Design of Finite Time Reduced Order H∞ Controller for Linear Discrete Time Systems
Abstract
1. Introduction
2. Preliminaries and Problem Definition
3. Main Results
3.1. FTB-H∞ Filter-Based Controller Synthesis
- The filter is unbiased: the error does not depend explicitly on and if ;
- The effect of disturbances on controlled output is minimized if ;
- The FTB-H∞ of the closed-loop system is guaranteed.
- If we choose the condition (41), the Equation (40) becomes:
- Now, either we use the condition (42) or the condition (43). Choosing the last condition, the Equation (40) becomes:
3.2. LMI Synthesis Conditions
4. Design Algorithm
- Set appropriate values for the parameters and α where .
- Solve the matrices (12) and (13), and deduce , , and .
- If these results are derived, then solve the matrices (60) and (61) for the given values of parameters and .
- Next, if the result is feasible, go then to Step 5; otherwise go back to Step 2.
- Finally, compute .
- Furthermore, the parameters and are computed using (34)–(39), (50)–(52), (53)–(55), (24), and (20).
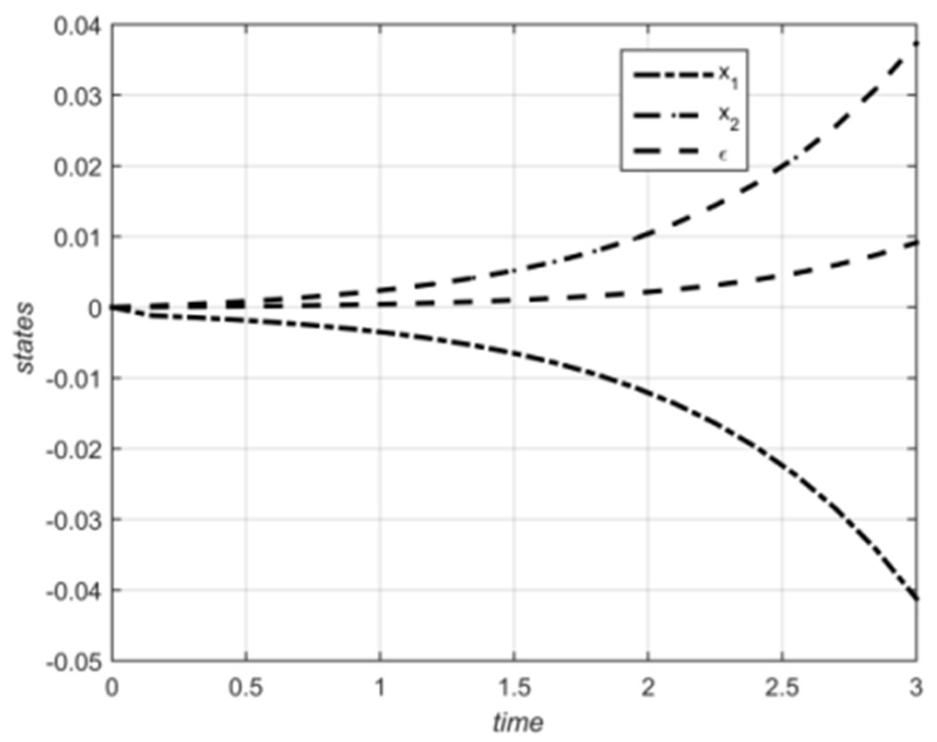
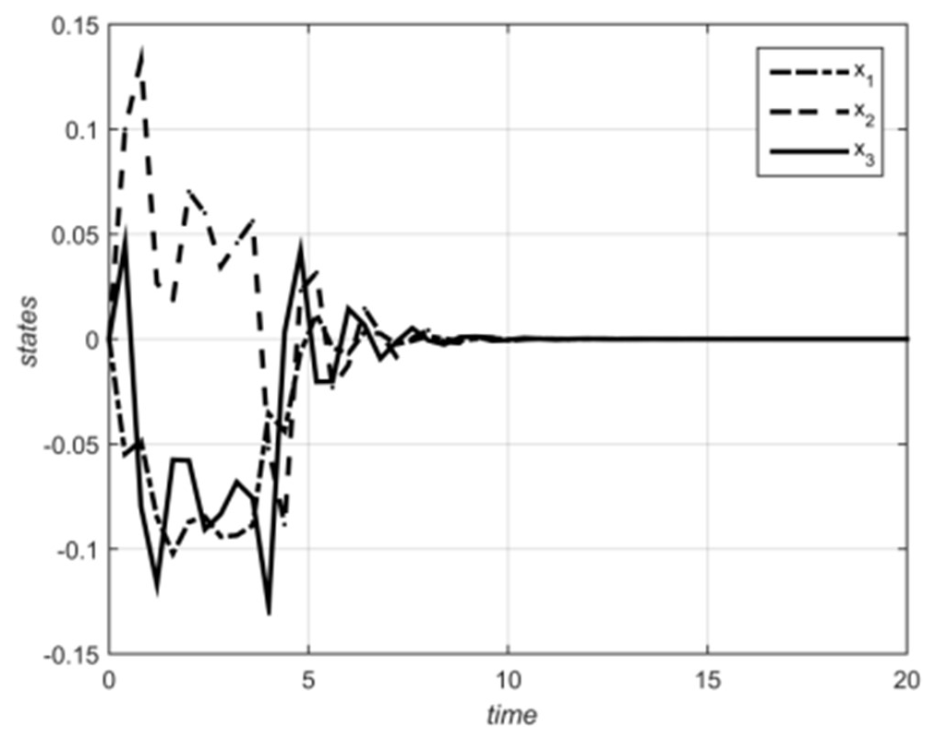
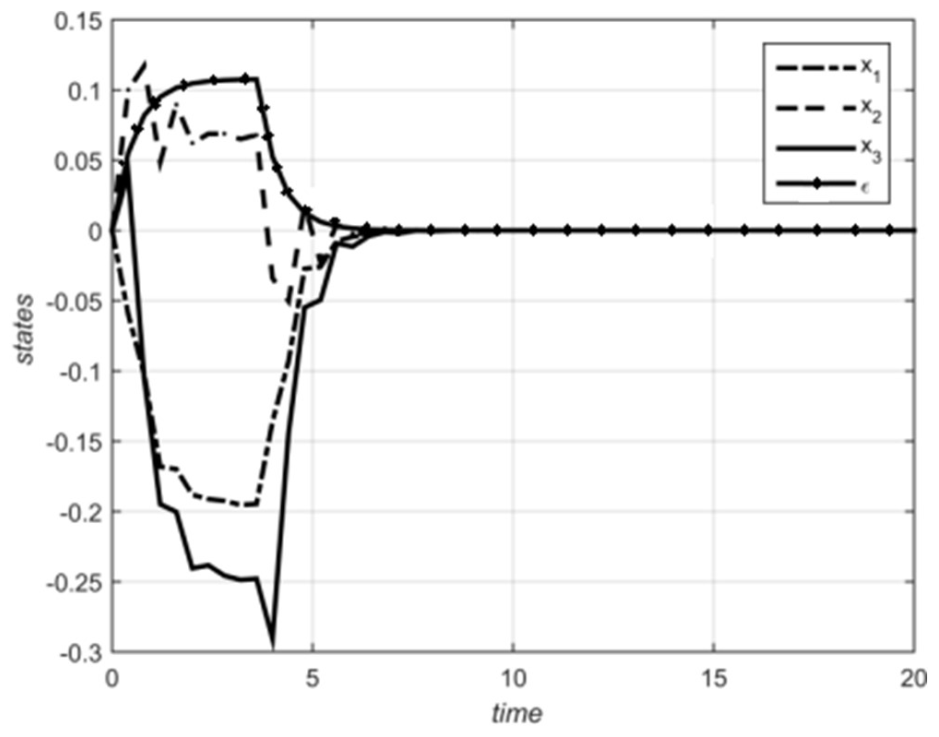
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baleanu, D.; Sajjadi, S.S.; Jajarmi, A.; Defterli, Ö. On a nonlinear dynamical system with both chaotic and nonchaotic behaviors: A new fractional analysis and control. Adv. Differ. Equ. 2021, 34, 1–17. [Google Scholar] [CrossRef]
- Baleanu, D.; Sajjadi, S.S.; Asad, J.H.; Jajarmi, A.; Estiri, E. Hyperchaotic behaviors, optimal control, and synchronization of a nonautonomous cardiac conduction system. Adv. Differ. Equ. 2021, 157, 1–24. [Google Scholar] [CrossRef]
- Baleanu, D.; Zibaei, S.; Namjoo, M.; Jajarmi, A. A nonstandard finite difference scheme for the modeling and nonidentical synchronization of a novel fractional chaotic system. Adv. Differ. Equ. 2021, 308, 1–19. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D.; Vahid, K.Z.; Mobayen, S. A general fractional formulation and tracking control for immunogenic tumor dynamics. Math. Methods Appl. Sci. 2022, 45, 667–680. [Google Scholar] [CrossRef]
- Jajarmi, A.; Pariz, N.; Effati, S.; Kamyad, A.V. Infinite horizon optimal control for nonlinear interconnected large-scale dynamical systems with an application to optimal attitude control. Asian J. Control 2012, 14, 1239–1250. [Google Scholar] [CrossRef]
- El Fezazi, N.; El Fakir, Y.; Bender, F.A.; Idrissi, S. AQM congestion controller for TCP/IP networks: Multiclass traffic. J. Control Autom. Electr. Syst. 2020, 31, 948–958. [Google Scholar] [CrossRef]
- El Fezazi, N.; Frih, A.; Lamrabet, O. New H∞ dynamic observer design for time-delay systems subject to disturbances. Int. J. Syst. Sci. 2020, 51, 2610–2624. [Google Scholar]
- El Fezazi, N.; Tissir, E.H.; El Haoussi, F.; Bender, F.A.; Husain, A.R. Controllersynthesisforsteer-by-wiresystemperformanceinvehicle. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 43, 813–825. [Google Scholar] [CrossRef]
- Lamrabet, O.; El Fezazi, N.; El Haoussi, F.; Tissir, E.H.; Alvarez, T. Congestion control in TCP/IP routers based on sampled-data systems theory. J. Control Autom. Electr. Syst. 2020, 31, 588–596. [Google Scholar] [CrossRef]
- Yi, X.; Guo, R.; Qi, Y. Stabilization of chaotic systems with both uncertainty and disturbance by the UDE-based control method. IEEE Access 2020, 8, 62471–62477. [Google Scholar] [CrossRef]
- Gao, N.; Darouach, M.; Alma, M. Dynamic observer design for a class of nonlinear systems. In Proceedings of the 3rd Advanced Information Technology, Electronic and Automation Control Conference, Chongqing, China, 12–14 October 2018; pp. 373–376. [Google Scholar]
- Xiong, X.; Pal, A.K.; Liu, Z.; Kamal, S.; Huang, R.; Lou, Y. Discrete-timeadaptivesuper-twistingobserverwithpredefinedarbitraryconvergencetime. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 2057–2061. [Google Scholar]
- Zang, J.; Chen, X.; Hao, F. Observer-based event-triggered bipartite consensus of linear multi-agent systems. Int. J. Control Autom. Syst. 2021, 19, 1291–1301. [Google Scholar] [CrossRef]
- Zare, K.; Shasadeghi, M.; Izadian, A.; Niknam, T.; Asemani, M.H. Switching TS fuzzy model-based dynamic sliding mode observer design for non-differentiable nonlinear systems. Eng. Appl. Artif. Intell. 2020, 96, 103990. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Luenberger, D. An introduction to observers. IEEE Trans. Autom. Control 1971, 16, 596–602. [Google Scholar] [CrossRef]
- Li, H.; Wu, C.; Yin, S.; Lam, H.K. Observer-based fuzzy control for nonlinear networked systems under unmeasurable premise variables. IEEE Trans. Fuzzy Syst. 2016, 24, 1233–1245. [Google Scholar] [CrossRef]
- Qiu, J.; Sun, K.; Wang, T.; Gao, H. Observer-based fuzzy adaptive event-triggered control for pure-feedback nonlinear systems with prescribed performance. IEEE Trans. Fuzzy Syst. 2019, 27, 2152–2162. [Google Scholar] [CrossRef]
- Venkatesh, M.; Patra, S.; Ray, G. Observer-based controller design for linear time-varying delay systems using a new Lyapunov-Krasovskii functional. Int. J. Autom. Control 2021, 15, 99–123. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Hao, F. Observer-based disturbance rejection for linear systems by aperiodical sampling control. IET Control Theory Appl. 2017, 11, 1561–1570. [Google Scholar] [CrossRef]
- Boutat-Baddas, L.; Osorio-Gordillo, G.L.; Darouach, M. H∞ dynamic observers for a class of nonlinear systems with unknown inputs. Int. J. Control 2021, 94, 558–569. [Google Scholar] [CrossRef]
- Gao, N.; Darouach, M.; Voos, H.; Alma, M. New unified H∞ dynamic observer design for linear systems with unknown inputs. Automatica 2016, 65, 43–52. [Google Scholar] [CrossRef]
- Wang, L.; Wang, H.; Liu, P.X.; Ling, S.; Liu, S. Fuzzy finite-time command filtering output feedback control of nonlinear systems. IEEE Trans. Fuzzy Syst. 2020, 30, 97–107. [Google Scholar] [CrossRef]
- Darouach, M.; Zasadzinski, M. Optimal unbiased reduced order filtering for discrete-time descriptor systems via LMI. Syst. Control Lett. 2009, 58, 436–444. [Google Scholar] [CrossRef][Green Version]
- Kim, K.S.; Rew, K.H. Reduced order disturbance observer for discrete-time linear systems. Automatica 2013, 49, 968–975. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Madhavan, K. Reduced order linear functional observers for large scale linear discrete-time control systems. In Proceedings of the 4th International Conference on Computing, Communications and Networking Technologies, Tiruchengode, India, 4–6 July 2013; pp. 1–7. [Google Scholar]
- Wang, Y.; Sun, M.; Wang, Z.; Liu, Z.; Chen, Z. A novel disturbance-observer based friction compensation scheme for ball and plate system. ISA Trans. 2014, 53, 671–678. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Q. Finite-time adaptive fuzzy command filtered control for nonlinear systems with indifferentiable non-affine functions. Nonlinear Dyn. 2020, 100, 493–507. [Google Scholar] [CrossRef]
- Fu, C.; Wang, Q.G.; Yu, J.; Lin, C. Neural network-based finite-time command filtering control for switched nonlinear systems with backlash-like hysteresis. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3268–3273. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, P.; Nguang, S.K. Observer-based finite-time H∞ control for discrete singular stochastic systems. Appl. Math. Lett. 2014, 38, 115–121. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, P.; Nguang, S.K.; Karimi, H.R. Observer-based finite-time control for discrete fuzzy jump nonlinear systems with time delays. In Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 6394–6399. [Google Scholar]
- Bhiri, B.; Delattre, C.; Zasadzinski, M.; Abderrahim, K. A descriptor system approach for finite-time control via dynamic output feedback of linear continuous systems. IFAC-Pap. 2017, 50, 15494–15499. [Google Scholar] [CrossRef]
- Bhiri, B.; Delattre, C.; Zasadzinski, M.; Abderrahim, K. Results on finite-time boundedness and finite-time control of non-linear quadratic systems subject to norm-bounded disturbances. IET Control Theory Appl. 2017, 11, 1648–1657. [Google Scholar] [CrossRef]
- Bhiri, B.; Delattre, C.; Zasadzinski, M.; Souley-Ali, H.; Zemouche, A.; Abderrahim, K. Finite time H∞ controller design based on finite time H∞ functional filter for linear continuous systems. In Proceedings of the 4th International Conference on Systems and Control, Sousse, Tunisia, 28–30 April 2015; pp. 460–465. [Google Scholar]
- Delattre, C.; Bhiri, B.; Zemouche, A.; Souley-Ali, H.; Zasadzinski, M.; Abderrahim, K. Finite-time H∞ functional filter design for a class of descriptor linear systems. In Proceedings of the 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; pp. 1572–1577. [Google Scholar]
- Amato, F.; Carbone, M.; Ariola, M.; Cosentino, C. Finite-time stability of discrete-time systems. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 2, pp. 1440–1444. [Google Scholar]
- Amato, F.; Ariola, M. Finite-time control of discrete-time linear systems. IEEE Trans. Autom. Control 2005, 50, 724–729. [Google Scholar] [CrossRef]
- Cheng, J.; Zhu, H.; Zhong, S.; Zhang, Y. Finite-time boundness of H∞ filtering for switching discrete-time systems. Int. J. Control. Autom. Syst. 2012, 10, 1129–1135. [Google Scholar] [CrossRef]
- Darouach, M. H∞ Unbiased Filtering for Linear Descriptor Systems via LMI. IEEE Trans. Autom. Control 2009, 54, 1966–1972. [Google Scholar] [CrossRef]
- Du, X.; Yang, G. Improved LMI conditions for H∞ output feedback stabilization of linear discrete-time systems. Int. J. Control Autom. Syst. 2010, 10, 163–168. [Google Scholar] [CrossRef]
- Lee, Y.S.; Han, S.H.; Kwon, W.H. H2/H∞FIR Filters for Discrete-time State Space Models. Int. J. Control Autom. Syst. 2006, 4, 645–652. [Google Scholar]
- O’Brien, R.T., Jr.; Kiriakidis, K. Reduced-order H∞ filtering for discrete-time, linear, time-varying systems. In Proceedings of the American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 4120–4125. [Google Scholar]
- Xu, D.; Wu, D.; Hu, A.; Wu, S. Robust Unbiased Filtering for System with Unknown System Noise Input. J. Comput. Inf. Syst. 2012, 8, 3867–3877. [Google Scholar]
- Zhang, J.; Shi, P.; Xia, Y.; Yang, H. Discrete-time sliding mode control with disturbance rejection. IEEE Trans. Ind. Electron. 2018, 66, 7967–7975. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taoussi, M.; El Akchioui, N.; Bardane, A.; El Fezazi, N.; Farkous, R.; Tissir, E.H.; Al-Arydah, M. Design of Finite Time Reduced Order H∞ Controller for Linear Discrete Time Systems. Mathematics 2023, 11, 31. https://doi.org/10.3390/math11010031
Taoussi M, El Akchioui N, Bardane A, El Fezazi N, Farkous R, Tissir EH, Al-Arydah M. Design of Finite Time Reduced Order H∞ Controller for Linear Discrete Time Systems. Mathematics. 2023; 11(1):31. https://doi.org/10.3390/math11010031
Chicago/Turabian StyleTaoussi, Mohammed, Nabil El Akchioui, Adil Bardane, Nabil El Fezazi, Rashid Farkous, El Houssaine Tissir, and Mo’tassem Al-Arydah. 2023. "Design of Finite Time Reduced Order H∞ Controller for Linear Discrete Time Systems" Mathematics 11, no. 1: 31. https://doi.org/10.3390/math11010031
APA StyleTaoussi, M., El Akchioui, N., Bardane, A., El Fezazi, N., Farkous, R., Tissir, E. H., & Al-Arydah, M. (2023). Design of Finite Time Reduced Order H∞ Controller for Linear Discrete Time Systems. Mathematics, 11(1), 31. https://doi.org/10.3390/math11010031





