Parameter Identification for Lithium-Ion Battery Based on Hybrid Genetic–Fractional Beetle Swarm Optimization Method
Abstract
:1. Introduction
2. Preliminaries
2.1. Fractional-Order Calculus
2.2. Fractional-Order Capacitor
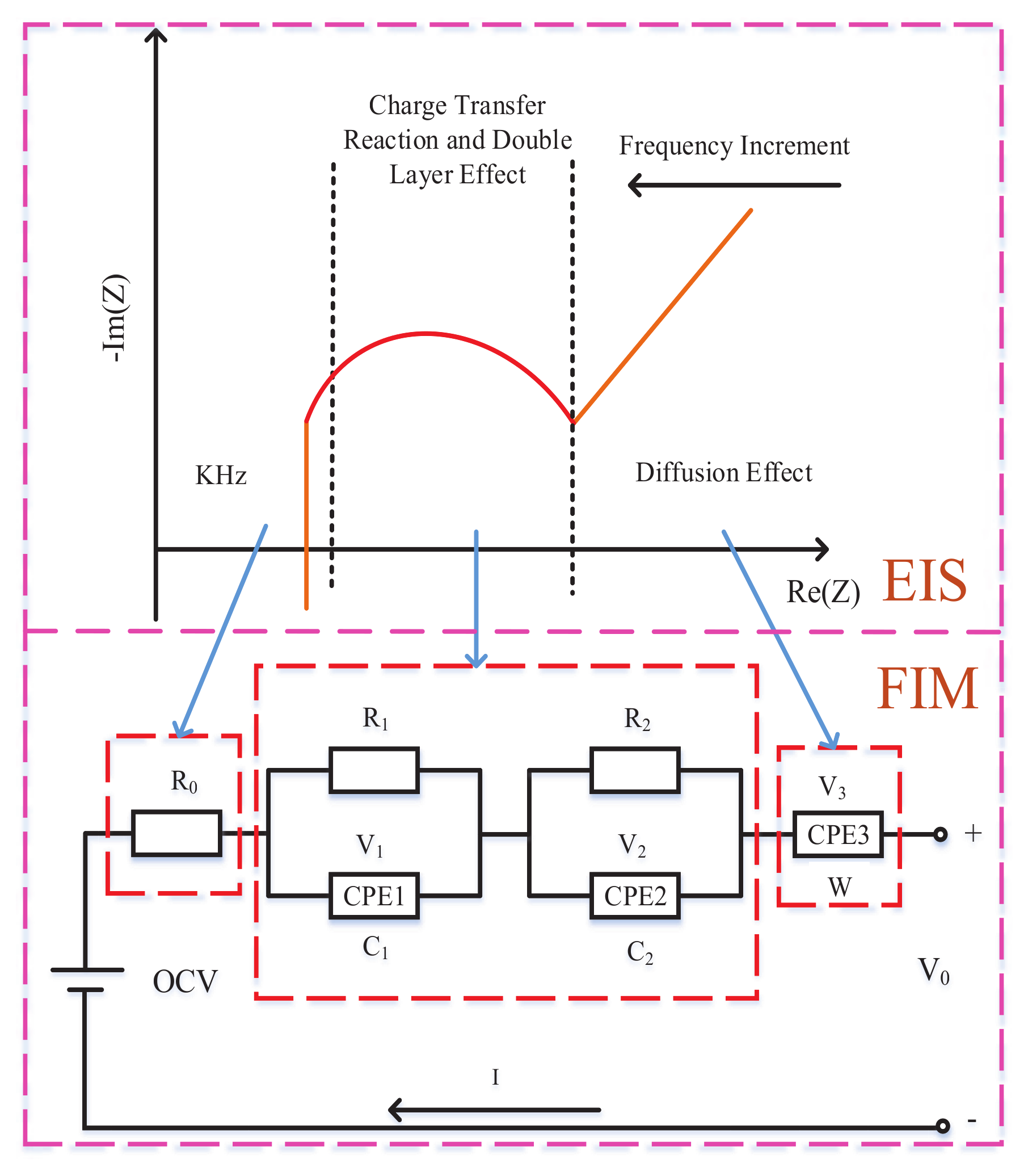
3. Fractional-Order Modeling of Libs
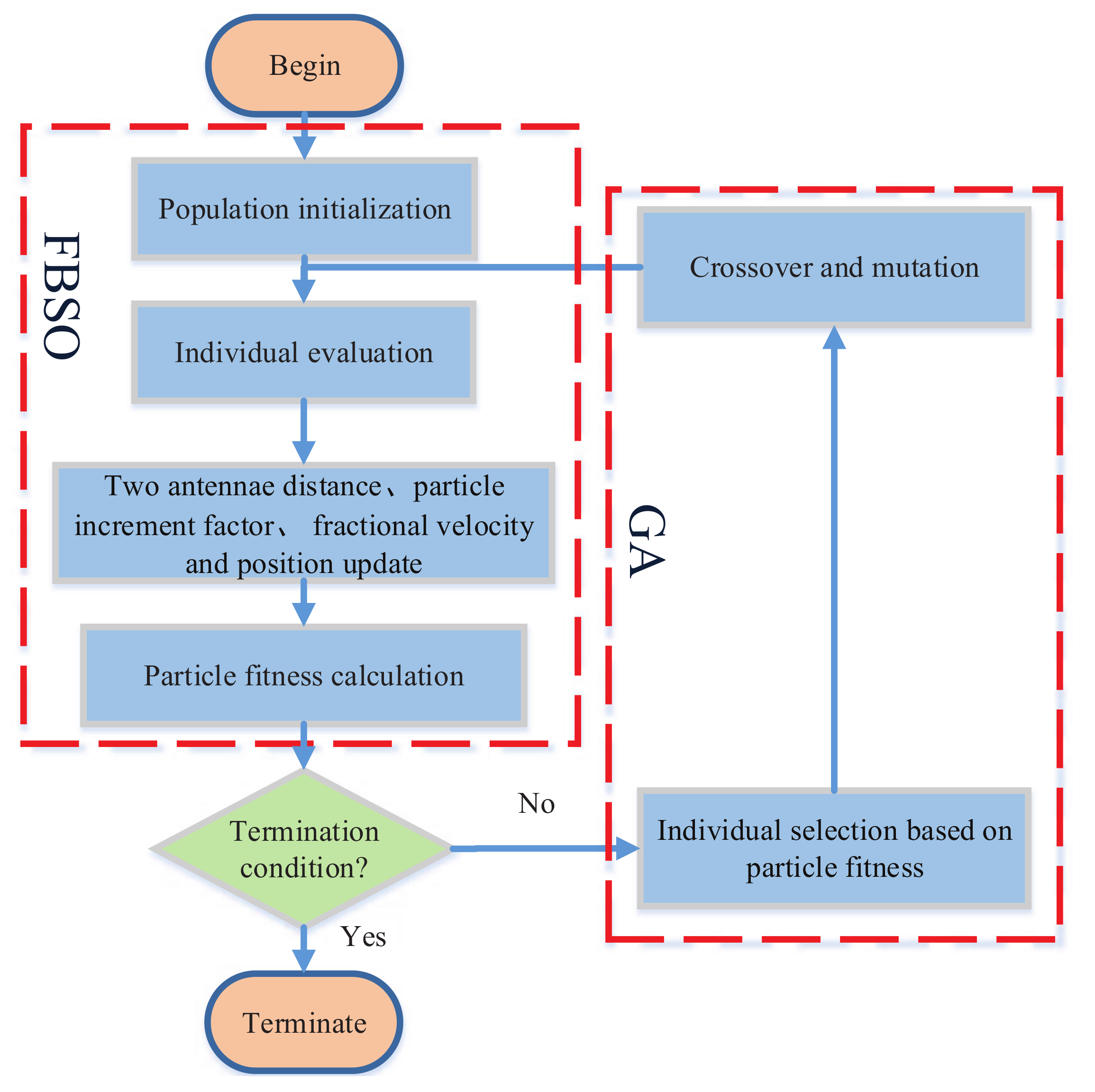
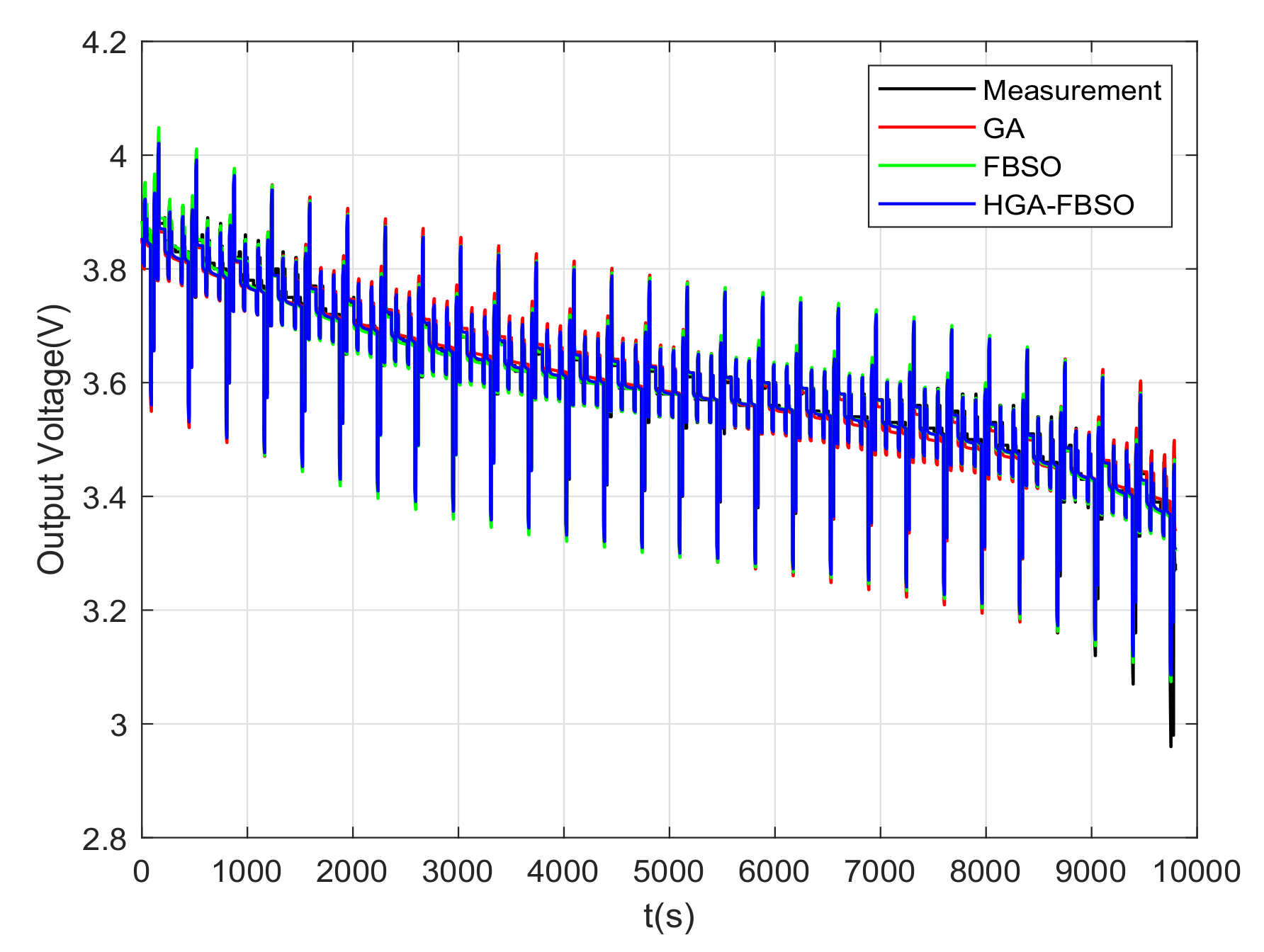
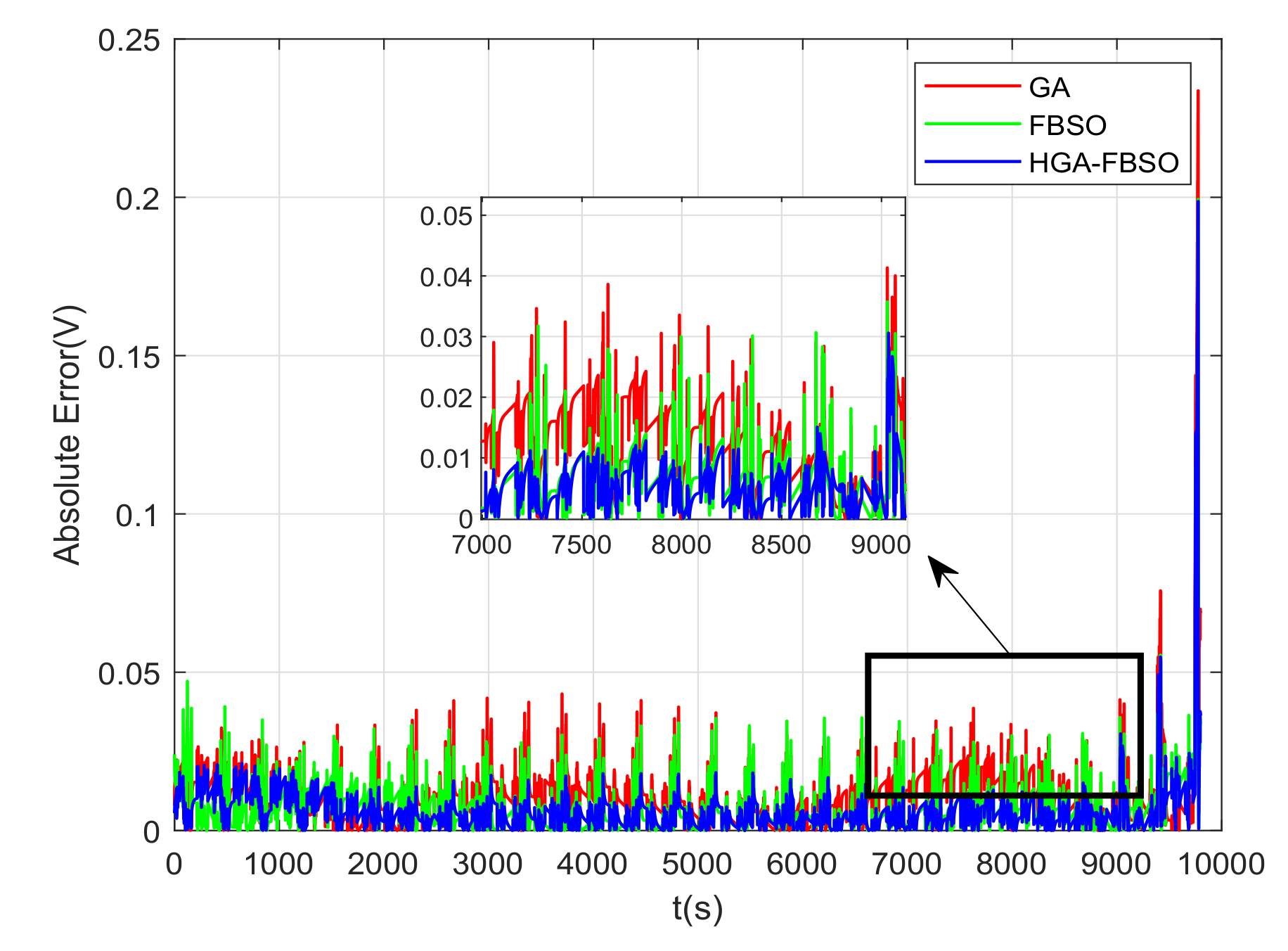
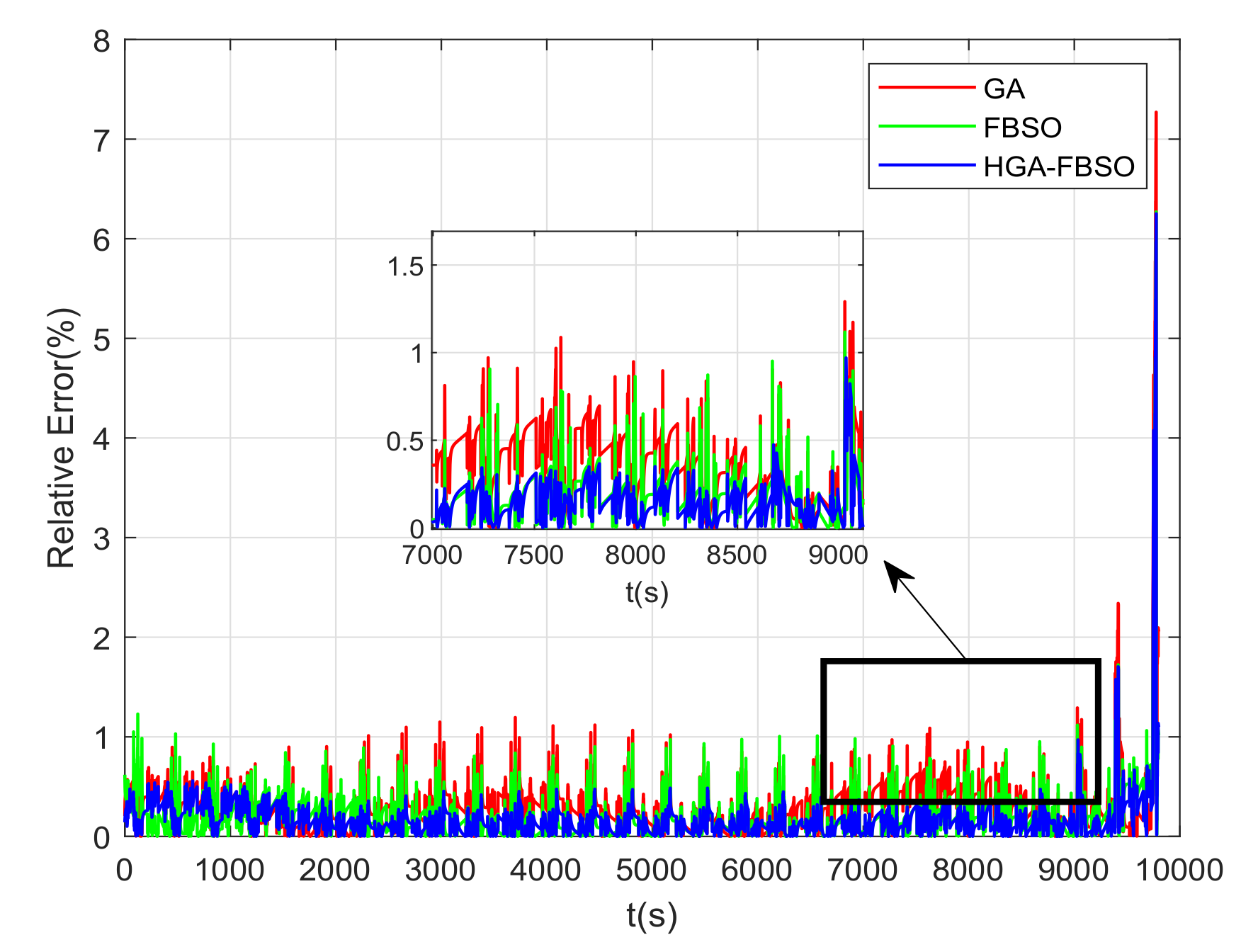
4. Model Parameter Identification and Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Comello, S.; Glenk, G.; Reichelstein, S. Transitioning to clean energy transportation services: Life-cycle cost analysis for vehicle fleets. Appl. Energy 2021, 285, 116408. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, G.; Zhen, D.; Gu, F.; Ball, A. A review on online state of charge and state of health estimation for lithium-ion batteries in electric vehicles. Energy Rep. 2021, 7, 5141–5161. [Google Scholar] [CrossRef]
- Chen, T.; Cai, L.; Wen, X.; Zhang, X. Experimental research and energy consumption analysis on the economic performance of a hybrid-power gas engine heat pump with LiFePO4 battery. Energy 2021, 214, 118913. [Google Scholar] [CrossRef]
- Shahjalal, M.; Roy, P.K.; Shams, T.; Fly, A.; Chowdhury, J.I.; Ahmed, M.R.; Liu, K. A review on second-life of Li-ion batteries: Prospects, challenges, and issues. Energy 2022, 241, 122881. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Yu, Q.; Jin, Q.; Yang, R. A set membership theory based parameter and state of charge co-estimation method for all-climate batteries. J. Clean. Prod. 2020, 249, 119380. [Google Scholar] [CrossRef]
- Seo, M.; Song, Y.; Kim, J.; Paek, S.W.; Kim, G.H.; Kim, S.W. Innovative lumped-battery model for state of charge estimation of lithium-ion batteries under various ambient temperatures. Energy 2021, 226, 120301. [Google Scholar] [CrossRef]
- Hua, X.; Zhang, C.; Offer, G. Finding a better fit for lithium ion batteries: A simple, novel, load dependent, modified equivalent circuit model and parameterization method. J. Power Sources 2021, 484, 229117. [Google Scholar] [CrossRef]
- Song, Z.; Hofmann, H.; Lin, X.; Han, X.; Hou, J. Parameter identification of lithium-ion battery pack for different applications based on Cramer-Rao bound analysis and experimental study. Appl. Energy 2018, 231, 1307–1318. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Chen, Z. Experimental study of fractional-order models for lithium-ion battery and ultra-capacitor: Modeling, system identification, and validation. Appl. Energy 2020, 278, 115736. [Google Scholar] [CrossRef]
- Lai, X.; He, L.; Wang, S.; Zhou, L.; Zhang, Y.; Sun, T.; Zheng, Y. Co-estimation of state of charge and state of power for lithium-ion batteries based on fractional variable-order model. J. Clean. Prod. 2020, 255, 120203. [Google Scholar] [CrossRef]
- Yu, M.; Li, Y.; Podlubny, I.; Gong, F.; Sun, Y.; Zhang, Q.; Shang, Y.; Duan, B.; Zhang, C. Fractional-order modeling of lithium-ion batteries using additive noise assisted modeling and correlative information criterion. J. Adv. Res. 2020, 25, 49–56. [Google Scholar] [CrossRef]
- He, L.; Wang, Y.; Wei, Y.; Wang, M.; Hu, X.; Shi, Q. An adaptive central difference Kalman filter approach for state of charge estimation by fractional order model of lithium-ion battery. Energy 2022, 244, 122627. [Google Scholar] [CrossRef]
- Chen, L.; Wu, X.; Tenreiro Machado, J.A.; Lopes, A.M.; Li, P.; Dong, X. State-of-Charge Estimation of Lithium-Ion Batteries Based on Fractional-Order Square-Root Unscented Kalman Filter. Fractal Fract. 2022, 6, 52. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Y.; Lopes, A.M.; Kong, H.; Wu, R. State of charge estimation of lithium-ion batteries based on fuzzy fractional-order unscented kalman filter. Fractal Fract. 2021, 5, 91. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, G.; Li, X.; Chen, Z. A fractional-order model-based state estimation approach for lithium-ion battery and ultra-capacitor hybrid power source system considering load trajectory. J. Power Sources 2020, 449, 227543. [Google Scholar] [CrossRef]
- Pang, H.; Mou, L.; Guo, L.; Zhang, F. Parameter identification and systematic validation of an enhanced single-particle model with aging degradation physics for Li-ion batteries. Electrochim. Acta 2019, 307, 474–487. [Google Scholar] [CrossRef]
- Tian, N.; Wang, Y.; Chen, J.; Fang, H. One-shot parameter identification of the Thevenin’s model for batteries: Methods and validation. J. Energy Storage 2020, 29, 101282. [Google Scholar] [CrossRef]
- Sun, C.; Lin, H.; Cai, H.; Gao, M.; Zhu, C.; He, Z. Improved parameter identification and state-of-charge estimation for lithium-ion battery with fixed memory recursive least squares and sigma-point Kalman filter. Electrochim. Acta 2021, 387, 138501. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, J.; Li, L.; Gu, J. Fractional modeling and parameter identification of lithium-ion battery. Ionics 2022, 28, 4135–4148. [Google Scholar] [CrossRef]
- Stark, O.; Pfeifer, M.; Hohmann, S. Parameter and order identification of fractional systems with application to a Lithium-Ion battery. Mathematics 2021, 9, 1607. [Google Scholar] [CrossRef]
- Kim, M.; Chun, H.; Kim, J.; Kim, K.; Yu, J.; Kim, T.; Han, S. Data-efficient parameter identification of electrochemical lithium-ion battery model using deep Bayesian harmony search. Appl. Energy 2019, 254, 113644. [Google Scholar] [CrossRef]
- Lai, X.; Wang, S.; Ma, S.; Xie, J.; Zheng, Y. Parameter sensitivity analysis and simplification of equivalent circuit model for the state of charge of lithium-ion batteries. Electrochim. Acta 2020, 330, 135239. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, G.; Liu, X.; Gu, F.; Ball, A. A novel method of parameter identification and state of charge estimation for lithium-ion battery energy storage system. J. Energy Storage 2022, 49, 104124. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, M.; Zhou, A.; Li, Y.; Li, S.; Fu, C.; Gong, C. State of charge estimation for lithium-ion batteries based on adaptive dual Kalman filter. Appl. Math. Model. 2020, 77, 1255–1272. [Google Scholar] [CrossRef]
- Yu, Z.; Huai, R.; Li, H. CPSO-Based Parameter-Identification Method for the Fractional-Order Modeling of Lithium-Ion Batteries. IEEE Trans. Power Electron. 2021, 36, 11109–11123. [Google Scholar] [CrossRef]
- Chen, L.; Wu, X.; Lopes, A.M.; Yin, L.; Li, P. Adaptive state-of-charge estimation of lithium-ion batteries based on square-root unscented Kalman filter. Energy 2022, 252, 123972. [Google Scholar] [CrossRef]
- Kwak, M.; Lkhagvasuren, B.; Park, J.; You, J.H. Parameter identification and SOC estimation of a battery under the hysteresis effect. IEEE Trans. Ind. Electron. 2019, 67, 9758–9767. [Google Scholar] [CrossRef]
- Li, L.; Wang, C.; Yan, S.; Zhao, W. A combination state of charge estimation method for ternary polymer lithium battery considering temperature influence. J. Power Sources 2021, 484, 229204. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, S.; Wu, B.; Fernandez, C.; Xiong, X.; Coffie-Ken, J. A state-of-charge estimation method of the power lithium-ion battery in complex conditions based on adaptive square root extended Kalman filter. Energy 2021, 219, 119603. [Google Scholar] [CrossRef]
- Moghaddasi, S.S.; Faraji, N. A hybrid algorithm based on particle filter and genetic algorithm for target tracking. Expert Syst. Appl. 2020, 147, 113188. [Google Scholar] [CrossRef]
- Peng, S.; Zhang, Z.; Liu, E.; Liu, W.; Qiao, W. A new hybrid algorithm model for prediction of internal corrosion rate of multiphase pipeline. J. Nat. Gas Sci. Eng. 2021, 85, 103716. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, X.; Hua, Y.; Zhou, X.; Yang, S. Adaptive model parameter identification for lithium-ion batteries based on improved coupling hybrid adaptive particle swarm optimization-simulated annealing method. J. Power Sources 2021, 482, 228951. [Google Scholar] [CrossRef]
- Ouyang, T.; Xu, P.; Chen, J.; Lu, J.; Chen, N. Improved parameters identification and state of charge estimation for lithium-ion battery with real-time optimal forgetting factor. Electrochim. Acta 2020, 353, 136576. [Google Scholar] [CrossRef]
- Guariglia, E.; Silvestrov, S. Fractional-wavelet analysis of positive definite distributions and wavelets on 𝔻′(ℂ). In Engineering Mathematics II; Springer: Berlin, Germany, 2016; pp. 337–353. [Google Scholar]
- Guariglia, E. Riemann zeta fractional derivative—Functional equation and link with primes. Adv. Differ. Equ. 2019, 2019, 261. [Google Scholar] [CrossRef]
- Zhang, Q.; Shang, Y.; Li, Y.; Cui, N.; Duan, B.; Zhang, C. A novel fractional variable-order equivalent circuit model and parameter identification of electric vehicle Li-ion batteries. ISA Trans. 2020, 97, 448–457. [Google Scholar] [CrossRef]
- Xiong, R.; Tian, J.; Shen, W.; Sun, F. A novel fractional order model for state of charge estimation in lithium ion batteries. IEEE Trans. Veh. Technol. 2018, 68, 4130–4139. [Google Scholar] [CrossRef]
- Hu, X.; Yuan, H.; Zou, C.; Li, Z.; Zhang, L. Co-estimation of state of charge and state of health for lithium-ion batteries based on fractional-order calculus. IEEE Trans. Veh. Technol. 2018, 67, 10319–10329. [Google Scholar] [CrossRef]
- Wang, T.; Yang, L. Beetle swarm optimization algorithm: Theory and application. arXiv 2018, arXiv:1808.00206. [Google Scholar] [CrossRef]
- Zheng, Y.; Huang, Z.; Tao, J.; Sun, H.; Sun, Q.; Sun, M.; Dehmer, M.; Chen, Z. A novel chaotic fractional-order beetle swarm optimization algorithm and its application for load-frequency active disturbance rejection control. IEEE Trans. Circ. Syst. II Express Briefs 2021, 69, 1267–1271. [Google Scholar] [CrossRef]
| 1.3006 | ||||||
| 1361.59 | 0.8616 | 965.09 | 185.86 | 0.3180 | 0.8951 | 0.5305 |
| 1.0946 | ||||||
| 636.01 | 0.8419 | 778.31 | 548.29 | 0.4033 | 0.6411 | 0.5563 |
| 0.9891 | ||||||
| 1101.56 | 0.4167 | 1892.57 | 1741.97 | 0.9477 | 0.4748 | 0.2180 |
| GA | FBSO | HGA-FBSO | |
|---|---|---|---|
| RMSE (mV) | 15.5 | 11.4 | 10.5 |
| MAE (%) | 1.0786 | 0.7017 | 0.6058 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, P.; Wu, X.; Lopes, A.M.; Cheng, A.; Xu, Y.; Chen, L. Parameter Identification for Lithium-Ion Battery Based on Hybrid Genetic–Fractional Beetle Swarm Optimization Method. Mathematics 2022, 10, 3056. https://doi.org/10.3390/math10173056
Guo P, Wu X, Lopes AM, Cheng A, Xu Y, Chen L. Parameter Identification for Lithium-Ion Battery Based on Hybrid Genetic–Fractional Beetle Swarm Optimization Method. Mathematics. 2022; 10(17):3056. https://doi.org/10.3390/math10173056
Chicago/Turabian StyleGuo, Peng, Xiaobo Wu, António M. Lopes, Anyu Cheng, Yang Xu, and Liping Chen. 2022. "Parameter Identification for Lithium-Ion Battery Based on Hybrid Genetic–Fractional Beetle Swarm Optimization Method" Mathematics 10, no. 17: 3056. https://doi.org/10.3390/math10173056
APA StyleGuo, P., Wu, X., Lopes, A. M., Cheng, A., Xu, Y., & Chen, L. (2022). Parameter Identification for Lithium-Ion Battery Based on Hybrid Genetic–Fractional Beetle Swarm Optimization Method. Mathematics, 10(17), 3056. https://doi.org/10.3390/math10173056








