Estimation of Coefficient of Variation Using Calibrated Estimators in Double Stratified Random Sampling
Abstract
1. Introduction
2. Linear Moments and Proposed Families of CV Estimators
2.1. Linear Moments
2.2. First Proposed Family of CV Estimators
2.3. Second Proposed Family of CV Estimators
3. Numerical Illustrations
- Step 1: Using from stratum , select a random sample with size .
- Step 2: Using a random sample in step 1, calculate the mean square errors (MSEs).
- Step 3: Replicate Step 1 and Step 2, times, and then
- Step 4: Calculate the percentage relative efficiency (PRE) as
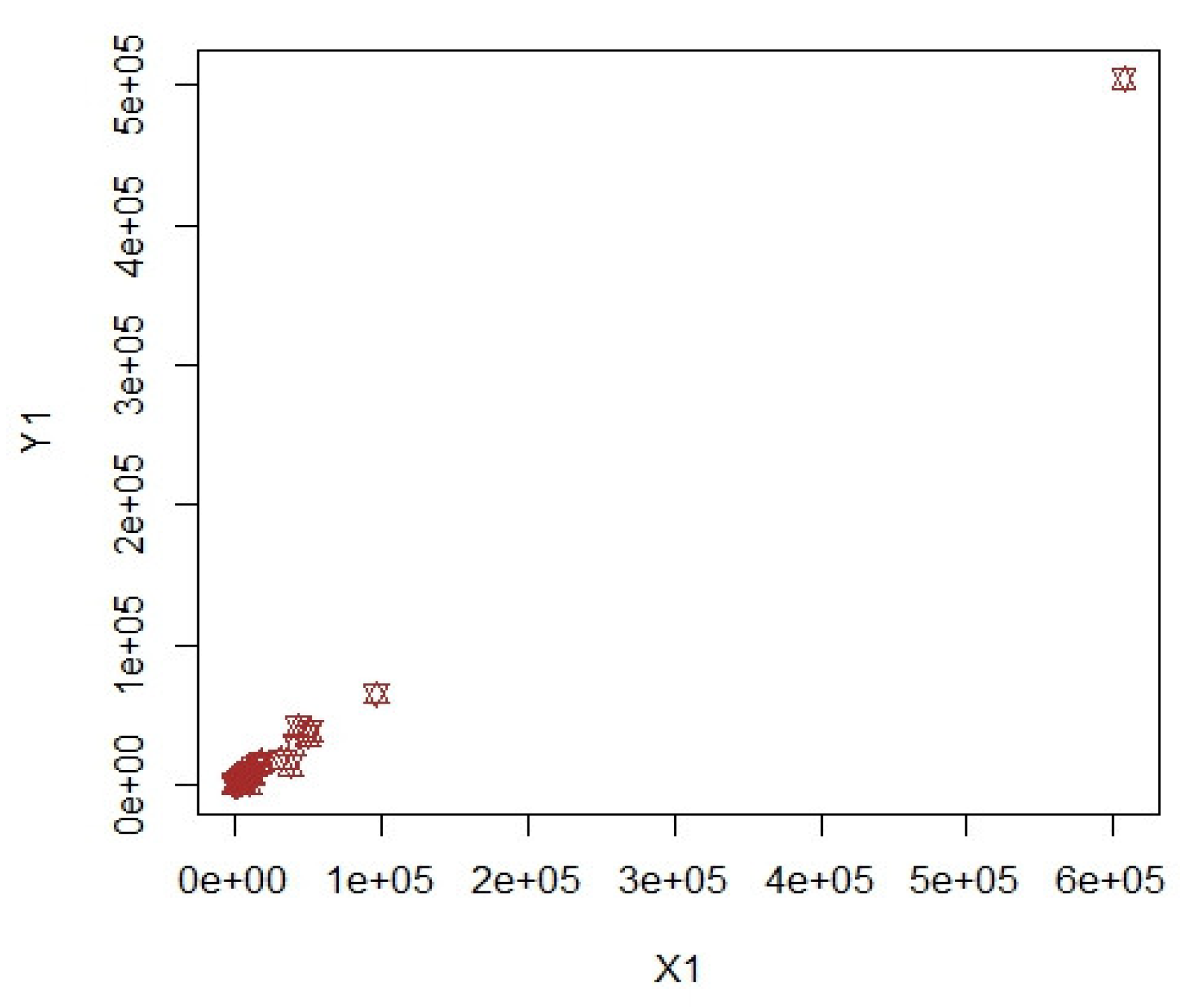
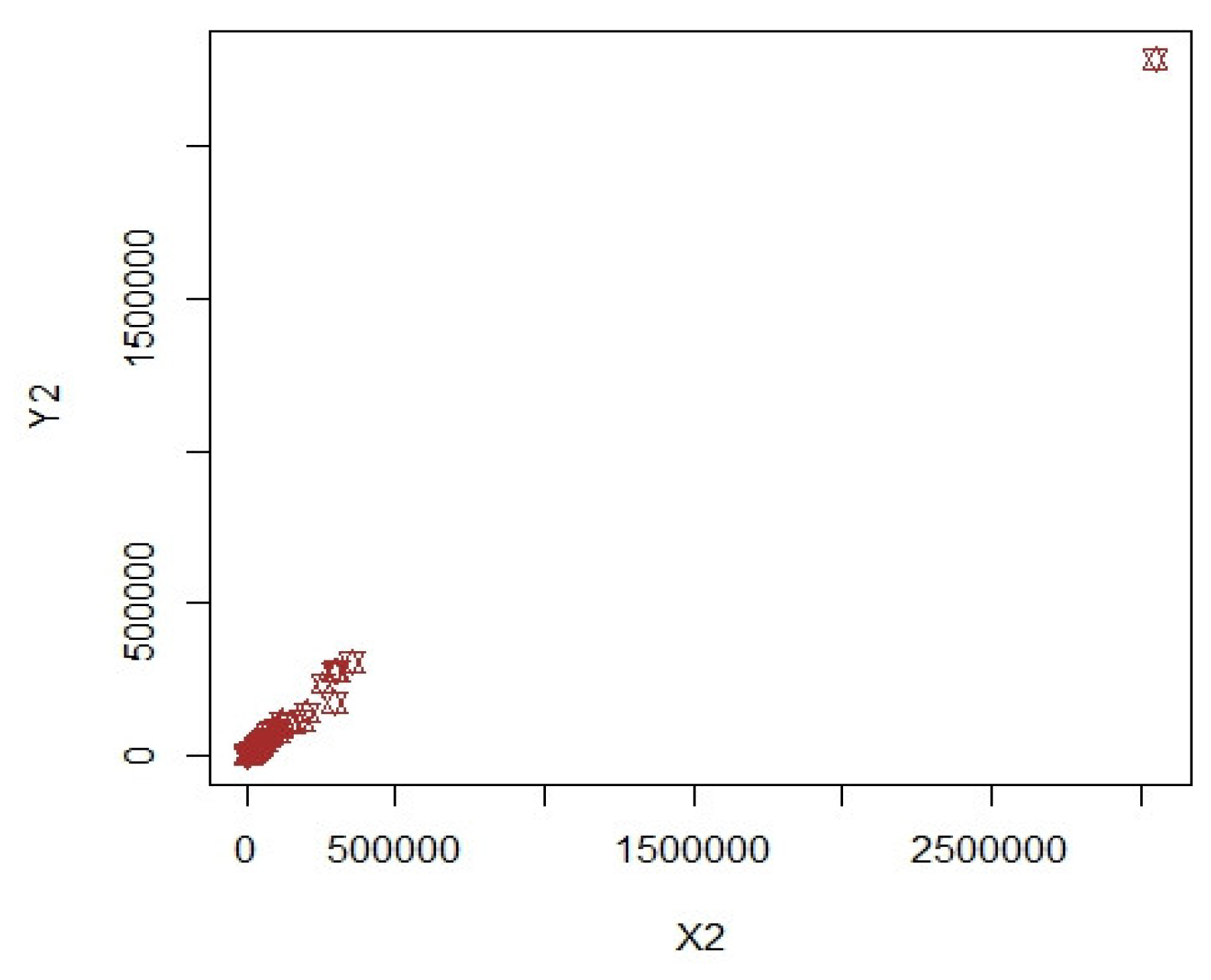
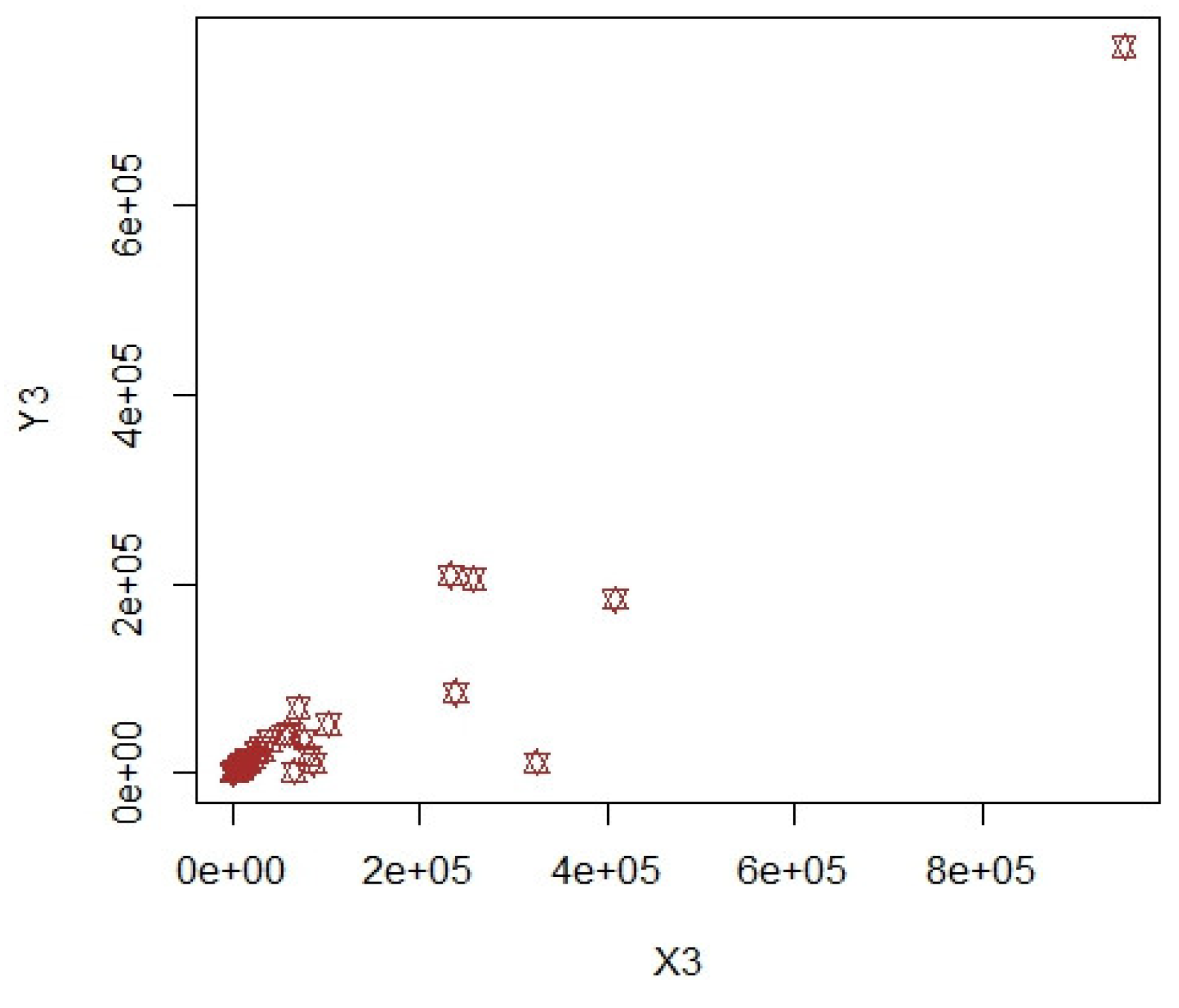
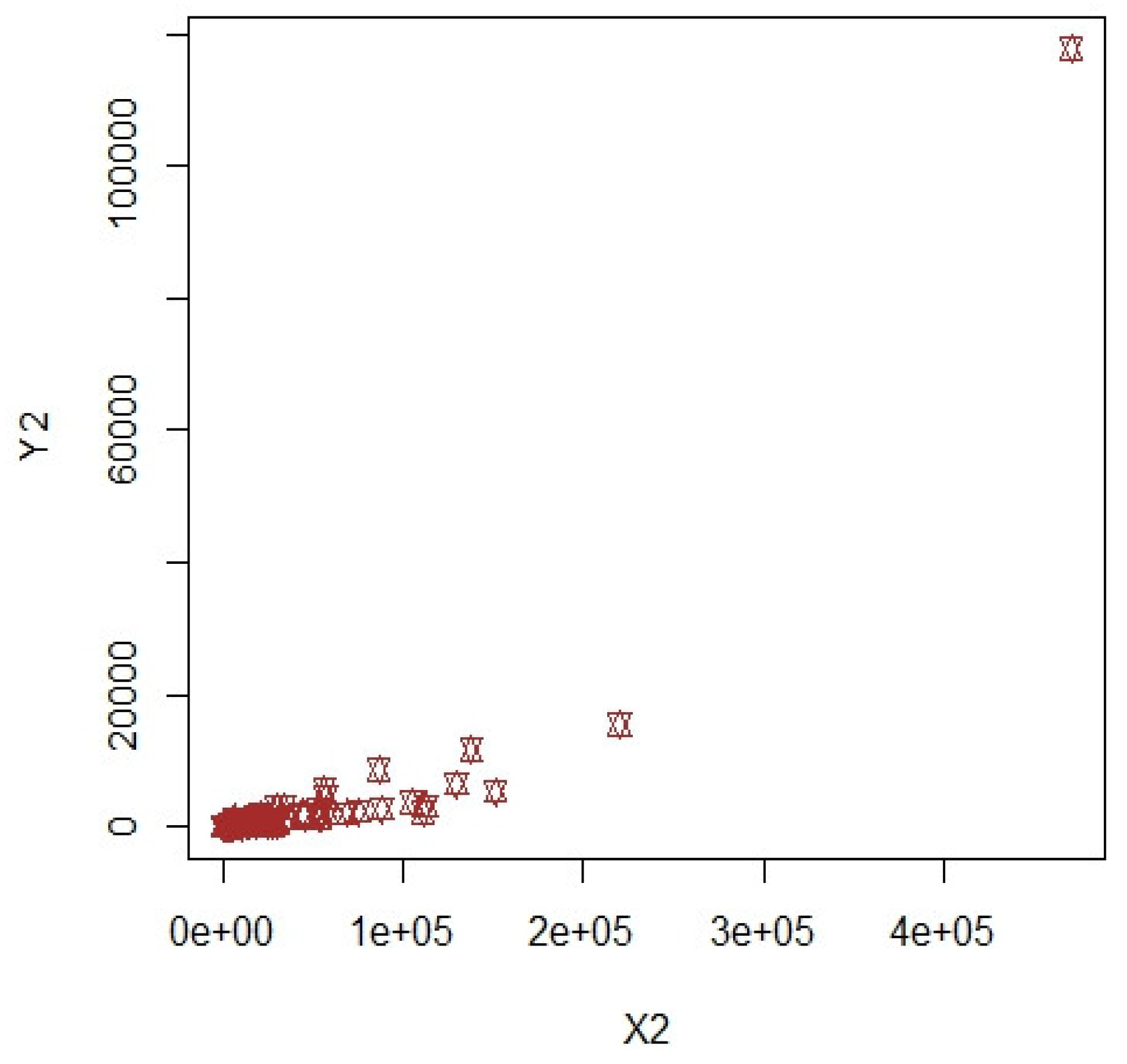
3.1. COVID-19 Data (Population-1)
3.2. Apple Data: Population-2 and Population-3
3.3. Discussion of Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Watson, D.J. The estimation of leaf area in field crops. J. Agric. Sci. 1937, 27, 474–483. [Google Scholar] [CrossRef]
- Cochran, W.G. The estimation of the yields of cereal experiments by sampling for the ratio of grain to total produce. J. Agric. Sci. 1940, 30, 262–275. [Google Scholar] [CrossRef]
- Zaman, T.; Bulut, H. Modified ratio estimators using robust regression methods. Commun. Stat. Theory Methods 2019, 48, 2039–2048. [Google Scholar] [CrossRef]
- Shahzad, U.; Al-Noor, N.H.; Hanif, M.; Sajjad, I. An exponential family of median based estimators for mean estimation with simple random sampling scheme. Commun. Stat. Theory Methods 2021, 50, 4890–4899. [Google Scholar] [CrossRef]
- Gagnon, F.; Lee, H.; Rancourt, E.; Särndal, C.E. Estimating the variance of the generalized regression estimator in the presence of imputation for the generalized estimation system. In Proceedings of the Survey Methods Section; Statistical Society of Canada: Ottawa, ON, Canada, 1997; pp. 151–156. [Google Scholar]
- Sorensen, J.B. The use and misuse of the coefficient of variation in organizational demography research. Sociol. Methods Res. 2002, 30, 475–491. [Google Scholar] [CrossRef]
- Wilson, C.A.; Payton, M.E. Modelling the coefficient of variation in factorial experiments. Commun. Stat. Theory Methods 2002, 31, 436–476. [Google Scholar] [CrossRef]
- Faber, D.S.; Korn, H. Applicability of the coefficient of variation method for analyzing synaptic plasticity. Biophys. J. 1991, 60, 1288–1294. [Google Scholar] [CrossRef] [PubMed]
- Banik, S.; Kibria, B.G. Estimating the population coefficient of variation by confidence intervals. Commun. Stat. Simul. Comput. 2011, 40, 1236–1261. [Google Scholar] [CrossRef]
- Yosboonruang, N.; Niwitpong, S.-A.; Niwitpong, S. Measuring the dispersion of rain-fall using Bayesian confidence intervals for coefficient of variation of delta-lognormal distribution: A study from Thailand. PeerJ 2019, 7, e7344. [Google Scholar] [CrossRef]
- Tian, L. Inferences on the common coefficient of variation. Stat. Med. 2005, 24, 2213–2220. [Google Scholar] [CrossRef]
- Mahmoudvand, R.; Hassani, H.; Wilson, R. Is the sample coefficient of variation a good estimator for the population coefficient of variation? World Appl. Sci. J. 2007, 2, 519–522. [Google Scholar]
- La-Ongkaew, M.; Niwitpong, S.-A.; Niwitpong, S. Confidence intervals for the difference between the coefficients of variation of Weibull distributions for analyzing wind speed dispersion. PeerJ 2021, 9, e11676. [Google Scholar] [CrossRef] [PubMed]
- Särndal, C.E.; Swensson, B.; Wretman, J. Model Assisted Survey Sampling; Springer: New York, NY, USA, 1992. [Google Scholar]
- Hosking, J.R. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. B Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Deville, J.C.; Särndal, C.E. Calibration estimators in survey sampling. J. Am. Stat. Assoc. 1992, 87, 376–382. [Google Scholar] [CrossRef]
- Koyuncu, N. Calibration estimator of population mean under stratified ranked set sampling design. Commun. Stat. Theory Methods 2018, 47, 5845–5853. [Google Scholar] [CrossRef]
- Shahzad, U.; Ahmad, I.; Almanjahie, I.; Al-Noor, N.H.; Hanif, M. A new class of L-moments based calibration variance Estimators. Comput. Mater. Contin. 2021, 66, 3013–3028. [Google Scholar] [CrossRef]
- Shahzad, U.; Ahmad, I.; Almanjahie, I.; Hanif, M.; Al-Noor, N.H. L-moments and calibration based variance estimators under double stratified random sampling scheme: An application of COVID-19 pandemic. Sci. Iran. 2021; in press. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Landweher, J.M.; Matales, N.C.; Wallis, J.R. Probability weighted moments: Definition and relation to parameters of several distributions expressible in inverse form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J. A comparison of unbiased and plotting-position estimators of L-moments. Water Resour. Res. 1995, 31, 2019–2025. [Google Scholar] [CrossRef]
- Elamir, E.A.H.; Seheult, A.H. Trimmed L-moments. Comput. Stat. Data Anal. 2003, 43, 299–314. [Google Scholar] [CrossRef]
- Bhushan, S.; Kumar, A.; Akhtar, M.T.; Lone, S.A. Logarithmic type predictive estimators under simple random sampling. AIMS Math. 2022, 7, 11992–12010. [Google Scholar] [CrossRef]
- Bhushan, S.; Kumar, A. Predictive estimation approach using difference and ratio type estimators in ranked set sampling. J. Comput. Appl. Math. 2022, 410, 114214. [Google Scholar] [CrossRef]








| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| 1 | |||
| L-Moments | ||||
| TL-Moments | ||||
| L-Moments | ||||
| TL-Moments | ||||
| L-Moments | ||||
| TL-Moments | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahzad, U.; Ahmad, I.; García-Luengo, A.V.; Zaman, T.; Al-Noor, N.H.; Kumar, A. Estimation of Coefficient of Variation Using Calibrated Estimators in Double Stratified Random Sampling. Mathematics 2023, 11, 252. https://doi.org/10.3390/math11010252
Shahzad U, Ahmad I, García-Luengo AV, Zaman T, Al-Noor NH, Kumar A. Estimation of Coefficient of Variation Using Calibrated Estimators in Double Stratified Random Sampling. Mathematics. 2023; 11(1):252. https://doi.org/10.3390/math11010252
Chicago/Turabian StyleShahzad, Usman, Ishfaq Ahmad, Amelia V. García-Luengo, Tolga Zaman, Nadia H. Al-Noor, and Anoop Kumar. 2023. "Estimation of Coefficient of Variation Using Calibrated Estimators in Double Stratified Random Sampling" Mathematics 11, no. 1: 252. https://doi.org/10.3390/math11010252
APA StyleShahzad, U., Ahmad, I., García-Luengo, A. V., Zaman, T., Al-Noor, N. H., & Kumar, A. (2023). Estimation of Coefficient of Variation Using Calibrated Estimators in Double Stratified Random Sampling. Mathematics, 11(1), 252. https://doi.org/10.3390/math11010252






