Combination of Functional and Disturbance Observer for Positive Systems with Disturbances
Abstract
1. Introduction
2. Preliminaries
- (i)
- The system is stable.
- (ii)
- The system matrix A is Hurwitz.
- (iii)
- There exists a vector such that .
3. Main Results
3.1. Structural Disturbance
3.2. Non-Structural Disturbance
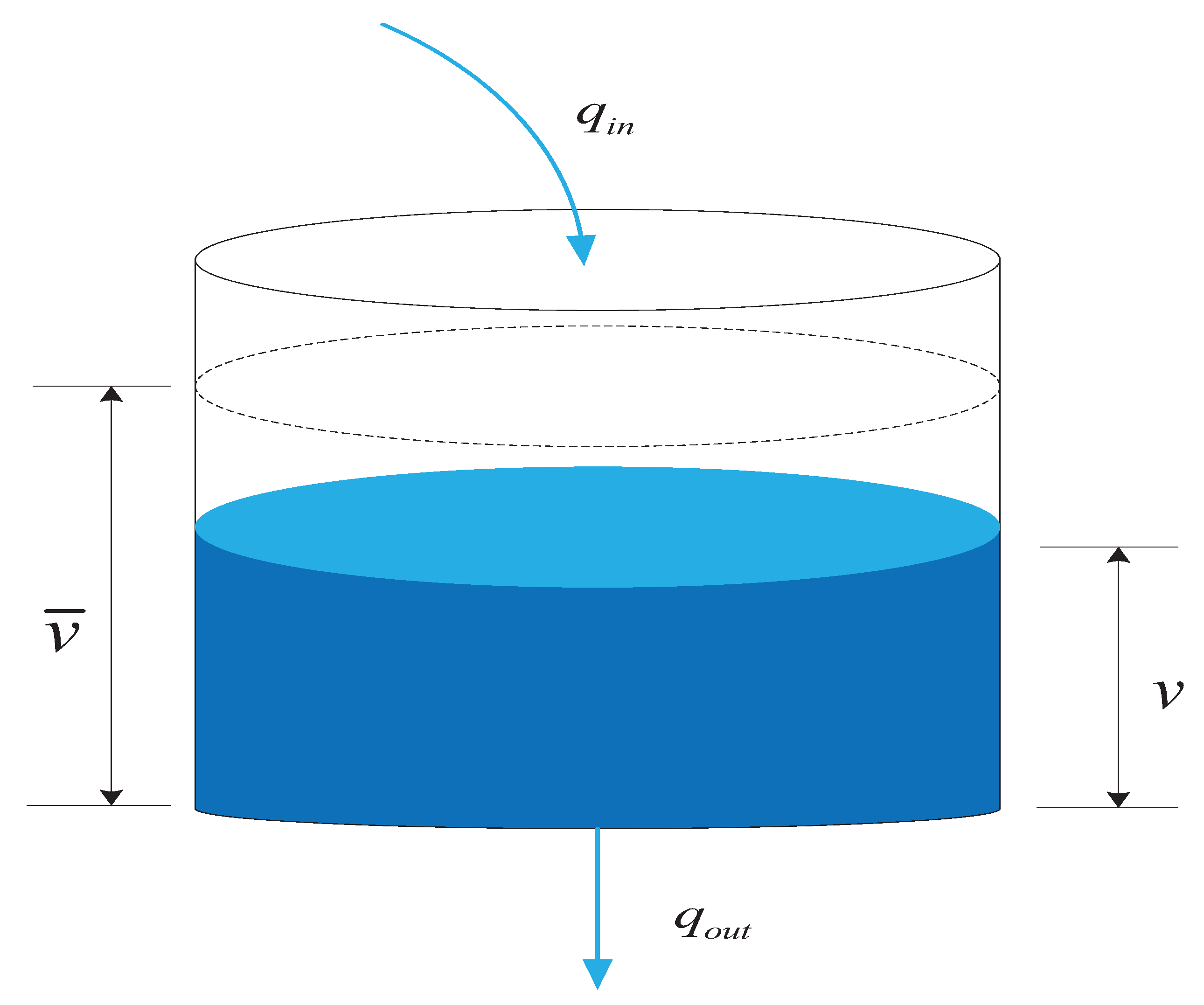
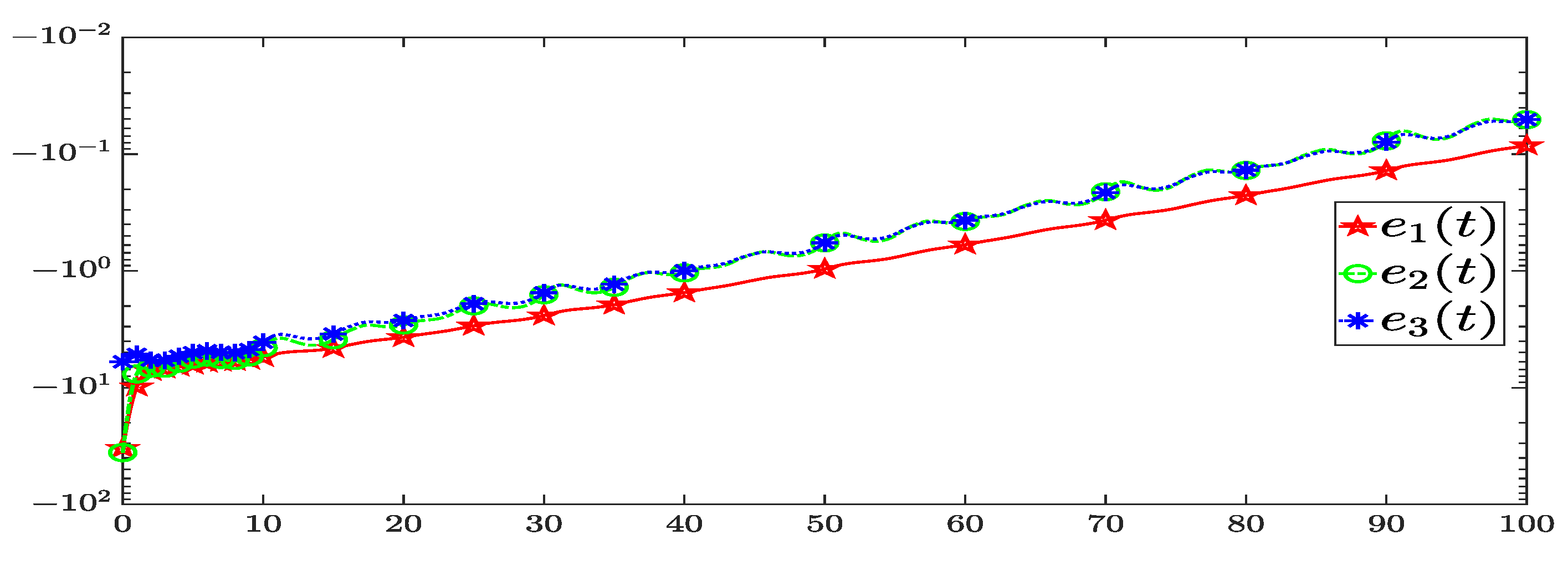
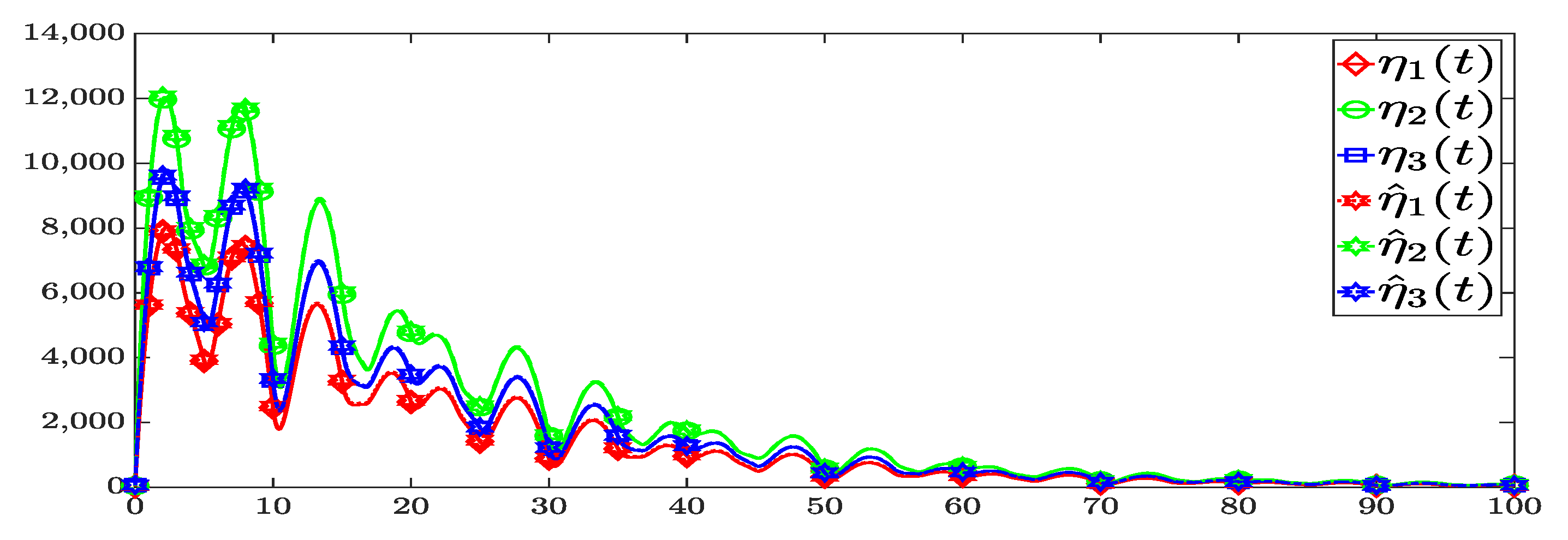
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luenberger, D.G. Observing the state of a linear system. IEEE Trans. Mil. Electron. 1964, 8, 74–80. [Google Scholar] [CrossRef]
- Fortmann, T.; Williamson, D. Design of low-order observers for linear feedback control laws. IEEE Trans. Autom. Control 1972, 17, 301–308. [Google Scholar] [CrossRef]
- Lien, C.H. Robust observer-based control of systems with state perturbations via LMI approach. IEEE Trans. Autom. Control 2004, 49, 1365–1370. [Google Scholar] [CrossRef]
- Rajamani, R. Observers for Lipschitz nonlinear systems. IEEE Trans. Autom. Control 1998, 43, 397–401. [Google Scholar] [CrossRef]
- Efimov, D.; Raïssi, T.; Chebotarev, S.; Zolghadri, A. Interval state observer for nonlinear time varying systems. Automatica 2013, 49, 200–205. [Google Scholar] [CrossRef]
- Tranninger, M.; Seeber, R.; Zhuk, S.; Steinberger, M.; Horn, M. Detectability analysis and observer design for linear time varying systems. IEEE Control Syst. Lett. 2019, 4, 331–336. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J. Reduced-order observer-based control design for nonlinear stochastic systems. Syst. Control Lett. 2004, 52, 123–135. [Google Scholar] [CrossRef]
- Eltag, E.; Aslam, M.S.; Chen, Z. Functional observer-based T-S fuzzy systems for quadratic stability of power system synchronous generator. Int. J. Fuzzy Syst. 2020, 22, 172–180. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, H.; Zhang, J.; Li, H. Multiple-mode observer design for a class of switched linear systems. IEEE Trans. Autom. Sci. Eng. 2013, 12, 272–280. [Google Scholar] [CrossRef]
- Chen, M.S.; Chen, C.C. Robust nonlinear observer for Lipschitz nonlinear systems subject to disturbances. IEEE Trans. Autom. Control 2007, 52, 2365–2369. [Google Scholar] [CrossRef]
- Penarrocha, I.; Sanchis, R.; Albertos, P. H∞ observer design for a class of nonlinear discrete systems. Eur. J. Control 2009, 15, 157–165. [Google Scholar] [CrossRef]
- Guan, Y.; Saif, M. A novel approach to the design of unknown input observers. IEEE Trans. Autom. Control 1991, 36, 632–635. [Google Scholar] [CrossRef]
- Zheng, G.; Bejaranoo, F.J.; Perruquetti, W.; Richard, J.P. Unknown input observer for linear time-delay systems. Automatica 2015, 61, 35–43. [Google Scholar] [CrossRef]
- Chen, W.H. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Yong, S.Z.; Zhu, M.; Frazzoli, E. Simultaneous input and state estimation for linear time-varying continuous-time stochastic systems. IEEE Trans. Autom. Control 2016, 62, 2531–2538. [Google Scholar] [CrossRef]
- Farina, L.; Rinaldi, S. Positive Linear Systems: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Kaczorek, T. Positive 1D and 2D Systems; Springer: London, UK, 2001. [Google Scholar]
- Fornasini, E.; Valcher, M.E. Stability and stabilizability criteria for discrete-time positive switched systems. IEEE Trans. Autom. Control 2011, 57, 1208–1221. [Google Scholar] [CrossRef]
- Briat, C. Robust stability and stabilization of uncertain linear positive systems via integral linear constraints: L1-gain and L-gain characterization. Int. J. Robust Nonlinear Control 2013, 23, 1932–1954. [Google Scholar] [CrossRef]
- Rami, M.A.; Tadeo, F.; Helmke, U. Positive observers for linear positive systems, and their implications. Int. J. Control 2011, 84, 716–725. [Google Scholar] [CrossRef]
- Ebihara, Y.; Peaucelle, D.; Arzelier, D. Analysis and synthesis of interconnected positive systems. IEEE Trans. Autom. Control 2016, 62, 652–667. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, G.; Feng, Y.; Chen, Y. Event-triggered state-feedback and dynamic output-feedback control of positive Markovian jump systems with intermittent faults. IEEE Trans. Autom. Control 2022. [Google Scholar] [CrossRef]
- Blanchini, F.; Colaneri, P.; Valcher, M.E. Co-positive Lyapunov functions for the stabilization of positive switched systems. IEEE Trans. Autom. Control 2012, 57, 3038–3050. [Google Scholar] [CrossRef]
- Knorn, F.; Mason, O.; Shorten, R. On linear co-positive Lyapunov functions for sets of linear positive systems. Automatica 2009, 45, 1943–1947. [Google Scholar] [CrossRef]
- Rami, M.A.; Tadeo, F. Controller synthesis for positive linear systems with bounded controls. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 151–155. [Google Scholar] [CrossRef]
- Shao, S.Y.; Chen, M.; Wu, Q.X. Stabilization control of continuous-time fractional positive systems based on disturbance observer. IEEE Access 2016, 4, 3054–3064. [Google Scholar] [CrossRef]
- Li, P.; Lam, J. Positive state-bounding observer for positive interval continuous-time systems with time delay. Int. J. Robust Nonlinear Control 2012, 22, 1244–1257. [Google Scholar] [CrossRef]
- Zaidi, I.; Chaabane, M.; Tadeo, F.; Benzaouia, A. Static state-feedback controller and observer design for interval positive systems with time delay. IEEE Trans. Circuits Syst. II Express Briefs 2014, 62, 506–510. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, R.; Chen, Y.; Fu, S. Linear programming based dynamic output-feedback controller for positive systems. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1281–1290. [Google Scholar]
- Qi, W.; Park, J.H.; Zong, G.; Cao, J.; Cheng, J. A fuzzy Lyapunov function approach to positive L1 observer design for positive fuzzy semi-Markovian switching systems with its application. IEEE Trans. Syst. Man Cybern. Syst. 2018, 51, 775–785. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Q.; Du, B. L1 fuzzy observer design for nonlinear positive Markovian jump system. Nonlinear Anal. Hybrid Syst. 2018, 27, 271–288. [Google Scholar] [CrossRef]
- Arogbonlo, A.; Huynh, V.T.; Oo, A.M.T.; Trinh, H. Functional observers design for positive systems with delays and unknown inputs. IET Control Theory Appl. 2020, 14, 1656–1661. [Google Scholar] [CrossRef]
- Oghbaee, A.; Shafai, B.; Nazari, S. Complete characterisation of disturbance estimation and fault detection for positive. IET Control Theory Appl. 2018, 12, 883–891. [Google Scholar] [CrossRef]
- Ocampo-Martínez, C.; Puig, V.; Cembrano, G.; Creus, R.; Minoves, M. Improving water management efficiency by using optimization-based control strategies: The Barcelona case study. Water Sci. Technol. Water Supply 2009, 9, 565–575. [Google Scholar] [CrossRef]
- Ocampo-Martínez, C.; Puig, V.; Cembrano, G.; Quevedo, J. Application of predictive control strategies to the management of complex networks in the urban water cycle. IEEE Control Syst. Mag. 2013, 3, 15–41. [Google Scholar]
- Zhang, J.; Yang, H.; Li, M.; Wang, Q. Robust model predictive control for uncertain positive time-delay systems. Int. J. Control. Autom. Syst. 2019, 17, 307–318. [Google Scholar] [CrossRef]
- Bonnabel, S.; Martin, P.; Rouchon, P. Symmetry-preserving observers. IEEE Trans. Auto-Matic Control 2008, 53, 2514–2526. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K.; Patton, R.J. Sliding mode observers for fault detection and isolation. Autom. Autom. 2000, 36, 541–553. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Zhao, X.; Lin, F.; Zhang, J. Combination of Functional and Disturbance Observer for Positive Systems with Disturbances. Mathematics 2023, 11, 200. https://doi.org/10.3390/math11010200
Huang L, Zhao X, Lin F, Zhang J. Combination of Functional and Disturbance Observer for Positive Systems with Disturbances. Mathematics. 2023; 11(1):200. https://doi.org/10.3390/math11010200
Chicago/Turabian StyleHuang, Lanai, Xudong Zhao, Fengyu Lin, and Junfeng Zhang. 2023. "Combination of Functional and Disturbance Observer for Positive Systems with Disturbances" Mathematics 11, no. 1: 200. https://doi.org/10.3390/math11010200
APA StyleHuang, L., Zhao, X., Lin, F., & Zhang, J. (2023). Combination of Functional and Disturbance Observer for Positive Systems with Disturbances. Mathematics, 11(1), 200. https://doi.org/10.3390/math11010200







