Solutions to the (4+1)-Dimensional Time-Fractional Fokas Equation with M-Truncated Derivative
Abstract
1. Introduction
2. M-Truncated Derivative
3. Wave Equation for the FFE
4. Exact Solutions of FFE
4.1. Extended Tanh–Coth Method
4.2. Jacobi Elliptic Function Method
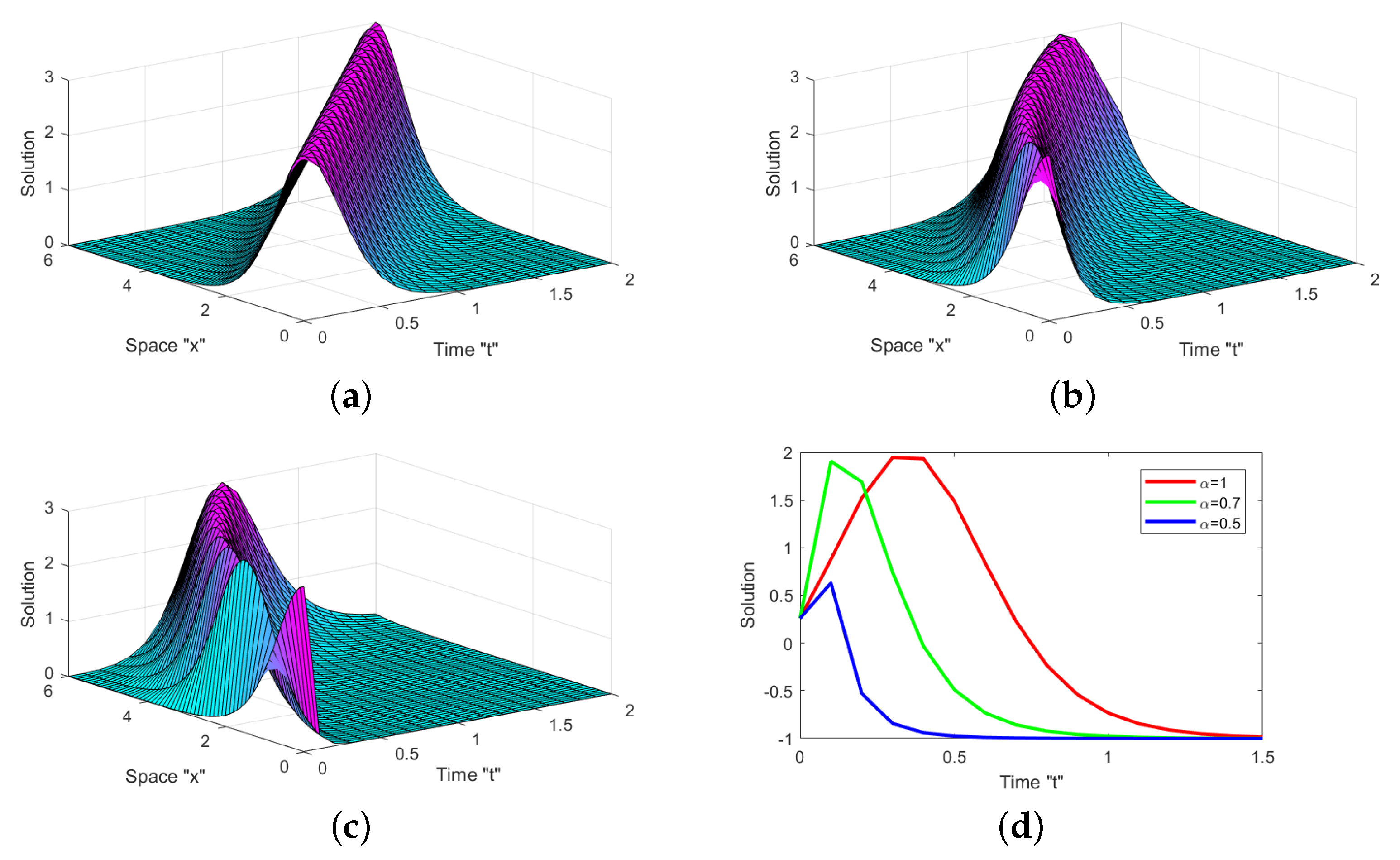
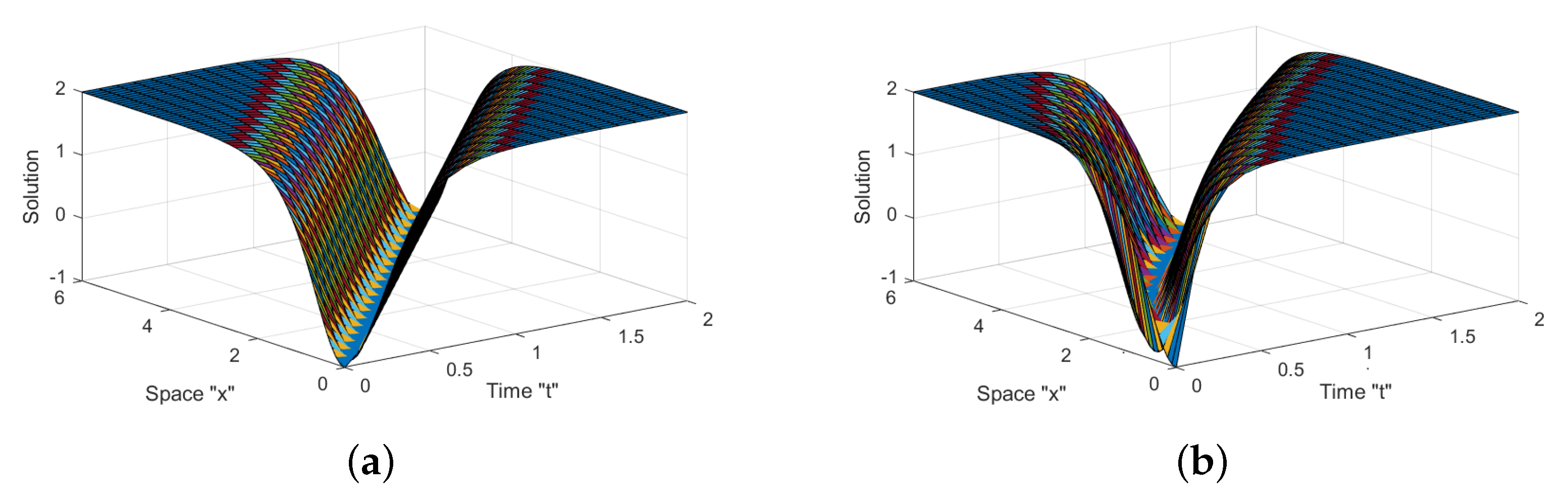
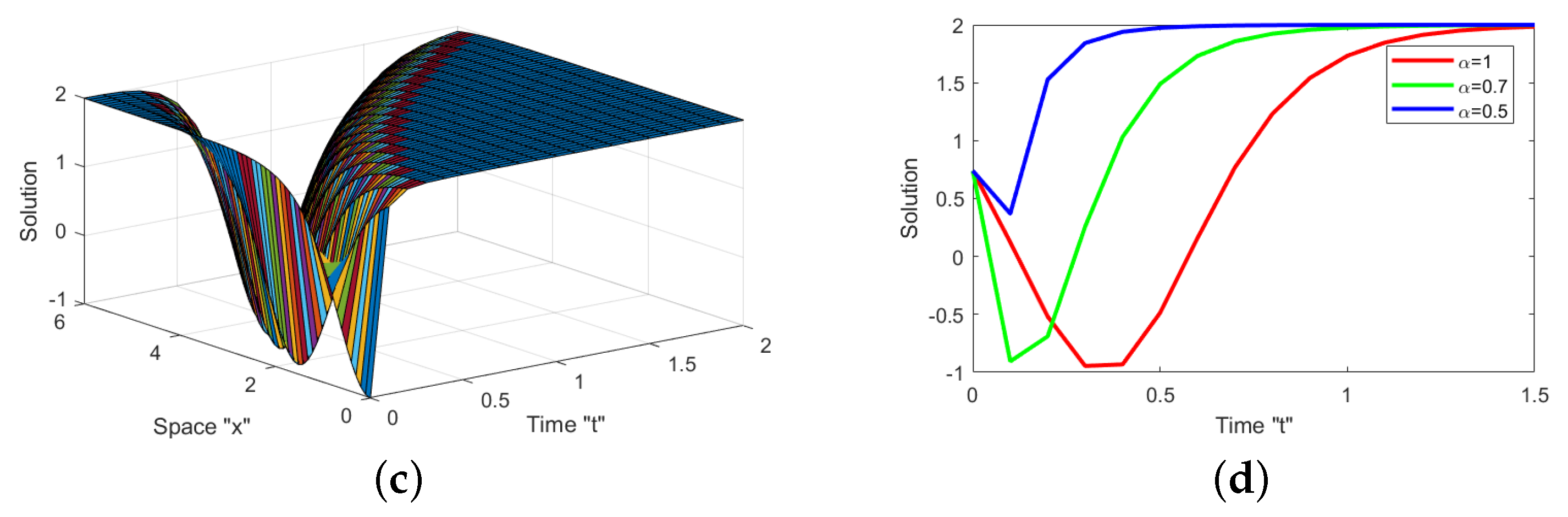
5. Graphical Representation and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Ntegration to Arbitrary Order, Vol. 11 of Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Mohammed, W.W.; Bazighifan, O.; Al-Sawalha, M.M.; Almatroud, A.O.; Aly, E.S. The influence of noise on the exact solutions of the stochastic fractional-space chiral nonlinear schrödinger equation. Fractal Fract. 2021, 5, 262. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations, Vol. 198 of Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing: Singapore, 2000. [Google Scholar]
- Oustaloup, A. La Commande CRONE: Commande Robuste d’Ordre Non Entier; Editions Hermès: Paris, France, 1991. [Google Scholar]
- Riesz, M. L’intégrale de Riemann-Liouville et le Problème de Cauchy pour L’équation des ondes. Bull. Société Mathématique Fr. 1939, 67, 153–170. [Google Scholar] [CrossRef]
- Wang, K.L.; Liu, S.Y. He’s fractional derivative and its application for fractional Fornberg-Whitham equation. Therm. Sci. 2016, 1, 54. [Google Scholar] [CrossRef]
- Miller, S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional differential without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel. Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. New properties of conformable derivative. Open Math. 2015, 13, 889–898. [Google Scholar] [CrossRef]
- Sousa, J.V.; de Oliveira, E.C. A new truncated Mfractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Diff. Equ. 2015, 1, 117–133. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Alshammari, M.; Cesarano, C.; El-Morshedy, M. Brownian Motion Effects on the Stabilization of Stochastic Solutions to Fractional Diffusion Equations with Polynomials. Mathematics 2022, 10, 1458. [Google Scholar] [CrossRef]
- Malfliet, W.; Hereman, W. The tanh method. I. Exact solutions of nonlinear evolution and wave equations. Phys. Scr. 1996, 54, 563–568. [Google Scholar] [CrossRef]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Hirota, R. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. The exp(-ψ(ς))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar]
- Mohammed, W.W. Approximate solution of the Kuramoto-Shivashinsky equation on an unbounded domain. Chin. Ann. Math. Ser. B 2018, 39, 145–162. [Google Scholar] [CrossRef]
- Mohammed, W.W. Modulation Equation for the Stochastic Swift–Hohenberg Equation with Cubic and Quintic Nonlinearities on the Real Line. Mathematics 2020, 6, 1217. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Yan, C. A simple transformation for nonlinear waves. Phys. Lett. A 1996, 224, 77–84. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Cesarano, C.; Mohammed, W.W. The analytical solutions of stochastic-fractional Drinfel’d-Sokolov-Wilson equations via (G′/G)-expansion method. Symmetry 2022, 14, 2105. [Google Scholar] [CrossRef]
- Zhang, H. New application of the (G′/G)-expansion method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3220–3225. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Belic, M.R.; Zhong, W.; Zhang, Y.; Xiao, M. Propagation dynamics of a light beam in a fractional Schrödinger equation. Phys. Rev. Lett. 2015, 115, 180403. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhong, H.; Belic, M.R.; Zhu, Y.; Zhong, W.; Zhang, Y.; Christodoulides, D.N.; Xiao, M. PT symmetry in a fractional Schrödinger Equation. Laser Photonics Rev. 2016, 10, 526–531. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Iqbal, N. Impact of the same degenerate additive noise on a coupled system of fractional space diffusion equations. Fractals 2022, 30, 2240033. [Google Scholar] [CrossRef]
- Fokas, A.S. Integrable nonlinear evolution partial differential equations in 4+2 and 3+1 dimensions. Phys. Rev. Lett. 2006, 96, 190210. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: New York, NY, USA, 1991. [Google Scholar]
- Davey, A.; Stewartson, K. On three-dimensional packets of surface waves. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1974, 338, 101–110. [Google Scholar]
- Zhang, S.; Chen, M. Painleve’ integrability and new exact solutions of the (4+1)-dimensional Fokas equation. Math. Probl. Eng. 2015, 2015, 367425. [Google Scholar] [CrossRef]
- He, Y. Exact solutions for (4+1)-dimensional nonlinear Fokas equation using extended F-expansion method and its variant. Math. Probl. Eng. 2014, 2014, 972519. [Google Scholar]
- Zhang, W.J.; Xia, T.C. Solitary wave, M-lump and localized interaction solutions to the (4+1)-dimensional Fokas equation. Phys. Scr. 2020, 95, 045217. [Google Scholar] [CrossRef]
- Al-Amr, M.O.; El-Ganaini, S. New exact traveling wave solutions of the (4+1)-dimensional Fokas equation. Comput. Math. Appl. 2017, 74, 1274–1287. [Google Scholar] [CrossRef]
- Kim, H.; Sakthivel, R. New exact traveling wave solutions of some nonlinear higher-dimensional physical models. Rep. Math. Phys. 2012, 70, 39–50. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A variety of multiple-soliton solutions for the integrable (4+1)-dimensional Fokas equation. Waves Random Complex Media 2018, 31, 46–56. [Google Scholar] [CrossRef]
- Sarwar, S. New soliton wave structures of nonlinear (4+1)-dimensional Fokas dynamical model by using different methods. Alex. Eng. J. 2021, 60, 795–803. [Google Scholar] [CrossRef]
- Yang, Z.-Z.; Yan, Z.-Y. Symmetry groups and exact solutions of new (4+1)-dimensional fokas equation. Commun. Theor. Phys. 2009, 51, 876. [Google Scholar]
- Lu, C.N.; Hou, C.J.; Zhang, N. Analytical and numerical solutions for a kind of high-dimensional fractional order equation. Fractal Fract. 2022, 6, 338. [Google Scholar] [CrossRef]
- Ullah, N.; Asjad, M.I.; Awrejcewicz, J.; Muhammad, T.; Baleanu, D. On soliton solutions of fractional-order nonlinear model appears in physical sciences. AIMS Math. 2022, 7, 7421–7440. [Google Scholar] [CrossRef]
- Hussain, A.; Jhangeer, A.; Abbas, N.; Khan, I.; Sherif, E.-S.M. Optical solitons of fractional complex Ginzburg–Landau equation with conformable, beta, and M-truncated derivatives: A comparative study. Adv. Differ. Equ. 2020, 2020, 612. [Google Scholar] [CrossRef]
- Peng, Y.Z. Exact solutions for some nonlinear partial differential equations. Phys. Lett. A 2013, 314, 401–408. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, W.W.; Cesarano, C.; Al-Askar, F.M. Solutions to the (4+1)-Dimensional Time-Fractional Fokas Equation with M-Truncated Derivative. Mathematics 2023, 11, 194. https://doi.org/10.3390/math11010194
Mohammed WW, Cesarano C, Al-Askar FM. Solutions to the (4+1)-Dimensional Time-Fractional Fokas Equation with M-Truncated Derivative. Mathematics. 2023; 11(1):194. https://doi.org/10.3390/math11010194
Chicago/Turabian StyleMohammed, Wael W., Clemente Cesarano, and Farah M. Al-Askar. 2023. "Solutions to the (4+1)-Dimensional Time-Fractional Fokas Equation with M-Truncated Derivative" Mathematics 11, no. 1: 194. https://doi.org/10.3390/math11010194
APA StyleMohammed, W. W., Cesarano, C., & Al-Askar, F. M. (2023). Solutions to the (4+1)-Dimensional Time-Fractional Fokas Equation with M-Truncated Derivative. Mathematics, 11(1), 194. https://doi.org/10.3390/math11010194






