Abstract
The original formulation of the firefighter problem defines a discrete-time process where a fire starts at a designated subset of the vertices of a graph G. At each subsequent discrete time unit, the fire propagates from each burnt vertex to all of its neighbors unless they are defended by a firefighter that can move between any pair of vertices in a single time unit. Once a vertex is burnt or defended, it remains in that state, and the process terminates when the fire can no longer spread. In this work, we present the moving firefighter problem, which is a generalization of the firefighter problem where the time it takes a firefighter to move from a vertex u to defend vertex v is determined by a function . This new formulation models situations such as a wildfire or a flood, where firefighters have to physically move from their current position to the location of an entity they intend to defend. It also incorporates the notion that entities modeled by the vertices are not necessarily instantaneously defended upon the arrival of a firefighter. We present a mixed-integer quadratically constrained program (MIQCP) for the optimization version of the moving firefighter problem that minimizes the number of burnt vertices for the case of general finite graphs, an arbitrary set of vertices where the fire breaks out, a single firefighter, and metric time functions .
Keywords:
firefighter problem; np-hard; mathematical programming; mixed-integer quadratically constrained programming (MIQCP); exact algorithm; spread and containment in networks MSC:
90-10; 90C35; 90C27; 90C11
1. Introduction
The firefighter problem was originally formulated by Bert Hartnell in 1995 [1]. It defines a discrete-time model of a diffusive process (e.g., a fire, a flood, an infectious disease, information, a computer virus, or an invasive species) on a graph , where a fire breaks out at a set of vertices . At each subsequent discrete time unit, the fire propagates from each burnt vertex to all of its neighbors unless they are defended by a firefighter. Once a vertex is burnt or defended, it remains in that state, and the process terminates when the fire can no longer spread. A solution to the problem defines the defending actions that have to be taken at each discrete time unit to optimally contain the spreading process by minimizing the number of burnt vertices or the time it takes to stop the diffusive process.
Over the years, the firefighter problem has gained growing relevance for its theoretical properties but also because it provides a simple model that can be used to study impactful phenomena such as the spreading and containment dynamics of viruses in social networks [2] and fires in oil terminals [3] and high-rise buildings [4].
Unfortunately, for the case of fighting actual fire outbreaks, the original formulation of the firefighter problem and its many variants and generalizations (e.g., [5,6,7,8,9,10,11,12,13,14,15,16,17,18]) fail to capture an important aspect that arises in more realistic scenarios, namely, that the process of transporting (or moving) a firefighter from her current location to defend an entity located at a different location may take a variable amount of time. In general, this time may be a function of the distance between the two locations and the particular properties of the terrain, the entity to be defended, and the firefighter herself. As a concrete example, when fighting a wildfire, any strategy has to consider the time it takes to move fire engines and perhaps heavy machinery to a given region and then defend that region by creating control lines containing no combustible material. This time may depend on many factors, such as the land topography and the type of fire engines. It is worth noting that designing efficient wildfire suppression strategies has become increasingly important. During the 2019/2020 bushfire season, the number of hectares burned in Australia surpassed 6.75 million [19], and 4.09 million hectares burned in the United States in 2020 [20]. In 2021, more than 75 thousand wildfire outbreaks were detected in the Amazon Rainforest [21].
In this work, we introduce the moving firefighter problem, which is a generalization of the firefighter problem that incorporates a function that determines the time it takes a firefighter to move from its current location at vertex to defend another vertex . Similarly to the original formulation of the firefighter problem, in this generalization, we assume that the time it takes the fire to spread from a burnt vertex to its neighbors in the graph is constant.
We present a mixed-integer quadratically constrained program (MIQCP) for the optimized version of the moving firefighter problem that minimizes the number of burnt vertices for the case of general finite graphs, an arbitrary set of vertices where the fire breaks out, a single firefighter, and metric time functions . We characterized the performance of the proposed solution through experiments on random graphs.
The rest of the paper is organized as follows. Section 2 presents a review of the extensive body of work on the firefighter problem and of its generalization and variants. Section 3 presents the formulation of the moving firefighter problem and the concepts and notation that are used throughout the paper. In this section, we also establish that the moving firefighter problem is indeed a generalization of the original firefighter problem, and hence, that it belongs to the class of -hard problems. Section 4 presents the proposed exact solution. Section 5 presents the results of a series of experiments, and Section 6 presents our concluding remarks and future work.
2. Related Work
The firefighter problem has been extensively studied. It has been determined that it is -hard for bipartite graphs [22], for cubic graphs [9], for trees of maximum degree three [22] and of pathwidth three [23], for co-bipartite graphs [23], and for unit disk graphs [24]. It has also been established that the problem is in P for caterpillars and P-trees [22], interval graphs, split graphs, permutation graphs, -free graphs for fixed k [24], and if the fire breaks out at a vertex of degree at most two, for graphs of maximum degree three [25].
For the case of firefighters, the problem is -complete for trees of maximum degree and -hard for the optimization version that maximizes the number of saved (unburnt) vertices for trees of maximum degree [11].
Regarding approximations, for the case of trees and a single firefighter, the greedy algorithm that every time selects the vertex that maximizes the number of protected vertices is a tight -approximation [2,26]. There is also a ()-approximation algorithm for rooted trees based on an LP-relaxation and randomized rounding [27]. The previous algorithm was used by Iwaikawa et al. to provide a 0.7144-approximation algorithm for ternary trees [28]. The problem is not -approximable on general graphs for any unless [8]. More recently, Adjiashvili et al. [29] presented a polynomial-time approximation scheme (PTAS) for trees.
From a parameterized point of view, the problem is W[1]-hard on general graphs for firefighters when parameterized by the number of saved vertices, protected vertices, and burned vertices [30].
Other generalizations of the firefighter problem include a version where the number of available firefighters at each time is not constant [7], a version where the objective is to protect a particular subset of the set of vertices [9,11], a version where the protection also propagates from each defended vertex to their non-burning neighbors [8,13], and a non-deterministic version where at each time the fire propagates to unprotected vertices with a given probability [14]. There is also a fractional version where vertices can be partially burned and protected, and partially burned vertices can propagate their fractions of the fire to their undefended or partially defended neighbors [5]. More recently, Coupechoux et al. introduced online versions of the firefighter and fractional firefighter problems where the number of available firefighters is revealed at each discrete time [16]. The k-firefighter problem is another generalization defined in terms of a two-player game where the fire propagates to at most k vertices in each round with the objective of burning as many vertices as possible while the firefighter defends vertices to contain the spread of the fire [6,10].
The geometric firefighter problem [12,15,17] is the closest variation to the moving firefighter problem because it considers the speed with which barriers are constructed to contain the fire. In this variation, the fire starts at a point inside a simple polygon and circularly propagates at a constant speed. A firefighter sequentially builds a series of one-dimensional barriers at a constant speed, which can be different from the fire propagation speed, to contain the propagation of the fire. Barriers have to be built continuously before the fire reaches any of its points. The objective is to maximize the protected area of , namely, the area separated from the fire by the barriers. Similarly to the original firefighter problem, the geometric firefighter problem assumes that the firefighter can be instantaneously transported from the last position of a recently constructed barrier to the origin of the next barrier in the solution.
In the traveling firefighter problem, also referred to as the -TSP (traveling salesman problem), a firefighter has to extinguish a set of wildfires located at positions modeled by vertices. The distance between vertices is defined by a function . A solution to this problem is a permutation of the vertices that minimize the total damage produced by the fires, which is a quadratic function of time elapsed from when the fires broke out to when the firefighter arrives [18].
Some other -hard problems that resemble the firefighter problem are the graph burning problem (GBP) [31,32,33] and the influence maximization problem (IMP) [34,35,36]. However, while they seek the rapid diffusion of information, the firefighter problem seeks diffusion containment. Nevertheless, very recently, the authors of [37] used the integer linear programming formulation (ILP) of the firefighter problem presented in [6] to derive the first exact solution to the graph burning problem.
Table 1 summarizes the main results discussed in this section.

Table 1.
Summary of related work.
3. The Moving Firefighter Problem
An instance of the moving firefighter problem () is defined as a 6-tuple , where is a simple graph; is a subset of the vertices where the fire breaks out; a is the depot where the firefighters are initially stationed (also referred as anchor point); is a function that determines the time it takes a firefighter to move from either the depot a or a vertex to any other vertex , and to defend v. f is the number of firefighters, and is a constant that defines the time it takes for the fire to spread from a burnt vertex to its unprotected neighbors in G.
From the assumption that the fire spreads uniformly at a constant rate, we can organize the time into time slots of length . Each time slot defines a burning round, where at the beginning of each time slot, the fire propagates from burnt vertices to their neighbors in G unless they were defended by a firefighter. Once a vertex is burnt or defended, it remains in that state, and the process terminates when the fire can no longer spread. We will say that a vertex is protected if it is neither burning nor defended at the end of the process. The diffusive process starts at time slot 0 where only the vertices in F are burning.
For the case of a single firefighter, a feasible solution to the is a valid sequence of vertices defended by the firefighter. We say that a sequence is valid if Equation (1) holds for each . In Equation (1), is the time at which a vertex would be burned if the defending sequence were truncated to .
The purpose of Equation (1) is to restrict the space of feasible solutions to that where the firefighter has enough time to defend every vertex in the sequence before the fire reaches them.
Figure 1 shows examples of an instance of the and of one of its solutions. The graph G is composed of the set of vertices and the set of edges . The fire breaks out at vertices , a single firefighter () is initially stationed at the depot a, and . The depot and the vertices in V are in the Euclidean plane. The number on top of the vertices indicates their shortest hop distance to their closest vertex in F, which in this example equals the smallest time slot in which they can burn. The figure also shows a feasible solution in which the firefighter moves from the depot a to defend vertex , then moves to defend vertex , and lastly moves to defend vertex . For this defending sequence , the value of equals 2 because vertex burns at time 2 when the truncated protecting sequence is applied, equals 2 because vertex burns at time 2 when the truncated protecting sequence is applied, and similarly, equals 3. is a valid sequence because , , and . The process ends after three burning rounds (at time slot three) because at that time, the fire can no longer spread. The value of this solution equals five because, at the end of the process, vertices , and are burnt.
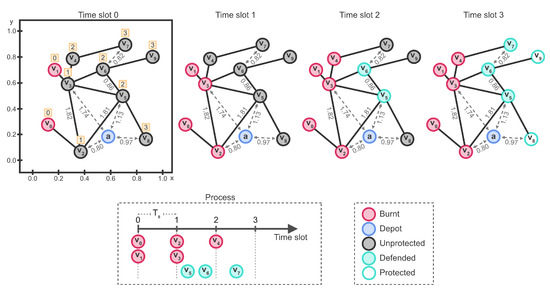
Figure 1.
Example of an instance of the MFP and one of its solutions.
For the instance of Figure 1, the firefighter cannot choose to defend vertex because for sequence . It could defend because for a sequence , but in this case no other vertex could be defended, giving a feasible solution of value nine. In these examples, the process also ends at time slot 3 when the fire can no longer spread.
For the case of firefighters, a feasible solution is a set of valid sequences of the vertices defended by each firefighter. In this case, has to be extended to compute the time in which a vertex in a is burnt if none of the defending sequences in includes vertices protected at a time posterior to for .
The objective of the minimization version of the is to find a feasible solution that minimizes the number of burnt vertices at the end of the process.
The decision version of the moving firefighter problem for a single firefighter (1-MFP) is as follows.
Definition 1.
Decision version of the 1-MFP problem:Given an arbitrary instance of 1-MFP and an integer , is there a valid sequence of vertices defended by the firefighter such that the number of burnt vertices at the end of the process is at most k?
1-MFP Is NP-Complete
In this section, we show that 1-MFP is NP-complete via a polynomial-time reduction () to the decision version of the firefighter problem for a single firefighter (1-FP), which can be defined as follows.
Definition 2.
Decision version of the 1-FP problem:Given an arbitrary instance of 1-FP, where is the set of vertices where the fire breaks out and an integer , is there a sequence of vertices defended by the firefighter such that the number of burnt vertices at the end of the process is at most k?
We start with two preliminary lemmas.
Lemma 1.
Given an instance of 1-FP, an instance of 1-MFP such that , , defending sequences for the instance of 1-FP, with for each for the instance of 1-MFP, and function with , and . The discrete time in which a vertex in is defended equals the time in which its corresponding vertex is defended in .
Proof of Lemma 1.
From the definition of , we can observe that the time in which a vertex is defended equals i. This is the same as the discrete-time in which the corresponding vertex is defended by , namely, i. □
Lemma 2.
Given an instance of 1-FP, an instance of 1-MFP such that , , defending sequences for the instance of 1-FP, with for each , for the instance of 1-MFP, and function with , , and . A vertex burns at discrete time t if and only if its corresponding vertex burns at the beginning of time slot t.
Proof of Lemma 2.
If a vertex burns at discrete time t, it means that there is a shortest path P of length t, from a vertex to v that does not contain any vertex in the truncated protecting sequence . Given that , this shortest path P also exists in and does not contain vertices in . From Lemma 1, and because the fire propagates at the beginning of each time slot of length , vertex has to burn at time t, a which equals the beginning of time slot t. A symmetric argument can be applied to show the other direction of the implication. □
Theorem 1.
1-MFP is NP-complete.
Proof of Theorem 1.
We first show that the 1-MFP is an NP. Given an arbitrary instance , , and a defending sequence , a certifier algorithm can check in polynomial-time if (1) holds for each , given that the firefighter defends each at time . Then, the certifier algorithm can execute, also in polynomial-time, the firefighting process to verify that the number of burnt vertices is, in fact, at most k.
Now, we show that 1-FP 1-MFP. Given an arbitrary instance of 1-FP and an integer k, we construct an instance of 1-MFP as with , , and with , and . Constructing this instance of 1-MFP takes steps.
Next, we claim that there is a defending sequence for the instance of the 1-FP such that at most k vertices of G burn, if and only if there is a valid defending sequence with for each , for the instance of the 1-MFP such that at most k vertices burn in .
(⇒) We first show that is valid. Let us proceed by contradiction and assume that is the vertex with the smallest index such that . However, from Lemma 1, we saw that the time a vertex in is defended by equals the discrete time its corresponding vertex in G is defended by . Since vertex is defended at discrete time j in the original firefighter process, it can not be burning at time j, which means that there is no path from a vertex to of length j or shorter that does not contain a vertex in the truncated protecting sequence . Since , there is no such a path in , and hence , a contradiction. From Lemma 2, at the end of the burning process, exactly the same number of vertices are burning in both instances. Therefore, if at most k vertices of G burn, then at most k vertices burn in .
(⇐) Since is valid for the 1-MFP instance, from Lemma 1 and 2, we know that all the vertices in can be defended in the 1-FP instance. From Lemma 2, we also know that if at most k vertices of burn, then at most k vertices of G burn. □
Table 2 summarizes the notation used throughout the paper.

Table 2.
Summary of notation.
4. Mixed-Integer Quadratically Constrained Program for the 1-MFP
Expressions (2) to (23) define a mixed-integer quadratically constrained program (MIQCP) for the optimization version of the 1-MFP. This MIQCP is based on the integer linear program (ILP) for the original firefighter problem (FP). For simplicity, let us assume that vertices are labeled as . In addition, let us consider the anchor point, a, as an isolated vertex in the graph. This way, the fire cannot catch this special vertex, and inconsistencies are not added to the formulation. As in the original FP, the proposed MIQCP for the 1-MFP requires an upper bound B on the number of burning rounds (or time slots) at which the diffusive process finishes. However, unlike the original FP, it also requires an upper bound D on the number of vertices that are defended within a single burning round. We will say that defending a vertex during a burning round defines a defense round within that burning round. The length of the defense rounds is a function of , and it is possible to have from 0 to D defense rounds in a given burning round.
The ILP for the original FP is relatively simple; it has binary variables and constraints, where is the graph’s largest vertex degree. In contrast, our proposed MIQCP for the 1-MFP has binary variables, linear constraints, and quadratic constraints. Since B and D are upper bounded by n, the numbers of variables and constraints are upper bounded by . In addition, this MIQCP assumes that function is normalized with respect to the length of the burning rounds (time slots), and hence that .
The ILP for the FP problem only has two sets of binary variables, and . Similarly, the main variables of the proposed MIQCP for the 1-MFP are and too. These variables report the state of each vertex i at the burning round, where and . Thus, if a vertex is burnt at round j, then ; otherwise, . If vertex is burnt at round j, it is because of one of the following reasons: it was originally burnt at some previous round (Constraint (3)), or it is in the neighborhood of some previously burnt vertex (Constraint (6)). In case vertex is defended at round j, then ; otherwise, . A vertex that is defended at any round will remain in that state (Constraint (4)), and if a vertex is in the neighborhood of some previously burnt vertex, then it has to be either burned or defended (Constraint (6)). By Constraint (5), a vertex cannot be simultaneously burnt and defended. For further clarification, we can organize these variables in two matrices (see Equations (24) and (25)), where matrix d can be further extended to matrices d’ and p (see Equations (26) and (27)), where .
Given that the 1-MFP allows sequentially defending many vertices within a burning round, we added a set of variables in order to report the sequence of defended vertices, where , , and . In more detail, if vertex is defended at the defense round, within the burning round, then ; otherwise, . Notice that D is an upper bound on the number of defended vertices within one burning round. We can organize these variables into B matrices of size . Thus, there is a matrix for each burning round (see Equation (26)).
By Constraint (7), all vertices defended at the burning round stay defended at the beginning of the first defense round of the following burning round, which is reported in the first column of . By Constraint (8), the state of the defended vertices at the end of the burning round (column D of d’) is copied into column j of matrix d. In other words, each column j of matrix d is a summary of what happens inside each matrix d’. Similarly to Constraint (4), Constraint (9) indicates that once a vertex is defended at the defense round of the burning round, it will stay defended.
Constraints (10)–(12) describe the relationship between the binary variables and variables . The goal of p is to report the last defended vertex at each defense round within each burning round. Notice that might mean two different things: vertex has been defended precisely at the defense round within burning round j (Constraints (10) and (11)), or vertex is the last vertex defended at some previous round. Constraint (12) guarantees that exactly one vertex is the last defended at each defense round. Please note that Constraint (18) establishes that the anchor point a is defended at the beginning of the process. For convenience, we can organize these variables in a matrix p for each burning round (see Equation (27)).
Constraints (13) and (14) guarantee that the information about the last defended vertex is copied into the following columns of p. When a new vertex becomes defended, these constraints are deactivated by making the right-hand side equal to zero. In this case, the subsequent columns are no longer a copy of the previous ones; instead, the currently defended vertex is updated. Constraints (15) and (16) guarantee that the time needed to carry out a sequence of defended vertices within the burning round does not exceed the current number j of time slots of the diffusive process. By these two constraints, Constraints (3) and (5)–(14), which define the relationship between the defended vertices and the dynamics of the diffusive process, the firefighter cannot defend a vertex that the fire has already spread to (which is consistent with Equation (1)).
The solution to an 1-MFP instance is obtained from the matrices by sequentially scanning them for the first time that a value of one appears in a row of one of such matrices. Remember that the first time that a value of one appears in row i of the matrix indicates that the vertex is defended at burning round j, and hence, that it is part of the resulting defending sequence . The ordering of the vertices in is obtained from the burning and defense rounds where they were defended.
For further clarification, Figure 2 shows the value of each variable in the solution of the example instance from Figure 1. In this example, we follow the convention of placing the anchor point in the last row of the matrices. Column represents the process’ initial conditions where vertices and are the initial fire sources and the firefighter is located at the anchor point. The remaining columns of matrices and report the state of the vertices at the subsequent burning rounds. The resulting defending sequence equals because the first value of one appears in the sixth row (the one corresponding to vertex ) of the first column of , the second value of one appears in the seventh row of , and the last value of one appears in the eighth row of the first column of . Time because no vertex is defended during the first burning round while because the firefighter moves from the anchor a to defend vertex and then from to defend , which takes 1.99 units of time. Similarly, because that is the time needed to complete the whole defending sequence , which is optimal for this instance.
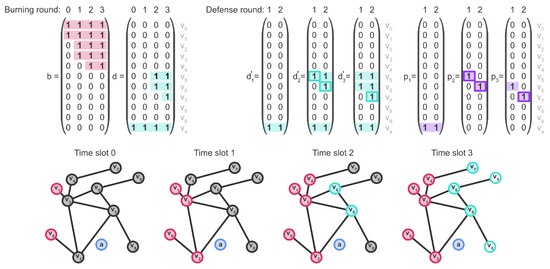
Figure 2.
State of the matrices defined by the MIQCP for the optimal solution of the instance defined in Figure 1. Here, , , and .
Regarding a MIQCP for the MFP with more than one firefighter, we conjecture that the number of variables and constraints might increase by an order of f. The precise formulation is left as future work.
5. Experimental Performance Evaluation
In this section, we present the results of a series of experiments that characterize the performance of the proposed MIQCP for the 1-MFP. The purpose was twofold: first, to evaluate the impacts of the size of the graph, the scale of function , and the number of vertices where the fire breaks out on the value of the objective function and the MIQCP’s running time; second, to provide a set of optimally solved instances that can be used for future performance comparison analyses of heuristic or approximated solutions.
For these experiments, we generated instances of the 1-MFP, where the number of firefighters f equals one, the length of the time slots also equals one, the number of initial fires is in , the graph with is randomly generated, and its vertices and the anchor point are placed uniformly at random inside a cube. To obtain a random graph G of size n, we generated a series of graphs of size following the Erdős–Rényi model with , until finding a with a connected component of size n which is used as G. Lastly, is obtained from the Euclidean distances between the locations of the vertices and the anchor point.
We implemented the proposed MIQCP using Python and a commercial version of Gurobi 9.5.1 [38]. Although there are other optimization solvers, not all of them can solve MIQCP problems. Gurobi and CPLEX [39] are among the best solvers with such capabilities. From them, we selected Gurobi because it is one of the fastest optimization solvers to date. All the experiments were executed using a computer running Ubuntu 20.04 on an Intel Core i7-6700 processor of 3.40 GHz with 32 GB of RAM.
For the results presented here, we used optimal values of the two hyperparameters introduced in the MIQCP—namely, the upper bound B for the number of time slots needed to complete the diffusive process and the upper bound D for the maximum number of vertices that can be defended in a single time slot. These optimal values were determined experimentally for each instance. As discussed in Section 4, the values of these upper bounds significantly impact the performance of the MIQCP because they determine the number of constraints. It is also important to highlight that underestimating these values precludes the MIQCP from finding optimal and even correct solutions.
Figure 3 presents the running times needed to solve instances with increasing numbers of vertices and initial fires, and when scaling function by a factor . The solid lines represent the average value computed over ten different random instances, and the shaded region represents the confidence interval for a confidence level of . The results are as expected. From the figure, we can observe that the running time increases rapidly as the size of the graphs (n) increases because the numbers of linear () and quadratic () constraints increase as a function of n. We can also observe that the running time tends to be smaller with a larger number of initial burnt vertices () because the upper bound B on the number of time slots needed to complete the diffusive process also tends to be smaller as increases. The latter is because B is proportional to the length of the shortest paths from vertices in F to the remaining vertices in G. Lastly, the running time decreases as the value of increases because the upper bound D on the number of vertices that can be defended in a single time slot decreases.
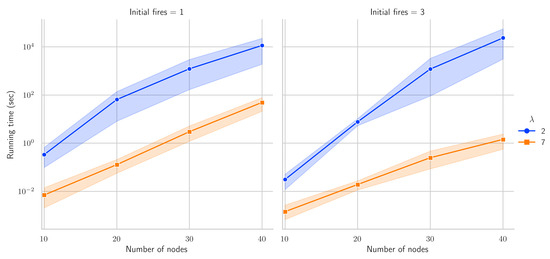
Figure 3.
Running time with one initial fire (left) and three initial fires (right). The x axis shows the number of vertices in the input graph, and the y axis shows the running time in seconds. The solid lines represent the average values over ten random instances, and the shaded regions are the confidence intervals for a confidence level of .
Figure 4 shows the average number of burnt vertices at the end of the diffusive processes when increasing the number of vertices, the number of initial fires, and the value of . As expected, the number of burnt vertices increases as the size of the graphs increases because, in general, the fire can propagate to a larger number of vertices. Increasing the number of initial fires increases the number of burnt vertices because the firefighter has to contain more than one diffusive process. This also reduces the objective function’s variability because having more than one initial fire makes the diffusive process less sensitive to the topological properties of the neighborhood where the fire breaks out. Lastly, the number of burnt vertices increases as the value of increases because this has the effect of making the firefighter slower.
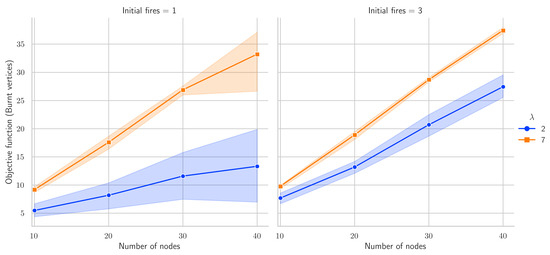
Figure 4.
Numbers of burnt vertices with one initial fire (left) and three initial fires (right). The x axis shows the number of vertices in the input graph, and the y axis shows the number of burnt vertices at the end of the process. The solid lines represent the average values over ten random instances, and the shaded regions are the confidence intervals for a confidence level of .
We performed experiments for graphs of size , but unfortunately, most of the executions did not end within a predefined time budget of 24 h, and in many cases, experienced memory crashes. This indicates a need for more scalable solutions for the MFP.
6. Conclusions
We presented the moving firefighter problem (MFP), a generalization of the original firefighter problem (FP) presented by Hartnell, which incorporates a function that determines the time it takes a firefighter to move from vertex u to vertex v in the input graph to defend v. We argue that this generalization allows modeling more realistic situations where the time needed to defend an entity modeled by a vertex is not the same for all the entities and where there is either a physical or logical distance between each pair of entities. This new formulation has practical applications for studying the spread and containment dynamics in networks.
Using polynomial time reduction from the decision version of the original firefighter problem for a single firefighter 1-FP, we showed that the decision version of the moving firefighter problem for a single firefighter 1-MFP is indeed a generalization of the 1-FP, and hence, that it belongs to the NP-complete class of problems.
We presented a mixed-integer quadratically constrained program (MIQCP) for the optimization version of the 1-MFP with metric functions that have binary variables, real-valued variables, linear constraints, and quadratic constraints. B and D are upper bounds to the numbers of burning and defense rounds, respectively. To empirically characterize the performance of the MIQCP, we solved 160 randomly generated instances. The results revealed that the running time of the MIQCP strongly depends on finding adequate values for B and D.
Future work includes designing scalable solutions for the 1-MFP, solutions for instances with more than one firefighter, and solutions specifically tailored for particular topologies such as trees. We also intend to design approximation algorithms and characterize the approximability of the MFP.
Author Contributions
Conceptualization, B.R.G.-D.-L.-P., J.G.-D., R.M.-M. (Rolando Menchaca-Méndez), M.A.M.-M., R.M.-M. (Ricardo Menchaca-Méndez) and O.A.G.-D.-L.-P.; Methodology, B.R.G.-D.-L.-P., J.G.-D., R.M.-M. (Rolando Menchaca-Méndez), M.A.M.-M., R.M.-M. (Ricardo Menchaca-Méndez) and O.A.G.-D.-L.-P.; Software, B.R.G.-D.-L.-P., J.G.-D., M.A.M.-M. and O.A.G.-D.-L.-P.; Validation, R.M.-M. (Ricardo Menchaca-Méndez); Formal analysis, B.R.G.-D.-L.-P., J.G.-D., R.M.-M. (Rolando Menchaca-Méndez), M.A.M.-M., R.M.-M. (Ricardo Menchaca-Méndez) and O.A.G.-D.-L.-P.; Writing—original draft, B.R.G.-D.-L.-P., J.G.-D., R.M.-M. (Rolando Menchaca-Méndez), M.A.M.-M., R.M.-M. (Ricardo Menchaca-Méndez) and O.A.G.-D.-L.-P.; Writing—review & editing, B.R.G.-D.-L.-P., J.G.-D., R.M.-M. (Rolando Menchaca-Méndez), M.A.M.-M., R.M.-M. (Ricardo Menchaca-Méndez) and O.A.G.-D.-L.-P.; Visualization, B.R.G.-D.-L.-P., J.G.-D. and O.A.G.-D.-L.-P.; Supervision, R.M.-M. (Rolando Menchaca-Méndez) and R.M.-M. (Ricardo Menchaca-Méndez); Project administration, R.M.-M. (Rolando Menchaca-Méndez). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “Consejo Nacional de Ciencia y Tecnología” of México and the “Instituto Politécnico Nacional”.
Data Availability Statement
The source code used in Section 5 is available at https://github.com/BrunoGupa/MovingFirefighterProblem. The same repository contains the specific instances and their corresponding optimal solutions that were used to obtain the results presented in Section 5.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Hartnell, B. Firefighter! an application of domination. In Proceedings of the the 24th Manitoba Conference on Combinatorial Mathematics and Computing, University of Manitoba, Winnipeg, ON, Canada, 30 September–2 October 1994. [Google Scholar]
- Finbow, S.; MacGillivray, G. The Firefighter Problem: A survey of results, directions and questions. Australas. J. Comb. 2009, 43, 57–78. [Google Scholar]
- Khakzad, N. A graph theoretic approach to optimal firefighting in oil terminals. Energies 2018, 11, 3101. [Google Scholar] [CrossRef]
- Wang, K.; Yuan, Y.; Chen, M.; Lou, Z.; Zhu, Z.; Li, R. A Study of Fire Drone Extinguishing System in High-Rise Buildings. Fire 2022, 5, 75. [Google Scholar] [CrossRef]
- Fogarty, P. Catching the Fire on Grids. Master’s Thesis, Department of Mathematics, University of Vermont, Burlington, VT, USA, 2003. [Google Scholar]
- Develin, M.; Hartke, S.G. Fire containment in grids of dimension three and higher. Discret. Appl. Math. 2007, 155, 2257–2268. [Google Scholar] [CrossRef][Green Version]
- Ng, K.L.; Raff, P. A generalization of the firefighter problem on Z × Z. Discret. Appl. Math. 2008, 156, 730–745. [Google Scholar] [CrossRef]
- Anshelevich, E.; Chakrabarty, D.; Hate, A.; Swamy, C. Approximation algorithms for the firefighter problem: Cuts over time and submodularity. In Proceedings of the International Symposium on Algorithms and Computation; Springer: Berlin, Germany, 2009; pp. 974–983. [Google Scholar]
- King, A.; MacGillivray, G. The firefighter problem for cubic graphs. Discret. Math. 2010, 310, 614–621. [Google Scholar] [CrossRef][Green Version]
- Bonato, A.; Messinger, M.E.; Prałat, P. Fighting constrained fires in graphs. Theor. Comput. Sci. 2012, 434, 11–22. [Google Scholar] [CrossRef][Green Version]
- Bazgan, C.; Chopin, M.; Ries, B. The firefighter problem with more than one firefighter on trees. Discret. Appl. Math. 2013, 161, 899–908. [Google Scholar] [CrossRef]
- Klein, R.; Levcopoulos, C.; Lingas, A. Approximation algorithms for the geometric firefighter and budget fence problems. In Proceedings of the Latin American Symposium on Theoretical Informatics; Springer: Berlin, Germany, 2014; pp. 261–272. [Google Scholar]
- Anshelevich, E.; Chakrabarty, D.; Hate, A.; Swamy, C. Approximability of the firefighter problem. Algorithmica 2012, 62, 520–536. [Google Scholar] [CrossRef]
- Michalak, K.; Knowles, J.D. Simheuristics for the multiobjective nondeterministic firefighter problem in a time-constrained setting. In Proceedings of the European Conference on the Applications of Evolutionary Computation; Springer: Berlin, Germany, 2016; pp. 248–265. [Google Scholar]
- Klein, R.; Levcopoulos, C.; Lingas, A. Approximation algorithms for the geometric firefighter and budget fence problems. Algorithms 2018, 11, 45. [Google Scholar] [CrossRef]
- Coupechoux, P.; Demange, M.; Ellison, D.; Jouve, B. Firefighting on trees. Theor. Comput. Sci. 2019, 794, 69–84. [Google Scholar] [CrossRef]
- Zambon, M.J.; de Rezende, P.J.; de Souza, C.C. Solving the geometric firefighter routing problem via integer programming. Eur. J. Oper. Res. 2019, 274, 1090–1101. [Google Scholar] [CrossRef]
- Farhadi, M.; Toriello, A.; Tetali, P. The Traveling Firefighter Problem. In Proceedings of the SIAM Conference on Applied and Computational Discrete Algorithms (ACDA21), Philadelphia, PA, USA, 19–21 July 2021; pp. 205–216. [Google Scholar]
- Granwal, L. Area of Bushfire Damage in Australia 2020 by Land Type. 2022. Available online: https://www.statista.com/statistics/1093799/australia-bushfire-damage-area-by-land-type/ (accessed on 14 April 2022).
- Sönnichsen, N. Acres Burned by Wildfires in the United States from 1983 to 2020. 2021. Available online: https://www.statista.com/statistics/203990/area-of-acres-burnt-due-to-wildland-fires-in-the-us/ (accessed on 14 April 2022).
- Alves, B. Number of Wildfires in Brazilian Biomes in 2021, by Type of Biome. 2022. Available online: https://www.statista.com/statistics/1044209/number-wildfires-brazil-biome/ (accessed on 14 April 2022).
- MacGillivray, G.; Wang, P. On the firefighter problem. JCMCC J. Comb. Math. Comb. Comput. 2003, 47, 57–78. [Google Scholar]
- Chlebíková, J.; Chopin, M. The firefighter problem: Further steps in understanding its complexity. Theor. Comput. Sci. 2017, 676, 42–51. [Google Scholar] [CrossRef]
- Fomin, F.V.; Heggernes, P.; van Leeuwen, E.J. The firefighter problem on graph classes. Theor. Comput. Sci. 2016, 613, 38–50. [Google Scholar] [CrossRef]
- Finbow, S.; King, A.; MacGillivray, G.; Rizzi, R. The firefighter problem for graphs of maximum degree three. Discret. Math. 2007, 307, 2094–2105. [Google Scholar] [CrossRef]
- Hartnell, B.; Li, Q. Firefighting on Trees: How Bad is the Greedy Algorithm? In Proceedings of the Thirty-First Southeastern International Conference on Combinatorics, Graph Theory and Computing. Congressus Numerantium 145, Boca Raton, FL, USA, 11 September 2000; pp. 187–192. [Google Scholar]
- Cai, L.; Verbin, E.; Yang, L. Firefighting on trees: (1- 1/e)–approximation, fixed parameter tractability and a subexponential algorithm. In Proceedings of the International Symposium on Algorithms and Computation; Springer: Berlin, Germany, 2008; pp. 258–269. [Google Scholar]
- Iwaikawa, Y.; Kamiyama, N.; Matsui, T. Improved approximation algorithms for firefighter problem on trees. IEICE Trans. Inf. Syst. 2011, 94, 196–199. [Google Scholar] [CrossRef]
- Adjiashvili, D.; Baggio, A.; Zenklusen, R. Firefighting on trees beyond integrality gaps. ACM Trans. Algorithms (TALG) 2018, 15, 1–33. [Google Scholar]
- Bazgan, C.; Chopin, M.; Cygan, M.; Fellows, M.R.; Fomin, F.V.; Van Leeuwen, E.J. Parameterized complexity of firefighting. J. Comput. Syst. Sci. 2014, 80, 1285–1297. [Google Scholar] [CrossRef]
- Bonato, A.; Janssen, J.; Roshanbin, E. Burning a graph as a model of social contagion. In Proceedings of the International Workshop on Algorithms and Models for the Web-Graph; Springer: Berlin, Germany, 2014; pp. 13–22. [Google Scholar]
- Bessy, S.; Bonato, A.; Janssen, J.; Rautenbach, D.; Roshanbin, E. Burning a graph is hard. Discret. Appl. Math. 2017, 232, 73–87. [Google Scholar] [CrossRef]
- García-Díaz, J.; Pérez-Sansalvador, J.C.; Rodríguez-Henríquez, L.M.X.; Cornejo-Acosta, J.A. Burning graphs through farthest-first traversal. IEEE Access 2022, 10, 30395–30404. [Google Scholar] [CrossRef]
- Kempe, D.; Kleinberg, J.; Tardos, É. Maximizing the spread of influence through a social network. In Proceedings of the Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 137–146. [Google Scholar]
- Banerjee, S.; Jenamani, M.; Pratihar, D.K. A survey on influence maximization in a social network. Knowl. Inf. Syst. 2020, 62, 3417–3455. [Google Scholar] [CrossRef]
- López-García, Á.O.; Rodríguez-Gómez, G.; López-López, A. A Physarum-Inspired Approach for Influence Maximization. In Proceedings of the International Conference on Metaheuristics and Nature Inspired Computing; Springer: Berlin, Germany, 2021; pp. 18–32. [Google Scholar]
- García-Díaz, J.; Rodríguez-Henríquez, L.M.X.; Pérez-Sansalvador, J.C.; Pomares-Hernández, S.E. Graph Burning: Mathematical Formulations and Optimal Solutions. Mathematics 2022, 10, 2777. [Google Scholar] [CrossRef]
- QMKPy: A Python Testbed for the Quadratic Multiple Knapsack Problem. arXiv 2022, arXiv:2211.17222.
- A two-stage algorithm for the Virtual Network Embedding problem. In Proceedings of the 2021 IEEE 46th Conference on Local Computer Networks (LCN), Edmonton, AB, Canada, 4–7 October 2021.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).