Design of Nonlinear Marine Predator Heuristics for Hammerstein Autoregressive Exogenous System Identification with Key-Term Separation

Abstract

Swarm-based metaheuristics have shown significant progress in solving different complex optimization problems, including the parameter identification of linear, as well as nonlinear, systems. Nonlinear systems are inherently stiff and difficult to optimize and, thus, require special attention to effectively estimate their parameters. This study investigates the parameter identification of an input nonlinear autoregressive exogenous (IN-ARX) model through swarm intelligence knacks of the nonlinear marine predators’ algorithm (NMPA). A detailed comparative analysis of the NMPA with other recently introduced metaheuristics, such as Aquila optimizer, prairie dog optimization, reptile search algorithm, sine cosine algorithm, and whale optimization algorithm, established the superiority of the proposed scheme in terms of accurate, robust, and convergent performances for different noise and generation variations. The statistics generated through multiple autonomous executions represent box and whisker plots, along with the Wilcoxon rank-sum test, further confirming the reliability and stability of the NMPA for parameter estimation of IN-ARX systems.

1. Introduction

Parameter estimation is widely used in various application areas, such as signal processing [1], machine learning [2], nonlinear systems [3], power [4], control [5], energy [6], system identification, energy, etc. [7]. An input nonlinear autoregressive exogenous (IN-ARX) model has been applied in different disciplines, such as multi-input multi-output (MIMO) systems [8], muscle modeling [9], data filtering [10], wireless sensor network [11], control systems [12], and electromyography [13].

Metaheuristics are applied in different engineering domains, since they treat optimization problems as a black box. Metaheuristics can be classified as evolutionary methods, human-based methods, physics-based methods, and swarm-based methods, as shown in Figure 1.

Evolutionary methods are inspired by biological processes, including reproduction, mutation, and selection in optimization. In differential evolution (DE) [14], the optimization is done by updating the solution based on mutation, crossover, and selection processes. In the genetic algorithm (GA) [15], the optimization is performed by selecting the fittest individuals for reproduction and producing offspring for the next generation. In the evolutionary mating algorithm [16], the optimization is performed by using the Hardy-Weinberg principle, crossover index, and environmental factors for solution updates in each generation. In the evolutionary algorithm [17], the optimization is done by using a parent-centric recombination operator, along with a fast population alteration model for solution updates.

Human-based methods were inspired by human problem-solving abilities for optimization. In teaching-learning optimization [18], the fitness function is optimized by stimulating a classroom environment. The optimization is divided into the teacher phase and learner phase, during which students learn from the teacher and then interact among themselves for knowledge sharing. In a heap-based optimizer [19], the optimization is performed by using corporate rank hierarchy, which depends on the interaction between subordinates and their boss, the interaction between colleagues, and the self-contribution of employees for each generation of optimization. In the human urbanization algorithm [20], the optimization is done by using multiple strategies, such as a combined search in open and limited scopes, along with the population management agent’s concentration during the search process. Forensic-based optimization [21] performs the optimization by using multiple processes used by police officers, such as investigation, location, and pursuit with fast convergence.

Physics-based methods were inspired by the laws of physics. In the gravitational search algorithm [22], optimization is done by interacting masses as search agents based on Newtonian gravity and the laws of motion. In big bang–big crunch [23], the optimization is performed in two phases, namely big bang and big crunch, respectively. In big bang, a random population is created around the center of masses in the search space, whereas, in big crunch, random particles were bought into order, creating only one mass so that both exploration and exploitation of the search space can be performed. In the circle search algorithm [24], the optimization is performed by using the geometric features of circles, such as the diameter, perimeter, and tangent lines. In the galaxy-based search algorithm [25], the optimization is done by using two modules, namely spiral chaotic move and local search. The spiral chaotic move performs the exploration, whereas the local search performs the exploitation.

Swarm-based methods were inspired by the behavior of swarms in nature. In particle swarm optimization (PSO) [26], the optimization is performed by constituting a swarm of particles around a search space for finding the local best and global best solutions. In the marine predator algorithm [27], the optimization is based on Levy and Brownian movements when encountering predator and prey. In a monkey search [28], the optimization is done by updating the solution on the basic food-searching process used by monkeys when climbing trees. With the ant lion optimizer [29], the optimization is performed by using hunting steps such as the random walk of ants, building traps, the entrapment of ants in traps, catching prey, and rebuilding traps.

Various techniques have been used in the literature for the identification of IN-ARX models. In [30], particle swarm optimization was applied for the identification of fractional nonlinear ARX models over several variations of generations and noise levels. In [31], a least mean support vector machine-based method was applied for the prediction of Hammerstein ARX through subspace-state space representation. In [32], a fractional hierarchical gradient descent method was applied for the identification of the nonlinear ARX model on several fractional order and noise conditions. In [33], genetic algorithms were applied for the identification of fractional Hammerstein ARX models in both noiseless and noisy conditions. In [34], fractional order particle swarm optimization, along with key term separation, were proposed. In [35], genetic algorithms and the key term separation principle were used for nonlinear Hammerstein ARX model identification. In [36], the marine predator algorithm was used for the identification of the nonlinear Hammerstein ARX model with key term separation.

Even though various metaheuristics were proposed and applied to different optimization problems, there is no single method that can solve all problems [37]. This leads researchers to develop new or improve existing metaheuristics for different real-world optimization problems [38]. Among the different approaches, swarm-based metaheuristics have been applied in various applications of parameter estimation, which are solar cells [39], electric vehicles [40], image processing [41], machine learning [42], multiple input multiple output systems [43], ARX estimation [44], economic dispatch [45], temperature processing plants [46], and nonlinear system identification [36].

The marine predator algorithm (MPA) was proposed in 2020 [27] and received an overwhelming response from the research community, with applications to solve a variety of optimization problems that arise in engineering, science, and technology, such as parameter estimation of photovoltaic modules [47], COVID-19 forecasting [48], heartbeats classification [49], optimal power allocation [50], human activity recognition [51], the control of hybrid power systems [52], etc. The nonlinear marine predator algorithm (NMPA) is an improved variant of the standard MPA proposed in 2022 [53] that effectively incorporates exploration and exploitation dynamics through an improved transition from a global search to a local search. The NMPA uses a set of nonlinear functions to change the search patterns of MPA. The superiority of the NMPA is well established in [53] over recent state-of-the-art counterparts, including the conventional MPA for a variety of benchmark functions, as well as real applications, such as fair power allocation in multiple access systems and Beyond 5G networks. Thus, accordingly, the research community has an opportunity to implement the stupendous knacks of the NMPA with expected outcomes better than the MPA and counterparts in stiff nonlinear optimization problems. These are the motivating factors for the authors to exploit the NMPA for the effective parameter estimation of nonlinear systems.

In the current study, the NMPA is investigated for the parameter estimation of IN-ARX models. The investigation is conducted on various noise levels, populations, and generations. Statistical comparisons of the NMPA with several methods were also conducted to establish robustness and reliability.

In Section 2, the mathematical model of IN-ARX is given. Section 3 provides the details of the NMPA scheme. The simulation results, along with the comparison of the NMPA with recent counterparts, are presented in Section 4, while the concluding remarks are given in Section 5.

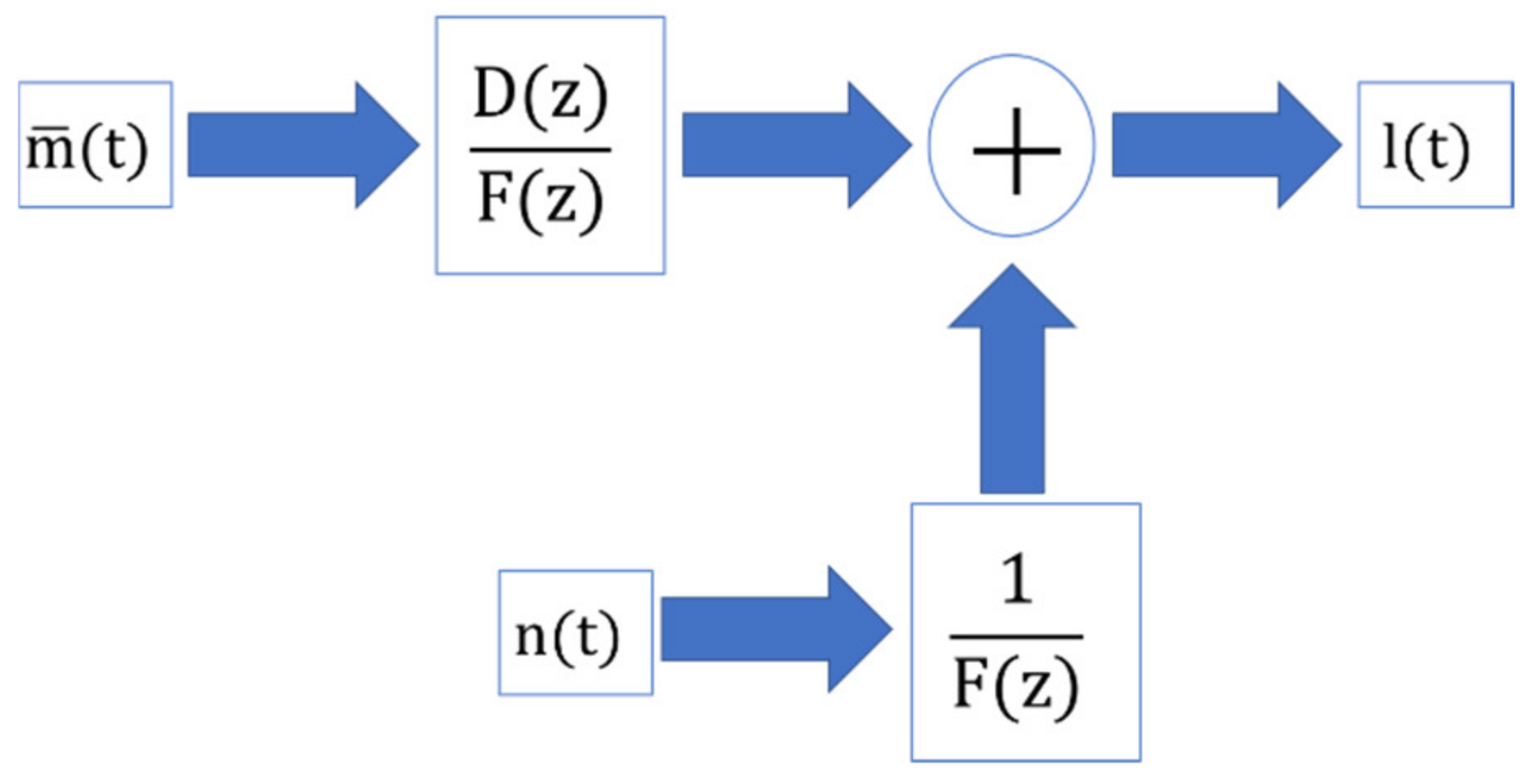
2. Input Nonlinear Autoregressive Exogenous Model Definition

The input nonlinear autoregressive exogenous (IN-ARX) model is a block-oriented structure in which there are two blocks: the first block is nonlinear, followed by a linear subsystem. In IN-ARX, normally, the nonlinear block is described by a polynomial-type nonlinearity, and the linear subsystem is characterized by a simple ARX structure. The IN-ARX is used to model different engineering problems arising in communication, signal processing, control systems, and biomedical sciences [8,9,10,11,12,13]. Figure 1 shows the block diagram representation of the IN-ARX model, while its mathematical representation is given in Equation (1)

$$l(t)=\frac{D(z)}{F(z)}\overline{m}(t)+\frac{1}{F(z)}n(t),$$

(1)

Simplify Equation (1) as given in Equation (2):

$$l(t)=(1-F(z))l(t)+D(z)\overline{m}(t)+n(t),$$

(2)

where $n(t)$ represents noise, and $m(t)/l(t)$ shows the input/output. $D(z)$, $F(z)$, and $\overline{m}(t)$ are defined in Equations (3)–(5), respectively.

$$D(z)=d_0+d_1{z}^{-1}+d_2{z}^{-2}+,\dots ,+d_{i_d}{z}^{-i_d}$$

(3)

$$F(z)=1+f_1{z}^{-1}+f_2{z}^{-2}+,\dots ,+f_{i_f}{z}^{-i_f}$$

(4)

$$\overline{m}(t)=b_1{h}_1[m(t)]+b_2{h}_2[m(t)]+,\dots ,+b_i{h}_i[m(t)].$$

(5)

Simplifying Equation (2) by incorporating Equations (3)–(5) and applying the key term separation technique by choosing $\overline{m}(t)$ as the key term with $d_0=1$ is given in Equation (6)

$$\begin{array}{c}l(t)=-{\displaystyle \sum _{k=1}^{i_f}{f}_k[l(t-k)]}+{\displaystyle \sum _{k=0}^{i_d}{d}_k\overline{m}(t-k)}\hfill \\ \hspace{1em}=-{\displaystyle \sum _{k=1}^{i_f}{f}_k[l(t-k)]}+d_0[\overline{m}(t)]+{\displaystyle \sum _{k=1}^{i_d}{d}_k\overline{m}(t-k)}+n(t)\hfill \\ \hspace{1em}=-{\displaystyle \sum _{k=1}^{i_f}{f}_k[l(t-k)]}+{\displaystyle \sum _{k=1}^{i_d}{d}_k[\overline{m}(t-k)}]+{\displaystyle \sum _{k=1}^p{b}_k{h}_k[m(t)]}+n(t)\hfill \end{array}.$$

(6)

The information/parameter vectors are expressed in Equations (7)–(9) and Equations (10)–(12), respectively

$${\gamma }_f(t)={[-l(t-1),-l(t-2),\dots ,-l(t-i_f)]}^T\in R^{i_f},$$

(7)

$${\gamma }_d(t)={[\overline{m}(t-1),\overline{m}(t-2),\dots ,\overline{m}(t-i_d)]}^T\in R^{i_d},$$

(8)

$$h(t)=h_1[m(t)],h_2[m(t)],\dots ,h_p{[m(t)]}^T\in R^p,$$

(9)

$$f={[f_1,f_2,\dots ,f_{i_f}]}^T\in R^{i_f},$$

(10)

$$d={[d_1,d_2,\dots ,d_{i_f}]}^T\in R^{i_d},$$

(11)

$$b={[b_1,b_2,\dots ,b_p]}^T\in R^p.$$

(12)

Using Equations (7)–(12) in Equation (6) represents the key term separation identification approach for the IN-ARX model, as given in Equation (13)

$$l(t)={\gamma }_f^T(t)f+{\gamma }_d^T(t)d+h^T(t)b+n(t).$$

(13)

3. Proposed Methodology

In this section, the parameter estimations of the IN-ARX model when using the nonlinear marine predator algorithm (NMPA) [47] are provided.

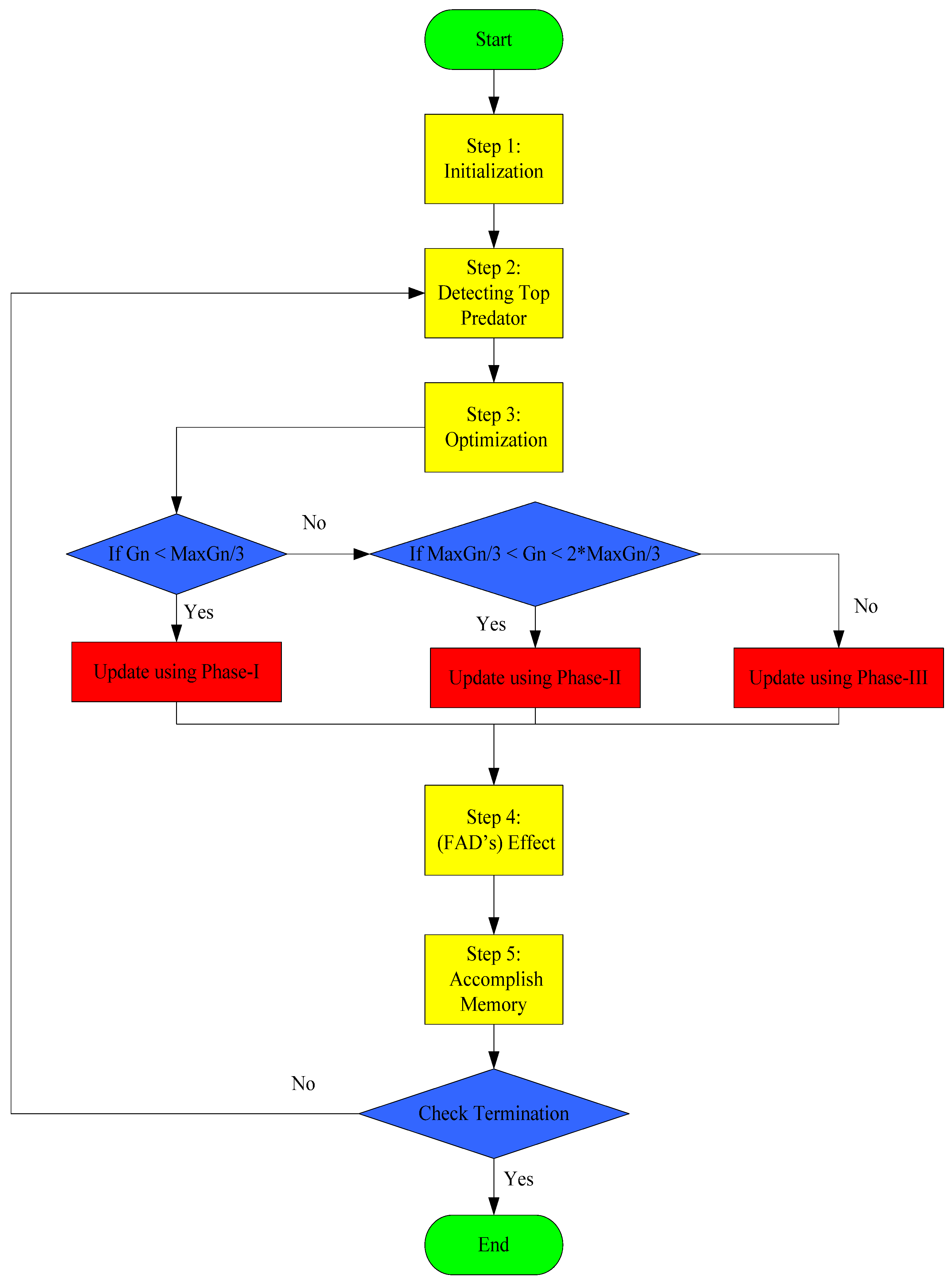
3.1. Nonlinear Marine Predator Algorithm

The NMPA is inspired by the performance of marine predators such as sharks, sunfish, and tunas to catch prey in oceans by using Brownian movements and Levy flight walk. Its mathematical steps are as follows.

3.1.1. Step 1: Initialization

In this step, the population is initialized over uniformly distributed search space, as given in Equation (14):

$$K_i=K_i^{\min }+\mathrm{rand}\times (K_i^{\max }-K_i^{\min })$$

(14)

where $K_i^{\max }$ and $K_i^{\min }$ are the maximum and minimum boundary values, respectively.

3.1.2. Step 2: Detecting Top Predator

The populations are arranged by constructing the Prey matrix ($P_m$) and Elite matrix ($E_m$). These matrices consist of random positions during step 1 and position vectors with the best fitness, as given in Equations (15) and (16):

$$P_m={\left(\begin{array}{ccc}{K}_{1,1}& \dots & K_{1,a}\\ ⋮& \ddots & ⋮\\ K_{Pn,1}& \cdots & K_{Pn,a}\end{array}\right)}_{P_n\times a}$$

(15)

$$E_m={\left(\begin{array}{ccc}{K}_{1,1}^I& \dots & K_{1,a}^I\\ ⋮& \ddots & ⋮\\ K_{Pn,1}^I& \cdots & K_{Pn,a}^I\end{array}\right)}_{P_n\times a}$$

(16)

where ${\overrightarrow{K}}^I$ represents the top predator vector.

3.1.3. Step 3: Brownian Movements and Levy Flight-Based Optimization

In this step, the optimization is done by considering different velocity ratios. It involves three phases, as given below.

Phase I

This phase involves an exploration at a high-velocity ratio by expanding the Brownian movement for one-third of the generations (Gn). The updated matrices are given in Equations (17) and (18):

$${\overrightarrow{SB}}_j={\overrightarrow{R}}_B\otimes (\overrightarrow{E_{m_j}}-(\overrightarrow{R_B}\otimes \overrightarrow{P_{m_j}})),j=1,2,\dots ,P_n$$

(17)

$$\overrightarrow{P_{m_i}}=\overrightarrow{P_{m_i}}+(E.\overrightarrow{B}\otimes \overrightarrow{S{B}_j})$$

(18)

where $R_B$ is a normal distributed vector, and $B$ is vector $\in [0.1]$.

Phase II

This phase involves both exploration and exploitation at a unit velocity ratio between 1/3 and 2/3 of the maximum generations (MaxGn). The updated matrices are given in Equations (19)–(22):

$${\overrightarrow{SB}}_j={\overrightarrow{R}}_L\otimes (\overrightarrow{E_{m_j}}-({\overrightarrow{R}}_L\otimes \overrightarrow{P_{m_j}})),j=1,2,\dots ,\frac{P_n}{2}$$

(19)

$$\overrightarrow{P_{m_i}}=\notin *\overrightarrow{P_{m_i}}+(E.\overrightarrow{B}\otimes \overrightarrow{S{B}_j})$$

(20)

where $\notin =2*\exp \left(-{\left(6*\frac{Gn}{MaxGn}\right)}^2\right)$ is a nonlinear parameter to balance the exploration and exploitation of the NMPA.

$${\overrightarrow{SB}}_j={\overrightarrow{R}}_B\otimes ({\overrightarrow{R}}_B\otimes (\overrightarrow{E_{m_j}}-\overrightarrow{P_{m_j}})),j=\frac{P_n}{2},\dots ,P_n$$

(21)

$$\overrightarrow{P_{m_i}}=\notin *\overrightarrow{E_{m_i}}+(E.A{F}_{new}\otimes \overrightarrow{S{B}_j})$$

(22)

where $A{F}_{new}=abs\left(2*\left(1-\frac{Gn}{MaxGn}\right)-2\right)$ is an adaptive factor for controlling predator movement step size increases linearly over interval $[0.2]$.

Phase III

This phase involves exploitation at a low-velocity ratio for the remaining generation (Gn). The updated matrices are given in Equations (23) and (24).

$${\overrightarrow{SB}}_j={\overrightarrow{R}}_L\otimes ({\overrightarrow{R}}_L\otimes (\overrightarrow{E_{m_j}}-\overrightarrow{P_{m_j}})),j=1,2,\dots ,P_n$$

(23)

$$\overrightarrow{P_{m_i}}=\overrightarrow{E_{m_i}}+(E.A{F}_{new}\otimes \overrightarrow{S{B}_j})$$

(24)

3.1.4. Step 4: Fish Aggregating Device (FAD) Effects

In this step, FAD effects are incorporated, as presented in Equations (25) and (26).

$$\overrightarrow{P_{m_j}}=\overrightarrow{P_{m_j}}+A{F}_{new}[K_{\min }+\overrightarrow{B}\otimes (K_{\max }-K_{\min })]\otimes \overrightarrow{U},\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\hspace{1em}s\le FAD’s$$

(25)

$$\overrightarrow{P_{m_j}}=\overrightarrow{P_{m_i}}+[FAD’s(1-s)+s(\overrightarrow{P_{m_{s1}}}-\overrightarrow{P_{m_{s2}}}),\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\hspace{1em}s\le FAD’s$$

(26)

where $\overrightarrow{U}$ is the binary vector, $s$ is a random number $\in [0,1]$, and $s_1$ and $s_2$ are subscripts of $\overrightarrow{P_m}$.

3.1.5. Step 5: Marine Memory

In this step, based on the performances of steps 1–4, the updated solution is compared with the previous solution.

The flowchart is shown in Figure 2.

The pseudo-code is given in Algorithm 1

Algorithm 1: Pseudo-code of NMPA

Initialize Population ($P_n$) by using (14). while check termination criteria Calculate Fitness value and construct matrices ($P_m$) and ($E_m$) by using (15) and (16). if $Gn<\frac{MaxGn}{3}$ Update by using (17) and (18). else if $\frac{MaxGn}{3}<Gn<\frac{2*MaxGn}{3}$ Update by using Equations (19) and (20) for first half. Update by using Equations (21) and (22) for other half. else if $Gn>\frac{2*MaxGn}{3}$ Update by using Equations (23) and (24). end Update by using Equations (25) and (26). Accomplish memory saving and update. end

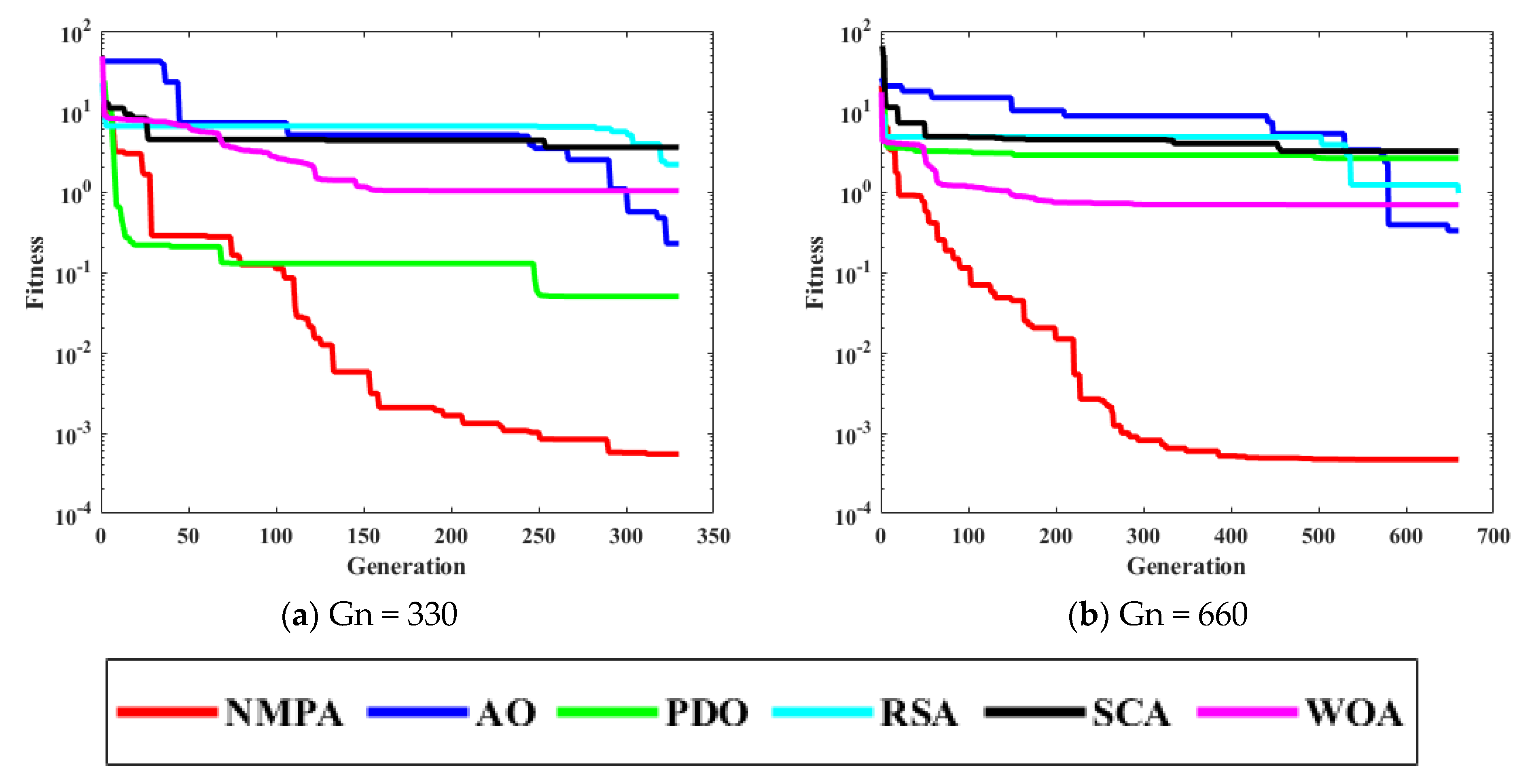
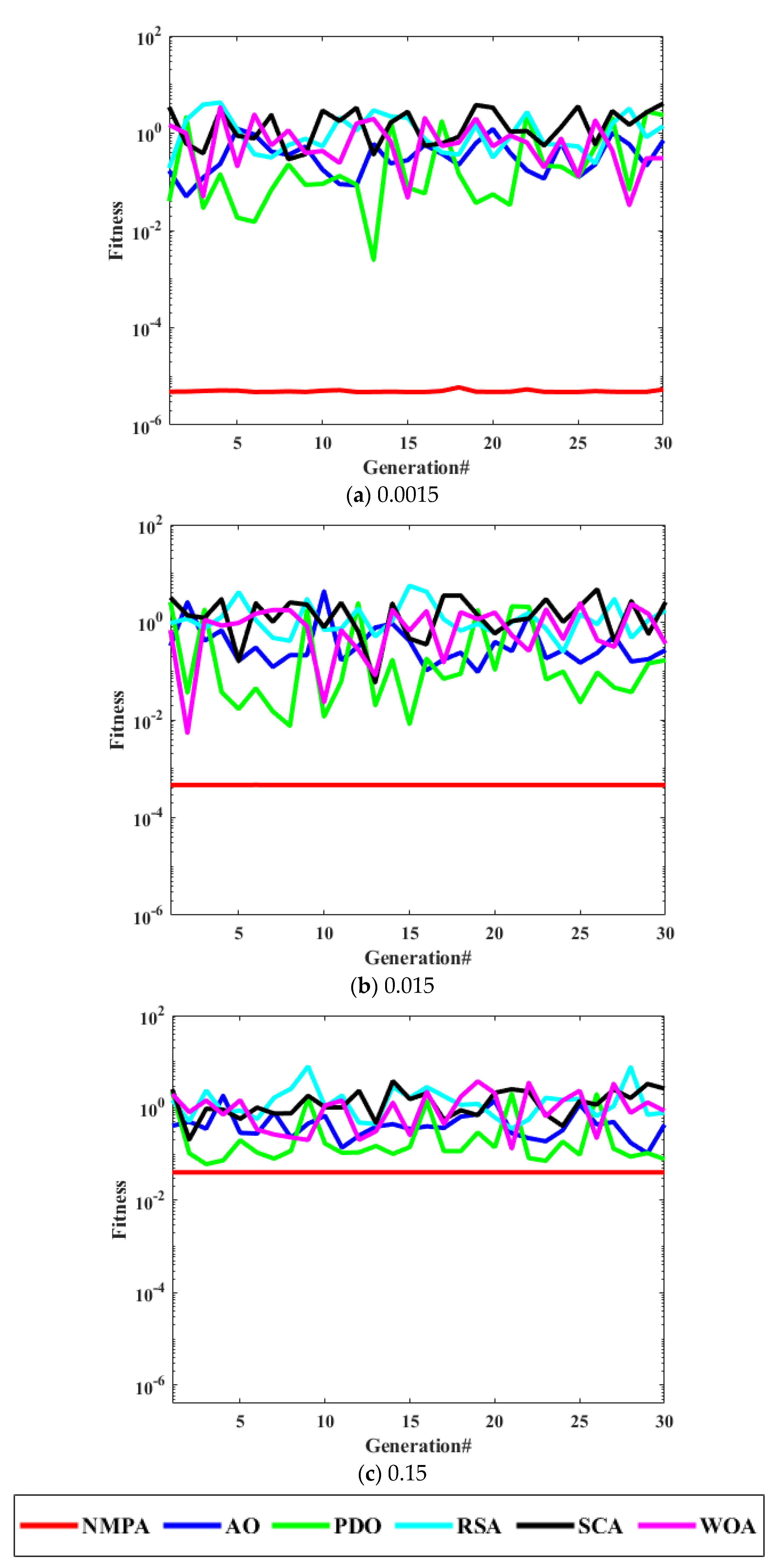
4. Performance Analysis

The simulation is performed using an Intel Core i5 system with 16 GB memory. The analysis is carried out on various generations (Gn), populations (Pn), and noise levels n(t) and is evaluated through fitness, calculated by Equation (27)

$$Fitness=\frac{1}{K}{\displaystyle \sum _{\tau =1}^K{[l(t_{\tau })-\tilde{l}(t_{\tau })]}^2},$$

(27)

where $l$/$\tilde{l}$ are the desired/approximated responses, and the IN-ARX approximated output is calculated by Equation (28)

$$l(t)={\gamma }_f^T(t)\tilde{f}+{\gamma }_d^T(t)\tilde{d}+h^T(t)\tilde{b}+n(t).$$

(28)

The estimated parameter vectors using the NMPA are given in Equations (29)–(31)

$$\tilde{f}={[{\tilde{f}}_1,{\tilde{f}}_2,\dots ,{\tilde{f}}_{i_f}]}^T\in R^{i_f},$$

(29)

$$\tilde{d}={[{\tilde{d}}_1,{\tilde{d}}_2,\dots ,{\tilde{d}}_{i_d}]}^T\in R^{i_d},$$

(30)

$$\tilde{b}={[{\tilde{b}}_1,{\tilde{b}}_2,\dots ,{\tilde{b}}_p]}^T\in R^p,$$

(31)

The objective is to minimize Equation (27) by using the NMPA. The desired parameter vectors taken from the recently reported literature [54] are given in Equations (32)–(35)

$$f={[f_1,f_2]}^T={[-0.8000,0.9000]}^T,$$

(32)

$$d={[d_1,d_2]}^T={[1.1000,0.6800]}^T,$$

(33)

$$b={[b_1,b_2,b_3]}^T={[0.9000,1.3000,-0.5000]}^T,$$

(34)

$$\tau ={[f_1,f_2,d_1,d_2,b_1,b_2,b_3]}^T={[-0.8000,0.9000,1.1000,0.68000,0.9000,1.3000,-0.5000]}^T.$$

(35)

The n(t) is the normal distributed noise with levels [0.0015, 0.015, 0.15]. The behavior of the NMPA is assessed based on the generations (Gn) [330, 660] and population (Pn = 45). The fitness curves are shown in Figure 3.

Figure 3a shows the convergence of the NMPA for all noise variances [0.0015, 0.015, 0.15] at Gn = 330, whereas Figure 3b shows convergence at Gn = 660. It can be observed from Figure 3a,b that, with the increasing Gn, the fitness decreases significantly. Moreover, at a low noise level [0.0015], the fitness of the NMPA is the minimum, whereas, for higher levels [0.015, 0.15], the fitness also increases.

The metaheuristics for the comparative study of the NMPA are selected after an exhaustive survey of the literature regarding the recently introduced metaheuristics. The NMPA is an improved variant of the conventional MPA, with established supremacy over various state-of-the-art counterparts, such as Differential Evolution (DE), Particle Swarm Optimization (PSO), Multi-Verse Optimization (MVO), Moth Flame Optimization (MFO), Grey Wolf Optimizer (GWO), Salp Swarm Algorithm (SSA), and the original marine predator algorithm (MPA) [53]. Therefore, in order to avoid redundancy and performing repeated investigations or experimentations, we selected ones other than these recently introduced metaheuristics. Thus, the performance of the NMPA is further investigated in comparison with other metaheuristics, which are Aquila optimizer (AO) [55], prairie dog optimization (PDO) [56], the reptile search algorithm (RSA) [57], sine cosine approach (SCA) [58], and whale optimization approach (WOA) [59], for the Gn = [330, 660] and noise levels [0.0015, 0.015, 0.15] for 30 independent runs.

AO is a population search-based metaheuristic motivated by Aquila’s strength to catch the prey. The optimization is divided into four steps. Two of them are used in exploration, while the remaining two are used in exploitation. It is applied in various optimization problems and applications of different domains. PDO is another population-based metaheuristic inspired by the natural habitat behavior of prairie dogs. The optimization involves exploration and exploitation based on foraging, borrowing, and communication. RSA is another population search-based heuristic motivated by hunting behavior of reptiles. The optimization is accomplished by using encircling and hunting during the exploration and exploitation phases. SCA is another population-based metaheuristic inspired by trigonometric functions used in mathematics. The exploration and exploitation of the search space are achieved by using adaptive random variables based on the sine and cosine functions. WOA is also a population-based metaheuristic inspired by the social behavior of hump whales. The exploration and exploitation of search spaces are performed by incorporating the bubble net hunting strategy in the optimization process.

Figure 4 shows the convergence curves of AO, PDO, RSA, and SCA for different scenarios of parameter tuning. The tuning is performed at Gn = 660, Pn = 45, and noise variance 0.0015 for ten independent runs. It is observed from Figure 4a that AO achieves the lowest fitness at alpha = 0.1 and delta = 0.1. Similarly, in Figure 4b–d, PDO, RSA, and SCA achieve the lowest fitness at rho = 0.005, alpha = 0.1, beta = 0.1, and a = 2, respectively.

The parameter settings of these metaheuristics are summarized in

Table 1. Parameter settings of the metaheuristics.

Metaheuristics	Parameter Values
NMPA	FAD = 0.2, $\mathrm{E}=0.5$
AO	alpha = 0.1, delta = 0.1
PDO	rho = 0.005
RSA	alpha = 0.1, beta = 0.1
SCA	a = 2
WOA [60]	a = [2 0]

.

Table 2. Estimated weights w.r.t generations (Gn) at the 0.0015 noise level.

Metaheuristics	Gn	Design Parameters							Best Fitness
		${\mathbf{f}}_1$	${\mathbf{f}}_2$	${\mathbf{d}}_1$	${\mathbf{d}}_2$	${\mathbf{b}}_1$	${\mathbf{b}}_2$	${\mathbf{b}}_3$
AO	330	−0.8192	0.9368	0.9891	0.4064	0.7439	1.6007	−0.2351	0.2012
	660	−0.7755	0.9014	1.5770	1.1252	0.4183	0.4834	−0.8811	0.0499
PDO	330	−0.8050	0.8939	1.6015	0.8107	0.3455	0.5423	−0.7053	0.0208
	660	−0.7903	0.8978	1.3308	0.8973	0.4988	0.7399	−0.7047	0.0024
RSA	330	−0.7326	0.8385	1.2840	1.7105	1.2003	0.8957	−0.9871	0.7066
	660	−0.7421	0.8642	1.1130	0.9510	0.8684	1.1687	−0.5634	0.1912
SCA	330	−0.7186	0.8537	0.9150	0.6195	1.0084	2.0000	0.0005	0.5935
	660	−0.7648	0.9200	1.7525	2.0000	−0.2438	−0.2213	−1.2119	0.2915
WOA	330	−0.8466	0.9521	0.9878	0.6570	0.6783	1.1143	−0.6393	0.1901
	660	−0.7862	0.9048	0.8771	0.6877	1.3408	1.8431	−0.3522	0.0331
NMPA	330	−0.7997	0.8997	1.1284	0.6982	0.8521	1.2310	−0.5231	2.4132 × 10−5
	660	−0.8000	0.8999	1.1067	0.6837	0.8861	1.2821	−0.5052	4.7671 × 10−6
Actual Values		−0.8000	0.9000	1.1000	0.6800	0.9000	1.3000	−0.5000	0

,

Table 3. Estimated weights w.r.t generations (Gn) at the 0.015 noise level.

Metaheuristics	Gn	Design Parameters							Best Fitness
		${\mathbf{f}}_1$	${\mathbf{f}}_2$	${\mathbf{d}}_1$	${\mathbf{d}}_2$	${\mathbf{b}}_1$	${\mathbf{b}}_2$	${\mathbf{b}}_3$
AO	330	−0.7942	0.8775	1.1663	0.7680	0.6776	0.9902	−0.6280	0.0561
	660	−0.7945	0.9099	1.5233	1.0325	0.0691	0.3455	−0.7981	0.0955
PDO	330	−0.7894	0.8941	1.4523	0.9153	0.4378	0.6399	−0.7182	0.0038
	660	−0.7959	0.8993	1.0815	0.7327	0.8041	1.2129	−0.5317	0.0075
RSA	330	−0.7220	0.9108	1.1243	1.0110	0.5696	1.0461	−0.5176	0.4078
	660	−0.7712	0.8883	1.0020	0.9802	0.8040	1.0051	−0.7028	0.2483
SCA	330	−0.7997	0.9340	1.8997	1.4184	−0.1877	−0.0817	−0.9527	0.2136
	660	−0.8026	0.8870	2.0000	1.2379	0.0353	0.0226	−0.9581	0.0586
WOA	330	−0.8374	0.8853	1.0703	0.2489	1.0443	1.9562	0.0293	0.2150
	660	−0.7864	0.8912	1.8573	1.1397	0.0551	0.1463	−0.8773	0.0053
NMPA	330	−0.8002	0.8988	1.1805	0.7246	0.7452	1.1017	−0.5584	4.7301 × 10−4
	660	−0.8003	0.8989	1.1751	0.7222	0.7556	1.1140	−0.5547	4.6813 × 10−4
Actual Values		−0.8000	0.9000	1.1000	0.6800	0.9000	1.3000	−0.5000	0

and

Table 4. Estimated weights w.r.t generations (Gn) at the 0.15 noise level.

Metaheuristics	Gn	Design Parameters							Best Fitness
		${\mathbf{f}}_1$	${\mathbf{f}}_2$	${\mathbf{d}}_1$	${\mathbf{d}}_2$	${\mathbf{b}}_1$	${\mathbf{b}}_2$	${\mathbf{b}}_3$
AO	330	−0.7755	0.8891	1.9109	1.8204	−0.1287	−0.1344	−1.0075	0.1621
	660	−0.8177	0.9021	1.0589	0.6413	1.1741	1.5627	−0.4029	0.1044
PDO	330	−0.8193	0.9085	0.9650	0.6171	1.0302	1.5850	−0.3628	0.0663
	660	−0.8218	0.8972	1.0634	0.5911	0.8280	1.3622	−0.3971	0.0608
RSA	330	−0.7640	0.9009	1.0093	0.9475	0.7496	1.2128	−0.5217	0.2810
	660	−0.7809	0.9042	0.9844	0.9097	0.5374	0.8729	−0.7874	0.3593
SCA	330	−0.7719	0.9252	1.5129	1.7924	0.0006	−0.0261	−1.1125	0.4162
	660	−0.7868	0.9022	1.6056	1.1461	−0.2537	0.0269	−0.8898	0.2069
WOA	330	−0.7691	0.9067	1.0330	1.1504	1.0278	1.1263	−0.7600	0.3160
	660	−0.8086	0.9049	0.9453	0.6698	0.7969	1.4578	−0.3311	0.1322
NMPA	330	−0.8033	0.8948	1.9997	1.1901	−0.1187	−0.0161	−0.8832	0.0405
	660	−0.8035	0.8943	2.0000	1.1789	−0.1210	−0.0139	−0.8781	0.0405
Actual Values		−0.8000	0.9000	1.1000	0.6800	0.9000	1.3000	−0.5000	0

display the presentation of all metaheuristics for the best fitness and the estimated parameters corresponding to the best fitness for the noise = [0.0015, 0.015, 0.15] scenarios. It is also seen that, for the low-noise scenario, i.e., 0.0015, the results of the NMPA are better when compared to relatively high-noise scenarios. Moreover, at the 0.0015 noise level, the estimated weights are more accurate. It is also distinguishable from Table 2, Table 3 and Table 4 that the best values of fitness for the 0.0015, 0.015, and 0.15 noise scenarios are $4.7\times {10}^{-6}$, $4.6\times {10}^{-4}$, and 0.0405, respectively. Thus, Table 2, Table 3 and Table 4 confirm that the NMPA fitness degrades a little bit for high-noise scenarios and improves by increasing generations.

Figure 5, Figure 6 and Figure 7 validate the convergence of the NMPA with AO, PDO, RSA SCA, and WOA for all noise levels. Figure 5a,b show the convergence for Gn = [330,660] for 0.0015 noise, whereas Figure 6a,b show convergence for 0.015 noise, and Figure 7a,b show convergence for the 0.15 noise level. It is distinguishable from Figure 5, Figure 6 and Figure 7 that, upon an increase in the noise levels, the fitness rises. Still, the NMPA attains the lowermost fitness compared to AO, PDO RSA, SCA, and WOA for all variations.

The statistical investigation of the NMPA against AO, PDO, RSA, SCA, and WOA at Pn = 45 and Gn = 660 for 30 autonomous executions is shown in Figure 8. It is distinguishable from Figure 8a–c that the fitness of the NMPA is lowest in comparison with AO, PDO, RSA, SCA, and WOA for all independent executions. Moreover, it is also confirmed that, upon an increase in the noise levels, the fitness rises for all metaheuristics.

The performance of the NMPA is explored and compared to AO, PDO, SCA, RSA, and WOA and the average fitness plots for all variations of Gn, Pn, and the noise levels, as shown in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. It is confirmed from Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 that the NMPA achieves the lowest fitness for all variations against other metaheuristics.

Figure 14 displays a boxplot analysis of the NMPA with AO, PDO, RSA, SCA, and WOA in terms of the average fitness for all variations. It is confirmed in Figure 14 that the NMPA achieves the lowest median and lowest first and third quartiles in comparison with the other metaheuristics.

The Wilcoxon rank sum test [61] is applied to the average fitness values of the NMPA vs. AO, NMPA vs. PDO, NMPA vs. RSA, NMPA vs. SCA, and NMPA vs. WOA. The performance values of expectation, std error, stat, and p-value are 39, 8.831, 2.038, and 0.020, respectively. These values indicate the efficacy of the NMPA against AO, PDO, RSA, SCA, and WOA.

5. Conclusions

The current study investigates the parameter estimation of nonlinear systems represented through the Hammerstein structure using the global search strength of recent novel metaheuristics. The parameters of the input nonlinear autoregressive exogenous IN-ARX model are estimated by exploiting the swarm intelligence of the nonlinear marine predators’ algorithm, the NMPA. The NMPA accurately estimates the parameters of the IN-ARX system and the detailed comparative analysis of the NMPA with other recently introduced metaheuristics, such as the Aquila optimizer, prairie dog optimization, reptile search algorithm, sine cosine algorithm, and whale optimization algorithm, demonstrating the effectiveness of the NMPA for different noise and generation variations. The statistical analyses were based on multiple autonomous executions of the scheme represented with box and whisker plots, and the Wilcoxon rank sum test further established the stable and reliable performance of the NMPA for the parameter estimations of IN-ARX systems. The promising results for nonlinear system identification reflect the potential of the NMPA to effectively solve other parameter estimation problems of complex engineering systems.