Optimal Elliptic-Curve Subspaces for Applications in Double-Authenticated Requests in Mobile Distributed Data Mining

Abstract

Mathematical models based on elliptic curves have been intensively studied since their applicability in data security systems was discovered. In this article, the authors describe the optimal way to select particular subspaces over which elliptic curves are defined, showing the applicability of these subspaces in secure data transfer. Access to large databases and analyses of the requests made to these databases are required daily by a variety of users, including legal entities. An attack on these communication systems causes violations in privacy and damage to/theft of data that can be worth EUR tens of billions annually. For requests made between computers, encryption methods can be used as these systems have adequate computing power and energy. For requests made from fixed and mobile systems, if the data are distributed heterogeneously, the computing power required to authenticate both the users and the answering entities determines the efficiency of the proposed solution. To address this limitation, our study proposes a double-authentication method based on particular elliptic-curve systems.

1. Introduction

In order to ensure the confidentiality of a request querying a complex database, techniques to authenticate the initiator and the answering entity and to encrypt the communication channel have been developed. Authentication based on the RSA-type digital signature—the Rivest, Shamir, and Adleman-based algorithm—was initially used ([1]). However, the power required to compute the parameters involved in this process increased with an increase in the length of the encryption keys. For a fixed computing system (computers and servers), the required power is provided by the involved entities; therefore, in the event that a request is made from and to a fixed computing system, the required computing power for the authentication protocols and for the communication encryption is provided by the query requester(s) and by the systems that store these distributed databases. In contrast, for mobile systems, energy consumption becomes an essential limiting factor; to address this limitation, we adopted elliptic-curve cryptography (ECC) as the solution for processes that require user authentication (as in [2], or quantum type on [3]). In the particular case of querying complex databases consisting of structures that are stored on several heterogeneous systems, as well as on physical structures and software, existing studies have proposed implementable solutions for each subcategory of case studies. In this sense, new solutions or their optimizations have continuously been illustrated, and the vulnerabilities of existing solutions have been highlighted. For the queries mentioned above, in situations in which an intelligent answer is necessary, only data mining ($DM$) techniques can be used. These intelligent answers are answers that actually provide an analysis of complex databases and algorithms and highlight certain aspects in their conclusions. More precisely, for situations where databases are heterogeneous complexes (that is, of different types and sizes), the data are stored heterogeneously (that is, on several types of computing systems, which can be personal computers, high-power computers, servers, and even mobile systems); we call these systems heterogeneous database systems ($HDBSs$). For HDBSs, an analysis does not yield only an individual answer—for example, finding not only some records that meet certain conditions but also some items with certain properties that are correlated with other items—and can provide a conclusion based on the correlation of several analyses comparing several databases. In situations where a query would be made from a mobile system to an $HDBS$-type system, the use of an algorithm from the RSA–C category would require a computing power that consumes more energy than is available.

The solution proposed by the authors comes from their experience and expertise gained from research projects and government contracts. The proposed method addresses the case where a query, which involves $DM$, needs to be made from a mobile system with an $HDBS$-type structure. A variant of this method was implemented in a functional system and used within an institutional entity.

2. Existing Solutions for Related Problems

In this section, we briefly describe the existing solutions for problems related to authentication models between systems that involve multiple authentications. The difference between cases solved by other solutions and the case treated by our proposed solution is also described.

Starting from the basic advantage of ECC-type communication security systems, solutions that implement authentication models have been developed, such as the one in [4,5]; communication confidentiality systems, such as those developed in [6,7,8]; and analysis models of their limits, also described in [9,10,11,12]. These models are based on an essential property of ECC systems, namely, the size difference of the cryptographic credentials used in the systems based on elliptic curves, compared with those of systems based on RSA-type models and their variants. This translates into the number of calculations required to create the cryptographic primitives as well as the transformation from plain text to encrypted text for messages that need to be protected against attacks in order to be transmitted on public communication channels.

Numerous studies on authentication and secure communication have been carried out, and more are underway, both within university research laboratories and within the research and development departments of large companies, to provide solutions regarding particular mathematical models that address concrete problems in applications of secure communication in the case of heterogeneous systems. The key models used can be classified into three categories, depending on the type of devices in which they are implemented:

1

Systems that are implemented for authentication and secured communications, in which the involved devices in the communication process are classified as servers and computers. In these cases, mathematical models and algorithms of the type described in [13,14] can be used. Particular variants of these solutions were implemented for this kind of model, by the authors, in such cases. For these models, the computing power required to compute the parameters involved in obtaining the cryptographic credentials can be assured by the devices in which they are implemented.

In the case studied by the authors, one of the restrictions is related to the computing power available for use in the process generating cryptographic credentials. Therefore, both the mathematical model used and the implemented algorithmic model must take this aspect into account.

2

Smart mobile system interconnections, in which unitary models are implemented to secure the communications. For this case, the computation of cryptographic credentials is ensured by a centralized system, and the mobile device uses the cryptographic primitives provided by a trusted party that manages the solution in a centralized way. Then, the mobile device has to use these parameters. Such models are described in [15,16]. The solution from [15] was proposed by a team that included one of the authors from the present study. This solution was implemented and is still being used.

In our studied case, the system is heterogeneous both from the point of view of the devices that are involved in the communication process and from the point of view of the security model for each of the groups of devices, with a solution being proposed for the case where the authentication will be carried out based on the parameters computed also by the mobile systems, with these devices generating their own cryptographic primitives.

3

Security models in which mobile devices are involved in the correlation with fixed systems, included in $SOTA$ (Secure Online Transaction Algorithm)-type models. In these cases, three parties are involved: consumer, retailer, and financial credit company. Solutions in this sense can be studied in [17].

The solution proposed by the authors is for the case where the volume of data transmitted is much higher than that in the case described above and where it is necessary to reduce the risk of malicious users, which in the above case does not need to be treated.

3. Description of The Parameters from Our Proposed Solution

This section describes the elements that define the treated case, the limitations imposed by the problem that needs to be solved, and the method of hierarchization for all the entities of the treated system.

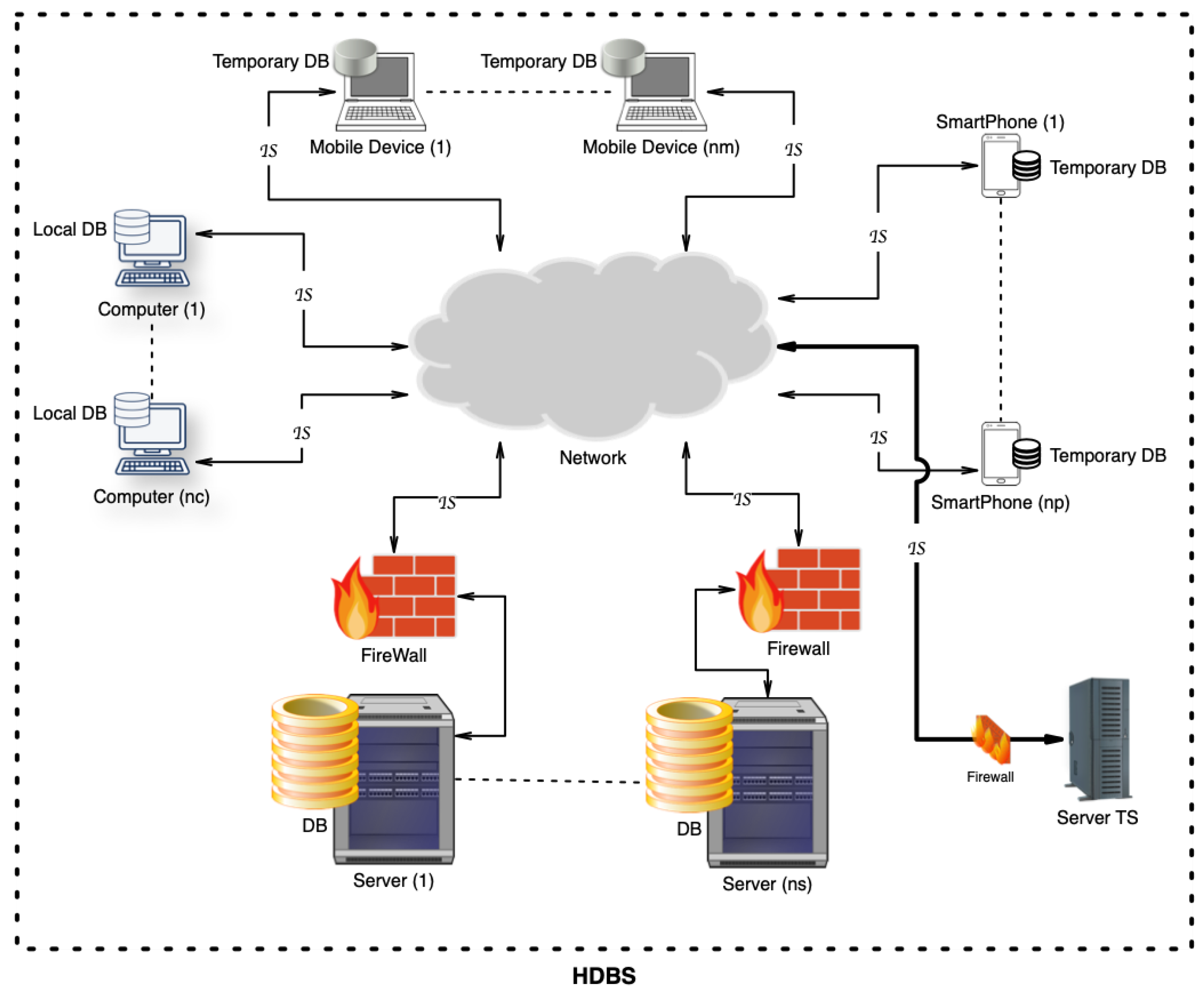
This study was carried out on an actual case in which an entity required a high degree of data security and communication confidentiality. We describe this case, first, by illustrating the components of this system. Let us take a heterogeneous set of computing systems, denoted as follows:

A set of

• $n_S$ server-type computing systems, denoted by $\mathcal{S}=\{S_1,S_2,...,S_{n_S}\}$;
• $n_C$ computers, denoted by $\mathcal{C}=\{C_1,C_2,...,C_{n_C}\}$;
• $n_M$ mobile devices, denoted by $\mathcal{M}=\{M_1,M_2,...,M_{n_M}\}$;
• $n_P$ smart mobile phones, denoted by $\mathcal{P}=\{P_1,P_2,...,P_{n_P}\}$.

The aforementioned devices contain databases, with temporary databases stored in $\mathcal{M}$ and $\mathcal{P}$, which means that the data will occasionally be transferred to specialized servers. The credentials required for the authentication and secure communications assurance systems are managed by a specialized device, called a trusted server ($TS$). The presented system is described in Figure 1.

All the above systems have ensured interconnections, but our proposed system involves different communication protocols, different types of physical communication, and different uptimes—the time during which they can be accessed. Let us denote the sets of communication types throughall systems as $\mathcal{IS}$.

Let $\mathcal{T}=〈\{\mathcal{S},\mathcal{C},\mathcal{M},\mathcal{P},\alpha TS\},\mathcal{IS}〉$. Then, $\mathcal{T}$ represents an $HDBS$.

Let $P_i$ be a smart mobile phone that makes a query in $\mathcal{T}$, where the result that will be provided involves an analysis of the whole $\mathcal{T}$ using DM algorithms. The data that pass between $P_i$ and $\mathcal{T}$ within the query request, as well as the result that $\mathcal{T}$ provides to $P_i$, represent a communication that requires double authentication and confidentiality of the communicated data; this is the treated case.

4. Our Solution to Ensure Authorized Access

This section presents the logical scheme of the studied system, the types of involved devices, the abstraction of the proposed model, and the proposed mathematical model for the generation of subspaces that are used in cryptographic processes.

In order to access $\mathcal{T}$’s query service, a complete security process is required, through which $P_i$ proves its identity and the $\mathcal{T}$ system identifies itself as the one to which $P_i$ wants to connect. This is the process of a double authentication: $P_i$ towards $\mathcal{T}$ and $\mathcal{T}$ towards $P_i$.

For the double-authentication technique, classic RSA-type algorithms can be used; such implementations require key lengths of 2048 bits for the involved security requests and the generation of keys on all computer systems within $\mathcal{T}$ for the treated case. For $\mathcal{S},\mathcal{C}$, and $\mathcal{M}$, this requirement can be fulfilled, but in the case of $\mathcal{P}$, the computing power required to generate the asymmetric keys of RSA involves the consumption of energy that is not available on such systems. To solve this requirement, which represents a class of data and communication security subproblems in which the confidentiality requirement is of a high degree and computing systems with low energy resources are involved, an ECC-based system can be used. First, we determine the cases of communication requests, and, depending on the type of devices involved, the mutual authentication method (double authentication) of the systems starts a data transfer process.

Involved devices:

• Case 1: sets from $〈\mathcal{S},\mathcal{C},\mathcal{M}〉$ and $TS$;
• Case 2: $〈\mathcal{P},\left\{AOT\right\}〉$, where $AOT$ represents any other device type, including $\mathcal{S},\mathcal{C},\mathcal{M},\mathcal{P},$ and $TS$.

For Case 1, the solution for the authentication was described in [15] and implemented, and it is still functional within a governmental entity. Let us describe the solution for Case 2.

4.1. Involved Device Authentication

In order to construct various types of quantiles of subspaces over which elliptic curves with cryptographic properties are defined, several studies have been carried out, among which we recommend [18,19,20,21,22,23]. From the authors’ previous studies for cases in which such subspaces were created for communication between devices with low computing power, i.e., smartphones, among those that demonstrated, in practice, superior results using models based on nonsupersingular elliptic curves, we recommend references [15,24] to interested readers. In order to define the number of subspaces required to obtain credentials in the double-authentication process for devices within $\mathcal{T}$, we build a model necessary for the particular case studied.

4.2. Mathematical Model for the Proposed Solution

Starting from the general space described in [24], let the values be generated by a series of integrals based on the partitions defining subspaces $\xi \left(K_{s_i}\right)$, as follows:

$$\left({\int }_{\xi }\frac{d\phi }{\sqrt{4{\phi }^3-{\tau }_2\phi -{\tau }_3}}\right)\frac{1}{\left|\xi \right|}$$

(1)

where $\xi$ represents the quantile considered from the curves series, $K_{s_i}$ is a partition of integer values, and $\phi$ is the variable defined over the subspace $\xi \left(K_{s_i}\right)$ and ${\tau }_2,{\tau }_3$ constants and represents the credential parameters of the series.

For each partition, we define its inverse as an elliptic curve from which points that have cryptographic properties in the sense of defining the credentials needed in the process of computing the keys involved in double authentication can be selected. To build this credential system, two constants, ${\nu }_1$ and ${\nu }_2$, as well as a periodic function defined over a set of real numbers, are selected. In the case considered in the current study, the Weierstrass equation for each $\xi$-partition is given by the following formula:

$${\left({\delta }^{\prime }\right)}^2={\left(4{\delta }^3-{\nu }_1\delta -{\nu }_2\right)}_{\xi }$$

(2)

where ${\nu }_1$ and ${\nu }_2$ are constants, and ${\nu }_1,{\nu }_2\in <\xi >$.

The two values $\delta ,{\delta }^{\prime }$ define a point of this curve:

$${\left({\iota }^2=4{\phi }^3-{\nu }_1\phi -{\nu }_2\right)}_{\xi }$$

(3)

for which the possibility of being considered as a point with cryptographic properties is computed. These subsets are defined for each partition $\xi$ of the above described system, thus obtaining a series of elliptic curves from which the points that will be part of the cryptographic algorithm are chosen.

5. Security Study of The Proposed Model

In this section, the security conditions of the proposed model are described.

Theorem 1.

The security condition, required by an $HDBS$ system, is that the inequality

$$\left|\xi \right|>\left(n_S+n_C+n_M+n_P\right)$$

(4)

has to be fulfilled.

Proof of Theorem 1.

If two devices are considered, let use denote them by $d_i,d_j\in <\mathcal{S},\mathcal{C},\mathcal{M},\mathcal{P}>$, where $i\ne j$, with ${\xi }_i$ and ${\xi }_j$, where the intersection of the partitions ${\xi }_i$ and ${\xi }_j$ is nonempty. According to [15,25], we have collisions in the process of establishing a cryptographic key required in step three of the communication protocols involved; therefore, $<{\xi }_i>\cap <{\xi }_j>=Ø$.    □

This theorem highlights the fact that each quantile considered in the series of studied elliptic curves will need to be defined independently from the others, a fact that emerges from the graphic representation illustrated in Figure 2. The quantities have to be selected in such a way as to comply with the requirement $<{\xi }_i>\cap <{\xi }_j>=Ø$.

Definition 1.

The elliptic curve corresponding to partition ${\xi }_i$ is represented by the sets of points of the form $(\varphi ,\iota )\in {\mathbb{Z}}_{\mu }\times {\mathbb{Z}}_{\mu }$ that meet the congruence conditions:

$${\iota }^2\equiv {\left(\left({\varphi }^3+{\nu }_1\varphi +{\nu }_2\right)\left(mod\mu \right)\right)}_{\xi }$$

(5)

and ${\iota }^2={\varphi }^3+{\nu }_1\varphi +{\nu }_2$, with $({\nu }_1,{\nu }_2)\in {\mathbb{Z}}_{\mu }$, where μ is a prime number greater than $\left({\xi }^2\right)$ and the $4{\nu }_1^3+27{\nu }_2^2\not\equiv 0\left(mod\mu \right)$ relation is satisfied, to which a special point $\mathcal{O}$ is added, called the point at infinity.

For the operations performed in order to compute the cryptographic parameters, using points selected from each quantile, optimizations of the standard computation methods are necessary for the involved operations, namely, for the specific addition of two such points and the multiplication of such a point by a scalar, in order to obtain the primary credentials. Among the optimal methods used in such operations, we can mention the studies in [26,27,28], where fundamental mathematical models with transformations of these modules and implementation optimizations in various private computing systems were described.

6. Implementation of the Proposed Model

This section illustrates the formulas used to compute the parameters of the subspaces over which the elliptic curves are defined, the graphic representation of these subspaces, and the computation algorithm proposed to compute these parameters.

For the implementations considered in the present case, we consider the optimal method of the type ${\varphi }_3={\gamma }^2-{\varphi }_1-{\varphi }_2$, ${\iota }_3=\gamma ({\varphi }_1-{\varphi }_3)-{\iota }_1$, where

$$\gamma =\left\{\begin{array}{c}({\iota }_2-{\iota }_1){({\varphi }_2-{\varphi }_1)}^{-1},forthecasethatthepointsintheoperanddiffer\hfill \\ (3{\varphi }_1^2+a){\left(2{\iota }_1\right)}^{-1},whenwehaveidenticalpoints\hfill \end{array}\right.$$

(6)

These operations are used to compute the intermediate points Q of coordinates $({\varphi }_3,{\iota }_3)$, using points $P_1$ of coordinates $({\varphi }_1,{\iota }_1)$ and $P_2$ of coordinates $({\varphi }_2,{\iota }_2)$. In the case of this type of computation, it is necessary to consider compliance with the restrictions established for each partition defined by ${\xi }_i$.

For each partition ${\xi }_i$, the number of points on the elliptic subcurve, defined over the corresponding space of this partition, can be computed by computing the trace of Frobenius for the particular studied case. Let ${\chi }_{\eta }$ be a subset of $K_{s_i}$, where $\eta$ represents the corresponding subsets for partition $s_i$. Thus, we have this value defined as $nop$ in the form $nop=\#\mathcal{E}{\left({\chi }_{\eta }\right)}_{\xi }=\eta +1-\kappa$, so for a space of size n, meaning $\left|\xi \right|=n$, it becomes $nop={\sum }_{i=1}^n\left(\left({\eta }_{\xi }+1\right)-{\kappa }_{\xi }\right)$, where ${\eta }_{\xi }$ represents a prime integer for partition $\xi$ and ${\kappa }_{\xi }$ represents the number of points from partition $\xi$.

Starting from the form described in [15], for the case of partitioning the parameter space with cryptographic properties for each partition, an endomorphism of the following form is defined:

$$\zeta =\left\{\begin{array}{c}\mathcal{E}\left({\chi }_{\eta }\right)\to \mathcal{E}\left(\overline{{\chi }_{\eta }}\right)\hfill \\ (\varphi ,\iota )\to ({\varphi }^{\eta },{\iota }^{\eta })\hfill \\ \mathcal{O}\to \mathcal{O}\hfill \end{array}\right.$$

(7)

For each partition ${\xi }_i$, with $1⩽i⩽n$, we have

$$\left|{\kappa }_{\xi }\right|⩽2\sqrt{{\eta }_{\xi }}$$

(8)

for each device involved in the double-authentication process.

There is the possibility to compute the number of points with cryptographic properties from the total set of points on these subspaces, according to the size of the partition and the chosen starting point in the process of computing a pair of primary credentials.

6.1. Graphic Representation

In this section, we provide graphic representations of the series of elliptic curves from which the ${\xi }_i$ subspaces are chosen and a representation of a point model with cryptographic properties resulting from the ESG algorithm.

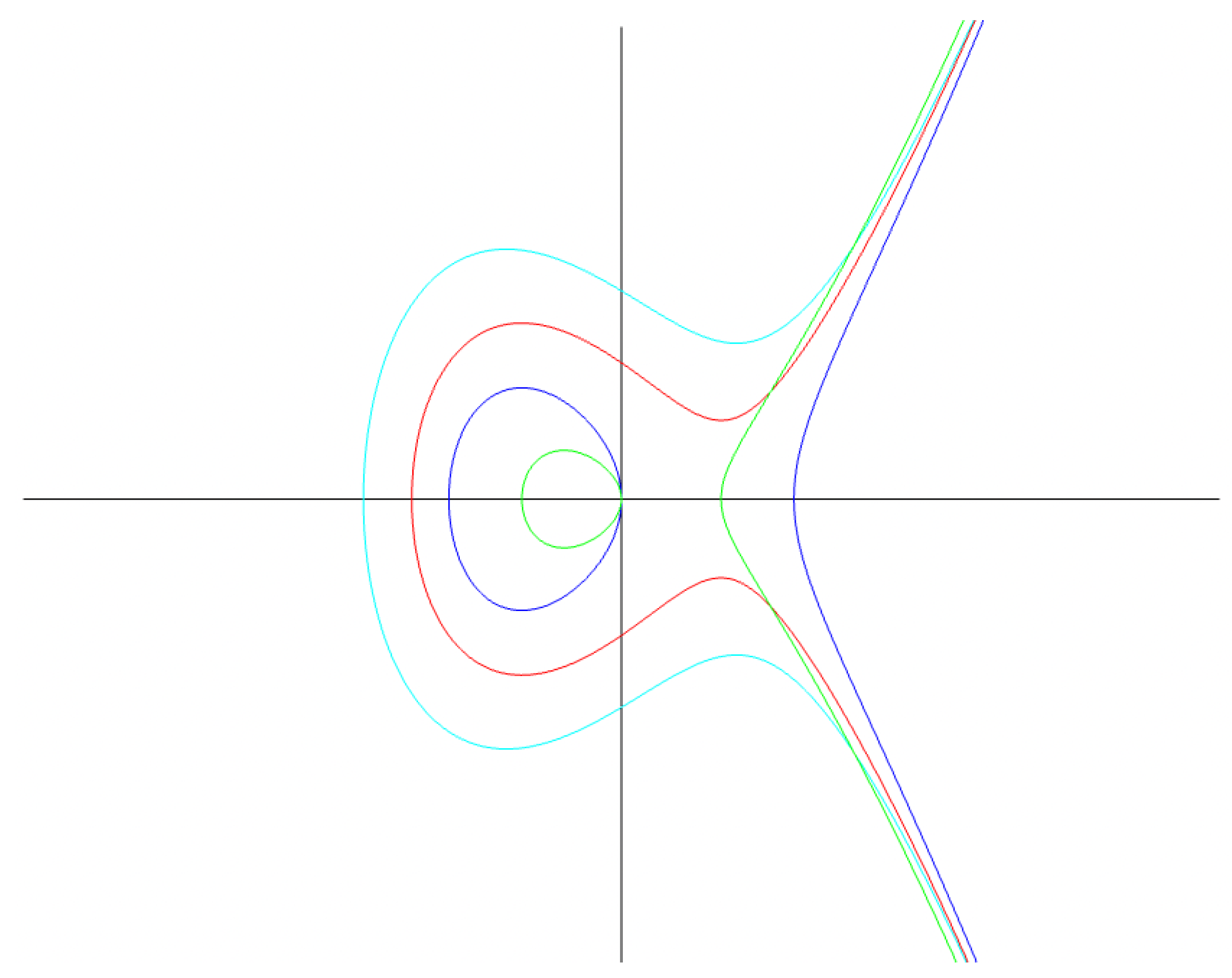
In this regards, in Figure 2, a series of curves generated according to predefined $K_{s_i}$ subspaces is represented and the choice of subspaces is made in compliance with the conditions from Theorem 1.

In Figure 3, three types of points are presented: green, representing those that passed the ESG algorithm test, from step 4, and that have cryptographic properties; gray, those that passed the test at the returned step according to the minimum standard ${\xi }_l^2$ value imposed by the security policies; and red, those that did not pass the test at step 5. They represent a limited number from possible sets and are computed for an interval within the subspaces within $d_i$; $P_j$ defines their credentials within the algorithm.

6.2. ESG Algorithm. Cryptographic Parameter Computation

In this section, we describe our proposed method to compute the cryptographic parameters for each partition ${\xi }_i$ using an $HDBS$-type device.

Each of the devices involved in the communication process initially select optimal parameters that will be used in the double authentication.

6.3. Double-Authentication Method

In this section, the proposed algorithm for the cryptographic parameter computation necessary for double authentication and for agreement with the communication security credentials is presented.

Algorithm 1 is the method by which two devices authenticate each other in the case where at least one device is from $\mathcal{P}$.

Algorithm 1: Subspace generation.

Initializations: ${\mathcal{E}}_j^{prec}$ is initialized at $\mathcal{O}$. 1. A partition ${\xi }_l$ is chosen for a value l generated pseudorandomly, and ${\mathcal{E}}_j^{current}$ is initialized at $\mathcal{O}$. 2. ${\mathcal{E}}_j$ is built based on ${\chi }_{\eta }$ coefficients. 3. An approximation of the number of points with cryptographic properties is computed, according to Equation (8), and ${\mathcal{E}}_j^{current}$ is created accordingly. 4. The degree of correlation between the parameters of the points on the elliptic curve is checked to verify the degree of resistance to cryptographic attacks, according to the methodology of [29,30]. In case this degree is greater than ${ϵ}_{{\xi }_l^1}$, certified according to the security policies established for $HDBS$, $max({\mathcal{E}}_j^{prec},{\mathcal{E}}_j^{current})$ is retained in ${\mathcal{E}}_j^{prec}$, and it returns to step 1. In other case, the current parameters are retained, in ${\mathcal{E}}_j^{current}$ 5. The simulation of the cryptographic computation of the primary parameters is carried out according to Equation (6). If the ${\xi }_l^2$ value is exceeded, the maximum accepted value for devices in $<\mathcal{P}>$, then it returns to step 1. Otherwise, the current parameters are retained in ${\mathcal{E}}_j^{current}$ 6. If the system returns a failure after testing the entire allocated partition, ${\mathcal{E}}_j^{prec}$ is returned together with a risk parameter allocated to this device. If the algorithm ends successfully, ${\mathcal{E}}_j^{current}$ is returned.

   All the communication processes that can be performed within an $HDBS$ can be reduced to several communications, including this particular type, because any multiple communication required in multiple query processes within data mining operations can be divided into a certain number of such dual communication processes, with the application of the protocol described by the algorithm in the following part.

Let $P_j$ be a device from $<\mathcal{P}>$, and let $d_i$ be another device from $<\mathcal{S},\mathcal{C},\mathcal{M},\mathcal{P}>$. Let it be the case where the $d_i$ device initiates the connection (the same procedure is followed in the opposite case). Device $d_i$ is checked to determineif it is in Case 1 or Case 2 according to the description of the possible cases in Section 4. For Case 1, the protocols described in [15] are applied.

In Case 2, the procedure is as follows: device $d_j$ uses in the double-authentication process its own pair of keys:

$$\left\{\begin{array}{c}\left((d_{p{b}_1}^{{{\xi }_d}_i},d_{p{b}_2}^{{{\xi }_d}_i}),d_{pr}^{{{\xi }_d}_i}\right)\hfill \\ \left(P_{p{b}_1}^{{{\xi }_P}_j},P_{p{b}_2}^{{{\xi }_P}_j}\right)\hfill \end{array}\right.$$

(9)

obtained from $TS$, and $P_j$ uses the key pair

$$\left\{\begin{array}{c}\left((P_{p{b}_1}^{{{\xi }_P}_j},d_{p{b}_2}^{{{\xi }_P}_j}),d_{pr}^{{{\xi }_P}_j}\right)\hfill \\ \left(d_{p{b}_1}^{{{\xi }_d}_i},d_{p{b}_2}^{{{\xi }_d}_i}\right)\hfill \end{array}\right.$$

(10)

obtained from $TS$.

The initiator of the process generates a pair of pseudorandom values, which are used in the combination process according to its partition and will initiate the connection $Challenge$. Upon such a request, the mobile device generates a pair of pseudorandom values that are combined according to the composition algorithm for mobile devices.

After this, the mobile device initiates the $Response$ process, through which it transmits the primary credentials necessary in the intermediate process required in the authentication of $P_j$ by $d_i$.

In order to perform a double authentication, a new round of communications is initiated from $d_i$ to $P_j$, called $CredentialAuthentication$, through which the parameters computed in the previous rounds by each of the participants are used as primary input data.

On this basis, at the end of the three rounds of communication, the two devices involved in the protocol will have completed the double-authentication process, through which each proved to the other its identity within the $\mathcal{T}$ system. A representation of this process is briefly shown in Figure 4.

6.4. DWA Authentication Algorithm

In this section, in accordance with the steps presented in Section 6.3, we describe the proposed protocol, presented as the following Algorithm 2:

During the creation of the credentials used to secure the communication, $d_i$ participates in the process using the data created by itself, namely, $Comp({\Delta }_1,{\Delta }_2)$, and $P_j$ participates in the construction of the credentials to secure the communication with the data generated independently of $d_i$, namely, $Comp({\mu }_1,{\mu }_2)$. On this basis, the final credentials are computed according to the combination of the data independently generated by each device involved in this process, which results in agreement with the credential protocol, not imposed credentials. Through this process of creating these credentials, there are also ensured authentications of $P_j$ by $d_i$, as well as of $d_i$ by $P_j$, which means that the man-in-the-middle attack is not possible.

Furthermore, the algorithm creates authenticated credentials for secure communication processes that take place between devices within a repeated query used to create a final answer given by a data mining action on $HDBS$. This procedure creates the credentials and takes into consideration a method of ensuring that cryptographic parameters are generated according to the parameters specific to each category of devices within $\mathcal{T}$. In this whole set of procedures initiated by elements from $\mathcal{T}$, it will be necessary for $TS$ to manage the certificates of each device from $\mathcal{T}$. Within the information stored about devices from $<\mathcal{M}$ and $\mathcal{P}>$, it is necessary to have descriptive data about each device from each class of devices and at each connection; for a device that contains an empty $TemporaryDB$, it is first transferred to the database servers within $HDBS$, and only then will the query continue.

The security level of the algorithm presented is in accordance with the attack resistance of a model based on $ECC$, with the difference being that, for a possible attacker, the analysis must be conducted on $<\xi >$, which represents the composition of all the parts stored by the models from each device, and not on ${\xi }_i$, a fact that increases the difficulty of processing the parameters and therefore increases the security level of the system in the case of a real attack on the protection model described for mobile devices within $\mathcal{P}$.

Algorithm 2: DWA.

♢ $d_i$ initiates the $Challenge$ process. 1. $({\varphi }_1,{\varphi }_2)\in {{\xi }_d}_i$ are generated, and $Combine({\varphi }_1,{\varphi }_2)$ is called. ${{\tau }_d}_i$ is returned. 2. The parameter ${\Delta }_1={{\tau }_d}_i\left({\left(d_{p{b}_1}^{{{\xi }_d}_i}\right)}^{-1}+d_{p{b}_2}^{{{\xi }_d}_i}\right)\frac{{\varphi }_1}{{\varphi }_2}$ is computed. 3. ${\Delta }_2$ is computed as the hash of the composition $Comp\left(d_{p{b}_1}^{{{\xi }_d}_i},{\Delta }_1\right)$. 4. ${\Delta }_3$ is computed as the asymmetric encryption of the message ${\Delta }_2$ using the secret key $d_{pr}^{{{\xi }_d}_i}$. 5. The $Comp({\Delta }_1,{\Delta }_2)$ values are communicated to $P_j$ (the $Challenge$ process). ♢ Upon receiving the ${\Delta }_3$ message, the $P_j$ device initiates the $Response$ process; generates two pseudorandom values $({\chi }_1,{\chi }_2)\in {\left({\xi }_P\right)}_j$; then calls the $Combine(P_{p{b}_1}^{{{\xi }_P}_j},{\Delta }_1)$ function, which respects the entropy principles from ([31,32]); computes ${\beta }_1^{P_j}$ as the hash of the result given by the $Comp(P_{p{b}_1}^{{{\xi }_P}_j},{\Delta }_1)$ function; and computes ${\beta }_2^{P_j}$ to be the encryption of ${\Delta }_2$ using $d_{p{b}_1}^{{{\xi }_d}_i}$’s public key. If the two computed parameters are not identical, the authentication of $d_i$ by $P_j$ ends in failure. Otherwise, the construction of the cryptographic parameters continues. 6. $P_j$ computes ${\mu }_1={\tau }_{P_j}\left({\left(P_{p{b}_1}^{{{\xi }_P}_j}\right)}^{-1}+P_{p{b}_2}^{{{\xi }_P}_j}\right)\frac{{\chi }_1}{ch{i}_2}$. 7. $P_j$ computes ${\mu }_2$ as the hash of $Comp(P_{p{b}_1}^{{{\xi }_P}_j},{\mu }_1)$. 8. ${\mu }_3$ is computed as the asymmetric encryption of the message ${\mu }_2$ using the secret key $P_{pr}^{{{\xi }_P}_j}$. ♢ The $Response$ process consists of $P_j$ sending $Comp({\mu }_1,{\mu }_2)$ values. Upon receiving the message from $P_j$, the device $d_i$ verifies the identity of $d_i$ in the same way as $d_i$ verified the identity of $P_j$. If the verification fails, the protocol ends with a failure. Otherwise, the protocol initiates the process for the $CredentialAuthentication$ phase. 9. $d_i$ computes ${\beta }_1^{P_j}$ as the hash of the result returned by the $Comp(P_{p{b}_1}^{{{\xi }_P}_j},{\mu }_1)$ function. 10. $d_i$ computes ${\beta }_2^{P_j}$ to be ${\mu }_2$’s encryption using $P_{p{b}_1}^{{{\xi }_P}_j}$’s public key. If the two calculated parameters do not have the same value, the credential authentication step fails. If the two parameters have the same value, the process ends successfully by authenticating the credentials approved by the two parameters and proceeds to calculate the final credentials of secure communication: $d_i$ computes a parameter ${\Delta }_4$ as the hash applied to the first three calculated parameters, encrypted with its public key, and transmits the result to $P_j$.

6.5. Performance Analysis

In this section, the performance of the implemented model ($ESG$) is described in comparison with two models previously implemented by the beneficiary, namely, $GN1$ (a variant based on solution presented in [15]) and $KMK$ (a variant based on solution presented in [33]), which were solutions that contributed to the dual authentication system, with the common feature being the space over which elliptic curves are defined, for an environment which contains 3 server centers, 87 users from the $\mathcal{C}$ category, and 212 users from the class $\mathcal{M}$, with heterogeneous systems.

The presented model was analyzed according to the computation time required to generate ${\mathcal{E}}_j^{prec}$-type subspaces for the presented solution, and the time generation and communication time of the results for previous solutions (in

Table 1. Parameter generation.

	GN1	KMK	ESG
Generation time	1.17	2.11	1.8
Assignment time	4.15	4.15	0.3
Recomputations	27	0	41
Generation errors	129	128	215

).

Below are descriptions of the properties represented in the table, as well as some remarks on the results.

Generation time–the time (in seconds) required to compute the parameters for elliptic curves. The time to compute the parameters is correlated with power consumption.

Assignment time–the time (in seconds) required to transfer data to other devices that are involved in the communication. The assignment time is correlated with power consumption.

Recomputations–the number of parameter recalculations (at each 1000 calls) according to the security policies established by the beneficiary. It should be noted here that they change over time depending on the problems found during the periodic security audit. The recomputation time is correlated with power consumption.

Generation errors–the number of failures (at each 1000 calls) in the process of generating a subspace in a space.

Moreover, a performance analysis with the required computation time was performed every 6 months to establish the cryptographic credentials and the number of detected attacks on the system (the last analysis is presented in

Table 2. Credential generation.

	GN1	KMK	ESG
Cryptographic credential generation time	0.72	1.12	0.3
Detected attacks	6	19	25

).

The data from this table are explained and interpreted below.

Cryptographic credential generation time–the time required to generate the cryptographic credentials used in double authentication and to secure the communication. The cryptographic credential generation time is correlated with power consumption.

Detected attacks–the number of detected attacks (at each 1000 calls).

As a general statement, the method of computing the cryptographic parameters, from the point of view of the allocated times/power consumption, depends on the initial generation method of the involved parameters and the security policy established by the beneficiary, which influences the number of recomputations and the generation time of the cryptographic parameters. This decision is made depending on the degree of security that is requested to be implemented.

6.6. Limitations of the Proposed Model

The proposed model ensures the creation of the necessary credentials in the cryptographic processes involved in securing communications and double authentication; otherwise, communications will be disallowed. This main limitation of the model is due to step 5 of Algorithm 1, where a ${\xi }_l^2$ value is exceeded only if it meets the maximum conditions for this parameter, established as the maximum value accepted for the devices in $<\mathcal{P}>$, according to the security policies, so the establishment of the security policies determines the number of repetitions of the process in certain cases. This practically translates into longer creation times for cryptographic credentials.

The second limitation involves the way in which double authentication is performed and the protection against man-in-the-middle attacks. This is present in all systems that respect this principle, namely, the creation of common cryptographic credentials is ensured, and in the case of an attack of the type mentioned above, communication is not allowed; the presence of such an attack can thus be signaled, but communication is not allowed.

7. Conclusions and Future Work

In this paper, we presented a method to determine the cryptographic parameters in the case of queries in an $HDBS$-type system; more precisely, we proposed a secure communication system for the case where smartphone-type devices are involved in this process and other heterogeneous devices are implied. The solution takes into account the particularities of these devices in terms of computing power and describes a way to generate cryptographic credentials for communications involving data-mining-type queries, as well as the transfer of base models defined as being of the $TemporaryDB$ type. This system was implemented and is functional within an entity that uses these types of queries. During the implementation and after consultation with the users of the system, as future research, an estimation of the degree of risk for the subspaces that are used and the establishment of methods to determine optimal ${ϵ}_{{\xi }_l^1}$ and ${ϵ}_{{\xi }_l^2}$ parameters within security policies were requested. These represent the next steps in the research to be undertaken.