LQR Chaos Synchronization for a Novel Memristor-Based Hyperchaotic Oscillator

Abstract

In a three-dimensional dissipative chaotic system circuit, by superimposing a cubic magnetron-type memristor and connecting a feedback circuit, a new four-dimensional synchronous controlling system is established. The control parameters have a significant impact on the system, and the system displays rich dynamic features such as hyperchaos, chaos, and period states. At the same time, the synchronization scheme for the chaotic system is designed based on the linear quadratic regulator (LQR), which effectively improves the system response speed and reduces the complexity of the synchronous controlling system. Further, numerical verification is carried out. Finally, a detailed verification of the chaotic system’s dynamic characteristics is performed by hardware simulation. Simulation results and performance analysis show that the proposed method has synchronous controlling performance. Compared to some existing synchronous controlling schemes, this method is more widely applicable.

1. Introduction

Standard nonlinear dynamic systems can usually be achieved using regular inputs and multipliers on electronic circuits, where the feedback capacitor and resistors link to execute the mathematical integration operation. This operation is a complete nonlinear operation with a four-quadrant implementation [1,2]. Memristor [3], a basic two-terminal electronic component with adjustable resistance or conductance [4] due to its unusual features of memory and nonlinearity, has great potential application in sundry linear dynamic circuits. Over the past decade, there has been an increasing trend to develop many other memristor models [5,6,7]. Many chaotic oscillators with memristive elements have been widely discussed, such as the memristive model controlled by the flux linkage [8,9] and the antiparallel two memristors [10]. For linear systems, sundry chaotic and hyper-chaotic flow loops based on memory barriers have been simply established, and research has been carried out [1,11]. After that, the system circuit realization of four-dimensional resistance hyperchaotic system with nonlinear coupling resistance has aroused researchers’ wide concern.

The study of the complexity of chaotic systems is one of the most popular research directions in the field of chaos, and many researchers have found simple nonlinear functions to construct chaotic ones [12,13]. Although there has been little work on memristive element-based chaotic systems, complex behaviors can be found in the existing literature. Some studies have been conducted on memristor-based chaotic oscillators and their importance in real-time engineering applications. The circuits’ performance is significantly impacted by the study of chaotic circuits because they have special properties such as unbalanced and hidden oscillations, line balance, and stable balance with nonlinear memristive models. Thus, the memristive Chua’s circuit is improved, and its physical realization presents an infinite balance of soft-hard excitation and bifurcation analysis [14]. The application of memristor-based circuit systems for weak signal detection and neural networks is also widely discussed [15,16,17]. Researchers have combined memristor elements with a Hopfield neural network to obtain complex chaotic systems with wide range of potential applications [18,19,20]. In addition, other researchers have proposed and studied a certain simple circuit implementation of a memristor, namely a bridge memristor circuit [21,22,23]. A simulator of the memory capacitor and memory inductor was designed using the current transmitter, and its dynamic characteristics were studied [24]. A novel memristive hyperchaotic system for image encryption was researched, indicating that memristor-based chaos generators are more sophisticated and practical in cryptography [25]. The memristive hyperchaotic system strongly attracts a great number of researchers to fight for its application in associative memory, brain science, information expression, pattern recognition, and synchronization control.

The chaotic synchronization of hyperchaotic systems based on complex memristor networks is an interesting challenge. In this case, the two systems must both exhibit the same chaotic behavior. These two systems can be coupled in one direction, also known as master-slave configuration, where the autonomous system with hyperchaotic dynamics is called the master system, and the other system forced to follow the hyperchaotic behavior by the coupling input is called the slave system. Many techniques have been introduced and successfully applied to synchronize identical or dissimilar chaotic systems including linear feedback control [26], sliding mode control [27,28,29], and so on. It is well known the controller plays a crucial role in synchronization implementation. Most of the principles of a controller design, such as impulsive control, pinning control, adaptive control, and feedback control, are assumed to be handily accessed. However, this assumption is too strict to realize synchronous control for the actual complex system. With the increasing use of memristors in chaotic systems, some workers have attempted to construct a synchronous controller based on memristor circuits [30,31]. Wang et al. [32] proposed an observer-based control method to estimate the state of memristive neural networks and ensure their synchronization in the presence of denial-of-service attacks and actuator saturation and finally achieved stable output. In 2022, by considering a cluster combination output behaviors among the neural nodes and designing multiple adjustable controllers based on adaptive control techniques, Wang et al. [33] applied a memristive neural networks synchronization strategy to reduce control costs and increase the anti-interference capacity of the control system, which accurately evaluated chaotic states and finally obtained unlimited control output. This study further proves that the synchronous control memristor-based system has lower costs and better resistance to interference capability. In the context of deep learning techniques being widely studied in various research fields, fuzzy neural network techniques have also started to be applied in chaotic synchronization [34].

Different control schemes are usually employed for engineering systems that have to change under demanding closed-loop conditions to obtain the desired output. PID controllers are a type of feedback control system that is commonly used in industrial and engineering settings. However, advanced control algorithms are required for chaotic and hyperchaotic systems with sensitive initial conditions and rapid response to parameter changes. Therefore, how to introduce a linear controller to reduce control difficulty in complex memristor chaotic systems becomes an inevitable issue. However, no related work has been reported yet, which lights a spark for this article to design a reliable controller to improve the sensitivity and linear stability of the chaotic synchronization system. LQR is an effective control strategy that is easy to implement. The static gain matrix K from LQR does not alter the order of the complex system’s closed-loop system.

The article is organized as follows. Section 2 proposes a new four-dimensional memristor-based hyperchaotic system, and its performance is discussed. In Section 3, we obtain the Lyapunov exponent map and bifurcation diagram to better comprehend the features of the chaotic system. In Section 4, we seek to construct a controller for the chaotic synchronization model with a feedback structure. In Section 5, the new hyperchaotic system’s circuit is established based on the operational amplifier and simulated in Multisim. The conclusion is summarized in Section 6.

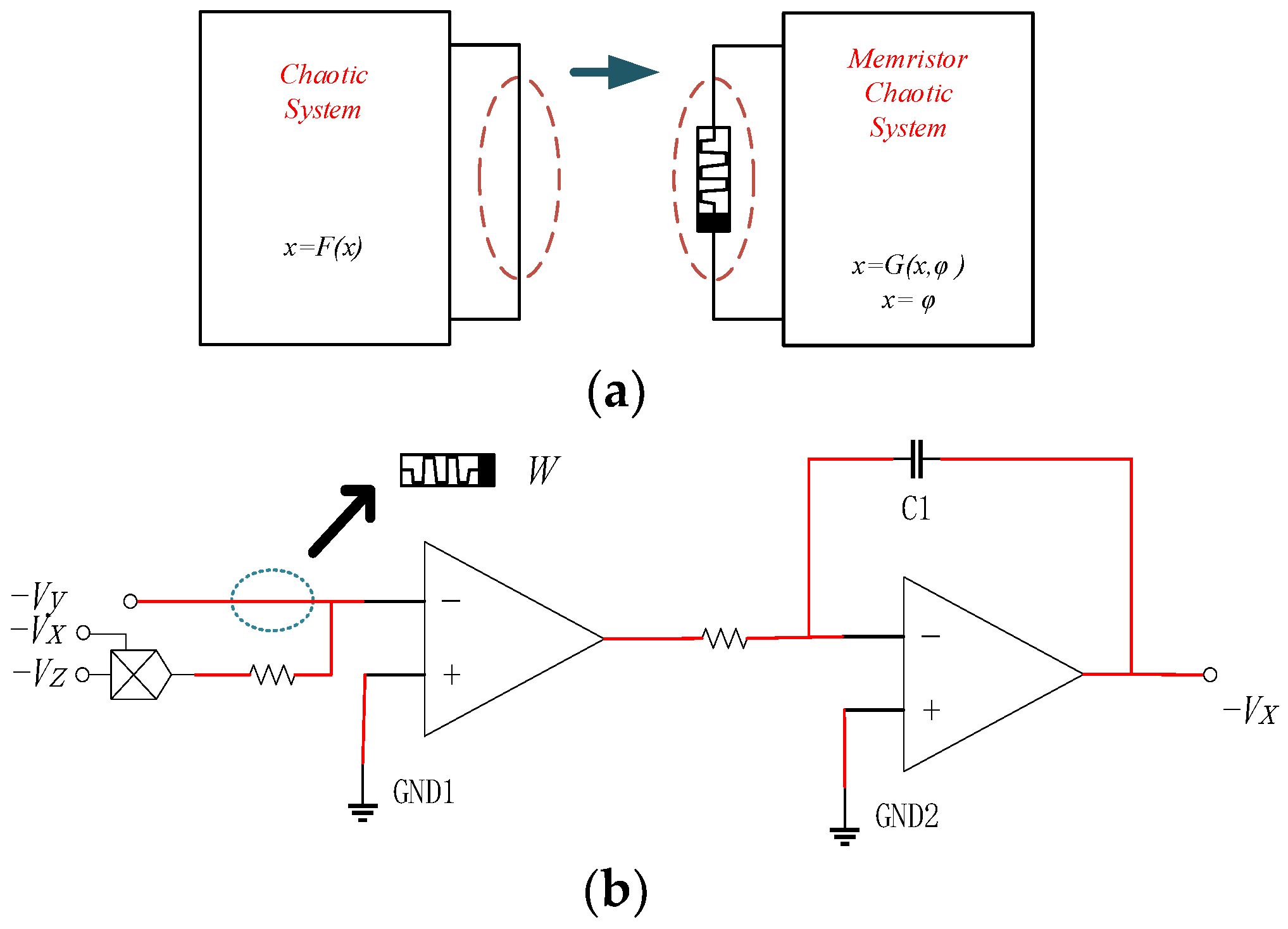
2. Hyperchaotic Systems Based on Memristor Circuit

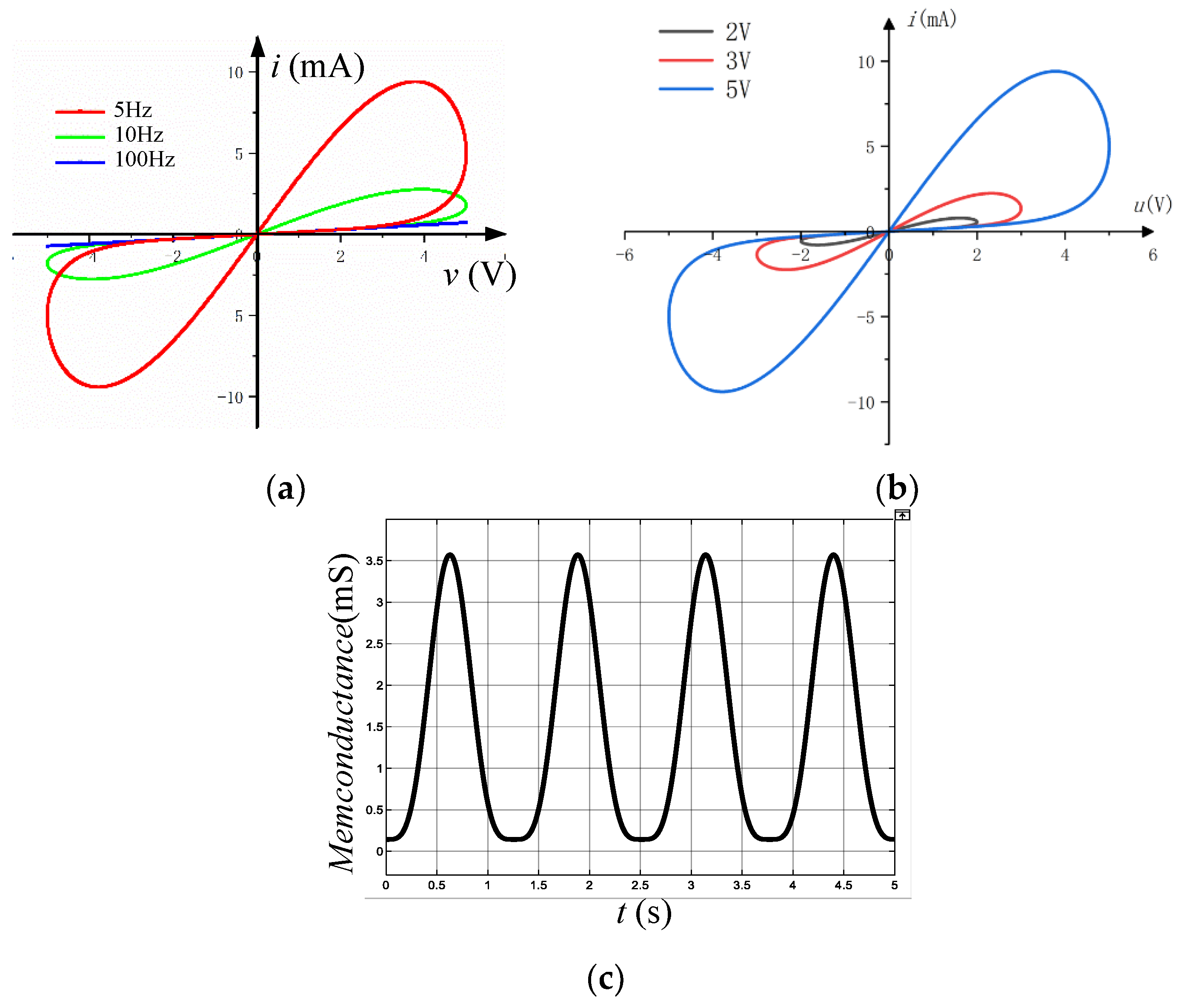
2.1. Construction of the System

A four-dimensional memristor-based hyperchaotic system is proposed in this section by adding a memristor to the implemented circuit of an existing three-dimensional chaotic system.

This is the most general parametric 3-D form containing all possible quadratic nonlinearities, as shown in [35], with a single non-quadratic term in the first equation:

$$\begin{array}{c}\{\begin{array}{l}\dot{x}=f\left(x,y\right)+a_1{x}^2+a_2{y}^2+a_3{z}^2+a_{4}xy+a_{5}xz+a_{6}yz,\hfill \\ \dot{\dot{y}=a_7{x}^2+}{a}_8{y}^2+a_9{z}^2+a_{10}xy+a_{11}xz+a_{12}yz,\hfill \\ \dot{\dot{z}=a_{13}{x}^2+}{a}_{14}{y}^2+a_{15}{z}^2+a_{16}xy+a_{17}xz+a_{18}yz,\hfill \end{array}\end{array}$$

(1)

Here, $f\left(x,y\right)$ are given by:

$$\begin{array}{c}f\left(x,y\right)=\{\begin{array}{c}\begin{array}{c}0,\\ 1,\end{array}\\ \begin{array}{c}\pm x,\\ y,\end{array}\end{array}\end{array}$$

(2)

We selected the $S{L}_{10}$, which is the tenth system in a series of chaotic systems proposed in reference [35]; its definition is as follows:

$$\begin{array}{c}\{\begin{array}{c}\dot{x}=y+pxz,\\ \dot{y}=xy-xz,\\ \dot{z}=xy+qyz,\end{array}\end{array}$$

(3)

Here, $p=0.2,q=3$.

In the same vein as the famous as Lorenz system [36], Chen system [37], and Lü system [38], system (3) is also an autonomous system that is a simple three-dimensional model, which is a simple task to implement this electronically with a circuit that uses multipliers and op-amps linked with resistors and/or capacitors. A memristor can be added to the realization circuit of the system (3) to create a novel memristor chaotic system; this system can be described as shown in Figure 1a. The memristor is represented by W and the self-variable resistor or linear coupling resistor is represented by R.

Based on the realization scheme of the memristor-based chaotic system in Figure 1a, a flux-controlled memristor $W$ was used to impact the y variable. In this manner, a memristor-based chaos system can be effortlessly assembled. For the memristor $W$, the intrinsic nonlinear relation between the input terminal voltage v and output terminal current i is given by:

$$\begin{array}{c}i=W\left(\phi \right)v,\dot{\phi }=v,\end{array}$$

(4)

where $W\left(\phi \right)$ is described as:

$$\begin{array}{c}W\left(\phi \right)=\alpha \phi +3\beta {\phi }^2,\end{array}$$

(5)

where $\alpha$ and $\beta$ are two constant parameters.

Here, we set the parameters $\alpha =1/7$, $\beta =2/7$. The pinched hysteresis lines in Figure 2a demonstrate how the voltage fluctuates when the sinusoidal excitation $v_s=V_{m}sin\left(2\pi ft\right)$ and $V_m$ = 5 V is used as the driving signal for the extended amnesia. When the excitation frequency is increased, the hysteresis area will decrease. The $v-i$ curves will span at the first and third quadrants. Figure 2b demonstrates how the voltage fluctuates when the sinusoidal excitation $v_s=V_{m}sin\left(2\pi ft\right)$ and $f$ = 5 rad/s is used as the driving signal for the extended amnesia. When the excitation voltage is increased, the hysteresis area will increase. The $v-i$ curves will span at the first and third quadrants. Figure 2c shows the variation of the hysteresis conductance of the memristor model with time, and it can be seen that the organization oscillates with time, which also indicates that the model has good nonlinear characteristics.

Correspondingly, a dimensionless state equation set of the proposed memristor system was modeled as:

$$\{\begin{array}{l}\dot{x}=\left(\alpha +3\beta w^2\right)\mathrm{y}+pxz,\\ \dot{y}=xy-xz,\\ \dot{z}=x^2+qxy,\\ \dot{w}=y,\end{array}$$

(6)

Finally, feedback was added to the system, the system was shown as:

$$\{\begin{array}{l}\dot{x}=\left(\alpha +3\beta w^2\right)\mathrm{y}+pxz+x,\\ \dot{y}=xy-xz-10x+z,\\ \dot{z}=x^2+qxy+w,\\ \dot{w}=y.\end{array}$$

(7)

2.2. Equilibrium Point and Stability Analysis

In our work, the parameters were set as α = 1/7, β = 2/7, $p=0.2, q=20$, respectively. The equilibrium points of the system can be calculated by setting the result of (7) equal to 0, which yields (0, 0, 0, 0) and (−1, 0, −5, −1). The Jacobi matrix at the equilibrium point S was then derived as:

$$J=\left(\begin{array}{cccc}pz& \left(\alpha +3\beta w^2\right)& px& 6\beta yw\\ y-z-10& x& 1-x& 0\\ 2x+qy& qx& 0& 1\\ 0& 1& 0& 0\end{array}\right).$$

(8)

Hence, by solving the following characteristic equations:

$$\begin{array}{c}P\left(\lambda \right)=\det \left(\mathbf{1}\lambda -\mathit{J}\right)=0,\end{array}$$

(9)

The eigenvalues at the two equilibrium points were obtained as such:

$$\begin{array}{c}\begin{array}{c}{S}_0:{\lambda }_{1,2}=0.7302\pm 0.7110i,{\lambda }_{3,4}=-0.2032\pm 0.9791i,\\ S_1:{\lambda }_1=-0.5374,{\lambda }_2=0.0541,{\lambda }_{3,4}=-0.2584\pm 5.8577i,\end{array}\end{array}$$

(10)

In the given parameter area, the zero-equilibrium point $S_0$ is always an unstable equilibrium point with two pairs of complex roots; the first pair has roots with positive real parts, and the second pair has roots with negative real parts. The other equilibrium point, $S_1$, has a positive real root, a negative real root, and a pair of conjugate complex roots with negative real parts. It is also an unstable equilibrium point where chaos can be aroused.

For the parameters, $\alpha =1/7$, $\beta =2/7$, $p=0.2, q=20$ and the initial values (4, 4, 4, 4) the system showed a hyperchaotic attractor as illustrated in Figure 3a,b. Figure 2c shows the time domain waveforms of state variables x, y, z, and w. Among them, the three state variables x, y and z had stable oscillation waveforms, while the amplitude of the oscillation waveform of the state variable w gradually decreased with time.

3. Properties of the MHS

As is well known, bifurcation diagrams and Lyapunov exponents spectra are wildly used to analyze the main dynamical property of the chaotic system. To study how various parameters impact the proposed memristor-based hyperchaotic system (6), the parameters were set as α = 1/7, β = 2/7, as along with the initial conditions (4, 4, 4, 4). The parameters p and q were adjusted separately and independently.

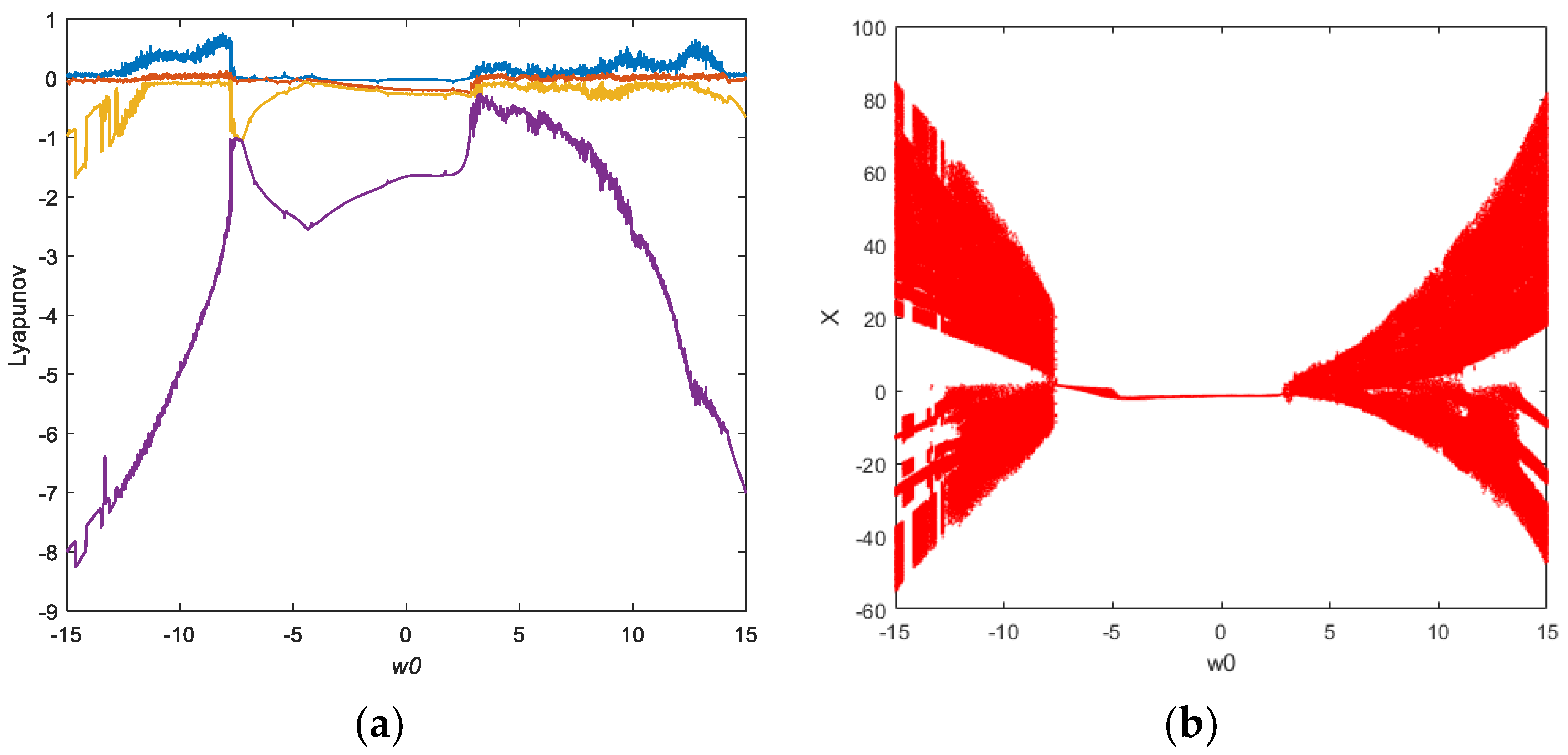
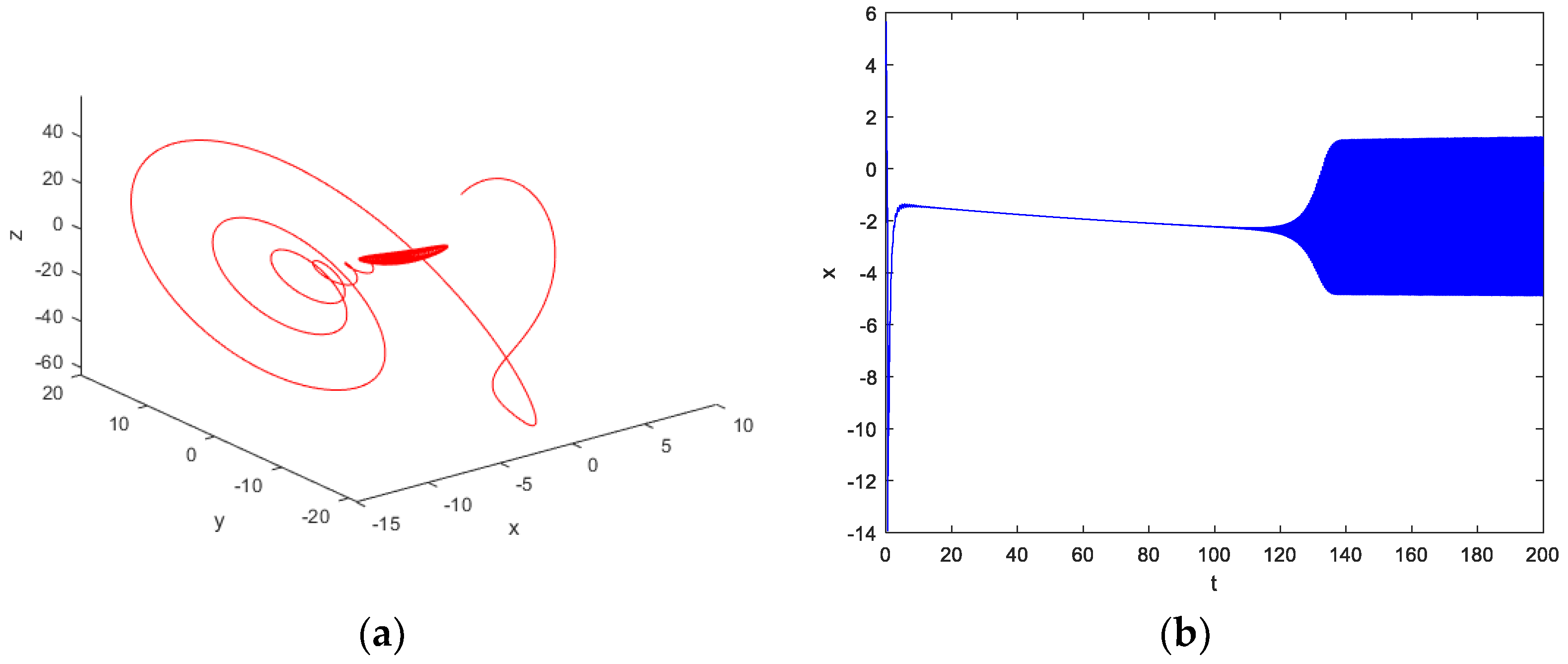
3.1. Hyperchaotic Behavior Depending on Parameters

The bifurcation diagram of the system state variable x, as well as the four Lyapunov exponents, are both plotted in Figure 4a and Figure 4c, respectively. The parameter p was set to 0.2, and q was increased gradually from 5 to 35. In a similar way, q = 20, and p was gradually increased from 0.1 to 0.7, Figure 4b,d show the bifurcation diagram of the system state variable x and its four Lyapunov exponents. The dynamical behaviors of chaos with one positive Lyapunov exponent and hyperchaotic with two positive Lyapunov exponents can be found in Figure 4, while we can also observe some periodic windows with non-positive maximum Lyapunov exponents. Moreover, the Lyapunov exponent of the system oscillated violently with the change of parameters p and q, which excited a rich dynamical behavior of the system. Furthermore, the consequence in Figure 4 indicates that the memristor-based system (7) was hyperchaotic for most of the interval of the parameter q. It is worth noting that if q increases, the dynamic amplitude of the state variable x will decrease, while the dynamic amplitude of the state variable x changes dramatically around the parameters p = 0.28 and p = 0.58.

3.2. Hyperchaotic Behavior Relying on Memristor Initial Condition

This section investigates the dynamic behavior of the memristor-based system under initial conditions. The fourth-state variable is critical to the memristor-based hyperchaotic system because it directly reflects the memristor’s internal state. Since the memristor has natural memory, its working state depends entirely on past behaviors. Therefore, if the initial condition of the fourth-state variable is different, it could make the dynamic behavior of the memristor-based chaotic system completely different.

The typical parameters α = 1/7, β = 2/7, p = 0.2, q = 20 and three initial conditions x (0) = 4, y (0) = 4, z (0) = 4 were fixed, where the memristor initial condition w (0) was varied in the region (–15, 15) When the memristor initial condition w (0) increased from −15 to 15, the bifurcation diagram of the state variable x and the four Lyapunov exponents are plotted in Figure 5a and Figure 5b, respectively. From Figure 5, the memristor-based system appeared to have hyperchaotic, chaotic, and periodic states based on the change of initial conditions. The vast majority of hyperchaotic systems with two positive Lyapunov exponents were found in the (−12, −8) and (3, 14) areas. Several narrow chaotic windows with a positive Lyapunov exponent were found in the hyperchaotic area at the same time. As w (0) increased, the dynamic amplitude of x varies approximately symmetrically. Whereas the periodic window was located in the (−8, 3) area, it should be noted that when the memristor’s initial state was the periodic state, the system variables will enter the periodic orbit after about 110 s of stagnation, as illustrated in Figure 6a,b.

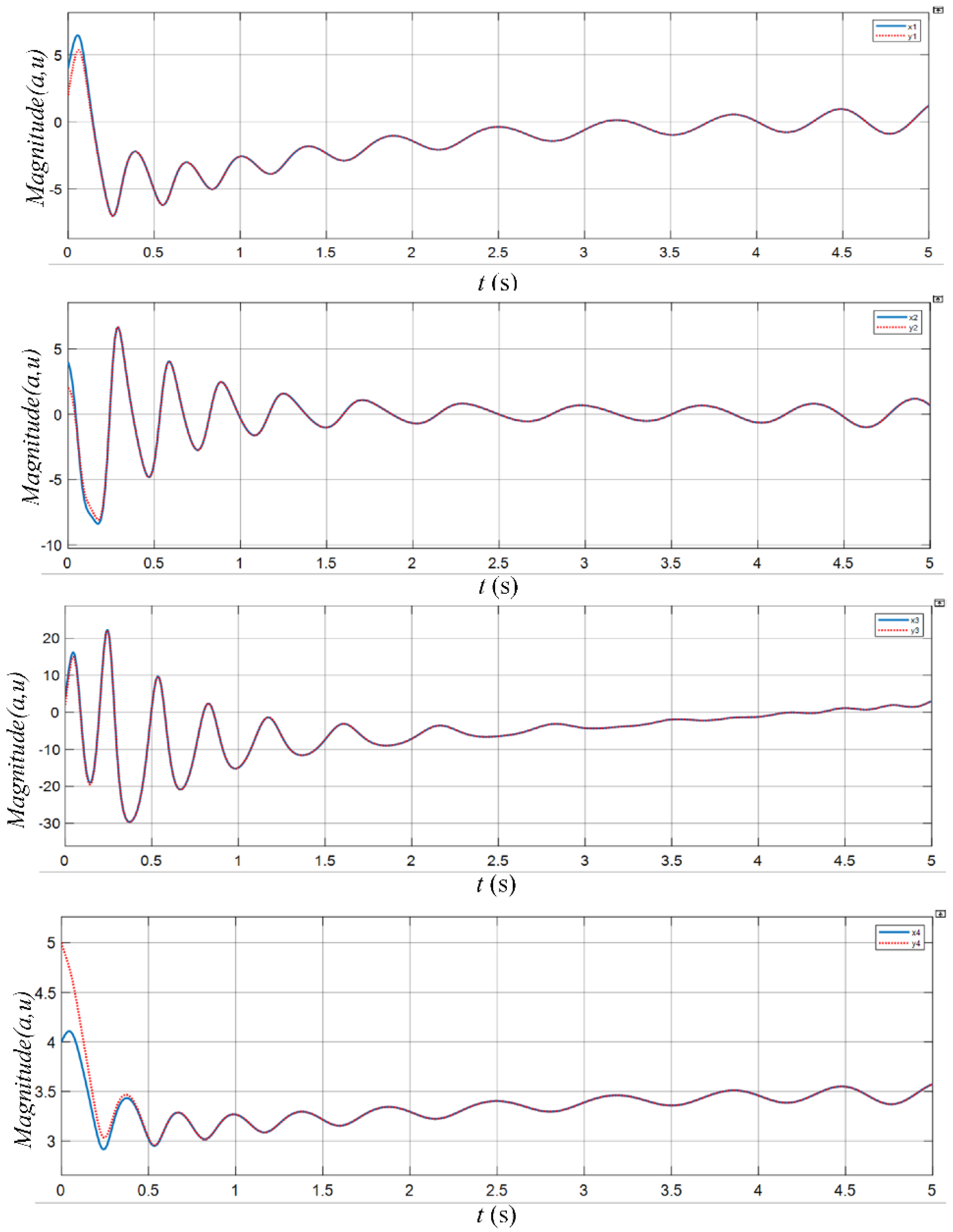
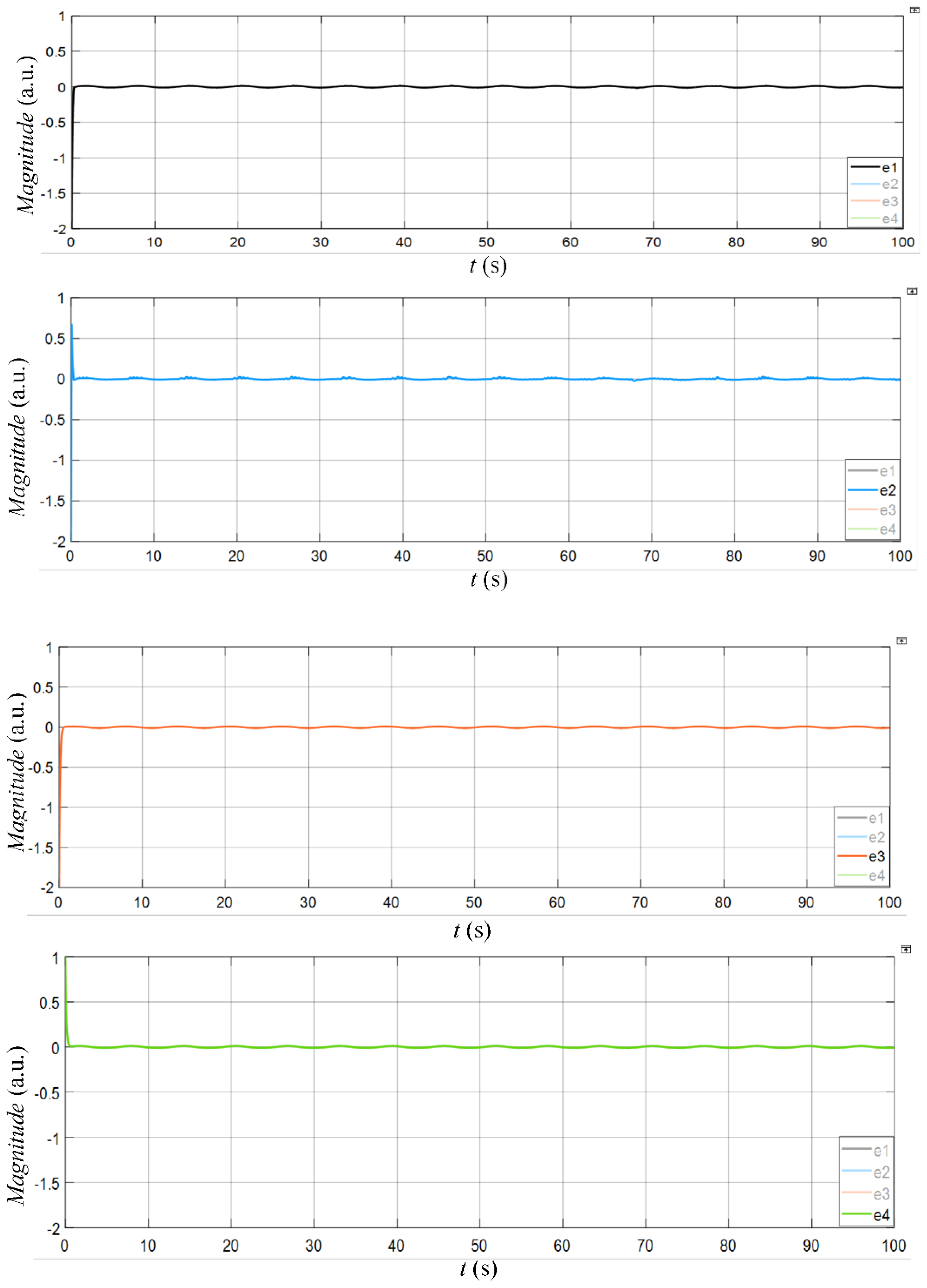
4. Synchronization by Using the LQR Method

The linear-quadratic problem is an optimal control problem that is studied when the system is linear and the performance index is the quadratic function of state variables and control variables. LQR, the linear quadratic regulator, is commonly used to solve linear-quadratic problems. LQR optimal design means that the designed state feedback controller K should minimize the quadratic objective function J, and K is uniquely determined by the weight matrices Q and R, so the selection of Q and R is critically important. LQR theory is one of the first and most well-developed state space design methods in modern control theory. It is particularly valuable that LQR can obtain the optimal control law of state linear feedback, which easily forms closed-loop optimal control.

If the master chaotic systems are assumed to be as follows:

$$\begin{array}{c}\dot{x}=Ax+f\left(x\right),\end{array}$$

(11)

Here, $x\in R^n$ is the state vector of the master system, $A\in R^{n\times n}$ is the linear parament matrix of the system, and $f\left(x\right)$ is the nonlinear part, the slave chaotic system is given by the following form:

$$\begin{array}{c}y=Ay+f\left(y\right)+u,\end{array}$$

(12)

$y\in R^n$ is the state vector of the slave system, and u is the controller. Synchronization error between the master system and the slave system is:

$$\begin{array}{c}e=y-x,\end{array}$$

(13)

According to Equations (11) and (12), the dynamic errors can be expressed as:

$$\begin{array}{c}\dot{e}=Ae+F\left(x,y\right)+u,\end{array}$$

(14)

where $F \left(x, y\right)=f\left(y\right)-f\left(x\right).$ The purpose of u is to make e(t)→0 when t→∞. For this purpose, controller u is separated into the linear and nonlinear terms, and it can be written as:

$$\begin{array}{c}u=-F\left(x,y\right)+B{u}_L,\end{array}$$

(15)

where $B\in R^{n\times r}$ is the control matrix, to achieve linear feedback $u_L$. Substituting Equation (15) into Equation (14), we achieve dynamic errors:

$$\begin{array}{c}\dot{e}=Ae+B{u}_L,\end{array}$$

(16)

We set $K\in R^{r\times n}$ as linear gain matrix. Therefore, linear control term $u_L$ is:

$$\begin{array}{c}{u}_L=-BKe,\end{array}$$

(17)

The dynamic errors can be written as:

$$\begin{array}{c}\dot{e}=\left(A-BK\right)e,\end{array}$$

(18)

For this reason, the linear error term can be transformed into a linear feedback system. Let us define the linear feedback system as follows:

$$\begin{array}{c}\dot{x}=Ax+B{u}_L,\end{array}$$

(19)

where:

$$\begin{array}{c}{u}_L=-Kx,\end{array}$$

(20)

The purpose is to derive the gain matrix (K) make the system (11) to the origin for linear control of (12). Furthermore, the proposed controller will make the closed-loop system Lyapunov stable and $Q=Q^T>0,R=R^T>0$.

$$\begin{array}{c}J={{\displaystyle \int }}_0^{\infty }\left(x^{T}Qx+u_L{}^{T}R{u}_L\right)dt,\end{array}$$

(21)

For the system (17), the controller calculation (20) can make Equation (21) as a minimum, which is computed as shown in Equation (13).

$$\begin{array}{c}{A}^{T}P+PA-Q+PB{R}^{-1}{B}^{T}P=0,\end{array}$$

(22)

$$\begin{array}{c}K=-R^{-1}{B}^{T}P,\end{array}$$

(23)

Thus, the closed-loop system of Equations (19) and (20) is obtained as follows:

$$\begin{array}{c}\dot{x}=\left(A-BK\right)x,\end{array}$$

(24)

From the controllability condition, the determinant of the system matrix will be:

$$\begin{array}{c}\left|A-BK\right|\ne 0.\end{array}$$

(25)

The system’s response to any given input can be fully determined. When the K state feedback control gain matrix is chosen correctly, the dynamic system will go to zero.

The master and slave of the 4D hyperchaotic system with control become:

$$A=\left(\begin{array}{cccc}1& 0& 0& 0\\ -10& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 1& 0& 0\end{array}\right),f\left(x\right)=\left(\begin{array}{c}M\left(x\right)\times x_2+p{x}_1{x}_3\\ x_1{x}_2-x_1{x}_2\\ x_1^2+q{x}_1{x}_3\\ 0\end{array}\right),f\left(y\right)=\left(\begin{array}{c}M\left(y\right)\times y_2+p{y}_1{y}_3\\ y_1{y}_2-y{y}_2\\ y_1^2+q{y}_1{y}_3\\ 0\end{array}\right)$$

The control matrix $I_{n\times n}$ is a unit matrix, and $B=I_{n\times n}.$ Because all conditions are satisfied with Equation (24), then all states of the system can be controlled. Therefore, the Lyapunov exponent nonlinear term −F (x, y) in u controller (10) was found.

The simulation block diagram based on these values is given in Figure 7 and Figure 8. According to the LQR method [39] given in the previous part, the performance index needs to be determined to calculate the linear control to $u_L K$ gain matrix. For this purpose, it is possible to take $Q=100\times I_{4\times 4},R=I_{4\times 4}$, and the $P$ and K matrices can be easily calculated as follows:

$$P=K=\left(\begin{array}{cccc} 13.9065& -4.1415& -0.2871& -0.1351\\ -4.1415& 9.1334& 0.4281& 0.5049\\ -0.2871& 0.4281& 10.0164& 0.5123\\ -0.1351& 0.5049& 0.5123& 10.0244\end{array}\right).$$

Therefore, the controller design was completed. In the Matlab/Simulink, the master and slave system initial values were set as $x_0=$ [4, 4, 4, 4] and $y_0=\left[2, 2, 2, 5\right]$. The simulation was performed by 0.001 s step and Runge-Kutta ODE45 solver for 5 s, and the results are given. The controller was active at the beginning. The error vector was equal to zero at t = 0.7 s. A comparison with other references in

Table 1. Comparison of our proposed synchronization method with other methods.

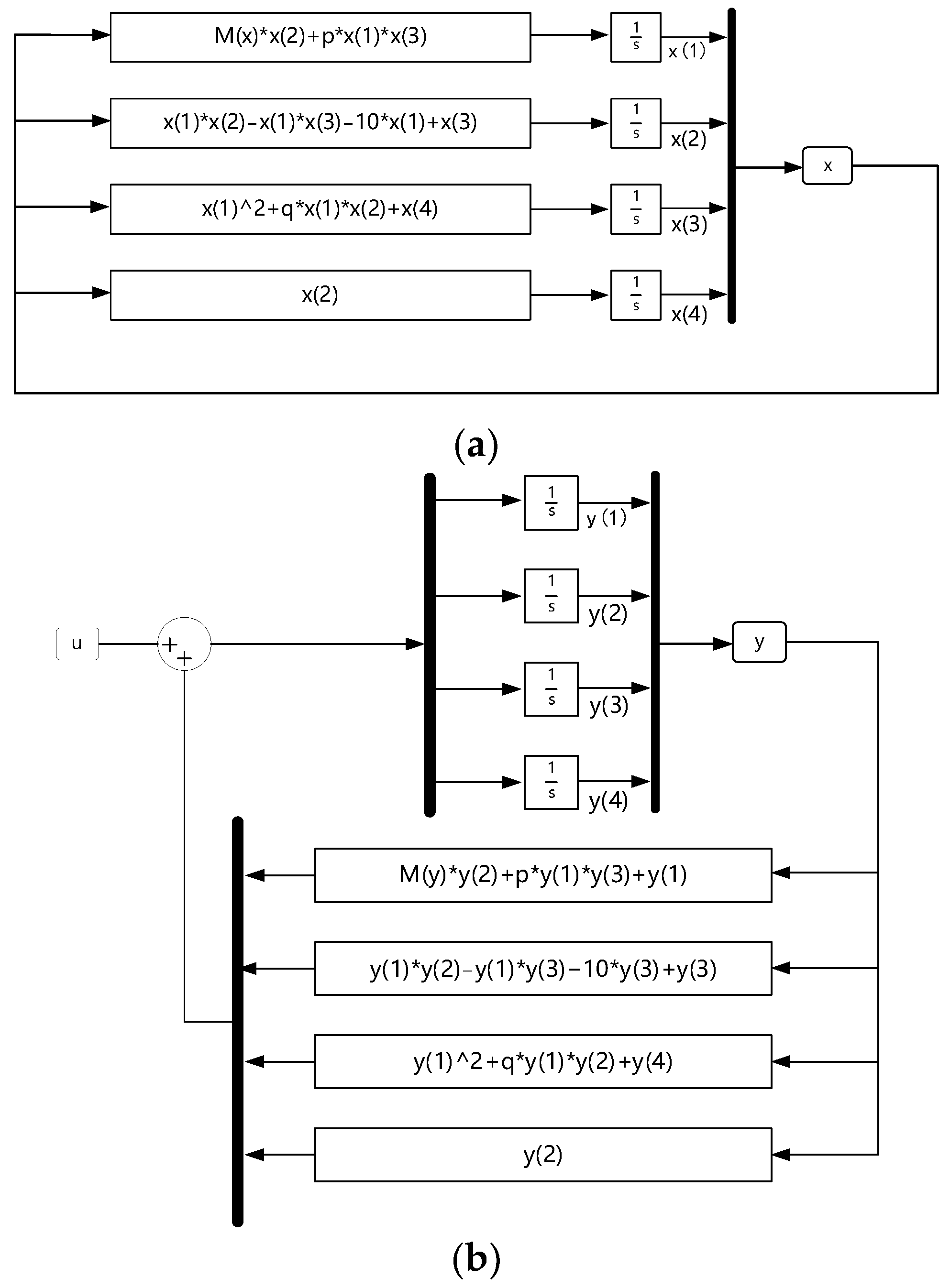
References	Types of System	Order	Methods	Time Required
[27]	Autonomous	5	Sliding mode control	t = 6.3 s
[26]	Non-autonomous	3	Linear feedback control	t = 8 s
[28]	Autonomous	4	Sliding mode control	t = 4.8 s
[29]	Autonomous	3	Sliding mode control	t = 4.1 s
[40]	Non-autonomous	5	Feedback control method	t = 13 s
[34]	Autonomous	2	Fuzzy neural network Function approximation	t = 1 s
[41]	Autonomous	3	Function approximation technique	t = 1 s
[42]	Non-autonomous	3	Feedback controller	t = 40 s
[43]	Non-autonomous	4	Generalized function projective	t = 6 s
this paper	Autonomous	4	Linear quadratic regulator	t = 0.7 s

shows that the synchronization results are excellent.

Figure 9 demonstrates that the error vector was equal to zero as soon as the controller started to work. Figure 10 shows the result of the master-slave system simulation. By increasing the value of the elements in the diagonal matrix Q, the continuous time to reach a steady state will be shortened, and the size of the control will increase. The simulation results show that our designed LQR controller with a memristor-based chaotic system had good synchronization performance and stability. In addition, the master-slave systems achieved synchronization quickly. Moreover, the system design is simple, and the synchronization control is extremely convenient.

The system we designed has more advantages than other synchronous control systems. First, our control method has good universality and can be widely applied to chaotic systems with different parameters. Second, the linear feedback controller can achieve a highly accurate controlling performance. Third, our synchronous control time is very short. Further, our controllers also have good robustness. As shown in Figure 11, a sine interference signal with an amplitude of 0.2 was added to the nonlinear term of the controller, and the simulation time was 100 s. We can observe that the four errors of the system synchronization were still controlled to 0 in a very short time; although there was a sine disturbance signal, the LQR controller still controlled the system error very well around e = 0 and did not make the system lose control because of the sensitive nature of the chaotic system.

5. Circuit Simulation

Based on hardware experimental circuits and Multisim circuit simulation models, the above complex dynamics implied by the proposed memristor-based hyperchaotic system can be demonstrated. Since it is difficult to specify the memristor’s initial conditions in hardware experiments [44,45,46,47], the dynamic behaviors of the memristor-based hyperchaotic system were obtained by Multisim circuit simulation.

Using Multisim Version 14.0 software with the circuit implementation of the memristor-based hyperchaotic system shown in Figure 1b, the circuit simulation model under typical circuit parameters was designed, as shown in Figure 12. When the simulated end time equals 100 s, the typical parameters $p=0.2$, $q=20$, $\alpha =1/7$, $\beta =2/7$, the value of the corresponding component in the circuit can be set as follows: R₁ = 5.0 MΩ, R₂ = 143 kΩ, R₃ = R₅ = R₈ = R₁₀ = R₁₇ = 1 MΩ, R₄ = 857 kΩ, R₉ = 50 kΩ, R₆ = R₇ = R₁₃ = R₁₅ = 100 kΩ, C₁ = C₂ = C₃ = C₄ = 1 µF, and the gains of seven multipliers are set to 1.

The memristor-based hyperchaotic system was found to have circuit-simulated phase portraits in different planes in Figure 13. The circuit simulation results are consistent with the numerical simulation results in Figure 2.

6. Conclusions

This paper first proposed a new hyperchaotic oscillator with a memristor nonlinearity and then discusses the various dynamical properties, including equilibrium states, attractors, Lyapunov exponents, and bifurcations of this system. Theoretical and experimental analyses indicate that compared to the initial chaotic system, the hyperchaotic system with added memristor exhibited more intense chaotic behavior with richer dynamical behavior and its trajectory preserved unsymmetrical distribution. Due to its complex hyperchaotic properties, it has the potential for future applications in information encryption. Further, we established a synchronization model of a chaotic system and analyzed its characteristics in detail. Moreover, we designed a synchronizing controller by applying the optimal linear quadratic regulator. Simulation results show that the control system achieved perfect performance, rapid response speed, and convenient controlling features. Finally, we implemented a detailed verification of the chaotic circuit by Multisim simulation. Compared to other existing synchronous controlling schemes, our synchronization method has the advantage of the short time required for synchronization; therefore, our proposed method is more advantageous. In future research, we will explore how to improve the robustness of the controller and apply the results of the work to simulate chaotic communication for better practical applications.