Performance Analysis of Regularized Convex Relaxation for Complex-Valued Data Detection
Abstract
:1. Introduction
2. Problem Formulation
2.1. Notation
2.2. Problem Setup
2.3. Performance Measures
2.4. Technical Assumptions
3. Asymptotic Performance Analysis
3.1. Main Asymptotic Results
3.2. Modulation Schemes
3.2.1. M-PSK Constellation
3.2.2. M-QAM Constellation
4. Numerical Simulation Results
5. Sketch of the Proof
5.1. CGMT: An Analysis Tool
5.2. Asymptotic Analysis
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T.L. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2013, 61, 1436–1449. [Google Scholar]
- Verdu, S. Multiuser Detection; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Mohammed, S.K.; Zaki, A.; Chockalingam, A.; Rajan, B.S. High-rate space–time coded large-MIMO systems: Low-complexity detection and channel estimation. IEEE J. Sel. Top. Signal Process. 2009, 3, 958–974. [Google Scholar] [CrossRef] [Green Version]
- Thrampoulidis, C.; Xu, W.; Hassibi, B. Symbol error rate performance of box-relaxation decoders in massive mimo. IEEE Trans. Signal Process. 2018, 66, 3377–3392. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, E.; Salehi, F.; Hassibi, B. Performance analysis of convex data detection in mimo. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 4554–4558. [Google Scholar]
- Atitallah, I.B.; Thrampoulidis, C.; Kammoun, A.; Al-Naffouri, T.Y.; Hassibi, B.; Alouini, M.S. Ber analysis of regularized least squares for bpsk recovery. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 4262–4266. [Google Scholar]
- Alrashdi, A.M.; Kammoun, A.; Muqaibel, A.H.; Al-Naffouri, T.Y. Optimum M-PAM Transmission for Massive MIMO Systems with Channel Uncertainty. arXiv 2020, arXiv:2008.06993. [Google Scholar]
- Atitallah, I.B.; Thrampoulidis, C.; Kammoun, A.; Al-Naffouri, T.Y.; Alouini, M.S.; Hassibi, B. The BOX-LASSO with application to GSSK modulation in massive MIMO systems. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 1082–1086. [Google Scholar]
- Aissa-El-Bey, A.; Pastor, D.; Sbai, S.M.A.; Fadlallah, Y. Sparsity-based recovery of finite alphabet solutions to underdetermined linear systems. IEEE Trans. Inf. Theory 2015, 61, 2008–2018. [Google Scholar] [CrossRef] [Green Version]
- Hajji, Z.; Aïssa-El-Bey, A.; Amis, K. Simplicity-based recovery of finite-alphabet signals for large-scale MIMO systems. Digit. Signal Process. 2018, 80, 70–82. [Google Scholar] [CrossRef] [Green Version]
- Sasahara, H.; Hayashi, K.; Nagahara, M. Multiuser detection based on MAP estimation with sum-of-absolute-values relaxation. IEEE Trans. Signal Process. 2017, 65, 5621–5634. [Google Scholar] [CrossRef]
- Hayakawa, R.; Hayashi, K. Asymptotic Performance of Discrete-Valued Vector Reconstruction via Box-Constrained Optimization With Sum of ℓ1 Regularizers. IEEE Trans. Signal Process. 2020, 68, 4320–4335. [Google Scholar] [CrossRef]
- Hayakawa, R.; Hayashi, K. Convex optimization-based signal detection for massive overloaded MIMO systems. IEEE Trans. Wirel. Commun. 2017, 16, 7080–7091. [Google Scholar] [CrossRef]
- Hayakawa, R.; Hayashi, K. Reconstruction of complex discrete-valued vector via convex optimization with sparse regularizers. IEEE Access 2018, 6, 66499–66512. [Google Scholar] [CrossRef]
- Thrampoulidis, C.; Abbasi, E.; Hassibi, B. Precise error analysis of regularized M-estimators in high dimensions. IEEE Trans. Inf. Theory 2018, 64, 5592–5628. [Google Scholar] [CrossRef] [Green Version]
- Stojnic, M. A framework to characterize performance of lasso algorithms. arXiv 2013, arXiv:1303.7291. [Google Scholar]
- Thrampoulidis, C.; Oymak, S.; Hassibi, B. Regularized linear regression: A precise analysis of the estimation error. In Proceedings of the Conference on Learning Theory, PMLR, Paris, France, 3–6 July 2015; pp. 1683–1709. [Google Scholar]
- Oymak, S.; Tropp, J.A. Universality laws for randomized dimension reduction, with applications. Inf. Inference J. IMA 2018, 7, 337–446. [Google Scholar] [CrossRef]
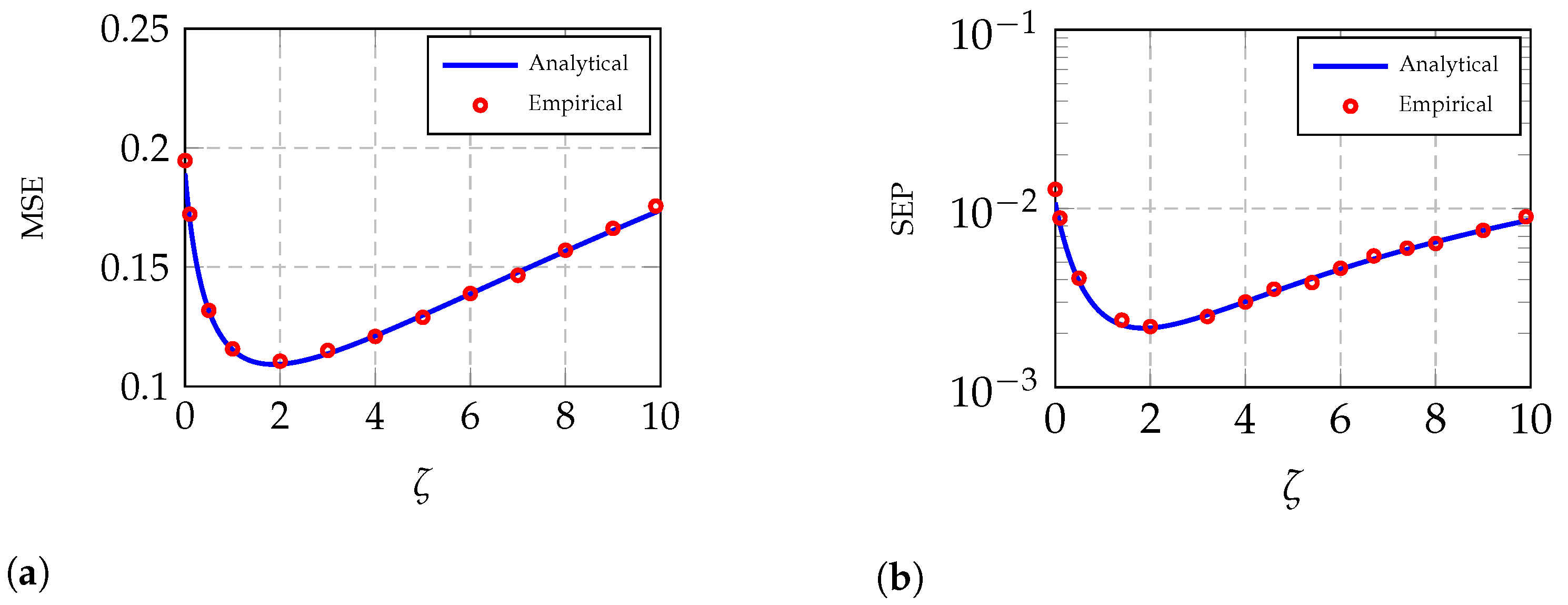
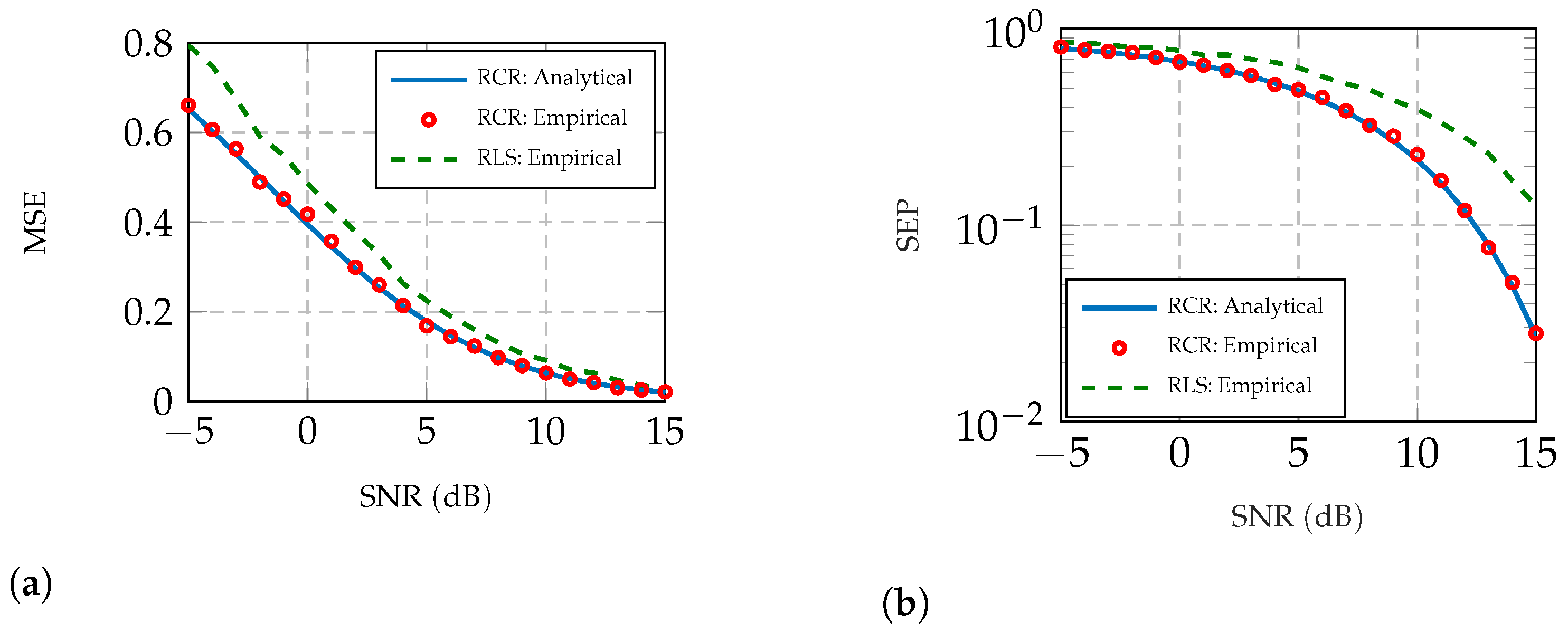

| SNR (dB) | MSE (RCR): Analytical | MSE (RCR): Empirical | MSE (RLS): Empirical |
|---|---|---|---|
| 0 | |||
| 5 | |||
| 10 | |||
| 15 | |||
| 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrashdi, A.M.; Sifaou, H. Performance Analysis of Regularized Convex Relaxation for Complex-Valued Data Detection. Mathematics 2022, 10, 1585. https://doi.org/10.3390/math10091585
Alrashdi AM, Sifaou H. Performance Analysis of Regularized Convex Relaxation for Complex-Valued Data Detection. Mathematics. 2022; 10(9):1585. https://doi.org/10.3390/math10091585
Chicago/Turabian StyleAlrashdi, Ayed M., and Houssem Sifaou. 2022. "Performance Analysis of Regularized Convex Relaxation for Complex-Valued Data Detection" Mathematics 10, no. 9: 1585. https://doi.org/10.3390/math10091585
APA StyleAlrashdi, A. M., & Sifaou, H. (2022). Performance Analysis of Regularized Convex Relaxation for Complex-Valued Data Detection. Mathematics, 10(9), 1585. https://doi.org/10.3390/math10091585






