Analytical Treatment of Unsteady Fluid Flow of Nonhomogeneous Nanofluids among Two Infinite Parallel Surfaces: Collocation Method-Based Study
Abstract
:1. Introduction
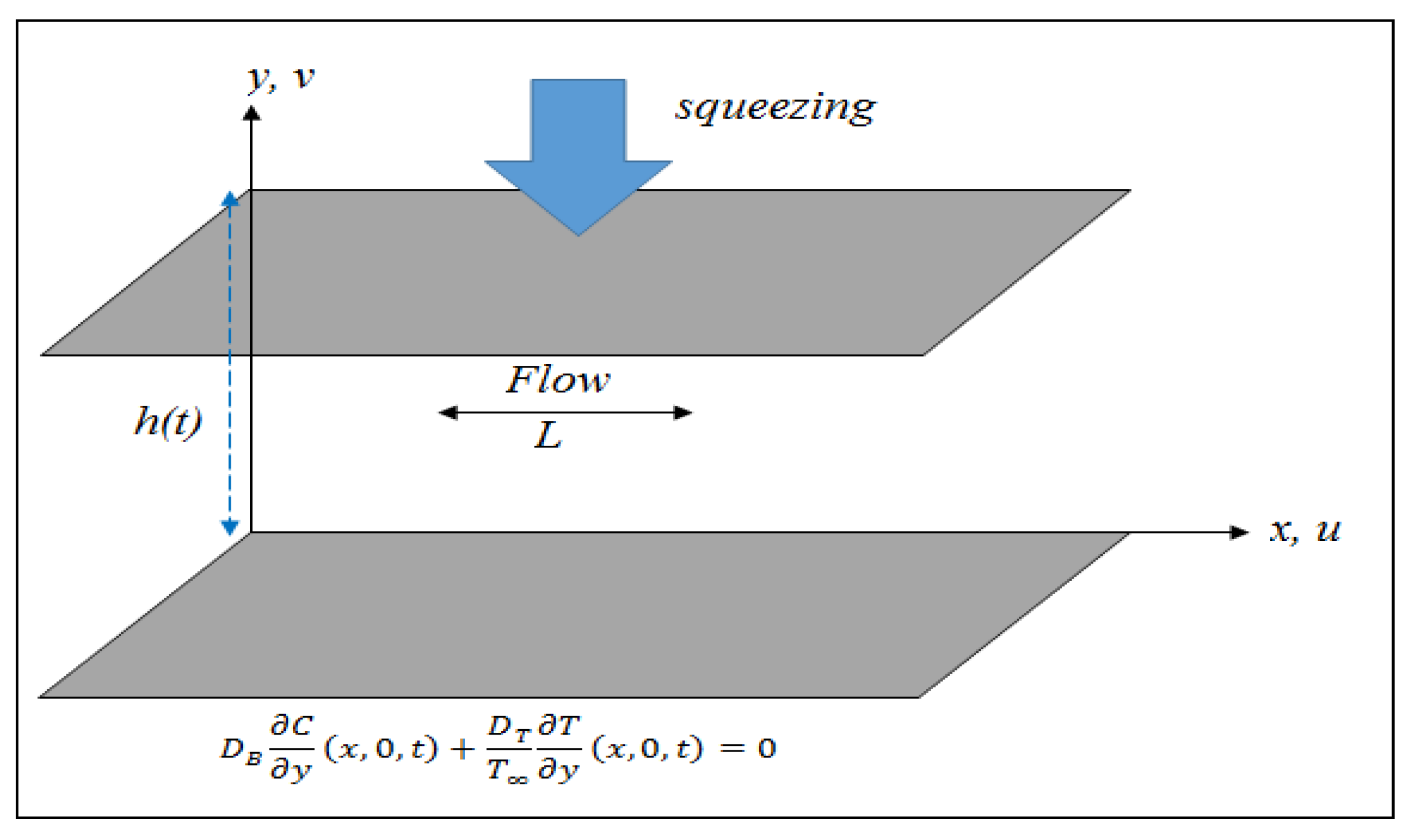
2. Mathematical Modeling
3. Solution Procedure via CM
4. Results and Discussion
5. Conclusions
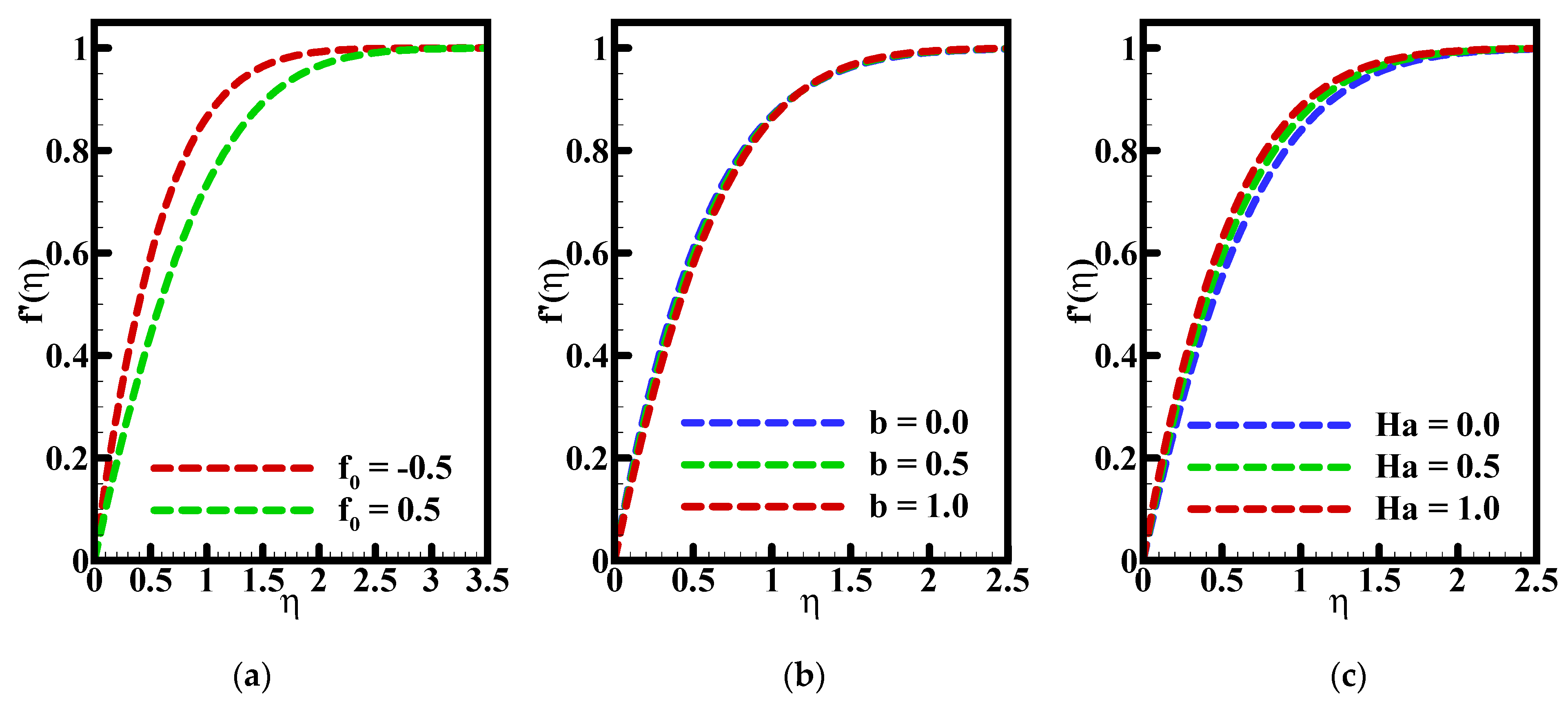
- The velocity is enhanced due to the higher impact of the parameter Ha (Hartmann number), while a different kind of behavior, actually a drop, is provided by the parameter f0.
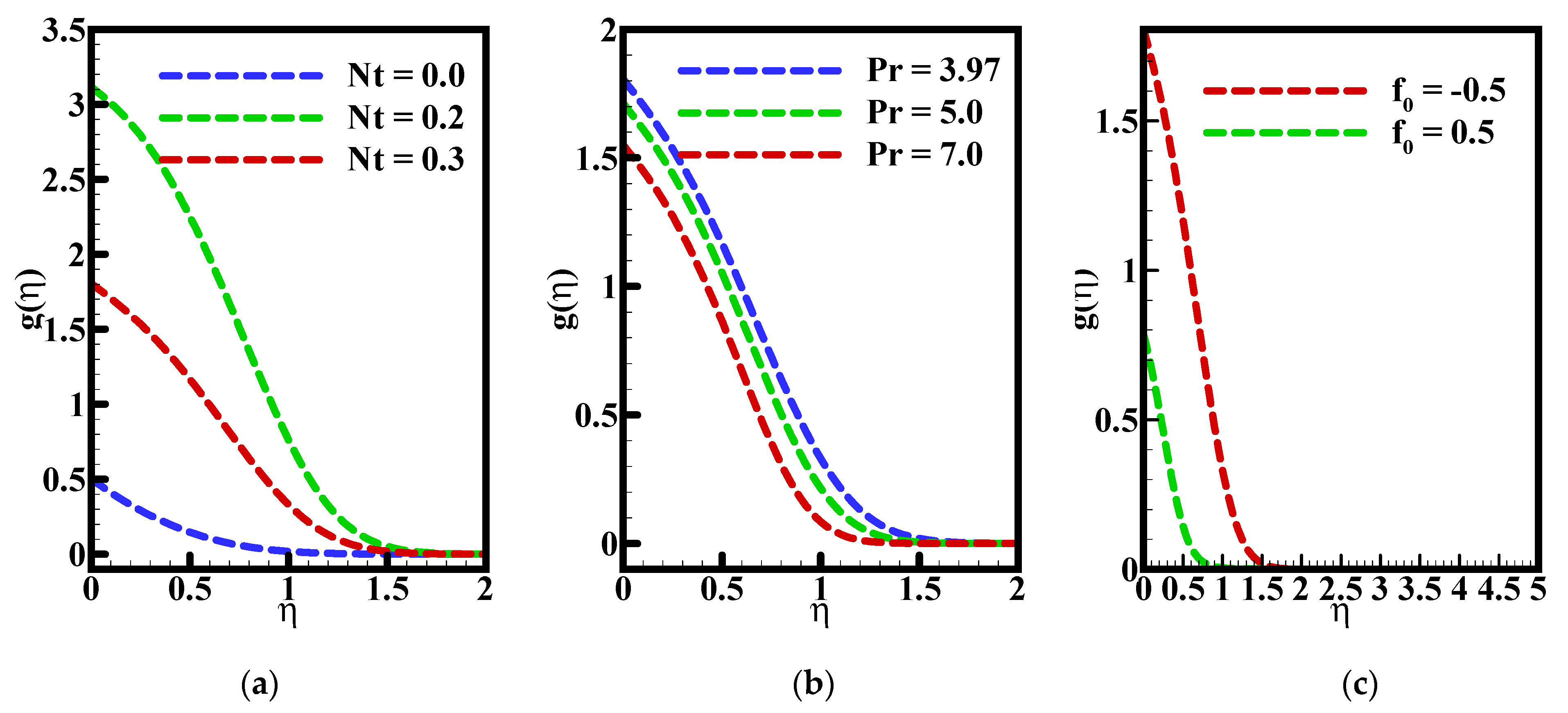
- The parameter Nt caused an efficient enhancement in the temperature distribution, while the parameters Nt and f0 provided a drop in the temperature that actually affected the rate of heat transmission.
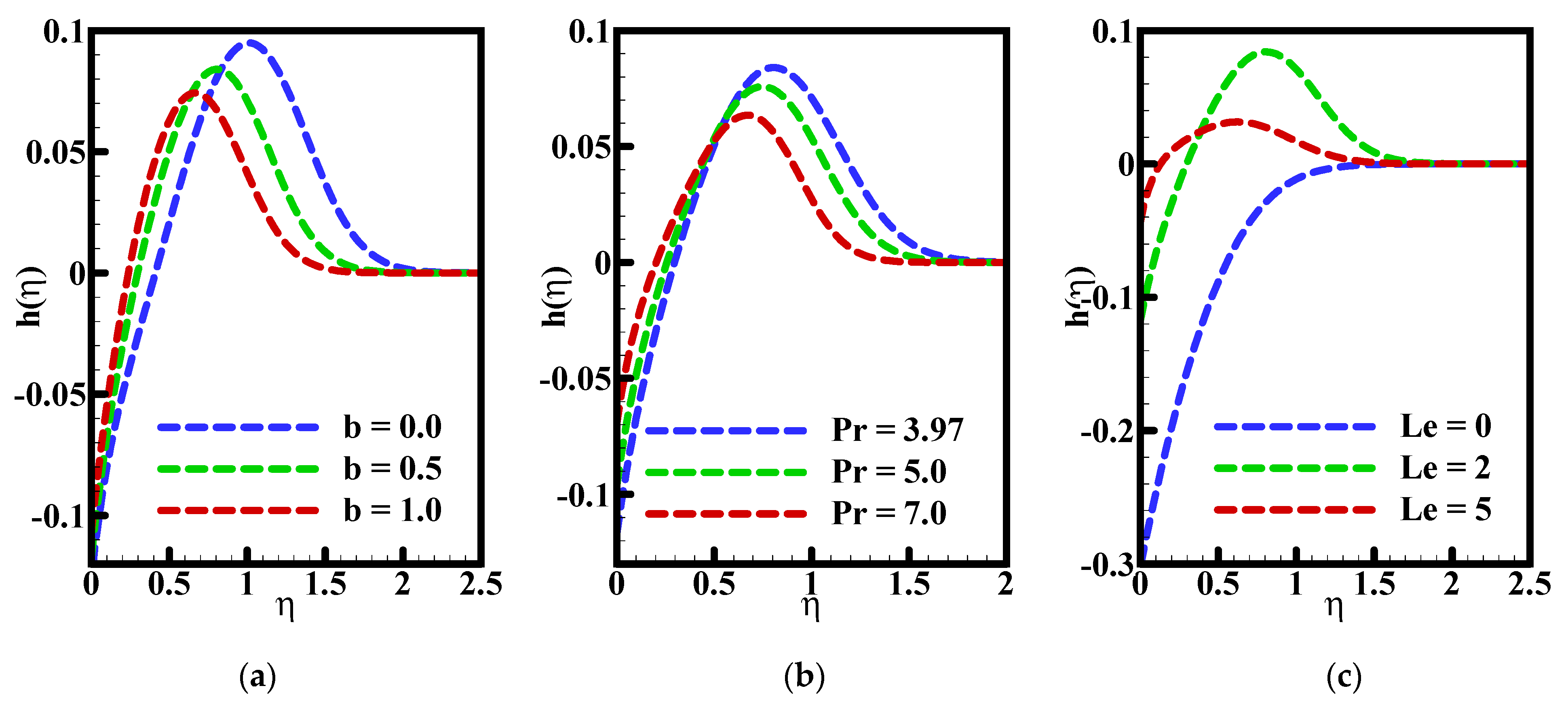
- Dual behavior of concentration is noted for parameter b, while it can be noted that mixed increasing behavior is available for the concentration against Le.
- The concentration and velocity profiles dropped due to the increasing values of parameter b, but the impact of parameter b is more significant on concentration. It showed a dual behavior for concentration after a particular stretch.
- It is observed that the proposed methodology is found to be really effective to deal with nonlinear mechanical or fluid dynamical problems.
- The presented method can be further used for a class of nonlinear problems arising in mechanics.
- The proposed scheme can be extended to investigate the solution of channel flow, fractional-order fluid flow, unsteady cavity models, etc.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Distance between two plates | |
| and | Velocity components in - and -directions |
| Free stream velocity | |
| Temperature of the fluid | |
| Concentration of the fluid | |
| B | Magnetic field |
| Pressure | |
| Kinematic viscosity | |
| Density | |
| Brownian parameter | |
| Thermophoresis diffusion parameter | |
| Free stream temperature | |
| Heat flux | |
| Velocity at sensor surface | |
| Ha | Hartmann number |
| Squeezed parameter | |
| Prandtl number | |
| Thermophoretic parameter | |
| Brownian motion parameter | |
| Lewis number | |
| Permeable velocity | |
| Re | Local Reynolds number |
| CM | Collocation method |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Xue, Q.; Xu, W.-M. A model of thermal conductivity of nanofluids with interfacial shells. Mater. Chem. Phys. 2005, 90, 298–301. [Google Scholar] [CrossRef]
- Usman, M.; Hamid, M.; Zubair, T.; Haq, R.U.; Wang, W. Cu-Al2O3/Water hybrid nanofluid through a permeable surface in the presence of nonlinear radiation and variable thermal conductivity via LSM. Int. J. Heat Mass Transf. 2018, 126, 1347–1356. [Google Scholar] [CrossRef]
- Hamid, M.; Usman, M.; Zubair, T.; Haq, R.U.; Wang, W. Shape effects of MoS2 nanoparticles on rotating flow of nanofluid along a stretching surface with variable thermal conductivity: A Galerkin approach. Int. J. Heat Mass Transf. 2018, 124, 706–714. [Google Scholar] [CrossRef]
- Usman, M.; Haq, R.U.; Hamid, M.; Wang, W. Least square study of heat transfer of water based Cu and Ag nanoparticles along a converging/diverging channel. J. Mol. Liq. 2018, 249, 856–867. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Hamid, M.; Usman, M.; Kanwal, A.; Zubair, T.; Wang, W.; Nazir, A. Rotating flow of nanofluid due to exponentially stretching surface: An optimal study. J. Algorithms Comput. Technol. 2019, 13, 1748302619881365. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Khan, S.A.; Alsaedi, A.; Zai, Q.Z. Computational analysis of heat transfer in mixed convective flow of CNTs with entropy optimization by a curved stretching sheet. Int. Commun. Heat Mass Transf. 2020, 118, 104881. [Google Scholar] [CrossRef]
- Wang, C. Stretching a surface in a rotating fluid. Z. Angew. Math. Und Phys. ZAMP 1988, 39, 177–185. [Google Scholar] [CrossRef]
- Yao, S.; Fang, T.; Zhong, Y. Heat transfer of a generalized stretching/shrinking wall problem with convective boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 752–760. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Bejawada, S.G.; Khan, Z.H.; Hamid, M. Heat generation/absorption on MHD flow of a micropolar fluid over a heated stretching surface in the presence of the boundary parameter. Heat Transf. 2021, 50, 6129–6147. [Google Scholar] [CrossRef]
- Soomro, F.A.; Haq, R.U.; Khan, Z.H.; Zhang, Q. Passive control of nanoparticle due to convective heat transfer of Prandtl fluid model at the stretching surface. Chin. J. Phys. 2017, 55, 1561–1568. [Google Scholar] [CrossRef]
- Naqvi, S.M.R.S.; Muhammad, T.; Saleem, S.; Kim, H.M. Significance of non-uniform heat generation/absorption in hydromagnetic flow of nanofluid due to stretching/shrinking disk. Phys. A Stat. Mech. Its Appl. 2020, 553, 123970. [Google Scholar] [CrossRef]
- Fan, S.; Wang, Y.; Cao, S.; Zhao, B.; Sun, T.; Liu, P. A deep residual neural network identification method for uneven dust accumulation on photovoltaic (PV) panels. Energy 2022, 239, 122302. [Google Scholar] [CrossRef]
- Stefen, M. Versuch Uber die scheinbare adhesion. Sitz. Akad. Wiss. Wien Math. Nat. 1874, 69, 713–721. [Google Scholar]
- Reynolds, O.I.V. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar]
- Mohyud-Din, S.T.; Usman, M.; Wang, W.; Hamid, M. A study of heat transfer analysis for squeezing flow of a Casson fluid via differential transform method. Neural Comput. Appl. 2018, 30, 3253–3264. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Qayyum, A.; Alsaedi, A.; Mustafa, M. On squeezing flow of nanofluid in the presence of magnetic field effects. J. Mol. Liq. 2016, 213, 179–185. [Google Scholar] [CrossRef]
- Haq, R.U.; Nadeem, S.; Khan, Z.H.; Noor, N.F. MHD squeezed flow of water functionalized metallic nanoparticles over a sensor surface. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 73, 45–53. [Google Scholar] [CrossRef]
- Chu, Y.M.; Khan, M.I.; Waqas, H.; Farooq, U.; Khan, S.U.; Nazeer, M. Numerical simulation of squeezing flow Jeffrey nanofluid confined by two parallel disks with the help of chemical reaction: Effects of activation energy and microorganisms. Int. J. Chem. React. Eng. 2021, 19, 717–725. [Google Scholar] [CrossRef]
- Waqas, H.; Wakif, A.; Al-Mdallal, Q.; Zaydan, M.; Farooq, U. Significance of magnetic field and activation energy on the features of stratified mixed radiative-convective couple-stress nanofluid flows with motile microorganisms. Alex. Eng. J. 2021, 61, 1425–1436. [Google Scholar] [CrossRef]
- Munawar, S.; Mehmood, A.; Ali, A. Three-dimensional squeezing flow in a rotating channel of lower stretching porous wall. Comput. Math. Appl. 2012, 64, 1575–1586. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Soomro, F.A.; Imtiaz, J. Influences of imposed magnetic force on treatment of hybrid nanofluid involving non-Darcy porous model. Int. Commun. Heat Mass Transf. 2021, 125, 105318. [Google Scholar] [CrossRef]
- Usman, M.; Zubair, T.; Hamid, M.; Haq, R.U.; Khan, Z.H. Unsteady flow and heat transfer of tangent-hyperbolic fluid: Legendre wavelet-based analysis. Heat Transf. 2021, 50, 3079–3093. [Google Scholar] [CrossRef]
- Nayak, M.K.; Akbar, N.S.; Pandey, V.S.; Khan, Z.H.; Tripathi, D. 3D free convective MHD flow of nanofluid over permeable linear stretching sheet with thermal radiation. Powder Technol. 2017, 315, 205–215. [Google Scholar] [CrossRef]
- Hussain, S.; Khan, Z.; Nadeem, S. Water driven flow of carbon nanotubes in a rotating channel. J. Mol. Liq. 2016, 214, 136–144. [Google Scholar] [CrossRef]
- Fan, S.; Wang, Y.; Cao, S.; Sun, T.; Liu, P. A novel method for analyzing the effect of dust accumulation on energy efficiency loss in photovoltaic (PV) system. Energy 2021, 34, 121112. [Google Scholar] [CrossRef]
- Haq, R.U.; Hammouch, Z.; Khan, W.A. Water-based squeezing flow in the presence of carbon nanotubes between two parallel disks. Therm. Sci. 2016, 20, 1973–1981. [Google Scholar] [CrossRef]
- Khan, Z.H.; Usman, M.; Zubair, T.; Hamid, M.; Haq, R.U. Brownian motion and thermophoresis effects on unsteady stagnation point flow of Eyring–Powell nanofluid: A Galerkin approach. Commun. Theor. Phys. 2020, 72, 125005. [Google Scholar] [CrossRef]
- Usman, M.; Mohyud Din, S.T.; Zubair, T.; Hamid, M.; Wang, W. Fluid flow and heat transfer investigation of blood with nanoparticles through porous vessels in the presence of magnetic field. J. Algorithms Comput. Technol. 2018, 13, 1748301818788661. [Google Scholar] [CrossRef] [Green Version]
- Ghalambaz, M.; Groşan, T.; Pop, I. Mixed convection boundary layer flow and heat transfer over a vertical plate embedded in a porous medium filled with a suspension of nano-encapsulated phase change materials. J. Mol. Liq. 2019, 293, 111432. [Google Scholar] [CrossRef]
- Mehryan, S.A.M.; Izadpanahi, E.; Ghalambaz, M.; Chamkha, A.J. Mixed convection flow caused by an oscillating cylinder in a square cavity filled with Cu–Al2O3/water hybrid nanofluid. J. Therm. Anal. Calorim. 2019, 137, 965–982. [Google Scholar] [CrossRef]
- Yang, S.; Tan, J.; Chen, B. Robust Spike-Based Continual Meta-Learning Improved by Restricted Minimum Error Entropy Criterion. Entropy 2022, 24, 455. [Google Scholar] [CrossRef]
- Li, P.; Gao, X.; Li, Z.; Zhou, X. Effect of the temperature difference between land and lake on photovoltaic power generation. Renewable Energy 2022, 185, 86–95. [Google Scholar] [CrossRef]
- Huang, L.; Zhou, W.; Xu, H.; Wang, L.; Zou, J.; Zhou, Q. Dynamic fluid states in organic-inorganic nanocomposite: Implications for shale gas recovery and CO2 sequestration. Chem. Eng. J. 2021, 411, 128423. [Google Scholar] [CrossRef]
- Zhu, T.; Li, Q.; Yu, A. Analysis of the solar spectrum allocation in a spectral-splitting photovoltaic-thermochemical hybrid system. Solar Energy 2022, 232, 63–72. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, J.; Tan, Z.; Tian, X.; Wang, Q. Numerical study on gravity-driven granular flow around tube out-wall: Effect of tube inclination on the heat transfer. Int. J. Heat Mass Transf. 2020, 174, 121296. [Google Scholar] [CrossRef]
- Cai, T.; Dong, M.; Liu, H.; Nojavan, S. Integration of hydrogen storage system and wind generation in power systems under demand response program: A novel p-robust stochastic programming. Int. J. Hydrogen Energy 2021, 47, 443–458. [Google Scholar] [CrossRef]
- Usman, M.; Hamid, M.; Mohyud Din, S.T.; Waheed, A.; Wang, W. Exploration of uniform heat flux on the flow and heat transportation of ferrofluids along a smooth plate: Comparative investigation. Int. J. Biomath. 2018, 11, 1850048. [Google Scholar] [CrossRef]
- Usman, M.; Hamid, M.; Rashidi, M.M. Gegenbauer wavelets collocation-based scheme to explore the solution of free bio-convection of nanofluid in 3D nearby stagnation point. Neural Comput. Appl. 2019, 31, 8003–8019. [Google Scholar] [CrossRef]
- Yu, D.; Zhao, X.; Wang, Y.; Jiang, L.; Liu, H. Research on Energy Management of a Virtual Power Plant Based on the Improved Cooperative Particle Swarm Optimization Algorithm. Front. Energy Res. 2022, 10, 785569. [Google Scholar] [CrossRef]
- Hamid, M.; Usman, M.; Haq, R.U.; Tian, Z. A spectral approach to analyze the nonlinear oscillatory fractional-order differential equations. Chaos Solitons Fractals 2021, 146, 110921. [Google Scholar] [CrossRef]
- Zaheer, M.; Khan, H.; Shah, S.H.; Mashwani, S.A.; ul Haq, E.; Manzoor, F. Solute transport modelling in low-permeability homogeneous and saturated soil media: Transport in low-permeability soil media. Rud.-Geološko-Naft. Zb. (Min. Geol. Pet. Bull.) 2021, 36, 25–32. [Google Scholar]
- Chamkha, A.J.; Aly, A.M.; Mansour, M.A. Similarity solution for unsteady heat and mass transfer from a stretching surface embedded in a porous medium with suction/injection and chemical reaction effects. Chem. Eng. Commun. 2010, 197, 846–858. [Google Scholar] [CrossRef]
- Sharidan, S.; Mahmood, T.; Pop, I. Similarity solutions for the unsteady boundary layer flow and heat transfer due to a stretching sheet. Int. J. Appl. Mech. Eng. 2006, 11, 647–654. [Google Scholar]
- Mukhopadhyay, S.; Gorla, R.S.R. Unsteady MHD boundary layer flow of an upper convected Maxwell fluid past a stretching sheet with first order constructive/destructive chemical reaction. J. Nav. Archit. Mar. Eng. 2012, 9, 123–133. [Google Scholar] [CrossRef]
- Bibi, M.; Rehman, K.U.; Malik, M.Y.; Tahir, M. Numerical study of Unsteady Williamson fluid flow and heat transfer in the presence of MHD through a permeable stretching surface. Eur. Phys. J. Plus 2018, 133, 154. [Google Scholar] [CrossRef]
- Kebede, T.; Haile, E.; Awgichew, G.; Walelign, T. Heat and mass transfer in unsteady boundary layer flow of Williamson nanofluids. J. Appl. Math. 2020, 2020, 1890972. [Google Scholar] [CrossRef]
- Khan, M.; Azam, M. Unsteady heat and mass transfer mechanisms in MHD Carreau nanofluid flow. J. Mol. Liq. 2017, 225, 554–562. [Google Scholar] [CrossRef]

| 0 | 0.5 | −0.5 | 3.97 | 0.3 | 0.5 | 2 | 1.41209 | 0.53992 | - |
| 1 | - | - | - | - | - | - | 1.60239 | 0.55369 | - |
| 2 | - | - | - | - | - | - | 1.77102 | 0.56518 | - |
| 0.5 | 0 | - | - | - | - | - | 1.71854 | 0.45771 | - |
| - | 0.5 | - | - | - | - | - | 1.60239 | 0.55370 | - |
| - | 1 | - | - | - | - | - | 1.48114 | 0.67073 | - |
| - | 0.25 | −0.5 | - | - | - | - | 1.66109 | 0.50362 | - |
| - | - | 0.5 | - | - | - | - | 1.09294 | −0.22818 | - |
| - | - | −0.5 | 3 | - | - | - | - | 0.48136 | - |
| - | - | - | 5 | - | - | - | - | 0.53414 | - |
| - | - | - | 7 | - | - | - | - | 0.59050 | - |
| - | - | - | 6.2 | 0.1 | - | - | - | 2.86340 | 0.2000 |
| - | - | - | - | 0.2 | - | - | - | 0.35443 | 0.4000 |
| - | - | - | - | 0.3 | - | - | - | 0.56881 | 0.6000 |
| - | - | - | - | 0.3 | 0.1 | - | - | - | 3.0000 |
| - | - | - | - | - | 0.2 | - | - | - | 1.5000 |
| - | - | - | - | - | 0.3 | - | - | - | 1.0000 |
| - | - | - | - | - | 0.5 | 0 | - | 3.09699 | - |
| - | - | - | - | - | - | 2 | - | 0.56881 | - |
| - | - | - | - | - | - | 5 | - | 0.65213 | - |
| Veclocity | Temperature | Concentration | |
|---|---|---|---|
| 0.00 | 0.00000000 | 1.80602974 | −0.11719518 |
| 0.30 | 0.40286279 | 1.46945390 | 0.00092259 |
| 0.60 | 0.66809369 | 0.99463258 | 0.06836315 |
| 0.90 | 0.82887854 | 0.47417323 | 0.08077955 |
| 1.20 | 0.91848603 | 0.13083488 | 0.04128107 |
| 1.50 | 0.96427592 | 0.01941746 | 0.00878368 |
| 1.80 | 0.98566979 | 0.00170315 | 0.00088685 |
| 2.10 | 0.99478720 | 0.00009441 | 0.00005156 |
| 2.40 | 0.99832789 | 0.00000335 | 0.00000187 |
| 2.70 | 0.99958484 | 0.00000007 | 0.00000004 |
| 3.00 | 1.00000000 | 0.00000000 | 0.00000000 |
| [47] | [48] | [49] | [50] | [51] | [52] | Present | |
|---|---|---|---|---|---|---|---|
| 0.0 | - | - | - | 1.0005 | 1.00000 | 1.00000 | 1.00000 |
| 0.2 | - | - | - | 1.0685 | 1.06874 | 1.06801 | 1.06871 |
| 0.4 | - | - | - | 1.1349 | 1.13521 | 1.13469 | 1.13522 |
| 0.6 | - | - | - | 1.1992 | 1.19930 | 1.19912 | 1.19924 |
| 0.8 | 1.261512 | 1.26104 | 1.261479 | - | 1.26099 | 1.26104 | 1.26092 |
| 1.2 | 1.378052 | 1.37772 | 1.377850 | - | 1.37755 | 1.37772 | 1.37761 |
| 2.0 | - | - | - | - | 1.58740 | 1.58737 | 1.58738 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, F.; Yu, D.; Sheng, Q. Analytical Treatment of Unsteady Fluid Flow of Nonhomogeneous Nanofluids among Two Infinite Parallel Surfaces: Collocation Method-Based Study. Mathematics 2022, 10, 1556. https://doi.org/10.3390/math10091556
Gao F, Yu D, Sheng Q. Analytical Treatment of Unsteady Fluid Flow of Nonhomogeneous Nanofluids among Two Infinite Parallel Surfaces: Collocation Method-Based Study. Mathematics. 2022; 10(9):1556. https://doi.org/10.3390/math10091556
Chicago/Turabian StyleGao, Fengkai, Dongmin Yu, and Qiang Sheng. 2022. "Analytical Treatment of Unsteady Fluid Flow of Nonhomogeneous Nanofluids among Two Infinite Parallel Surfaces: Collocation Method-Based Study" Mathematics 10, no. 9: 1556. https://doi.org/10.3390/math10091556
APA StyleGao, F., Yu, D., & Sheng, Q. (2022). Analytical Treatment of Unsteady Fluid Flow of Nonhomogeneous Nanofluids among Two Infinite Parallel Surfaces: Collocation Method-Based Study. Mathematics, 10(9), 1556. https://doi.org/10.3390/math10091556






