Abstract
This paper looks at adapting a recent approach found in the literature for pricing short-term American options to price American straddle options with two free boundaries. We provide a series solution in which explicit formulas for the coefficients are given. Hence, no complicated, recursive systems or nonlinear integral equations need to be solved, and the method efficiently provides fast solutions. We also compare the method with a numerical method and find that it gives very accurate prices not only for the option value, but also for the critical stock prices.
Keywords:
American straddle options; options valuation; analytical approximations; critical stock prices; free boundary problems MSC:
35R35; 91G50; 91-10
1. Introduction
A European straddle is a strategy that involves buying both a European call option and a European put option both with the same strike price and expiration date. The strategy is extremely popular in a volatile market as the more the underlying asset moves from the chosen strike price, the higher the value of the straddle. The European straddle can be exercised only at the expiry time, at which time the payoff is , where S is the value of the underlying asset at expiry and X is the strike price. The value of a European straddle is simply the sum of the component call and put options, which can be calculated using the famous Black–Scholes formulas (see, e.g., Kwok [1]). An American straddle also has the payoff at expiry of , but it can be exercised at any time before expiry and so there exist free boundaries, or optimal exercise boundaries (OEBs), which mark the borders between holding and exercising the straddle. Hence, its value is not simply the combination of an American call option and an American put option.
American options offer investors a means to offset their financial risk as well as a means to attain higher returns should their opinion on the market direction be correct. Given their immense popularity worldwide, it is as expected that their pricing has attracted considerable research. Unfortunately to date, even for the vanilla American call and put options, no fully analytical solution for their price and optimal exercise boundaries have been found. While the American call and put options each have one free boundary, the American straddle has two: an upper one, similar to that for a call option and a lower one, similar to that for a put option. This means the valuation of American straddles is even more challenging.
In 2002, Alobaidi and Mallier [2] attempted to use partial Laplace transforms on the Black–Scholes partial differential Equation (PDE) to find the value of the straddle option price. However they were not able to invert the value function in Laplace format. Then in 2006, the same authors [3] used a method due to Kim [4] to formulate an integral representation for the price of straddle options near expiry. They obtained a set of four coupled nonlinear (Volterra of the second kind) integral equations governing the locations of the free boundaries, which were then solved asymptotically to find their locations close to expiry. Both the value function and the free boundaries were written as series in functions of time-to-expiry, and to determine each coefficient involved solving complicated nonlinear systems of equations.
A related derivative to the American straddle is the American strangle. The payoff of strangle options is defined as , where K is the higher strike price and L is the lower strike price, satisfying . Hence, the strangle is similar to the straddle, but uses different strike prices. From the definition of the payoff function, this option will be in-the-money when the stock price S is in the regions and .
The strangle was studied by Chiarella and Ziogas [5] who used the Fourier transform method to formulate a coupled integral equation system for the value of the strangle’s two free boundaries. The system was solved numerically and the free boundaries were then used to find the price of the American strangle.
Additionally, Detemple [6] got the same early exercise premium representation for the value of American strangle options as was found in Chiarella and Ziogas [5], which again was suitable for applying a numerical method to calculate the option price.
Numerical methods, such as lattice methods, have also been studied for pricing American strangles. This includes the work of Gao et al. [7], who used lattice methods for pricing American strangles and then compared the results with the least square Monte Carlo method via numerical examples.
More recently, Kang et al. [8] attempted to price American strangles using Laplace–Carson transforms. However, although they derived in the Laplace–Carson space an analytic expression of the value function and a nonlinear system of equations in the transformed variables of the two free boundaries, this nonlinear system had to be solved using numerical Laplace inversion techniques.
The majority of the above references used the integral equation approach to price the American strangle or straddle. However, this generally means no closed-form solutions for the optimal exercise boundaries and value function. The nonlinear integral equations are also difficult to solve efficiently using numerical methods. In a different approach, Ma et al. [9] constructed upper and lower bounds for the value of an American strangle and proposed an algorithm to approximate the early exercise boundary of the American strangle option.
Also using an integral equation approach, Qiu [10] showed that the double optimal stopping boundaries for American strangle and straddle options with finite maturity can be described as the unique pair of solution to a system of two nonlinear integral equations. These equations were derived using an early exercise premium representation. To calculate the double free-boundaries in the system of two integral equations he introduced a numerical method. Through computer simulation he showed intuitively that with respect to time, the lower and upper boundaries were increasing and decreasing, respectively. He also showed (in his Theorem 8) that for American strangle options, when time t approaches maturity T, the upper and lower free-boundaries converge respectively to the early exercise boundaries of the American call and put options, i.e., where are the risk-free interest rate and continuous dividend yield, respectively.
In this paper, we adapt and improve on the method of Medvedev and Scaillet [11], who proposed a new analytical approximation method to price short-term American put options. The main idea behind their proposal was to replace the optimal exercise rule with a simple suboptimal exercise rule so that as soon as the option’s moneyness reached some desired level, then the option should be exercised. The American option price was given as an asymptotic series with respect to time to maturity. They say their method [11] ‘is both computationally tractable and general enough to be successfully applied to a three factor diffusion model without jumps’. However a major weakness of the method is that complicated recursive systems need to be solved in order to calculate the coefficients of their asymptotic series. With investors requiring quick answers, this is a significant issue. In this paper, we modify their method to present an analytic approximation to American straddle options. However, rather than solving a recursive system, we provide explicit formulas for the coefficients in the series solution. Free boundary problems are notoriously hard to solve and the American straddle option problem has two free boundaries: an upper and a lower. The solution for the options as well as the critical stock prices are derived and then compared to those found by the numerical Crank–Nicolson method. Our solutions are found to be very accurate and the solution method highly efficient compared to the time-consuming numerical method. We also examine the asymptotic behavior of the free boundaries as time to expiry tends to zero.
2. The Mathematical Model and Solution
We now present the main result of the paper, in which we present the series representation for the American straddle option price. Explicit formulas are given for the coefficients in the series.
We let be the price of an American straddle option with exercise price X and expiry T and assume that the stock price S follows the risk-neutral lognormal process, i.e.,
In (1), and are, respectively, the constant risk-free interest rate, dividend yield and volatility and is an increment in a Wiener process Z, under a risk-neutral measure. Then, if we denote the upper optimal exercise boundary (OEB) by and the lower optimal exercise boundary by then in the continuation region, the value satisfies the Black–Scholes Equation (see Appendix A)
subject to
In pricing an American put option with price and free boundary , Medvedev and Scaillet [11] replaced the smooth-pasting condition by an explicit exercise rule and assumed that the OEB had the form
where y is a decision variable determining the suboptimal rule. Hence, the American put option was treated as a barrier put option that is exercised when the normalized level of moneyness, , reaches the barrier level y. The same application is used in our paper where there is now an upper and lower barrier. We will use a similar idea for both of the free boundaries of the straddle option and, unlike Medvedev and Scaillet, give explicit formulas for the coefficients in the series representation for the American straddle. The following theorem gives our main result.
Theorem 1.
Let and The approximation to the short-term American straddle option price in where and , respectively, are the upper and lower OEBs is
where
with and M and U represent the confluent hypergeometric functions, Kummer-M and Kummer-U, respectively (see [12]).
The coefficients and are given by
where
with
The upper and lower optimal exercise boundaries are given respectively by
and
, where approximations for the true early exercise level of moneyness, are given by
and
where and are implicitly defined in (5).
Note: Outside the continuation region, the option should be exercised. Hence, for and for .
Proof.
It is useful to divide the continuation domain into the 2 regions and . In the continuation region of the American straddle option, the option price satisfies Equation (2), which in
necessitates being solved subject to
and in , subject to
Note: As indicated in (6), we will be formulating a solution of the form
where , and where g and are given functions found by comparing (15) with (6).
With fixed, when , and . This means the payoff is implied by the form (15) and hence the final condition (3a) will be satisfied.
We also require that across the strike price we have continuity of the value of the option and its derivative, i.e.,
We note that continuity of the second derivative across the strike price is also required for an exact, classical solution to the second-order PDE (2). This will be shown to follow automatically.
Making the substitutions
PDE (2) becomes
We note that a similar PDE of parabolic type was considered by Covei [13] where the author connected the considered equation with a production planning problem. We solve (16) on subject to and on subject to The continuity conditions become
Now letting where reduces (16) to the classical heat equation
Finally, we let to get
to be solved on subject to
and on subject to
with continuity conditions
Equation (18) admits separable solutions of the form
where M and U are the confluent hypergeometric functions, Kummer-M and Kummer-U functions, respectively. In (21), we have used the separation constant where i is a positive integer. This was chosen as power series in square root of time have been shown to be effective in solving other free boundary problems that involve linear diffusion equations (see, e.g., Tao [14]). We will use (21) to describe the solutions in .
For we use different constants and write
- Determining the Solution Coefficients
For the limit conditions at (or the corresponding x conditions across ) to be satisfied we need
so that we set and .
We point out here that the continuity at of the second derivative necessitates
However, this follows directly from (23). This means derivatives of all orders are continuous at . Hence, we have
To determine the constants and we first apply the boundary condition at , which in series form is
where and are defined in (9d)–(9j). Hence equating coefficients of we get
Plots of American straddle prices are given in Figure 1, using parameter values for and . The upper, and lower, , critical stock prices are indicated on the plots. The values in the continuation region, i.e., are calculated using Theorem 1 and this part of the graph merges smoothly into the payoff functions for and for . As expected, the minimum values are at and options with the longer time to expiry have higher values in the continuation region. The difference between the two plots decreases with distance from the strike price.
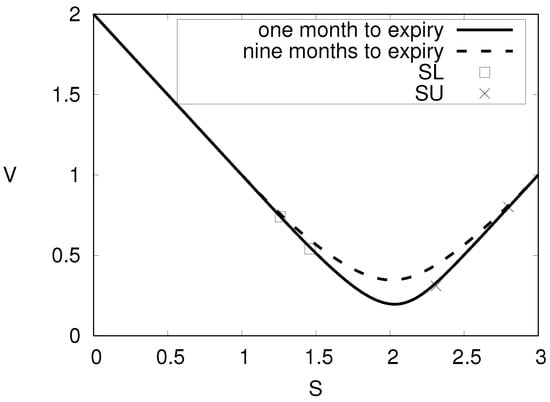
Figure 1.
American straddle prices with parameters for and .
Plots of optimal exercise boundaries, and for calculated using Theorem 1 are given in Figure 2 using and a variety of parameter values for and q. From the figures it can be seen that at , when that and ; when that and and when , . This is in agreement with the results of Qiu [10]. From increases, (at first more sharply) while decreases with .
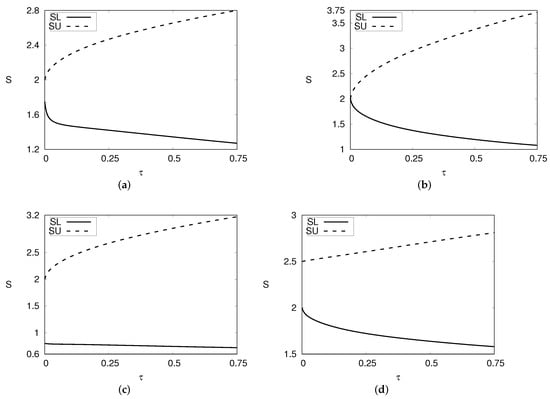
Figure 2.
Optimal exercise stock prices for using and (a) , (b) , (c) and (d) .
3. Early Exercise Price at Small Maturities
Recall that in the previous section we defined where . In this section, we demonstrate how our representation of the solution when leads to an approximation of the early exercise level for the lower boundary in (11) as tends to 0 which is similar to asymptotic results found in the literature for the free boundary in American put options (see, e.g., Lamberton Villeneuve [12] and Kwok [1]). However, when the behavior differs from that of the American put free boundary as tends to zero. For the upper boundary, the behaviors are interchanged.
Proposition 1.
Proof.
We have in ,
where
From (13), we have that for small , . This leads to
Now, using the relation that for large z
we get
We now examine the leading order term of when which is
Using (31) the leading order behavior is found to be
Hence, from (32) we have
This makes sense only if and so for this case we get on rearranging (34)
When then for the leading order behavior of we go to
Using (31) we get the leading order behavior .
Hence, we have
From this, we get
Hence, where is the Lambert function (see Abramowitz and Stegun [15]). □
Remark 1.
When the right hand side of (34) would be negative and thus the above analysis fails. In this case, we cannot use the leading order of as in (33) even though the terms in eventually go to zero. It is believed that in this case by comparing (11) and the known behavior at expiry of American put options when (see, e.g., Kwok [1]), which is evidenced in our solutions.
Proposition 2.
Proof.
The proof for this proposition is similar to that for Proposition 4.1. We have in
where
From (12) we have that . This leads to
We now look at the leading order term of , namely
This only makes sense if in which case so that
When then the leading order behavior of is
Hence, from (38) (but with the RHS now ) we have
From this, we get
Hence □
We now make a similar remark as for the previous proposition.
Remark 2.
When the right hand side of (41) would be negative and thus the above analysis fails. So for we are unable to use the leading order of as in (42), however the terms in eventually go to zero. By comparing (10) and the known behavior at expiry of American call options when (see, e.g., Kwok [1]), it is presumed that in this case This is supported by our solutions.
4. Some Comparisons with a Numerical Method
We now assess the performance of the formula in Theorem 1 (T1) for pricing American straddle options up to 9 months maturity with that obtained numerically using (2), (3a)–(3e). The solution method in this paper is designed for American straddles with a short time to maturity, e.g., up to 1 year, as the majority of American options have a lifespan of less than 9 months. The numerical method we used was the Crank–Nicolson (CN) method with successive over-relaxation which is accurate to (see Wilmott [16]) where and are the increments in time and asset price respectively (note that the increment sizes and obviously affect the speed and accuracy of the CN scheme. If the largest S value in the grid is denoted then the number of S intervals is and the size of the coefficient matrices are . Here, we used and chose increments so that when halved, did not alter the solution to 4 decimal places. Typically, this was and or ).
In Table 1 we compare American straddle prices V using Theorem 1 (T1) with that obtained using the CN method. We used and a variety of other parameter values for and S and with maturity times from 1 to 9 months. As can be seen from the table, the price solutions agree remarkably well with mostly 4 decimal place accuracy and with root mean square errors (RMSEs) for all the maturities being less than .

Table 1.
Comparison of American straddle option prices with using Theorem 1 (T1) and the Crank–Nicolson scheme (CN).
In Table 2, we compare the upper and lower optimal exercise boundaries obtained using (12) and (13) with that obtained numerically. The values agree extremely well in all cases. Hence, the solution as described in Theorem 1 has shown to be remarkably accurate not just for the option values, but also for the OEBs values.

Table 2.
Comparison of optimal exercise stock prices ( the upper price and the lower price) with using Theorem 1 (1) and the Crank–Nicolson scheme (CN).
As a further test, we compared the computational times for the Crank–Nicolson numerical method with that of the proposed solution in this paper. Using the computer algebra package Maple [17] on a Dell x64 PC, (Intel Core i7 processor, 16 GB RAM, CPU @3.6 GHz) we found that using terms in the series expansions for the American straddle price, the new solution presented in this paper took under one and a half seconds in real time or under one second in CPU time, to yield the straddle price. Using terms took about 3 s in real time or 2.56 s in CPU time. In comparison, the numerical CN method could take between 25 and 300 s depending on the time to maturity, or between 86 and 1000 s CPU time. Given that fast and accurate answers are critical in practice, this is an important development in the area of option pricing.
5. Conclusions
There are currently close to 5 million options listed on the Chicago Board of Exchange (CBOE) (see https://markets.cboe.com/, accessed on 21 April 2022) with over 376 million open interest. The overwhelming majority of these options have less than 9 months to maturity. Hence, with short-tenor American options, whether they be vanilla or exotic, being in such demand, it is no surprise that the matter of pricing these options is so useful and crucial. In this paper, we have provided a very accurate and efficient analytical approximation for American straddle options with short-tenor in the form of a series solution; the coefficients of which are in terms of standard mathematical functions. As such, solutions of all orders can be found extremely swiftly. We have also demonstrated that the solution provides very accurate results. While some analytic approximations proposed in the literature might yield good results in some cases for either the option price or the critical stock price, remarkably our solution provides very accurate results for both for the option price and for the critical stock prices. This is a highlight of the solution method as many analytic approximations to American options yield either good option prices or critical stock prices, but not both. We have also examined the behavior of the critical boundaries near expiry and found they were dependent on the relative values of the risk-free interest rate r and the dividend yield q. Like American put options, when , the lower boundary of the American straddle tends to the strike price, X, in the parabolic-logarithmic form, and when , the upper boundary of the American straddle behaves like the free boundary of American call options and tends to the strike price in the parabolic-logarithmic form. However, when , the behaviors differ from their American vanilla counterparts. In the case for the lower boundary and for the upper boundary, we surmised and observed they tended towards parabolically as time to expiry tended towards zero.
Author Contributions
Writing—review and editing, J.G. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University for funding this work through Research Group no. RG-21-09-19.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We assume that the stock price S follows the risk-neutral lognormal process given in Equation (1). Now, consider a portfolio, with value , that consists of a long position of a straddle option contract and short positions in the stock S (i.e., ). Then, the instantaneous change in the portfolio, , can be found by applying Itô’s Lemma:
Note that the stock pays a dividend of in a time . With a judicious choice of , this becomes
In excess of the risk-free return , we have
When it is optimal to hold the option, i.e., in the continuation region , then we must have , which leads to the Black–Scholes Equation (2).
References
- Kwok, Y. Mathematical Models of Financial Derivatives; Springer: Singapore, 1998. [Google Scholar]
- Alobaidi, G.; Mallier, R. Laplace transforms and the American straddle. J. Appl. Math. 2002, 3, 121–129. [Google Scholar] [CrossRef]
- Alobaidi, G.; Mallier, R. The American straddle close to expiry. Bound. Value Probl. 2006, 2006, 32835. [Google Scholar] [CrossRef][Green Version]
- Kim, I. The analytic valuation of American options. Rev. Financ. Stud. 1990, 3, 547–572. [Google Scholar] [CrossRef]
- Chiarella, C.; Ziogas, A. Evaluation of American strangles. J. Econ. Dyn. Control 2005, 3, 31–62. [Google Scholar] [CrossRef]
- Detemple, J. American-Style Derivatives: Valuation and Computation; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Gao, X.; Deng, D.; Shan, Y. Lattice methods for pricing American strangles with two-dimensional stochastic volatility models. Discrete Dyn. Nat. Soc. 2014, 1, 1–6. [Google Scholar] [CrossRef]
- Kang, M.; Jeon, J.; Han, H.; Lee, S. Analytic solution for American strangle options using Laplace–Carson transforms. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 292–307. [Google Scholar] [CrossRef]
- Ma, J.; Li, W.; Cui, Z. Valuation of American Strangles Through an Optimized Lower–Upper Bound Approach. J. Oper. Res. Soc. China 2018, 6, 25–47. [Google Scholar] [CrossRef]
- Qiu, S. American Strangle options. Appl. Math. Financ. 2020, 7, 228–263. [Google Scholar] [CrossRef]
- Medvedev, A.; Scaillet, O. Pricing American options under stochastic volatility and stochastic interest rates. J. Financ. Econ. 2010, 98, 145–159. [Google Scholar] [CrossRef]
- Lamberton, D.; Villeneuve, S. Critical price near maturity for an American option on a dividend-paying stock. Ann. Appl. Probab. 2003, 13, 800–815. [Google Scholar] [CrossRef]
- Covei, D. On a parabolic partial di¤erential equation and system modeling a production planning problem. Electron. Res. Arch. 2022, 30, 1340–1453. [Google Scholar] [CrossRef]
- Tao, L. On free boundary problems with arbitrary initial and flux conditions. J. Appl. Math. Phys. 1979, 30, 416–426. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions With Formulas, Graphs, and Mathematical Tables; U.S. Government Publishing Office: Washington, DC, USA, 1998.
- Wilmott, P. Derivatives: The Theory and Practice of Financial Engineering; John Wiley & Sons: Chichester, UK, 1998. [Google Scholar]
- Maple. Maplesoft; A Division of Waterloo Maple Inc.: Waterloo, ON, Canada, 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).