Observer-Based PID Control Strategy for the Stabilization of Delayed High Order Systems with up to Three Unstable Poles
Abstract
:1. Introduction
2. Problem Statement
Preliminary Results
3. Main Results
3.1. System with Three Unstable Poles
3.1.1. State Feedback Controller
3.1.2. Auxiliary Output Injection Structure
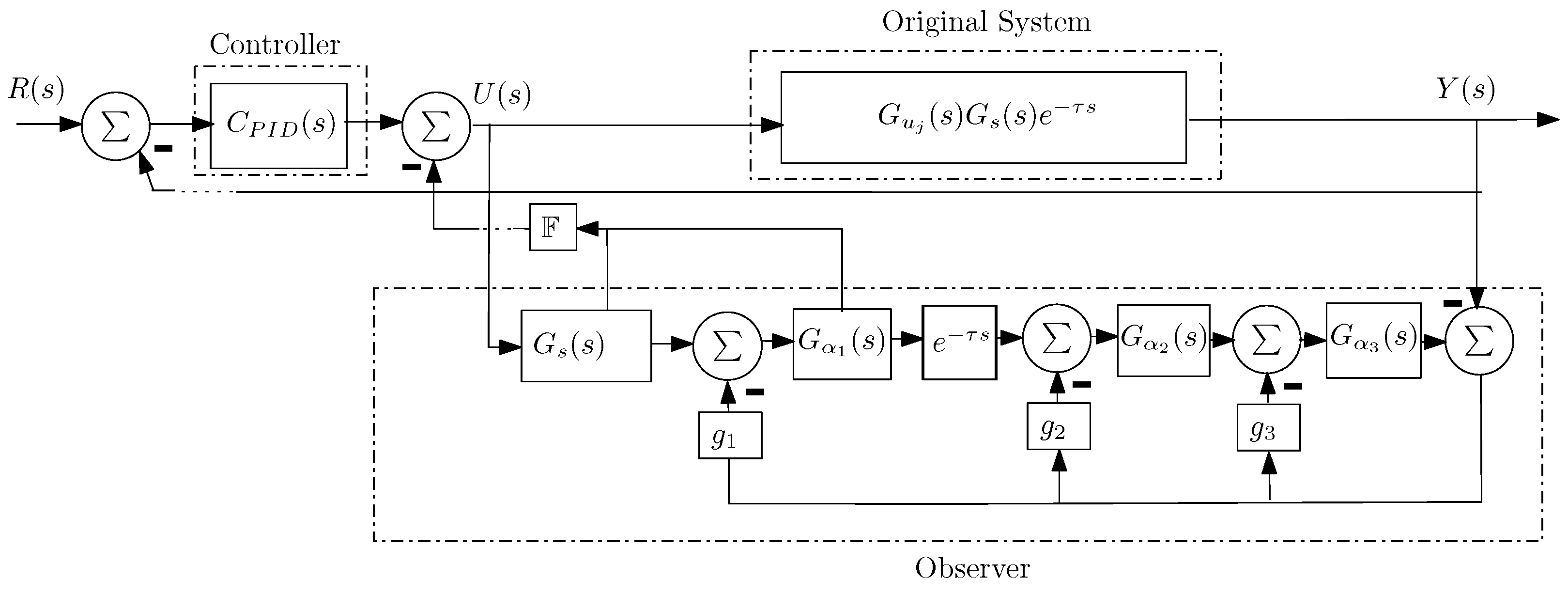
3.1.3. Observer-Based PID Control Scheme
3.1.4. Controller Parameters Selection
- (a)
- (b)
- Consider Figure 2. Select and to move poles and to positions and , satisfying relation (24). Again the new poles should be placed far from the origin. Then, we use a Nyquist diagram to select , stabilizing the new subsystem: . Parameter must be such that the Nyquist diagram encircle once the point in counter-clockwise direction;
- (c)
- Consider Figure 1. The PID controller must stabilize the closed loop subsystem (17); a system with two unstable poles and stable (relocated by ) poles. The existence of a PID controller is guarantee by relation (18) and the parameters can be selected by the methodology proposed in [25] or, in an alternative way, trough trail and error, by using again a Nyquist diagram, noting that a PID controller is equivalent to a pole at the origin, two free zeros and a free gain. The location of the two free zeros must be such that there exists a free gain value making the Nyquist diagram to encircle twice the point in counter-clockwise direction.
3.2. System with Two Unstable Poles
3.2.1. State Feedback Controller
3.2.2. Output Injection Structure
3.2.3. Observer-Based Control Scheme for the Case of Two Unstable Poles
3.3. System with One Unstable Pole
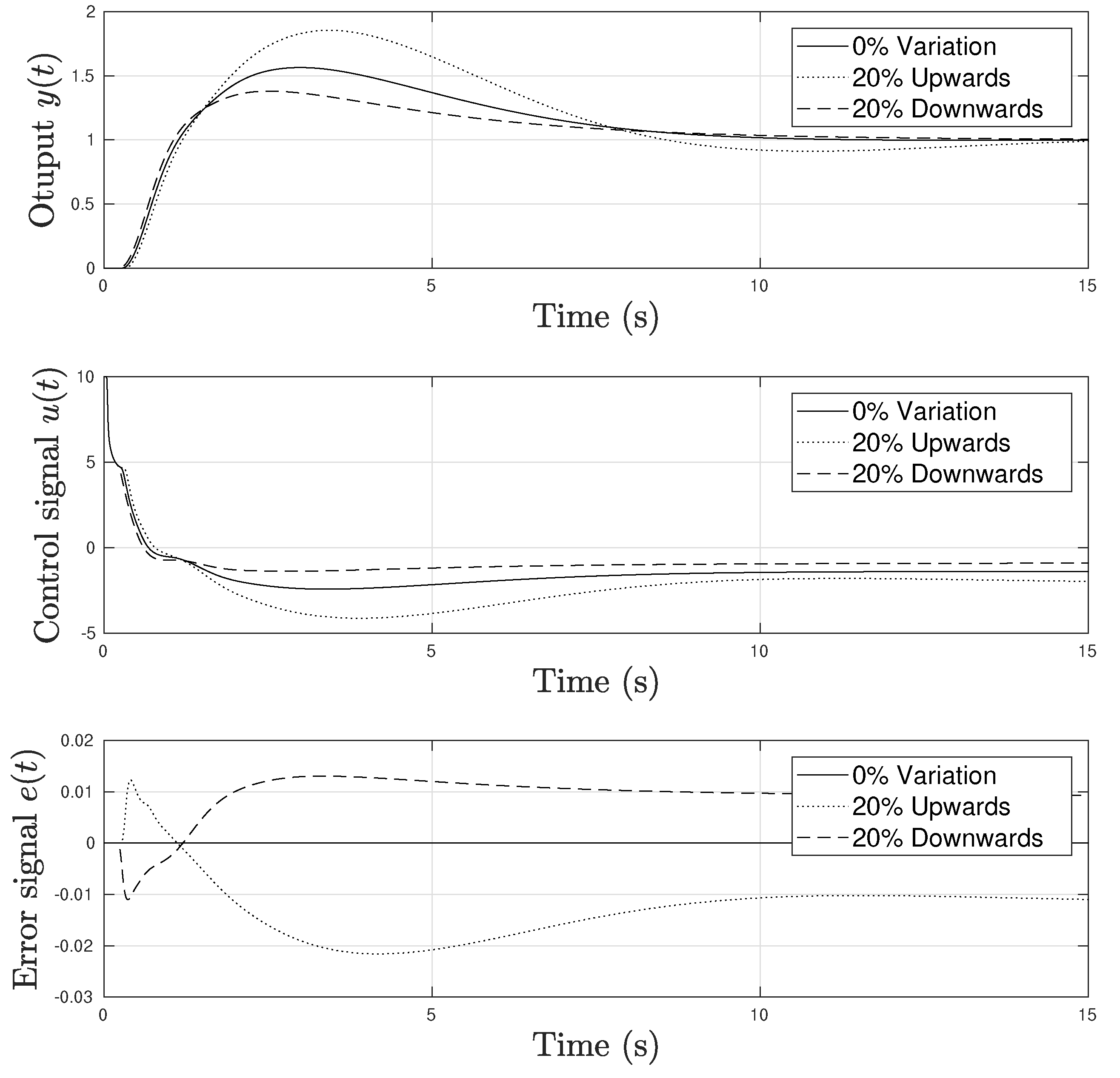
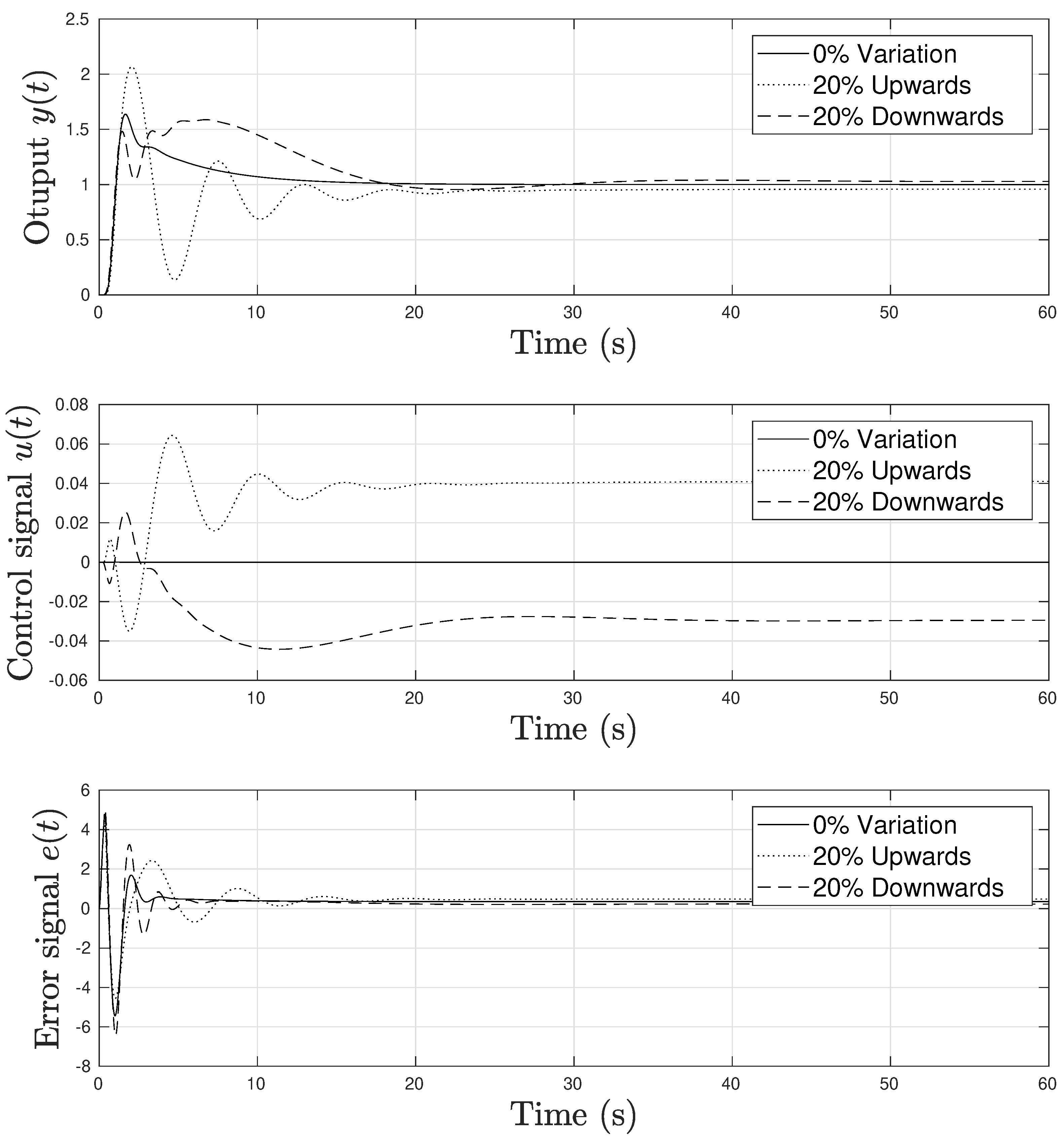
4. Numerical Experiments
4.1. Example 1: Delayed System with One Unstable Pole
4.2. Example 2: Fourth Order Linear System with Delay and Two Unstable Poles
4.3. Example 3: Three Unstable Poles
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, W.C. Dynamics and control of a financial system with time-delayed feedbacks. Chaos Solitons Fractals 2008, 37, 1198–1207. [Google Scholar] [CrossRef]
- Milton, J.G. Time delays and the control of biological systems: An overview. IFAC-PapersOnLine 2015, 48, 87–92. [Google Scholar] [CrossRef]
- Hamdy, M.; Ramadan, A. Design of Smith Predictor and Fuzzy Decoupling for Mimo Chemical Processes with Time Delays. Asian J. Control 2017, 19, 57–66. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A. Networked non-linear control for an aluminum plate thermal process with time-delays. Int. J. Syst. Sci. 2008, 39, 1075–1080. [Google Scholar] [CrossRef]
- Al-Wais, S.; Khoo, S.; Lee, T.H.; Shanmugam, L.; Nahavandi, S. Robust H cost guaranteed integral sliding mode control for the synchronization problem of nonlinear tele-operation system with variable time-delay. ISA Trans. 2018, 72, 25–36. [Google Scholar] [CrossRef]
- Min, H.; Wang, S.; Sun, F.E.A. Robust consensus for networked mechanical systems with coupling time delay. Int. J. Control Autom. Syst. 2012, 10, 227–237. [Google Scholar] [CrossRef]
- Zhang, C.K.; Jiang, L.; Wu, Q.H.; He, Y.; Wu, M. Delay-Dependent Robust Load Frequency Control for Time Delay Power Systems. IEEE Trans. Power Syst. 2013, 28, 2192–2201. [Google Scholar] [CrossRef]
- Bolognani, S.; Ceschia, M.; Mattavelli, P.; Paccagnella, A.; Zigliotto, M. Improved FPGA-based dead time compensation for SVM inverters. In Proceedings of the Second International Conference on Power Electronics, Machines and Drives (PEMD 2004), Edinburgh, UK, 31 March–2 April 2004; Volume 2, pp. 662–667. [Google Scholar]
- Deng, W.; Yao, J.; Wang, Y.; Yang, X.; Chen, J. Output feedback backstepping control of hydraulic actuators with valve dynamics compensation. Mech. Syst. Signal Process. 2021, 158, 107769. [Google Scholar] [CrossRef]
- Tang, Y.; Xing, X.; Karimi, H.R.; Kocarev, L.; Kurths, J. Tracking Control of Networked Multi-Agent Systems Under New Characterizations of Impulses and Its Applications in Robotic Systems. IEEE Trans. Ind. Electron. 2016, 63, 1299–1307. [Google Scholar] [CrossRef]
- Sipahi, R.; Niculescu, S.I.; Abdallah, C.T.; Michiels, W.; Gu, K. Stability and Stabilization of Systems with Time Delay. IEEE Control Syst. Mag. 2011, 31, 38–65. [Google Scholar]
- Smith, O.J.M. Closer Control of Loops With Dead Time. Chem. Eng. Prog. 1957, 53, 217–219. [Google Scholar]
- Rao, A.S.; Rao, V.S.R.; Chidambaram, M. Simple Analytical Design of Modified Smith Predictor with Improved Performance for Unstable First-Order Plus Time Delay (FOPTD) Processes. Ind. Eng. Chem. Res. 2007, 46, 4561–4571. [Google Scholar] [CrossRef]
- Levine, W.S. The Control Handbook—Electrical Engineering Handbook, 1st ed.; CRC-Press: Boca Raton, FL, USA, 1996; Volume 1. [Google Scholar]
- Wu, Z.; Yuan, J.; Li, D.; Xue, Y.; Chen, Y. The proportional-integral controller design based on a Smith-like predictor for a class of high order systems. Trans. Inst. Meas. Control 2021, 43, 875–890. [Google Scholar] [CrossRef]
- Lee, S.C.; Wang, Q.G.; Xiang, C. Stabilization of all-pole unstable delay processes by simple controllers. J. Process Control 2010, 20, 235–239. [Google Scholar] [CrossRef]
- Hernández-Pérez, M.A.; del Muro-Cuéllar, B.; Velasco-Villa, M. PID for the stabilization of high-order unstable delayed systems with possible complex conjugate poles. Asia-Pac. J. Chem. Eng. 2015, 10, 687–699. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Q.G.; Zhang, Y. Relationship on Stabilizability of LTI Systems by P and PI Controllers. Can. J. Chem. Eng. 2007, 85, 374–377. [Google Scholar] [CrossRef]
- Novella Rodríguez, D.F.; del Muro-Cuéllar, B.; Sename, O. Observer-based scheme for the control of high order systems with two unstable poles plus time delay. Asia-Pac. J. Chem. Eng. 2014, 9, 167–180. [Google Scholar] [CrossRef] [Green Version]
- Vázquez, C.; Márquez, J.; del Muro, B.; Novella, D.; Hernandez, M.; Duchen, G. Observer-PI scheme for the stabilization and control of high order delayed systems with one or two unstable poles. IFAC-PapersOnLine 2018, 51, 432–437. [Google Scholar] [CrossRef]
- Rosas, C.D.V.; Rubio, J.F.M.; del Muro Cuéllar, B.; Rodríguez, D.F.N.; Sename, O.; Dugard, L. Stabilizing High-order Delayed Systems with Minimum-phase Zeros Using Simple Controllers. Stud. Inform. Control 2019, 28, 381–390. [Google Scholar]
- Duchén, G.; BDM, B.; Márquez, J.; Hernández, M.; Ramírez, E.; Cruz, C. Estabilización y control de sistemas de alto orden con retardo y dos polos inestables: Esquema PD-observador. In Proceedings of the Congreso Nacional de Control Automático, Puebla, Mexico, 23–25 October 2019; pp. 291–296. [Google Scholar]
- Duchén Sánchez, G.; del Muro Cuéllar, B.; Márquez Rubio, J.F.; Velasco Villa, M.; Hernández Pérez, M.A. Observer-Based PD Controller for a Class of High Order Linear Unstable Delayed Systems. IEEE Lat. Am. Trans. 2021, 100, 291–300. [Google Scholar] [CrossRef]
- Dev, A.; Novella Rodríguez, D.F.; Anand, S.; Sarkar, M.K. Multi Observer-Based Sliding Mode Load Frequency Control With Input Delay Estimation. ASME Lett. Dyn. Syst. Control 2021, 1, 041009. [Google Scholar] [CrossRef]
- Novella-Rodríguez, D.F.; del Muro Cuéllar, B.; Márquez-Rubio, J.F.; Hernández-Pérez, M.A.; Velasco-Villa, M. PD-PID controller for delayed systems with two unstable poles: A frequency domain approach. Int. J. Control 2019, 92, 1196–1208. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz-Díaz, C.; del Muro-Cuéllar, B.; Duchén-Sánchez, G.; Márquez-Rubio, J.F.; Velasco-Villa, M. Observer-Based PID Control Strategy for the Stabilization of Delayed High Order Systems with up to Three Unstable Poles. Mathematics 2022, 10, 1399. https://doi.org/10.3390/math10091399
Cruz-Díaz C, del Muro-Cuéllar B, Duchén-Sánchez G, Márquez-Rubio JF, Velasco-Villa M. Observer-Based PID Control Strategy for the Stabilization of Delayed High Order Systems with up to Three Unstable Poles. Mathematics. 2022; 10(9):1399. https://doi.org/10.3390/math10091399
Chicago/Turabian StyleCruz-Díaz, César, Basilio del Muro-Cuéllar, Gonzalo Duchén-Sánchez, Juan Francisco Márquez-Rubio, and Martín Velasco-Villa. 2022. "Observer-Based PID Control Strategy for the Stabilization of Delayed High Order Systems with up to Three Unstable Poles" Mathematics 10, no. 9: 1399. https://doi.org/10.3390/math10091399
APA StyleCruz-Díaz, C., del Muro-Cuéllar, B., Duchén-Sánchez, G., Márquez-Rubio, J. F., & Velasco-Villa, M. (2022). Observer-Based PID Control Strategy for the Stabilization of Delayed High Order Systems with up to Three Unstable Poles. Mathematics, 10(9), 1399. https://doi.org/10.3390/math10091399






