1. Introduction
In the engineering field, due to the limitations of engineering measurement technology, some information that is required for engineering calculations can be difficult to obtain. Such problems are called inverse problems. The lack of information about inverse problems can be mainly classified into two modes: the detection of the boundary location and the determination of boundary conditions. Chang, Yeih and Shieh (2001) [
1] showed that neither the traditional Tikhonov’s regularization method, nor the singular value decomposition method can yield an acceptable numerical result for the inverse Cauchy problem of Laplace equations, when the influence matrix is highly ill-posed. In order to obtain sufficiently stable and accurate numerical results for inverse Cauchy problems, different numerical methods have been studied by scholars in previous works.
In order to obtain stable solutions, some mesh-based methods have been widely used to solve inverse problems, including the finite element method (FEM) [
2], the finite difference method (FDM) [
3] and the boundary element method (BEM) used by Lesnic et al. [
4,
5,
6]. However, as a mesh-based method, it is still nontrivial of the BEM to generate a well-behaved mesh for complex-shaped surfaces. As a competitor to the mesh-based method, the meshless method has been proposed by researchers to solve inverse Cauchy problems. Similar to the FEM, the domain-type meshless method needs to employ arbitrarily distributed interior and boundary collocations to represent the domain and boundary of the problem. The domain-type meshless methods are the radial basis function method (RBFCM) and the generalized finite-difference method (GFDM), which are commonly used recently. The RBFCM was proposed by Kansa in 1990 [
7,
8], after which the selection of its optimal parameters was studied [
9,
10,
11], and then this method became popular [
12]. The GFDM has been applied to inverse problems and is widely used for engineering problems [
13,
14,
15,
16]. Similar to the BEM, boundary-type methods have the advantages of reducing the calculation dimensions and can easily obtain highly accurate numerical results. Considering their merits, boundary-type methods, including the Trefftz method [
17,
18,
19], the modified collocation Trefftz method (MCTM) [
20,
21], the singular boundary method (SBM) [
22] and the boundary particle method (BPM) have been widely studied for use in inverse Cauchy problems [
23].
It is worth emphasizing that among the boundary-type meshless methods, the method of fundamental solutions (MFS) proposed by Kupradze and Aleksidze in 1964 [
24] is the most popular in the application of inverse problems [
25,
26] due to its high accuracy. Young [
27] studied the condition number of MFS in a Cauchy problem, and Fan [
28] further extended the scheme to solve a Cauchy problem involving Stokes equations. Despite the popularity of the method, determining the appropriate location of the source nodes is one of the difficulties that the MFS needs to overcome. Therefore, in 2002, Chen and Tanaka [
29,
30] proposed a boundary-type method with a nonsingular general solution instead of a singular fundamental solution as its basis function, named the boundary knot method (BKM). Since then, the BKM has also been applied to solve different problems [
31,
32], especially inverse problems [
33,
34].
In recent years, the concept of localization has been proposed to overcome the problems caused by the full matrix. The localized radial basis function collocation method (LRBFCM) [
35,
36,
37,
38], the first localized meshless method, was developed from the combination of the localization method and the RBFCM. Then, this method was applied to the study of an inverse Cauchy problem by Chan and Fan in 2013 [
39]. After that, in 2019, in order to expand the application of the MFS in large-scale problems, Fan [
40] proposed the localized method of fundamental solutions (LMFS) by combining a similar localization concept with MFS. This localized method was used to solve inverse Cauchy problems by Wang [
41], who proved its accuracy. In addition, the localized Trefftz method (LTM) and the localized singular boundary method (LSBM) were studied by Liu et al. [
42] and Wang et al. [
43], respectively. In this paper, the traditional BKM is improved into a localized meshless method, which is called the localized boundary knot method (LBKM). Moreover, large-scale problems that were difficult to solve in the past using the traditional methods can be solved efficiently by the LBKM, and successful tests for solving direct problems can be found in recent works [
44,
45]. Considering the merits of the LBKM, we take the Laplace equation as the governing equation and discuss the application of the LBKM for the inverse Cauchy problem for the first time.
The structure of this paper can be studied as follows: In the first section, we introduce previous research on the use of numerical methods in inverse problems and discuss their merits and drawbacks. In the second section, we give the details and formulations of the inverse Cauchy problem. In the third section, we illustrate the LBKM calculation process with a specific description. Six numerical examples are shown in the fourth section. Then, the defined errors and numerical results are compared and analyzed. In the last section, the discussion and conclusions about the entire work can be found.
2. Inverse Cauchy Problem
In this paper, we use the localized boundary knot method to solve the two-dimensional Cauchy inverse problem. The core of the problem is that some of the boundary conditions are unknown, so we need to add the overdetermined boundary condition to the known boundary section. The governing equation and boundary conditions are:
where
is the two-dimensional Laplacian,
represents any unknown variable in the field
,
is the boundary of the computational domain and we assume that the boundary
consists of two components that are disjointed from each other
.
and
are the Dirichlet boundary condition and the Neumann boundary condition, respectively.
represents the boundary portions with overspecified boundary conditions.
represents the boundary portions without boundary conditions.
is the unit outward normal vector on the boundary.
and
are the given boundary conditions.
3. Numerical Method
In this study, we used a localized BKM to solve this two-dimensional Cauchy inverse problem, whose governing equation is the Laplace equation. However, the traditional boundary knot method is extended from the method of the fundamental solution, and this study improves the global-type meshless method by changing it into the local type.
is assumed to represent the total number of points to be calculated, where
represents the number of internal points, while
and
represent the points of two kinds of boundary, i.e.,
and
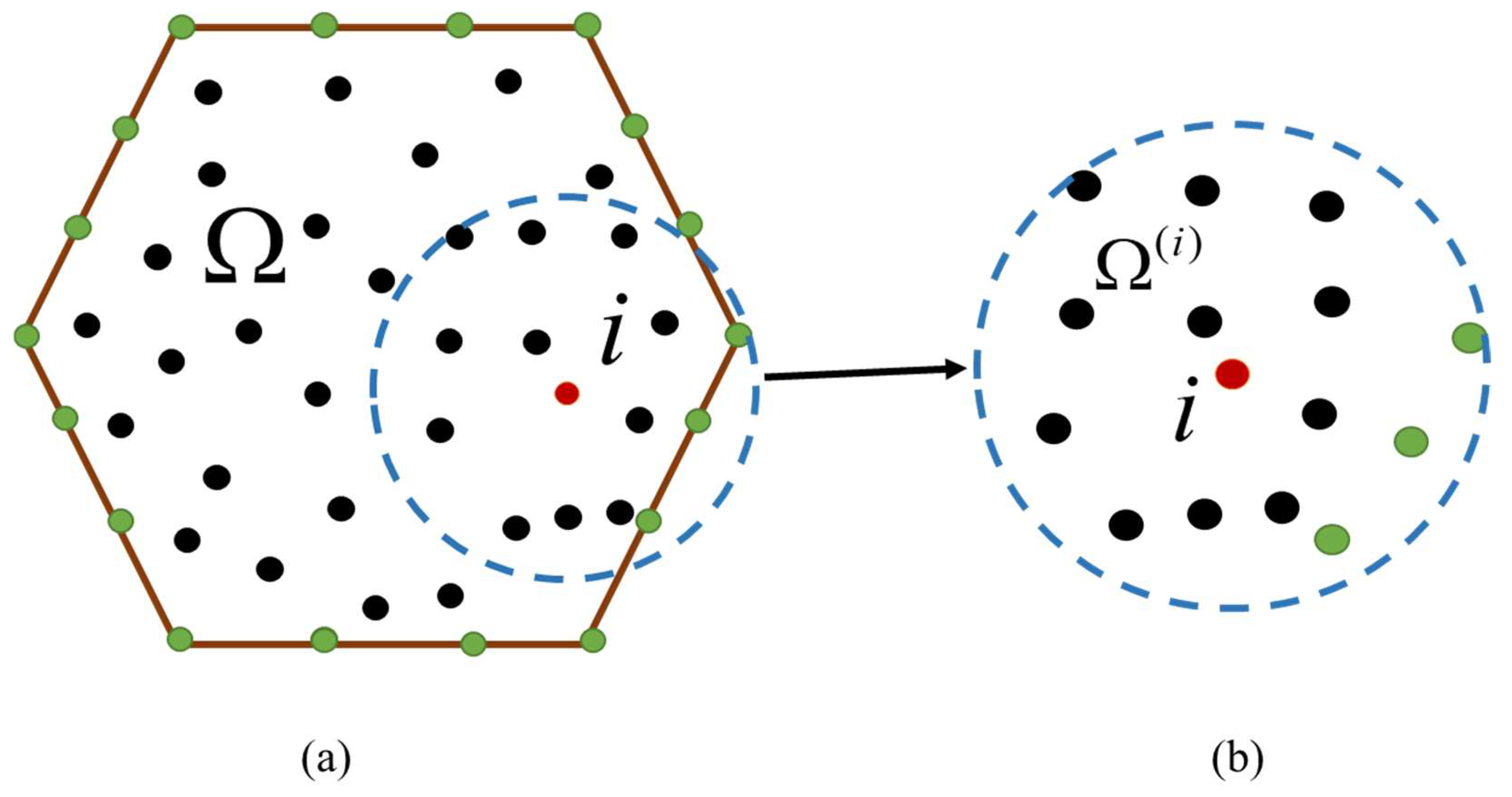
, respectively. A schematic diagram of the calculation nodes of the localized BKM method is shown in
Figure 1a.
In the localized BKM method, a subdomain is formed in each node, as shown in
Figure 1b. The numerical solution for each subdomain can be approximately expressed as follows:
in which
stands for the unknown coefficients, and
N is the number of adjacent nodes.
is the BKM basis function, which satisfies the two-dimensional Laplace equation.
is the number of nodes in a subdomain.
c is the shape parameter.
is adopted in the following case.
is the Euclidean distance, where
and
represent the
x and
y coordinates of the local node near the computing node, respectively. The source points are obtained from the nearest computing nodes in the subdomain.
By introducing the spatial coordinates of the nearest nodes into Equation (6), the following system is obtained:
where
is the vector of unknown variables at
nodes, and
is the vector of the unknown coefficients.
C is the coefficient matrix. The unknown coefficients can be expressed by unknown variables:
The inverse matrix is calculated by using the MATLAB command pinv, and we set the tolerance to be 10−3–10−4 in this article.
The numerical solution for the
ith node can be obtained from introducing the node coordinates of this point into Equation (7). The form is as follows:
where
is the vector of the fundamental solution at the
ith node.
represents the weighting coefficients.
In addition, according to Equation (3), we have
and
where
In order to obtain the expression for the Neumann boundary conditions, we can bring Equations (10) and (11) into Equation (3):
The linear equations that satisfy the Laplace equation, Dirichlet boundary conditions and Neumann boundary conditions are combined to form sparse linear algebraic equations,
where
is the sparse coefficient matrix that avoids the ill-conditioned matrix,
is the unknown field quantity at every node and
represents the known conditions. Therefore,
can be calculated from Equation (15). The localized BKM, which combines BKM with the localization concept of localized MFS, is simple and clear, and the method of determining local points is also novel. In addition, due to the sparse matrix generated in the calculation of linear algebraic equations, it can also be applied to some complex fields.
4. Numerical Results and Comparisons
In this section, we present an analysis and comparison of the results of five cases. These five examples include a simply connected domain and a multi-connected domain. At the same time, different levels of noise are added to the boundary conditions to verify the stability of the localized BKM. For the last case, we carry out the process of forward calculation and then reverse calculation by guessing the analytical solution and relative error of the Laplace equation. In this paper, we compare the analytical solution
with the numerical solution
and take the maximum relative error as the index of error analysis.
4.1. Case 1
In the first example, we use a square computing field, as shown in
Figure 2. The field is denoted by
. The boundary corner points are removed, and the internal points and boundary points are evenly distributed throughout the entire calculation domain. The analytical solution of the applied boundary condition is as follows:
where the
boundary is unknown, and the overdetermined boundary conditions (Dirichlet and Neumann) are added to the remaining edges, which are
and
. Hence, the points on this edge are calculated as interior points. The following parameters are used in this example:
, where
N is the number of total nodes, while
is the number of boundary nodes.
In order to reflect the real boundary conditions, different levels of noise
are added to the boundary to consider possible errors in advance. Therefore, the boundary conditions take the following forms:
where
s is the percentage of added noise,
rand is the random number and the range is
. The function
rand in MATLAB software is used in this paper to generate the noise.
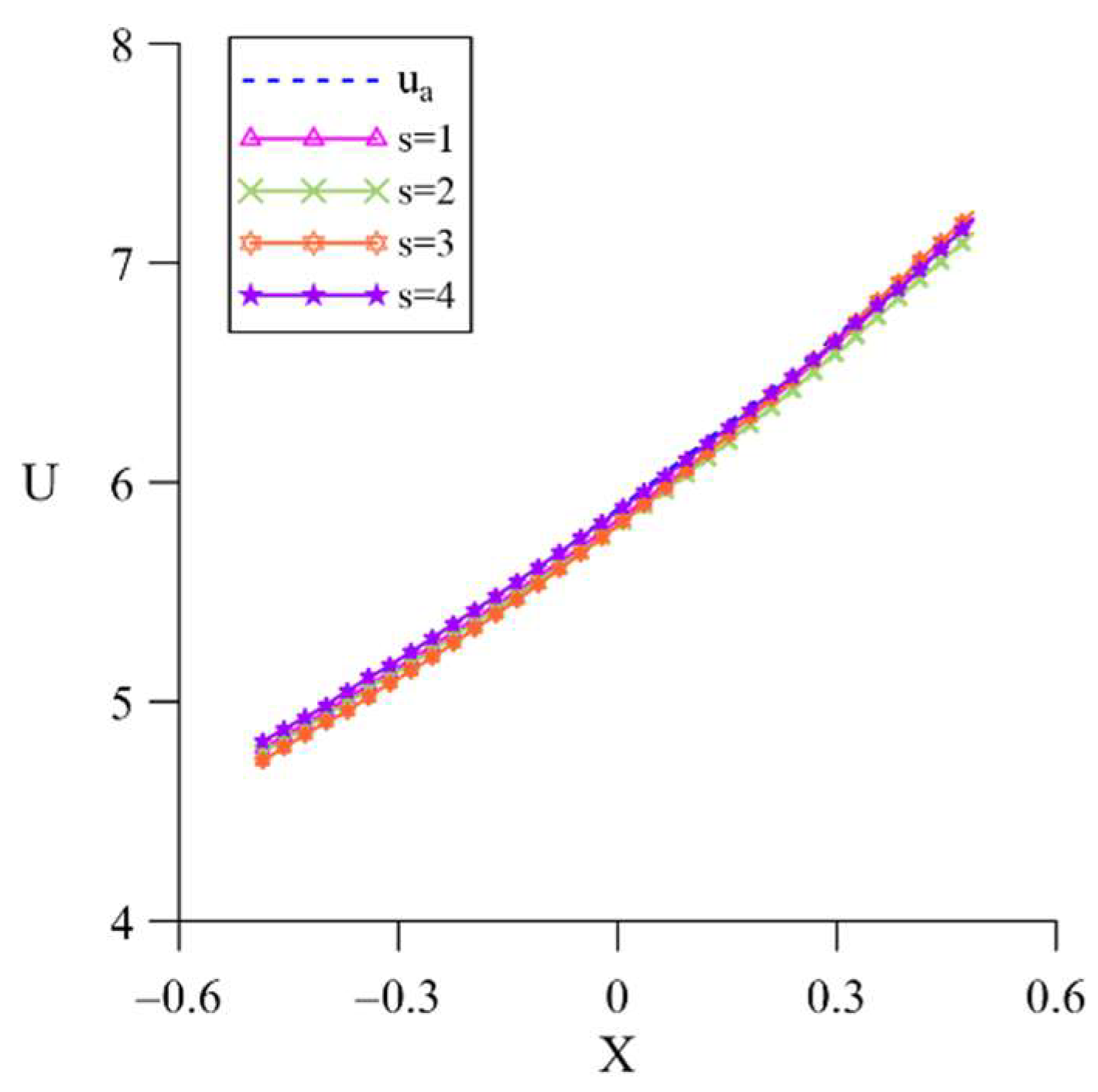
In order to show the calculation results more clearly, we draw the solution along the boundary
, as shown in
Figure 3. In this figure, we can see that, although different degrees of noise interference are added, the numerical solution along the boundary
is relatively stable, and the line-fitting degree with the analytical solution is relatively high.
In
Figure 4, we use a solid line to represent the internal numerical solution and a dotted line to represent the internal analytical solution. It can be seen from these four pictures that the errors increase with an increase in added noise, but they are all within the acceptable range, and those near the unknown boundary increase significantly. In
Table 1, we describe the maximum relative error corresponding to different degrees of disturbance in detail.
4.2. Case 2
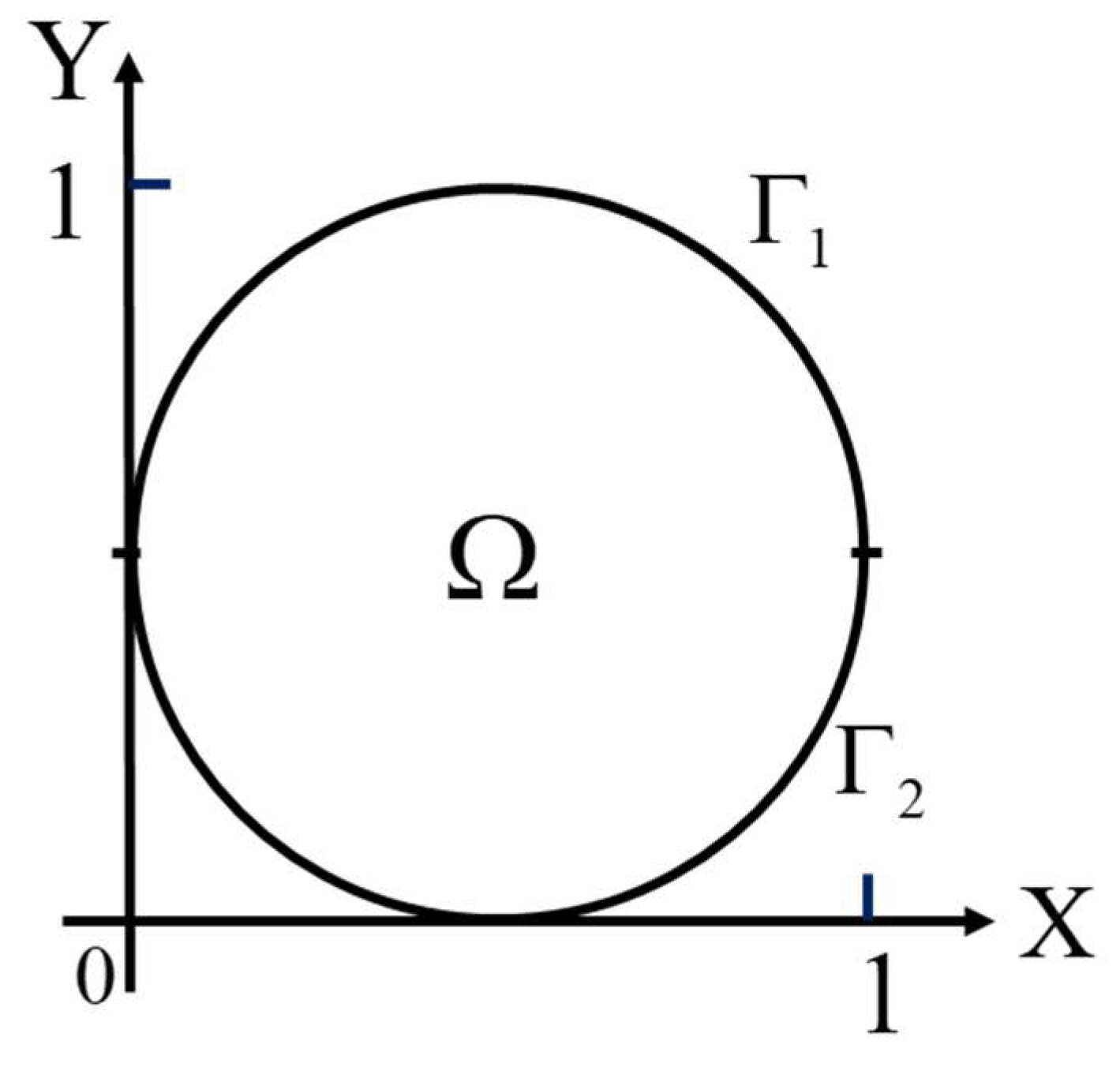
In this case, a circle is used as the calculation domain, as shown in
Figure 5. The radius of the circle is 1, and half of the boundary is unknown.
is an unknown boundary, while
is a known boundary. The analytical solution for this example is:
The following parameters are used in this example:
. The boundary conditions take the following forms:
The marked solid lines in
Figure 6 represent the numerical results for the unknown boundary
under different noise disturbances, and the dotted line represents the analytical solution curve of
. Obviously, the numerical solutions are in good agreement with the analytical solution.
In
Table 2, we list the maximum relative error obtained when adding different degrees of noise, and they are all very small. In
Figure 7, we draw the internal distributions under different disturbances. The error near the unknown boundary is relatively large but is still within the acceptable range. The analytical solution line and the numerical solution line near the boundary with known boundary conditions fit well.
4.3. Case 3
For the third inverse problem, we use a doubly connected domain. The computational domain is concentric annular, as shown in
Figure 8. The radius of the outer circle is 2, and the radius of the inner circle is 1. The analytical solution for this example is:
The outer boundary has two kinds of boundary conditions, while the inner boundary has no boundary conditions. The given boundary conditions are obtained by the analytical solution, and the nodes are uniformly distributed in the computational domain and on the boundary. The parameters used in this example are as follows:
, where and represent the numbers of nodes on the outer and inner boundaries, respectively.
In
Table 3, we list the maximum relative errors obtained when adding different degrees of noise, and the errors are also stable. A comparison of the analytical and numerical solutions drawn along the unknown boundary is shown in
Figure 9. An internal contour map of different degrees of disturbance is shown in
Figure 10. It can be seen from the figures that the numerical solution and the analytical solution are very similar.
4.4. Case 4
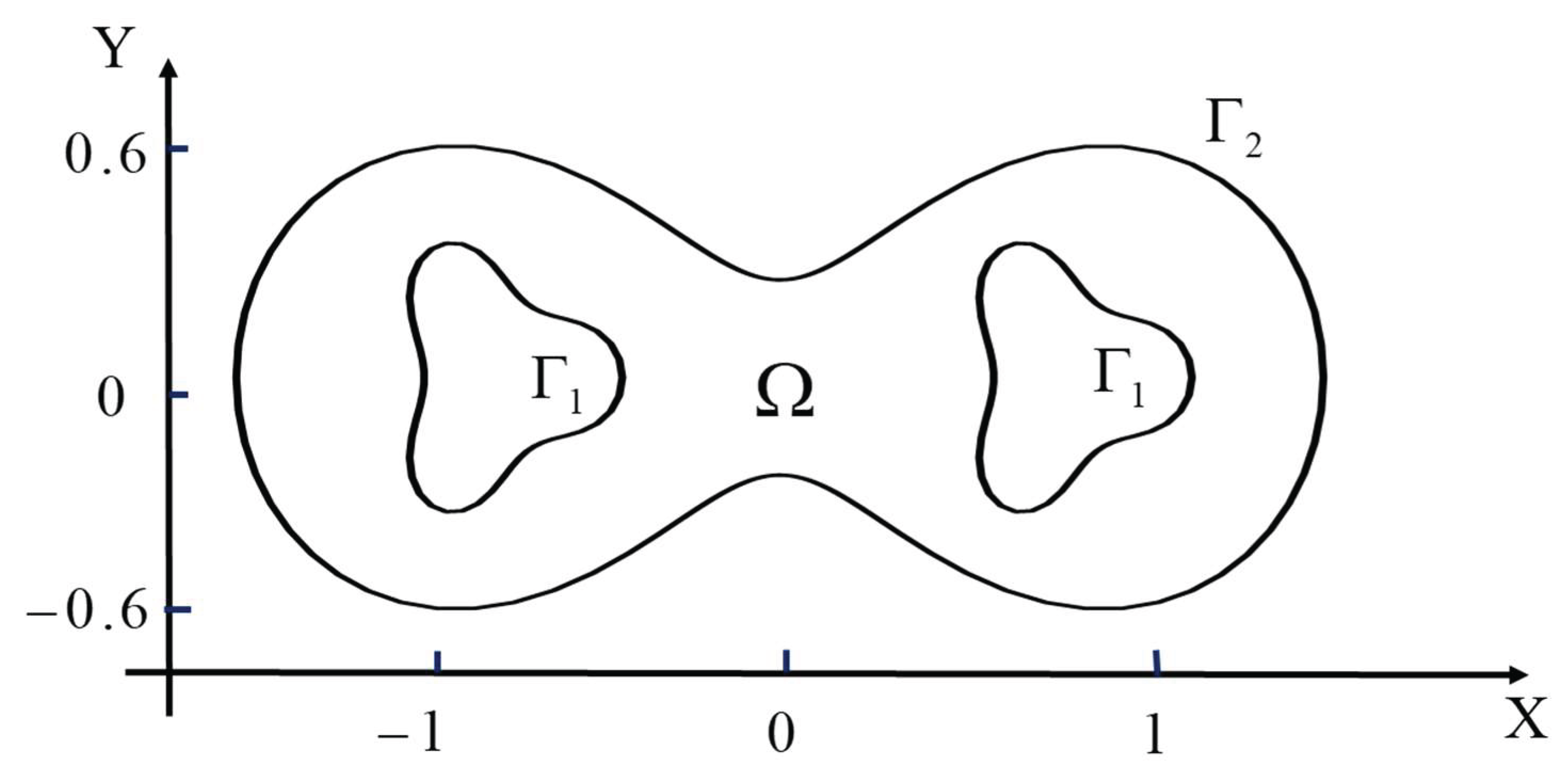
In order to verify the stability of the numerical method, we use the multi-connected domain as the computational domain in this case, as shown in
Figure 11. In this case, we take the outer boundary
as the unknown boundary and the inner boundary
as the known boundary. Therefore, two kinds of boundary conditions are added to the inner boundary. The analytical solution for this example is:
The boundary of the peanut shape is regarded as an unknown boundary, so the points on the boundary are calculated as internal nodes. Two internal wave elimination blocks are used as known boundaries, and a Dirichlet boundary condition and Neumann boundary condition are added. The parameters used in this example are as follows:
In
Table 4, we list the maximum relative errors obtained when adding different degrees of noise, and the errors are also stable. A comparison of the analytical and numerical solutions drawn along the unknown boundary is shown in
Figure 12. The data from tables and graphs show that the error is relatively stable and small.
4.5. Case 5
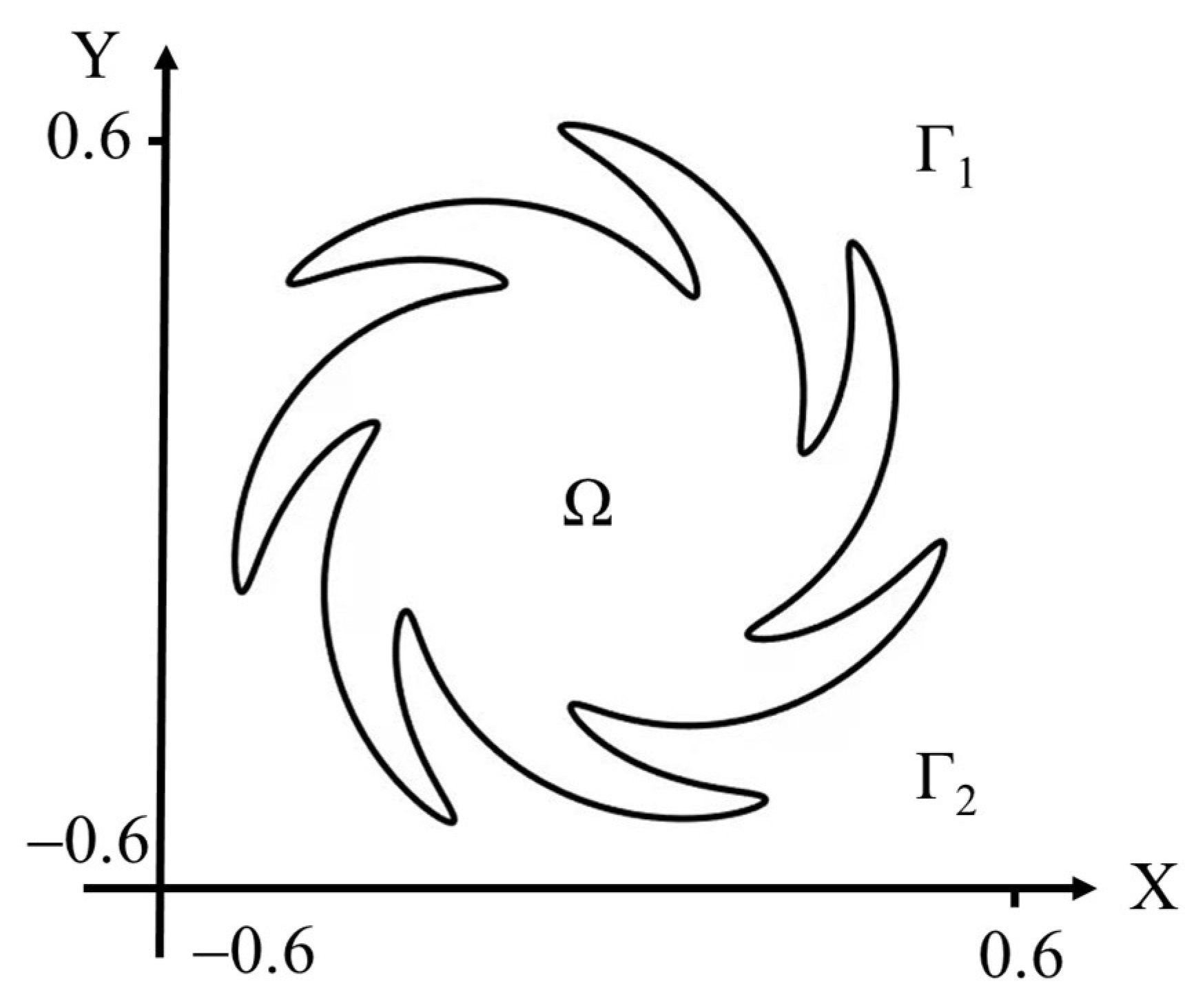
In this example, the geometry of this computational domain is more complex and there are many sharp angles at the boundary; its schematic diagram is shown in
Figure 13. The equation for the gear shape is as follows:
where
.
We set the boundary conditions (
) of the upper half as unknown and the boundary conditions of the lower half (
) as given. The Dirichlet boundary condition and the Neumann boundary condition are given by the following analytical solution:
The following parameters are used: .
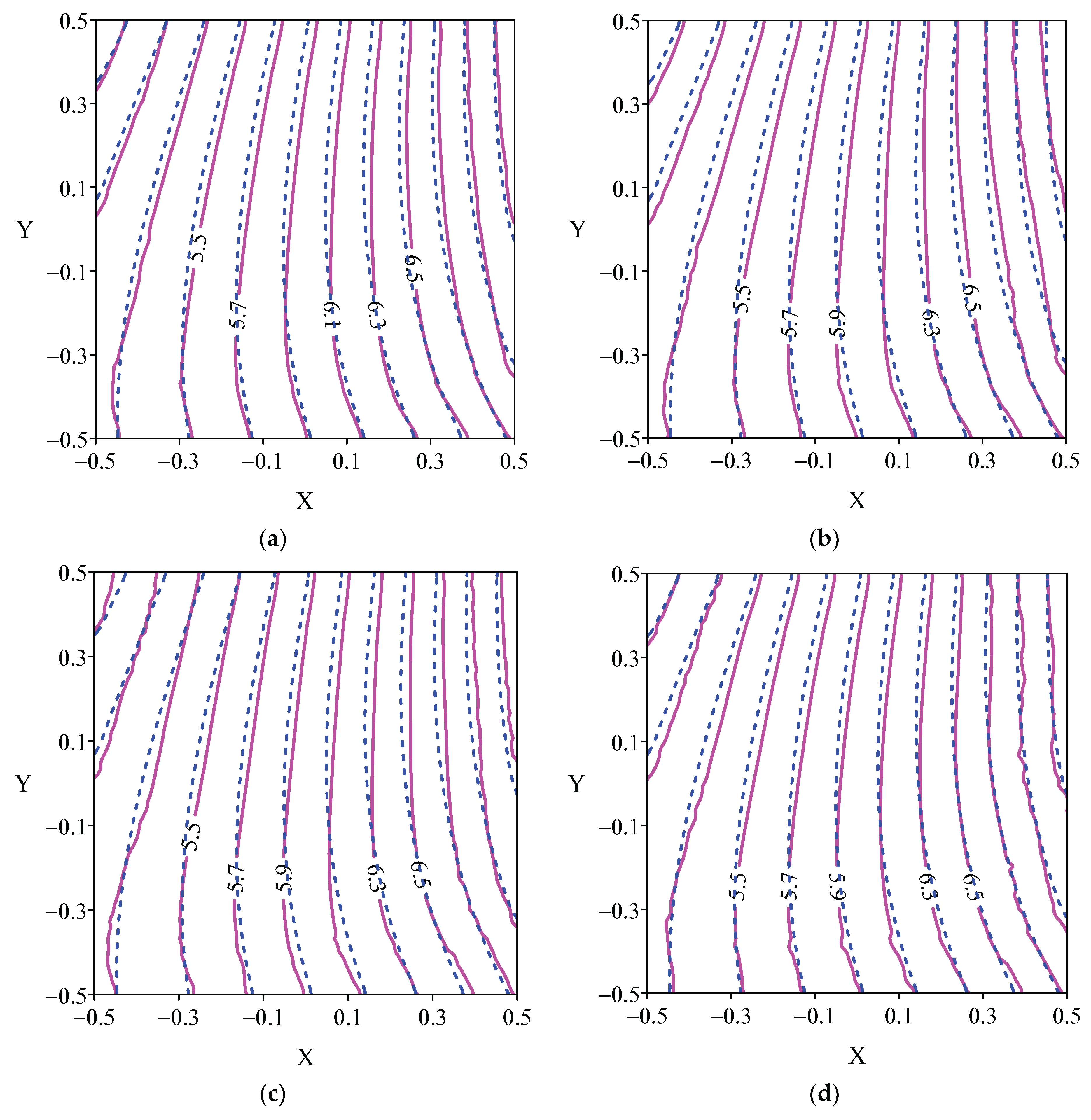
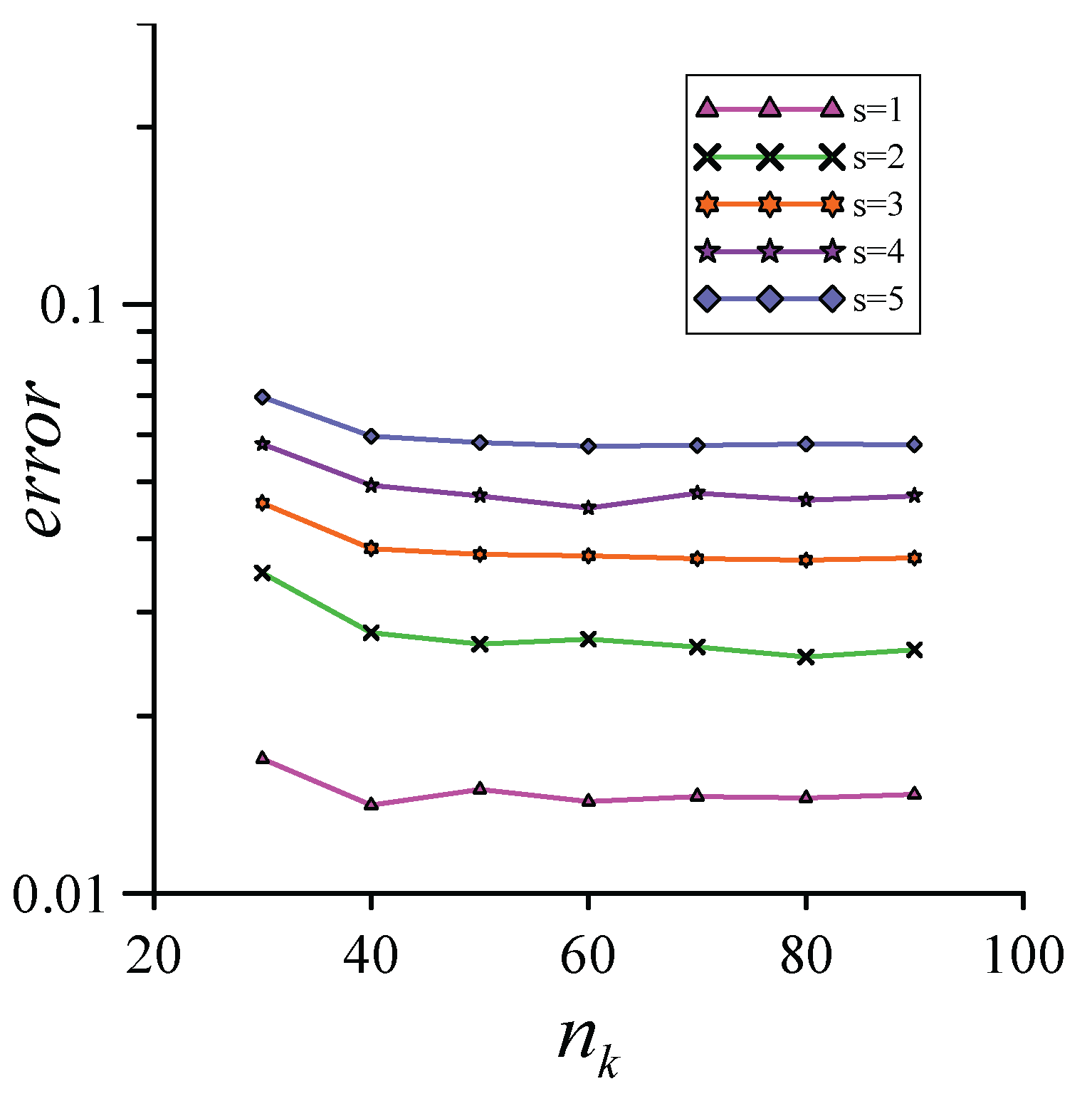
From
Table 5, it can be observed that even the geometry of the boundary is more complex under the setting of different levels of noise, and we can use the localized boundary knot method to solve this inverse Cauchy problem and still maintain a stable level of accuracy. Additionally,
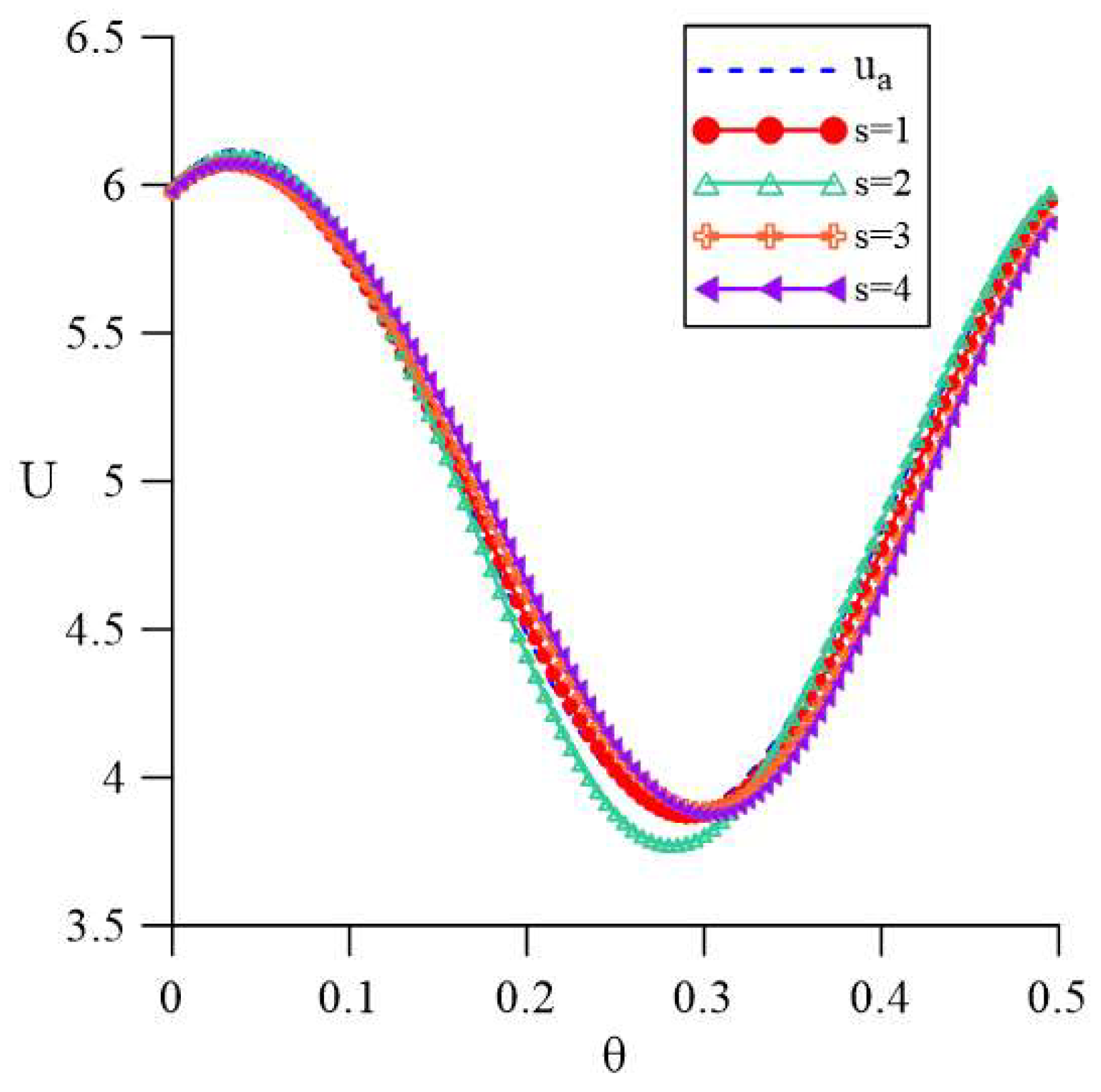
Figure 14 clearly shows the error curves obtained by applying different percentages of noise under different numbers of local points. This means that when the number of local points increases, the maximum relative error from the analytical solution approaches a stable state. In
Figure 15, we show that (a)
, (b)
, (c)
and (d)
. These four graphs show that there is indeed a certain degree of deviation in the upper half of the lack of boundary information, but the numerical results in the domain are consistent with the analytical solution.
4.6. Case 6
In order to further verify the accuracy of the localized BKM, in the last case, we also use the circle as the calculation domain, where a quarter of the boundary is used as the unknown boundary, namely
. We assume that the boundary conditions do not satisfy the analytical solution. This means that the corresponding analytical solution cannot be derived from the governing equations and boundary conditions. The known boundary satisfies the following conditions:
In Step 1, the boundary is set as the Neumann boundary condition, and the boundary is set as the Dirichlet boundary condition. The numerical solutions can be solved by LBKM.
In Step 2, is selected as the unknown boundary condition and the numerical solution obtained from the previous solution and the Neumann boundary condition on the boundary are used. For the first of the step calculation, the total number of nodes is , the number of boundary nodes is , the number of local domain nodes is , and the shape parameter is , and for the second step of the calculation, the total number of nodes is , the number of boundary nodes is , and the shape parameter is . We analyze the maximum relative error of the numerical solutions for Step 1 and Step 2.
To show the stability of the numerical method, we solved this problem by using different numbers of local points, and the maximum relative error is presented in
Table 6. The change in maximum relative error corresponding to the change in total points is recorded in
Table 7. It can be seen from the test of different total points
and local points
that, in the case where the boundary conditions do not use analytical solutions, the maximum relative error can still remain accurate and stable.
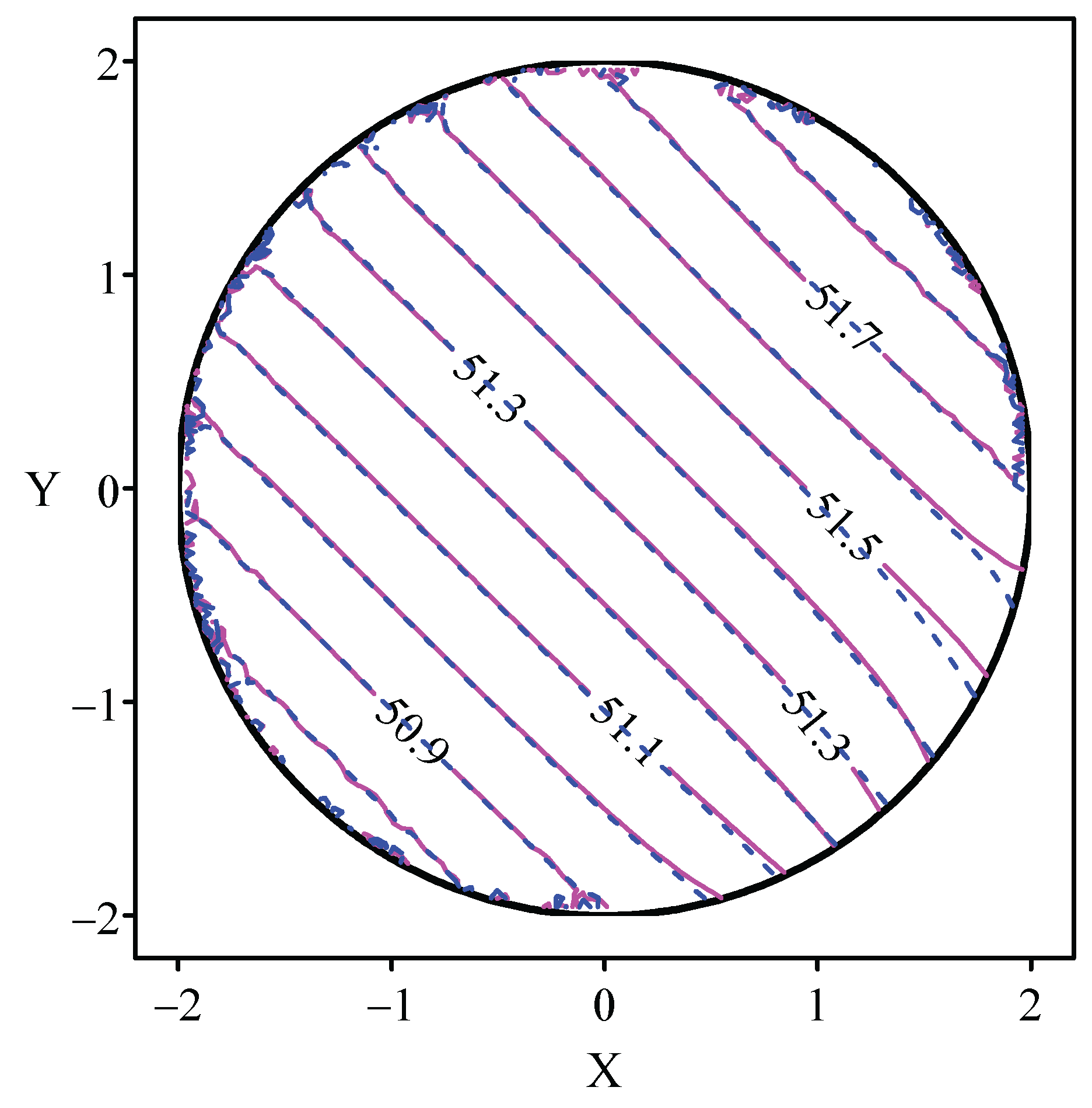
The distributions of numerical solutions to the direct and inverse problems are shown in
Figure 16. In this figure, it can be seen that numerical solutions to the inverse problem are basically the same as in Step 1, and the maximum relative error is
.
5. Conclusions
In this paper, the localized BKM was used to solve an inverse Cauchy problem controlled by a two-dimensional Laplace equation. The localized BKM is a method that combines the BKM of the meshless method with the localization concept. This method does not need grid generation and numerical integration, and it eliminates border radius issues with source points. For Cauchy problems, some boundary conditions are not readily available or there are measurement errors, so the numerical simulation is unstable. Therefore, we used the localized BKM to calculate such problems and verify the accuracy of this method.
We presented five examples that illustrate the stability and accuracy of this method for solving inverse problems. With different percentages of noise on the boundaries, the maximum relative error remained stable and within the acceptable range. In particular, in the last case, the direct algorithm was first used to obtain the data with an extra boundary and was then applied to the reverse calculation in the second step. From the results of the error analysis presented in this paper, the localized BKM was shown to be more stable and accurate for solving Cauchy inverse problems.
In the future, the localized BKM will be applied to various mathematical and physical problems as well as more complex problems, for example, moving boundary problems and three-dimensional problems.