Abstract
This paper presents results from a study about problem solving related to the concept of the greatest common divisor with secondary school students. The perspective of the analysis is the meaningful learning of the constructivist theory. The main objectives are to assess the students’ competence in the resolution of such problems and analyze if the difficulties in the acquisition of this competence are influenced by the kinds of magnitudes or the context of the problem. The results suggest that some contexts generate more difficulties to perform the use of the greatest common divisor. Moreover, some erroneous patterns have been detected. On one hand, students tend to relate and confuse the concepts of greatest common divisor and lowest common multiple. On the other hand, they have a predisposition to simplify problems, performing only the operation to obtain the greatest common divisor, and without thinking that additional arithmetic operations can be performed.
Keywords:
greatest common divisor; word problems; secondary school education; context; erroneous patterns; learning difficulties MSC:
97D70; 97F70
1. Introduction
As Godino, Batanero, and Font pointed out in [1], “all theories about teaching-learning mathematics agree on the need to identify students’ errors in the learning process, determine its causes and organize the teaching process taking into account that information”. A high level of error is related to difficulties for students when faced with a learning activity. Thus, the identification of errors could lead to finding difficulties and their causes. Providing (teaching) solutions to reduce such difficulties is the main purpose of the research in didactics of mathematics.
This work studies the difficulties that secondary education students face when solving arithmetic word problems, particularly those related to the greatest common divisor (g.c.d.) concept, and reveals that these difficulties often appear associated with the contexts in which such problems are proposed.
The study is based on Ausubel’s meaningful learning [2] from the constructivist theory, making it clear that the lack of such learning entails difficulties such as those observed here, which stem from experiences of mechanical learning. To improve the teaching–learning process, some teaching actions are recommended to overcome difficulties found.
The research methodology consists of a preliminary percentage analysis and a qualitative study, which determine the degree of difficulty the students face and the influence that the context or the quantities used have over errors that appear when problem solving.
2. Theoretical Framework
The two most relevant theoretical models on learning mathematics are the conductist model and the constructivist model [3]. The conductist model theorizes that the student learns only and exclusively what the teacher explains in class, while the constructivist model centers around the idea that the learning of mathematics is constructed by the pupils themselves. In relation to the latter, Castro points out in [4] that “learning is achieved by incorporating the characteristics of the concepts learned in their mental structures, creating a new structure that fits these properties, as if returning to equilibrium, but incorporating the new properties and concepts.” The constructivist model finds its epistemological roots in the theories inspired by Piaget, which include the following principles: all knowledge is constructed; and there are cognitive structures that are activated in the processes of knowledge construction.
Obviously, it would be preposterous to think that mathematics learning is built on nothing by the subjects themselves or without help from anyone. Concerning this, Ausubel [2] (p. 2), in his theory of meaningful learning, points out that “the most important factor influencing learning is what the student already knows,” what, in [5], Rayas calls prior knowledge and defines as “the conceptions students have acquired about different knowledge, not only those constructed from experiences external to systematic teaching, but also those created in the educational processes.” Likewise, Godino, Batanero, and Font [1] (p. 13) point out the crucial role of the teacher in the organization, direction, and promotion of their students’ personal learning construction, in addition to the relevance of their cooperation and social interaction.
To promote the process of building knowledge and activate cognitive structures on the part of the teacher, various authors propose to organize the activities in a sequential way, following a series of phases. For example, in [6], Pantano establishes four phases in their constructive development of the teaching–learning process: initiation and introduction; development and restructuring; deepening and application; and evaluation.
Meaningful learning can be considered the construction of new knowledge, based on reflection and restructuring of previous knowledge, which both allow the possibility to expand upon learned information and apply it in problem solving, as well as transfer its application to other contexts or different problem situations. In [2], Ausubel calls meaningful such type of learning, to distinguish it from rote or mechanical learning, based on acquisition of knowledge by pure memorization, without the need for any kind of reflection or relationship with prior knowledge and without consideration of (or application to) problem situations different from the known ones, where they can appear. The main characteristics or indicators of meaningful learning and an experience of its measurement can be seen in [7].
The immediate consequence of non-meaningful learning is the appearance of difficulties, errors, and, in the worst case, blockages [8]. The appearance of errors is also possible in a constructivist learning model. However, this does not suppose any contradiction, but simply that the construction of knowledge has failed in some respect and learning is not entirely meaningful. It is therefore a matter of detecting these failures in construction, which are the causes of difficulties, errors, and, sometimes, blockages, and organizing teaching actions for their correction.
In [9], Carrillo distinguishes three types of difficulties in learning mathematics based on their potential causes: the very nature (complexity) of the math; the personnel, methods and resources used for their teaching; and problems of the student himself (cognitive factors, beliefs, attitudes, etc.). Godino, Batanero, and Font establish a different classification in [1] (pp. 74–77), which corresponds to a large extent with the one in [9], but instead with six types: caused by lack of competence on previous content; caused by the content itself; caused by the sequence of proposed activities; caused by the organization of the center; caused by the psychological development of the pupil; and caused by student motivation.
In the field of didactics of mathematics, there is related research that shows some difficulties in learning and understanding divisibility, which include difficulties associated with the concept of g.c.d. Thus, several studies have verified that the understanding of divisibility is a subject fraught with difficulties at different educational stages. In [10], Zazkis and Campbell, in a study with student teachers on the main elements of divisibility, observed the low capacity of students in this area, as well as a great predisposition to use purely procedural reasoning, typical of mechanical learning, even in the cases in which they evidenced an adequate understanding of the concepts. Recent studies confirm this lack of comprehension in other educational stages. In addition, Ordoñez [11] studied the understanding of primary school students concerning the concepts of multiple and divisor, and Vallejo [12] reviewed the difficulties of first year high school students in concepts related to divisibility, proposing a course of action that can help to overcome these difficulties. Regarding divisibility, and more specifically in the study of the concept of g.c.d., Noblet [13] demonstrated that students of different educational levels have problems assimilating the concept of g.c.d., specifically in problem solving and posing. Along the same lines, Gutiérrez-Gutiérrez, Gómez, and Rico [14] accredited that even student teachers lack mathematical knowledge in the properties of g.c.d. Specifically, in [15], Martínez, González-Calero, and Sotos showed that student teachers present difficulties in this topic, confusing the concepts of g.c.d. and l.c.m. In addition, elementary school students also have a marked erroneous pattern when performing a subtraction of the quantities present in the statement instead of calculating g.c.d. [16].
In this sense, the existing studies on this subject suggest that the origin of these difficulties is based on the fact that knowledge about these concepts is usually supported by unintuitive rules for students (see, for example, [17]), as teaching practices currently focus on learning calculations rather than the structure, representation, and properties of calculations’ numbers (see [18,19]).
3. Objectives
Although different papers review the mathematical competence in divisibility in different educational stages, this work aims to study more specifically the different types of word problems linked to the concept g.c.d., and detect different erroneous resolution patterns and their causes.
Specifically, this work sets the following objectives:
- (O1)
- Study competence in solving verbal problems in different situations of divisibility involving the concept of g.c.d.
- (O2)
- Analyze whether some contexts present greater difficulties than others do.
- (O3)
- Find different erroneous resolution patterns and inquire about their origin.
4. Methodology
This research was developed in two stages: a (percentage) preliminary analysis and a posterior qualitative study, with a test group composed of students who all passed the divisibility content of high school education. In the preliminary stage, an “ex post facto” type investigation was used to establish cause-and-effect relationships for an observed effect whose cause lies in the past. This preliminary examination also serves to identify some erroneous patterns and to study them more deeply in the second part of the analysis. Then, to complete the research, a qualitative study was carried out. For this qualitative study, while considering the school complex and/or educational culture, the use of a naturalistic strategy was chosen in order to establish an interpretive approach (see [20]).
Seventy-one (71) students participated in the preliminary phase. In this phase, the participants had to solve a written test composed of 9 word problems with each of their resolutions requiring the calculation of the g.c.d. of the two quantities present in the statement. Specifically, the instrument used in the percentage analysis combines two elements:
- (1)
- Problems with solutions obtained directly through the calculation of the g.c.d. or the g.c.d. and a division operation.
- (2)
- Problems in five different contexts: length, area, volume, discrete sets, and decontextualized numbers.
The problems were obtained from a combination of these elements. In addition to these problems used in the written test, 5 control problems were added to prevent students from discovering the g.c.d. pattern and solving all the problems in the same way without deep reflection on the statements.
The statements of the problems used in the written test are presented in Table 1. A key has been created to identify each type of problem. The key breaks down each specific problem statement:

Table 1.
Word problems from the written test.
- GCDDQ problem: problem whose data refer to discrete sets and in which the g.c.d. must be obtained for its resolution, and division must be performed.
- GCDDL problem: problem whose data refer to continuous sets measuring length (meters) and in which the g.c.d. must be obtained for its resolution and division must be performed.
- GCDDC problem: problem whose data refer to continuous sets measuring volume (liters) and in which the g.c.d. must be obtained for its resolution and division must be performed.
- GCDDA problem: problem whose data refer to area and in which the g.c.d. must be obtained for its resolution and division must be performed.
- GCDQ problem: problem whose data refer to discrete sets and in which only the g.c.d. must be obtained for its resolution.
- GCDL problem: problem whose data refer to continuous sets measuring length (meters) and in which only the g.c.d. must be obtained for its resolution.
- GCDC problem: problem whose data refer to continuous sets measuring capacity (liters) and in which only the g.c.d. must be obtained for its resolution.
- GCDA problem: problem whose data refer to areas and in which only the g.c.d. must be obtained for its resolution.
- GCDD problem: problem whose data refer to discrete decontextualized quantities and in which only the g.c.d. should be obtained for its resolution.
To carry out the written test, students were given a time of 50 min to solve the problems. Different versions were made of the written test in order to avoid all students receiving the same one; the only factor changed was the order of the given problems.
The analysis of the students’ results in the percentage analysis served to identify erroneous performance patterns or trends when solving the problems and thus to facilitate the selection of participants in a subsequent qualitative study, testing the origin of these trends or patterns.
The subsequent qualitative analysis consisted of a case study of the participants who had shown interesting behaviors from a didactic point of view when completing the written tests. Specifically, pairs of students who performed similarly on the written test were selected and recorded solving the same or similar word problems.
5. Preliminary Analysis
Table 2 shows the percentage of correct resolutions of the participants for each of the problems studied. A resolution is considered correct when it is evident that the student has tried to calculate the g.c.d., either algorithmically or by another procedure, such as the direct comparison of divisors.

Table 2.
Percentage of correct resolutions for each problem.
The data reveals a low efficiency in the students’ problem solving, as only 14 students of the 71 performed all the problems well and, on average, only 19.7% of the group has an adequate knowledge of the analyzed content.
Taking into account the efficacy with the type of problem, significant differences emerge. The problems that measured area presented greater difficulties (around 30% of correct answers), while those of discrete lengths and quantities were more easily tackled (between 40 and 70% of correct answers). This difficulty was later the object of the qualitative study, to discover why these contexts are particularly difficult and the students fail to see the involvement of the divisors of the two numbers in their answer.
Table 3 shows a classification of incorrect resolutions. The main difficulties of the students are noted, broken down by type of problem. Among the incorrect answers, four different categories have been considered: g.c.d., l.c.m., Others, and Blank. The g.c.d. and l.c.m. have been individually evaluated, as they are considered of special relevance as they appeared as two repetitive patterns among the students’ answers in the sample.

Table 3.
Classification of incorrect student resolutions by type of problem.
The g.c.d. category refers to those resolutions in which the g.c.d. is performed only when another subsequent operation is necessary (for example, division). This incorrect pattern only applies to GCDDQ, GCDDL, GCDDC, and GCDDA contexts.
The l.c.m. category corresponds to students who confused the calculation of the g.c.d. and l.c.m. and, therefore, solved the problem by relating the quantities present in the statement using the l.c.m. instead of the g.c.d.
The Others category includes those resolutions made incompletely or erroneously, which did not show any of the trends defined in the two previous categories.
Finally, the Blank category includes erroneous actions in which the problem has not been addressed.
As shown in Table 3, a considerable portion (16.1%) of the students tended to apply l.c.m. instead of g.c.d. methods, especially when the g.c.d. needs an additional operation (about 20% of the cases). In Figure 1, an example of this type of action is presented in the GCDDL problem: “For one of the camp tests, a scout group needs to prepare equal length ribbons as long as possible from two strings, one of 15 cm and another of 24 cm, how many ribbons can they get without leftover strings?” This difficulty was later a subject of the qualitative study, to investigate its causes.

Figure 1.
Example of answer calculating l.c.m. for GCDDL problem.
The results in Table 3 also allow us to check that the students often (on an average of 26.4% of cases) do not notice the need of performing another operation in addition to the calculation of the g.c.d. An example of this type of action in the GCDDQ problem is shown in Figure 2: “Carla has 36 strawberry candies and 60 chocolate candies. She wants to separate them in identical boxes with the largest number of candies without mixing flavors. How many boxes does she need?” When setting out the task the teacher made it clear that identical means same number of candies.
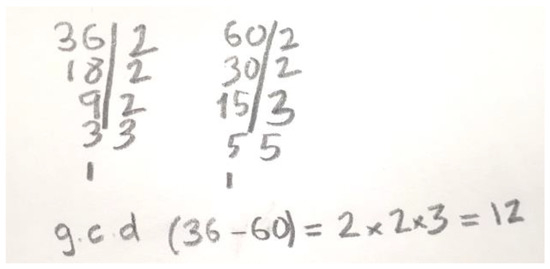
Figure 2.
Example of answer with direct calculation g.c.d. for problem GCDDQ.
Although a great variety of different answers were given (e.g., performing the subtraction of the two quantities in the statement, taking the average, indicating the unit as an answer, etc.), none of them clearly suggests an observable pattern. However, most of the problem solving seems to have a common predisposition towards immediate execution, that is, to perform an arithmetic operation without notably reflecting on the statement. In Figure 3, an example of this type of action is presented.
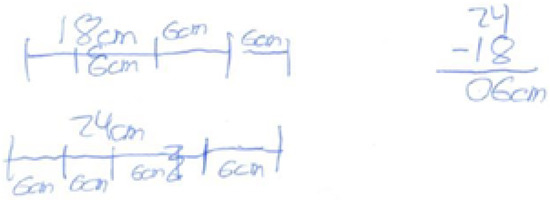
Figure 3.
Example of answer with subtraction predisposition for GCDL problem.
Finally, although in Table 2 and Table 3 the procedure for calculating the g.c.d. is not specifically distinguished, it can be observed that the problem solving procedure chosen by the students is majorly algorithmic (94.6%). This suggests that the introduction of algorithmic calculus in secondary school implies the cancellation of other types of more intuitive procedures, with a greater sense, the direct comparison of divisors.
6. Qualitative Analysis: Case Study
The precedent percentage analysis presents three areas of didactic interest. Firstly, they allow us to realize that certain contexts in the statements provoke greater difficulties in resolution. Secondly, they point out that there is a strong predisposition to use the l.c.m. instead of the g.c.d. Finally, they reveal that students present a great predisposition to perform only the calculation of the g.c.d., even if the problem requires an additional operation. In view of this, the qualitative analysis of these cases was carried out to record the resolution process made by pairs of students who had shown similar behaviors in the cases considered.
6.1. Case of Context: Areas
For this case study, we interviewed two students, who we will call Student C and Student X, both presenting problems in solving area problems in the written test.
Thus, they were asked to solve another problem equivalent to GCDA together. The problem solving was carried out on the blackboard in a classroom, with only the aforementioned students and the researcher. The problem posed was the following:
“You want to parcel out a field, 36 m long and 45 m wide, in square plots as large as possible, how long will these plots measure?”
Students proceed to read the problem and then:
- Student C:
- Buff, this problem is like the one the other day, buff, I don’t know… (referring to the similar problem they did in the written test)
- Student X:
- Okay, but let’s see what you ask for…
- Student C:
- I don’t know how to do it, ask what the plots will be like
- Student X:
- Let’s see…
The interviewer noticed that the students did not know how to solve the problem, as expected, as a result of their performances in the previous written test. Thus, he tried to guide the students to see if they understand the problem.
- Interviewer:
- Why do you find this problem difficult?
- Student C:
- It is asking what the plots measure.
- Interviewer:
- Ok, can you describe the problem in your own words?
- Student C:
- We have a piece of land and…
- Student X:
- We want to divide it into large squares
- Interviewer:
- Ok, what is the data?
- Student C:
- The land is 36 and 45 m (write the data on the board)
- Interviewer:
- Are the data of the same type?
- Student X:
- Uh… yeah… it’s meters.
- Interviewer:
- What is required?
- Student C:
- Ehh… what the plots measure.
- Interviewer:
- Is the unknown the same type as the data?
- Student C:
- Well, ask for the area, I think…
- Student X:
- Good or the side of the plot.
- Student C:
- Yes, now.
- Interviewer:
- Is it the same type?
- Student C:
- It will be meters too.
From their answers, it can be inferred that the students did not correctly interpret the statement of the problem. In response to this, the interviewer advocated clarifying to see if they also had difficulty studying the conception of a plan.
- Interviewer:
- Draw the terrain (Student X draws a square on the board).
- Interviewer:
- Now put in a possible plot (Student X draws a small square in the upper right corner of the plot of land).
- Interviewer:
- What is required?
- Student C:
- This… (pointing to the small square).
- Interviewer:
- So what is asked is the side of the plot, right?
- Student C:
- Oh sure, okay.
- Interviewer:
- So, can you explain in your words what you have to do?
- Student C:
- Yes, we have to calculate the side of the plots, knowing that the total land is that (indicating the drawing).
Although it seemed that they had already understood the statement, the interviewer continued the interview to see if there were also difficulties in analyzing the problem:
- Interviewer:
- How are the data and the unknown related?
- Student C:
- Everything is meters.
- Student X:
- The plots are smaller.
- Interviewer:
- So is there a concept that relates the data and the unknown?
- Student C:
- What operation could we do?
Analogously, although it seemed that they had understood the problem, they had a hard time finding the divisor ideas behind the data.
- Interviewer:
- Do you think that the g.c.d. of the two quantities could be the solution?
- Student C:
- Ehh… no.
- Interviewer:
- Why?
- Student C:
- Well, the 18 m are here and the others are below (indicating the vertical and horizontal lines of the drawing of the terrain on the board).
- Interviewer:
- And that, what does it mean?
- Student C:
- Well, there cannot be common divisors.
- Interviewer:
- Why do you think they have no common divisors?
- Student C:
- They are not the same, they are in different places…
From Student C’s interventions, it can be deduced that, as the data belong to different directions within the same geometric figure, the g.c.d. cannot be applied. Although they seemed to understand that the g.c.d. relates the divisors of two numbers, in this case, it did not seem possible. Finally, the researcher inquired if the problem had been associated with length.
- Interviewer:
- So if it were 2 strings…
- Student C:
- So yeah
- Interviewer:
- And you, what do you think?—referring to Student X-
- Student X:
- The same, if it were two strings we could do the g.c.d.
Consequently, it can be inferred that students do not associate the g.c.d. with geometrical data, but they do in other contexts. They (erroneously) assume that the g.c.d. only applies when dealing with independent things: two strings, two discrete sets, etc.
6.2. Case of l.c.m.
For the study of this case, a couple of students, which we will call Student G and Student L, who had similar resolutions in the written test, were interviewed.
Analogously to the previous case, they were asked to solve in pairs and on the blackboard another problem equivalent to GCDDQ, in this case. The problem posed was the following:
“Marc has 18 stickers for soccer players and 30 for basketball players. If you want to put them in envelopes with the same number of stickers without mixing the soccer players with the basketball players and getting the greatest number of players per envelope, how many envelopes do you have to prepare?”
Once read, they tried to analyze it:
- Student G:
- Let’s see, fifteen… And of the others, twenty-four.
- Student L:
- Same envelopes.
- Student G:
- And they ask us how many envelopes.
- Student L:
- Yes.
- Student G:
- As we distribute the cards, we draw… it seems to me that the greatest common divisor, but…
- Student L:
- Uh… okay.
Student G’s verbalizations indicated that he considers that, to distribute the chocolates, they should find a divisor. Therefore, they proposed to use the g.c.d., with which Student L agrees.
The couple proceeded to calculate the g.c.d. by means of factorial decomposition, obtaining the number 6 as a result.
- Student L:
- Get 6 stickers.
- Student G:
- But you ask us the number of envelopes, right?
- Student L:
- Ah… and then what?
- Student G:
- Buff, then it will be the l.c.m.
- Student L:
- It could be
Student G decided to calculate the l.c.m. of the statement data. Student G’s interventions indicate that the students based their approaches on choosing to relate the statement data by means of some known concept (in this case l.c.m.), which seems to indicate a random search by trial and error of the number sought.
After calculating the l.c.m., the couple stated that 90 envelopes are needed. None of the students evaluated the result in the context of the problem and did not show doubts about the validity of the solution. Therefore, the interviewer advocated investigating the retrospective view of the problem.
- Interviewer:
- Do you think the result is in line with what was requested?
- Student L:
- Yes, that’s 90 envelopes.
- Interviewer:
- If you read the statement again, knowing the resulting envelopes, is it possible?
- Student G:
- Let’s see if we have 18 for soccer and 30 for basketball and we put them in 90 envelopes… oh!… It can’t be.
- Student L:
- They have to be less envelopes, of course.
- Student G:
- Buff… well I don’t know
The verbalizations of the students point out they realized that the result is illogical, what confirms that the review of the results is a useful tool in the detection of errors.
6.3. Case of g.c.d.
For the study of this case, a couple of students, who we will call Student M and Student S, who had similar resolutions in the written test, were interviewed.
In the same way as in the precedent cases, they were asked to solve another problem equivalent to GCDDQ on the blackboard. The problem posed was the following:
“Marc has 18 stickers for soccer players and 30 for basketball players. If you want to put them in envelopes with the same number of stickers without mixing the soccer players with the basketball players and that there is the greatest number of players per envelope, how many envelopes do you have to prepare? “
Once read, they tried to analyze it:
- Student M:
- I put the data, okay?
- Student S:
- Ok.
Student M puts on the board F = 18, B = 30 and envelopes?
- Student S:
- That’s it, there is no more data.
- Student M:
- We have to find out the envelopes…
- Student S:
- So we have to divide, find the greatest common divisor, right?
- Student M:
- Well, but… yes, okay.
The verbalizations made by Student S indicate he considers that distributing the cards is related to the division. Therefore, he proposed to use the g.c.d., with which Student M, although hesitant, finally agrees.
The couple proceeded to calculate the g.c.d. by means of factorial decomposition, obtaining the number 6 as a result.
- Student S:
- Get 6 envelopes.
- Student M:
- Good.
Thus, the couple stated that 6 envelopes were needed. Again, none of the students evaluated whether it would be envelopes or stickers and they did not show doubts about the validity of the solution.
For this reason, the interviewer advocated asking directly how they know that it is about envelopes and not stickers:
- Interviewer:
- Just one question, is the result envelopes or stickers?
- Student S:
- They ask us for the envelopes.
- Student M:
- Of course… you have to distribute in envelopes, therefore divide. It is a divisor, … the g.c.d. are the envelopes.
The students’ interventions indicate that they based their statements on the fact that, if the statement implies the g.c.d., this is the only calculation to be performed, and no further operations are needed.
7. Discussion
In line with previous works (see [21] and the references therein), the results of this research corroborate a certain lack of competence at this educational level regarding divisibility, and show that the type of magnitudes used in the statement influence these difficulties, revealing they originate from a scarce understanding and relation of the quantities present in the problems (and of the mathematics in general) with the measures and units to which they refer in real life, which is typical of a low meaningful learning.
In relation to the first objective of this work (O1) on the competence in solving verbal problems that involve the concept of g.c.d., the results presented indicate serious difficulties in the group of students analyzed. These results confirm that, according to other previous studies [13,14,15,16,22,23,24,25], learning of these concepts is not meaningful. In line with this research, the study presented here suggests that the difficulties encountered could be due to methodological causes. Specifically, it occurs in a non-meaningful instruction based more on the learning of routine procedures than on solving problem situations.
Regarding the second objective (O2), related to the analysis of the context, it has been shown that those statements with contexts in which the measures and units that are handled are areas present greater difficulties, probably due to the scarce mathematical approach to geometric elements of the real life. The most successful contexts are those in which quantities are part of a discrete set, whose relationships between quantities and real life are easier for them to assimilate. These types of difficulties in secondary education students, caused by the inability to relate mathematics to the context, also appear in other types of mathematical problems [26].
Furthermore, with respect to the third objective of this work (O3), two erroneous resolution patterns have been detected that, although different, have a certain relationship due to a tendency to simplify the problem. In this sense, on the one hand, a confusion has been observed between the g.c.d. and l.c.m. in these students, due to a strong predisposition to solve problems with a single operation. The interventions of the students show that, although at some point, arguments arise about the idea of divisor, they immediately discard them if they must be completed with another operation; and, basing their approaches on the use of a single operation, they decide on the use of another type of operation, entering a trial-and-error process for troubleshooting. This issue, together with the fact that students resort to procedures typical of mechanical learning, such as algorithmic ones for calculating the g.c.d. and the l.c.m. (see [27,28]), demonstrates that, at no point in the resolution process, no solid reflection arises on the ideas of multiple and divisor (typical of meaningful learning), leading students to make wrong statements. Students also make a very common mistake when solving the problem and not checking if the result they have obtained is feasible. This error was also previously observed in other types of arithmetic problems, such as [26], where it was shown that students give answers with inconsistent results, without paying attention to them.
On the other hand, some students intuit the need to calculate the g.c.d. However, due to a strong predisposition to simplify the problem, they present the g.c.d. as its solution, without questioning the validity of the result or whether some type of additional operation is needed. This fact can be highly influenced by the habits in solving arithmetic problems, which can drag from their stage in primary school, in which the problems lead to the application of the identified (unique) operation, in order to immediately obtain the solution of the problem (see, for example, [29,30]).
In addition, this type of action indicates a little control of the students over the concept of g.c.d., since they do not have a clear idea about which unit it should refer to. It may be influenced by the fact that these students mainly use algorithmic resolutions. This suggests that, once the algorithmic calculation of these elements is introduced in secondary education, students stop using graphic resolutions, which are more didactic, as they facilitate the understanding of these situations. This becomes a very important obstacle to be taken into account.
Concerning the didactical implications, these findings point to the need to increase the quality and variety of verbal problems, considering multiple variables (for example, different contexts, type of measures or units, number of operations, etc.) in the teaching process, in order to connect mathematics with real life and that they can build a meaningful learning of the subject in question. In the same way, it is important to reinforce the verification of the results, either through the final check or through the use of other more intuitive g.c.d. calculation procedures, which allow a better analysis of the problems and make it easier for students to notice their errors by themselves, and rectify or expand their analysis.
Regarding the limitations of this study, as the influence of the type of magnitude had not been analyzed until now, it would be convenient to carry out more work on the subject. In particular, it would be beneficial to analyze samples of different sizes and levels. In addition, as a possible line of future research, qualitative studies could be carried out to explore the mental representations of the subjects, depending on the type of magnitudes, to improve the understanding of these types of difficulties and to provide (teaching) solutions to reduce them.
Author Contributions
Conceptualization, S.M. and J.C.V.; Data curation, S.M. and J.C.V.; Formal analysis, S.M. and J.C.V.; Investigation, S.M. and J.C.V.; Methodology, S.M. and J.C.V.; Writing—original draft, S.M. and J.C.V.; Writing—review & editing, S.M. and J.C.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Godino, J.; Batanero, C.; Font, V. Matemáticas y su Didáctica Para Maestros; Universidad de Granada: Granada, Spain, 2003. [Google Scholar]
- Ausubel, D. Teoría del Aprendizaje Significativo. 1983. Available online: https://www.academia.edu/10435788/teoría_teoria_del_aprendizaje_significativo (accessed on 23 August 2020).
- Chamorro, M.D.C. Didáctica de las Matemáticas Para Educación Infantil; Pearson Educación: Madrid, Spain, 2005. [Google Scholar]
- Castro, E. Didáctica de la Matemática en la Educación Primaria; Síntesis, S.A.: Madrid, Spain, 2001. [Google Scholar]
- Rayas, J. El Reconocimiento de las Ideas Previas Como Condición Necesaria Para Mejorar las Posibilidades de los Alumnos en los Procesos Educativos en Ciencias Naturales. Revista Xictli de la Unidad UPD. n. 94. 2004. Available online: http://189.208.102.74/u094/revista/54/02.html (accessed on 23 August 2020).
- Pantano, L.V. Enseñando adición y sustracción a partir del método para el aprendizaje natural de las matemáticas y la granja de Don Juan. Góndola Enseñanza Aprendiz. Cienc. 2014, 9, 60–78. [Google Scholar] [CrossRef][Green Version]
- Arias-Rueda, J.H.; Arias-Rueda, C.A.; Burgos-Hernández, C.A. Procesos aplicados por los estudiantes en la resolución de problemas matemáticos: Caso de estudio sobre la función cuadrática. Góndola Enseñanza Y Aprendiz. Cienc. 2020, 15, 129–147. [Google Scholar] [CrossRef]
- Blanco, M.; Bermejo, V. Dificultades de aprendizaje en matemáticas. In Cómo Enseñar Matemáticas para Aprender Mejor; Editorial CCS: Madrid, Spain, 2004; pp. 215–238. [Google Scholar]
- Carrillo, B. Dificultades en el Aprendizaje Matemático. Innovación Exp. Educ. 2009, 16, 1–10. Available online: https://archivos.csif.es/archivos/andalucia/ensenanza/revistas/csicsif/revista/pdf/Numero_16/BEATRIZ_CARRILLO_2.pdf (accessed on 3 March 2022).
- Zazkis, R.; Campbell, S. Divisibility and multiplicative structure of natural numbers: Preservice teacher’s understanding. J. Res. Math. Educ. 1996, 27, 540–563. [Google Scholar] [CrossRef]
- Ordoñez, C. La Construcción de la Noción de División y Divisibilidad de Números Naturales, Mediada por Justificaciones, en Alumnos de Tercer Grado de Nivel de Primaria. Educación Matemática Master’s Thesis, Pontificia Universidad Católica del Perú, Lima, Perú, 2014. [Google Scholar]
- Vallejo, E. Análisis y Propuesta en Torno a las Justificaciones en la Enseñanza de la Divisibilidad en el Primer Grado de Secundaria. Educación Matemática Master’s Theisis, Pontificia Universidad Católica del Perú, Lima, Perú, 2012. [Google Scholar]
- Noblet, K. Preservice elementary teachers’ understanding of greatest common factor story problems. In Proceedings of the 16th Annual Conference on Research in Undergraduate Mathematics Education, Denver, CO, USA, 21–23 February 2013; Sigma: Denver, CO, USA, 2013; pp. 219–225. [Google Scholar]
- Gutiérrez-Gutiérrez, A.; Gómez, P.; Rico, L. Conocimiento matemático sobre números y operaciones de los estudiantes de Magisterio. Educ. XX1 2016, 19, 135–158. [Google Scholar] [CrossRef][Green Version]
- Martínez, S.; González-Calero, J.A.; Sotos, M.A. La influencia del enunciado en la relación de problemas de m.c.d. y m.c.m. de estudiantes para maestro. In Investigación en Educación Matemática XIX; Fernández, C., Molina, M., Planas, N., Eds.; SEIEM: Alicante, Spain, 2015; pp. 343–350. [Google Scholar]
- González-Calero, J.A.; Martínez, S.; Sotos, M.A. La tendencia a restar en la resolución de problemas de g.c.d. en alumnos de primaria. In Investigación en Educación Matemática XX; Macías, J.A., Jiménez, A., González, J.L., Sánchez, M.T., Hernández, P., Fernández, C., Ruiz, F.J., Fernández, T., Berciano, A., Eds.; SEIEM: Málaga, Spain, 2016; p. 295. [Google Scholar]
- Dias, A. Using lattice models to determine greatest common factor and least common multiple. Int. J. Math. Teach. Learn. 2005, 730–738. Available online: https://www.cimt.org.uk/journal/dias.pdf (accessed on 3 March 2022).
- Zazkis, R.; Gadowsky, K. Attending to transparent features of opaque representations of natural numbers. In NCTM 2001 Yearbook: The Roles of Representation in School Mathematics; Cuoco, A., Ed.; NCTM: Reston, VA, USA, 2001; pp. 41–52. [Google Scholar]
- Zazkis, R.; Liljedahl, P. Understanding primes: The role of representation. J. Res. Math. Educ. 2004, 35, 164–186. [Google Scholar] [CrossRef][Green Version]
- Uribe, L.C. Estrategias cualitativas de investigación en Educación Matemática. In Proceedings of the XV Conferencia Interamericana de Educación Matemática, Medellín, Colombia, 5–10 May 2019. [Google Scholar]
- Bodí, S. Análisis de la Comprensión de Divisibilidad en el Conjunto de los Números Naturales. Ph.D. Thesis, Universitat d’Alacant, Alicante, Spain, 2006. [Google Scholar]
- Dwi Hastuti, I.; Listiawan, T.; Komariah, A.; Dabirnia, M. Fourth-grade primary school students’ misconception on greatest common factor and least common multiple. Educ. Res. Int. 2021, 2021, 6581653. [Google Scholar]
- Li, H.C.; Tsai, T.L. The effects of a problem-based learning intervention on primary students’ performance on greatest common factor and least common multiple and on their attitudes towards mathematics. Int. J. Innov. Learn. 2022, 31, 51–69. [Google Scholar] [CrossRef]
- Nortes Martinez-Artero, R.; Nortes Checa, A. Los problemas de m.c.d. y m.c.m. en futuros maestros. In Investigaciones Sobre la Formación Docente en el Siglo XXI; Maquilón Sánchez, J.J., Izquierdo Rus, T., Belmonte Almagro, M.L., Alfageme González, M.B., Eds.; Ediciones de la Universidad de Murcia: Murcia, Spain, 2018; pp. 91–104. [Google Scholar]
- Puri, R.I.I. Developing learning trajectory using traditional games in supporting students learning greatest common divisor in Indonesian primary school. In Proceedings of the 12th ICME, Soul, Korea, 8–15 July 2012; Volume 1, p. 7721. [Google Scholar]
- Macnab, D.S.; Cummine, J.A. La Enseñanza de las Matemáticas de 11 a 16: Un Enfoque Centrado en la Dificultad; Aprendizaje Visor: Madrid, Spain, 1992. [Google Scholar]
- Alba, M.Á.B.; Mellado, F.J.C.; Compaña, M.T.S.; Palacián, M.A. Pensamiento matemático avanzado y scratch: El caso del máximo común divisor. Pensam. Matemático 2017, 7, 43–64. [Google Scholar]
- Baeza Alba, M.Á.; Arnal Palacián, M.; Claros Mellado, F.J.; Sánchez Compaña, M.T. Comprensión del máximo común divisor: Propuesta didáctica con scratch. Uno Rev. Didáctica Matemáticas 2018, 80, 43–47. [Google Scholar]
- Bell, A.; Fischbein, E.; Greer, B. Choice of operation in verbal arithmetic problems: The effects of number size, problem structure and context. Educ. Stud. Math. 1984, 15, 129–147. [Google Scholar] [CrossRef]
- Puig, L.; Cerdán, F. Problemas Aritméticos Escolares; Síntesis: Madrid, Spain, 1988. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).