A Comparative Study of Different Schemes Based on Bézier-like Functions with an Application of Craniofacial Fractures Reconstruction

Abstract

Cranial implants, especially custom made implants, are complex, important and necessary in craniofacial fracture restoration surgery. However, the classical procedure of the manual design of the implant is time consuming and complicated. Different computer-based techniques proposed by different researchers, including CAD/CAM, mirroring, reference skull, thin plate spline and radial basis functions have been used for cranial implant restoration. Computer Aided Geometric Design (CAGD) has also been used in bio-modeling and specifically for the restoration of cranial defects in form of different spline curves, namely $C^1,C^2,G{C}^{1}G{C}^2,$ rational curves, B-spline and Non-Uniform Rational B-Spline (NURBS) curves. This paper gives an in-depth comparison of existing techniques by highlighting the limitations and advantage in different contexts. The construction of craniofacial fractures is made using different Bézier-like functions (Ball, Bernstein and Timmer basis functions) and is analyzed in detail. The $C^1,G{C}^1$ and $G{C}^2$ cubic Ball curves are performed well for construction of the small fractured part. Any form of fracture is constructed using this approach and it has been effectively applied to frontal and parietal bone fractures. However, B-spline and NURBS curves can be used for any type of fractured parts and are more friendly user.

1. Introduction

The most complex part of the human body is the craniofacial region because it consists of different bones integrated together in a very complex way. The bones that make up this region are shown in Figure 1, taken from [1]. There can be several reasons for cranial fractures such as sports injury, falls, trauma and home violence. Different tools, including X-rays, Magnetic Resonance Imaging (MRI) and Computed tomography (CT) scan are used to diagnose the craniofacial fractures. The main goal of craniofacial fracture reconstruction is to get and restore both normal physiological function and esthetics. As discussed earlier, the cranial part is a complicated anatomical region of the body. Therefore, to diagnose the craniofacial region is always a challenging task both for the surgeon and the radiologist. Most of the time, only radiologists can detect the fractures using radiological imaging tools.

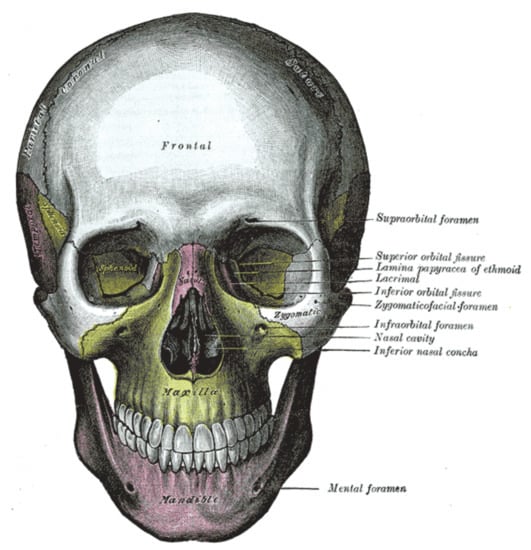
Figure 1. Craniofacial bones [1].

To overcome this problem, the latest computer technology has opened new doors for engineers, doctors and mathematicians to guide in construction and diagnosis of fractures caused by trauma and tumors. The CAD/CAM process has been used by [2,3] for the construction of the cranial area. This CAD/CAM process is time consuming and requires technical staff help, which causes high costs and low efficiency. One more down side of this process is that this method is not good for the construction of large format fractures. Cubic trigonometric B-spline basis functions have been used by [4] for geometric modeling. Craniofacial fractures in 3D form have been constructed by [1] using Bézier-like functions. The mirroring method for craniofacial fractures was proposed by [5]. This method is applicable for the fracture on the single side of the skull and will not work for multiple bone fractures. The surface interpolation or deformation method is proposed by [6]. Using this method, the fractured part is constructed using the non-fractured part. Wu et al. [7] and Shui et al. [8] introduced the adaptive deformation method for the restoration of a cranial implant. This method is based on a reference skull by first constructing the reference skull then constructing the patients fracture. The authors in [9] suggested a computer imaging system to generate $2D$ manual construction; to maintain the accuracy, they construct 20 different parts involving nose, contours, hairstyle and eyes. Meanwhile, a technique based on soft tissue thickness was proposed by [10].

Rational cubic Ball curves with $C^1$ continuity and two shape parameters have been used by [11] for frontal bone fracture reconstruction. Occipital bone fracture has been constructed by [12] using cubic B-spline curves. The parietal bone has been reconstructed using $G{C}^1$ rational Ball curves by [13]. NURBS curves with degree three have been used for the construction of multiple bone fractures by [14]. Hierarchical B-spline curve was used by [15,16] for cranial implants. They developed markers to use computer technology to recreate the face area. Kang [17] and Shui et al. [18] utilized thirty seven landmarks to construct craniofacial fractures. Facial reconstruction is dependent on the registration of dense points. Suetens et al. [19] used Thin Plate Spline (TPS) to reconstruct the craniofacial fracture taking 52 landmarks. Turner et al. [20] adopted Iterative Closest Point (ICP), taking into account a 30-skull model database. Claes et al. [21] presented Principal Component Analysis (PCA). Carr et al. [22] used radial basis function. Parietal bone fracture has been constructed by [23] using a parallel curve algorithm.

The scheme based on 37 land marks was used by [17,18] for the restoration of the fractured part. Radial bases functions and thin plate spline were used by [19,22] for facial reconstruction. In thin plate spline, authors used 52 landmarks. Thirty skull model databases were used in adopted iteration closest point for facial fracture reconstruction by [20]. Principal component analysis was used by [21] for fracture reconstruction.

This paper carries out the following two comparisons:

• A comparison between the existing scheme-like techniques (mirroring, reference skull, thin plate spline, iterative closest point, radial basis functions, the technique using CAD/CAM) and the techniques using spline curves.
• A comparative analysis of techniques based on spline curves.

The rest of the paper is organized in four sections. In Section 2, different Bézier-like functions and curves with their applications are discussed. Different continuity conditions between two curve segments are also a part of this section. Section 3 deals the two types of comparison analyses. First, the comparison between exiting techniques and the techniques based on Bézier-like functions. Second, the comparison between the different techniques based on Bézier-like functions. The last section is for conclusions.

2. Theoretical Foundation

This section explains different techniques based on spline curves, which have been used for the construction of craniofacial fractures.

2.1. Bézier-like Functions

Different cubic basis functions $B_i\left(\psi \right),i=0:1:3$ are defined in [24] as:

$$\begin{array}{c}{B}_0\left(\psi \right)={(1-\psi )}^2(1+(2-m)\psi ),B_1\left(\psi \right)=m\psi {(1-\psi )}^2,\hfill \\ B_2\left(\psi \right)=m{\psi }^2(1-\psi ),B_3\left(\psi \right)={\psi }^2(1+(2-m)(1-\psi )).\hfill \end{array}$$

(1)

Here, m is a positive integer. When $m=2$ the functions become a Ball basis defined by [25], and for $m=3,4$ equation one represents the Bézier and Timmer basis functions defined in [26,27]. The graphical behavior of the basis functions for different values of m is represented in Figure 2; $m=2$ has been used in this work.

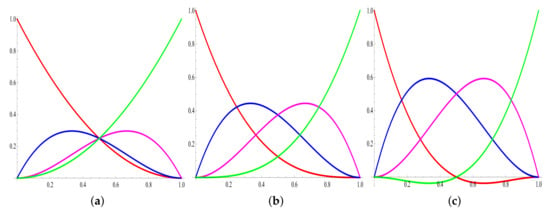
Figure 2. Graphical behavior of basis functions with different values of m. (a) Ball basis functions $(m=2)$; (b) Bézier basis functions $(m=3)$; (c) Timmer basis functions $(m=4)$.

The Bézier-like functions defined in Equation (1) satisfy the basic properties such as non-negativity, symmetricity, monotonicity and partition of unity.

2.2. Curve Segment and Continuity

The cubic Ball curve is defined as $T\left(\psi \right)={\sum }_{i=0}^3{Q}_i{B}_i\left(\psi \right)$. Here, $Q_i\in R^2$ are control points and $B_i\left(\psi \right)$ are Ball basis functions defined in Equation (1). The cubic Ball curve obeys all basic properties, including convex hull, coordinate system independence and the variation diminishing property.

In order to construct the craniofacial fractures, two or more curve segments are required. The smoothness and continuity between two curve segments (at knot points) is an important issue. Parametric and geometric continuities are commonly used to get the smoothness at the knots. Another use of the parametric and geometric condition is that it provides the relation to evaluate the intermediate control points.

2.3. Parametric and Geometric Continuity

Let $T_1\left(\psi \right)$ and $T_2\left(\psi \right)$ be two curve segments. The parametric continuity between two segments is defined as:

$C^m$ continuity: where m is the number of derivatives at the adjacent end points, which are the same:

$$T_2^i\left(1\right)=T_1^i\left(0\right)i=0,1,\dots ,m.$$

(2)

$C^0$, $C^1$ and $C^2$ are the continuity between two segments, as shown in Figure 3. The geometric continuity between segments can be defined as:

$$\begin{array}{c}\hfill G{C}^0:\mathrm{if}{T}_1\left(0\right)=T_2\left(1\right)\\ \hfill G{C}^1:\mathrm{if}{T}_2\left(0\right)=T_1\left(1\right),\mathrm{and}\\ \hfill T_2^{\prime }\left(0\right)=\lambda T_1^{\prime }\left(1\right),\lambda >0.\end{array}$$

$$\begin{array}{c}\hfill G{C}^2:\mathrm{if}{T}_2\left(0\right)=T_1\left(1\right),\mathrm{and}\\ \hfill T_2^{\prime }\left(0\right)=\lambda T_1^{\prime }\left(1\right),\mathrm{and}\\ \hfill T_2^{″}\left(0\right)={\lambda }^2{T}_1^{″}\left(1\right)+\gamma T_1^{\prime }\left(1\right),\end{array}$$

where $\lambda >0,\gamma$ is an arbitrary value.

Figure 3. Parametric continuity. (a) $C^0$ continuity $T_2\left(1\right)=T_1\left(0\right)$; (b) $C^1$ continuity $T_2^i\left(1\right)=T_1^i\left(0\right)$, $i=0,1$; (c) $C^2$ continuity $T_2^i\left(1\right)=T_1^i\left(0\right),i=0,1,2$.

For $\lambda =1$, $G{C}^1$ continuity reduces to $C^1$ continuity. The graphical representation of geometric continuity between two segments is given in Figure 4.

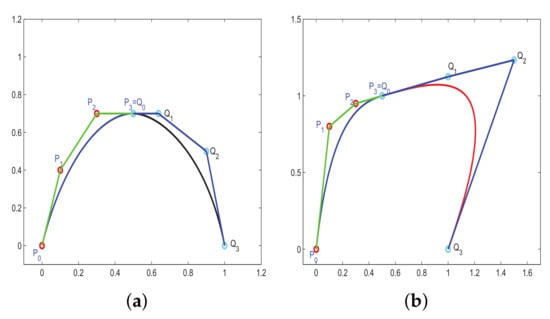
Figure 4. Geometric continuity. (a) $G{C}^1$ continuity $\lambda =1.3$; (b) $G{C}^2$ continuity $\lambda =0.5,\gamma =1.2$.

In the literature, different rational Ball curves with $C^1$, $G{C}^1$ and $G{C}^2$ continuity have been used for fracture reconstruction. $C^1$ rational cubic Ball curve has been used in [11], which is defined as:

$$\begin{array}{c}\hfill R_i\left(\psi \right)=\frac{L_i\left(\psi \right)}{M_i\left(\psi \right)},i=1,\dots n-1\mathrm{with}0\le \psi \le 1,\end{array}$$

(3)

where:

$$\begin{array}{c}\hfill L_i\left(\psi \right)=f_i{(1-\psi )}^2+V_i{(1-\psi )}^2\psi +W_i(1-\psi ){\psi }^2+f_{i+1}{\psi }^2,\\ \hfill M_i\left(\psi \right)={(1-\psi )}^2+c_i{(1-\psi )}^2\psi +d_i(1-\psi ){\psi }^2+{\psi }^2,\\ \hfill 0={\psi }_0<{\psi }_1<{\psi }_2<{\psi }_3.\dots <{\psi }_n=1,\end{array}$$

$$\begin{array}{c}\hfill V_i=c_i{g}_i+h_i{t}_i,\\ \hfill W_i=d_i{g}_{i+1}-h_i{t}_{i+1},\end{array}$$

satisfies the following conditions:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{R}_i\left({\psi }_0\right)=g_i,R_i\left({\psi }_n\right)=g_{i+1},\hfill \\ R_i^{\prime }\left({\psi }_0\right)=t_i,R_i^{\prime }\left({\psi }_n\right)=t_{i+1}.\hfill \end{array}\right.\end{array}$$

(4)

where $c_i$, $d_i$ are positive shape parameters, the endpoints of each segment is represented by $g_i$, $g_{i+1}$ and tangent vectors at $g_i$ and $g_{i+1}$, are $t_i$, $t_{i+1}$, respectively.

The above scheme with $C^1$ continuity has been used for the construction of frontal bone fracture, as shown in Figure 5.

Figure 5. Fracture reconstruction using $C^1$ rational cubic Ball curves.

In [28], the authors have constructed the fractured part using $G{C}^1$ rational Ball curves, which is defined as:

$$R_i\left(\theta \right)=\frac{L_i\left(\psi \right)}{M_i\left(\psi \right)},0\le \psi \le 1,$$

(5)

where:

$$\begin{array}{c}{L}_i\left(\psi \right)=E_i{(1-\psi )}^2+F_i{(1-\psi )}^2\psi +G_i(1-\psi ){\psi }^2+H_i{\psi }^2,\hfill \\ M_i\left(\psi \right)={(1-\psi )}^2+c_i{(1-\psi )}^2\psi +d_i(1-\psi ){\psi }^2+{\psi }^2.\hfill \end{array}$$

and $E_i$, $F_i$, $G_i$ and $H_i$ represents the control points and $c_i$, $d_i$ are shape parameters. $G{C}^1$ and $G{C}^2$ continuity between two adjacent segments can be defined as:

$$R_i\left(\psi \right)=\frac{L_i\left(\psi \right)}{M_i\left(\psi \right)},i=1,\dots ,n-1,$$

(6)

$$R_{i+1}\left(\psi \right)=\frac{L_{i+1}\left(\psi \right)}{M_{i+1}\left(\psi \right)},i=1,\dots ,n-1.$$

(7)

where:

$$\begin{array}{c}{L}_i\left(\psi \right)=A_i{(1-\psi )}^2+B_i{(1-\psi )}^2\psi +C_i(1-\psi ){\psi }^2+D_i{\psi }^2,\hfill \\ M_i\left(\psi \right)={(1-\psi )}^2+c_i{(1-\psi )}^2\psi +d_i(1-\psi ){\psi }^2+{\psi }^2,\hfill \\ L_{i+1}\left(\psi \right)=A_{i+1}{(1-\psi )}^2+B_{i+1}{(1-\psi )}^2\psi +C_{i+1}(1-\psi ){\psi }^2+D_{i+1}{\psi }^2,\hfill \\ M_{i+1}\left(\psi \right)={(1-\psi )}^2+c_{i+1}{(1-\psi )}^2\psi +d_{i+1}(1-\psi ){\psi }^2+{\psi }^2.\hfill \end{array}$$

Using the geometric continuity condition definition, the $G{C}^1$ continuity condition has been derived as follows:

$$\left\{\begin{array}{c}{R}_i\left(0\right)=E_i=g_i,R_i\left(1\right)=H_i=g_{i+1},\hfill \\ R_{i+1}\left(0\right)=E_{i+1}=g_{i+1},R_{i+1}\left(1\right)=H_{i+1}=g_{i+2},\hfill \\ H_i=E_{i+1}=g_{i+1},\hfill \\ F_{i+1}=(c_{i+1}+{\lambda }_i{d}_i)g_{i+1}-{\lambda }_i{G}_i.\hfill \end{array}\right.$$

(8)

where $g_i,g_{i+1},g_{i+2},i=1:1:n-2$ are control points and $c_i,d_i,{\lambda }_i$ are shape controls to be calculated. Figure 6 shows the parietal bone fracture using the $G{C}^1$ rational Ball curve.

Figure 6. Construction of fractured part using $G{C}^1$ rational Ball curves.

In [13], the authors used $G{C}^2$ rational Ball curves for fracture reconstruction with four shape parameters. The $G{C}^2$ continuity conditions are:

$$\left\{\begin{array}{c}{R}_i\left(0\right)=g_i=D_i,R_i\left(1\right)=g_{i+1}=H_i,\hfill \\ R_{i+1}\left(0\right)=g_{i+1},R_{i+1}\left(1\right)=g_{i+2},\hfill \\ H_{i+1}=E_{i+1}=g_{i+1},\hfill \\ F_{i+1}=(c_{i+1}+{\lambda }_i{d}_i)g_{i+1}-{\lambda }_i{G}_i,\hfill \\ G_{i+1}={\lambda }_i^2{g}_i+{\lambda }_i^2{F}_i+(-{\lambda }_i^2{d}_i-{\gamma }_i/2-{\lambda }_i{c}_{i+1})G_i\hfill \\ +(-{\lambda }_i^2{c}_i-{\lambda }_i^2+{\lambda }_i^2{d}_i^2+{\gamma }_i{d}_i/2-4c_{i+1}+d_{i+1}+1+2c_{i+1}^2+{\lambda }_i{c}_{i+1}{d}_i)g_{i+1}-g_{i+2}.\hfill \end{array}\right.$$

(9)

where $g_i,g_{i+1},g_{i+2},i=1,2,\dots n-2$ represents the control points on the curve and $c_i,d_i,{\lambda }_i$ and ${\gamma }_i$ represents the shape control to be calculated. The $G{C}^2$ rational Ball curve has been used for the construction of parietal bone fracture, which is shown in Figure 7.

Figure 7. Construction of fractured part using $G{C}^2$ rational Ball curves.

To define the cubic B-spline basis, consider the set of the knot vector with non-decreasing elements (knots), i.e., $w_j⩽w_{j+1},j=0,\dots m-1$; say $W^{*}=\{w_0,\dots ,w_m\}$. The cubic B-spline of the jth order with degree n is defined as:

$$S_{j,0}\left(w\right)=\left\{\begin{array}{c}1,\mathrm{if}w\in [w_j,w_{j+1}),\hfill \\ 0,otherwise.\hfill \end{array}\right.$$

(10)

$$X_{j,n}\left(w\right)=\frac{w-w_j}{w_{j+n}-w_j}{S}_{j,n-1}\left(w\right)+\frac{w_{j+n+1}-w}{w_{j+n+1}-w_{j+1}}{S}_{j+1,n-1}\left(w\right)$$

(11)

for $j=0,\dots ,m$ and $n\ge 1.$ These bases have been used for the construction of the occipital bone fracture by [12]. The reconstructed occipital fracture is shown in Figure 8.

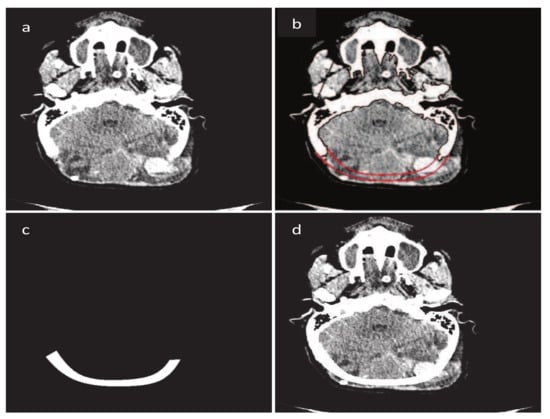
Figure 8. Construction of fractured part using B-spline. (a) Original CT scan image; (b) Construction of fractured part boundary curves; (c) Fractured part in DICOM format; (d) Implanted fractured part.

In [14], the authors used NURBS curves. The dth-degree NURBS curve is defined by:

$$X\left(w\right)=\frac{{\sum }_{j=0}^n{N}_{j,d}\left(w\right)w{\ast }_j{P}_j}{{\sum }_{j=0}^n{N}_{j,d}\left(w\right)w{\ast }_j},a\le w\le b.$$

(12)

where $\left\{w{\ast }_i\right\}$ are the weights, $\left\{P_j\right\}$ are the control points and $\left\{N_{j,d}\left(t\right)\right\}$ represents the dth-degree B-spline functions on non-uniform knots.

$$W=\{\underset{d+1}{\underbrace{a,\dots a}},w_{d+1},\dots ,w_{m-p-1},\underset{d+1}{\underbrace{b,\dots ,b}}\}.$$

as:

$$X_{i,0}\left(w\right)=\left\{\begin{array}{c}1,\mathrm{if}w\in [w_i,w_{i+1}),\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

(13)

$$X_{i,d}\left(w\right)=\frac{w-w_i}{w_{i+d}-w_i}{N}_{i,d-1}\left(w\right)+\frac{w_{i+d+1}-w}{w_{i+d+1}-w_{i+1}}{N}_{i+1,d-1}\left(w\right)$$

(14)

for $i=0,\dots ,n$ and $d\ge 1.$

For simplicity, assume that $a=0,b=1$ and $w{*}_i>0$ for all $i.$ Setting:

$$X_{i,d}\left(w\right)=\frac{N_{i,d}\left(w\right)w{\ast }_i}{{\sum }_{j=0}^n{N}_{i,d}\left(w\right)w{\ast }_j},$$

(15)

Equation (15) can be written as:

$$X\left(w\right)=\sum _{i=0}^n{R}_{i,d}\left(w\right)P_i.$$

(16)

The $R_{i,d}\left(w\right)$ are the rational basis functions.

These bases are piecewise rational functions on $w\in [0,1].$ The authors used the NURBS curve for the construction of the parietal bone fracture on the left hand side, as shown in Figure 9.

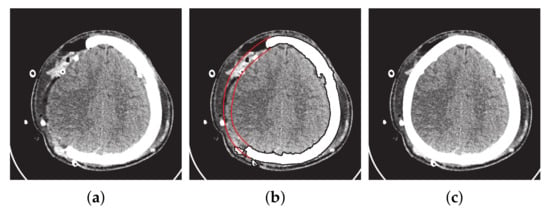
Figure 9. Construction of fractured part using NURBS curves. (a) Original image. (b) Fractured part boundary curves reconstruction (red curves show the inner and outer boundary curves). (c) Reconstruction of fracture part into DICOM format.

3. Comparative Analysis

3.1. Existing vs. Bézier-like Function Techniques

This subsection addresses the comparison between the existing techniques and the techniques based on spline curves. Table 1 gives a detailed comparison of the different techniques.

Table 1. Comparison of existing techniques and techniques based on spline curves.

Sr. No.	Parameter	Existing Methods	Methods Based on Bézier-like Functions
1	Technical staff	Refs. [2,3] used CAD/CAM process for craniofacial fracture reconstruction. It required technical staff/tools, which causes low efficiency and high cost	In this method, no need for staff/tools, reconstruction is based on patient CT scan DICOM data
2	Mirroring Method	Ref. [5] constructed the cranial part using the mirroring method. This method is not suitable for the patient with multiple bone fractures	The scheme based on spline functions is independent of mirroring and will work for any type of fractures.
3	Reference skull	Refs. [7,8] used adaptive deformation method for reconstruction. This scheme is dependent on reference skull	There is no need to take the reference skull using this method and reconstruction is based on CT scan data.
4	Thin plate spline	Ref. [19] proposed the thin plate spline and it is also based on the reference skull	Proposed method is independent of reference skull, construction will start directly using patient data.
5	Radial basis function	Radial basis functions have been used by [22]. In this method, authors consider the average thickness of bone and use a large number of data points	In this scheme, the user can attain the required thickness of the skull within a contour.
6	Iterative closest point	Ref. [20] used iterative closest point (ICP) algorithm to reconstruct the mandible bone fracture using non-fractured contour as a reference point	This scheme is independent of the reference skull. The reconstructed fractured part can be controlled and adjusted by shape parameters in the proposed method. The reconstructed implant is custom-made for each individual patient; thus, it is time saving and efficient.

3.2. Comparison of Techniques Using Spline Curves

This subsection addresses the critical analysis of different schemes based on Bézier-like functions such as $G{C}^2$, $G{C}^1$, $C^1$ rational cubic Ball curves, NURBS curves and B-spline curve of degree three. Different types of fractures have been constructed using CT scan, such as in Figure 10. Initially, the $C^1$ rational cubic Ball curve is used to construct the boundary curve of the fractured part, as shown in Figure 11. This scheme works well for small fractures but it reduces the smoothness and flexibility when the defected part become bigger and irregular, as shown in Figure 12 and Figure 13. However, the results obtained by $G{C}^1$, $G{C}^2$ rational cubic Ball curves are better, smoother and more flexible than the $C^1$ rational cubic Ball curve due to the presence of more shape parameters, as shown in Figure 14. The comparison of all curves is shown in Figure 15. In this figure, the red curve is obtained using the $G{C}^1$ rational Ball, the blue and green curves are obtained using the $C^1$ rational Ball.

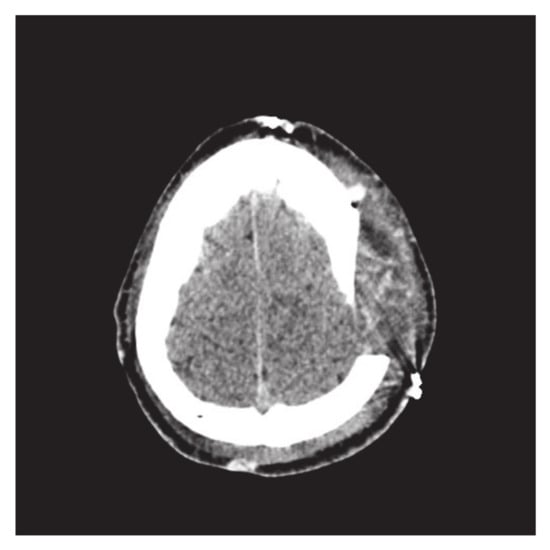
Figure 10. Parietal bone fracture.

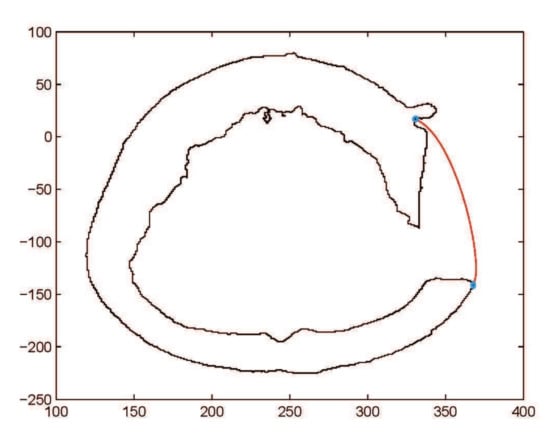
Figure 11. Construction of fractured part curve using $C^1$ rational Ball curves.

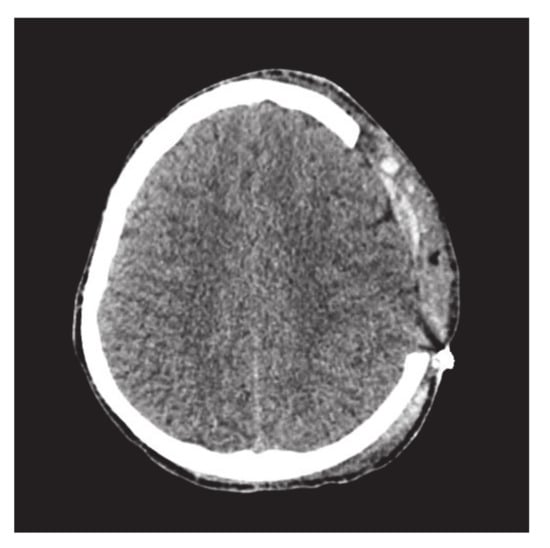
Figure 12. CT scan image of slice 170.

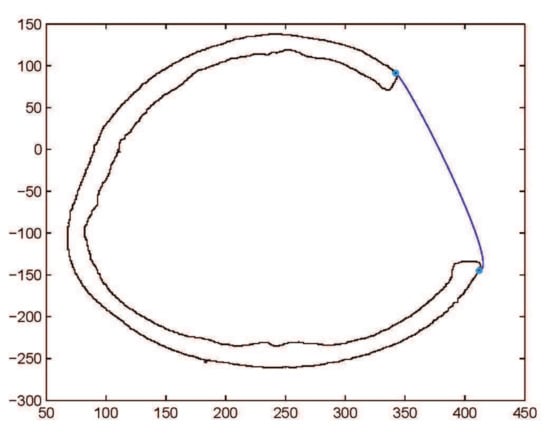
Figure 13. Construction of fractured part curve using $C^1$ rational Ball curves.

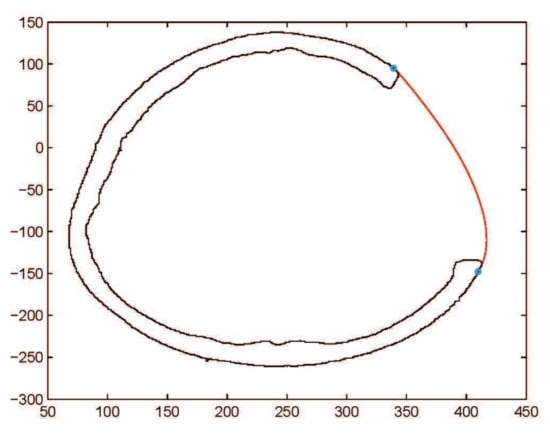
Figure 14. Construction of fractured part curve using $G{C}^1$ rational Ball curves.

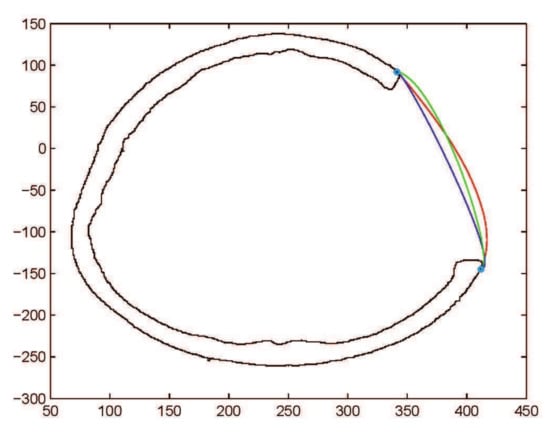
Figure 15. Comparison of $C^1$, $G{C}^1$ rational Ball curves (purple and green curves are constructed using $C^1$ and red curve is constructed using $G{C}^1).$

To check the validity of $G{C}^1$ and $G{C}^2$ curves, they are applied to construct the comparatively bigger fractured part, as shown in Figure 16. The results of curve fitting using $G{C}^1$, $G{C}^2$ curves show the rigidity of the curve resulting in limitation of these methods, as shown in Figure 17, Figure 18 and Figure 19. By dividing the fractured part into segments, the curve become smoother and flexible. The flexibility and smoothness is totally dependent on the number of segments of the fractured part. However, by increasing the number of segments, the required number of control points and and shape parameters are also increased, which is not easy to handle and increases the computational cost.

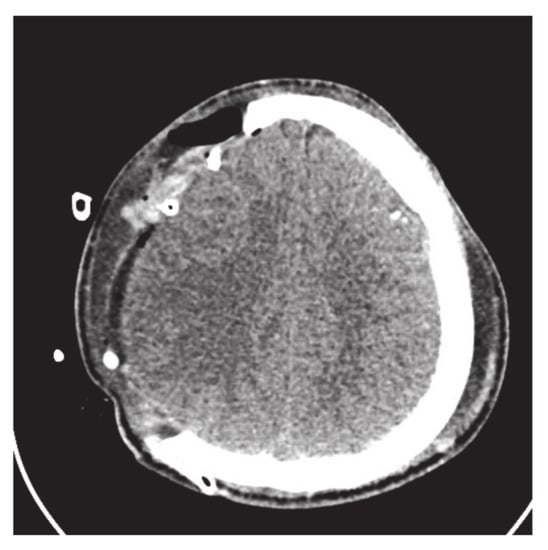
Figure 16. CT scan slice with big fractured part.

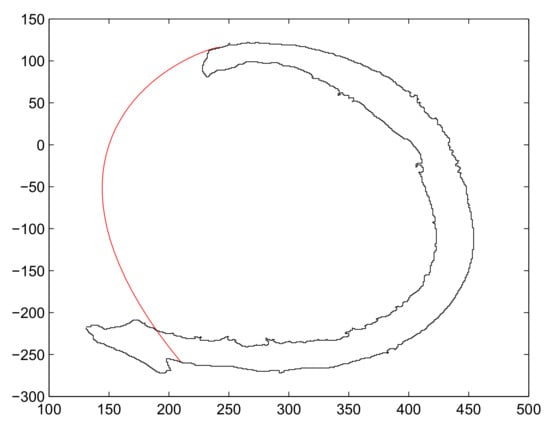
Figure 17. Construction of fractured part curve using $G{C}^1$ rational Ball curves with one segments.

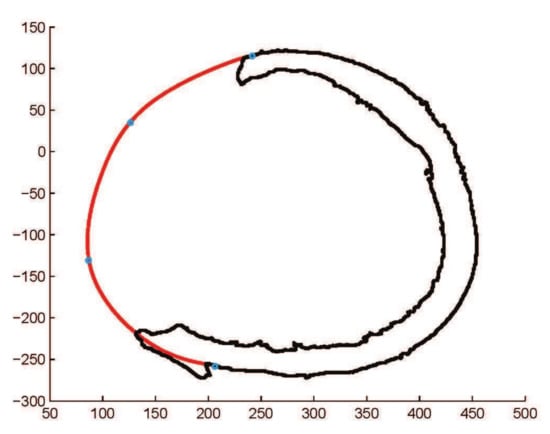
Figure 18. Construction of fractured part curve using $G{C}^1$ rational Ball curves with three segments.

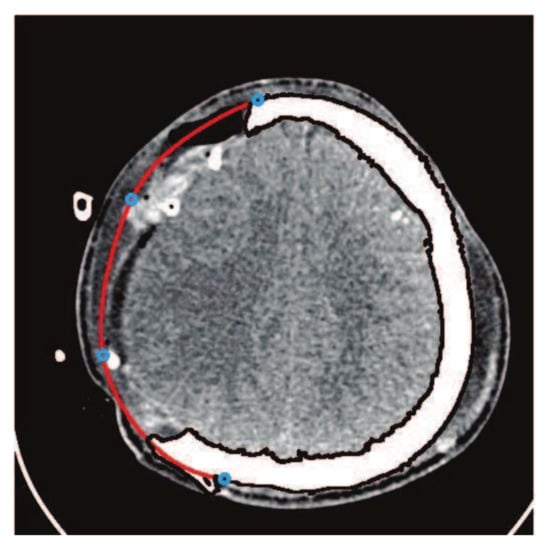
Figure 19. Construction of fractured part curve using $G{C}^2$ rational Ball curves with three segments.

To reduce the number of control points and overcome the computational cost, cubic B-spline is used to restore the cranial implant. It is very user friendly, one can get the desired curve just clicking on the CT scan image and there is no need to tackle shape parameters, as shown in Figure 20. Using the B-spline curve, there is no need to define and generate the continuity condition between two segments, in contrast to $G{C}^1$ and $G{C}^2$ where the continuity has to be generated. The main controlling tool in the B-spline curve is the knot points; one can change and adjust the curve using knot points. In order to make more flexible and smooth NURBS curves, it has been used for fracture reconstruction, as shown in Figure 21. The NURBS curve is a modified form of the B-spline and is more flexible due to the presence of weights.

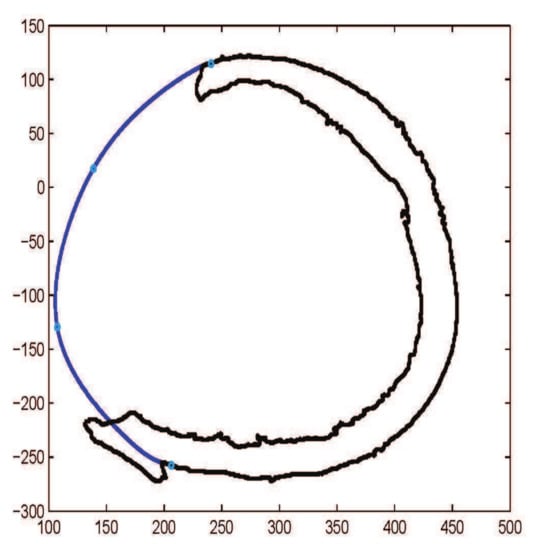
Figure 20. Construction of fractured part curve using B-spline curves with three segments.

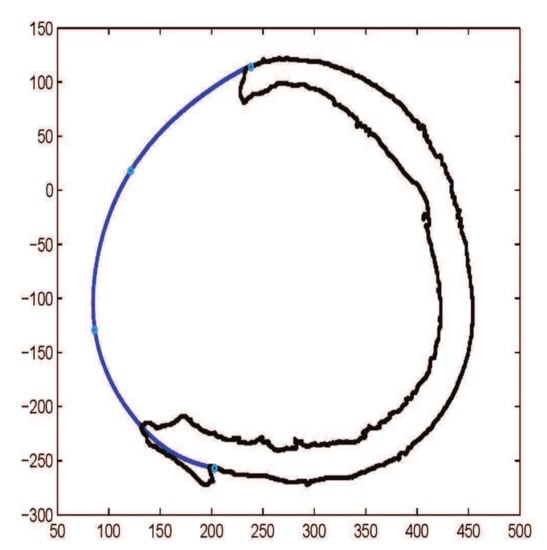
Figure 21. Construction of fractured part curve using NURBS curve with three segments.

The $G{C}^1$, $G{C}^2$ rational Ball, B-spline and NURBS curves have been employed on the same image, as shown in Figure 22. The fractured part curves are constructed with three segments. The $G{C}^1$ curve needs 9 free shape parameters and 10 control points. The $G{C}^2$ curve needs 12 free shape parameters and 10 control points. The B-spline curve needs only 6 control points and in the last NURBS curve, needs 6 control points and 6 weights. Table 2 shows the comparison of all parameters and computational time used in Figure 22. Table 3 gives the comparison of different curves used for the construction of craniofacial fractures.

Figure 22. Pink curve from $G{C}^1$, green curve from $G{C}^2$, black curve from B-spline and blue curve from NURBS curve.

Table 2. Comparison of spline curves with three curve segments.

Sr. No.	Curve	Number of Control Points Used	Number of Shape Parameters Used	Computational Time in Sec
1	$G{C}^1$ Ball curve	10	9	0.057
2	$G{C}^2$ Ball curve	10	12	0.067
3	B-spline curve	6	0	0.034
4	NURBS curve	6	6	0.043

Table 3. Comparison of cubic Bézier-like, B-Spline and NURBS curve.

Sr. No.	Bézier-like Curve	B-Spline	NURBS Curve
1	Interpolated curve	Approximated curve	Interpolated curve
2	Global control	Local control	Local control
3	Need to develop the continuity between two curve segments	No need to develop continuity; gives $C^2$ continuity	No need to develop continuity; gives $C^2$ continuity.
4	Need 4 control points for 1 curve segment	Need 4 control points for 1 curve segment	Need 4 control points for 1 curve segment
5	Need 7 and 10 control points for 2 and 3 curve segments, respectively	Need 5 and 6 control points for 2 and 3 curve segments, respectively	Need 5 and 6 control points for 2 and 3 curve segments, respectively
6	Need two shape parameter for 1 curve segment	No need for shape parameter	Need 4 weights (shape parameter for 1 segment)
7	$C^1$ needs 4 shape parameters for 2 curve segments, $G{C}^1$ needs 6 and $G{C}^2$ needs 8	B-spline is independent of shape parameters. Control points are the only way to handle the curve	Need 5 control points for 2 consecutive curve segments
8	Need to find intermediate control points using different techniques	The control points can be evaluated by using knots and B-spline basis	The control points can be evaluated by using knots and b-spline basis

4. Conclusions

The existing techniques for the construction of craniofacial fractures gives effective solutions in different contexts. However, techniques based on spline curves give more advantages by being non-dependent on the reference skull, mirroring and external help. Different Bézier-like functions have been used for the construction of craniofacial fractures and analyzed in detail. Cubic Ball curves with $C^1$, $G{C}^1$ and $G{C}^2$ continuity worked well for the small fractured part. Using this method, any type of fracture can be constructed and applied on the frontal and parietal bone fractures successfully. The constructed fracture is flexible due to the presence of shape parameters. The computational cost will be high if it will be used for large fractures. To overcome this problem, B-spline and NURBS curves can be used.