Evaluation Method of Highway Plant Slope Based on Rough Set Theory and Analytic Hierarchy Process: A Case Study in Taihang Mountain, Hebei, China
Abstract
:1. Introduction
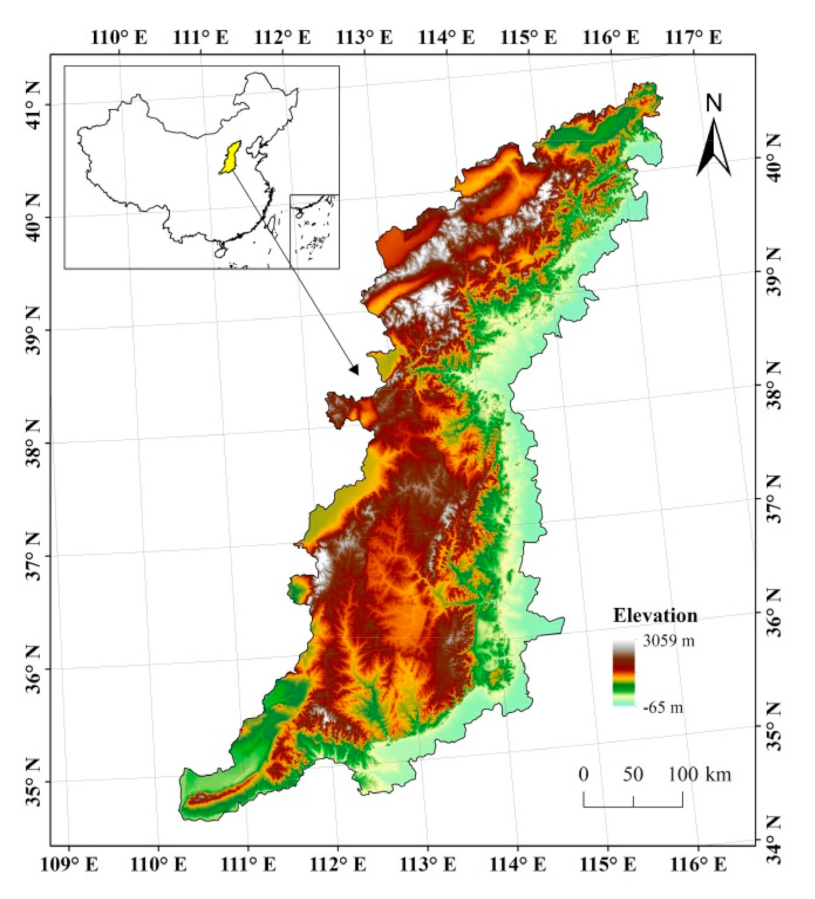
2. Study Site Description
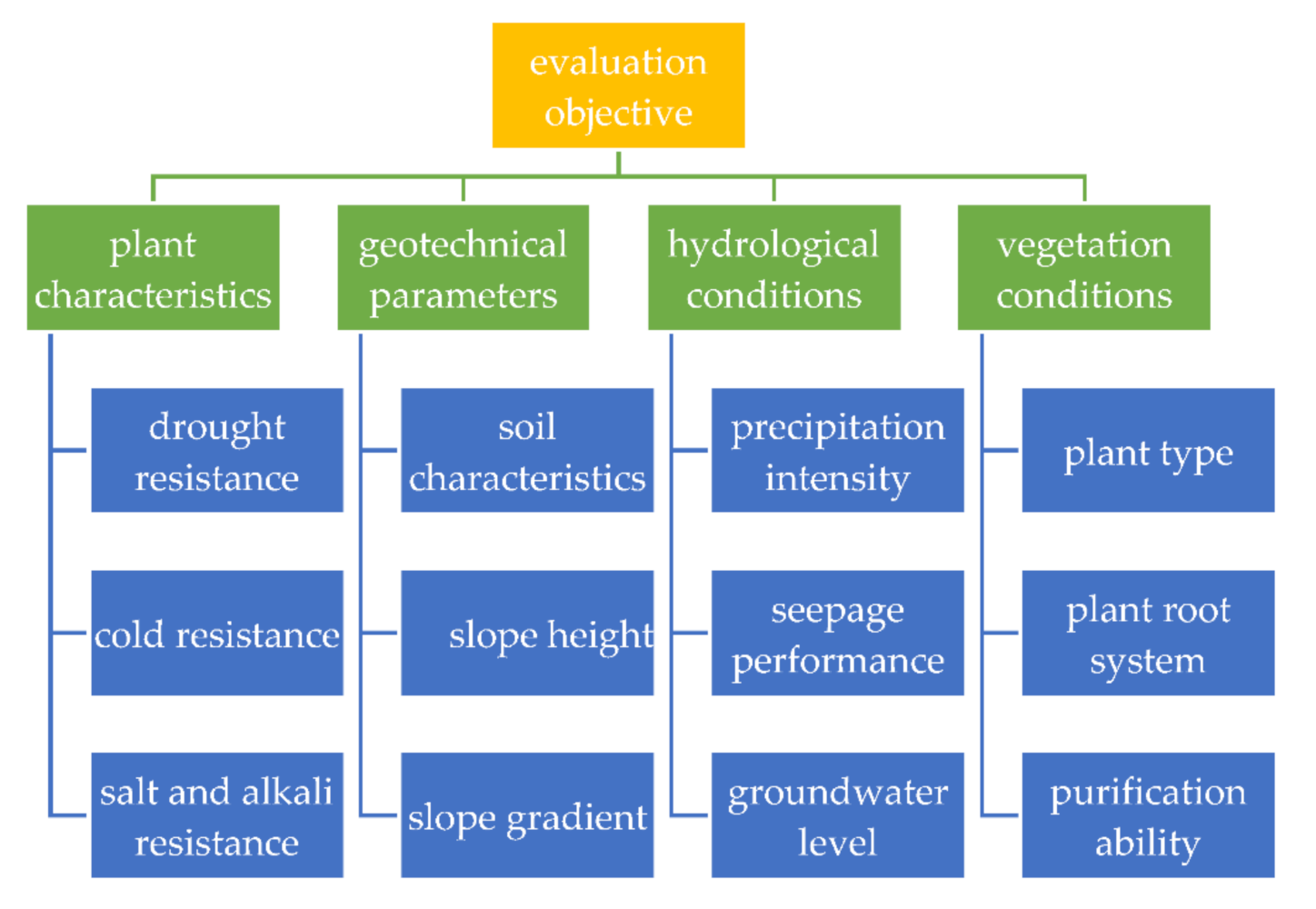
3. Construction of Performance Evaluation Index System of the Slope
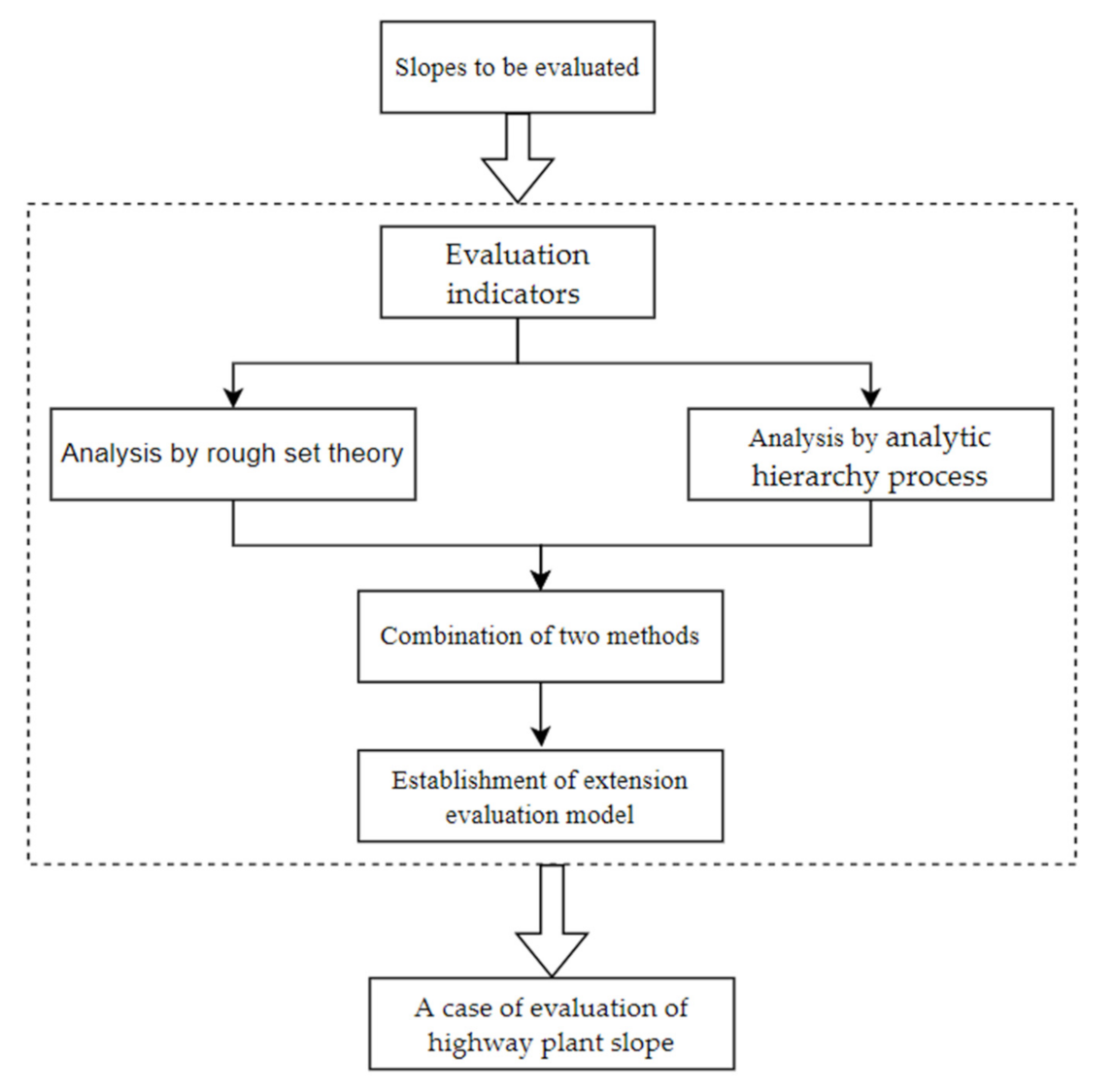
4. Construct the Evaluation Model of Highway Plant Slope
4.1. Calculation Steps of Rough Set Theory
4.2. Analytic Hierarchy Process Calculation Steps
4.3. Weight Results of First-Level Indicators
4.4. Secondary Index Weight Results
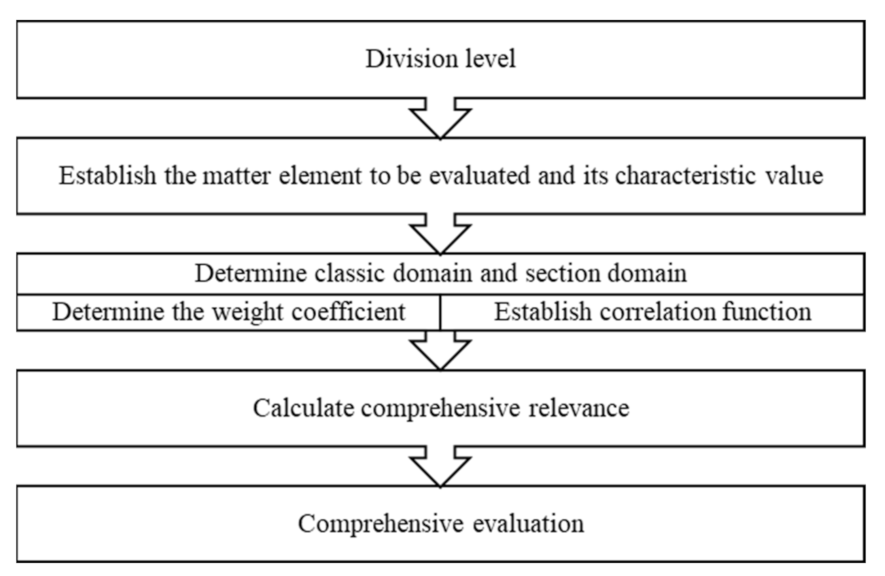
4.5. Establishment of Evaluation Model
5. A Case of Evaluation of Highway Plant Slope
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pandit, D.; Kaushik, K.; Cirillo, C. Coupling National Performance Management Research Data Set and the Highway Performance Monitoring System Datasets on a Geospatial Level. Transp. Res. Rec. 2019, 2673, 583–592. [Google Scholar] [CrossRef]
- Al-Hmouz, R.; Pedrycz, W.; Awadallah, M.; Al-Hmouz, A. Fuzzy relational representation, modeling and interpretation of temporal data. Knowl.-Based Syst. 2022, 244, 108548. [Google Scholar] [CrossRef]
- Le, C.; Jeong, H.; Damnjanovic, I. Network Theory–Driven Construction Logic Knowledge Network: Process Modeling and Application in Highway Projects. J. Constr. Eng. Manag. 2021, 147, 04021114. [Google Scholar] [CrossRef]
- Koteleva, N.; Frenkel, I. Digital Processing of Seismic Data from Open-Pit Mining Blasts. Appl. Sci. 2021, 11, 383. [Google Scholar] [CrossRef]
- Mokarram, M.; Pourghasemi, H.; Tiefenbacher, J. Comparison analytic network and analytical hierarchical process ap-proaches with feature selection algorithm to predict groundwater quality. Environ. Earth Sci. 2019, 78, 625. [Google Scholar] [CrossRef]
- Sakkas, G.; Misailidis, I.; Sakellariou, N.; Kouskouna, V.; Kaviris, G. Modeling landslide susceptibility in Greece: A weighted linear combination approach using analytic hierarchical process, validated with spatial and statistical analysis. Nat. Hazards 2016, 84, 1873–1904. [Google Scholar] [CrossRef]
- Jia, W.; Xu, Y.; Li, D.; Hu, R. Stochastic Analysis of Predator–Prey Models under Combined Gaussian and Poisson White Noise via Stochastic Averaging Method. Entropy 2021, 23, 1208. [Google Scholar] [CrossRef]
- Alemu, M.; Birhanu Wubneh, Z.; Adugna Ayanaw, M. Antidiarrheal Effect of 80% Methanol Extract and Fractions of the Roasted Seed of Coffea arabica Linn (Rubiaceae) in Swiss Albino Mice. Evid.-Based Complementary Altern. Med. 2022, 2022, 9914936. [Google Scholar] [CrossRef]
- Liu, W.; Yan, X.; Huang, S.; Yang, C.; Wang, G. Advanced Control for Singular Systems with Applications. Math. Probl. Eng. 2018, 2018, 1819540. [Google Scholar] [CrossRef]
- Chen, Z.S.; Liu, X.L.; Chin, K.S.; Pedrycz, W.; Tsui, K.L.; Skibniewski, M.J. Online-review analysis based large-scale group decision-making for determining passenger demands and evaluating passenger satisfaction: Case study of high-speed rail system in China. Inf. Fusion 2021, 69, 22–39. [Google Scholar] [CrossRef]
- Pham, V.; Volos, C.; Jafari, S.; Kapitaniak, T. Coexistence of hidden chaotic attractors in a novel no-equilibrium sys-tem. Nonlinear Dyn. 2016, 87, 2001–2010. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Pawlak, Z.; Skowron, A. Rudiments of rough sets. Inf. Sci. 2007, 1, 3–27. [Google Scholar] [CrossRef]
- Dai, J.; Hu, H.; Wu, W.; Qian, Y.; Huang, D. Maximal-Discernibility-Pair-Based Approach to Attribute Reduction in Fuzzy Rough Sets. IEEE Trans. Fuzzy Syst. 2018, 26, 2174–2187. [Google Scholar] [CrossRef]
- Xue, Y.; Liu, H.; Bai, C.; Su, M.; Qiu, D.; Zhou, B.; Yu, Y.; Jiang, X. Extension prediction model of soft rock tunnel deformation grade based on entropy weight method and rough set. Environ. Earth Sci. 2021, 81, 24. [Google Scholar] [CrossRef]
- Charles, W.N. Atmosphere-plant-soil interactions: Theories and mechanisms. Chin. J. Geotech. Eng. 2017, 39, 1–47. [Google Scholar] [CrossRef]
- Qiao, J.; Sun, X. Extension Stability Evaluation Model of Soil-rock Mixture Slope of Mountain Roads Based on Rough Set Weighting. J. Beijing Univ. Technol. 2020, 46, 508–514. [Google Scholar] [CrossRef]
- Abu-Gdairi, R.; El-Gayar, M.A.; Al-shami, T.M.; Nawar, A.S.; El-Bably, M.K. Some Topological Approaches for Generalized Rough Sets and Their Decision-Making Applications. Symmetry 2022, 14, 95. [Google Scholar] [CrossRef]
- Geng, S.; Shi, P.; Zong, N.; Zhu, W. Using Soil Survey Database to Assess Soil Quality in the Heterogeneous Taihang Mountains, North China. Sustainability 2018, 10, 3443. [Google Scholar] [CrossRef] [Green Version]
- Volpe, E.; Ciabatta, L.; Salciarini, D.; Camici, S.; Cattoni, E.; Brocca, L. The Impact of Probability Density Functions Assessment on Model Performance for Slope Stability Analysis. Geosciences 2021, 11, 322. [Google Scholar] [CrossRef]
- Theocharis, A.I.; Zevgolis, I.E.; Deliveris, A.V.; Karametou, R.; Koukouzas, N.C. From Climate Conditions to the Numerical Slope Stability Analysis of Surface Coal Mines. Appl. Sci. 2022, 12, 1538. [Google Scholar] [CrossRef]
- Wu, L.; Liu, X.; Yu, Y.; Ma, X. Biochar, grass, and cross-ridge reshaped the surface runoff nitrogen under consecutive rainstorms in loessial sloping lands. Agric. Water Manag. 2022, 261, 107354. [Google Scholar] [CrossRef]
- Valentin, C.; Poesen, J.; Li, Y. Gully erosion: Impacts, factors and control. CATENA 2005, 63, 132–153. [Google Scholar] [CrossRef]
- Liu, R.; Thomas, B.; Shi, X.; Zhang, X.; Wang, Z.; Zhang, Y. Effects of ground cover management on improving water and soil conservation in tree crop systems: A meta-analysis. CATENA 2021, 199, 105085. [Google Scholar] [CrossRef]
- Tong, D.; Tan, F.; Ma, B.; Jiao, Y.-Y.; Wang, J. A Suitability Evaluation Method of Urban Underground Space Based on Rough Set Theory and Conditional Entropy: A Case Study in Wuhan Changjiang New Town. Appl. Sci. 2022, 12, 1347. [Google Scholar] [CrossRef]
- da Luz, M.P.; Aparicio Ardila, M.A.; dos Santos Junior, R.D.; Valentin, C.A.; Schliewe, M.S.; Coelho, A.T.; Lins da Silva, J. Geomats Used to Control Erosion on Reservoir Margins in Brazilian Hydroelectric Power Plants. Water 2021, 13, 1444. [Google Scholar] [CrossRef]
- Kubler, S.; Robert, J.; Derigent, W.; Voisin, A.; Le Traon, Y. A state-of the-art survey & testbed of fuzzy AHP (FAHP) appli-cations. Expert Syst. Appl. 2016, 65, 398–422. [Google Scholar] [CrossRef]
- Nadi, B.; Askari, F.; Farzaneh, O.; Fatolahzadeh, S.; Mehdizadeh, R. Reliability Evaluation of Regression Model for Estimating Co-seismic Landslide Displacement. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 165–173. [Google Scholar] [CrossRef]
- Ponti, S.; Cannone, N.; Guglielmin, M. A new simple topo-climatic model to predict surface displacement in paraglacial and periglacial mountains of the European Alps: The importance of ground heating index and floristic components as ecological indicators. Ecol. Indic. 2021, 120, 106889. [Google Scholar] [CrossRef]
- Prakasam, C.; Aravinth, R.; Nagarajan, B.; Kanwar, V.S. Site-specific geological and geotechnical investigation of a debris landslide along unstable road cut slopes in the Himalayan region, India. Geomat. Nat. Hazards Risk 2020, 11, 1827–1848. [Google Scholar] [CrossRef]
- Li, B.; Li, T.; Xu, N.; Dai, F.; Chen, W.; Tan, Y. Stability assessment of the left bank slope of the Baihetan Hydropower Station, Southwest China. Int. J. Rock Mech. Min. Sci. 2018, 104, 34–44. [Google Scholar] [CrossRef]
- Cerdà, A.; Lucas-Borja, M.; Franch-Pardo, I.; Úbeda, X.; Novara, A.; López-Vicente, M.; Popović, Z.; Pulido, M. The role of plant species on runoff and soil erosion in a Mediterranean shrubland. Sci. Total Environ. 2021, 799, 149218. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Zhang, K.; Guo, Z. Runoff and soil erosion from highway construction spoil deposits: A rainfall simulation study. Transp. Res. Part D Transp. Environ. 2012, 17, 8–14. [Google Scholar] [CrossRef]
- Xu, Y.-Q.; Jin, L.-S.; Chen, Z.-S.; Yager, R.R.; Špirková, J.; Kalina, M.; Borkotokey, S. Weight Vector Generation in Multi-Criteria Decision-Making with Basic Uncertain Information. Mathematics 2022, 10, 572. [Google Scholar] [CrossRef]
- Sobol, N.; Gabbasova, I.; Komissarov, M. Effect of rainfall intensity and slope steepness on the development of soil erosion in the Southern Cis-Ural region (A model experiment). Eurasian Soil Sci. 2017, 50, 1098–1104. [Google Scholar] [CrossRef]
- Shinohara, Y.; Otani, S.; Kubota, T.; Otsuki, K.; Nanko, K. Effects of plant roots on the soil erosion rate under simulated rainfall with high kinetic energy. Hydrol. Sci. J. 2016, 61, 2435–2442. [Google Scholar] [CrossRef] [Green Version]
- Durán Zuazo, V.; Rodríguez Pleguezuelo, C. Soil-erosion and runoff prevention by plant covers. A review. Agron. Sustain. Dev. 2008, 28, 65–86. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Ai, S.; Liu, J.; Yang, H.; Wang, L.; Zhu, M.; Fu, D.; Yang, S.; Ai, X.; Ai, Y. The life span and influencing factors of metal mesh in artificial soil on railway rock-cut slopes in humid areas. Sci. Total Environ. 2019, 671, 41–51. [Google Scholar] [CrossRef]
- Xing, Z.; Wang, Y.; Zong, Q. Test of Ecological Riverbank Protection with Concrete. Appl. Mech. Mater. 2013, 438–439, 194–196. [Google Scholar] [CrossRef]
- Verma, S.; Midha, V.; Choudhary, A. Runoff erosion control performance of structurally modified coir geomeshes on different soil type and slope angle. J. Nat. Fibers 2021, 1–13. [Google Scholar] [CrossRef]
- Rossi, N.; Bačić, M.; Kovačević, M.S.; Librić, L. Fragility Curves for Slope Stability of Geogrid Reinforced River Levees. Water 2021, 13, 2615. [Google Scholar] [CrossRef]
- Kleyner, A. Effect of field stress variance on test to field correlation in accelerated reliability demonstration testing. Eng. Int. 2015, 31, 783–788. [Google Scholar] [CrossRef]
- Wei, X.; Fan, X.; Li, F.; Liu, X.; Liang, L.; Li, Q. Uncertainty analysis of hydraulic fracture height containment in a layered formation. Environ. Earth Sci. 2018, 77, 664. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, B.; Tan, R.; Tseng, M.-L.; Lin, R.C.-W.; Lim, M.K. Using Neighborhood Rough Set Theory to Address the Smart Elderly Care in Multi-Level Attributes. Symmetry 2020, 12, 297. [Google Scholar] [CrossRef] [Green Version]
- Ouma, Y.O.; Tateishi, R. Urban Flood Vulnerability and Risk Mapping Using Integrated Multi-Parametric AHP and GIS: Methodological Overview and Case Study Assessment. Water 2014, 6, 1515–1545. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Specifications for Design of Highway Subgrades: JTG D30-2004; China Communications Press: Beijing, China, 2004.
- Casquilho, J. A methodology to determine the maximum value of weighted Gini–Simpson index. SpringerPlus 2016, 5, 1143. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Luo, G. Grey system analysis and evaluation of slope stability based on experience. Chin. J. Geotech-Nical Eng. 1999, 21, 34–44. [Google Scholar]
- Gu, X.; Wu, S.; Ji, X.; Zhu, Y. The Risk Assessment of Debris Flow Hazards in Banshanmen Gully Based on the Entropy Weight-Normal Cloud Method. Adv. Civ. Eng. 2021, 2021, 8841310. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Labella, Á.; Nuñez-Cacho, P.; Molina-Moreno, V.; Martínez, L. A comprehensive minimum cost consensus model for large scale group decision making for circular economy measurement. Technol. Forecast. Soc. Change 2022, 175, 121391. [Google Scholar] [CrossRef]
- Liu, L.; Qiao, J.; Dou, Y. Tensile performance of PE-HD vegetation net and single-layer geonet. Eng. Plast. Appl. 2021, 49, 110–114. [Google Scholar] [CrossRef]
- Ulén, B.; Aronsson, H.; Bechmann, M.; Krogstad, T.; Øygarden, L.; Stenberg, M. Soil tillage methods to control phosphorus loss and potential side-effects: A Scandinavian review. Soil Use Manag. 2010, 26, 94–107. [Google Scholar] [CrossRef]
- Saaty, T.L. How to Make a Decision Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 9–16. [Google Scholar] [CrossRef]
- Nurnaini, R.; Wijayanto, D.; Fitri, A. Analysis of small-scale fish handling development in rembang waters. Russ. J. Agric. Socio-Econ. Sci. 2019, 90, 130–134. [Google Scholar] [CrossRef]
- Hu, C.; Ma, Y.; Chen, T. Application on Online Process Learning Evaluation Based on Optimal Discrete Hopfield Neural Network and Entropy Weight TOPSIS Method. Complexity 2021, 2021, 2857244. [Google Scholar] [CrossRef]
- Cai, W. Matter-Element Analysis; Guangdong Higher Education Press: Guangzhou, China, 1987. [Google Scholar]
- Saaty, T.L. Decision Making with the Analytic Hierarchy Process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J.; Yang, Q.; Lu, L. Study on Performance Evaluation of Service Supply Chain by Extension Method. Discret. Dyn. Nat. Soc. 2021, 2021, 1223577. [Google Scholar] [CrossRef]
- Xiaoxiao, L.; Zhengnan, H.; Ming, T.; Shengxian, Z. Engineering Internal Control Analysis Based on AHP-FCE Taking Wind Power Enterprise as an Example. E3S Web Conf. 2021, 253, 03048. [Google Scholar] [CrossRef]
- Mishra, P.; Vasudeva Reddy, C.; Satish Kumar, U. An evaluation of furrows for managing soil and water loss from a shallow Alfisol under simulated rainfall. Soil Use Manag. 2008, 24, 171–180. [Google Scholar] [CrossRef]
- Luo, X.; Wang, Z.; Lu, L.; Guan, Y. Supply Chain Flexibility Evaluation Based on Matter-Element Extension. Complexity 2020, 2020, 8057924. [Google Scholar] [CrossRef]
- Fu, K.; Xu, Y.; Yang, J.; Zhang, W. System Availability Test Procedure with Minimum Operating Time. Adv. Mater. Res. 2013, 706–708, 2053–2056. [Google Scholar] [CrossRef]
- Mirauda, D.; De Vincenzo, A.; Pannone, M. Statistical characterization of flow field structure in evolving braided gravel beds. Spat. Stat. 2019, 34, 100268. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014, update 2015 International soil classification system for naming soils and creating legends for soil maps. In World Soil Resources Reports No. 106; FAO: Rome, Italy, 2015. [Google Scholar]
| Region | Side Slope Grade | Slope Defects | Geologic Environment |
|---|---|---|---|
| Tuling | 1:1.5 | There are valleys on the right side of the slope, the catchment area is large, the valley mouth of the lower river is comprehensive, and there are signs of ancient debris flow | Silty clay soil, stone |
| Shangjiaosi | 1:1.25 | Medium soil collapse degree | Loess-like silt, with gravel |
| Lingdi | 1:1 | Strongly weathered collapsed rubble visible on both sidesRed clay deposit, poor geology. | Artificial fill, block stone, weathered marl, silt, and other combinations |
| Indicators | Notations | Corresponding Grade | Discrete Values |
|---|---|---|---|
| Drought resistance | C1 | Excellent | 1 |
| Good | 2 | ||
| Average | 3 | ||
| Poor | 4 | ||
| Cold resistance | C2 | Excellent | 1 |
| Good | 2 | ||
| Average | 3 | ||
| Poor | 4 | ||
| Salt and alkali resistance | C3 | Excellent | 1 |
| Good | 2 | ||
| Average | 3 | ||
| Poor | 4 | ||
| Soil characteristics | C4 | Excellent | 1 |
| Good | 2 | ||
| Average | 3 | ||
| Poor | 4 | ||
| Slope height/m | C5 | 0–5 | 1 |
| 5–10 | 2 | ||
| 10–15 | 3 | ||
| >15 | 4 | ||
| Slope gradient/(°) | C6 | 0–20 | 1 |
| 20–40 | 2 | ||
| 40–60 | 3 | ||
| >60 | 4 | ||
| Precipitation intensity/mm | C7 | 0–20 | 1 |
| 20–60 | 2 | ||
| 60–120 | 3 | ||
| >120 | 4 | ||
| Seepage performance | C8 | Excellent | 1 |
| Good | 2 | ||
| Average | 3 | ||
| Poor | 4 | ||
| Groundwater level | C9 | Dry | 1 |
| Wet | 2 | ||
| Dripping | 3 | ||
| Bubbling | 4 | ||
| Plant type | C10 | Trees, shrubs and herbs are reasonable | 1 |
| Fewer trees, reasonable shrubs and herbs | 2 | ||
| Few trees, reasonable shrubs, more reasonable herbs | 3 | ||
| No trees, few shrubs, more reasonable herbs | 4 | ||
| Purification ability | C11 | Excellent | 1 |
| Good | 2 | ||
| Average | 3 | ||
| Poor | 4 | ||
| Vegetation cover | C12 | 85–100% | 1 |
| 65–85% | 2 | ||
| 45–65% | 3 | ||
| 10–45% | 4 |
| Rank | Range of Values |
|---|---|
| 1 | [90, 100] |
| 2 | [60, 90) |
| 3 | [40, 60) |
| 4 | [0, 40) |
| Rank | Slope Stability Condition |
|---|---|
| One | very stable |
| Two | stable |
| Three | unstable |
| Four | severely unstable |
| U | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | D |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U1 | 2 | 3 | 1 | 2 | 3 | 4 | 3 | 2 | 4 | 3 | 3 | 3 | Four |
| U2 | 2 | 3 | 3 | 2 | 3 | 1 | 3 | 2 | 3 | 4 | 4 | 3 | Three |
| U3 | 3 | 4 | 4 | 2 | 4 | 2 | 3 | 1 | 3 | 4 | 3 | 4 | Four |
| U4 | 2 | 2 | 3 | 2 | 3 | 4 | 1 | 3 | 2 | 3 | 3 | 2 | Two |
| U5 | 2 | 3 | 4 | 2 | 2 | 3 | 3 | 2 | 1 | 1 | 2 | 3 | Two |
| U6 | 4 | 3 | 1 | 2 | 3 | 4 | 3 | 2 | 4 | 3 | 3 | 3 | One |
| U7 | 2 | 2 | 3 | 2 | 3 | 1 | 3 | 2 | 3 | 4 | 4 | 3 | One |
| U8 | 1 | 4 | 2 | 1 | 2 | 2 | 3 | 2 | 2 | 3 | 2 | 1 | Two |
| U9 | 2 | 3 | 4 | 2 | 2 | 3 | 3 | 2 | 1 | 2 | 2 | 3 | Four |
| U10 | 2 | 3 | 4 | 2 | 2 | 3 | 3 | 2 | 3 | 1 | 2 | 3 | Three |
| U11 | 2 | 2 | 4 | 2 | 3 | 4 | 1 | 3 | 2 | 3 | 3 | 2 | Two |
| U12 | 3 | 4 | 4 | 2 | 4 | 2 | 3 | 1 | 3 | 2 | 3 | 4 | Three |
| U13 | 2 | 3 | 3 | 2 | 2 | 1 | 4 | 1 | 2 | 3 | 2 | 3 | Two |
| U14 | 2 | 2 | 3 | 2 | 3 | 4 | 1 | 3 | 4 | 3 | 3 | 2 | Four |
| U15 | 3 | 4 | 2 | 2 | 4 | 2 | 3 | 1 | 3 | 4 | 3 | 4 | Two |
| Canonical Scale | Definition | Explanation |
|---|---|---|
| 1 | Equally important | One factor is as important as the other |
| 3 | A little important | One factor is slightly more important than the other |
| 5 | Clearly important | The importance of one factor outweighs the other |
| 7 | Strongly important | One factor is significantly more important than the other |
| 9 | Absolutely important | One factor is more essential than the other |
| A0 | A1 | A2 | A3 | A4 | Weight | Other Values |
|---|---|---|---|---|---|---|
| A1 | 1 | 2 | 4 | 3 | 0.4427 | CR = 0.0859 |
| A2 | 1/2 | 1 | 5 | 4 | 0.3545 | |
| A3 | 1/4 | 1/5 | 1 | 2 | 0.1123 | |
| A4 | 1/3 | 1/4 | 1/2 | 1 | 0.0905 |
| Indicator | Analytic Hierarchy Process Weight | Rough Set Weight | Coupling Weight |
|---|---|---|---|
| W1 | 0.3025 | 0.0503 | 0.2086 |
| W2 | 0.0885 | 0.0527 | 0.0639 |
| W3 | 0.0517 | 0.0959 | 0.0680 |
| W4 | 0.0921 | 0.0743 | 0.0938 |
| W5 | 0.1463 | 0.0767 | 0.1538 |
| W6 | 0.1161 | 0.0983 | 0.1564 |
| W7 | 0.0780 | 0.0792 | 0.0847 |
| W8 | 0.0107 | 0.0815 | 0.0120 |
| W9 | 0.0236 | 0.1007 | 0.0326 |
| W10 | 0.0516 | 0.1031 | 0.0729 |
| W11 | 0.0088 | 0.0818 | 0.0098 |
| W12 | 0.0301 | 0.1055 | 0.0435 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Dou, Y.; Qiao, J. Evaluation Method of Highway Plant Slope Based on Rough Set Theory and Analytic Hierarchy Process: A Case Study in Taihang Mountain, Hebei, China. Mathematics 2022, 10, 1264. https://doi.org/10.3390/math10081264
Liu L, Dou Y, Qiao J. Evaluation Method of Highway Plant Slope Based on Rough Set Theory and Analytic Hierarchy Process: A Case Study in Taihang Mountain, Hebei, China. Mathematics. 2022; 10(8):1264. https://doi.org/10.3390/math10081264
Chicago/Turabian StyleLiu, Luliang, Yuanming Dou, and Jiangang Qiao. 2022. "Evaluation Method of Highway Plant Slope Based on Rough Set Theory and Analytic Hierarchy Process: A Case Study in Taihang Mountain, Hebei, China" Mathematics 10, no. 8: 1264. https://doi.org/10.3390/math10081264
APA StyleLiu, L., Dou, Y., & Qiao, J. (2022). Evaluation Method of Highway Plant Slope Based on Rough Set Theory and Analytic Hierarchy Process: A Case Study in Taihang Mountain, Hebei, China. Mathematics, 10(8), 1264. https://doi.org/10.3390/math10081264





