Abstract
Combining multiple biomarkers to provide predictive models with a greater discriminatory ability is a discipline that has received attention in recent years. Choosing the probability threshold that corresponds to the highest combined marker accuracy is key in disease diagnosis. The Youden index is a statistical metric that provides an appropriate synthetic index for diagnostic accuracy and a good criterion for choosing a cut-off point to dichotomize a biomarker. In this study, we present a new stepwise algorithm for linearly combining continuous biomarkers to maximize the Youden index. To investigate the performance of our algorithm, we analyzed a wide range of simulated scenarios and compared its performance with that of five other linear combination methods in the literature (a stepwise approach introduced by Yin and Tian, the min-max approach, logistic regression, a parametric approach under multivariate normality and a non-parametric kernel smoothing approach). The obtained results show that our proposed stepwise approach showed similar results to other algorithms in normal simulated scenarios and outperforms all other algorithms in non-normal simulated scenarios. In scenarios of biomarkers with the same means and a different covariance matrix for the diseased and non-diseased population, the min-max approach outperforms the rest. The methods were also applied on two real datasets (to discriminate Duchenne muscular dystrophy and prostate cancer), whose results also showed a higher predictive ability in our algorithm in the prostate cancer database.
MSC:
62H30; 62J12; 62P10
1. Introduction
In clinical practice, it is usual to obtain information on multiple biomarkers to diagnose diseases. Combining them into a single biomarker is a widespread practice that often provides better diagnostics than each of the biomarkers alone [1,2,3,4,5,6]. Although recent studies have analyzed the diagnostic accuracy of built models in the presence of covariates and binary biomarkers [7,8,9], the combination of continuous biomarkers should provide a better discrimination ability. Linear combination methods have been widely developed and applied for both binary and multi-class classification problems in medicine [10,11] for their ease of interpretation and good performance. The accuracy of a diagnostic marker is usually analyzed using statistics derived from the receiver operating characteristic (ROC) curve, such as sensitivity and specificity, the area or partial area under the ROC curve or the Youden index, which allow for its discriminatory capacity to be measured.
The formulation of algorithms to estimate binary classification models that maximize the area under the ROC curve is a widely developed line of research. Su and Liu [12], using a discriminant function analysis, provided the best linear combination that maximizes area under ROC curve (AUC) under the multivariate normality assumption. Pepe and Thompson [13] proposed a distribution-free approach to estimate the linear model that maximizes AUC based on the Mann–Whitney U statistic [14]. This formulation has given rise to the development of non-parametric and semiparametric approaches in the construction of classifiers under optimality criteria derived from the ROC curve.
The process that Pepe and Thompson proposed lies in a discrete optimization that is based on a grid search over the parameter vector for a set of selected values. However, this process requires a great computational effort when the number of biomarkers is greater than or equal to three. In order to address the computational burden, various methods were proposed. Liu et al. [15] developed a non-parametric min-max approach, reducing the problem to a linear combination of two markers (minimum and maximum of biomarker values). Pepe et al. [13,16] also suggested the use of stepwise algorithms, where a new variable is introduced into the model at each stage searching for the partial combination of variables that maximizes AUC. Esteban et al. [17] implemented this approach, providing strategies to handle ties that appear in the sequencing of partial optimizations. Kang et al. [10,18] proposed a less computationally demanding stepwise approach based on a descending order of the AUC values corresponding to the predictor variables.
Other authors have developed algorithms focused on optimizing other parameters derived from the ROC curve. Liu et al. [19] analyzed the optimal linear of diagnostic markers that maximize sensitivity over a range of specificity. Yin and Tian [20] analyzed the joint inference on sensitivity and specificity at the optimal cut-off point associated with the Youden index. More recently, Yu and Park [21], Yan et al. [22] and Ma et al. [23] explored methods for the linear combination of multiple biomarkers that optimizes the pAUC.
The Youden index has also been used in different clinical studies and is both an appropriate summary for making the diagnosis and a good criterion for choosing the best cut-off point to dichotomize a biomarker [24]. The Youden index defines the effectiveness of a biomarker, as it maximize the sum of the sensitivity and specificity when an equal weight is given for both values [25]. Thus, the cut off point that simultaneously maximizes the probability of correctly classifying positive and negative subjects or minimizes the maximum of the misclassification error probability is chosen. It ranges from 0 to 1, where a 0 value indicates that the biomarker is equally distributed on the positive and the negative populations, whereas a value of 1 indicates completely separate distributions [26].
Based on the stepwise approach of Kang et al. [18], Yin and Tian [27] carried out a study aimed at optimizing the Youden index. These authors also analyzed the optimization of the AUC and Youden index simultaneously and presented both a parametric and a non-parametric approach to estimate the joint confidence region for the AUC and the Youden index [28]. However, the usual procedure is to estimate models that maximize either the AUC or the Youden index separately.
Unlike the AUC, the study and exploration of methods that optimize the Youden index has not received enough attention in the literature. The aim of our study was to propose a new stepwise distribution-free approach to find the optimal linear combination of continuous biomarkers based on maximizing the Youden index. In order to analyze its performance, our method was compared with five other linear methods from the literature (the Yin and Yan stepwise approach, the min-max method, logistic regression, a parametric approach under multivariate normality and a non-parametric kernel smoothing approach) adapted to optimize the Youden index, both in simulated data and in real datasets.
2. Materials and Methods
Firstly, we introduce the non-parametric formulation of Pepe et al. [13,16] and their suggestions for the estimation of the parameter vector of the linear model, which are the basis for the formulation and estimation of our proposed algorithm and of the analyzed algorithms. Then, we introduce our proposed method and five existing models in the literature adapted to optimize the Youden index to be compared: stepwise algorithm proposed by Yin and Tian, min-max approach, logistic regression, parametric method under multivariate normality and non-parametric kernel smoothing method. Finally, the simulated scenarios, as well as the real datasets considered, are described. All methods were programmed and applied using free software R [29]. In particular, a library in R (SLModels) [30] openly available to the scientific community was created that incorporates our proposed stepwise algorithm, among other linear algorithms.
Suppose that p continuous biomakers are measured for individuals with disease: and for individuals without it: . denotes the vector of p biomarkers for the individual of group k = 1,2 (disease and non-disease) and the biomarker () for the individual of group k = 1,2.
Given as the parameter vector, the linear combination for the disease and non-disease group is represented as follows:
The Youden index (J) is defined as
where c denotes the cut-off point and the cumulative distribution function of random variable
Denoting by as the optimal cut-off point and substituting (1) in (2), the empirical estimate of Youden index () is obtained as follows:
where I denotes the indicator function.
2.1. Background: Non Parametric Approach
By contrast to Su and Liu [12], who provided best linear model under multivariate normality, Pepe and Thompson [13] proposed a non-parametric approach to estimate the linear model that maximizes the AUC evaluated by the Mann–Whitney U statistic,
considering the linear model formulation as follows:
where p denotes the number of biomarkers, the biomarker and the parameter to be estimated. In order to be able to address the computational burden, Pepe et al. [13,16] suggest, for the estimation of the parameter , a discrete optimization that is based on a grid search over 201 equally spaced values in the interval [−1,1]. The justification for choosing this range lies in the property of the ROC curve that is invariant to any monotonic transformation. Consider, for simplicity, the linear combination of biomarkers . Then, due to the invariant property of the ROC curve for any monotonic transformation, dividing by the value does not change the value of the sensitivity and specificity pair. That is, estimating for and is equivalent to estimating for and, therefore, all possible values of are covered.
However, the search for the best linear combination in (5) is still computationally costly when . To solve this problem, Pepe et al. [13,16] suggested using stepwise algorithms by turning a computationally intractable problem into an approachable problem of single-parameter estimation (linear combination of two variables) times.
2.2. Our Proposed Stepwise Approach
Our proposed stepwise linear modelling (SLM) is an adaptation of the one proposed by Esteban et al. [17] for Youden index maximization. The general idea of this approach, as Pepe et al. [13,16] suggest, is to follow a step by step algorithm that includes a new variable in each step, selecting the best combination (or combinations) of two variables, in terms of maximizing the Youden index. The following steps explain the algorithm in detail:
- Firstly, given p biomarkers, the linear combination of the two biomarkers that maximizes the Youden index is chosen,using empirical search proposed by Pepe et al.: for each biomarker pair, for each value of the 201 , the optimal cut-off point that maximizes Youden index is selected. The final value chosen is the one with the highest Youden obtained;
- Once the pair of biomarkers and the parameter that maximizes the Youden index are chosen, this linear combination is considered as a single variable. For simplicity, suppose the linear combination . Then, in the same way as point 1, the biomarker (of the remaining s) and the parameter whose new linear combination maximize the Youden index are selected:Specifically, either the combination (7) or (8) that maximizes the Youden index is selected. This new linear combination will be considered as a new variable in the next step;
- The process (2) is repeated for the rest of biomarkers (i.e., times) until all of them are included in the model.
At each step, the maximum Youden index can be reached for more than one optimal linear combination. Our proposed algorithm considers each of these combinations and generates a branch to be explored by the algorithm. That is, it considers all ties at each stage and drags them forward until they are broken in the next steps (whenever possible) or until the end of the algorithm.
2.3. Yin and Tian’s Stepwise Approach
The stepwise non-parametric approach with downward direction (SWD) introduced by Yin and Tian [27] is an adaptation of the step-down approach proposed by Kang et al. [10,18] for the Youden index maximization. As the stepwise approach previously described, the general idea is to introduce a new variable at each stage and find the combination of two variables that maximizes the Youden index using the empirical search for combination parameters proposed by Pepe et al. [13,16].
Unlike our proposed stepwise approach, where, in each step, a search is performed not only for the parameter but also for the new biomarker that obtains the best linear combination, the approach proposed by Yin and Tian sets the biomarker that is entered in each step, based on the values ordered from largest to smallest of the empirical Youden index, obtained for each biomarker as follows:
Therefore, the approach is reduced to choosing, in each step, the parameter whose linear combination achieves the highest Youden index. Another difference from our proposed stepwise algorithm is that the Yin and Tian approach does not handle ties but chooses only one combination from among the optimal ones at each step.
Therefore, the approach presented by Yin and Tian could be considered as a simpler particular case of our proposed stepwise approach, where the new biomarkers of each stage are fixed from the beginning and where the ties are not considered.
2.4. Min-Max Approach
The non-parametric min-max approach (MM) was proposed by Liu et al. [15]. The aim was to reduce the order of the linear combination by considering only two markers (maximum value and the minimum value of all the p biomarkers) and estimate only the parameter of the linear combination that maximizes the AUC. Under this idea, the min-max approach can be adapted to maximize the Youden index with an expression as follows:
where and for and each , and , following Pepe et al’s. [13,16] suggestion of the empirical search for the optimal value of .
2.5. Logistic Regression
The logistic regression [31] (LR) (or logit regression) is a statistical model that models the probability of an event (disease or non-disease) given a set of independent variables through the logistics function. Assuming that the set of predictive independent variables for patient i is , the classification problem becomes the estimation of the parameters , such that:
and linear dependence:
For the application of the logistic regression model, the R function glm() was used.
2.6. Parametric Approach under Multivariate Normality
The parametric approach to estimate the Youden index under multivariate normality (MVN) is based on the results presented by Schisterman and Perkins [32].
Suppose and the single marker , the result of linear combination is , where:
for (disease and non-disease groups, respectively).
The formula for the Youden index and the optimal cut-off point differs depending on whether (i.e., ) or (i.e., ). Under the first scenario (), for , the Youden index () and the optimal cut-off point are expressed as follows:
where indicates the normal cumulative distribution function. Under the second one (), the expressions are the following:
These formulations are also valid under Box–Cox-type transformations [33].
Note that the Youden index () is a continuous differentiable function with respect to the parameter vector and its estimation () can be numerically optimized from quasi-Newton algorithms. Specifically, the R package optimr() was used to estimate the parameter vector from a initial parameter vector.
2.7. Non-Parametric Kernel Smoothing Approach
When no distributional hypothesis can be assumed, empirical distribution functions are often used, and their estimations can be performed using kernel-type approximations. In particular, a non-parametric Kernel Smoothing approach (KS) was applied in our study, whose estimation of the Youden index is as follows:
where the kernel function is the normal cumulative distribution function and the general-purpose bandwidth [34,35,36,37] is:
where and denote the standard deviation and the interquartile range of the combined marker , respectively.
Note that the Youden index () is a continuous differentiable function with respect to the parameter vector and . As in the previous approach, the R package optimr() was used to numerically optimize the Youden index from an initial vector . Thus, the estimated parameter vector can be obtained.
2.8. Simulations
A wide range of simulated scenarios were explored in order to compare the performance of the algorithms. Four () biomarkers were considered in each simulation scenario. Different joint and marginal distributions were considered, ranging from normal to non-normal distributions, with the aim of broadening the range for the evaluation and comparison of methods beyond normality.
A wide range of combinations were considered for the generation of simulated data following normal distributions: biomarkers with equal or different means (i.e., different capacity to discriminate between biomarkers) and independent or non-independent biomarkers, with negative or positive correlations with low, medium and high intensity, as well as the same and different covariances matrix for the group with disease and without disease. For each scenario, 1000 random samples from the underlying distribution were considered, with different sample sizes for the diseased and non-diseased population: . Each method was applied on each simulated dataset and the maximum Youden index for the optimal linear combination of biomarkers was obtained.
In terms of the scenarios of normal distributions, the null vector is considered in all scenarios as the mean vector of the non-diseased population (). With respect to the diseased population (), scenarios are explored with the same mean for each biomarker, as well as with mean vectors with different values. As for the covariance matrix, scenarios are analyzed with both the same covariance matrices for both populations and with different covariance matrices. For simplicity, the variance of each biomarker is set to be 1 in all cases and, therefore, the covariances equal to the correlations. The same correlation value for all pairs of biomarkers is assumed. Both positive and negative correlations are considered. Concerning negative correlations, the values and are considered. Regarding positive correlations, four types of correlations are assumed depending on the intensity: independence (), low (), medium () and high (). Specifically, the following covariance matrices ( for diseased and non-diseased population, respectively) are considered in the different scenarios: (independent biomarkers), ··J (low correlation), ··J (medium correlation), ··J (high correlation) and ··J, ··J (different correlations), where I is the identity matrix and J a matrix of all of them.
In terms of scenarios that do not follow a normal distribution, the following scenarios were considered: simulated data with different marginal distributions (multivariate chi-square/normal/gamma/exponential distributions via normal copula) and simulated data following the multivariate log-normal skewed distribution. The latter simulated data were generated from the normal scenario configurations and then exponentiated to obtain these multivariate log-normal observations.
2.9. Application in Clinical Diagnosis Cases
The analyzed methods were also applied to two real data examples related to clinical diagnosis cases. In particular, a Duchenne muscular dystrophy dataset and a prostate cancer dataset were analyzed through their respective biomarkers. Duchenne Muscular Dystrophy (DMD) is a progressive and recessive muscular disorder that is transmitted from a mother to her children. Percy et al. [38] analyzed the effectiveness in detecting the following four biomarkers of blood samples: serum creatine kinase (CK), haemopexin (H), pyruvate kinase (PK) and lactate dehydrogenase (LDH). The available data contain complete information on these four biomarkers of 67 women who are carriers of the progressive recessive disorder DMD and 127 women who are not carriers.
Prostate cancer is the second most common cancer in males worldwide after lung cancer [39] and it is therefore a matter of social and medical concern. The detection of clinically significant prostate cancer (Gleason score ≥ 7) through the combination of clinical characteristics and biomarkers has been an important line of study in recent years [40,41]. The data set used contains complete information on 71 people who were diagnosed with clinically significant prostate cancer and 398 with non-significant prostate cancer in 2016 at Miguel Servet University Hospital (Zaragoza, Spain) on the following four biomarkers: prostate-specific antigen (PSA), age, body mass index (BMI) and free PSA.
2.10. Validation
To analyze the performance of the compared algorithms in prediction scenarios, we validated built models for simulation and real data. For each scenario of simulated data, we built 100 models using small (50) and large (500) sample sizes, and then we validated these models by estimating the mean of the 100 Youden indexes calculated for new data simulated using the same setting of parameters and sample sizes. For real data, a 10-fold cross validation procedure was performed.
3. Results
This section first presents the results of the simulations for the training set. Then, the results of simulated scenarios for the validation data are presented. Finally, for a specific scenario, the time carried out in each of the methods is also presented in order to illustrate the computational cost of each one of them.
3.1. Simulations
Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10 show the results of the performance of each algorithm for each simulated data scenario. In particular, for each simulated dataset (1000 random samples), the mean and standard deviation (SD) of the empirical estimates of the Youden index of each biomarker are shown. In addition, for each method, the mean and standard deviation of the maximum Youden indexes obtained in each of the 1000 samples, as well as the probability of obtaining the highest Youden index, are presented. These results and conclusions drawn in terms of performance in the simulated scenarios are presented below.
3.1.1. Normal Distributions. Different Means and Equal Positive Correlations for Diseased and Non-Diseased Population
Table 1, Table 2, Table 3 and Table 4 show the results obtained in the scenarios under multivariate normal distribution with mean vectors and and independent biomarkers, low correlations, medium correlations and high correlations, respectively.
The results in Table 1 show that our proposed stepwise method outperforms the rest of the methods in all scenarios and with a remarkable estimated probability of yielding the largest Youden index of 0.5 or more in most of them. It is followed by Yin and Tian’s stepwise approach and the non-parametric kernel smoothing approach, which perform similarly in general. Logistic regression and the parametric approach under multivariate normality perform comparably in general. The min-max approach is the one with the worst results in such scenarios. The same conclusions are drawn from the results reported in Table 2.



Table 1.
Normal distributions: Different means. Independence ( = I).
Table 1.
Normal distributions: Different means. Independence ( = I).
| Mean (SD) | Probability Greater than or Equal to Youden Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (, ) | Mean (SD) Variables | SLM | SWD | MM | LR | MVN | KS | SLM | SWD | MM | LR | MVN | KS |
| (10, 20) | = (0.2737, 0.3560, 0.5178, 0.4314) | 0.7782 | 0.731 | 0.6352 | 0.6926 | 0.6937 | 0.7272 | 0.5962 | 0.1389 | 0.0588 | 0.0532 | 0.0355 | 0.1175 |
| = (0.1357, 0.1395, 0.1421, 0.1457) | (0.1022) | (0.1104) | (0.119) | (0.1346) | (0.1253) | (0.1179) | |||||||
| (30, 30) | = (0.2063, 0.3024, 0.4663, 0.3673) | 0.6737 | 0.6402 | 0.5556 | 0.6057 | 0.6050 | 0.6395 | 0.6480 | 0.1350 | 0.0453 | 0.0221 | 0.0161 | 0.1335 |
| = (0.0943, 0.0991, 0.0990, 0.1053) | (0.0836) | (0.0876) | (0.0962) | (0.0957) | (0.0946) | (0.0891) | |||||||
| (50, 30) | = (0.1933, 0.2975, 0.4630, 0.3603) | 0.6434 | 0.6278 | 0.5424 | 0.5895 | 0.5896 | 0.6203 | 0.5806 | 0.1756 | 0.0448 | 0.0179 | 0.0176 | 0.1636 |
| = (0.0846, 0.0937, 0.0894, 0.0898) | (0.0771) | (0.0778) | (0.0812) | (0.0839) | (0.0828) | (0.0806) | |||||||
| (50, 50) | = (0.1764, 0.2784, 0.4484, 0.3458) | 0.6219 | 0.6005 | 0.5193 | 0.5693 | 0.5693 | 0.5998 | 0.6586 | 0.1428 | 0.0272 | <0.01 | 0.0132 | 0.1495 |
| = (0.0736, 0.0789, 0.0774, 0.0796) | (0.0667) | (0.0702) | (0.0736) | (0.0732) | (0.0732) | (0.0701) | |||||||
| (100, 100) | = (0.1487, 0.2498, 0.4254, 0.3214) | 0.5734 | 0.5623 | 0.4837 | 0.5412 | 0.5409 | 0.5620 | 0.6174 | 0.1543 | 0.0132 | 0.0171 | 0.0137 | 0.1844 |
| = (0.0533, 0.0590, 0.0560, 0.0590) | (0.0506) | (0.051) | (0.0526) | (0.0538) | (0.0537) | (0.0528) | |||||||
| (500, 500) | = (0.1062, 0.2185, 0.3991, 0.2925) | 0.5213 | 0.5191 | 0.4447 | 0.5120 | 0.5119 | 0.5196 | 0.4545 | 0.1824 | <0.01 | 0.0332 | 0.0317 | 0.2982 |
| = (0.0257, 0.0282, 0.0274, 0.0280) | (0.0257) | (0.0257) | (0.027) | (0.0262) | (0.0263) | (0.0258) | |||||||
| (10, 20) | = (0.3359, 0.5120, 0.6604, 0.5815) | 0.9134 | 0.8783 | 0.8042 | 0.8771 | 0.8594 | 0.8786 | 0.4822 | 0.1128 | 0.0350 | 0.1913 | 0.0565 | 0.1221 |
| = (0.1413, 0.1386, 0.1275, 0.1402) | (0.074) | (0.0834) | (0.1013) | (0.0158) | (0.0958) | (0.0886) | |||||||
| (30, 30) | = (0.2699, 0.4695, 0.6172, 0.5299) | 0.8488 | 0.8190 | 0.7463 | 0.8086 | 0.8044 | 0.8242 | 0.5826 | 0.1304 | 0.0319 | 0.0692 | 0.0420 | 0.1438 |
| = (0.0989, 0.0988, 0.0911, 0.1019) | (0.0645) | (0.0690) | (0.0787) | (0.0778) | (0.0750) | (0.0719) | |||||||
| (50, 30) | = (0.2586, 0.4636, 0.6133, 0.5218) | 0.8310 | 0.8172 | 0.7400 | 0.8005 | 0.7960 | 0.8162 | 0.5270 | 0.1755 | 0.0372 | 0.0540 | 0.0362 | 0.1700 |
| = (0.0905, 0.0926, 0.0810, 0.0854) | (0.0598) | (0.0621) | (0.069) | (0.0676) | (0.0666) | (0.0633) | |||||||
| (50, 50) | = (0.2444, 0.4475, 0.6010, 0.5099) | 0.8144 | 0.7972 | 0.7235 | 0.7840 | 0.7806 | 0.8007 | 0.5841 | 0.1403 | 0.0199 | 0.0436 | 0.0295 | 0.1826 |
| = (0.0791, 0.0796, 0.0695, 0.0772) | (0.0545) | (0.0569) | (0.0624) | (0.0598) | (0.0584) | (0.0573) | |||||||
| (100, 100) | = (0.2178, 0.4243, 0.5821, 0.4906) | 0.7827 | 0.7728 | 0.6987 | 0.7620 | 0.7611 | 0.7749 | 0.5701 | 0.1690 | <0.01 | 0.0262 | 0.0286 | 0.2036 |
| = (0.0570, 0.0579, 0.0526, 0.0562) | (0.04) | (0.0412) | (0.0456) | (0.0423) | (0.0423) | (0.0412) | |||||||
| (500, 500) | = (0.1809, 0.3997, 0.5604, 0.4673) | 0.7483 | 0.7461 | 0.6692 | 0.7424 | 0.7422 | 0.7471 | 0.4667 | 0.1695 | <0.01 | 0.0431 | 0.0359 | 0.2848 |
| = (0.0271, 0.0272, 0.0255, 0.0260) | (0.02) | (0.0199) | (0.0223) | (0.0201) | (0.0201) | (0.0199) | |||||||

Table 2.
Normal distributions: Different means. Low correlation ( = 0.7·I + 0.3·J).
Table 2.
Normal distributions: Different means. Low correlation ( = 0.7·I + 0.3·J).
| Mean (SD) | Probability Greater than or Equal to Youden Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (, ) | Mean (SD) Variables | SLM | SWD | MM | LR | MVN | KS | SLM | SWD | MM | LR | MVN | KS |
| (10, 20) | = (0.2666, 0.3621, 0.5180, 0.4226) | 0.7348 | 0.6811 | 0.5730 | 0.6380 | 0.6385 | 0.6755 | 0.6163 | 0.1309 | 0.0617 | 0.0404 | 0.0312 | 0.1195 |
| = (0.1378, 0.1439, 0.1377, 0.1427) | (0.1063) | (0.1158) | (0.1294) | (0.1389) | (0.1358) | (0.1266) | |||||||
| (30, 30) | = (0.2037, 0.3051, 0.4700, 0.3774) | 0.6228 | 0.5873 | 0.4842 | 0.5472 | 0.5483 | 0.5844 | 0.6869 | 0.1276 | 0.0343 | 0.0103 | 0.0125 | 0.1284 |
| = (0.0951, 0.1029, 0.1002, 0.1004) | (0.0848) | (0.0896) | (0.0948) | (0.0994) | (0.0982) | (0.0939) | |||||||
| (50, 30) | = (0.1963,0.2917,0.4606,0.3620) | 0.5905 | 0.5701 | 0.4677 | 0.5278 | 0.5284 | 0.5628 | 0.6378 | 0.1491 | 0.0322 | 0.0151 | 0.0141 | 0.1517 |
| = (0.0841, 0.0888, 0.0899, 0.0903) | (0.0788) | (0.0787) | (0.0831) | (0.0868) | (0.0862) | (0.0852) | |||||||
| (50, 50) | = (0.1771, 0.2780, 0.4448, 0.3459) | 0.5641 | 0.5380 | 0.4435 | 0.5030 | 0.5038 | 0.5354 | 0.7324 | 0.1176 | 0.0165 | 0.0123 | 0.0113 | 0.1098 |
| = (0.0751, 0.0798, 0.0778, 0.0805) | (0.0683) | (0.0707) | (0.0753) | (0.0752) | (0.0756) | (0.0717) | |||||||
| (100, 100) | = (0.1464, 0.2526, 0.4270, 0.3230) | 0.5148 | 0.5012 | 0.4078 | 0.4770 | 0.4768 | 0.4984 | 0.6986 | 0.1268 | <0.01 | 0.013 | <0.01 | 0.1457 |
| = (0.0515, 0.0593, 0.0580, 0.0591) | (0.0546) | (0.0550) | (0.0542) | (0.0584) | (0.0585) | (0.0563) | |||||||
| (500, 500) | = (0.1063, 0.2178, 0.3980, 0.2923) | 0.4524 | 0.449 | 0.3586 | 0.4404 | 0.4402 | 0.4488 | 0.5629 | 0.1693 | <0.01 | 0.0234 | 0.0222 | 0.2221 |
| = (0.0262, 0.0282, 0.0278, 0.0278) | (0.0264) | (0.0265) | (0.0271) | (0.0269) | (0.0268) | (0.0265) | |||||||
| (10, 20) | = (0.3272, 0.5176, 0.6594, 0.5757) | 0.8558 | 0.8128 | 0.7198 | 0.7941 | 0.7847 | 0.809 | 0.5515 | 0.1334 | 0.0565 | 0.1059 | 0.0445 | 0.1081 |
| = (0.1436, 0.1440, 0.1291, 0.1388) | (0.0907) | (0.1001) | (0.1174) | (0.1256) | (0.1137) | (0.1056) | |||||||
| (30, 30) | = (0.2685, 0.4690, 0.6182, 0.5362) | 0.7751 | 0.7433 | 0.6514 | 0.7196 | 0.7175 | 0.7433 | 0.6647 | 0.1203 | 0.0238 | 0.0329 | 0.0271 | 0.1313 |
| = (0.1006, 0.1013, 0.0920, 0.0949) | (0.0742) | (0.0772) | (0.0892) | (0.0852) | (0.0841) | (0.082) | |||||||
| (50,30) | = (0.2629, 0.4602, 0.6113, 0.5246) | 0.7515 | 0.7343 | 0.6393 | 0.7057 | 0.7047 | 0.7291 | 0.643 | 0.1586 | 0.0228 | 0.0243 | 0.0204 | 0.1308 |
| = (0.0891, 0.0909, 0.0813, 0.0870) | (0.0681) | (0.0705) | (0.078) | (0.0779) | (0.0762) | (0.0733) | |||||||
| (50, 50) | = (0.2441, 0.4483, 0.5975, 0.5108) | 0.7307 | 0.7107 | 0.6204 | 0.6883 | 0.6870 | 0.7109 | 0.6652 | 0.1333 | 0.0168 | 0.0217 | 0.021 | 0.142 |
| = (0.0793, 0.0795, 0.0729, 0.0761) | (0.0609) | (0.0646) | (0.0702) | (0.0675) | (0.0673) | (0.0648) | |||||||
| (100, 100) | = (0.2160, 0.4258, 0.5829, 0.4909) | 0.6934 | 0.6818 | 0.5922 | 0.6642 | 0.6641 | 0.6814 | 0.655 | 0.1473 | <0.01 | 0.0229 | 0.0229 | 0.1485 |
| = (0.0537, 0.0578, 0.0529, 0.0567) | (0.0488) | (0.0488) | (0.0496) | (0.0525) | (0.0516) | (0.0492) | |||||||
| (500, 500) | = (0.1803, 0.3987, 0.5594, 0.4663) | 0.6453 | 0.643 | 0.5543 | 0.6379 | 0.6378 | 0.6436 | 0.4826 | 0.1741 | <0.01 | 0.0363 | 0.0354 | 0.2717 |
| = (0.0277, 0.0274, 0.0252, 0.0266) | (0.023) | (0.023) | (0.0244) | (0.0237) | (0.0238) | (0.0229) | |||||||
The results reported in Table 3 show that, in general, our proposed stepwise method dominates over the rest of the algorithms. The non-parametric kernel smoothing approach slightly outperforms Yin and Tian’s approach in terms of the average Youden index, and even for large sample sizes (), its mean Youden index is even slightly higher than that of our proposed stepwise method. This behaviour is accentuated in the scenarios of Table 4, where Yian and Tian’s stepwise approach performs significantly worse than the non-parametric kernel smoothing approach, and even their average values are lower than those achieved by logistic regression or the parametric approach under multivariate normality.



Table 3.
Normal distributions: Different means. Medium correlation ( = 0.5·I + 0.5·J).
Table 3.
Normal distributions: Different means. Medium correlation ( = 0.5·I + 0.5·J).
| Mean (SD) | Probability Greater than or Equal to Youden Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (, ) | Mean (SD) Variables | SLM | SWD | MM | LR | MVN | KS | SLM | SWD | MM | LR | MVN | KS |
| (10, 20) | = (0.2713, 0.3657, 0.5268, 0.428) | 0.7314 | 0.667 | 0.5534 | 0.6404 | 0.6432 | 0.674 | 0.4883 | 0.1566 | 0.0399 | 0.0496 | 0.0804 | 0.1851 |
| = (0.1353, 0.1477, 0.1423, 0.1427) | (0.1093) | (0.1181) | (0.1271) | (0.1387) | (0.1356) | (0.1306) | |||||||
| (30, 30) | = (0.2030, 0.3020, 0.4665, 0.3668) | 0.62 | 0.5647 | 0.4598 | 0.548 | 0.5433 | 0.5777 | 0.5478 | 0.1417 | 0.0118 | 0.0244 | 0.0572 | 0.2171 |
| = (0.0933, 0.1014, 0.0991, 0.1008) | (0.0847) | (0.0882) | (0.0945) | (0.0972) | (0.0952) | (0.0921) | |||||||
| (50, 30) | = (0.1931, 0.2928, 0.4581, 0.3632) | 0.5874 | 0.5568 | 0.4415 | 0.5288 | 0.5297 | 0.5631 | 0.4942 | 0.1885 | <0.01 | 0.0295 | 0.0282 | 0.2543 |
| = (0.0847, 0.0908, 0.0883, 0.0905) | (0.0769) | (0.0764) | (0.0811) | (0.0856) | (0.0842) | (0.0831) | |||||||
| (50, 50) | = (0.1753, 0.2761, 0.4472, 0.3495) | 0.5637 | 0.5274 | 0.4187 | 0.5096 | 0.5094 | 0.5401 | 0.5076 | 0.1588 | <0.01 | 0.0247 | 0.0502 | 0.2528 |
| = (0.0742, 0.0798, 0.0787, 0.0791) | (0.0677) | (0.0717) | (0.0738) | (0.0755) | (0.0746) | (0.0738) | |||||||
| (100, 100) | = (0.1449, 0.2487, 0.4250, 0.3236) | 0.5114 | 0.4907 | 0.3806 | 0.4766 | 0.4766 | 0.5005 | 0.4238 | 0.3977 | <0.01 | 0.0152 | <0.01 | 0.1548 |
| = (0.0520, 0.0578, 0.0591, 0.0595) | (0.0539) | (0.0551) | (0.056) | (0.0583) | (0.0584) | (0.0566) | |||||||
| (500, 500) | = (0.1063, 0.2187, 0.3994, 0.2921) | 0.4511 | 0.443 | 0.3325 | 0.4429 | 0.4429 | 0.4516 | 0.3103 | 0.3948 | <0.01 | 0.0237 | 0.0204 | 0.2508 |
| = (0.0261, 0.0280, 0.0264, 0.0279) | (0.0256) | (0.0276) | (0.0272) | (0.0265) | (0.0265) | (0.0256) | |||||||
| (10, 20) | = (0.3339, 0.5172, 0.6658, 0.5790) | 0.844 | 0.7906 | 0.6879 | 0.7838 | 0.7736 | 0.7996 | 0.4078 | 0.1614 | 0.0258 | 0.1348 | 0.0884 | 0.1817 |
| = (0.1406, 0.1442, 0.1287, 0.1370) | (0.0934) | (0.1050) | (0.1184) | (0.1288) | (0.1167) | (0.1107) | |||||||
| (30, 30) | = (0.2685, 0.4669, 0.6160, 0.5254) | 0.7609 | 0.7139 | 0.6157 | 0.7084 | 0.7007 | 0.7294 | 0.5169 | 0.1461 | 0.0115 | 0.0512 | 0.0628 | 0.2116 |
| = (0.0998, 0.1025, 0.0945, 0.0954) | (0.0766) | (0.0801) | (0.0906) | (0.0876) | (0.087) | (0.0804) | |||||||
| (50, 30) | = (0.2580, 0.4621, 0.6105, 0.5264) | 0.7348 | 0.7101 | 0.6034 | 0.6945 | 0.6929 | 0.7177 | 0.4785 | 0.1823 | <0.01 | 0.0643 | 0.0438 | 0.2257 |
| = (0.0887, 0.0908, 0.0807, 0.0862) | (0.0686) | (0.0707) | (0.0782) | (0.0773) | (0.0743) | (0.0721) | |||||||
| (50, 50) | = (0.2428, 0.4477, 0.5994, 0.5124) | 0.7162 | 0.6874 | 0.5831 | 0.6778 | 0.6762 | 0.7013 | 0.4817 | 0.1485 | <0.01 | 0.0496 | 0.0575 | 0.2574 |
| = (0.0782, 0.0810, 0.0723, 0.0769) | (0.0620) | (0.0649) | (0.0715) | (0.0697) | (0.0665) | (0.0639) | |||||||
| (100, 100) | = (0.2146, 0.4235, 0.5816, 0.4916) | 0.6755 | 0.6572 | 0.5535 | 0.6519 | 0.6513 | 0.6684 | 0.5904 | 0.083 | <0.01 | 0.04 | 0.0382 | 0.2475 |
| = (0.0554, 0.0572, 0.0550, 0.0580) | (0.0480) | (0.0493) | (0.0524) | (0.0510) | (0.0509) | (0.0494) | |||||||
| (500, 500) | = (0.1808, 0.3990, 0.5606, 0.4663) | 0.6286 | 0.6239 | 0.5165 | 0.6258 | 0.6255 | 0.6317 | 0.379 | 0.1055 | <0.01 | 0.0561 | 0.0563 | 0.403 |
| = (0.0270, 0.0277, 0.0244, 0.0260) | (0.0236) | (0.0242) | (0.0251) | (0.0232) | (0.0232) | (0.023) | |||||||

Table 4.
Normal distributions: Different means. High correlation ( = 0.3·I + 0.7·J).
Table 4.
Normal distributions: Different means. High correlation ( = 0.3·I + 0.7·J).
| Mean (SD) | Probability Greater than or Equal to Youden Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (, ) | Mean (SD) Variables | SLM | SWD | MM | LR | MVN | KS | SLM | SWD | MM | LR | MVN | KS |
| (10, 20) | = (0.2708, 0.3672, 0.5202, 0.4299) | 0.754 | 0.6634 | 0.5546 | 0.6702 | 0.6704 | 0.6962 | 0.5549 | 0.1035 | 0.0211 | 0.0879 | 0.0684 | 0.1642 |
| = (0.1361, 0.1398, 0.1435, 0.1447) | (0.1036) | (0.119) | (0.1268) | (0.1418) | (0.1383) | (0.1317) | |||||||
| (30, 30) | = (0.2005, 0.3040, 0.4663, 0.3703) | 0.6514 | 0.5668 | 0.4559 | 0.5844 | 0.5834 | 0.6166 | 0.5812 | 0.0826 | 0.0116 | 0.0521 | 0.0397 | 0.2329 |
| = (0.0936, 0.1025, 0.1045, 0.1038) | (0.0817) | (0.0937) | (0.0946) | (0.0981) | (0.0972) | (0.0940) | |||||||
| (50, 30) | = (0.1951, 0.2932, 0.4625, 0.3591) | 0.6175 | 0.5628 | 0.4401 | 0.5689 | 0.5690 | 0.6000 | 0.5288 | 0.1146 | <0.01 | 0.0414 | 0.0324 | 0.2768 |
| = (0.0815, 0.0877, 0.0893, 0.0914) | (0.0779) | (0.0834) | (0.0817) | (0.0882) | (0.0874) | (0.0859) | |||||||
| (50, 50) | = (0.1781, 0.2779, 0.4479, 0.3450) | 0.5983 | 0.5325 | 0.4166 | 0.5527 | 0.5521 | 0.5805 | 0.5430 | 0.0799 | <0.01 | 0.0454 | 0.0431 | 0.2858 |
| = (0.0735, 0.0787, 0.0800, 0.0806) | (0.0671) | (0.0754) | (0.0747) | (0.0782) | (0.0774) | (0.0741) | |||||||
| (100, 100) | = (0.1461, 0.2526, 0.4243, 0.3207) | 0.5472 | 0.4969 | 0.3773 | 0.5203 | 0.5202 | 0.5413 | 0.4680 | 0.2348 | <0.01 | 0.0173 | 0.0222 | 0.2577 |
| = (0.0534, 0.0597, 0.0566, 0.0606) | (0.0515) | (0.0567) | (0.0548) | (0.0547) | (0.0547) | (0.0530) | |||||||
| (500, 500) | = (0.1057, 0.2177, 0.3992, 0.2928) | 0.4949 | 0.4587 | 0.3313 | 0.4893 | 0.4892 | 0.4972 | 0.3588 | 0.1517 | <0.01 | 0.0418 | 0.0358 | 0.4118 |
| = (0.0267, 0.0281, 0.0276, 0.0278) | (0.0257) | (0.0308) | (0.0274) | (0.0260) | (0.0259) | (0.0255) | |||||||
| (10, 20) | = (0.3322, 0.5204, 0.6594, 0.5826) | 0.8612 | 0.7759 | 0.6874 | 0.8091 | 0.7979 | 0.8204 | 0.5229 | 0.0699 | 0.0183 | 0.1656 | 0.0730 | 0.1503 |
| = (0.1426, 0.1414, 0.1301, 0.1402) | (0.0882) | (0.1107) | (0.1232) | (0.1266) | (0.1156) | (0.1099) | |||||||
| (30, 30) | = (0.2669, 0.4678, 0.6169, 0.5312) | 0.7842 | 0.7095 | 0.6146 | 0.7393 | 0.7369 | 0.7607 | 0.5373 | 0.0759 | <0.01 | 0.0856 | 0.0629 | 0.2325 |
| = (0.0982, 0.0999, 0.0961, 0.1011) | (0.0702) | (0.0854) | (0.0884) | (0.0835) | (0.0821) | (0.0782) | |||||||
| (50,30) | = (0.2620, 0.4584, 0.6136, 0.5234) | 0.7596 | 0.7128 | 0.6007 | 0.7304 | 0.7283 | 0.7514 | 0.4932 | 0.0898 | <0.01 | 0.0842 | 0.0564 | 0.2714 |
| = (0.0865, 0.0865, 0.0817, 0.0866) | (0.0682) | (0.0722) | (0.078) | (0.0760) | (0.0735) | (0.0696) | |||||||
| (50, 50) | = (0.2458, 0.4465, 0.6006, 0.5098) | 0.7394 | 0.6899 | 0.5806 | 0.7165 | 0.7149 | 0.7361 | 0.4764 | 0.0643 | <0.01 | 0.0650 | 0.0637 | 0.3282 |
| = (0.0776, 0.0776, 0.0756, 0.0769) | (0.0612) | (0.0717) | (0.0729) | (0.0676) | (0.0663) | (0.0638) | |||||||
| (100, 100) | = (0.2155, 0.4256, 0.5809, 0.4890) | 0.7018 | 0.6658 | 0.5523 | 0.6898 | 0.6886 | 0.7036 | 0.4592 | 0.0528 | <0.01 | 0.0712 | 0.0544 | 0.3625 |
| = (0.0562, 0.0606, 0.0520, 0.0570) | (0.042) | (0.0525) | (0.0502) | (0.0469) | (0.047) | (0.0458) | |||||||
| (500, 500) | = (0.1802, 0.3992, 0.5603, 0.4668) | 0.6588 | 0.6451 | 0.5148 | 0.6643 | 0.6643 | 0.6701 | 0.1175 | 0.2240 | <0.01 | 0.0793 | 0.0653 | 0.5138 |
| = (0.0280, 0.0267, 0.0250, 0.0256) | (0.0226) | (0.0270) | (0.0253) | (0.0222) | (0.0222) | (0.0220) | |||||||
Given the reported results of these simulations, it could be concluded that, in scenarios of multivariate normal distributions with different means and equal positive correlations, our proposed stepwise method dominates generally over the rest of the algorithms, followed by the non-parametric kernel smoothing approach and Yin and Tian’s stepwise approach, with the former being better in scenarios of higher correlations.
3.1.2. Normal Distributions. Different Means and Unequal Positive Correlations for Diseased and Non-Diseased Population
Table 5 shows the results obtained in the scenarios under multivariate normal distribution with mean vectors and and different correlations for the diseased and non-diseased populations (··J, ··J). The results indicate that our proposed stepwise approach outperforms the other algorithms in most scenarios. It is followed by the non-parametric kernel smoothing approach and Yin and Tian’s stepwise approach. The min-max approach is the worst performer. Logistic regression and the parametric approach under multivariate normality performed comparably in general.


Table 5.
Normal distributions: Different means. Different correlation ( = 0.3·I + 0.7·J, = 0.7·I + 0.3·J).
Table 5.
Normal distributions: Different means. Different correlation ( = 0.3·I + 0.7·J, = 0.7·I + 0.3·J).
| Mean (SD) | Probability Greater than or Equal to Youden Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (, ) | Mean (SD) Variables | SLM | SWD | MM | LR | MVN | KS | SLM | SWD | MM | LR | MVN | KS |
| (10, 20) | = (0.2706, 0.3608, 0.5172, 0.4272) | 0.736 | 0.6644 | 0.5952 | 0.637 | 0.6408 | 0.669 | 0.4899 | 0.1413 | 0.0987 | 0.0536 | 0.0679 | 0.1486 |
| = (0.1367, 0.1405, 0.1453, 0.1456) | (0.0998) | (0.116) | (0.1258) | (0.1328) | (0.1338) | (0.1292) | |||||||
| (30, 30) | = (0.2023, 0.3027, 0.4703, 0.3748) | 0.6268 | 0.5745 | 0.5086 | 0.5512 | 0.5527 | 0.5871 | 0.5236 | 0.1399 | 0.0877 | 0.0244 | 0.038 | 0.1864 |
| = (0.0948, 0.1002, 0.0979, 0.1003) | (0.0825) | (0.0869) | (0.0905) | (0.0973) | (0.0928) | (0.0896) | |||||||
| (50, 30) | = (0.1957, 0.2895, 0.4586, 0.3606) | 0.5986 | 0.567 | 0.4958 | 0.5373 | 0.5383 | 0.5717 | 0.4958 | 0.1717 | 0.0993 | 0.0327 | 0.0282 | 0.1723 |
| = (0.0832, 0.0925, 0.0862, 0.0918) | (0.0794) | (0.0775) | (0.0827) | (0.0907) | (0.0868) | (0.0856) | |||||||
| (50, 50) | = (0.1785, 0.2736, 0.4439, 0.3447) | 0.5727 | 0.5297 | 0.4708 | 0.5096 | 0.5129 | 0.5426 | 0.5447 | 0.1275 | 0.0869 | 0.0149 | 0.0376 | 0.1883 |
| = (0.0735, 0.0793, 0.077, 0.0831) | (0.0669) | (0.0719) | (0.0745) | (0.0772) | (0.0763) | (0.0741) | |||||||
| (100, 100) | = (0.1465, 0.2526, 0.4273, 0.3225) | 0.5198 | 0.4946 | 0.4378 | 0.482 | 0.4835 | 0.508 | 0.4783 | 0.3068 | 0.0648 | 0.0128 | 0.0113 | 0.1258 |
| = (0.052, 0.0572, 0.0576, 0.0598) | (0.052) | (0.0539) | (0.0557) | (0.0557) | (0.0556) | (0.0529) | |||||||
| (500, 500) | = (0.1063, 0.2181, 0.3994, 0.2929) | 0.4576 | 0.4482 | 0.3916 | 0.4446 | 0.4464 | 0.4565 | 0.3803 | 0.3227 | <0.01 | 0.0122 | 0.0187 | 0.2593 |
| = (0.0264, 0.0271, 0.0272, 0.0276) | (0.0256) | (0.0264) | (0.0271) | (0.0271) | (0.0268) | (0.026) | |||||||
| (10, 20) | = (0.3328, 0.5141, 0.6583, 0.5798) | 0.8422 | 0.7851 | 0.6824 | 0.7763 | 0.7697 | 0.7934 | 0.4419 | 0.1638 | 0.0412 | 0.1108 | 0.0785 | 0.1637 |
| = (0.1429, 0.1394, 0.1338, 0.1404) | (0.091) | (0.1103) | (0.1244) | (0.1259) | (0.1146) | (0.1113) | |||||||
| (30, 30) | = (0.2664, 0.4658, 0.6184, 0.5334) | 0.7628 | 0.7199 | 0.6068 | 0.7102 | 0.7055 | 0.7333 | 0.5186 | 0.1604 | 0.013 | 0.0512 | 0.056 | 0.2007 |
| = (0.1005, 0.0991, 0.0921, 0.0971) | (0.0752) | (0.0803) | (0.089) | (0.0869) | (0.0846) | (0.0802) | |||||||
| (50, 30) | = (0.2627, 0.4576, 0.6125, 0.5232) | 0.7403 | 0.7154 | 0.5945 | 0.6961 | 0.6947 | 0.7219 | 0.5055 | 0.2028 | 0.0115 | 0.0428 | 0.0379 | 0.1996 |
| = (0.0894, 0.0924, 0.0783, 0.088) | (0.0714) | (0.0713) | (0.0773) | (0.0827) | (0.0767) | (0.0722) | |||||||
| (50, 50) | = (0.2455, 0.4442, 0.5970, 0.5088) | 0.7176 | 0.687 | 0.5735 | 0.6765 | 0.6759 | 0.6998 | 0.5134 | 0.1669 | <0.01 | 0.048 | 0.045 | 0.2182 |
| = (0.0782, 0.0794, 0.0700, 0.0784) | (0.0617) | (0.0668) | (0.0713) | (0.0706) | (0.0676) | (0.0649) | |||||||
| (100, 100) | = (0.2150, 0.4275, 0.5840, 0.4909) | 0.6804 | 0.661 | 0.5473 | 0.6543 | 0.6545 | 0.6724 | 0.4505 | 0.3459 | <0.01 | 0.0262 | 0.021 | 0.1555 |
| = (0.0546, 0.0565, 0.0523, 0.0558) | (0.0477) | (0.0486) | (0.0537) | (0.0512) | (0.0509) | (0.0488) | |||||||
| (500, 500) | = (0.1807, 0.3992, 0.5600, 0.4667) | 0.6309 | 0.6258 | 0.5091 | 0.6255 | 0.6258 | 0.6326 | 0.2942 | 0.3528 | <0.01 | 0.0317 | 0.0346 | 0.2868 |
| = (0.0278, 0.0270, 0.0251, 0.0258) | (0.0233) | (0.0237) | (0.0256) | (0.024) | (0.0239) | (0.0235) | |||||||
3.1.3. Normal Distributions. Different Means and Equal Negative Correlations for Diseased and Non-Diseased Population
Table 6 and Table 7 show the results obtained in the scenarios under multivariate normal distribution with mean vectors and and equal negative correlations (, respectively).



Table 6.
Normal distributions: Different means. Negative correlation (−0.1).
Table 6.
Normal distributions: Different means. Negative correlation (−0.1).
| Mean (SD) | Probability Greater than or Equal to Youden Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (, ) | Mean (SD) Variables | SLM | SWD | MM | LR | MVN | KS | SLM | SWD | MM | LR | MVN | KS |
| (10, 20) | = (0.2651, 0.3652, 0.5164, 0.4329) | 0.8127 | 0.7625 | 0.678 | 0.7395 | 0.7356 | 0.7664 | 0.4308 | 0.1033 | 0.0474 | 0.1301 | 0.08 | 0.2084 |
| = (0.1298, 0.1462, 0.1450,0.1438) | (0.0967) | (0.105) | (0.1216) | (0.1334) | (0.1259) | (0.1163) | |||||||
| (30, 30) | = (0.2064, 0.3013, 0.4704, 0.3718) | 0.7108 | 0.6747 | 0.5997 | 0.6603 | 0.6599 | 0.6905 | 0.4499 | 0.0831 | 0.0309 | 0.0744 | 0.0694 | 0.2924 |
| = (0.0949, 0.0980, 0.1005, 0.1040) | (0.0799) | (0.0823) | (0.0893) | (0.092) | (0.0904) | (0.0847) | |||||||
| (50, 30) | = (0.1947, 0.2934, 0.4588, 0.3593) | 0.6862 | 0.6681 | 0.5863 | 0.6422 | 0.6413 | 0.6692 | 0.4088 | 0.132 | 0.0245 | 0.058 | 0.0495 | 0.3272 |
| = (0.0836, 0.0880, 0.0879, 0.0926) | (0.072) | (0.0742) | (0.0799) | (0.0829) | (0.0801) | (0.0788) | |||||||
| (50, 50) | = (0.1755, 0.2784, 0.4466, 0.3465) | 0.6667 | 0.6419 | 0.568 | 0.6297 | 0.6288 | 0.654 | 0.4187 | 0.1011 | 0.0219 | 0.065 | 0.0756 | 0.3177 |
| = (0.0717, 0.0792, 0.0787, 0.0800) | (0.0622) | (0.0672) | (0.0721) | (0.0716) | (0.0704) | (0.0676) | |||||||
| (100, 100) | = (0.1445, 0.2522, 0.4264, 0.3212) | 0.6252 | 0.6135 | 0.5321 | 0.6054 | 0.6053 | 0.6229 | 0.3913 | 0.1198 | <0.01 | 0.05 | 0.0572 | 0.3759 |
| = (0.0531, 0.0578, 0.0579, 0.0585) | (0.0502) | (0.0507) | (0.0534) | (0.0515) | (0.0516) | (0.05) | |||||||
| (500, 500) | = (0.1068, 0.2180, 0.3989, 0.2923) | 0.5784 | 0.5761 | 0.4947 | 0.5734 | 0.5735 | 0.5804 | 0.3137 | 0.1578 | <0.01 | 0.0484 | 0.0567 | 0.4234 |
| = (0.0263, 0.0277, 0.0275, 0.0273) | (0.0237) | (0.0239) | (0.0251) | (0.0243) | (0.0244) | (0.0238) | |||||||
| (10, 20) | = (0.3266, 0.5185, 0.6594, 0.5868) | 0.9466 | 0.9098 | 0.8538 | 0.9296 | 0.9078 | 0.922 | 0.3156 | 0.1426 | 0.056 | 0.267 | 0.0912 | 0.1276 |
| = (0.1344, 0.1434, 0.1322, 0.1347) | (0.0619) | (0.0752) | (0.0916) | (0.0898) | (0.0825) | (0.0757) | |||||||
| (30, 30) | = (0.2701, 0.4666, 0.6203, 0.5327) | 0.8952 | 0.8625 | 0.8046 | 0.8737 | 0.8652 | 0.8835 | 0.3993 | 0.1047 | 0.026 | 0.168 | 0.0824 | 0.2195 |
| = (0.0986, 0.0999, 0.0926, 0.1011) | (0.056) | (0.0622) | (0.0697) | (0.0655) | (0.0625) | (0.0581) | |||||||
| (50, 30) | = (0.2602, 0.4611, 0.6101, 0.5226) | 0.8806 | 0.8672 | 0.7964 | 0.8604 | 0.8545 | 0.8714 | 0.3853 | 0.1296 | 0.0278 | 0.1445 | 0.0751 | 0.2376 |
| = (0.0888, 0.0855, 0.0793, 0.0905) | (0.0516) | (0.0533) | (0.0644) | (0.0609) | (0.0578) | (0.055 | |||||||
| (50, 50) | = (0.2427, 0.4476, 0.6006, 0.5110) | 0.8677 | 0.8508 | 0.7835 | 0.8503 | 0.8454 | 0.8616 | 0.381 | 0.1215 | 0.0217 | 0.1144 | 0.0651 | 0.2963 |
| = (0.0757, 0.0791, 0.0731, 0.0765) | (0.0448) | (0.0477) | (0.0574) | (0.0506) | (0.0485) | (0.0476) | |||||||
| (100, 100) | = (0.2138, 0.4268, 0.5832, 0.4905) | 0.8442 | 0.8342 | 0.757 | 0.8329 | 0.831 | 0.8427 | 0.3815 | 0.1121 | <0.01 | 0.0856 | 0.0672 | 0.351 |
| = (0.0573, 0.0578, 0.0533, 0.0558) | (0.0367) | (0.0379) | (0.0422) | (0.037) | (0.0367) | (0.0356) | |||||||
| (500, 500) | = (0.1813, 0.3989, 0.5598, 0.4665) | 0.8152 | 0.8127 | 0.7294 | 0.8108 | 0.8105 | 0.8145 | 0.3765 | 0.1367 | <0.01 | 0.0724 | 0.0619 | 0.3525 |
| = (0.0273, 0.0270, 0.0255, 0.0255) | (0.0180) | (0.0182) | (0.0208) | (0.0176) | (0.0175) | (0.0173) | |||||||

Table 7.
Normal distributions: Different means. Negative correlation (−0.3).
Table 7.
Normal distributions: Different means. Negative correlation (−0.3).
| Mean (SD) | Probability Greater than or Equal to Youden Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (, ) | Mean (SD) Variables | SLM | SWD | MM | LR | MVN | KS | SLM | SWD | MM | LR | MVN | KS |
| (10, 20) | = (0.2624, 0.3591, 0.5238, 0.4281) | 0.976 | 0.8938 | 0.845 | 0.9963 | 0.9874 | 0.9902 | 0.2058 | 0.0617 | 0.0166 | 0.2782 | 0.2115 | 0.2261 |
| = (0.1354, 0.1447, 0.1413, 0.1425) | (0.0468) | (0.0964) | (0.0935) | (0.0189) | (0.0289) | (0.0258) | |||||||
| (30, 30) | = (0.2057, 0.3046, 0.4707, 0.3672) | 0.9589 | 0.8946 | 0.7906 | 0.9875 | 0.9746 | 0.9821 | 0.1978 | 0.0499 | <0.01 | 0.3625 | 0.15661 | 0.2331 |
| = (0.0942, 0.1007, 0.1004, 0.1008) | (0.0472) | (0.0852) | (0.0717) | (0.0254) | (0.027) | (0.0243) | |||||||
| (50, 30) | = (0.1967, 0.2948, 0.4565, 0.3621) | 0.9405 | 0.9125 | 0.7819 | 0.9835 | 0.9725 | 0.9802 | 0.1498 | 0.0712 | <0.01 | 0.3874 | 0.1407 | 0.2504 |
| = (0.0868, 0.0899, 0.0933, 0.0903) | (0.0577) | (0.0726) | (0.0674) | (0.0267) | (0.0269) | (0.0243) | |||||||
| (50, 50) | = (0.1769, 0.2795, 0.4447, 0.3482) | 0.9471 | 0.9052 | 0.7678 | 0.9775 | 0.9668 | 0.975 | 0.192 | 0.0609 | <0.01 | 0.3861 | 0.1163 | 0.2447 |
| = (0.0754, 0.0805, 0.0780, 0.0789) | (0.0447) | (0.0718) | (0.0583) | (0.0255) | (0.0243) | (0.0218) | |||||||
| (100, 100) | = (0.1435, 0.2540, 0.4258, 0.3240) | 0.9421 | 0.9178 | 0.7469 | 0.9652 | 0.9606 | 0.9674 | 0.1053 | 0.1346 | <0.01 | 0.2778 | 0.1168 | 0.3655 |
| = (0.0543, 0.0544, 0.0591, 0.0595) | (0.0345) | (0.0503) | (0.0431) | (0.0202) | (0.019) | (0.0177) | |||||||
| (500, 500) | = (0.1067, 0.2173, 0.3981, 0.2919) | 0.9365 | 0.9309 | 0.7161 | 0.9509 | 0.9502 | 0.9531 | 0.1671 | 0.0586 | <0.01 | 0.1500 | 0.1057 | 0.5185 |
| = (0.0270, 0.0284, 0.0280, 0.0276) | (0.0195) | (0.0217) | (0.0215) | (0.0096) | (0.0097) | (0.0093) | |||||||
| (10, 20) | = (0.3223, 0.5169, 0.6668, 0.5786) | 0.9998 | 0.9876 | 0.9734 | 1.0000 | 1.0000 | 1.0000 | 0.1838 | 0.1479 | 0.1131 | 0.1851 | 0.1851 | 0.1851 |
| = (0.1401, 0.1425, 0.1279, 0.1364) | (0.0034) | (0.0311) | (0.0413) | (0.00000) | (0.0000) | (0.0000) | |||||||
| (30, 30) | = (0.2701, 0.4693, 0.6214, 0.5251) | 0.9997 | 0.9891 | 0.9519 | 1.0000 | 1.0000 | 0.9999 | 0.201 | 0.1504 | 0.0378 | 0.2037 | 0.2037 | 0.2032 |
| = (0.0990, 0.1018, 0.0922, 0.0968) | (0.0031) | (0.0249) | (0.0384) | (0.0000) | (0.0000) | (0.0015) | |||||||
| (50, 30) | = (0.2631, 0.4635, 0.6084, 0.5255 | 0.999 | 0.9958 | 0.9503 | 1.0000 | 1.0000 | 1.0000 | 0.1952 | 0.1699 | 0.0217 | 0.2046 | 0.2043 | 0.2043 |
| = (0.0933, 0.0889, 0.0858, 0.0867) | (0.0064) | (0.0132) | (0.0355) | (0.0000) | (0.0006) | (0.0006) | |||||||
| (50, 50) | = (0.2436, 0.4498, 0.5975, 0.5118) | 0.9995 | 0.9953 | 0.9431 | 1.0000 | 0.9999 | 1.0000 | 0.2018 | 0.1672 | <0.01 | 0.2082 | 0.2066 | 0.2082 |
| = (0.0795, 0.0802, 0.0713, 0.0768) | (0.0033) | (0.013) | (0.0322) | (0.0000) | (0.0015) | (0.0000) | |||||||
| (100, 100) | = (0.2131, 0.4277, 0.5819, 0.4917) | 0.9996 | 0.9981 | 0.933 | 1.0000 | 0.9999 | 1.0000 | 0.1985 | 0.1723 | <0.01 | 0.2107 | 0.2077 | 0.2107 |
| = (0.0578, 0.0541, 0.0543, 0.0577) | (0.0022) | (0.0057) | (0.0243) | (0.0000) | (0.001) | (0.0000) | |||||||
| (500, 500) | = (0.1812, 0.3992, 0.5598, 0.4662) | 0.9995 | 0.9992 | 0.916 | 0.9999 | 0.9996 | 0.9998 | 0.1821 | 0.1581 | <0.01 | 0.247 | 0.1911 | 0.2217 |
| = (0.0278, 0.0277, 0.0255, 0.0262) | (0.0011) | (0.0016) | (0.0121) | (0.0005) | (0.0009) | (0.0006) | |||||||
The same conclusions as in the previous tables can be deduced from Table 6 for the mean vector scenario , globally. The results show that our proposed stepwise approach, in general, outperforms over the other algorithms. After it, the non-parametric kernel smoothing approach and Yin and Tian’s stepwise approach are the best performers, the results of the former being slightly better than those of the latter. Logistic regression and the parametric approach under multivariate normality conditions obtain similar results. The min-max approach is the worst performer.
However, the results provided by the simulated data with mean vector (Table 6) show that Yin and Tian’s stepwise approach and logistic regression perform comparably. In these scenarios, the algorithms achieve a superior performance than when considering simulated data with mean vector , as is the case in all tables. Moreover, in this scenario (; Table 6), the algorithms discriminate successfully, with the average Youden index achieved by all algorithms being higher than 0.8, with the exception of min-max, which ranges between 0.72 and 0.85. Table 7 shows that these are also scenarios where the combination of biomarkers discriminates satisfactorily. This result could be in line with the literature, where Pinsky and Zhu [42] already unveiled a remarkable increase in performance when considering the combination of highly negatively correlated variables. The results in Table 7 show that the stepwise approaches are worse than the other algorithms, although all of them achieve a perfect or near-perfect performance in some scenarios, with the exception of the min-max approach.
3.1.4. Normal Distributions. Same Means for Diseased and Non-Diseased Population
Table 8 shows the results obtained from the multivariate normal distribution simulations with mean vector under the low correlation (··J) and different correlation (··J, ··J) scenarios.


Table 8.
Normal distributions: Same means: .
Table 8.
Normal distributions: Same means: .
| Mean (SD) | Probability Greater than or Equal to Youden Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (, ) | Mean (SD) Variables | SLM | SWD | MM | LR | MVN | KS | SLM | SWD | MM | LR | MVN | KS |
| Same Correlation. Low Correlation ( = 0.7·I + 0.3·J) | |||||||||||||
| (10, 20) | = (0.5178, 0.5176, 0.5180, 0.5150) | 0.8023 | 0.7592 | 0.704 | 0.7158 | 0.7128 | 0.7505 | 0.5881 | 0.1306 | 0.0969 | 0.0468 | 0.0263 | 0.1113 |
| = (0.1439, 0.1440, 0.1377, 0.1427) | (0.0993) | (0.1061) | (0.1177) | (0.1335) | (0.1256) | (0.1165) | |||||||
| (30, 30) | = (0.4661, 0.469, 0.4700, 0.4741) | 0.7069 | 0.6756 | 0.6379 | 0.6384 | 0.6377 | 0.6682 | 0.6635 | 0.1258 | 0.0902 | 0.0201 | 0.0167 | 0.0836 |
| = (0.1023, 0.1013, 0.1002, 0.0993) | (0.0822) | (0.0843) | (0.0891) | (0.0965) | (0.0947) | (0.0895) | |||||||
| (50, 30) | = (0.4642, 0.4602, 0.4606, 0.4605) | 0.6793 | 0.6629 | 0.6267 | 0.6224 | 0.6218 | 0.6523 | 0.6006 | 0.1586 | 0.1148 | 0.0118 | 0.0169 | 0.0972 |
| = (0.0882, 0.0909, 0.0899, 0.0881) | (0.0729) | (0.0742) | (0.0775) | (0.0822) | (0.0827) | (0.078) | |||||||
| (50, 50) | = (0.4491, 0.4483, 0.4448, 0.4479) | 0.6564 | 0.634 | 0.606 | 0.6039 | 0.6044 | 0.6307 | 0.6627 | 0.1242 | 0.1036 | <0.01 | 0.0138 | 0.0867 |
| = (0.0787, 0.0795, 0.0778, 0.0782) | (0.0644) | (0.0674) | (0.0719) | (0.0724) | (0.072) | (0.0689) | |||||||
| (100, 100) | = (0.4266, 0.4258, 0.4270, 0.4252) | 0.6102 | 0.5989 | 0.5779 | 0.5793 | 0.5788 | 0.5979 | 0.5803 | 0.1536 | 0.1003 | 0.014 | 0.0129 | 0.1389 |
| = (0.0536, 0.0578, 0.0580, 0.0581) | (0.0484) | (0.0499) | (0.0499) | (0.0518) | (0.0515) | (0.0503) | |||||||
| (500, 500) | = (0.3998, 0.3987, 0.3980, 0.3989) | 0.5556 | 0.5536 | 0.5387 | 0.5479 | 0.5478 | 0.555 | 0.3932 | 0.2252 | 0.0557 | 0.0337 | 0.0241 | 0.2681 |
| = (0.0264, 0.0274, 0.0278, 0.0272) | (0.0247) | (0.0251) | (0.025) | (0.0253) | (0.0255) | (0.0247) | |||||||
| Different Correlation ( = 0.3·I + 0.7·J, = 0.7·I + 0.3·J) | |||||||||||||
| (10, 20) | = (0.5149, 0.5141, 0.5172, 0.5203) | 0.7563 | 0.7156 | 0.7406 | 0.6664 | 0.6654 | 0.7022 | 0.3382 | 0.2086 | 0.2474 | 0.0590 | 0.0363 | 0.1104 |
| = (0.1438, 0.1394, 0.1453, 0.1453) | (0.1051) | (0.1141) | (0.1139) | (0.1372) | (0.1345) | (0.1261) | |||||||
| (30, 30) | = (0.4640, 0.4658, 0.4703, 0.4718) | 0.6641 | 0.6353 | 0.6782 | 0.5896 | 0.5905 | 0.6224 | 0.3442 | 0.0746 | 0.4400 | 0.0210 | 0.0160 | 0.1041 |
| = (0.1016, 0.0991, 0.0979, 0.0981) | (0.0853) | (0.0877) | (0.0846) | (0.0964) | (0.0959) | (0.0912) | |||||||
| (50, 30) | = (0.4625, 0.4576, 0.4586, 0.4598) | 0.6424 | 0.6256 | 0.6669 | 0.5791 | 0.5813 | 0.6119 | 0.2979 | 0.0744 | 0.4954 | 0.0119 | 0.0142 | 0.1062 |
| = (0.0902, 0.0924, 0.0862, 0.0906) | (0.0735) | (0.0752) | (0.0762) | (0.0839) | (0.0818) | (0.0785) | |||||||
| (50, 50) | = (0.4481, 0.4442, 0.4439, 0.4457) | 0.6145 | 0.5936 | 0.6465 | 0.5552 | 0.5562 | 0.5826 | 0.3163 | 0.0587 | 0.5325 | <0.01 | <0.01 | 0.0800 |
| = (0.0805, 0.0794, 0.0770, 0.0822) | (0.0653) | (0.0686) | (0.0696) | (0.0745) | (0.075) | (0.0728) | |||||||
| (100, 100) | = (0.4253, 0.4275, 0.4273, 0.4254) | 0.5658 | 0.5551 | 0.6220 | 0.5297 | 0.53 | 0.5491 | 0.1722 | 0.0516 | 0.7520 | <0.01 | <0.01 | 0.0187 |
| = (0.0564, 0.0565, 0.0576, 0.0578) | (0.05) | (0.0513) | (0.0504) | (0.0538) | (0.0534) | (0.0527) | |||||||
| (500, 500) | = (0.3994, 0.3992, 0.3994, 0.3993) | 0.5085 | 0.5058 | 0.5870 | 0.5004 | 0.5005 | 0.5069 | <0.01 | <0.01 | 0.9930 | <0.01 | <0.01 | <0.01 |
| = (0.0275, 0.0270, 0.2720, 0.0267) | (0.025) | (0.0253) | (0.0240) | (0.026) | (0.0262) | (0.0256) | |||||||
In contrast to the results in Table 2 (different means and low correlation), the results in Table 8 show that the min-max approach performs better in scenarios with biomarkers with the same means. This means that these are scenarios in which the biomarkers have a similar discriminatory capacity, as can be seen in the second column of the table, where the empirical estimates of the Youden index for each biomarker are presented. The table shows that, for scenarios with a low correlation, the min-max algorithm performs similar to the logistic regression and parametric approach under multivariate normality. In this scenario, our proposed stepwise approach dominates the other algorithms. However, this is not the case in the scenario of different covariance matrices (··J, ··J), where the min-max approach is the best performer, becoming more and more prominent as the sample size increases. Specifically, in almost 100% of the 1000 simulations of sample size , the min-max approach performs best.
3.1.5. Non-Normal Distributions. Different Marginal Distributions
Table 9 shows the results obtained from simulations of multivariate chi-square, normal, gamma and exponential distributions via normal copula with a dependence/correlation parameter between biomarkers of 0.7 and 0.3 for the diseased and non-diseased population, respectively. Biomarkers for the non-diseased population were considered to be marginally distributed as , , and , where the considered probability density function for the gamma distribution , using the shape-rate parametrization, is
and, for the exponential distribution , denoting the rate parameter, the following:
In the case of the diseased population, two scenarios were considered: , , , and , , , . Since the range of values for each of the four biomarkers was markedly different, it was necessary to normalize the values for each biomarker.


Table 9.
Non-normal distributions: Different marginal distributions.
Table 9.
Non-normal distributions: Different marginal distributions.
| Mean (SD) | Probability Greater than or Equal to Youden Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (, ) | Mean (SD) Variables | SLM | SWD | MM | LR | MVN | KS | SLM | SWD | MM | LR | MVN | KS |
| / | |||||||||||||
| (10, 20) | = (0.2111, 0.2710, 0.6032, 0.2119) | 0.7476 | 0.7004 | 0.4910 | 0.6047 | 0.5436 | 0.6672 | 0.5544 | 0.1723 | 0.0531 | 0.0767 | 0.0187 | 0.1237 |
| = (0.1249, 0.1339, 0.1215, 0.1247) | (0.099) | (0.1076) | (0.1258) | (0.16) | (0.1809) | (0.1283) | |||||||
| (30, 30) | = (0.1494, 0.2072, 0.5553, 0.1453) | 0.661 | 0.6294 | 0.4306 | 0.5214 | 0.4585 | 0.6101 | 0.5692 | 0.1607 | 0.0112 | 0.0367 | <0.01 | 0.2129 |
| = (0.0875, 0.0942, 0.0940, 0.0854) | (0.0803) | (0.0876) | (0.0916) | (0.1278) | (0.1488) | (0.1144) | |||||||
| (50, 30) | = (0.1364, 0.1939, 0.5476, 0.1328) | 0.6413 | 0.6218 | 0.4300 | 0.5136 | 0.4492 | 0.6015 | 0.5183 | 0.1802 | 0.0170 | 0.0312 | <0.01 | 0.2460 |
| = (0.0757, 0.0828, 0.0876, 0.0745) | (0.0778) | (0.0809) | (0.0798) | (0.1212) | (0.1447) | (0.1059) | |||||||
| (50, 50) | = (0.1161, 0.1752, 0.5384, 0.1126) | 0.6239 | 0.6031 | 0.3957 | 0.4926 | 0.4455 | 0.5940 | 0.5254 | 0.1658 | <0.01 | 0.0142 | 0.0104 | 0.2828 |
| = (0.0656, 0.0720, 0.0744, 0.0610) | (0.0651) | (0.0704) | (0.0726) | (0.1048) | (0.1275) | (0.0878) | |||||||
| (100, 100) | = (0.0847, 0.1466, 0.5216, 0.0829) | 0.5869 | 0.5755 | 0.3728 | 0.4651 | 0.4403 | 0.5834 | 0.3691 | 0.1404 | <0.01 | <0.01 | 0.0102 | 0.4759 |
| = (0.0459, 0.0551, 0.0537, 0.0460) | (0.047) | (0.05) | (0.0564) | (0.0773) | (0.1037) | (0.0620) | |||||||
| (500, 500) | = (0.0387, 0.1061, 0.4968, 0.0387) | 0.5423 | 0.5369 | 0.3497 | 0.4423 | 0.4404 | 0.5716 | 0.0395 | 0.0155 | <0.01 | <0.01 | 0.0115 | 0.9335 |
| = (0.0201, 0.0265, 0.0252, 0.0206) | (0.0235) | (0.0253) | (0.0260) | (0.0439) | (0.0652) | (0.0271) | |||||||
| / | |||||||||||||
| (10, 20) | = (0.2111, 0.3666, 0.7690, 0.2119) | 0.8899 | 0.8479 | 0.5380 | 0.804 | 0.7612 | 0.8296 | 0.5278 | 0.1513 | <0.01 | 0.1438 | 0.0396 | 0.1282 |
| = (0.1249, 0.1412, 0.1005, 0.1247) | (0.0756) | (0.0868) | (0.1301) | (0.1413) | (0.1563) | (0.1097) | |||||||
| (30, 30) | = (0.1494, 0.3073, 0.7331, 0.1453) | 0.8406 | 0.8013 | 0.5206 | 0.7626 | 0.7249 | 0.8042 | 0.6367 | 0.1127 | <0.01 | 0.07 | 0.0154 | 0.1622 |
| = (0.0875, 0.0997, 0.0797, 0.0854) | (0.0685) | (0.0723) | (0.0909) | (0.1083) | (0.1202) | (0.0807) | |||||||
| (50, 30) | = (0.1364, 0.2940, 0.7280, 0.1328) | 0.8283 | 0.7992 | 0.5504 | 0.7622 | 0.7188 | 0.7974 | 0.6465 | 0.1148 | <0.01 | 0.0707 | 0.0111 | 0.1558 |
| = (0.0757, 0.0891, 0.0763, 0.0745) | (0.0651) | (0.0686) | (0.0811) | (0.1012) | (0.1125) | (0.0766) | |||||||
| (50, 50) | = (0.1161, 0.2745, 0.7216, 0.1126) | 0.8178 | 0.786 | 0.4974 | 0.7476 | 0.7158 | 0.7916 | 0.6727 | 0.0982 | <0.01 | 0.0583 | 0.0152 | 0.1557 |
| = (0.0656, 0.0785, 0.0654, 0.0610) | (0.0554) | (0.0603) | (0.0768) | (0.089) | (0.0999) | (0.0635) | |||||||
| (100, 100) | = (0.0847, 0.2516, 0.7089, 0.0829) | 0.7976 | 0.771 | 0.4836 | 0.7354 | 0.7114 | 0.7805 | 0.7245 | 0.0628 | <0.01 | 0.0304 | <0.01 | 0.1727 |
| = (0.0459, 0.0605, 0.0457, 0.0460) | (0.0399) | (0.0424) | (0.0579) | (0.0651) | (0.0733) | (0.0433) | |||||||
| (500, 500) | = (0.0387, 0.2177, 0.6886, 0.0387) | 0.7774 | 0.7547 | 0.4635 | 0.7221 | 0.6929 | 0.7698 | 0.8105 | 0.0217 | <0.01 | <0.01 | <0.01 | 0.1645 |
| = (0.0201, 0.0274, 0.0215, 0.0206) | (0.0193) | (0.0217) | (0.0256) | (0.0347) | (0.0373) | (0.0194) | |||||||
The results in Table 9 show that our stepwise approach also generally dominates the other approaches in non-normal scenarios with different marginal distributions. It is followed by Yin and Tian’s stepwise approach and the non-parametric kernel smoothing approach. Logistic regression outperforms the parametric approach under multivariate normality. The min-max approach is the worst performer.
3.1.6. Non-Normal Distributions. Log-Normal Distributions
Table 10 shows the results obtained from simulated data following a log-normal distribution. Specifically, three scenarios were analyzed under this distribution: independent biomarkers with different means ( and ), biomarkers correlated with a medium intensity and different means (··J and ) and biomarkers correlated with a medium intensity and same means (··J and ).


Table 10.
Non-normal distributions: Log-normal distributions.
Table 10.
Non-normal distributions: Log-normal distributions.
| Mean (SD) | Probability Greater than or Equal to Youden Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size (, ) | Mean (SD) Variables | SLM | SWD | MM | LR | MVN | KS | SLM | SWD | MM | LR | MVN | KS |
| Different means: . Independence ( = I) | |||||||||||||
| (10, 20) | = (0.2737, 0.3560, 0.5178, 0.4314) | 0.765 | 0.7189 | 0.627 | 0.6548 | 0.6284 | 0.7051 | 0.6045 | 0.1424 | 0.0867 | 0.0424 | 0.0157 | 0.1082 |
| = (0.1357, 0.1395, 0.1421, 0.1457) | (0.1013) | (0.1097) | (0.1222) | (0.1448) | (0.1524) | (0.1194) | |||||||
| (30, 30) | = (0.2063, 0.3024, 0.4663, 0.3673) | 0.6545 | 0.6235 | 0.5527 | 0.5651 | 0.5422 | 0.6162 | 0.6476 | 0.1413 | 0.0772 | 0.0152 | <0.01 | 0.1121 |
| = (0.0943, 0.0991, 0.0990, 0.1053) | (0.0835) | (0.0857) | (0.0959) | (0.1014) | (0.1088) | (0.0892) | |||||||
| (50, 30) | = (0.1933, 0.2975, 0.4630, 0.3603) | 0.6289 | 0.6137 | 0.5397 | 0.5539 | 0.5313 | 0.6023 | 0.5810 | 0.1785 | 0.0862 | 0.0164 | <0.01 | 0.1317 |
| = (0.0846, 0.0937, 0.0894, 0.0898) | (0.0742) | (0.0758) | (0.0816) | (0.0888) | (0.0942) | (0.0798) | |||||||
| (50, 50) | = (0.1764, 0.2784, 0.4484, 0.3458) | 0.605 | 0.5829 | 0.5163 | 0.5308 | 0.5139 | 0.5735 | 0.6739 | 0.1518 | 0.0638 | <0.01 | <0.01 | 0.0996 |
| = (0.0736, 0.0789, 0.0774, 0.0796) | (0.0663) | (0.0682) | (0.0737) | (0.0796) | (0.0832) | (0.0715) | |||||||
| (100, 100) | = (0.1487, 0.2498, 0.4254, 0.3214) | 0.5507 | 0.5399 | 0.4802 | 0.5027 | 0.4911 | 0.5322 | 0.6514 | 0.1676 | 0.0418 | 0.0105 | <0.01 | 0.1223 |
| = (0.0533, 0.0590, 0.0560, 0.0590) | (0.0498) | (0.0514) | (0.0528) | (0.0560) | (0.0578) | (0.0526) | |||||||
| (500, 500) | = (0.1062, 0.2185, 0.3991, 0.2925) | 0.4926 | 0.4904 | 0.4412 | 0.4779 | 0.4745 | 0.4890 | 0.5157 | 0.2015 | <0.01 | 0.0257 | 0.0198 | 0.2308 |
| = (0.0257, 0.0282, 0.0274, 0.0280) | (0.0255) | (0.0255) | (0.0267) | (0.0265) | (0.0269) | (0.0259) | |||||||
| Different means: . Medium Correlation ( = 0.5·I + 0.5·J) | |||||||||||||
| (10, 20) | = (0.2713, 0.3657, 0.5268, 0.4280) | 0.7319 | 0.6647 | 0.5354 | 0.6227 | 0.5784 | 0.6732 | 0.5570 | 0.1647 | 0.0280 | 0.0741 | 0.0245 | 0.1518 |
| = (0.1353, 0.1477, 0.1423, 0.1427) | (0.1064) | (0.1185) | (0.1314) | (0.1429) | (0.1568) | (0.1191) | |||||||
| (30, 30) | = (0.2032, 0.3020, 0.4665, 0.3668) | 0.6177 | 0.5641 | 0.4490 | 0.5177 | 0.4834 | 0.5712 | 0.5712 | 0.1799 | 0.0124 | 0.0354 | 0.0101 | 0.1911 |
| = (0.0933, 0.1014, 0.0991, 0.1008) | (0.0836) | (0.0885) | (0.0981) | (0.1016) | (0.1153) | (0.0899) | |||||||
| (50, 30) | = (0.1931, 0.2928, 0.4581, 0.3632) | 0.5848 | 0.5579 | 0.4333 | 0.5066 | 0.4713 | 0.5564 | 0.5245 | 0.2395 | <0.01 | 0.0220 | 0.011 | 0.1972 |
| = (0.0847, 0.0908, 0.0883, 0.0905) | (0.0767) | (0.0786) | (0.0838) | (0.0896) | (0.1036) | (0.082) | |||||||
| (50, 50) | = (0.1753, 0.2761, 0.4472, 0.3495) | 0.5619 | 0.5243 | 0.4121 | 0.4864 | 0.4546 | 0.5268 | 0.5553 | 0.1843 | <0.01 | 0.0260 | <0.01 | 0.2243 |
| = (0.0742, 0.0798, 0.0787, 0.0791) | (0.0676) | (0.0712) | (0.0767) | (0.0792) | (0.0899) | (0.0745) | |||||||
| (100, 100) | = (0.1449, 0.2487, 0.4250, 0.3236) | 0.5089 | 0.4845 | 0.378 | 0.4567 | 0.4345 | 0.4859 | 0.5573 | 0.2003 | <0.01 | 0.0208 | <0.01 | 0.2118 |
| = (0.0520, 0.0578, 0.0591, 0.0595) | (0.0539) | (0.056) | (0.0567) | (0.0608) | (0.0677) | (0.0582) | |||||||
| (500, 500) | = (0.1063, 0.2187, 0.3994, 0.2921) | 0.4446 | 0.4374 | 0.3329 | 0.4285 | 0.4202 | 0.4394 | 0.5233 | 0.1825 | <0.01 | 0.0315 | <0.01 | 0.2538 |
| = (0.0261, 0.0280, 0.0264, 0.0279) | (0.0261) | (0.0257) | (0.0273) | (0.0265) | (0.0282) | (0.0265) | |||||||
| Same means: . Medium Correlation ( = 0.5·I + 0.5·J) | |||||||||||||
| (10, 20) | = (0.5224, 0.5172, 0.5268, 0.5197) | 0.7619 | 0.7249 | 0.66 | 0.663 | 0.6254 | 0.7041 | 0.5180 | 0.2036 | 0.0794 | 0.0675 | 0.0183 | 0.1132 |
| = (0.1405, 0.1442, 0.1423, 0.1404) | (0.1032) | (0.1127) | (0.1267) | (0.1402) | (0.1508) | (0.1187) | |||||||
| (30, 30) | = (0.4685, 0.4669, 0.4665, 0.4640) | 0.6624 | 0.6291 | 0.5882 | 0.5676 | 0.5385 | 0.6089 | 0.5416 | 0.2341 | 0.0776 | 0.0251 | <0.01 | 0.1123 |
| = (0.1024, 0.1025, 0.0991, 0.0991) | (0.0851) | (0.0878) | (0.0926) | (0.101) | (0.1092) | (0.0939) | |||||||
| (50, 30) | = (0.4586, 0.4621, 0.4581, 0.4627) | 0.6337 | 0.6167 | 0.5758 | 0.5566 | 0.5263 | 0.5949 | 0.5167 | 0.2714 | 0.0851 | 0.0171 | 0.0107 | 0.0991 |
| = (0.0878, 0.0908, 0.0883, 0.0878) | (0.0759) | (0.0773) | (0.082) | (0.0871) | (0.102) | (0.083) | |||||||
| (50, 50) | = (0.4459, 0.4477, 0.4472, 0.4479) | 0.6089 | 0.5887 | 0.5562 | 0.5335 | 0.5061 | 0.5688 | 0.5359 | 0.2648 | 0.0887 | 0.0127 | <0.01 | 0.0929 |
| = (0.0769, 0.0810, 0.0787, 0.0789) | (0.0673) | (0.0715) | (0.0737) | (0.0795) | (0.087) | (0.0758) | |||||||
| (100, 100) | = (0.4243, 0.4235, 0.4250, 0.4263) | 0.5598 | 0.5457 | 0.5266 | 0.5081 | 0.4879 | 0.5331 | 0.5434 | 0.2628 | 0.0996 | 0.0128 | <0.01 | 0.0772 |
| = (0.0569, 0.0572, 0.0591, 0.0597) | (0.0498) | (0.0525) | (0.0537) | (0.0565) | (0.0638) | (0.0544) | |||||||
| (500, 500) | = (0.3993, 0.3990, 0.3994, 0.3992) | 0.4963 | 0.4934 | 0.4883 | 0.4819 | 0.4748 | 0.4908 | 0.4802 | 0.2588 | 0.1300 | 0.0135 | <0.01 | 0.1105 |
| = (0.0268, 0.0277, 0.0264, 0.0270) | (0.0254) | (0.0255) | (0.0256) | (0.0265) | (0.0277) | (0.0259) | |||||||
The results in Table 10 indicate that, in these scenarios of skewed distributions, our stepwise approach performs significantly better than the other methods. Yin and Tian’s stepwise approach performs slightly better than the non-parametric kernel smoothing approach in most scenarios, especially in scenarios where the biomarkers have a similar mean. Logistic regression globally outperforms the parametric approach under multivariate normality and the min-max approach performs better than the logistic approach in biomarker scenarios with the same predictive ability.
From the results provided under sample scenarios of non-normal distributions, it can be deduced that our proposed stepwise approach remains the method that achieves the best overall performance, followed by Yin and Tian’s stepwise approach and the non-parametric kernel smoothing approach. The min-max method follows a similar behaviour to that found in normal distribution scenarios, increasing its performance in biomarker samples with a similar predictive ability. Unlike most simulated normal sample data scenarios, in scenarios under non-normal distributions, logistic regression outperforms the parametric approach under multivariate normality.
3.2. Simulations. Validation
Table 11, Table 12, Table 13, Table 14, Table 15 and Table 16 show the results of the validation of each algorithm for every simulated data scenario. In particular, for all simulated setting of parameters, using 100 random samples, and for each method, the mean and standard deviation (in brackets) of the maximum Youden indexes obtained in the analysis of the 100 validation samples are presented.

Table 11.
Normal distributions: Different means and equal positive correlations. Validation.

Table 12.
Normal distributions: Different means and unequal positive correlations. Validation.

Table 13.
Normal distributions: Different means and equal negative correlations. Validation.

Table 14.
Normal distributions: Same means. Validation.

Table 15.
Non-normal distributions: Different marginal distributions. Validation.

Table 16.
Non-normal distributions: Log-normal distributions. Validation.
These results and conclusions drawn in terms of validation in the simulated scenarios are presented below.
3.2.1. Normal Distributions. Different Means and Equal Positive Correlations for Diseased and Non-Diseased Population
The results in Table 11 show that, for normal simulated data, different means and equal positive correlation, the logistic regression and the parametric approach under multivariate normality outperform the rest of the methods in all scenarios for small or large sample sizes. The non-parametric kernel smoothing approach shows lower but comparable results to the logistic regression and non-parametric approach, especially in large sample sizes. Our stepwise approach outperforms Yin and Tian’s stepwise approach, especially and significantly in the high correlation scenario. Our stepwise approach is closer in performance to the non-parametric kernel smoothing approach for large sample sizes. The min-max approach is the one with the worst results in such scenarios.
3.2.2. Normal Distributions. Different Means and Unequal Positive Correlations for Diseased and Non-Diseased Population
For normal simulated data, different means and unequal positive correlation for diseased and non-diseased population, the results displayed in Table 12 show logistic regression and the parametric approach under multivariate normality as the best models, and as very similar to the non-parametric kernel smoothing approach, with the stepwise approaches slightly worse and the min-max method with clearly lower values.
3.2.3. Normal Distributions. Different Means and Equal Negative Correlations for Diseased and Non-Diseased Population
The performance of the algorithms for normal simulated data, different means and equal negative correlation was very similar to previous results. It can be seen in Table 13 that logistic regression and the parametric approach under multivariate normality were the best models, followed by the non-parametric kernel smoothing approach, our stepwise approach and Yin and Tian’s stepwise approach, with worse results for the min-max algorithm.
3.2.4. Normal Distributions. Same Means for Diseased and Non-Diseased Population
Regarding scenarios with normal simulated data and same means for the diseased and non-diseased populations, the results in Table 14 present clear differences with previous simulations. For scenarios of the same correlation, the min-max algorithm is not the worst and all algorithms show a very similar mean Youden index in large samples. However, for scenarios of different correlations, the min-max algorithm clearly outperforms the rest of the algorithms.
Thus, in summary, for normal simulated data, our stepwise approach, Yin and Tian’s stepwise model, logistic regression, parametric under multivariate normality and non-parametric kernel smoothing algorithms showed a close performance, with the best results for logistic regression and the parametric approach under multivariate normality, an intermediate position for the kernel smoothing algorithm and lower values for our proposed stepwise approach, which is still better than Yin and Tian’s stepwise algorithm in most cases, and significantly for high correlations. By contrast, the min-max algorithm has a worse performance for scenarios with different means, but is clearly superior for simulations generated with the same mean for disease markers and different correlations for disease and non-disease populations.
3.2.5. Non-Normal Distributions. Different Marginal Distributions
Table 15 shows results for the non-normal scenario with different marginal distributions, which is a scenario that is probably closer to the reality of the actual data, where asymmetries occur when patients have different degrees of a disease. In this cases, the stepwise approaches clearly outperform the rest of the algorithms, with the better results for our proposed stepwise algorithm. For large sample sizes, the non-parametric kernel smoothing shows markedly superior results to the logistic and the parametric approach. As in some previous cases, the min-max method fails to provide similar results in these scenarios.
3.2.6. Non-Normal Distributions. Log-Normal Distributions
Table 16 shows the results for the simulated log-normal distributions. Similar conclusions can be drawn for the simulated normal data. We can infer that, for distributions that can be converted into normal distributions by means of monotonic transformations, we expect to find similar conclusions as for the simulations under the normality hypothesis.
3.3. Computational Times
In addition to the performance of the algorithms in terms of the Youden index, in practice, it can be important to also consider the computational time taken by the algorithm to be used. Although our proposal is an algorithm of an extensive search, when k is the number of values of to be considered and p is the number of markers, the number of Youden indexes necessary to estimate the parameters of the model is reduced from the order using the comprehensive Pepe and Thompson algorithm [13] to the order using the stepwise procedure.
Without a loss of generality, Table 17 shows the average computational time of 1000 simulations of each of the analyzed algorithms for the scenario of normal distributions, a low positive correlation and vector of means () (Table 2), both for the smallest sample size () and for the largest sample size ().

Table 17.
Total computational time for each algorithm (estimated by mean of 1000 samples).
Table 17 shows that the stepwise algorithms have a longer computational time than the other algorithms. Our proposed algorithm entails a noticeably higher computational time compared to Yin and Tian’s stepwise approach. This difference in the computational time is due to the biomarker search that optimizes the linear combination at each step and the handling of ties in our algorithm, which gets worse at small sample sizes where ties are more common. As a consequence, there is a high disparity between computational times with small sample sizes. This computational burden increases significantly for a larger number of biomarkers. However, although this high computational time presents a limitation in our algorithm, it addresses a correct handling of ties, leading to better discriminatory ability results. Furthermore, the computational time of a single simulation is, for four biomarkers, in any case, addressable. It should also be noted that the computational times of derivative-based numerical search methods (such as the non-parametric kernel smoothing approach) significantly depend on the initial values.
3.4. Application in Clinical Diagnosis Cases
Figure 1 and Figure 2 show the distribution of each biomarker for the Duchenne muscular dystrophy and prostate cancer dataset, respectively, where disease refers to clinically significant prostate cancer.
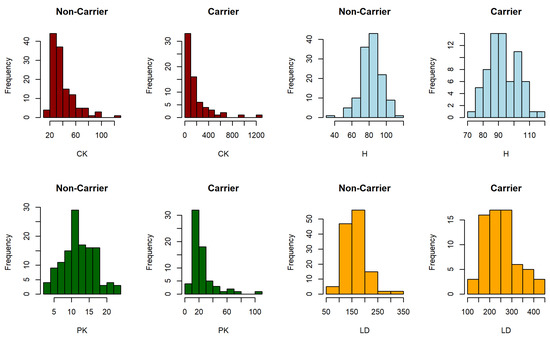
Figure 1.
Marginal distributions of biomarkers. DMD dataset. CK: serum creatine kinase, H: haemopexin, PK: pyruvate kinase, LD: lactate dehydrogenase.
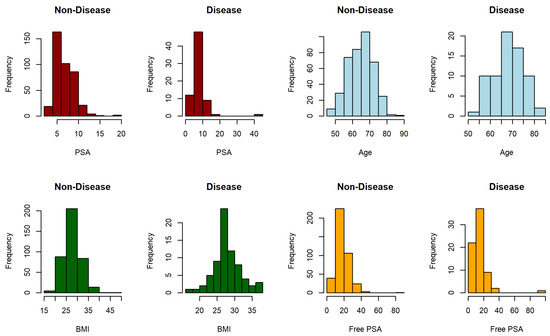
Figure 2.
Marginal distributions of biomarkers. Prostate cancer dataset. PSA: prostate specific antigen, Age: age in years, BMI: body mass index, Free PSA: percentage of Free PSA.
Table 18 and Table 19 show the empirical estimates of the Youden index of each biomarker and the optimal cut-off point (threshold), as well as the characteristics of each of them in terms of mean, standard deviations (SD) and correlations between them for both the disease and non-disease group, considered as a non-carrier for the Duchenne muscular dystrophy dataset and non-clinically significant prostate cancer for the prostate cancer dataset, respectively.

Table 18.
DMD dataset information.

Table 19.
Prostate cancer dataset information.
Concerning the performance achieved by each method, Table 20 and Table 21 present the linear combination for the optimal cut-off point that maximizes the Youden index, as well as the sensitivity and specificity values achieved, for the Duchenne muscular dystrophy and prostate cancer dataset, respectively. Table 22 and Table 23 show these metrics after applying the 10-fold cross validation procedure.

Table 20.
Linear combination that maximizes the Youden index for each method. DMD dataset.

Table 21.
Linear combination that maximizes the Youden index for each method. Prostate cancer dataset.

Table 22.
Ten-fold cross validation. DMD dataset.

Table 23.
Ten-fold cross validation. Prostate dataset.
3.4.1. Duchenne Muscular Dystrophy Dataset
The mean values of each biomarker and the correlations between them are very different and differ between carriers and non-carriers. Likewise, the variances of the four biomarkers are very different and, therefore, it is necessary to normalize the values of each variable before applying the min-max method. In this way, different units of measurement are avoided so that a correct use of the min-max algorithm is made, where all biomarkers must be in the same unit. The estimates of the Youden index of each biomarker (CK, H, PK, LD) in a univariate way were 0.6124, 0.4172, 0.5079 and 0.5776.
The linear methods (combination of biomarkers) achieved a remarkable Youden index in training data, with values above 0.8 for most of them. Stepwise methods followed by logistic regression and the non-parametric method based on kernel smoothing are the ones that obtained the best results. Our proposed stepwise approach achieved the best performance in training data (Youden index = 0.8255) with the linear combination , but the logistic regression showed the best result in a 10-fold cross validation procedure (Youden index = 0.7861) with the linear combination . It is followed by the kernel algorithm and our stepwise approach. These results are in concordance with those of normal simulated data or variables that can be converted into normal distributions by means of monotonic transformations.
3.4.2. Prostate Cancer Dataset
Although to a lesser extent than the previous example, there is a notable difference between the variances of the biomarkers, so the values were also normalized before applying the min-max approach. The correlations between biomarkers are close to zero (independent biomarkers). The Youden index estimates for each biomarker (PSA, age, BMI, free PSA) in a univariate way were lower than the previous data set: 0.1571, 0.2202, 0.0953 and 0.0141.
Our proposed stepwise algorithm and the non-parametric method based on kernel smoothing dominate all of the other methods. Our algorithm achieved the best performance in training and validation data (maximum Youden index = 0.4857, 0.3844 for training and validation data respectively) with the linear combination . In these cases, PSA and free PSA are markers that usually present a marked asymmetry, showing a greater or lower degree of progress of the cancer disease; in this scenario, simulated data also showed the superiority of the stepwise algorithm.
4. Discussion
Although continuous markers usually provide better adjusted predictions, in classification problems, the ultimate goal is to assign a class 0/1 for any individual. Choosing threshold probabilities to dichotomize a predictive or prognostic model is the key to solve this problem. There are different methods to provide the cut-off point depending on the purpose of the classification, but there is a consensus that, without a clear reason to provide higher values for sensitivity or specificity, the Youden index provides an optimized balance of sensitivity/specificity [43].
Thus, the Youden index has been the most usual method to classify patients according to predictive or prognostic models in medicine. As previous studies provide methods to estimate the parameter of linear models in order to optimize ROC parameters, in this work, we have proposed a stepwise algorithm that maximizes the Youden index. This algorithm is based on sequential optimizations, as they happen in dynamic programming, thus following the Bellman’s optimality principle [44]. Unlike similar algorithms that use partial optimizations, we explore, at any step, the candidate biomarkers to be added to the model that provide linear combinations with the highest Youden index, following Pepe and Thompson’s parameter search approach. In addition, our proposal also considers the ties that appear in the sequencing of the partial optimizations.
Our proposed approach has been explored in extensive simulation scenarios and compared with other methods. In particular, five other linear combination methods from the literature adapted to optimize the Youden index have been considered for comparison. Two of them are also based on Pepe and Thompson’s empirical search (the Yin and Tian stepwise approach and the min-max approach) and three methods in numerical search based on derivatives (the classical logistic regression approach, a parametric approach and a non-parametric kernel smoothing approach).
The results obtained show that our proposed stepwise approach is superior to all other compared methods in most of the simulated scenarios considered for training data, but remains close to the rest for validation data, except in cases that are far from the verification of the normality hypothesis, in which, it is the best method for both training and validation data. It is globally followed by the Yin and Tian stepwise approach and the non-parametric kernel smoothing approach, the latter being slightly better in scenarios of higher correlation normal distributions for training data. However, in normal distributions scenarios, the non-parametric kernel smoothing approach outperformed Yian and Tian’s stepwise approach for the validation data. In normal distribution scenarios, logistic regression and the parametric approach under multivariate normality showed a comparable performance overall, inferior to the non-parametric kernel smoothing approach in training data but superior or similar to the rest in validation data. However, the performance of the parametric approach worsened compared to logistic regression in non-normal distribution scenarios, as expected.
The min-max approach performed the worst in scenarios with different biomarker predictive capacities. However, it performed better in scenarios with the same predictive capacity of biomarkers (both in normal and non-normal distributions) and it outperformed the other algorithms when the covariance matrices differed between the diseased and non-diseased population. Among the wide range of simulated scenarios, highly negatively correlated biomarker scenarios were also included. In these scenarios, most algorithms achieved a very high performance, a result that is in agreement with the study by Pinsky and Zhu, who reported an increase in performance when considering highly negatively correlated biomarkers. In cases where they achieved near-perfect Youden indexes, the stepwise approaches performed worse than the other algorithms, with the exception of the min-max approach.
The performance of the linear combination methods was also analyzed on real datasets. The results obtained derived similar conclusions to those deduced from the simulated data. Remarkably, the stepwise approach performance is superior to the rest of the algorithms for the prostate cancer database in training and validation data. This is a data set where the PSA and free PSA variables for screening populations, or without previous treatment, present clear asymmetries that reflect the progression of the disease. This situation will occur for many other diseases where markers do not present results under the hypothesis of normality and the triggered values are associated with advanced stages of a disease. In these scenarios, the stepwise algorithm that we have proposed performs better than parametric algorithms where the non-verification of the hypothesis (normality or logistic relation) results in a loss of prediction capacity in the models.
The stepwise approaches and the non-parametric kernel smoothing approach achieved a good performance in general. Logistic regression also achieved one of the best discriminative capabilities on the DMD dataset (the best in the validation data), whose performance was relatively high overall.
Therefore, given the results of the spectrum analyzed, we could suggest the reader to use the min-max algorithm in scenarios with biomarkers with a similar predictive power and different covariance matrices between the disease and non-disease group, and our proposed stepwise approach in other scenarios, especially for those apart from the normality hypothesis. In addition, we have created a library in R (SLModels) that can be used to implement these algorithms.
However, in terms of the computational time, stepwise approaches and, in particular, our proposal entail a significantly higher computational time due to the handling of ties, which may be more present in small sample sizes. This may be a limitation in the use of our algorithm, since, in practice, a faster computational speed is desired, especially when the number of biomarkers increases (). In these cases, the other algorithms (non-stepwise or min-max approach) have the advantage of being much more efficient. However, it has been shown that the min-max approach may not be sufficient in terms of discrimination in some scenarios. Aznar-Gimeno et al. [45] proposed a new approach that extends the min-max approach in order to analyze whether it increased predictive capacity while also being computationally tractable independently of the number of biomarkers.
As a line of future work, it is intended to optimize the proposed stepwise algorithm, with the aim of reducing its computational burden. It is intended to create tie handling strategies in such a way that the least pernicious criteria are used to break ties and not to drag them through many stages. The idea is to balance a certain increase in performance against an increase in computational load. Readers are also encouraged to adapt our algorithm using other target metrics to optimize and validate it in other scenarios, such as to explore and analyze the algorithm in multi-class classification problems using ROC surfaces.
5. Conclusions
In this work, we present a stepwise algorithm that complements and extends related existing ideas to optimize ROC-curve-derived parameters for linear models. We used, as the optimization parameter, the Youden index, which is the most used threshold point to dichotomize markers. As a strength, the developed method is a fully non-parametric distribution-free approach that showed a better performance in some scenarios. In addition, it captures the full predictive ability of a set of variables, in contrast to methodologies that try to reduce them. Additionally, the research has led to the creation of the R library SLModels, which incorporates our proposed algorithm, can be used and is openly available to the scientific community. We believe that the findings of this research will provide insight for the development and application of algorithms for classification problems in medicine.
Author Contributions
Conceptualization, R.A.-G. and L.M.E.; methodology, R.A.-G., L.M.E. and G.S.; software, R.A.-G., L.M.E. and R.d.-H.-A.; validation, R.A.-G. and L.M.E.; formal analysis, R.A.-G. and L.M.E.; investigation, R.A.-G., L.M.E. and G.S.; resources, R.A.-G., L.M.E. and Á.B.-F.; data curation, R.A.-G., L.M.E. and Á.B.-F.; writing—original draft preparation, R.A.-G. and L.M.E.; writing—review and editing, R.A.-G., L.M.E., G.S., R.d.-H.-A. and Á.B.-F.; visualization, R.A.-G. and L.M.E.; supervision, R.A.-G., L.M.E., G.S. and R.d.-H.-A.; funding acquisition, G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Government of Aragon (Stochastic Models Research group, grant number E46_20R), and Ministerio de Ciencia e Innovación (grant number PID2020-116873GB-I00).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Patient consent was waived due to the retrospective observational nature of this study; data could be fully anonymized.
Data Availability Statement
Data from the prostate cancer dataset were retrieved from the Miguel Servet University Hospital database and are not shared. The Duchenne muscular dystrophy dataset can be found at https://hbiostat.org/data/, accessed on 19 February 2022.
Acknowledgments
Research of Luis Mariano Esteban, Gerardo Sanz and Ángel Borque was supported by the Stochastic Models Research group of the Government of Aragon, grant number E46_20R and Ministerio de Ciencia e Innovación, grant number PID2020-116873GB-I00. In addition, we would like to thank Instituto Tecnológico de Aragón (ITAINNOVA), Zaragoza, Spain for the support of the work of Rocío Aznar-Gimeno and Rafael del-Hoyo-Alonso, belonging to the Integration and Development of Big Data and Electrical Systems (IODIDE) group (T17_20R).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Esteban, L.M.; Sanz, G.; Borque, A. Linear combination of biomarkers to improve diagnostic accuracy in prostate cancer. Monografías Matemáticas García de Galdeano 2013, 38, 75–84. [Google Scholar]
- Bansal, A.; Pepe, M.S. When does combining markers improve classification performance and what are implications for practice? Stat. Med. 2013, 32, 1877–1892. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, L.; Tian, L.; Liu, S. Combining large number of weak biomarkers based on AUC. Stat. Med. 2015, 34, 3811–3830. [Google Scholar] [CrossRef] [Green Version]
- Lyu, T.; Ying, Z.; Zhang, H. A new semiparametric transformation approach to disease diagnosis with multiple biomarkers. Stat. Med. 2019, 38, 1386–1398. [Google Scholar] [CrossRef]
- Amini, M.; Kazemnejad, A.; Zayeri, F.; Amirian, A.; Kariman, N. Application of adjusted-receiver operating characteristic curve analysis in combination of biomarkers for early detection of gestational diabetes mellitus. Koomesh 2019, 21, 751–758. [Google Scholar]
- Ma, H.; Yang, J.; Xu, S.; Liu, C.; Zhang, Q. Combination of multiple functional markers to improve diagnostic accuracy. J. Appl. Stat. 2022, 49, 44–63. [Google Scholar] [CrossRef]
- Yu, S. A Covariate-Adjusted Classification Model for Multiple Biomarkers in Disease Screening and Diagnosis. Ph.D. Thesis, Kansas State University, Manhattan, AR, USA, 2019. [Google Scholar]
- Ahmadian, R.; Ercan, I.; Sigirli, D.; Yildiz, A. Combining binary and continuous biomarkers by maximizing the area under the receiver operating characteristic curve. Commun. Stat. Simul. Comput. 2020, 1–14. [Google Scholar] [CrossRef]
- Hu, X.; Li, C.; Chen, J.; Qin, G. Confidence intervals for the Youden index and its optimal cut-off point in the presence of covariates. J. Biopharm. Stat. 2021, 31, 251–272. [Google Scholar] [CrossRef]
- Kang, L.; Xiong, C.; Crane, P.; Tian, L. Linear combinations of biomarkers to improve diagnostic accuracy with three ordinal diagnostic categories. Stat. Med. 2013, 32, 631–643. [Google Scholar] [CrossRef] [Green Version]
- Maiti, R.; Li, J.; Das, P.; Feng, L.; Hausenloy, D.; Chakraborty, B. A distribution-free smoothed combination method of biomarkers to improve diagnostic accuracy in multi-category classification. arXiv 2019, arXiv:1904.10046. [Google Scholar]
- Su, J.Q.; Liu, J.S. Linear combinations of multiple diagnostic markers. J. Am. Stat. Assoc. 1993, 88, 1350–1355. [Google Scholar] [CrossRef]
- Pepe, M.S.; Thompson, M.L. Combining diagnostic test results to increase accuracy. Biostatistics 2000, 1, 123–140. [Google Scholar] [CrossRef] [PubMed]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, C.; Liu, A.; Halabi, S. A min–max combination of biomarkers to improve diagnostic accuracy. Stat. Med. 2011, 30, 2005–2014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pepe, M.S.; Cai, T.; Longton, G. Combining predictors for classification using the area under the receiver operating characteristic curve. Biometrics 2006, 62, 221–229. [Google Scholar] [CrossRef]
- Esteban, L.M.; Sanz, G.; Borque, A. A step-by-step algorithm for combining diagnostic tests. J. Appl. Stat. 2011, 38, 899–911. [Google Scholar] [CrossRef]
- Kang, L.; Liu, A.; Tian, L. Linear combination methods to improve diagnostic/prognostic accuracy on future observations. Stat. Methods Med. Res. 2016, 25, 1359–1380. [Google Scholar] [CrossRef] [Green Version]
- Liu, A.; Schisterman, E.F.; Zhu, Y. On linear combinations of biomarkers to improve diagnostic accuracy. Stat. Med. 2005, 24, 37–47. [Google Scholar] [CrossRef]
- Yin, J.; Tian, L. Joint inference about sensitivity and specificity at the optimal cut-off point associated with Youden index. Comput. Stat. Data Anal. 2014, 77, 1–13. [Google Scholar] [CrossRef]
- Yu, W.; Park, T. Two simple algorithms on linear combination of multiple biomarkers to maximize partial area under the ROC curve. Comput. Stat. Data Anal. 2015, 88, 15–27. [Google Scholar] [CrossRef]
- Yan, Q.; Bantis, L.E.; Stanford, J.L.; Feng, Z. Combining multiple biomarkers linearly to maximize the partial area under the ROC curve. Stat. Med. 2018, 37, 627–642. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Halabi, S.; Liu, A. On the use of min-max combination of biomarkers to maximize the partial area under the ROC curve. J. Probab. Stat. 2019, 2019, 8953530. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perkins, N.J.; Schisterman, E.F. The inconsistency of “optimal” cutpoints obtained using two criteria based on the receiver operating characteristic curve. Am. J. Epidemiol. 2006, 163, 670–675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Youden, W.J. Index for rating diagnostic tests. Cancer J. 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Martínez-Camblor, P.; Pardo-Fernández, J.C. The Youden Index in the Generalized Receiver Operating Characteristic Curve Context. Int. J. Biostat. 2019, 15, 20180060. [Google Scholar] [CrossRef]
- Yin, J.; Tian, L. Optimal linear combinations of multiple diagnostic biomarkers based on Youden index. Stat. Med. 2014, 33, 1426–1440. [Google Scholar] [CrossRef]
- Yin, J.; Tian, L. Joint confidence region estimation for area under ROC curve and Youden index. Stat. Med. 2014, 33, 985–1000. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: http://www.r-project.org/index.html (accessed on 19 February 2022).
- SLModels: Stepwise Linear Models for Binary Classification Problems under Youden Index Optimisation. R Package Version 0.1.2. Available online: https://cran.r-project.org/web/packages/SLModels/index.html (accessed on 19 February 2022).
- Walker, S.H.; Duncan, D.B. Estimation of the probability of an event as a function of several independent variables. Biometrika 1967, 54, 167–179. [Google Scholar] [CrossRef]
- Schisterman, E.F.; Perkins, N. Confidence intervals for the Youden index and corresponding optimal cut-point. Commun. Stat. Simul. Comput. 2007, 36, 549–563. [Google Scholar] [CrossRef]
- Faraggi, D.; Reiser, B. Estimation of the area under the ROC curve. Stat. Med. 2002, 21, 3093–3106. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on some nonparametric estimates of a density function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Fluss, R.; Faraggi, D.; Reiser, B. Estimation of the Youden Index and its associated cutoff point. Biom. J. J. Math. Biol. 2005, 47, 458–472. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Routledge: London, UK, 2018. [Google Scholar]
- Percy, M.E.; Andrews, D.F.; Thompson, M.W. Duchenne muscular dystrophy carrier detection using logistic discrimination: Serum creatine kinase, hemopexin, pyruvate kinase, and lactate dehydrogenase in combination. Am. J. Med. Genet. A 1982, 13, 27–38. [Google Scholar] [CrossRef] [PubMed]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef]
- Rubio-Briones, J.; Borque-Fernando, A.; Esteban, L.M.; Mascarós, J.M.; Ramírez-Backhaus, M.; Casanova, J.; Collado, A.; Mir, C.; Gómez-Ferrer, A.; Wong, A.; et al. Validation of a 2-gene mRNA urine test for the detection of >=GG2 prostate cancer in an opportunistic screening population. Prostate 2020, 80, 500–507. [Google Scholar] [CrossRef]
- Morote, J.; Schwartzman, I.; Borque, A.; Esteban, L.M.; Celma, A.; Roche, S.; de Torres, I.M.; Mast, R.; Semidey, M.E.; Regis, L.; et al. Prediction of clinically significant prostate cancer after negative prostate biopsy: The current value of microscopic findings. In Urologic Oncology: Seminars and Original Investigations; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Pinsky, P.F.; Zhu, C.S. Building Multi-Marker Algorithms for Disease Prediction—The Role of Correlations among Markers. Biomark. Insights 2011, 6, 83–93. [Google Scholar] [CrossRef]
- Rota, M.; Antolini, L. Finding the optimal cut-point for Gaussian and Gamma distributed biomarkers. Comput. Stat. Data Anal. 2014, 69, 1–14. [Google Scholar] [CrossRef]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Aznar-Gimeno, R.; Esteban, L.M.; Sanz, G.; del-Hoyo-Alonso, R.; Savirón-Cornudella, R.; Antolini, L. Incorporating a New Summary Statistic into the Min–Max Approach: A Min–Max–Median, Min–Max–IQR Combination of Biomarkers for Maximising the Youden Index. Mathematics 2021, 9, 2497. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).