Effects of the Wiener Process on the Solutions of the Stochastic Fractional Zakharov System
Abstract
:1. Introduction
2. Preliminaries
- is a constant,
- 1.
- 2.
- is continuous function of t,
- 3.
- For is independent,
- 4.
- has a Gaussian distribution with mean 0 and variance .
3. Wave Equation for SFSZS
4. The Analytical Solutions of the SFSZS
4.1. Riccati–Bernoulli Sub-ODE Method
4.2. The Jacobi Elliptic Function Method
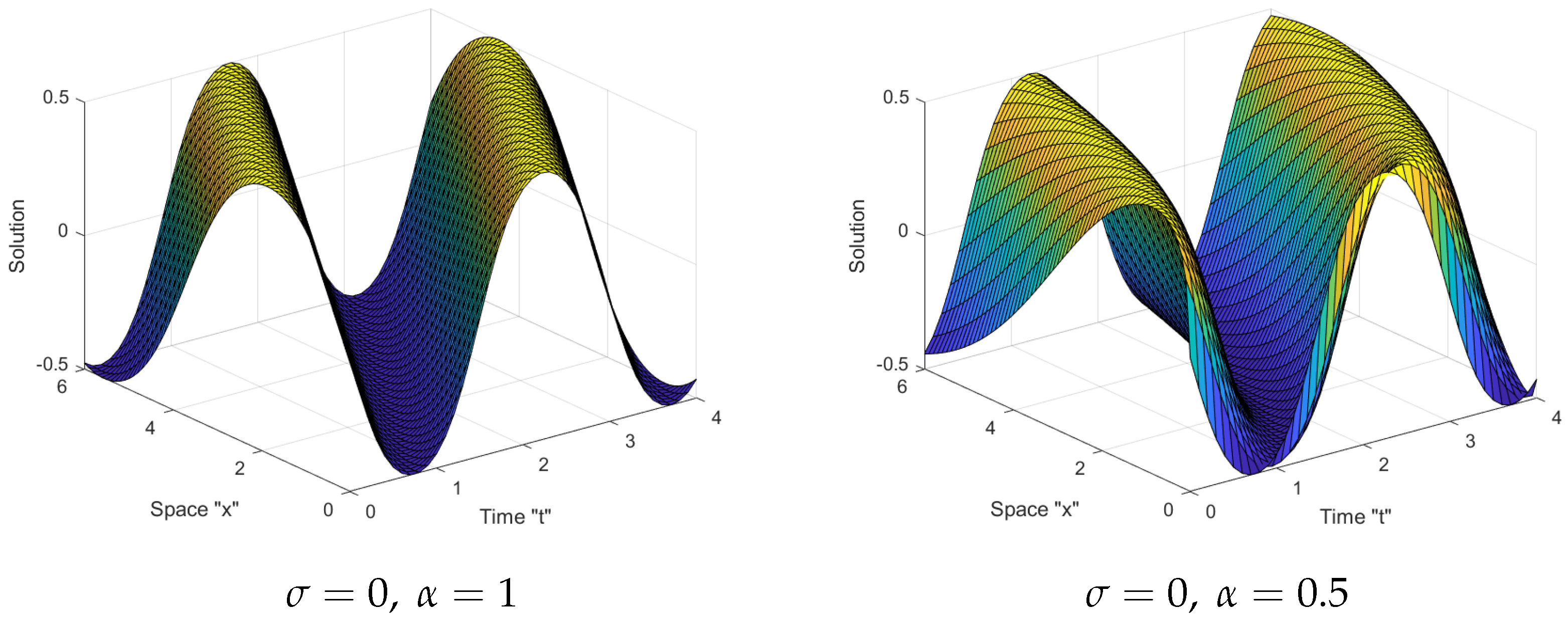
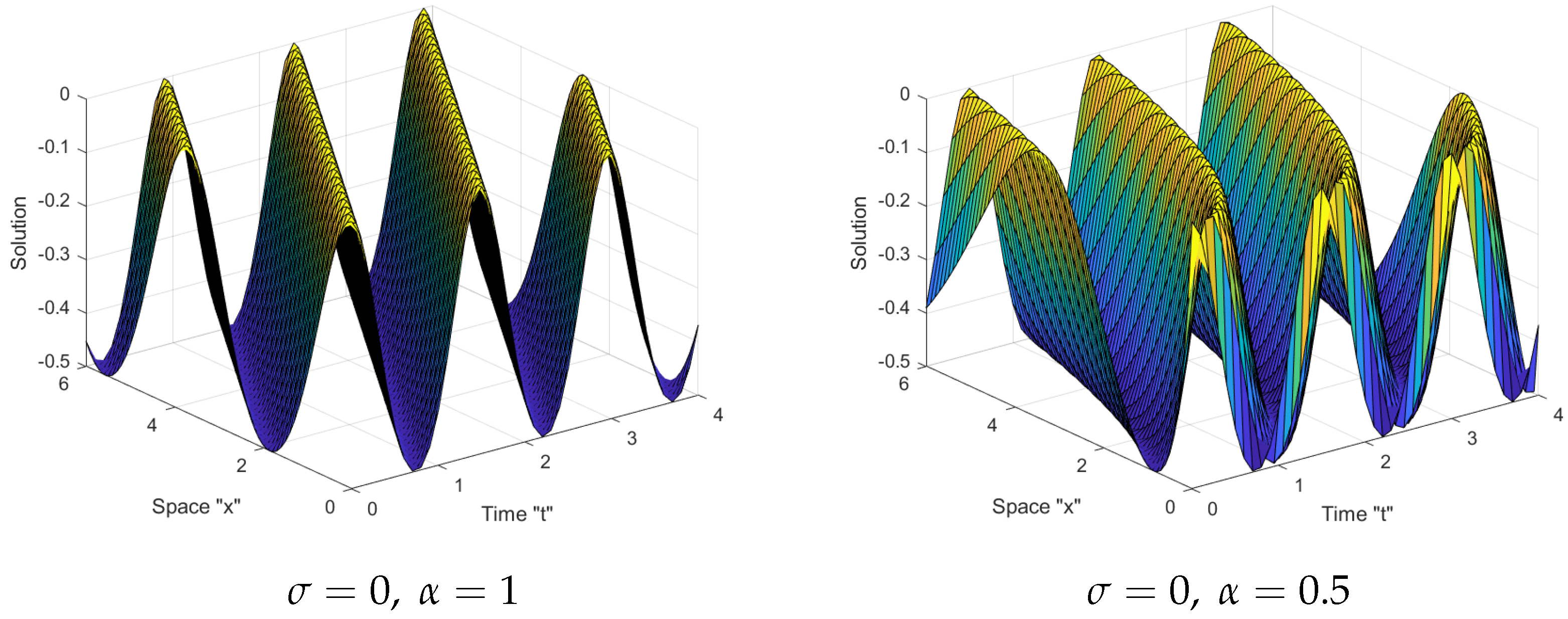
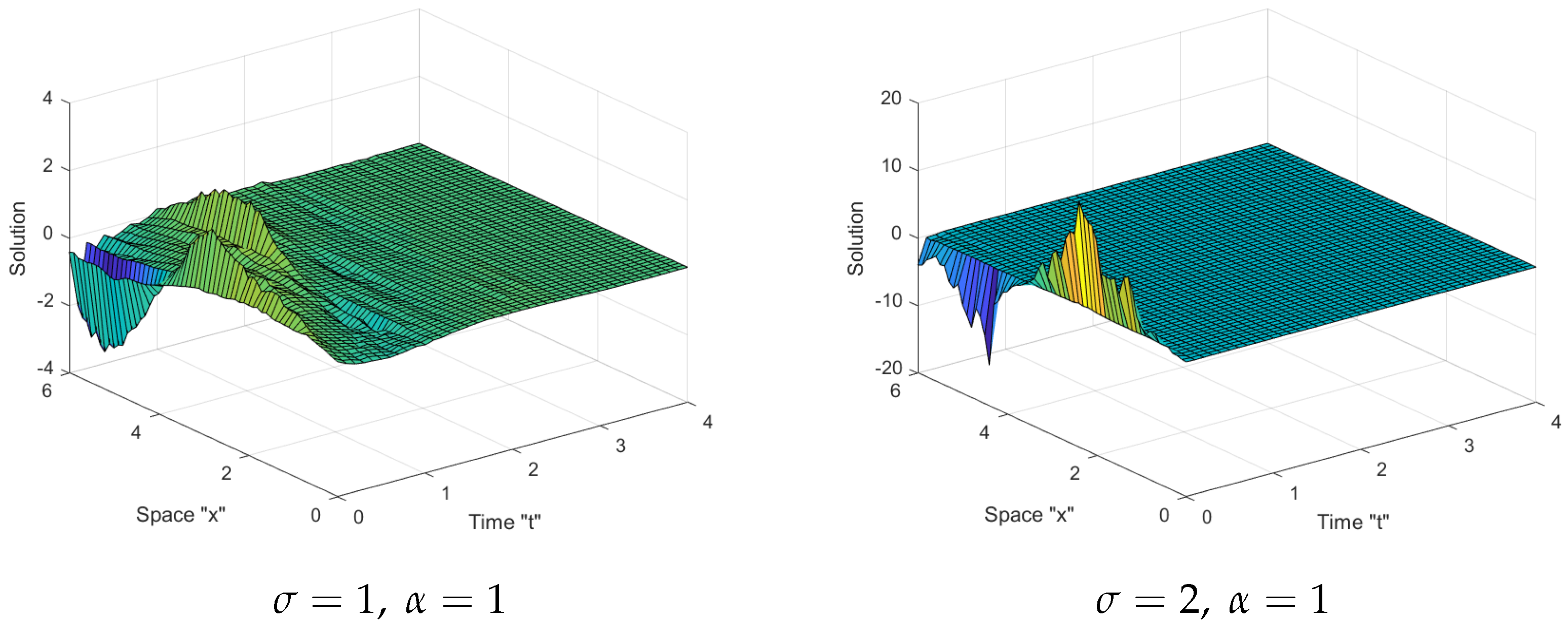
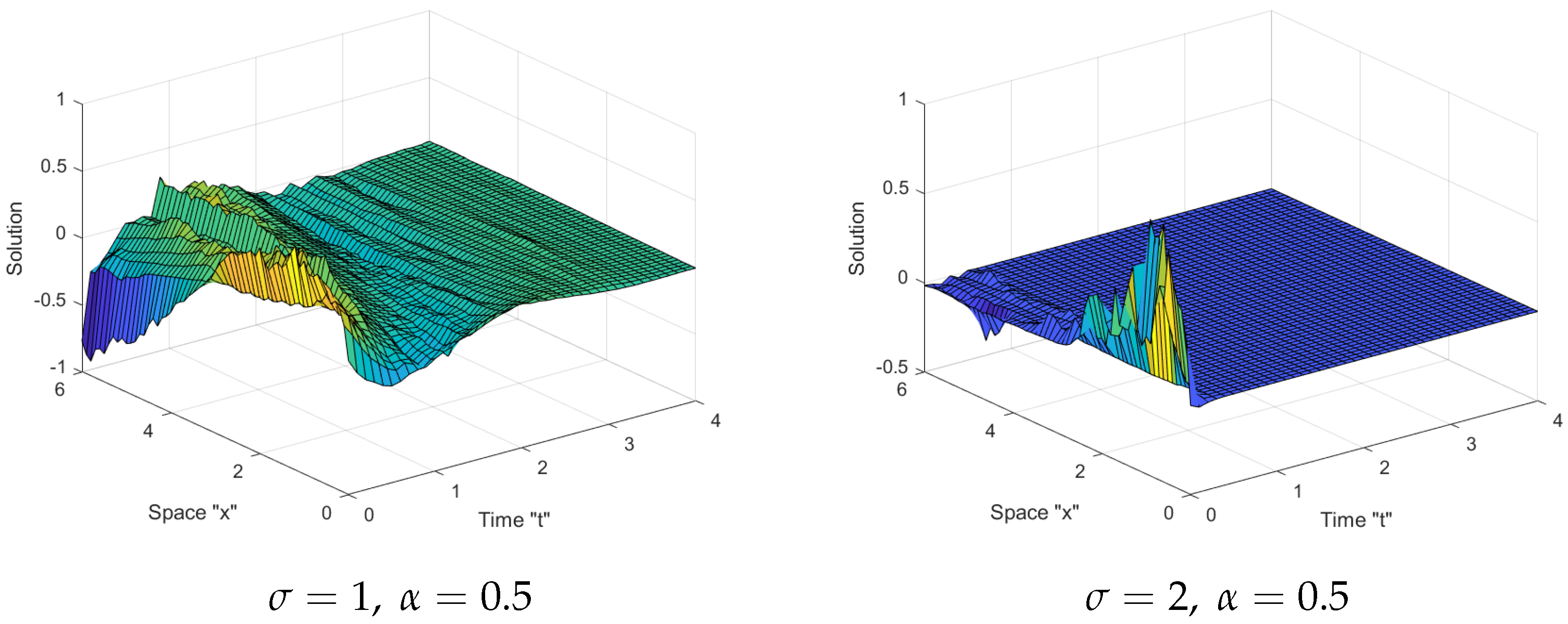
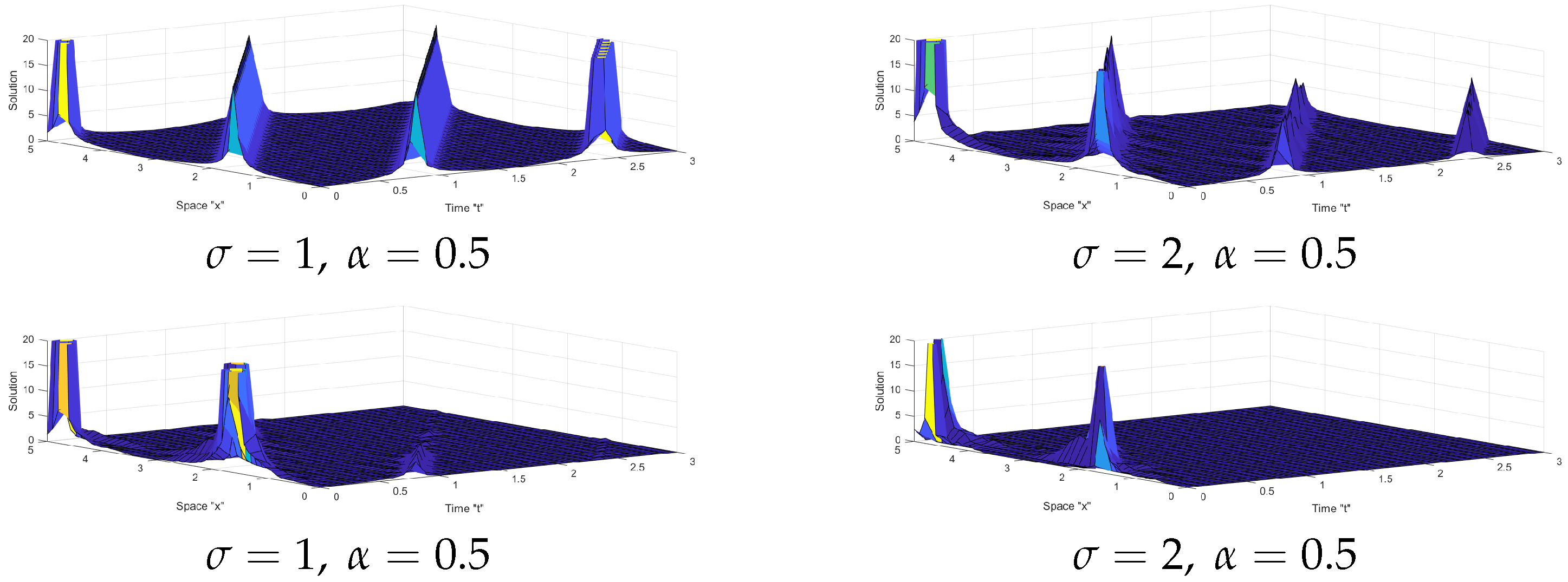
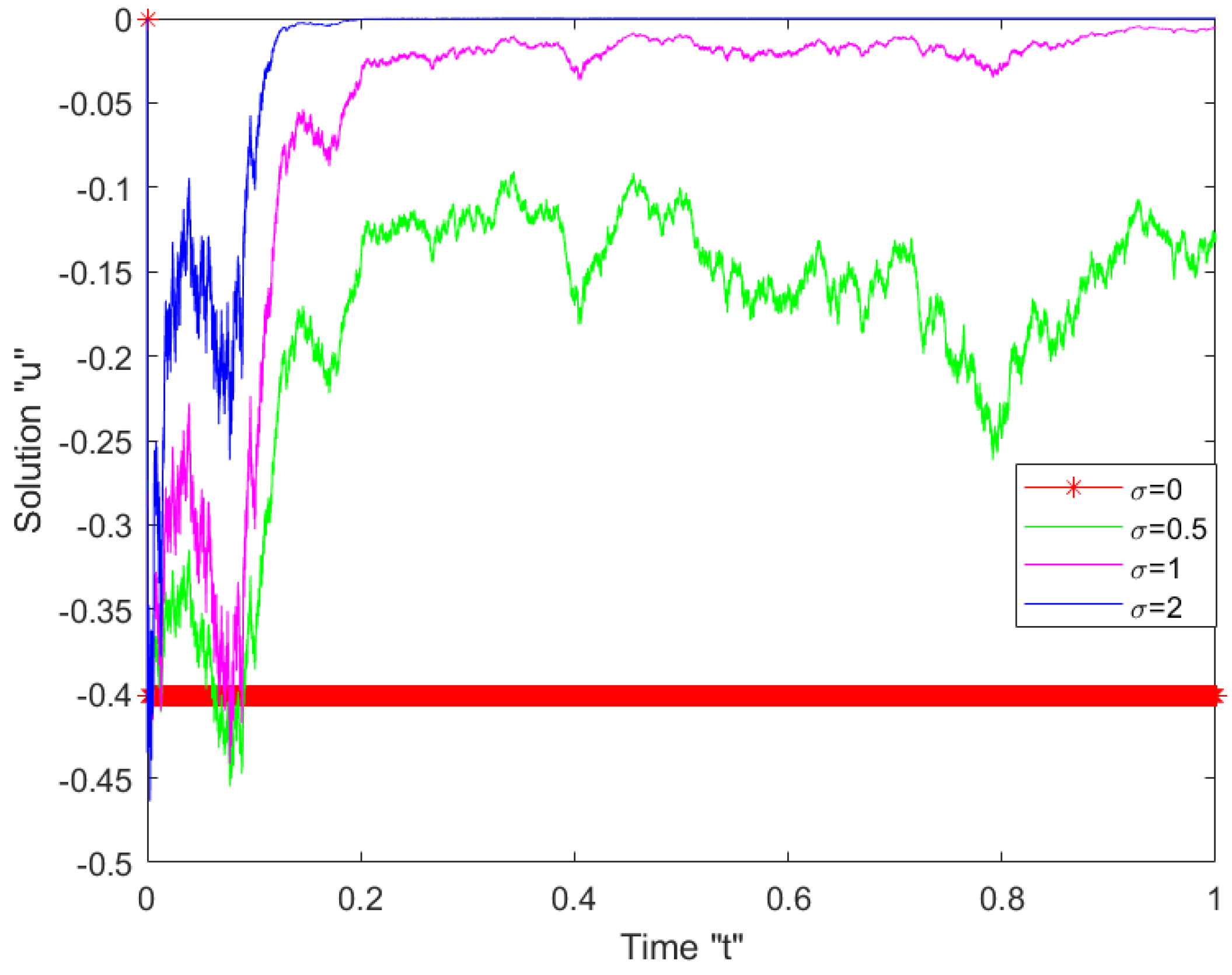
5. The Influence of Noise on SFSZS Solutions
- The surface expands as the fractional order increases;
- Multiplicative Wiener process stabilizes the solutions of SFSBE around zero.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zakharov, V.E. Collapse of Langmuir waves. Sov. J. Exper. Theor. Phys. 1972, 35, 908–914. [Google Scholar]
- Goubet, O.; Moise, I. Attractors for dissipative Zakharov equations. Nonlinear Anal. TMA 1998, 31, 823–847. [Google Scholar] [CrossRef]
- Guo, B. On the IBVP for some more extensive Zakharov equations. J. Math. 1987, 7, 269–275. [Google Scholar]
- Li, Y. On the initial boundary value problems for two dimensional systems of Zakharov equations and of complex-Schrödinger-real-Boussinesq equations. J. Partial Diff. Equ. 1992, 5, 81–93. [Google Scholar]
- Masselin, V. A result on the blow-up rate for the Zakharov equations in dimension 3. SIAM J. Math. Anal. 2001, 33, 440–447. [Google Scholar] [CrossRef]
- Guo, B.; Sheng, L. The global existence and uniqueness of classical solutions of periodic initial boundary problems of Zakharov equations. Acta Math. Appl. Sin. 1982, 5, 310–324. [Google Scholar]
- Song, M.; Liu, Z. Traveling wave solutions for the generalized Zakharov equations. Math. Probl. Eng. 2012, 2012, 747295. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z. Extended F-expansion method and periodic wave solutions for the generalized Zakharov equations. Phys. Lett. A 2005, 343, 48–54. [Google Scholar] [CrossRef]
- Javidi, M.; Golbabai, A. Construction of a solitary wave solution for the generalized Zakharov equation by a variational iteration method. Comput. Math. Appl. 2007, 54, 1003–1009. [Google Scholar] [CrossRef] [Green Version]
- Taghizadeh, N.; Mirzaadsh, M.; Farahrooz, F. Exact solutions of the generalized-Zakharov (GZ) equation by the infinite series method. Appl. Appl. Math. 2010, 5, 621–628. [Google Scholar]
- Hong, B.; Lu, D.; Sun, F. The extended Jacobi Elliptic Functions expansion method and new exact solutions for the Zakharov equations. World J. Model. Simul. 2009, 5, 216–224. [Google Scholar]
- Yuste, S.B.; Acedo, L.; Lindenberg, K. Reaction front in an A + B → C reaction–subdiffusion process. Phys. Rev. E 2004, 69, 036126. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, W.W.; Iqbal, N. Impact of the same degenerate additive noise on a coupled system of fractional space diffusion equations. Fractals 2022, 30, 2240033. [Google Scholar] [CrossRef]
- Iqbal, N.; Yasmin, H.; Ali, A.; Bariq, A.; Al-Sawalha, M.M.; Mohammed, W.W. Numerical Methods for Fractional-Order Fornberg-Whitham Equations in the Sense of Atangana-Baleanu Derivative. J. Funct. Spaces 2021, 2021, 2197247. [Google Scholar] [CrossRef]
- Mohammed, W.W. Approximate solutions for stochastic time-fractional reaction–diffusion equations with multiplicative noise. Math. Methods Appl. Sci. 2021, 44, 2140–2157. [Google Scholar] [CrossRef]
- Iqbal, N.; Wu, R.; Mohammed, W.W. Pattern formation induced by fractional cross-diffusion in a 3-species food chain model with harvesting. Math. Comput. Simul. 2021, 188, 102–119. [Google Scholar] [CrossRef]
- Barkai, E.; Metzler, R.; Klafter, J. From continuous time random walks to the fractional Fokker–Planck equation. Phys. Rev. 2000, 61, 132–138. [Google Scholar] [CrossRef]
- Arnold, L. Random Dynamical Systems; Springer: Berlin, Germany, 1998. [Google Scholar]
- Weinan, E.; Li, X.; Vanden-Eijnden, E. Some Recent Progress in Multiscale Modeling, Multiscale Modeling and Simulation; Lect. Notes in Computer Science Engineering; Springer: Berlin, Germany, 2004; Volume 39, pp. 3–21. [Google Scholar]
- Mohammed, W.W.; Blömker, D. Fast diffusion limit for reaction-diffusion systems with stochastic Neumann boundary conditions. SIAM J. Math. Anal. 2016, 48, 3547–3578. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, W.W. Modulation Equation for the Stochastic Swift–Hohenberg Equation with Cubic and Quintic Nonlinearities on the Real Line. Mathematics 2020, 6, 1217. [Google Scholar] [CrossRef] [Green Version]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Guo, B.; Lv, Y.; Yang, X. Dynamics of Stochastic Zakharov Equations. J. Math. Phys. 2009, 50, 052703. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, B.; Li, D. Global random attractors for the stochastic dissipative Zakharov equations. Acta Math. Appl. Sin. 2014, 30, 289–304. [Google Scholar] [CrossRef]
- Guo, Y.F.G.B.; Li, D. Asymptotic behavior of stochastic dissipative quantum Zakharov equations. Stoch. Dyn. 2013, 13, 1250016. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: New York, NY, USA, 1995. [Google Scholar]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Diff. Equ. 2015, 1, 117–133. [Google Scholar] [CrossRef] [Green Version]
- Fan, E.; Zhang, J. Applications of the Jacobi elliptic function method to special-type nonlinear equations. Phys. Lett. A 2002, 305, 383–392. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Askar, F.M.; Mohammed, W.W.; Alshammari, M.; El-Morshedy, M. Effects of the Wiener Process on the Solutions of the Stochastic Fractional Zakharov System. Mathematics 2022, 10, 1194. https://doi.org/10.3390/math10071194
Al-Askar FM, Mohammed WW, Alshammari M, El-Morshedy M. Effects of the Wiener Process on the Solutions of the Stochastic Fractional Zakharov System. Mathematics. 2022; 10(7):1194. https://doi.org/10.3390/math10071194
Chicago/Turabian StyleAl-Askar, Farah M., Wael W. Mohammed, Mohammad Alshammari, and M. El-Morshedy. 2022. "Effects of the Wiener Process on the Solutions of the Stochastic Fractional Zakharov System" Mathematics 10, no. 7: 1194. https://doi.org/10.3390/math10071194
APA StyleAl-Askar, F. M., Mohammed, W. W., Alshammari, M., & El-Morshedy, M. (2022). Effects of the Wiener Process on the Solutions of the Stochastic Fractional Zakharov System. Mathematics, 10(7), 1194. https://doi.org/10.3390/math10071194






