Proving Feasibility of a Docking Mission: A Contractor Programming Approach
Abstract
1. Introduction
1.1. Context
1.2. State of the Art
1.3. Contribution
2. Formalization
2.1. Formalizing Robots as Dynamical Systems
- T is the system’s time set in which the time parameter t evolves;
- is the system’s state space containing the system’s state ;
- is the identity function, ;
- for any and for any .
2.2. Accounting for System’s Uncertainties
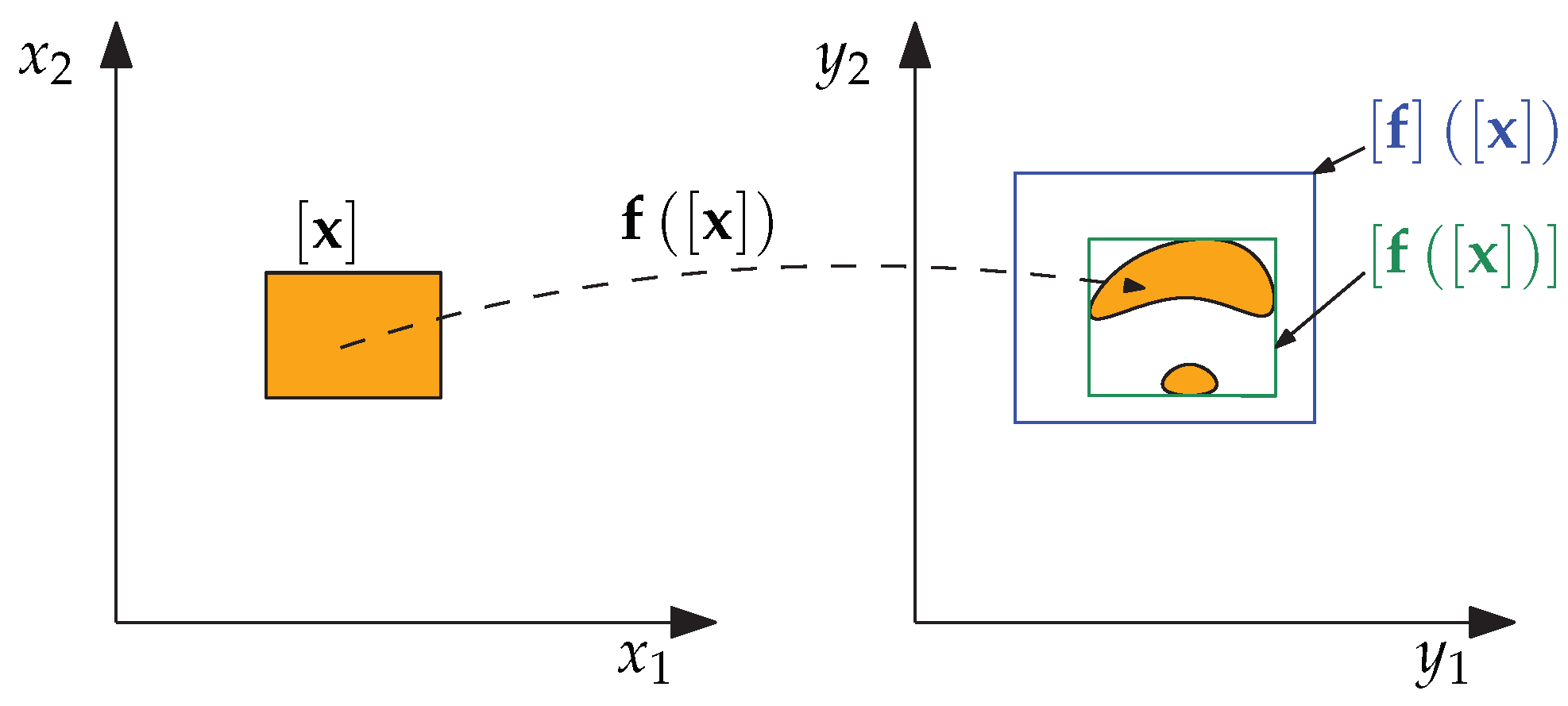
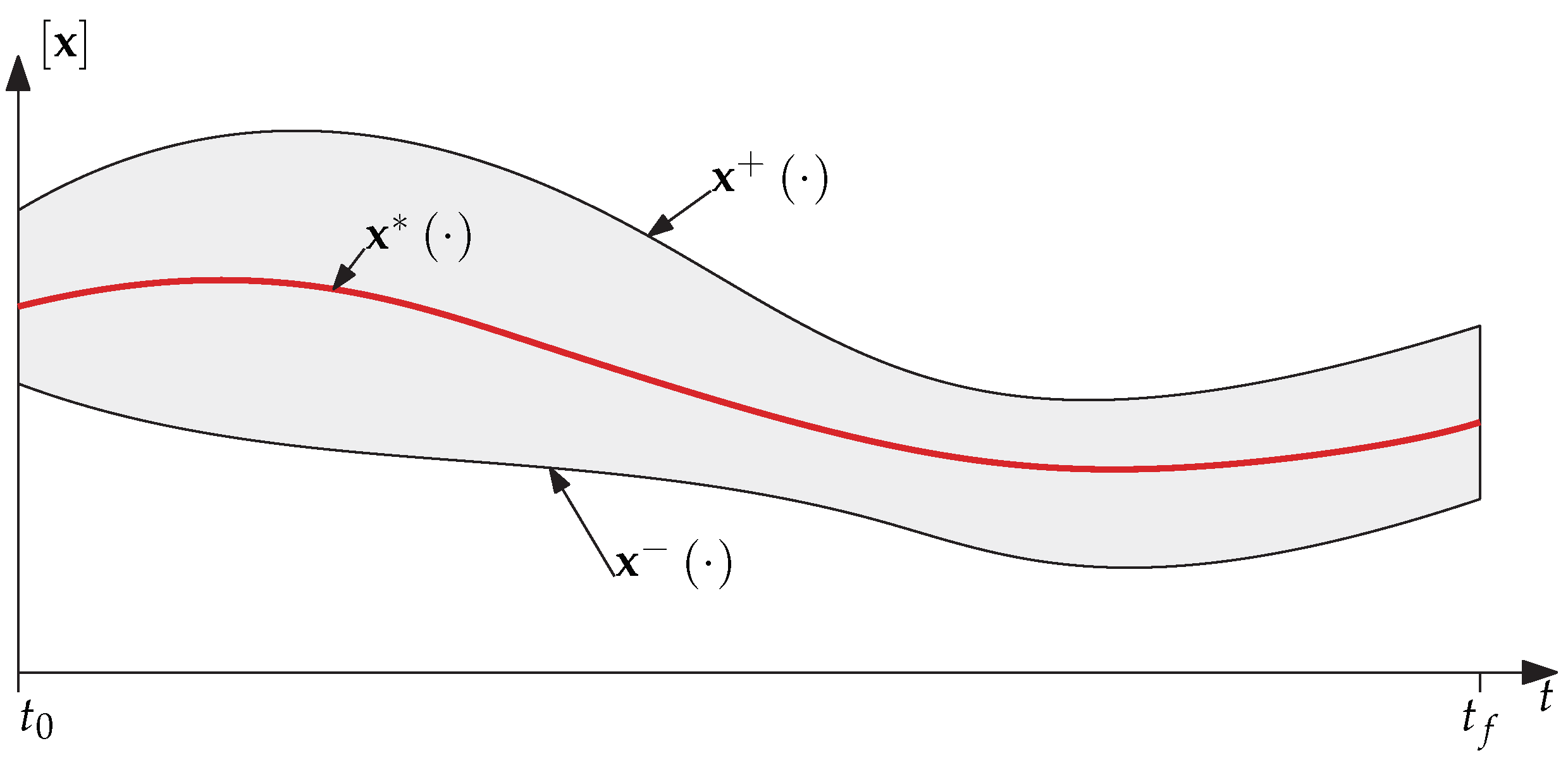
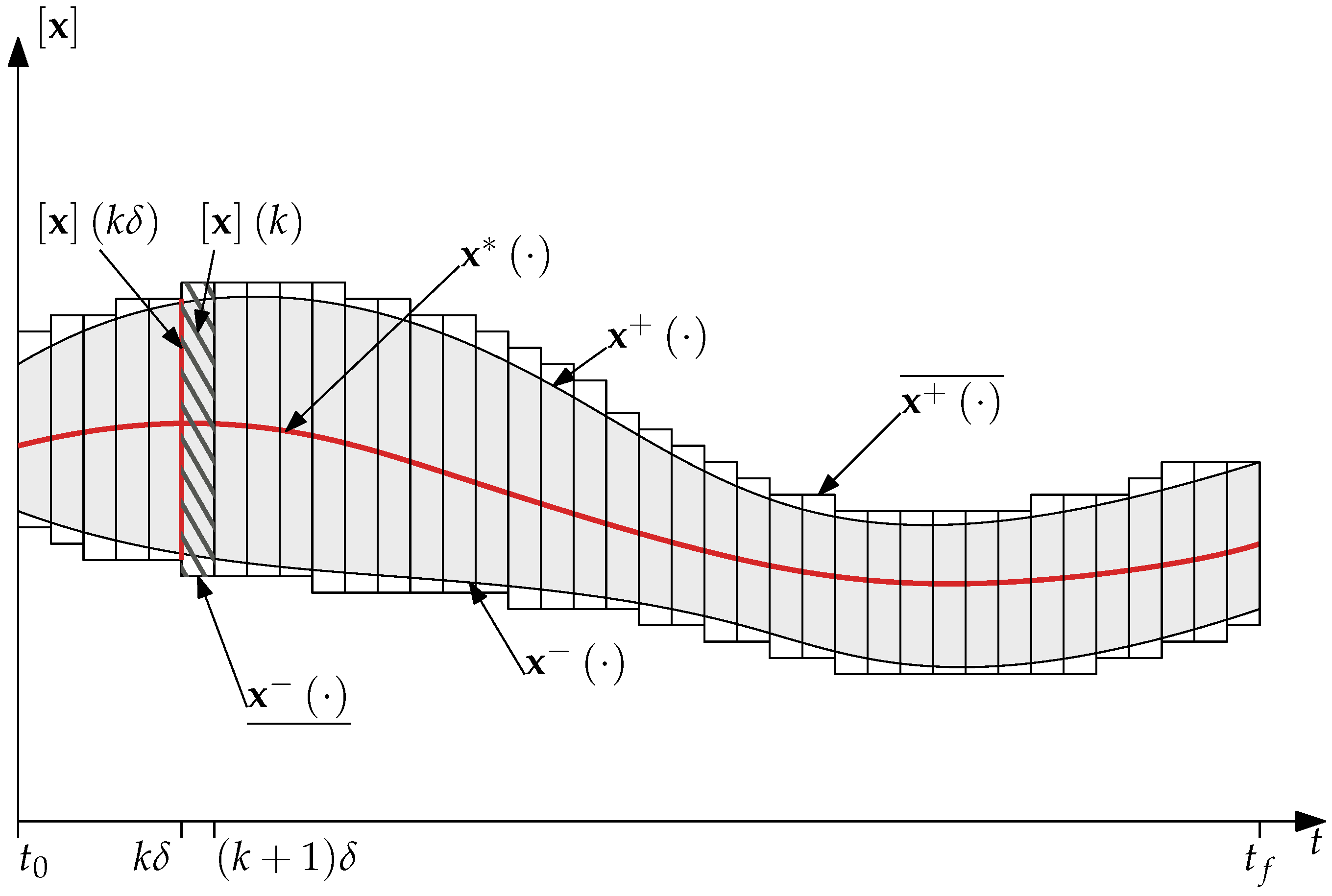
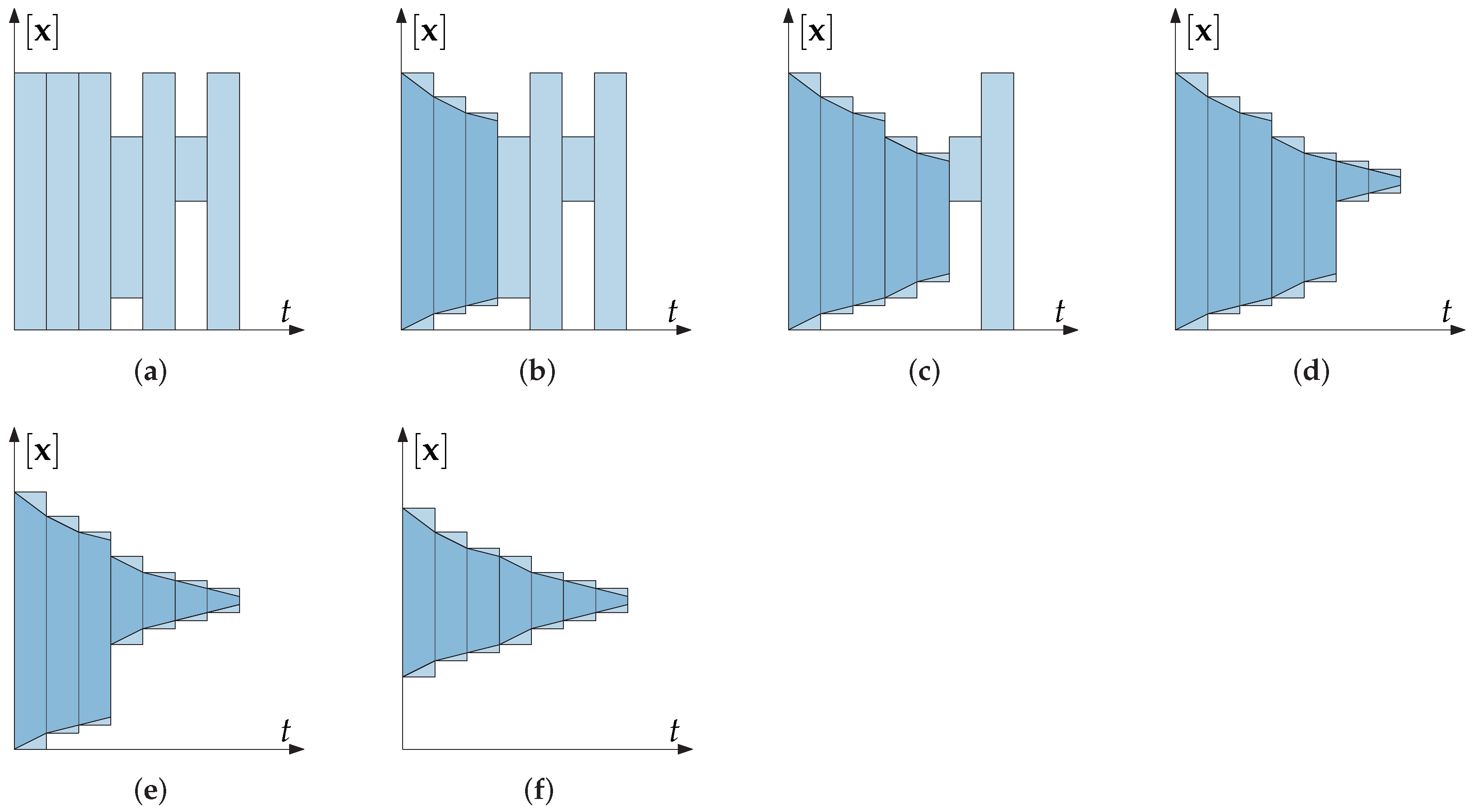
2.3. Tube Arithmetic
2.4. Constraint Programming
2.5. Tube Implementation and the Codac Library
3. Guaranteed Integration: A Constraint Programming Approach
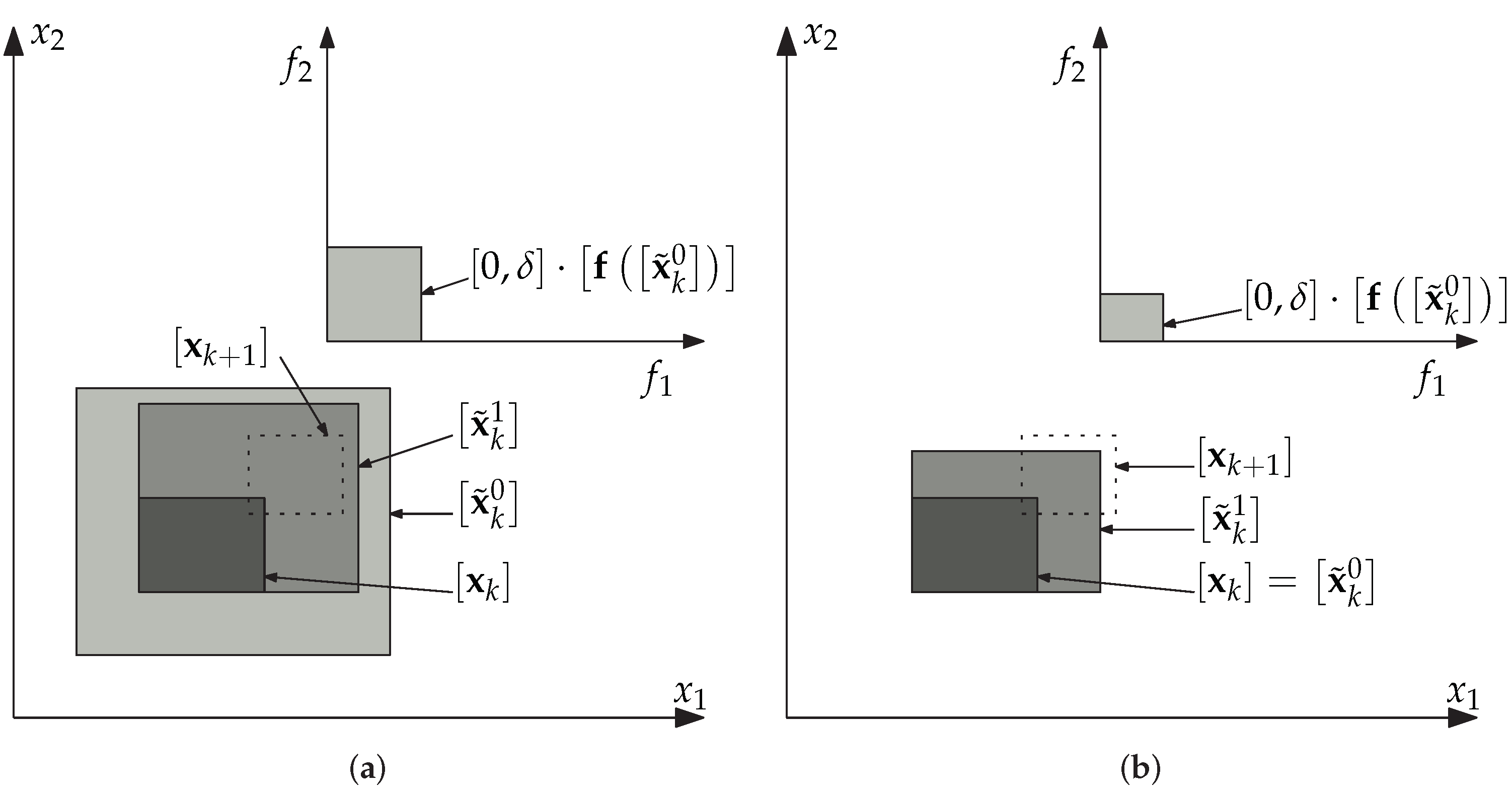
3.1. Lohner Algorithm
- Find a global enclosure for the system’s trajectories over the time interval ;
- Using , find an enclosure for the state at time , i.e., .
- Given an initial state enclosure , Algorithm 2 can compute a sequence of boxes that contains the system’s state at time ;
- For all , the enclosure is actually represented by a tilted box in Algorithm 2: , where both and represent the system’s state enclosure, respectively, in the canonical basis and in the one defined by the orthogonal matrix ;
- Algorithm 2 computes at each time step k the global enclosure , such that for all and for all , .
| Algorithm 1GlobalEnclosure (in: , , , , out: , inout: ) | |
| |
| |
| Increase the number of iterations | |
| |
| Reset the iteration counter | |
| Reduce the time step by a factor |
| Reset the a priori estimates | |
| |
| |
| Inflate the a priori estimate | |
| Compute the new a priori estimate |
| |
| |
| Algorithm 2SimpleLohner (in: , , N, out: ) | |
| initialisation | |
| |
| |
| |
| |
| |
| orthogonal part of the QR factorisation | |
| |
| |
| |
| |
3.2. Lohner Contractor
- can be seen as the input gate of slice 0 and the system’s initial condition, i.e., forming an IVP;
- can be interpreted as the kth slice’s input gate, the th slice’s output gate, and the system’s state enclosure at time ;
- is the kth slice of , thus containing all the system trajectories over the time interval . can therefore be seen as a global enclosure for the system over .
- Assume that we initialize the algorithm with the initial box ;
- Then, all the system trajectories during the time interval must be contained both in the slice and in the global enclosure ;
- Consider the kth slice: at time , the system’s state is enclosed by , and at time , it is enclosed both in the slice’s output gate and in the box computed by Algorithm 2;
- Finally, we have .
| Algorithm 3 (inout: ) | |
| |
| |
| |
| |
| |
| |
| see Algorithm 2 |
| |
| |
| orthogonal part of the QR factorization | |
| |
| |
| |
| contracts |
| adjusts the center of the tilted box | |
| contracts uncertainties in tilted frame |
| contracts the slice and the output gate | |
| |
4. Applications
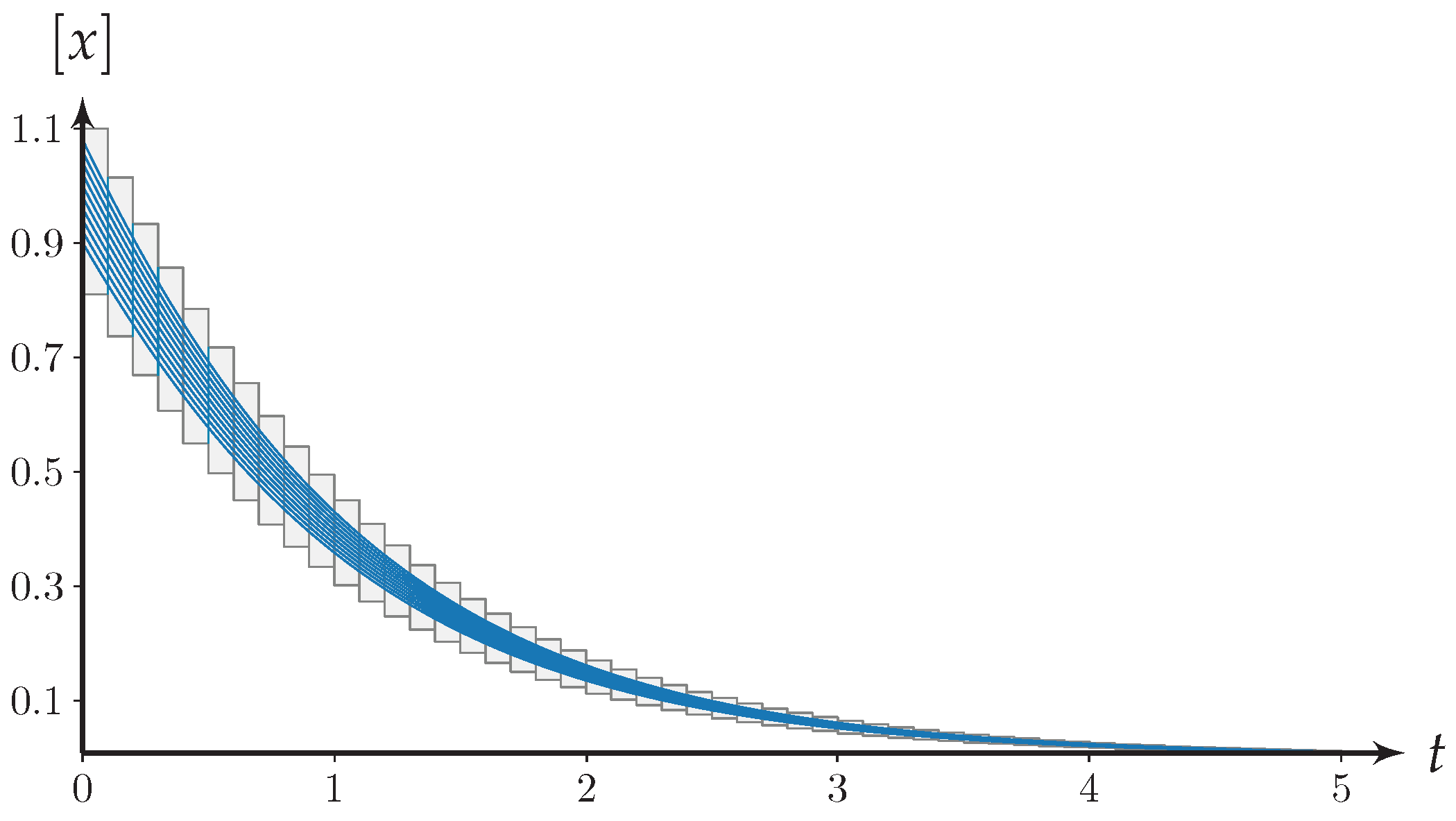
4.1. Simple Illustrating Example
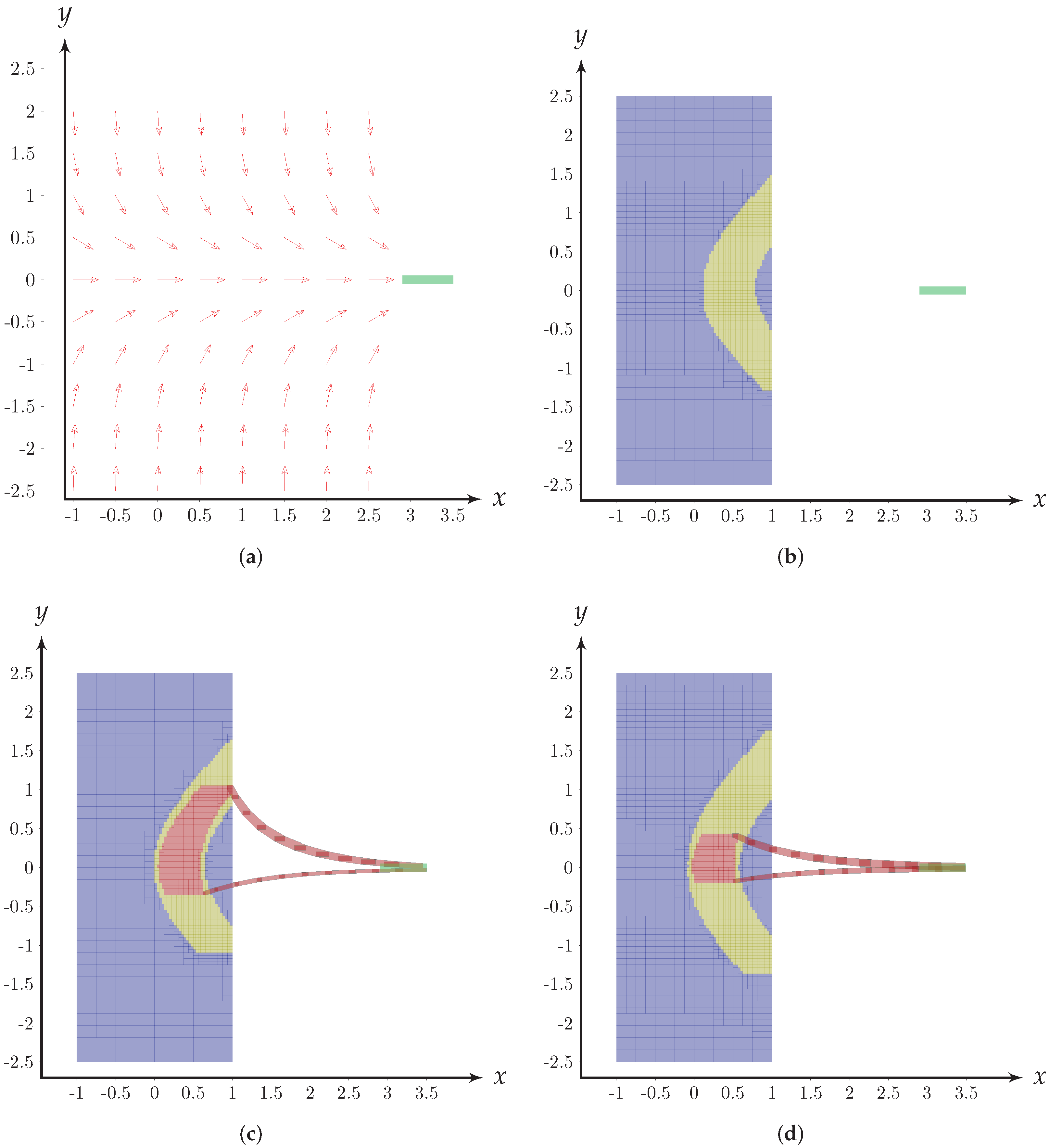
4.2. Underwater Docking Mission Feasibility
4.2.1. Modeling the Robot as a Dynamical System
4.2.2. Computing
| Algorithm 4(in: , , ) | |
| |
| |
| |
| |
| |
| pop a box from the temporary list |
| initialize the tubewith | |
| contract the initial tube with |
| |
| |
| |
| |
| |
| bisectto obtain a thinner trajectory |
| |
| |
| |
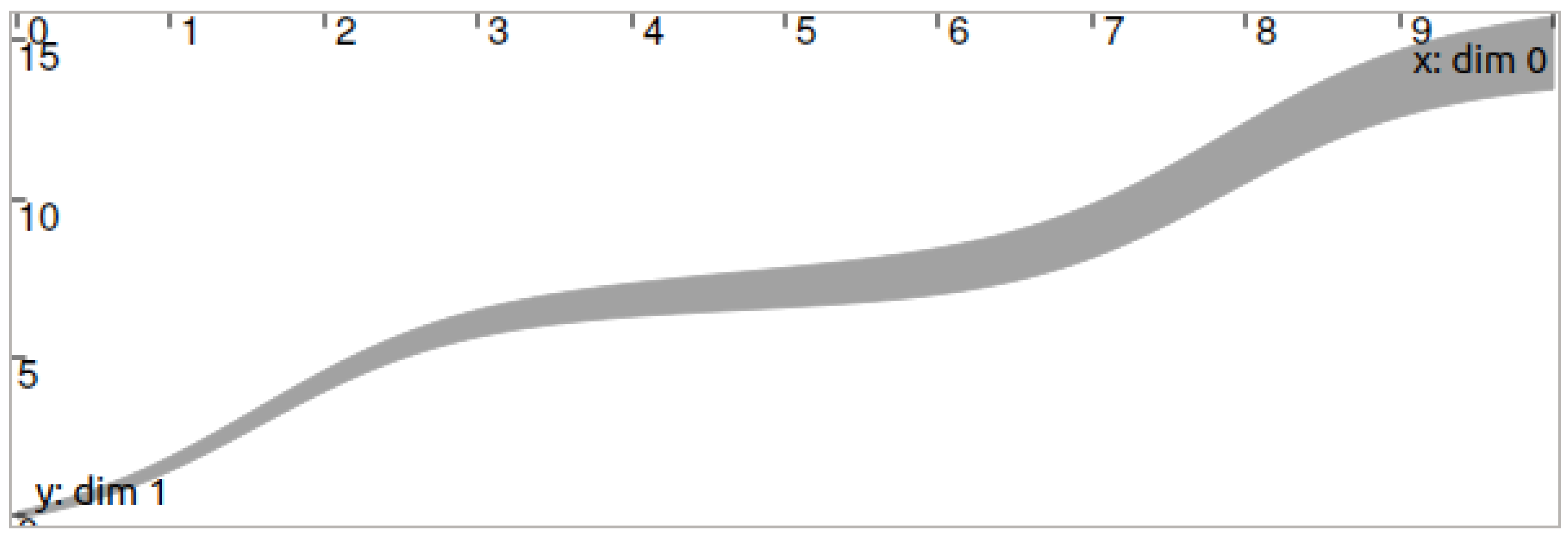
4.2.3. Numerical Results
4.2.4. Discussion
5. Conclusions and Outlook on Future Work
5.1. Summary
5.2. Future Recommendations
- The first contractor that could be of use in robotics is the one enforcing a differential constraint of the form , where is not computed using the robot’s state but another tube of trajectories in the command space, possibly without analytical expression. This would come down to dealing with non-autonomous and time-varying differential equations , which can be useful, for example, when the command is simply measured or when the system is operated in an open-loop mode and the mission is to compute the actual robot’s trajectory using this command and the available sensor data;
- A second contractor could extend Poincaré maps to the world of contractor programming. A Poincaré map returns the impact point, where the trajectory of a dynamical system transversely crosses an arbitrary surface (we refer the reader to [24,46,47] for more details). This contractor could help solve the docking problem presented in this article, as the trajectories would not be limited by the time constraint modeled by T anymore: any trajectory “impacting” the entrance of the docking station could be considered valid. The method for stability analysis, extended to Poincaré maps, can also be used to analyze more general dynamic systems such as systems with hybrid dynamics in which the state transitions result from event-triggered control approaches.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Abbreviations
| PID | Proportional, Integral, Derivative |
| IVP | Initial Value Problem |
| ROV | Remotely Operated Vehicle |
| CAPD | Computer-Assisted Proofs in Dynamics |
References
- Trslic, P.; Rossi, M.; Robinson, L.; O’Donnel, C.W.; Weir, A.; Coleman, J.; Riordan, J.; Omerdic, E.; Dooly, G.; Toal, D. Vision based autonomous docking for work class ROVs. Ocean Eng. 2020, 196, 106840. [Google Scholar] [CrossRef]
- Schjølberg, I.; Utne, I.B. Towards autonomy in ROV operations. IFAC-PapersOnLine 2015, 48, 183–188. [Google Scholar] [CrossRef]
- Vallicrosa, G.; Bosch, J.; Palomeras, N.; Ridao, P.; Carreras, M.; Gracias, N. Autonomous homing and docking for AUVs using range-only localization and light beacons. IFAC-Pap. 2016, 49, 54–60. [Google Scholar] [CrossRef]
- Colaço, J.L.; Pagano, B.; Pouzet, M. Scade 6: A formal language for embedded critical software development. In Proceedings of the 2017 International Symposium on Theoretical Aspects of Software Engineering (TASE), Sophia Antipolis, France, 13–15 September 2017; pp. 1–11. [Google Scholar] [CrossRef]
- Asarin, E.; Maler, O.; Pnueli, A. Reachability analysis of dynamical systems having piecewise-constant derivatives. Theor. Comput. Sci. 1995, 138, 35–65. [Google Scholar] [CrossRef][Green Version]
- Bourke, T.; Pouzet, M. Zélus: A synchronous language with ODEs. In Proceedings of the 16th International Conference on Hybrid Systems: Computation and Control, Philadelphia, PA, USA, 8–11 April 2013; pp. 113–118. [Google Scholar] [CrossRef]
- Taha, W.; Duracz, A.; Zeng, Y.; Atkinson, K.; Bartha, F.A.; Brauner, P.; Duracz, J.; Xu, F.; Cartwright, R.; Konečný, M.; et al. Acumen: An open-source testbed for cyber-physical systems research. In International Internet of Things Summit; Springer: Berlin/Heidelberg, Germany, 2015; pp. 118–130. [Google Scholar] [CrossRef]
- Bourgois, A.; Jaulin, L. Interval centred form for proving stability of non-linear discrete-time systems. In Proceedings of the SNR 2020: 6th International Workshop on Symbolic-Numeric Methods for Reasoning about CPS and IoT, Online, 31 August 2020. [Google Scholar] [CrossRef]
- Bourgois, A.; Jaulin, L. Proving the stability of a limit cycle of a hybrid system. LITES-Leibniz Trans. Embed. Syst. 2020. Submitted. [Google Scholar]
- Alur, R. Formal verification of hybrid systems. In Proceedings of the Ninth ACM International Conference on Embedded Software, Taipei, Taiwan, 9–14 October 2011; pp. 273–278. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar] [CrossRef]
- Asarin, E.; Dang, T.; Girard, A. Hybridization methods for the analysis of nonlinear systems. Acta Inform. 2007, 43, 451–476. [Google Scholar] [CrossRef][Green Version]
- Girard, A. Reachability of Uncertain Linear Systems Using Zonotopes. In Hybrid Systems: Computation and Control; Springer: Berlin/Heidelberg, Germany, 2005; pp. 291–305. [Google Scholar] [CrossRef]
- Goubault, E.; Mullier, O.; Putot, S.; Kieffer, M. Inner approximated reachability analysis. In Proceedings of the 17th International Conference on Hybrid Systems: Computation and Control, Berlin, Germany, 15–17 April 2014; pp. 163–172. [Google Scholar] [CrossRef]
- Le Mézo, T.; Jaulin, L.; Zerr, B. Bracketing the solutions of an ordinary differential equation with uncertain initial conditions. Appl. Math. Comput. 2018, 318, 70–79. [Google Scholar] [CrossRef]
- Ramdani, N.; Nedialkov, N.S. Computing reachable sets for uncertain nonlinear hybrid systems using interval constraint-propagation techniques. Nonlinear Anal. Hybrid Syst. 2011, 5, 149–162. [Google Scholar] [CrossRef]
- Rauh, A.; Kersten, J.; Aschemann, H. Techniques for Verified Reachability Analysis of Quasi-Linear Continuous-Time Systems. In Proceedings of the 2019 24th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 26–29 August 2019; pp. 18–23. [Google Scholar] [CrossRef]
- Rohou, S.; Jaulin, L.; Mihaylova, L.; Le Bars, F.; Veres, S.M. Guaranteed computation of robot trajectories. Robot. Auton. Syst. 2017, 93, 76–84. [Google Scholar] [CrossRef]
- dit Sandretto, J.A. Confidence-based Contractor, Propagation and Potential Clouds for Differential Equations. Acta Cybern. 2021, 25, 49–68. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Son: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Giunti, M. Computation, Dynamics, and Cognition; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Hirsch, M.W.; Smale, S.; Devaney, R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar] [CrossRef]
- Corke, P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB® Second, Completely Revised; Springer: Berlin/Heidelberg, Germany, 2017; Volume 118. [Google Scholar] [CrossRef]
- Moore, R.E. Interval Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1966; Volume 4. [Google Scholar]
- Moore, R.E.; Kearfott, R.B.; Cloud, M.J. Introduction to Interval Analysis; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar] [CrossRef]
- Jaulin, L.; Kieffer, M.; Didrit, O.; Walter, E. Applied Interval Analysis, with Examples in Parameter and State Estimation, Robust Control and Robotics; Springer: London, UK, 2001. [Google Scholar] [CrossRef]
- Tucker, W. Validated Numerics: A Short Introduction to Rigorous Computations; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Mayer, G. Interval Analysis: And Automatic Result Verification; De Gruyter: Berlin, Germany, 2017. [Google Scholar] [CrossRef]
- Kurzhanski, A.B.; Filippova, T.F. On the theory of trajectory tubes—A mathematical formalism for uncertain dynamics, viability and control. In Advances in Nonlinear Dynamics and Control: A Report from Russia; Springer: Berlin/Heidelberg, Germany, 1993; pp. 122–188. [Google Scholar] [CrossRef]
- Rohou, S.; Jaulin, L.; Mihaylova, L.; Le Bars, F.; Veres, S.M. Reliable Robot Localization: A Constraint-Programming Approach over Dynamical Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Bethencourt, A.; Jaulin, L. Solving non-linear constraint satisfaction problems involving time-dependant functions. Math. Comput. Sci. 2014, 8, 503–523. [Google Scholar] [CrossRef]
- Rohou, S.; Desrochers, B.; Jaulin, L.; Chabert, G.; Damers, J.; Voges, R.; Le Bars, F.; Bourgois, A.; Le Mezo, T.; Bouvier, C.; et al. The Codac (Catalog of Domains and Contractors) Library—Constraint-Programming for Robotics. 2017. Available online: https://codac.io/ (accessed on 29 January 2022).
- Rohou, S.; Jaulin, L.; Mihaylova, L.; Le Bars, F.; Veres, S.M. Reliable non-linear state estimation involving time uncertainties. Automatica 2018, 93, 379–388. [Google Scholar] [CrossRef]
- Lohner, R.J. Enclosing the Solutions of Ordinary Initial and Boundary Value Problems; Wiley-Teubner: Stuttgart, Germany, 1987; pp. 225–286. [Google Scholar]
- Joudrier, H. Guaranteed Deterministic Global Optimization Using Constraint Programming through Algebraic, Functional and Piecewise Differential Constraints. Ph.D. Thesis, Université Grenoble Alpes, Saint-Martin-d’Heres, France, 2018. [Google Scholar]
- Bourgois, A. Safe & Collaborative Autonomous Underwater Docking. Ph.D. Thesis, ENSTA Bretagne, Brest, France, 2021. Available online: https://hal.archives-ouvertes.fr/tel-03151588v1 (accessed on 29 January 2022).
- Moore, R.E. Methods and Applications of Interval Analysis; SIAM: Philadelphia, PA, USA, 1979. [Google Scholar] [CrossRef]
- Nedialkov, N.S.; Jackson, K.R. A new perspective on the wrapping effect in interval methods for initial value problems for ordinary differential equations. In Perspectives on Enclosure Methods; Springer: Berlin/Heidelberg, Germany, 2001; pp. 219–263. [Google Scholar] [CrossRef]
- Freihold, M.; Hofer, E.P. Derivation of Physically Motivated Constraints for Efficient Interval Simulations Applied to the Analysis of Uncertain Dynamical Systems. Int. J. Appl. Math. Comput. Sci. 2009, 19, 485–499. [Google Scholar] [CrossRef]
- Rauh, A.; Krasnochtanova, I.; Aschemann, H. Quantification of overestimation in interval simulations of uncertain systems. In Proceedings of the 2011 16th International Conference on Methods & Models in Automation & Robotics, Miedzyzdroje, Poland, 22–25 August 2011. [Google Scholar] [CrossRef]
- Corliss, G.F.; Rihm, R. Validating an a priori enclosure using high-order Taylor series. Math. Res. 1996, 90, 228–238. [Google Scholar]
- Nedialkov, N.S.; Jackson, K.R.; Pryce, J.D. An effective high-order interval method for validating existence and uniqueness of the solution of an IVP for an ODE. Reliab. Comput. 2001, 7, 449–465. [Google Scholar] [CrossRef]
- Kapela, T.; Mrozek, M.; Wilczak, D.; Zgliczyński, P. CAPD::DynSys: A flexible C++ toolbox for rigorous numerical analysis of dynamical systems. Commun. Nonlinear Sci. Numer. Simul. 2020, 101, 105578. [Google Scholar] [CrossRef]
- Perko, L. Differential Equations and Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 7. [Google Scholar] [CrossRef]
- Tucker, W. Computing accurate Poincaré maps. Phys. D Nonlinear Phenom. 2002, 171, 127–137. [Google Scholar] [CrossRef]
- Kletting, M.; Antritter, F. Robustness Comparison of Tracking Controllers Using Verified Integration. In Modeling, Design, and Simulation of Systems with Uncertainties; Springer: Berlin/Heidelberg, Germany, 2011; pp. 95–115. [Google Scholar] [CrossRef]
- Antritter, F.; Kletting, M.; Hofer, E.P. Robust analysis of flatness based control using interval methods. Int. J. Control 2007, 80, 816–823. [Google Scholar] [CrossRef]

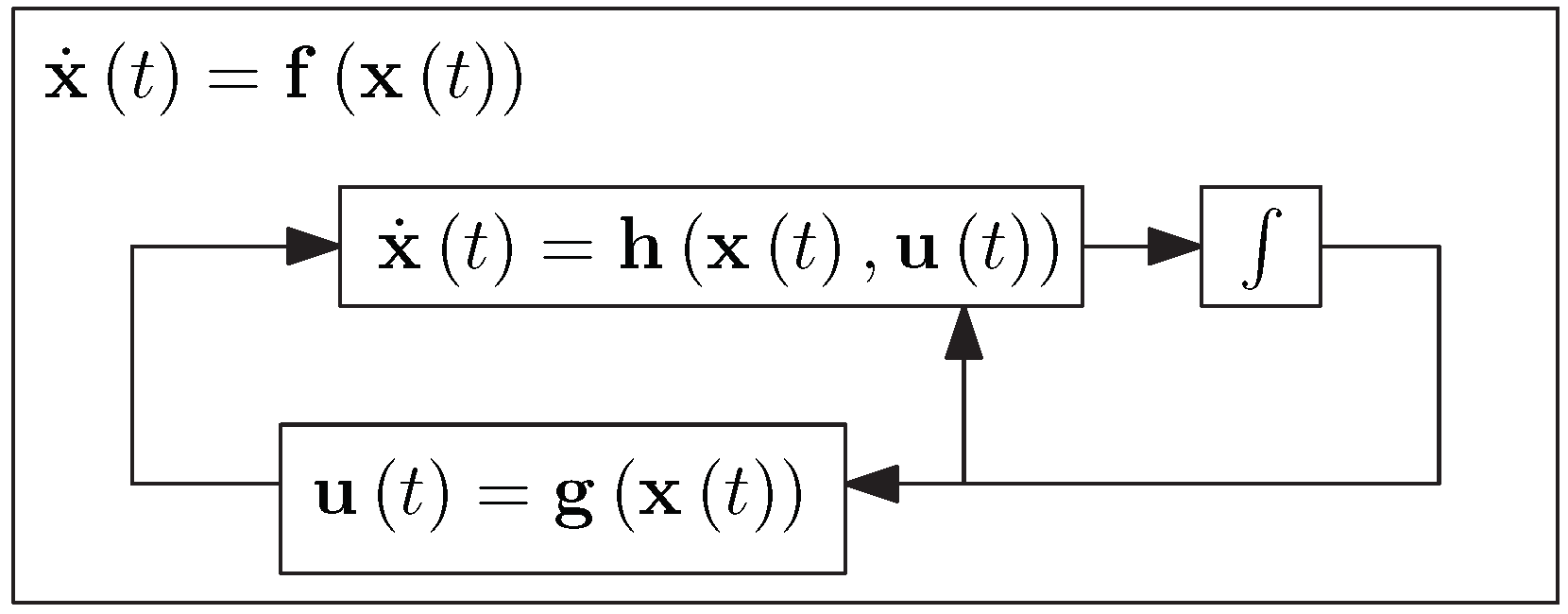


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bourgois, A.; Rohou, S.; Jaulin, L.; Rauh, A. Proving Feasibility of a Docking Mission: A Contractor Programming Approach. Mathematics 2022, 10, 1130. https://doi.org/10.3390/math10071130
Bourgois A, Rohou S, Jaulin L, Rauh A. Proving Feasibility of a Docking Mission: A Contractor Programming Approach. Mathematics. 2022; 10(7):1130. https://doi.org/10.3390/math10071130
Chicago/Turabian StyleBourgois, Auguste, Simon Rohou, Luc Jaulin, and Andreas Rauh. 2022. "Proving Feasibility of a Docking Mission: A Contractor Programming Approach" Mathematics 10, no. 7: 1130. https://doi.org/10.3390/math10071130
APA StyleBourgois, A., Rohou, S., Jaulin, L., & Rauh, A. (2022). Proving Feasibility of a Docking Mission: A Contractor Programming Approach. Mathematics, 10(7), 1130. https://doi.org/10.3390/math10071130







