Abstract
In this study, under the considerations of symbolic computation with the help of Mathematica software, various types of solitary wave solutions for the (3 + 1)-dimensional Jimo–Miwa (JM) equation are successfully constructed based on the extended modified rational expansion method. The constructed solutions are novel and more general for the JM equation named kink wave solutions, anti-kink wave solutions, bright and dark solutions, mixed solutions in the shape of bright-dark solutions, and periodic waves, which do not exist in the existing literature. The physical phenomena of the demonstrated results is represented graphically by two-dimensional, three-dimensional, and contour images with the help of Mathematica. The obtained results will be widely used to explain the various interesting physical structures in the areas of optics, plasma, gas, acoustics, classical mechanics, fluid dynamics, heat transfer, and many others.
Keywords:
(3 + 1)-dimensional Jimo–Miwa equation; new mathematical technique; bright and dark solutions; kink and anti-kink wave solutions; mixed solutions; periodic solitary wave solutions MSC:
35J05; 35J10; 35K05; 35L05
1. Introduction
A lot of research have been conducted on the investigation of nonlinear evolution equations (NLEEs), which involves the study of nonlinear structures in applied and natural sciences. The researcher investigate the various kinds of nonlinear evolution equations to describe some interesting physical phenomena. For instance, the Kortewege–de Vries (KdV) equation describes the development of one dimensional long waves in many physical phenomena such as waves on the surface of shallow water with weakly nonlinear restoring forces, long internal waves in a density stratified ocean, ion acoustic waves in plasmas, and acoustic waves on a crystal lattice [1,2,3,4]. The Schrödinger equation is established to model the surface waves in deep waters as well as electromagnetic waves in optical fibers [5]. The Kadomtsev–Petviashvili (KP) equation explain the dynamics of long wavelength and small amplitude solitary waves in two dimensions [6]. The Whitham–Broer–Kaup (WBK) equation describes the small amplitude regime for dispersive long waves in shallow water. The WBK equation also describes the propagation of waves in shallow water with different dispersion relations [7].
Moreover, it is of more significant importance to determine techniques for solving the NLEEs, if the exact solutions of the NLEEs are available, then they can provide enhanced knowledge of certain application problems such as optical communications. With the solutions of these NLEEs people can know the physical phenomena of master and matter its routes, for example, in the areas of fiber optics, heat transfer, electromagnetism, classical mechanics, field physics, fluid dynamics, acoustics, aerospace, and so on. The partial differential equations have been importantly established and solving the PDEs has become more and more popular [8,9,10,11,12,13,14,15,16,17,18,19]. From the solutions of PDEs, it is very difficult to solve the nonlinear partial differential equations. With the passage of time increasing the power of computing tools, such as the computer softwares Mathematica, Maple, Matlab, etc., we can determine rogue waves, lump solutions, and solitary wave solutions successfully by symbolic computations.
The NLPDEs have marvelous applications in the area of nonlinear sciences to understand the behavior of physical phenomena. The difficulties and problems are that for the construction of exact and solitary wave solutions of NLPDEs, the efficient and powerful methods are required to analytically investigate the NLPDEs. According to this aspect, large groups of mathematicians and engineers have developed various types of methods, including the Sine-Gorden expansion method [20], the F-expansion method [21], the lamped Galerkin method [22], the extended simple equation method, the Exp-function method [23], the Backlund transformation [24], the modified Kudryashov method [25], the spectral collection method [26], extended direct algebraic technique [27,28], Modified auxiliary mapping technique [29,30,31,32], the binary bell polynomials [33], and the (G/G)-expansion method [34].
The (3 + 1)-dimensional Jimo–Miwa equation is the second equation in the well-known KP hierarchy of integrable systems. The JM equation describes the interesting (3 + 1)-dimensional phenomena of waves in physics. Many researchers have investigated and found various solutions for the (3 + 1)-dimensional Jimo–Miwa equation in previous literature. Zhuosheng Lü et al. constructed the exact solutions in the form of bi-solutions for the (3 + 1)-dim JM equation with Bäcklund transformation [35]. Runfa Zhang et al. found the exact solutions for (3 + 1)-dim JM equation named cross-kink wave, periodic wave with generalized bilinear method in [36] and demonstrated the periodic lump wave and interaction solutions via the Hirota bilinear method in [37]. Yong Zhang et al. found the rational and semi-rational solutions named lump, breather, and rogue wave [38] for (3 + 1)-dim JM equation via the Hirota bilinear method. Bintao Cao calculated the two families of explicit exact solutions with the help of two methods named stable-range and logarithmic stable-range methods in [39,40,41,42,43,44].
In this study, we investigate the JM equation with the modified mathematical technique named the extended modified rational expansion method [45]. The constructed solutions are novel and more general for the JM equation named kink wave solutions, anti-kink wave solutions, bright and dark solutions, mixed solutions in the shape of bright-dark solutions, and periodic waves, which does not exist in the literature.
The rest of the article is organized as follows: In Section 2, we explain the algorithm of the applied technique. In Section 3, we applied the proposed technique on the (3 + 1)-dimensional Jimo–Miwa equation for the construction of solitary wave solutions. We discuss the obtained results in Section 4. In the last section, the conclusion is given (Section 5) (See Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14).
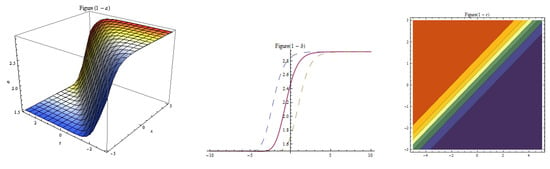
Figure 1.
Three-dim, two-dim, and contour plots for Equation (11) represent the kink wave solution with , , , , , , , , , , , .
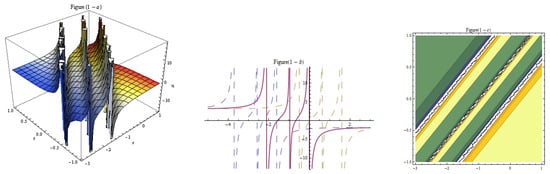
Figure 2.
Three-dim, two-dim, and contour plots for Equation (12) represent the solitary wave with , , , , , , , , , , , , .
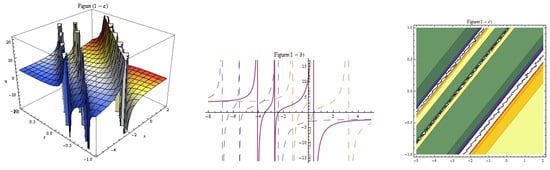
Figure 3.
Three-dim, two-dim, and contour plots for Equation (13) represent the solitary wave with , , , , , , , , , , , , , .
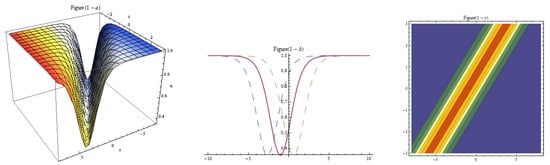
Figure 4.
Three-dim, two-dim, and contour plots for Equation (15) represent the dark solution with , , , , , , , , , , , .
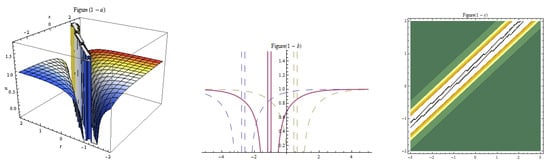
Figure 5.
Three-dim, two-dim, and contour plots for Equation (16) represent the mixed solution with , , , , , , , , , , , , .
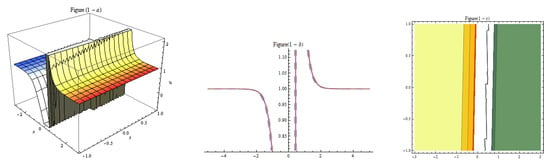
Figure 6.
Three-dim, two-dim, and contour plots for Equation (19) represent the solitary wave with , , , , , , , , , , , .
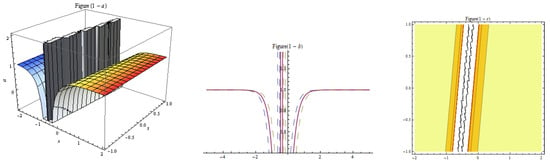
Figure 7.
Three-dim, two-dim, and contour plots for Equation (20) represent the mixed solution with , , , , , , , , , , , , .
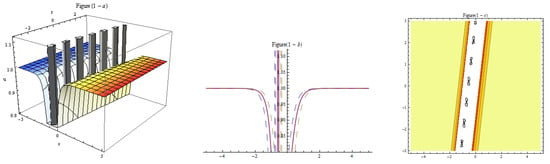
Figure 8.
Three-dim, two-dim, and contour plots for Equation (21) represent the mixed solution with , , , , , , , , , , , , , .
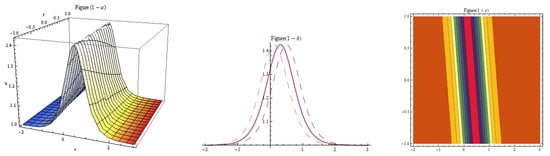
Figure 9.
Three-dim, two-dim, and contour plots for Equation (23) representing the bright solution with , , , , , , , , , , , .
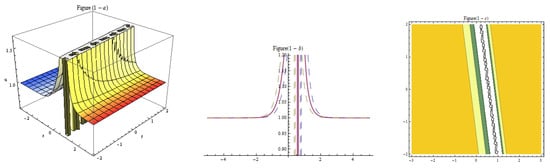
Figure 10.
Three-dim, two-dim, and contour plots for Equation (25) representing the mixed solution with , , , , , , , , , , , , , .
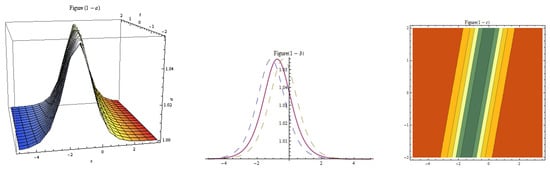
Figure 11.
Three-dim, two-dim, and contour plots for Equation (27) representing bright solutions with , , , , , , , , , , , , .
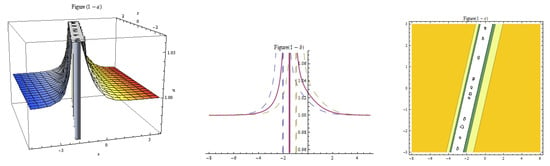
Figure 12.
Three-dim, two-dim, and contour plots for Equation (29) representing mixed solutions with , , , , , , , , , , , , .
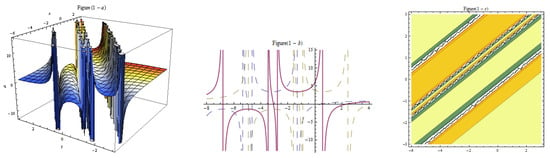
Figure 13.
Three-dim, two-dim, and contour plots for Equation (32) representing solitary waves with , , , , , , , , , , , .
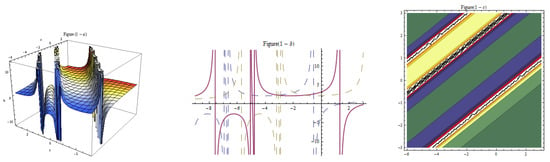
Figure 14.
Three-dim, two-dim, and contour plots for Equation (33) representing solitary waves with , , , , , , , , , , , , .
2. Algorithm of Proposed Technique
We consider the NLPDEs as:
where denotes the polynomial function of and their derivatives. The main structures of the EMRE method (extended modified rational expansion method) is described as:
Step 1. We take the transformations of traveling wave as:
The ODE of Equation (1), is obtained as:
In Equation (3), represents the polynomial function in and its derivatives.
Step 2. The series solution of Equation (3), is considered as:
Here are constants, which are determined to be latter, the and their derivatives satisfy the following auxiliary equation:
In Equation (5), are real constants which are found later.
Step 3. For determining the value of n for Equation (4), we balance the nonlinear terms and derivative of higher order in Equation (3).
3. Application of Proposed Technique for the (3 + 1)-Dimensional Jimo–Miwa Equation
Here, we apply the proposed method (extended modified rational expansion method) on the (3 + 1)-dimensional Jimo–Miwa Equation for the constructions of solitary wave solutions. The (3 + 1)-dimensional Jimbo–Miwa equation is given as:
Applying the traveling wave transformation on Equation (1):
Substituting Equation (11) into Equation (1) and integratating once with respect to , then Equation (1) changes into the ODE as:
Using the homogeneous principle on Equation (16), we obtain n = 1. The trial solution of Equation (16), is taken as:
Substituting Equation (9) in Equation (8) and collecting the coefficients of then making every coefficient equal to zero, obtaining a family of equations, and solving these families of equations by Mathematica software, the parameter values are obtained as:
Case-I
Case-II
Case-III
Case-IV
Case-V
Case-VI
4. Results and Discussion
In this section we describe the similarities and differences between constructed solutions for the (3 + 1)-dimensional Jimo–Miwa equation in this study which have already been demonstrated in the previous literature. In this work, we have constructed novel and interesting results named solitary solutions. The series solution is the significant result in this study with the variety of five parameters, which have diverse constructions. The constant parameter values were collected with symbolic computation, then Equation (5) had different kinds of results named rational, trigonometric, and elliptic functions. The constructed results are novel, more general, and interesting solutions via this powerful and efficient method. Now, we compare our calculated results with other techniques (See Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14).
1. Bäcklund transformation:
Zhuosheng Lü et al. constructed the exact solutions in the form of bi-solutions for the (3 + 1)-dimensional Jimo–Miwa equation with Bäcklund transformation in [35]. However, our constructed results are novel, interesting, and have different physical structures.
2. Generalized bilinear method:
Runfa Zhang et al. found the exact solutions for the JM equation named cross-kink wave and periodic wave with generalized bilinear methods in [36]. However, our constructed results are novel, interesting, and have different physical structure.
3. Hirota bilinear method:
Runfa Zhang et al. demonstrated the periodic lump wave and interaction solutions in [37] and Yong Zhang et al. found the rational and semi-rational solutions named lump, breather, and rogue wave [38] for (3 + 1)-dim JM equation via the Hirota bilinear method. However, our constructed results are novel, interesting, and have different physical structures.
4. Stable-range and logarithmic stable-range methods:
Bintao Cao calculated the two families of explicit exact solutions with the help of two methods named stable-range and logarithmic stable-range methods in [39]. However, our constructed results are novel, interesting, and have different physical structures.
In this work, the demonstrated new results named elliptic, rational, and trigonometric kink wave solutions, anti-kink wave solutions, bright and dark solutions, and mixed solutions in the shape of bright-dark solutions and periodic solitary waves for (3 + 1)-dim JM equations.
From the above detailed discussion and compression, we accomplish that the constructed results are novel, interesting, and more general, which have not been calculated in the previous literature by other methods. The current study shows that applied method is more powerful, efficient, and reliable for the investigation of other nonlinear evolution equations.
5. Conclusions
Under the investigation of the EMRE method (extended modified rational expansion method), we have successfully constructed the novel, more general, and interesting results for the the (3 + 1)-dimensional Jimo–Miwa (JM) equation. In this current work, the demonstrated new results named elliptic, rational, and trigonometric, in the shape of kink wave solutions, anti-kink wave solutions, bright and dark solutions, mixed solutions in the shape of bright-dark solutons and periodic solitary waves. The physical behavior of the demonstrated results is represented by images via two-dimensional, three-dimensional, and contour plots with Mathematica. The constructed solutions are novel, more general, interesting, and do not exist in the existing literatures, which will be widely used to describe the many interesting physical phenomena in the area of optics, plasma, gas, acoustics, classical mechanics, fluid dynamics, heat transfer, and many others. The current research shows that the proposed method is more powerful, reliable, and efficient for the study of other nonlinear evolution equations.
Author Contributions
Funding acquisition, H.Z.; Methodology, M.I.; Supervision, A.R.S. All authors have read and agreed to the published version of the manuscript.
Funding
Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work the project number (141/442).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work the project number (141/442). The authors would also like to extend their appreciation to Taibah University for its supervision support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: London, UK, 1991. [Google Scholar]
- Zhang, Y.; Wang, Z.; Nie, Z.; Li, C.; Chen, H.; Lu, K.; Xiao, M. Four-Wave Mixing Dipole Soliton in Laser-Induced Atomic Gratings. Phys. Rev. Lett. 2011, 106, 093904. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.; Seadawy, A.R.; Lu, D. Dispersive solitary wave solutions of nonlinear further modified Kortewege-de Vries dynamical equation in a unmagnetized dusty plasma via mathematical methods. Mod. Phys. Lett. A 2018, 33, 1850217. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Iqbal, M. Propagation of the nonlinear damped Korteweg-de Vries equation in an unmagnetized collisional dusty plasma via analytical mathematical methods. Math. Methods Appl. Sci. 2021, 44, 737–748. [Google Scholar] [CrossRef]
- Zakharov, V.E.; Shabat, A.B. Exact theory of two-dimentional self-focusing and one-dimentional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62–69. [Google Scholar]
- Kadomtsev, B.B.; Petviashvili, V.I. On the stability of solitary waves in weakly dispersive media. Sov. Phys. Dokl. 1970, 15, 539–541. [Google Scholar]
- Zhang, C.; Tian, B.; Meng, X.H.; Lu, X.; Cai, K.J.; Geng, T. Painlevéintegrability and N-soliton solution for the Whitham-Broer-Kaup shallow water model using symbolic computation. Z. Naturforsch. A 2008, 63, 253–260. [Google Scholar] [CrossRef]
- Iqbal, M.; Seadawy, A.R. Instability of modulation wave train and disturbance of time period in slightly stable media for unstable nonlinear Schrödinger dynamical equation. Mod. Phys. Lett. B 2020, 34 (Suppl. 1), 2150010. [Google Scholar] [CrossRef]
- Huang, L.L.; Yue, Y.F.; Chen, Y. Localized waves and interaction solutions to a (3 + 1)-dimensional generalized KP equation. Comput. Math. Appl. 2018, 76, 831–844. [Google Scholar] [CrossRef]
- Yue, Y.F.; Huang, L.L.; Chen, Y. N-solitons, breathers, lumps and rogue wave solutions to a (3 + 1)-dimensional nonlinear evolution equation. Comput. Math. Appl. 2018, 75, 2538–2548. [Google Scholar] [CrossRef]
- Fang, T.; Wang, Y.H. Interaction solutions for a dimensionally reduced Hirota bilinear equation. Comput. Math. Appl. 2018, 76, 1476–1485. [Google Scholar] [CrossRef]
- Seadawy, A.R. Stability analysis for Zakharov-Kuznetsov equation of weakly nonlinear ion-acoustic waves in a plasma. Comput. Math. Appl. 2014, 67, 172–180. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The Hirota’s direct method for multiple-soliton solutions for three model equations of shallow water waves. Appl. Math. Comput. 2008, 201, 489–503. [Google Scholar] [CrossRef]
- Seadawy, A.R. Stability analysis for two-dimensional ion-acoustic waves in quantum plasmas. Phys. Plasm. 2014, 21, 052107. [Google Scholar] [CrossRef]
- Chen, S.T.; Ma, W.X. Lump solutions of a generalized Calogero-Bogoyavlenskii-Schiff equation. Comput. Math. Appl. 2018, 76, 1680–1685. [Google Scholar] [CrossRef]
- Manukure, S.; Zhou, Y.; Ma, W.X. Lump solutions to a (2+1)-dimensional extended KP equation. Comput. Math. Appl. 2018, 75, 2414–2419. [Google Scholar] [CrossRef] [Green Version]
- Yong, X.L.; Ma, W.X.; Huang, Y.H.; Liu, Y. Lump solutions to the Kadomtsev-Petviashvili I equation with a self-consistent source. Comput. Math. Appl. 2018, 75, 3414–3419. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.P.; Akhmediev, N. Rogue wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef]
- Eslami, M.; Mirzazadeh, M. Optical solitons with Biswas-Milovic equation for power law and dual-power law nonlinearities. Nonlinear Dynam. 2016, 83, 731–738. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, Z. New exact solutions of (2+1)-dimensional Gardner equation via the new sine-Gordon equation expansion method. Chaos Solitons Fractals 2005, 26, 399–406. [Google Scholar] [CrossRef]
- Zhao, Y.M. F-expansion method and its application for finding new exact solutions to the Kudryashov-Sinelshchikov equation. J. Appl. Math. 2013, 2013, 895760. [Google Scholar] [CrossRef] [Green Version]
- McLean, W. A spectral Galerkin method for a boundary integral equation. Math. Comp. 1986, 47, 597–607. [Google Scholar] [CrossRef]
- Zhang, S. Exp-function method for solving Maccari’s system. Phys. Lett. A 2007, 371, 65–71. [Google Scholar] [CrossRef]
- Zuo-nong, Z.H.U. Painleve property, Bäcklund transformation, Lax pairs and solitonlike solutions for a variable coefficient KP equation. Phys. Lett. A 1993, 152, 277–281. [Google Scholar]
- Kabir, M.M.; Khajeh, A.; Aghdam, E.A.; Koma, A.Y. Modified Kudryashov method for finding exact solitary wave solutions of higher-order nonlinear equations. Math. Method Appl. Sci. 2011, 34, 213–219. [Google Scholar] [CrossRef]
- Li, M.; Xu, T.; Wang, L. Dynamical behaviors and soliton solutions of a generalized higher-order nonlinear Schrödinger equation in optical fibers. Nonlinear Dyn. 2015, 80, 1451–1461. [Google Scholar] [CrossRef]
- Iqbal, M.; Seadawy, A.R.; Lu, D. Applications of nonlinear longitudinal wave equation in a magneto-electro-elastic circular rod and new solitary wave solutions. Mod. Phys. Lett. B 2019, 33, 1950210. [Google Scholar] [CrossRef]
- Seadawy, A.R. Approximation solutions of derivative nonlinear Schrödinger equation with computational applications by variational method. Eur. Phys. J. Plus 2015, 130, 182. [Google Scholar] [CrossRef]
- Seadawy, A.R. Ion acoustic solitary wave solutions of two-dimensional nonlinear Kadomtsev–Petviashvili–Burgers equation in quantum plasma. Math. Methods Appl. Sci. 2017, 40, 1598–1607. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.R.; Iqbal, M. Mathematical method via construction of traveling and solitary wave solutions of three coupled system of nonlinear partial differential equations and their applications. Results Phys. 2018, 11, 1161–1171. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.R.; Iqbal, M. Construction of new solitary wave solutions of generalized Zakharov-Kuznetsov-Benjamin-Bona-Mahony and simplified modified form of Camassa-Holm equations. Open Phys. 2018, 16, 896–909. [Google Scholar] [CrossRef]
- Iqbal, M.; Seadawy, A.R.; Lu, D.; Xia, X. Construction of bright–dark solitons and ion-acoustic solitary wave solutions of dynamical system of nonlinear wave propagation. Mod. Phys. Lett. A 2019, 34, 1950309. [Google Scholar] [CrossRef]
- Javidi, M.; Golbabai, A. Numerical studies on nonlinear Schrödinger equations by spectral collocation method with preconditioning. J. Math. Anal. Appl. 2007, 333, 1119–1127. [Google Scholar] [CrossRef] [Green Version]
- Li, B.Q.; Ma, Y.L. New application of the (G′/G)-expansion method to excite soliton structures for nonlinear equation. Z. Naturfors. Sect. A 2010, 65, 518–524. [Google Scholar] [CrossRef]
- Lü, Z.; Su, J.; Xie, F. Construction of exact solutions to the Jimbo–Miwa equation through Bäcklund transformation and symbolic computation. Comput. Math. Appl. 2013, 65, 648–656. [Google Scholar] [CrossRef]
- Zhang, R.; Bilige, S.; Fang, T.; Chaolu, T. New periodic wave, cross-kink wave and the interaction phenomenon for the Jimbo–Miwa-like equation. Comput. Math. Appl. 2019, 78, 754–764. [Google Scholar] [CrossRef]
- Zhang, R.; Bilige, S. New interaction phenomenon and the periodic lump wave for the Jimbo–Miwa equation. Mod. Phys. Lett. B 2019, 33, 1950067. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, S.; Dong, H. Hybrid solutions of (3 + 1)-dimensional Jimbo-Miwa equation. Math. Probl. Eng. 2017, 2017, 5453941. [Google Scholar] [CrossRef]
- Cao, B. Solutions of jimbo-miwa equation and konopelchenko-dubrovsky equations. Acta Appl. Math. 2010, 112, 181–203. [Google Scholar] [CrossRef] [Green Version]
- Rizvi, S.T.R.; Seadawy, A.R.; Ali, I.; Bibi, I.; Younis, M. Chirp-free optical dromions for the presence of higher order spatio-temporal dispersions and absence of self-phase modulation in birefringent fibers. Mod. Phys. Lett. B 2020, 34, 2050399. [Google Scholar] [CrossRef]
- Younas, U.; Seadawy, A.R.; Younis, M.; Rizvi, S.T.R. Dispersive of propagation wave structures to the Dullin-Gottwald-Holm dynamical equation in a shallow water waves. Chin. J. Phys. 2020, 68, 348–364. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Cheemaa, N. Applications of extended modified auxiliary equation mapping method for high order dispersive extended nonlinear schrodinger equation in nonlinear optics. Mod. Phys. Lett. B 2019, 33, 1950203. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Cheemaa, N. Propagation of nonlinear complex waves for the coupled nonlinear Schrödinger Equations in two core optical fibers. Phys. A Stat. Mech. Its Appl. 2019, 529, 121330. [Google Scholar] [CrossRef]
- Özkan, Y.S.; Yaşar, E.; Seadawy, A.R. On the multi-waves, interaction and Peregrine-like rational solutions of perturbed Radhakrishnan–Kundu–Lakshmanan equation. Phys. Scr. 2020, 95, 085205. [Google Scholar] [CrossRef]
- Iqbal, M.; Seadawy, A.R.; Khalil, O.H.; Lu, D. Propagation of long internal waves in density stratified ocean for the (2+1)-dimensional nonlinear Nizhnik-Novikov-Vesselov dynamical equation. Results Phys. 2020, 16, 102838. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).