Multiple Benefit Thresholds Problem in Online Social Networks: An Algorithmic Approach

Abstract

An important problem in the context of viral marketing in social networks is the Influence Threshold (IT) problem, which aims at finding some users (referred to as a seed set) to begin the process of disseminating their product’s information so that the benefit gained exceeds a predetermined threshold. Even though, marketing strategies exhibit different in several realistic scenarios due to market dependence or budget constraints. As a consequence, picking a seed set for a specific threshold is not enough to come up with an effective solution. To address the disadvantages of previous works with a new approach, we study the Multiple Benefit Thresholds (MBT), a generalized version of the IT problem, as a result of this phenomenon. Given a social network that is subjected to information distribution and a set of thresholds, $T=\{T_1,T_2,\dots ,T_k\},T_i>0$, the issue aims to seek the seed sets $S_1,S_2,\dots ,S_k$ with the lowest possible cost so that the benefit achieved from the influence process is at the very least $T_1,T_2,\dots ,T_k$, respectively. The main challenges of this problem are a #NP-hard problem and the estimation of the objective function #P-Hard under traditional information propagation models. In addition, adapting the exist algorithms many times to different thresholds can lead to large computational costs. To address the abovementioned challenges, we introduced Efficient Sampling for Selecting Multiple Seed Sets, an efficient technique with theoretical guarantees (ESSM). At the core of our algorithm, we developed a novel algorithmic framework that (1) can use the solution to a smaller threshold to find that of larger ones and (2) can leverage existing samples with the current solution to find that of larger ones. The extensive experiments on several real social networks were conducted in order to show the effectiveness and performance of our algorithm compared with current ones. The results indicated that our algorithm outperformed other state-of-the-art ones in terms of both the total cost and running time.

1. Introduction

In recent years, there has been a rapid development of the global economy thanks to the contribution of the Online Social Network (OSN), based on the provision of a powerful platform for communication and information dissemination in the field of marketing, media, and advertising, particularly in social networks with billions of users. The strong underpinnings of problems of social influences in OSNs are information diffusion models. Kempe et al. [1] first introduced two classic models, named Independent Cascade (IC) and Linear Threshold (LT), and formulated the Influence Maximization (IM) problem, which aims to select k nodes that may impact the largest number of users a social network. This work has inspired many studies on social influence [2,3,4,5,6,7,8,9,10], misinformation/rumors detection, and control [11,12,13,14,15].

In the context of viral marketing for product promotion, hosts (companies) often devise a marketing campaign including the distribution of product samples to selected users and expect that they persuade their friends, friends of friends, etc. The number of people who have been impacted reaches a certain level. Influence Threshold (IT) was inspired by this phenomenon and a slew of research backed it up; it looks for a node set with the smallest size possible so that the number of impacted nodes reaches or surpasses a predetermined threshold $\gamma$ [8,16,17]. The value of $\gamma$ can determine the scale of of the viral marketing. However, in some realistic scenarios, there is a distinct cost to persuade a user who promotes a sample product [4,18]. Besides, each influenced user often offers a different benefit when one is influenced after the marketing process. Customers with significant financial resources, for example, will be able to purchase more things than others. As a result, the existing algorithms for IT problem may offer an inaccurate solution of a marketing purpose. Moreover, the marketing strategies are often adjusted since the market can vary in a short time. Consequently, a particular solution for a benefit is insufficient to be the overall effective solution. This can be overcome by finding solutions for multiple thresholds and selecting the best one that suits their budget and current market.

For instance, assume that a company wants to come up with a strategy that can influence customers on an online social network. Nonetheless, or due to budget fluctuations or the instability of the market, they may consider strategies of spreading with the different number of influenced customers such as 1000, 2000, 3000, 5000, etc. In this case, the company wants to find solutions, where the benefit function of each is above the corresponding threshold and then that company can select a solution with a reasonable cost so as to execute its marketing plan well.

Our goal in this study is to develop an answer to a novel Multiple Benefit Thresholds (MBT) problem, which is expressed as follows. For a social network $G=(V,E)$ given a set of k benefit thresholds $T=\{T_1,T_2,\dots ,T_k\}$, each user u has a distinct cost price $c\left(u\right)>0$. The issue is to seek for the various seed sets $\{S_1,S_2,\dots ,S_k\}$, in which each $S_i$ has the cheapest total cost $c\left(S_i\right)$ by a result of each seed set’s earned benefit $S_i$, characterized by $\mathbb{B}\left(S_i\right)$, and is at least $T_i$ for $i=1\dots ,k$. There are two main challenges for solving MBT problem. First ones are to find MBT as #NP-Hard and to calculate the benefit function #P-Hard. Secondly, finding numerous seed sets for multiple thresholds needs more time and memory than other information propagation challenges, as well as the IT problem. It is necessary to run the existing algorithms for a single threshold k times to prove it is costly and, hence, not applicable to large networks. To overcome the challenges, in this paper, we propose a highly efficient algorithm to solve the problem. This not only guarantees a solution but also produces good results in practice. This work revised and extended the our conference paper [19] by providing all the proofs more detail and experiment evaluation.

The following is a list of our contributions as a whole:

• The Multiple Benefit Thresholds (MBT) is first formulated with the Independent Cascade (IC) information diffusion model.
• With a view to developing the solution, the Efficient Sampling for Multiple Seed Set Selection (ESSM) is proposed, a theoretical approximation algorithm bounds by developing a novel algorithmic framework that utilizes the sample technique to estimate the benefit function, denoted as $\mathbb{B}(·)$, and leverages the seed set and the samples with smaller benefit threshold with the purpose of finding the seed set of the larger ones. Accordingly, our algorithm can find multiple seed sets in only one run. For solution guarantee, our algorithm returns multiple seed sets $S_i$ satisfying $\mathbb{B}\left(S_i\right)\ge \frac{1-ϵ}{1+ϵ}{T}_i-ϵ$ and the total cost $c\left(S_i\right)\le (1+ln\frac{(T_i-ϵT_i)}{ϵ})c\left(S_i^{*}\right)$ a strong possibility (w.h.p), where $ϵ>0$ is an input and $S_i^{*}$ is the best seed set in terms of threshold $T_i$ for all $i=1,2,\dots ,k$.
• Extensive experiments on six real-world networks are performed, including Gnutella, Email-Enron, Net-Hept, Net-Phy, Amazon, and DBLP for the comparison of the efficiency between our algorithm and other state-of-the-art ones. The results of experiments indicated that our algorithm outperformed the state-of-the-art ones in respect of both the cost and the running time.

Organization. The rest of the paper is structured as follows. In Section 2, we review previous relevant works of influence maximization. Section 3 presents the model, problem definition, and main algorithm. The experiment results are shown and explained in Section 4. Finally, Section 5 brings the paper to the conclusion.

2. Related Works

In this section, we review previous studies related to our abovementioned problem, including Information propagation models, Influence Maximization, and Influence Threshold.

Information propagation models and Influence Maximization. Social networks provide a convenient environment for business marketing through the word-of-mouth effect. Influence Maximization (IM) [1], which seeks out k nodes (seed set) in a social network that can influence the greatest number of nodes is one of the most important challenges in social network influence. Kempe et al. originally investigated IM as an #NP-hard combinatorial optimization under two famous information diffusion models: Linear Threshold (LT) and Independent Cascade (IC). Furthermore, the challenge of solving IM also coming from calculating the influence function under two above models is #P-hard models—that is, it is impossible to calculate in polynomial time with input size [5,6]. However, due to the enormous application of IM in commerce, several efficient algorithms were proposed for solving the problem in large-scale networks, such as approximation algorithm [1,2,3,20,21] and heuristics without theoretical guarantee [7,22,23]. Notably, Borg et al. [24] made a theoretical breakthrough by proposing a $(1-1/e-ϵ)$-approximation algorithm in $O\left({ϵ}^{-3}k{l}^2(m+n){log}^{2}n\right)$ with a probability at least $1-n^{-l}$. The main idea of Borg’ algorithm is that they proposed a sample technique, namely, Reverse Reachable (RR) set, to estimate the number of influenced nodes under stochastic information propagation models and an algorithmic framework that finds the solution in generated samples with theoretical bound. Tang et al. [2] proposed the TIM/TIM++ algorithms reducing the time complexity to $O({ϵ}^{-2}(k+l)(m+n)logn)$ while maintaining the performance guarantees and demonstrated the high efficiency of their algorithm in billion-scale networks. Later on, several algorithms have been devised in an attempt to reduce the sample complexity and running time but they still maintained an approximate ratio by modifying the RIS framework, including IMM [3], SSA/DSSA [21], OPIM [25], etc. Recently, Akram et al. mentioned finding influential communities in a social network with fuzzy competition hypergraphs notion [26,27].

In other directions, numerous studies were carried out on variations of IM for many scenarios of viral marketing. The authors in [28,29,30] considered IM under topic queries by introducing the information diffusion model that can enable many topics to spread. Additionally, the advance in geoposition enabled devices and services makes OSNs able to integrate a user’s location. The authors in [31] investigated the location-aware influence maximization (LIM) problem in which some nodes were selected and the largest number of nodes was influenced in a given distance; [32] considered the role of distance among users to promote the influence process of viral marketing. Moreover, several other variations of $\mathsf{IM}$ including competitive-aware [5,33] and time-aware [34] have been introduced and studied.

Recently, Nguyen et al. [35] has studied IM under the budget constraint where each node has the limited cost to adopt a sample product and the total budget was required. In the seminal paper, it showed that the greedy algorithm can achieve an approximation ratio of $1-1/\sqrt{e}$ and further proposed efficient heuristic algorithms without any performance guarantees. Later, Nguyen et al. [4] studied the Cost-aware Targeted Viral Marketing (CTVM) problem, a generalization of IM. In this problem, each node u has an arbitrary cost $c\left(u\right)$ and a benefit $b\left(u\right)$. The goal of CTVM was to select a seed set within a given budget B so that the total benefit was maximized. They proposed a benefit sampling technique and a $1-\frac{1}{\sqrt{e}}-ϵ$ approximation algorithm with probability at least $1-\delta$ in $O({ϵ}^{-2}nlog\left(\left(\genfrac{}{}{0pt}{}{n}{k}\right)\right)/\delta )$. In this study, the sampling technique in [4] is adapted to estimate the benefit function. However, BCT could not adapt to solving our problem due to the difference between MBT and CTVM.

Influence Threshold. Influence Threshold (IT), which seeks the smallest size seed set S such that the influence spread, defined as $\sigma \left(S\right)$, is at least a specified threshold $\gamma$, is the problem that comes closest to ours. Goyal et al. [36] were the first to investigate the IT problem using IC models. Using the influence function’s monotone submodular characteristic, they proposed a greedy algorithm combining with Monte Carlo simulation method [1] to estimate $\sigma \left(S\right)$. The algorithm returns a seed set S satisfying $\sigma \left(S\right)\ge \gamma -ϵ$ and $\left|S\right|\le |S^{*}|·(1+ln\frac{\gamma }{ϵ})$ in $O\left(n^{2}R\right)$ time complexity, where $ϵ>0$ is an input, $S^{*}$ is the optimal solution, and R is number of Monte Carlo simulations with setting $R=10.000$. Due to its high time complexity, it is difficult to apply this algorithm to large networks. By utilizing the sampling technique method in [37], Kuhnle et al. [8] developed a $(1-2\alpha ,1+4\alpha \gamma +log\gamma )$—bicriteria approximation algorithm for a special case of IT where cost of the vertices is the same (We call an algorithm is an $(\alpha ,\beta )$-bicriteria approximation for IT problem if it returns a solution S satisfying $\sigma \left(S\right)\ge \alpha ·T$ and $\left|S\right|\le \beta ·|S^{*}|$, where $\alpha ,\beta >0$ and $S^{*}$ is the optimal solution.) in $O({\alpha }^2(m+n)log\left(n\right)|S\left|\right)$ time complexity, where $\alpha \in (0,1)$ is an input and $n,m$ refer to the number of nodes, edges in the network.

The authors of [17] recently explored IT in a noisy model resembling a real-world situation, where we only estimate the influence spread function within an error bound. The greedy algorithm under noise with theoretical bound was proposed but it retained time complexity as in [38]. In these studies, they ignored the point that each affected user provided a different benefit in these experiments. The benefits of the nodes and different benefit thresholds are considered for identifying the appropriate seed sets in our MBT problem. In the case of the great similarity in benefits of nodes, the above algorithms can be used for each threshold $T_i$, but it is imperative to run k times to find the k seed sets. On the other hand, our proposed algorithm not only provides theoretical bounds but also returns multiple seed sets for set of benefit thresholds at a single time.

3. Methodology

In this section, Independent Cascade (IC) model is presented, as the well-known original model related to the IM problems. [1,2,3,4,20,21]. Our notations and symbols are summarized in

Table 1. Table of symbols.

Notional	Description
$n,m$	The number of nodes and of edges in G, respectively
$N_{in}\left(v\right),N_{out}\left(v\right)$	The incoming and outgoing neighbor node set of v.
$S_i$	The solution returned by our algorithm for threshold $T_i$
$\mathbb{B}\left(S\right),\widehat{\mathbb{B}}\left(S\right)$	Define the benefit function and an estimation of benefit function
$\Gamma$	$\Gamma ={\sum }_{u\in V}b\left(u\right)$
$S_i^{*}$	The optimal seed set for threshold $T_i$
$N(i,j)$	$N(i,j)=\frac{(2+\frac{2}{3}ϵ)\Gamma }{{ϵ}^2(T_i-ϵT_i)}ln(\left(\genfrac{}{}{0pt}{}{n}{j}\right)/\delta )$
$N_{max}^i$	$N_{max}^i={max}_{j:1\dots |S_i|}\frac{(2+\frac{2}{3}ϵ)\Gamma }{{ϵ}^2(T_i-ϵT_i)}ln(\left(\genfrac{}{}{0pt}{}{n}{j}\right)/\delta )$
$i_{max}$	$i_{max}=arg{max}_{i=1\dots |S_k|}ln\left(\left(\genfrac{}{}{0pt}{}{n}{i}\right)\right)$

.

3.1. Independent Cascade Model

In this work, a social network is abstracted by a directed graph $G=(V,E)$. V and E represent the set of users and the set of links in the network, respectively. In this model, each edge $e=(u,v)\in E$ has a probability $p(u,v)\in (0,1)$ representing the influence transmission from u to v. Given a seed set $S\subseteq V$, each node is in one of two states: active and inactive, which reflects whether it is influenced by the seed set or not. The diffusion process starts from S and works as follows:

• At the beginning (step $t=0$), all nodes in the seed set are active.
• At the next steps (step $t\ge 1$), an node u, which is activated in previous steps, has a single chance to influence each of its neighbors v with the probability of success $p(u,v)$.
• All active nodes retain their status until the end of the diffusion process, and the process ends at step t if there is no new activated node in this step.

Kempe et al. [1] showed that the IC model was equivalent to sample graph model, defined as follows. The live-edge model first generates a sample graph $g=(E_g,V_g)$ by selecting $e=(u,v)\in E$ with probability $p\left(e\right)=p(u,v)$ and not selecting $e=(u,v)\in E$ with probability $1-p(u,v)$. The sample graph g is generated with probability

$$\begin{array}{c}\hfill Pr[g◃G]=\prod _{e\in E_g}p\left(e\right)·\prod _{e\in E\backslash E_g}(1-p\left(e\right))\end{array}$$

(1)

In our model setting, we will gain a benefit $b\left(u\right)>=0$ if the node u becomes active, as in [4]. Benefit function $\mathbb{B}\left(S\right)$, denoted as the total benefit over all influenced nodes, is calculated as follows:

$$\begin{array}{c}\hfill \mathbb{B}\left(S\right)=\sum _{g◃G}Pr[g◃G]\sum _{u\in R(g,S)}b\left(u\right)\end{array}$$

(2)

where $R(g,S)$ is the set of nodes that can reach from any node in S in graph g. In additional, each node $u\in V$ has a cost $c\left(u\right)>0$, which we have to pay to user u to initiate the influence process from u and $c\left(S\right)={\sum }_{u\in S}c\left(u\right)$.

3.2. Problem Definition

We formally introduce our studied problem, Multiple Benefit Thresholds (MBT), as follows:

Definition 1

(MBT). Given a graph $G=(V,E)$ under the IC model and the set of benefit thresholds $T=\{T_1,T_2,\dots ,T_k\}$. For each $T_i\in T$, the problem is required to find $S_i\in V$ with smallest cost $c\left(S_i\right)$ so that $\mathbb{B}\left(S_i\right)\ge T_i$.

In the case when $b\left(u\right)=1,\forall u\in V$, the benefit function $\mathbb{B}(·)$ becomes the influence spread function [1]. Ref. [6] showed that it was #P-hard to compute the number of influence nodes (influence spread function) exactly, so calculating $\mathbb{B}(·)$ was also #P-hard. Besides, the IT problem [8,17,38], a special case of MBT problem with $b\left(u\right)=c\left(u\right)=1,\forall u\in V$ and $k=1$, is NP-hard, which implies that MBT is also #NP-hard.

3.3. Our Proposed Algorithm

In this section, the Efficient Sampling for Selecting Multiple seed sets (ESSM), an efficient algorithm for MBT problem with theoretical guarantee, is introduced. Our novel technique is to develop a method that combines two following ideas: (1) finds the candidate seed set for each threshold via the benefit sampling; (2) uses the seed set with a smaller threshold for finding the seed sets with bigger ones, which can improve the running time as well as memory usage. Moreover, the sampling technique with martingale theory is in use to estimate the benefit function effectively.

3.3.1. Benefit Sampling

We first recap the concept of Benefit Sample (BS) in [4] to estimate the $\mathbb{B}(·)$.

Definition 2

(Benefit Sample). A BS is generated from $G=(V,E)$ under the IC model by following steps: (1) Choose a source node u with probability $\frac{b\left(u\right)}{\Gamma }$, (2) create a sample graph g from G, and (3) return $R_j$ as the set of nodes that can reach node u in g.

The Algorithm 1 in [4] can be used to generate a BS for IC model.

Algorithm 1: An algorithm for generating a BS under the IC model.

Input: Graph $G=(V,E)$ under IC model

Output: A BS set $R_j$

1: Choose a source node u with probability $\frac{b\left(u\right)}{\Gamma }$

2: Initialize a queue $Q=\left\{u\right\}$ and $R_j=\left\{u\right\}$

3: while Q is not empty do

4:   $v\leftarrow Q.pop\left(\right)$

5:   for $u\in N_{in}\left(v\right)\backslash (R_j\cup Q)$ do

6:    With probability $p(u,v)$ do: $Q.push\left(u\right)$, $R_j\leftarrow R_j\cup \left\{u\right\}$;

7:   end for

8: end while

9: return $R_j$

Given $\mathcal{R}$ is a collection of BSes, a seed set S, we define a random variable $X_j\left(S\right)$ as follows:

$$X_j\left(S\right)=\left\{\begin{array}{c}1,\mathrm{If}{R}_j\cap S\ne \varnothing \hfill \\ 0,\mathrm{Otherwise}\hfill \end{array}\right.$$

(3)

We can estimate the benefit function $\mathbb{B}\left(S\right)$ by the following Lemma in [4].

Lemma 1

(Lemma 2, [4]). For any set of nodes $S\subseteq V$, we have: $\mathbb{B}\left(S\right)=\Gamma ·\mathbb{E}\left[X_j\left(S\right)\right]$

The function $\mathbb{B}(·)$ is monotone and submodular [4], i.e., for any $S\subseteq T\subseteq V$, and $v\notin T$, we have

$$\begin{array}{cc}\hfill & \mathbb{B}\left(T\right)\ge \mathbb{B}\left(S\right)\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \mathbb{B}(S+\{v\left\}\right)-\mathbb{B}\left(S\right)\ge \mathbb{B}(T+\{v\left\}\right)-\mathbb{B}\left(T\right)\hfill \end{array}$$

(5)

We can calculate an estimation $\widehat{\mathbb{B}}\left(S\right)$ of $\mathbb{B}\left(S\right)$ via a collection $\mathcal{R}$ of BSes as follows:

$$\widehat{\mathbb{B}}\left(S\right)=\frac{\Gamma }{\left|\mathcal{R}\right|}\sum _{R_j\in \mathcal{R}}{X}_j\left(S\right)$$

(6)

It can be seen that $X_j\left(S\right)\in [0,1]$. We define a random variable $Y_i={\sum }_{j=1}^i(X_j\left(S\right)-\mu ),\forall i\ge 1$, where $\mu =\mathbb{E}\left[X_j\right]$ and a sequence random variables $Y_1,Y_2,\dots$, we have

$$\mathbb{E}\left[Y_i\right|Y_1,\dots ,Y_{j-1}]=\mathbb{E}\left[Y_{i-1}\right]+\mathbb{E}[Y_i\left(S\right)-\mu ]=\mathbb{E}\left[Y_{i-1}\right]$$

Therefore, $Y_1,Y_2,\dots$ are a form of martingale [39]. Thus, we have the following Lemma [39].

Lemma 2

([39]). Given a collection $\mathcal{R}$ with $T=\left|\mathcal{R}\right|$ and $\lambda >0$, we have

$$\begin{array}{cc}\hfill Pr\left[\sum _{j=1}^T{X}_j\left(S\right)-T·\mu \ge \lambda \right]& \le exp\left\{-\frac{{\lambda }^2}{2\lambda \frac{2}{3}+\mu T}\right\}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill Pr\left[\sum _{j=1}^T{X}_j\left(S\right)-T·\mu \le -\lambda \right]& \le exp\left\{-\frac{{\lambda }^2}{2\mu T}\right\}\hfill \end{array}$$

(8)

Let $\lambda =ϵT\mu$ in Lemma 2, we obtain

$$\begin{array}{cc}\hfill Pr[\widehat{\mathbb{B}}\left(S\right)\ge (1+ϵ)\mathbb{B}\left(S\right)]& \le exp\left\{-\frac{{ϵ}^2\mu T}{2+\frac{2}{3}ϵ}\right\}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill Pr[\widehat{\mathbb{B}}\left(S\right)\le (1-ϵ)\mathbb{B}\left(S\right)]& \le exp\left\{-\frac{{ϵ}^2\mu T}{2}\right\}\hfill \end{array}$$

(10)

If the number of BSs is at least $T\ge (2+\frac{2}{3})\frac{1}{\mu }\frac{1}{{ϵ}^2}ln\left(\frac{1}{\delta }\right)$ for $\delta \in (0,1)$, ${\widehat{\mathbb{B}}}_{\mathcal{R}}\left(S\right)$ is an $(ϵ,\delta )$-approximation of $\mathbb{B}\left(S\right)$, i.e.,

$$Pr[(1-ϵ)\mathbb{B}\left(S\right)\le \widehat{\mathbb{B}}\left(S\right)\le (1+ϵ)\mathbb{B}\left(S\right)]\ge 1-\delta$$

(11)

The characteristics of the martingale sequence play an important role in devising our algorithm in the next subsection.

3.3.2. ESSM Algorithm

Our proposed algorithm is now described. On a high level, our algorithm combines two methods: (1) We provide a $(\delta ,ϵ)$-approximation of the benefit function via martingale theory. (2) In each iteration, we propose the algorithmic framework that finds some candidate seed sets for a threshold and then choose the final seed set, which guarantees the solution quality by checking static evidence. (3) We reuse the seed set for smaller threshold for finding the seed sets with the larger threshold. Our proposed algorithm is presented in Algorithm 2.

Algorithm 2: ESSM algorithm.

Input: A graph $G=(V,E)$, $T=\{T_1,\dots ,T_k\}$, $ϵ,\delta \in (0,1)$

Output:$S_1,S_2,\dots ,S_k$

1: Generate ${\mathcal{R}}_0$ containing $\frac{(2+\frac{2}{3}ϵ)\Gamma }{{ϵ}^2(T_i-ϵT_i)}(lnn+ln(1/\delta ))$ BSs by using Algorithm 1

2: $S_0\leftarrow \varnothing$

3: for $i=1$ to k do

4:   ${\mathcal{R}}_i\leftarrow {\mathcal{R}}_{i-1}$

5:   $S_i\leftarrow S_{i-1}$

6:    Calculate $\widehat{\mathbb{B}}\left(S_i\right)$ by Equation (6)

7:   while $\widehat{\mathbb{B}}\left(S_i\right)<T_i-ϵT_i-ϵ$ do

8:    $u\leftarrow arg{max}_{v\in V\backslash S_i}\frac{min(\widehat{\mathbb{B}}(S_i\cup v),T_i-ϵT_i-ϵ)-\widehat{\mathbb{B}}\left(S_i\right)}{c\left(v\right)}$

9:    $S_i\leftarrow S_i\cup \left\{u\right\}$

10:    $j\leftarrow |S_i|$

11:    $N(i,j)\leftarrow \frac{(2+\frac{2}{3}ϵ)\Gamma }{{ϵ}^2(T_i-ϵT_i)}ln(\left(\genfrac{}{}{0pt}{}{n}{j}\right)/\delta )$

12:    if $|{\mathcal{R}}_i|<N(i,j)$ then

13:     Generate more $N(i,j)-|{\mathcal{R}}_i|$ BSs and add them into ${\mathcal{R}}_i$

14:     $N\leftarrow N(i,j)$

15:     $S_i\leftarrow \varnothing$

16:    end if

17:   end while

18: end for

19: return $S_1,S_2,\dots ,S_k$

At the beginning of the algorithm, it generates collection ${\mathcal{R}}_0$ that contains $\frac{(2+\frac{2}{3}ϵ)\Gamma }{{ϵ}^2(T_i-ϵT_i)}(lnn+ln(1/\delta ))$ BSs by using Algorithm 1 and initiates a seed set $S_1$ as empty.

At each iteration i of first loop (line 3–18), it finds the seed set with respect to threshold $T_i$. Denote $f\left(S_i\right)=min(\widehat{\mathbb{B}}\left(S_i\right),T_i-ϵT_i-ϵ)$. At each iteration of the second loop (line 7–18), the algorithm finds a seed $S_i$, by iteratively selecting a node u with maximum marginal of the estimation function f as per its cost, i.e., $(f(S_i\cup \left\{u\right\})-f\left(S_i\right))/c\left(v\right)$ and (2) checking the condition of the number of samples (line 12). If the number of samples is sufficient to give an $(\delta ,ϵ)$-approximation (by Lemma 3), the algorithm moves into next iterations and keeps current seed set $S_i$; otherwise, the algorithm generates more samples (line 13) so that the number of samples is $N(i,j)$ and adds them into $R_i$. In this case, the seed set $S_i$ is suitable for new collection $R_i$. The second loop terminates when it satisfies the condition $\widehat{\mathbb{B}}\left(S_i\right)\ge T_i-ϵT_i-ϵ$. Next, the algorithm reuses the current samples and seed set to find the seed set for larger threshold (lines 4–5) by using similar steps with previous iteration.

The theoretical bounds of the algorithm are now analyzed. Firstly, the satisfactory number of BSes is provided to estimate $\mathbb{B}(·)$ is shown in Lemma 3.

Lemma 3.

If $\left|\mathcal{R}\right|\ge \frac{(2+\frac{2}{3}ϵ)\Gamma }{{ϵ}^2(T_i-ϵT_i)}(lnn+ln\frac{1}{\delta })$ then $Pr[\widehat{\mathbb{B}}\left(S_i^{*}\right)\ge T_i-T_iϵ]\ge 1-\delta$

Proof. 

Denote $\mu =\mathbb{B}\left(S_i^{*}\right)/\Gamma ,\widehat{\mu }=\widehat{\mathbb{B}}\left(S_i^{*}\right)/\Gamma$, we have

$$\begin{array}{cc}\hfill & Pr[\widehat{\mathbb{B}}\left(S_i^{*}\right)\le T_i-T_iϵ]\le Pr[\widehat{\mathbb{B}}\left(S_i^{*}\right)\le (1-ϵ)\mathbb{B}\left(S_i^{*}\right)]\hfill \\ \hfill & =Pr[\widehat{\mu }\le (1-ϵ)\mu ]\left(\mathrm{By}\mathrm{applying}\right(10\left)\right)\hfill \\ \hfill & \le exp\left(\frac{-{ϵ}^2\left|\mathcal{R}\right|\mu }{2}\right)\hfill \\ \hfill & \le exp\left(\frac{-{ϵ}^2\left|\mathcal{R}\right|\widehat{\mu }}{2(1-ϵ)}\right)(\mathrm{Due}\mathrm{to}\mu \ge \widehat{\mu }/(1-ϵ))\hfill \\ \hfill & \le exp\left(-\frac{(2+\frac{2}{3}ϵ)\widehat{\mathbb{B}}\left(S_i^{*}\right)}{2(1-ϵ)(T_i-ϵT_i)}ln\frac{1}{\delta }\right)\le \delta \hfill \end{array}$$

which implies the proof. □

The theoretical guarantee of Algorithm 2 is stated as follows.

Theorem 1.

For any inputs $ϵ,\delta \in (0,1)$, the Algorithm 2 returns a set of seed sets $S=\{S_1,S_2,\dots ,S_k\}$ satisfying

(a) 

$Pr[c\left(S_i\right)\le (1+ln\frac{T_i-ϵT_i}{ϵ})c\left(S_i^{*}\right)]\ge 1-\delta /n$.

(b) 

$Pr\left(\mathbb{B}\left(S_i\right)\ge T_i·\frac{1-ϵ}{1+ϵ}-ϵ\right)\ge 1-\delta$.

Proof. 

At any i-th iterator of the first loop (line 3 to 19) in Algorithm 2, denote $S_i=S_i^t=\{s_i^1,s_i^2,\dots ,s_i^t\}$ as the solution of algorithm with respect to the threshold $T_i$, and $P_i=\{v_1^i,v_2^i,\dots ,v_l^i\}$ as a set of nodes with minimum cost satisfying $\widehat{\mathbb{B}}\left(P_i\right)\ge T_i-ϵT_i$ and $C_i=c\left(P_i\right)$. Due to the checking condition in line 12, the number of BSes at the end of iteration i obtains at least

$$\begin{array}{c}\hfill N_{min}^i=\frac{(2+\frac{2}{3}ϵ)\Gamma }{{ϵ}^2(T_i-ϵT_i)}ln(\left(\genfrac{}{}{0pt}{}{n}{|S_i|}\right)/\delta )\end{array}$$

(12)

and obtains at most,

$$\begin{array}{c}\hfill N_{max}^i=\underset{j:1\dots |S_i|}{max}\frac{(2+\frac{2}{3}ϵ)\Gamma }{{ϵ}^2(T_i-ϵT_i)}ln(\left(\genfrac{}{}{0pt}{}{n}{j}\right)/\delta )\end{array}$$

(13)

Prove (a) As $\widehat{\mathbb{B}}(·)$ is submodular, we have

$$\begin{array}{cc}\hfill & T_i-ϵT_i-\widehat{\mathbb{B}}\left(S_i^{t-1}\right))\le \widehat{\mathbb{B}}\left(P_i\right)-\widehat{\mathbb{B}}\left(S_i^{t-1}\right))\hfill \\ \hfill & \le \widehat{\mathbb{B}}(P_i\cup S_i^{t-1})-\widehat{\mathbb{B}}(S_i^{t-1}))\hfill \\ \hfill & \le \sum _{v\in P_i\backslash S_i^{t-1}}(\widehat{\mathbb{B}}(S_i^{t-1}\cup \left\{v\right\})-\widehat{\mathbb{B}}\left(S_i^{t-1}\right))\hfill \\ \hfill & \le \frac{C_i}{c\left(S_i^{t-1}\right)}\sum _{v\in P_i\backslash S_i^{t-1}}(\widehat{\mathbb{B}}(S_i^{t-1}\cup \left\{v\right\})-\widehat{\mathbb{B}}\left(S_i^{t-1}\right))\hfill \end{array}$$

For any positive numbers $a_1,\dots a_l$ and $b_1,\dots ,b_l$. According to [40], we have

$$\begin{array}{c}\hfill \underset{i=1\dots l}{min}\frac{a_i}{b_i}\le \frac{{\sum }_{i=1}^l{a}_i}{{\sum }_{i=1}^l{b}_i}\le \underset{i=1\dots l}{max}\frac{a_i}{b_i}\end{array}$$

(14)

Applying the above inequality, we obtain

$$\begin{array}{cc}\hfill T_i-ϵT_i-\widehat{\mathbb{B}}\left(S_i^t\right)& \le \frac{C_i}{c\left(s_i^t\right)}(\widehat{\mathbb{B}}\left(S_i^t\right)-\widehat{\mathbb{B}}\left(S_i^{t-1}\right))\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & \le (1-\frac{c\left(s_i^t\right)}{C_i})(T_i-ϵT_i-\widehat{\mathbb{B}}\left(S_i^{t-1}\right))\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & \le e^{-\frac{c\left(s_i^t\right)}{C_i}}(T_i-ϵT_i-\widehat{\mathbb{B}}(S_i^{t-1}))\hfill \end{array}$$

(17)

The (17) condition must satisfy $x+1\le e^x$, for any $x>0$. Therefore,

$$\begin{array}{cc}\hfill T_i-ϵT_i-\widehat{\mathbb{B}}\left(S_i^t\right)& \le e^{-\frac{1}{C_i}{\sum }_{j=1}^{t}c\left(s_i^t\right)}(T_i-ϵT_i)\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & =e^{-\frac{1}{C_i}c\left(S_i^t\right)}(T_i-ϵT_i)\hfill \end{array}$$

(19)

By the definition of $S_i^t$ and because $S_i$ satisfies the condition in line 7, we have $\widehat{\mathbb{B}}\left(S_i^{t-1}\right)<T_i-ϵT_i-ϵ$ and $\widehat{\mathbb{B}}\left(S_i^t\right)\ge T_i-ϵT_i-ϵ$. Combining with (19), we have

$$\begin{array}{cc}\hfill (T_i-ϵT_i)e^{-\frac{1}{C_i}c\left(S_i^{t-1}\right)}& \ge T_i-ϵT_i-\widehat{\mathbb{B}}\left(S_i^{t-1}\right)\hfill \\ \hfill & >T_i-ϵT_i-(T_i-ϵT_i-ϵ)=ϵ\hfill \end{array}$$

implying that $c\left(S_i^{t-1}\right)<C_{i}ln\frac{T_i-ϵT_i}{ϵ}$. On the other hand, from (17), we obtain

$$\begin{array}{c}\hfill c\left(s_i^t\right)\le C_{i}ln\frac{T_i-ϵT_i-\widehat{\mathbb{B}}\left(S_i^{t-1}\right)}{T_i-ϵT_i-\widehat{\mathbb{B}}\left(S_i^t\right)}\le 1\end{array}$$

(20)

Thus, $c\left(S_i^t\right)=c\left(S_i^{t-1}\right)+c\left(s_i^t\right)\le C_i(1+ln\left(\frac{T_i-ϵT_i}{ϵ}\right))$, where $S_i$ is the candidate solution for threshold $T_i$. After i-th iteration of the first loop, $|{\mathcal{R}}_i|=N(i,j)=\frac{(2+\frac{2}{3}ϵ)\Gamma }{{ϵ}^2(T_i-ϵT_i)}ln(\left(\genfrac{}{}{0pt}{}{n}{j}\right)/\delta )$. By applying Lemma 3, after iterator i, we have $Pr[\mathbb{B}\left(S_i^{*}\right)\ge T_i-ϵT_i]\ge 1-\delta /\left(\genfrac{}{}{0pt}{}{n}{j}\right)$. Combining with the definition of $P_i$, the following events happen with a probability of at least $1-\delta /\left(\genfrac{}{}{0pt}{}{n}{t}\right)\ge 1-\delta /n$:

$$\begin{array}{cc}\hfill c\left(S_i\right)& \le C_i(1+ln(\frac{T_i-ϵT_i}{ϵ}))\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & \le c\left(S_i^{*}\right)(1+ln(\frac{T_i-ϵT_i}{ϵ}))\hfill \end{array}$$

(22)

Prove (b) The i-th iteration of the first loop ends when $\widehat{\mathbb{B}}\left(S_i\right)\ge T_i-T_iϵ-ϵ$, we obtain

$$\begin{array}{cc}\hfill Pr\left(\mathbb{B}\left(S_i\right)\le T_i\frac{1-ϵ}{1+ϵ}-ϵ\right)& \le Pr\left(\mathbb{B}\left(S_i\right)\le \frac{T_i-T_iϵ-ϵ}{1+ϵ}\right)\hfill \\ \hfill & \le Pr\left(\mathbb{B}\left(S_i\right)\le \frac{\widehat{\mathbb{B}}\left(S_i\right)}{1+ϵ}\right)\hfill \\ \hfill & \le e^{\frac{-{ϵ}^2\left|{\mathcal{R}}_i\right|\widehat{\mathbb{B}}\left(S_i\right)}{2\Gamma (1+ϵ)}}\left(\mathrm{By\; applying}\right(10\left)\right)\hfill \\ \hfill & \le e^{\frac{-ln(\left(\genfrac{}{}{0pt}{}{n}{j}\right)/\delta )}{1+ϵ}}\hfill \\ \hfill & \le 1-\delta /\left(\genfrac{}{}{0pt}{}{n}{j}\right)\hfill \end{array}$$

Since $|S_i|=j$ there are at most $\left(\genfrac{}{}{0pt}{}{n}{j}\right)$ possible solutions $S_i$. By applying the union bound of the probability of events, we have $Pr\left(\forall S_i,\mathbb{B}\left(S_i\right)\le T_i·\frac{1-ϵ}{1+ϵ}-ϵ\right)\le \delta$. Hence, $Pr\left(\mathbb{B}\left(S_i\right)\ge T_i·\frac{1-ϵ}{1+ϵ}-ϵ\right)\ge 1-\delta$. The proof is completed. □

Theorem 2

(Number of required BSes). For any $ϵ,\delta \in (0,1)$, the sample complexity of ESSM is $O({ϵ}^{-2}nln(\left(\genfrac{}{}{0pt}{}{n}{i_{max}}\right)/\delta ))$, where $i_{max}=arg{max}_{i=1\dots |S_k|}ln\left(\left(\genfrac{}{}{0pt}{}{n}{i}\right)\right)$.

Proof. 

The number of BSes for finding seed set $S_i$ is at most $N_{max}^i$. The algorithm reuses the set of BSes for current seed set for next iteration, so the number of BSes generated by the algorithm is at most $N_{max}^k$. On the other hand, $\Gamma ={\sum }_{u\in V}b\left(u\right)\le b_{max}n=O\left(n\right)$. Therefore, the number of samples used in the algorithm is

$$\begin{array}{c}\hfill \frac{(2+\frac{2}{3}ϵ)\Gamma }{{ϵ}^2(T_1-ϵT_1)}ln(\left(\genfrac{}{}{0pt}{}{n}{i_{max}}\right)/\delta )=O({ϵ}^{-2}nln(\left(\genfrac{}{}{0pt}{}{n}{i_{max}}\right)/\delta ))\end{array}$$

which completes the proof. □

Denote $M,(M\le n)$ is the expected running time for generating one BS, and $j_{max}$ is the largest number of iterations of selecting a seed set. The time complexity of the algorithm is $O({ϵ}^{-2}nk{j}_{max}Mln(\left(\genfrac{}{}{0pt}{}{n}{N_{max}^k}\right)/\delta ))$.

4. Experiments and Discussion

In this section, some extensive experiments are carried out to show the performance of the ESSM algorithm in comparison with other state-of-the-art algorithms on three important metrics: running time, cost of seed sets, and memory usage.

4.1. Experiment Settings

4.1.1. Datasets

For a comprehensive experiment, six networks are selected for information propagation problems [1,2,3,4,5,21] of different sizes. The description of used datasets is presented in

Table 2. Datasets.

Dataset	#Nodes	#Edges	Avg. Degree	Source
Gnutella	6301	20,777	3.3	[41]
Enron	36,692	183,831	5.0	[42]
Net-Hept	15,233	58,891	5.5	[43]
Net-Phy	37,154	231,584	13.4	[5]
Amazon	262,111	1,234,877	9.4	[44]
DBLP	317,080	1,049,866	6.6	[45]

.

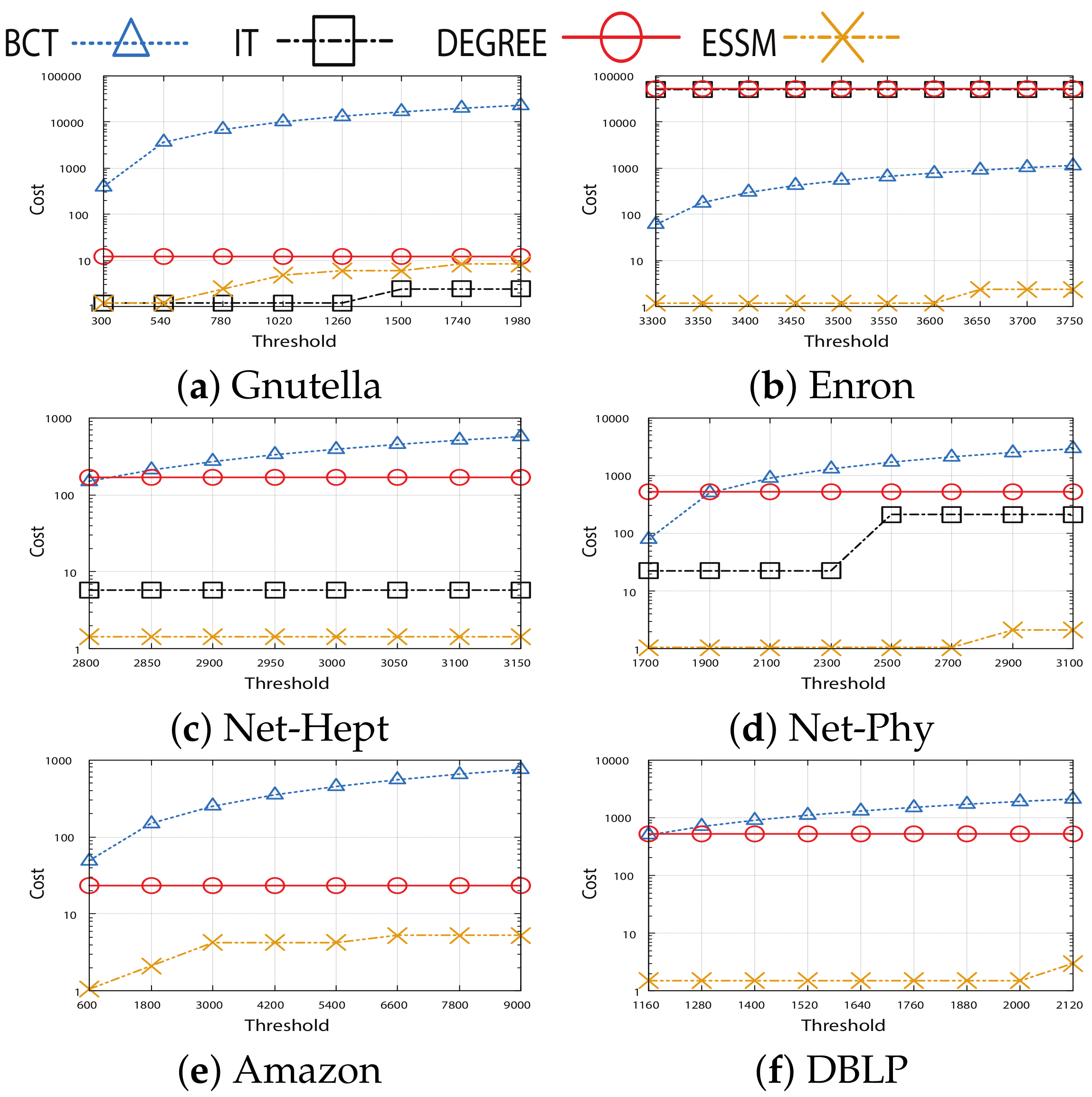
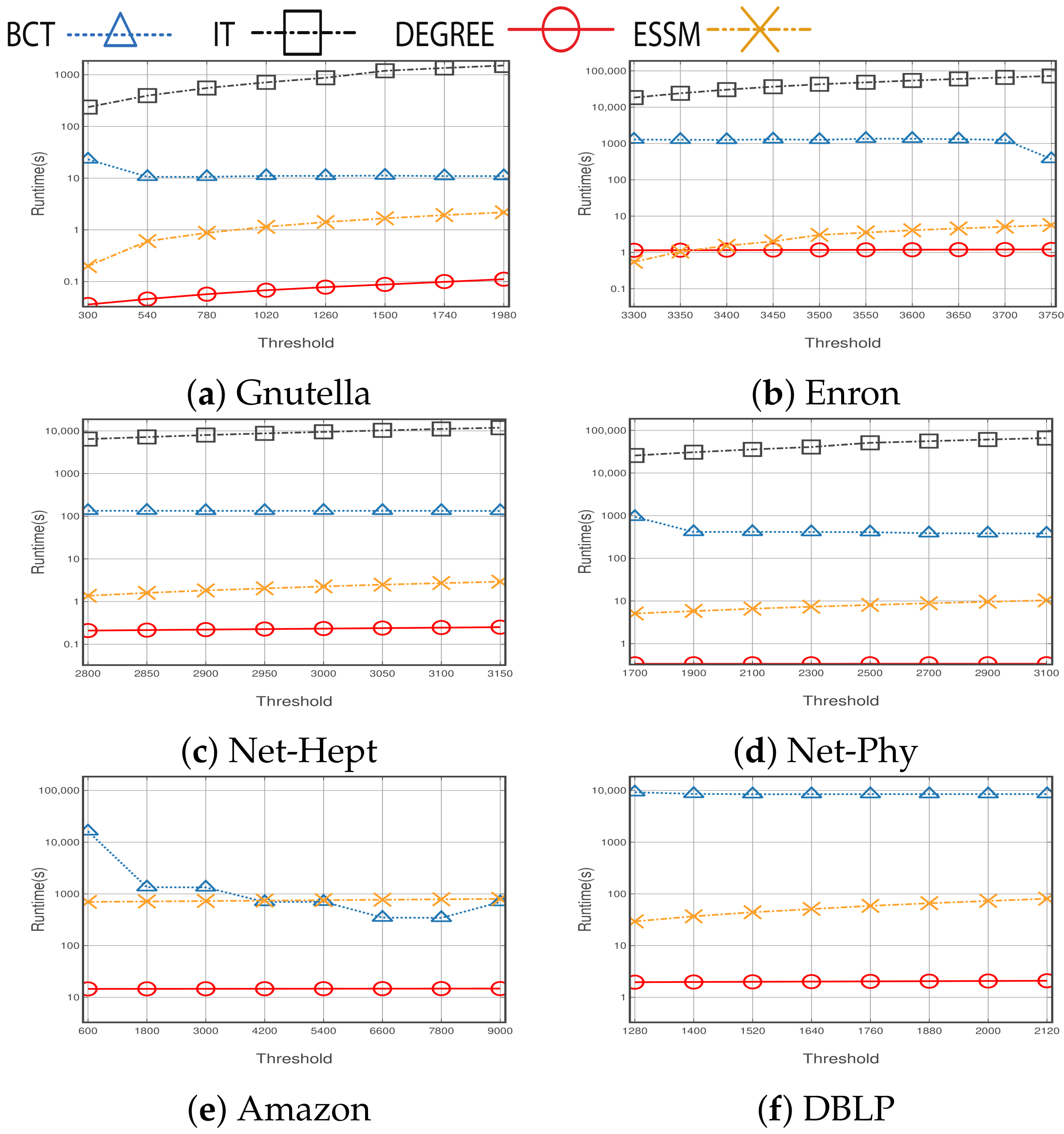
• Gnutella [41] represents Gnutella peer-to-peer file sharing network in August 2002. In this network, 20,777 edges among 6301 nodes show connections among hosts in the Gnutella network topology.
• Email-Enron [42] network covers all the email communication within a dataset of around half a million emails. These originally public data were posted on the web, by the Federal Energy Regulatory Commission during its investigation. Nodes of the network are email addresses and if an address i has sent at least one email to address j, the graph contains an undirected edge. Note that non-Enron email addresses act as sinks and sources in the network as their communication with the Enron email addresses is only under observation. The Enron email data were originally released by William Cohen at CMU.
• Net-Hept [43] and Net-Phy [5] are collaborative networks from the “high-energy physics theory” section and “physics” section, in which the nodes represent the authors and undirected edges represent papers written by the same authors.
• Amazon [44] was collected in 2 March 2003 by crawling the Amazon website. It is based on customers who bought an item and also bought features of the Amazon website. If a product i is frequently copurchased with product j, the graph contains a directed edge from i to j.
• DBLP computer science bibliography [45] provides a comprehensive list of research papers in computer science. If two authors publish at least one publication together, they establish a coauthorship network.

4.1.2. Algorithms Compared

Since IT [36] and CTVM [4] are the problems most closely related to MBT problem, ESSM is compared with their algorithms with some modifications in our experiment. In addition, the DEGREE algorithm, a popular baseline algorithm for information propagation problems [1,2,5,6], is in use. Compared algorithms are listed below.

• BCT is an algorithm for CTVM problem [4]. BCT is used by comparison due to the similarity between the BCT and CTVM problem by considering the costs and benefits of the nodes. However, due to the differences between MBT and CTVM, BCT is adapted with some modifications as follows: For each threshold $T_i$, we use a binary search on the cost from range $[0,{\sum }_{u}c\left(u\right)]$ until the reached benefit function falls in $[T_i(1-ϵ),T_i]$, where $ϵ=0.1$ and returns the seed set with minimum cost.
• IT is a greedy algorithm for the Influence Threshold problem in [36]. In order to adapt IT algorithm for MBT problem, the Monte Carlo simulation is used to estimate benefit function with 10,000 time simulations as in [1,5].
• DEGREE is one of common baseline algorithms for influence problem [1,4,22], which select the highest degree of nodes until the benefit of the selection set exceeds thresholds.

4.1.3. Parameter Settings

For computing the transmission probability in IC model, the conventional computation as in [1,2,3,4] is followed and the transmission probability is calculated as $p(u,v)=\frac{1}{|N_{in}\left(v\right)|}$. We set $c\left(u\right)=\frac{n.N_{out}\left(u\right)}{{\sum }_{v\in V}{N}_{out}\left(v\right)}$ and randomly choose $20\%$ of nodes in each network and set the benefit to 1, the rest assign to 0 as in [4]. Finally, $ϵ=0.1$ and $\delta =1/n$ are set as a default setting [2,3,4] in all the experiments.

We utilize a Linux computer with 2 × Intel(R) Xeon(R) CPU E5-2630 v4 processors running at 2.20 GHz and used 64 GB DDR4 RAM performing at 2400 MHz. Our algorithms are developed in C/C++ using the g++11 compiler.

4.2. Experimental Results

4.2.1. Comparison of the Cost

Figure 1 showed the costs of seed sets returned by algorithms in which the smaller one was better. Our algorithm ESSM outperformed other algorithms by a large gap in most datasets except the Gnutella network. Particularly, ESSM returned the seed sets whose costs are 1875 to 116,000 times more than that of other algorithms. The results also confirmed that our framework algorithm was more efficient than the others.

The IT algorithm only produced good results on the Gnutella dataset and produced worse results than ESSM did on the rest. However, it delivered better results than the rest algorithms did, because the algorithm always finds important seed nodes with low and rational cost as our algorithm do. With large datasets (Amazon and DBLP), IT did not finish within the time limit. This showed that the Monte Carlo method was not suitable for large networks due to its high complexity. DEGREE algorithm selected the highest out-degree of nodes to prioritize as seed nodes, so the highest degree value affected the cost of computing formula, leading to considerable increase in cost, even when the variety of found seed nodes were small. Especially in the Email-Enron dataset, at the first threshold $T_i$, where a seed node was loaded with the highest out-degree, the DEGREE algorithm resulted in the high cost value, even higher than that of the BCT algorithm; although, BCT was also based on the use of BS samples but produced worse results because it used binary search, which could give much larger results than the optimal solution.

4.2.2. Comparison of Running Time

The running times of algorithms were demonstrated in Figure 2. ESSM was significantly faster than the others on all datasets. ESSM algorithm was 6900 to 127,710 times faster and 39 to 2120 times faster than IT and BCT, respectively. The running time of IT was the longest and could not finish within time limit for Amazon and DBLP networks. This was caused by the long time IT spent on accessing Monte Carlo simulation to estimate the benefit function.

The running times of algorithms are shown in Figure 2. ESSM was significantly faster than the others on all datasets. ESSM algorithm is 6900 to 127,710 times faster and 39 to 2120 times faster than IT and BCT, respectively. The running time of IT was the longest and it could not finish within time limit for Amazon and DBLP networks. This resulted from IT spending a long time on calling Monte Carlo simulation to estimate benefit function.

BCT was significantly faster than IT even though it used many loops for binary search for the reason that the BCT used BS samples to estimate the benefit function instead of Monte Carlo simulation method. However, BCT was significantly slower than our algorithm because it did not have a mechanism for reusing the seed set in finding other seed sets with a larger benefit threshold. The larger number of vertices of the datasets, the more time it took BCT to find a solution. The above results were consistent with our assessment that the seed selection strategy in the reuse of solution could shorten the running time of the algorithm. The above results were consistent with our assessment that the seed selection strategy with the reuse seed sets in our algorithm could shorten the time to find the solution.

DEGREE algorithm was also based on the use of a Monte-Carlo-like IT algorithm. Nevertheless, choosing seed nodes was easily dependent on the existing seed set without predicting the next seed nodes. As a consequence, DEGREE ran for a few seconds and was 4 to 54 times faster than our algorithm.

4.2.3. Comparison of Memory Usage

The memory usage of algorithms are illustrated in

Table 3. Memory usage of compared algorithms.

Dataset	Threshold	Algorithm
		BCT	IT	DEGREE	ESSM
Gnutella	300	0.758	0.77	0.855	1.02
	540	0.805	0.75	0.852	1.02
	780	0.805	0.758	0.719	1.02
	1020	0.758	0.789	0.75	1.02
	1260	0.758	0.789	0.723	1.02
	1500	0.809	0.816	0.723	1.02
	1740	0.824	0.855	0.785	1.02
	1980	0.824	0.813	0.746	1.02
Email-Enron	3300	4859.98	1.051	0.746	0.813
	3350	4874.96	1.051	0.855	0.809
	3400	4841.89	1.051	0.77	0.715
	3450	4863.27	1.051	0.75	0.855
	3500	4839.59	2.328	0.809	0.75
	3550	4856.99	2.582	0.711	0.816
	3600	4858.67	2.582	0.746	0.7
	3650	4835.6	2.582	0.855	0.715
Net-Hept	2800	0.723	0.711	0.711	0.77
	2850	0.723	0.742	0.855	0.77
	2900	0.723	0.75	0.754	0.77
	2950	0.77	0.75	0.855	0.77
	3000	0.805	0.77	0.754	0.77
	3050	0.746	0.809	0.809	0.77
	3100	0.75	0.715	0.75	0.77
	3150	0.75	0.754	0.809	0.77
Net-Phy	1700	2800.25	0.805	20.66	1.117
	1900	1444.21	0.723	20.66	1.117
	2100	1446.43	0.82	20.66	1.117
	2300	1442.56	0.82	20.66	1.117
	2500	1434.55	0.867	20.66	1.117
	2700	1429.17	0.75	20.66	1.117
	2900	1426.53	0.758	20.66	1.117
	3100	1437.99	0.793	20.66	1.117
Amazon	600	0.195	N/A	0.723	12.453
	1800	0.742	N/A	0.789	12.453
	3000	0.742	N/A	0.809	12.512
	4200	0.746	N/A	0.719	12.512
	5400	0.715	N/A	0.813	12.512
	6600	0.715	N/A	0.746	12.512
	7800	0.805	N/A	0.758	12.512
	9000	0.715	N/A	0.742	12.512
DBLP	1280	26,316.8	N/A	0.711	19.121
	1400	41,369.6	N/A	0.715	19.227
	1520	26,009.6	N/A	0.813	19.227
	1640	24,883.2	N/A	0.816	19.227
	1760	24,883.2	N/A	0.719	19.227
	1880	24,883.2	N/A	0.711	19.227
	2000	24,883.2	N/A	0.711	19.227
	2120	24,883.2	N/A	0.754	19.227

. The memory of our ESSM algorithm was not the lowest in small and medium datasets, depending on the characteristics of the data, but the difference was not fairly significant. In the remaining medium and large datasets, the ESSM algorithm clearly offered its advantages with a reduction in memory usage of more than 20,000 times compared with the BCT algorithm in the DBLP dataset. The ESSM algorithm will be more likely to be used on larger datasets while the BCT and IT algorithms will be less likely.

The BCT algorithm does not inherit the sample set across multiple thresholds, such as regenerating independent time-consumption and memory usage for sample sets at each threshold. With a lower threshold, the formula for calculation requires the large number of samples. Whereas the threshold increases, the total required sample set decreases. As a result, the memory usage must decrease and the threshold value must increase. Moreover, the BCT’s sampling algorithm does not guarantee the consistency of the number of samples at a certain threshold, leading to an unusual variation in memory usage among these closing thresholds $T_i$, which was clearly displayed in small datasets using the close thresholds in the experiments as Gnutella, Net-Hept.

During the experiment, the IT algorithm always consumed the highest running time among the algorithms, caused by the use of the classical Monte Carlo sampling algorithm, which consumed the memory usage as well as the run-times. Two large datasets as Amazon and DBLP could not experiment with the IT algorithm partly because during the sampling process, the algorithm overloaded the memory usage. This exhibited the disadvantage of IT algorithm compared with other algorithms. On the contrary, IT used less memory than BCT and ESSM did in some cases because of its no need of storing BS samples such as the other two mentioned algorithms. Finally, similar to IT, DEGREE used the least amount of memory because of its simplicity with no inheritance in building solutions.

4.3. Discussions

The primary difference between our algorithm and the other algorithms was its permission for the reuse of solutions at lower thresholds for higher thresholds while still ensuring the quality of solutions. To ensure approximate guarantee for MBT problem, current state-of-the-art algorithms require to do this once for each threshold $T_i$. Our algorithm only needs to be performed one time for all thresholds of the problem. Consequently, it saves time and performs well with large networks. This is consistent with our experimental results. For most datasets, our algorithm guarantees solution quality (total cost of reaching thresholds) but is significantly faster than the other algorithms. Furthermore, our algorithm also offers significantly better solution quality than the other algorithms do. The reason is that the candidate solutions are still checked by the sampling method with the appropriate number of samples.

5. Conclusions and Future Work

In this paper, motivated by applications in viral marketing, we the investigate MBT problem, which finds seed sets $S_1,S_2,\dots ,S_k$ so that their influence benefits are at least given thresholds $T_1,T_2,\dots ,T_k$, respectively, under the well-known Independent Cascade model. In the above model, the relationships among users in a social network are represented by a propagation probability or transmission probability.

The problem of our study generalizes the IT problem by considering the following factors: the benefit of each node and finding many seed sets with many thresholds. Although the current IT algorithms are applicable to our problem, multiple repetitions of these are required to find solutions for all thresholds, which makes them expensive and time-consuming.

In order to address the above challenge, we devise ESSM, an efficient algorithm that not only provides solutions with theoretical bounds but also can find multiple seed sets at once. The results confirmed the effectiveness of our algorithm and indicated that it highly outperformed the state-of-the-art algorithms in terms of both solution quality and running time.

One question that arises is whether our algorithm can keep solution guarantees as well as performance against other information propagation models. In the future work, further investigation into MBT problem is going to reveal under other information diffusion models and efficient algorithms are further proposed.

Another interesting question about our research is whether our algorithm is still efficient when each user relationship is affected by different topics. In the future, this issue will be thoroughly under discussion and an algorithm that is appropriate for that context is recommended.