Branching Random Walks with Two Types of Particles on Multidimensional Lattices
Abstract
:1. Introduction
2. Description of the Model
3. The First Moments
3.1. Differential Equations for Moments
3.2. Solutions of Differential Equations for the First Moments
3.3. Asymptotic Behavior in the Case of Finite Variance of Jumps
4. The Second Moments
4.1. Differential Equations for Moments
4.2. Solutions of Differential Equations for the Second Moments
5. Clustering for BRWs with Two Types of Particles with a Critical Reproduction Law
5.1. Degeneration Probability
5.2. Clustering
6. Example
6.1. Description of the Model
6.2. The First Moments
6.3. The Second Moment for
6.4. Intermittency for
6.5. The Second Moment for
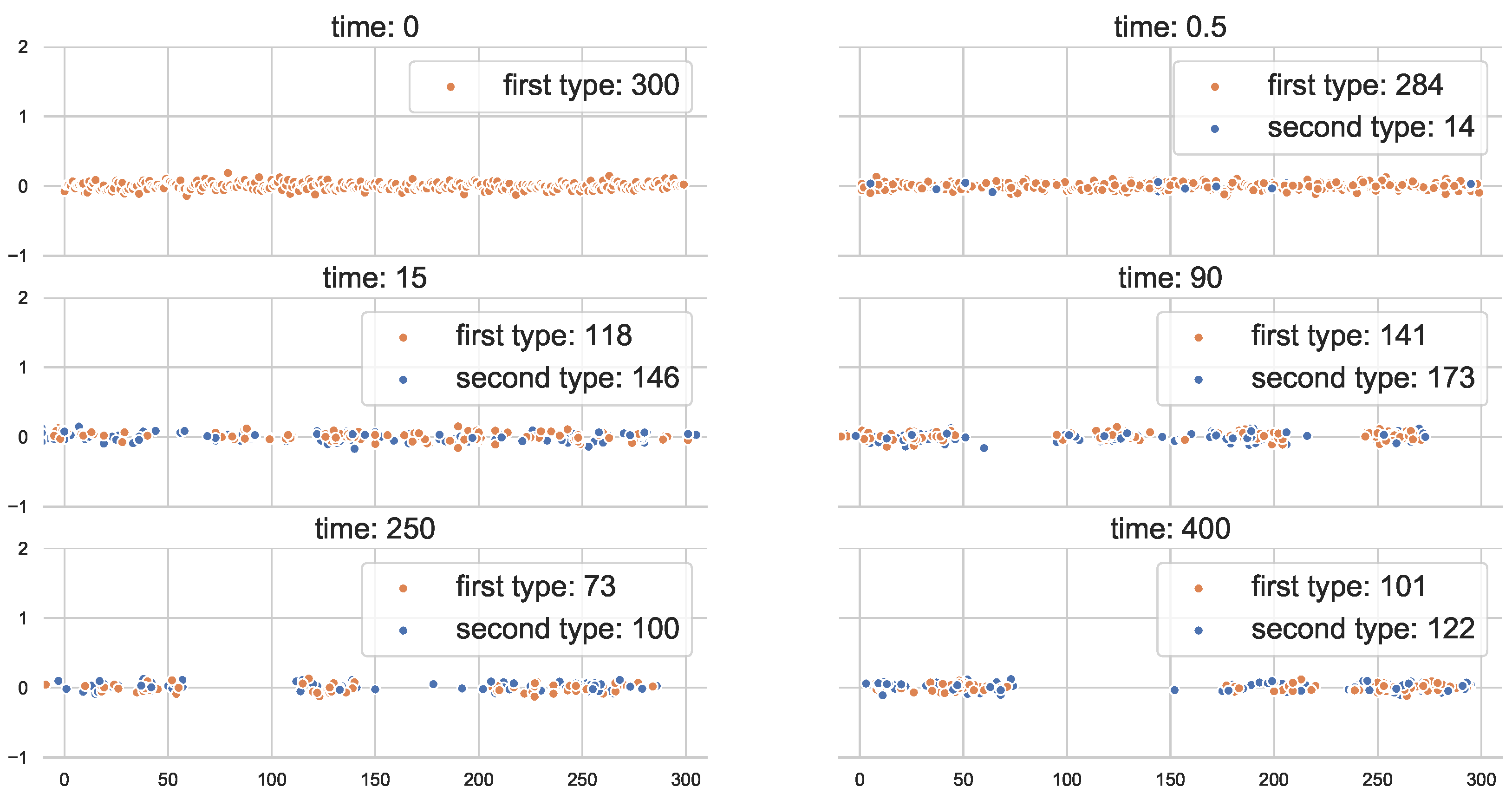
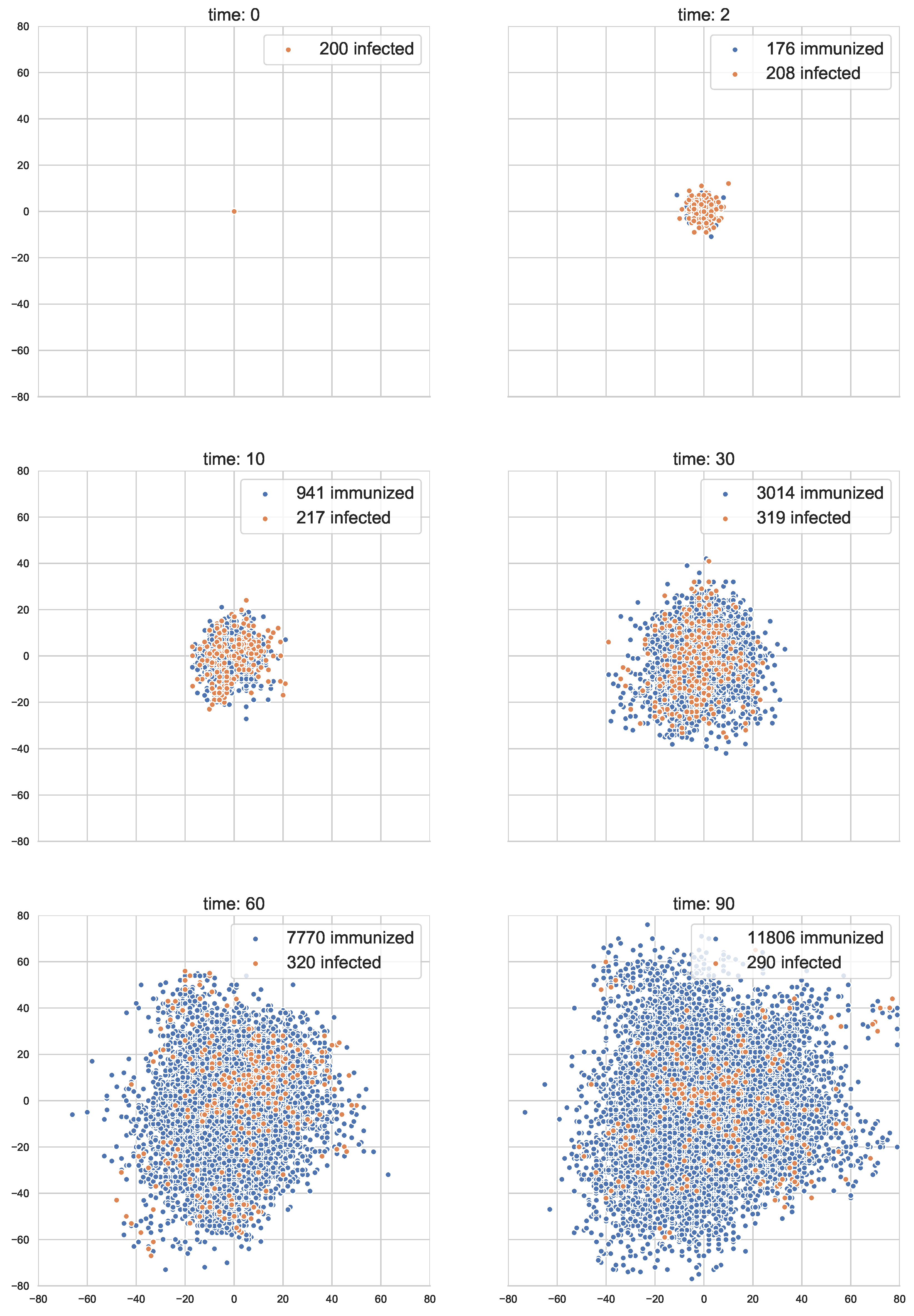
7. Simulation of BRW
- d is the lattice dimension;
- R is the array consisting of a finite number of lists characterizing types i and particle positions at the initial moment of time;
- are diffusion coefficients;
- are matrices of the random walk intensities, by which the generators (3) are determined;
- are the death intensities;
- are the birth intensities;
- is the intensity of degeneration from the first type to the second;
- is the duration of evolution under consideration.
- with probability dies;
- with probability divides into particles, then we append k lists and l lists to the array;
- with probability jumps from position x to position , then we append to the array;
- with probability turns into a particle of the second type, then we append to the array.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Yarovaya, E.B. Branching Random Walks in a Heterogeneous Environment; Center of Applied Investigations of the Faculty of Mechanics and Mathematics of the Moscow State University: Moscow, Russian, 2007. (In Russian) [Google Scholar]
- Bulinskaya, E.V. Spread of a catalytic branching random walk on a multidimensional lattice. Stochastic Process. Appl. 2018, 128, 2325–2340. [Google Scholar] [CrossRef] [Green Version]
- Barczy, M.; Li, Z.; Pap, G. Stochastic differential equation with jumps for multi-type continuous state and continuous time branching processes with immigration. ALEA Lat. Am. J. Probab. Math. Stat. 2015, 12, 129–169. [Google Scholar]
- Barczy, M.; Nedényi, F.K.; Pap, G. On aggregation of multitype Galton-Watson branching processes with immigration. Mod. Stoch. Theory Appl. 2018, 5, 53–79. [Google Scholar] [CrossRef] [Green Version]
- Makarova, Y.; Han, D.; Molchanov, S.; Yarovaya, E. Branching random walks with immigration. Lyapunov stability. Markov Process. Related Fields 2019, 25, 683–708. [Google Scholar]
- Makarova, Y.; Kutsenko, V.; Yarovaya, E. On Two-Type Branching Random Walks and Their Applications for Genetic Modelling. In Recent Developments in Stochastic Methods and Applications; Shiryaev, A.N., Samouylov, K.E., Kozyrev, D.V., Eds.; Springer: Cham, Switzerland, 2021; Volume 371, pp. 255–268. [Google Scholar] [CrossRef]
- Molchanov, S.; Whitmeyer, J. Spatial models of population processes. In Modern Problems of Stochastic Analysis and Statistics; Springe: Cham, Switzerland, 2017; Volume 208, pp. 435–454. [Google Scholar] [CrossRef]
- Sevast’yanov, B.A. Vetvyashchiesya Protsessy; Izdat. “Nauka”: Moscow, Russian, 1971; p. 436. (In Russian) [Google Scholar]
- Braunsteins, P.; Hautphenne, S. Extinction in lower Hessenberg branching processes with countably many types. Ann. Appl. Probab. 2019, 29, 2782–2818. [Google Scholar] [CrossRef] [Green Version]
- Braunsteins, P.; Hautphenne, S. The probabilities of extinction in a branching random walk on a strip. J. Appl. Probab. 2020, 57, 811–831. [Google Scholar] [CrossRef]
- Vatutin, V.; Wachtel, V. Multi-type subcritical branching processes in a random environment. Adv. Appl. Probab. 2018, 50, 281–289. [Google Scholar] [CrossRef] [Green Version]
- Vatutin, V.A.; D’yakonova, E.E. The survival probability for a class of multitype subcritical branching processes in random environment. Math. Notes 2020, 107, 189–200. [Google Scholar] [CrossRef] [Green Version]
- Molchanov, S.A.; Yarovaya, E.B. Large deviations for a symmetric branching random walk on a multidimensional lattice. Proc. Steklov Inst. Math. 2013, 282, 186–201. [Google Scholar] [CrossRef]
- Yarovaya, E.B.; Stoyanov, J.M.; Kostyashin, K.K. On conditions for a probability distribution to be uniquely determined by its moments. Theory Probab. Appl. 2020, 64, 579–594. [Google Scholar] [CrossRef]
- Stoyanov, J.M. Counterexamples in Probability; Dover Publications, Inc.: Mineola, NY, USA, 2013. [Google Scholar]
- Yarovaya, E.B. Spectral properties of evolutionary operators in branching random walk models. Math. Notes 2012, 92, 115–131. [Google Scholar] [CrossRef]
- Filippov, A.F. Sbornik Zadach po Differentsial’nym Upravleniyam. Uchebnoe Posobie; Moskva: Nauka, Russian, 1992; p. 128. [Google Scholar]
- Molchanov, S.A.; Yarovaya, E.B. Limit theorems for the Green function of the lattice Laplacian under large deviations for a random walk. Izv. Math. 2012, 76, 1190–1217. [Google Scholar] [CrossRef]
- Balashova, D.; Molchanov, S.; Yarovaya, E. Structure of the particle population for a branching random walk with a critical reproduction law. Methodol. Comput. Appl. Probab. 2021, 23, 85–102. [Google Scholar] [CrossRef] [Green Version]
- Gikhman, I.I.; Skorokhod, A.V. Vedenie v Teoriyu Sluchaĭnykh Protsessov, 2nd ed.; Izdat. “Nauka”: Moscow, Russian, 1977; p. 567. [Google Scholar]
- Getan, A.; Molchanov, S.; Vainberg, B. Intermittency for branching walks with heavy tails. Stoch. Dyn. 2017, 17, 1750044. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makarova, I.; Balashova, D.; Molchanov, S.; Yarovaya, E. Branching Random Walks with Two Types of Particles on Multidimensional Lattices. Mathematics 2022, 10, 867. https://doi.org/10.3390/math10060867
Makarova I, Balashova D, Molchanov S, Yarovaya E. Branching Random Walks with Two Types of Particles on Multidimensional Lattices. Mathematics. 2022; 10(6):867. https://doi.org/10.3390/math10060867
Chicago/Turabian StyleMakarova, Iuliia, Daria Balashova, Stanislav Molchanov, and Elena Yarovaya. 2022. "Branching Random Walks with Two Types of Particles on Multidimensional Lattices" Mathematics 10, no. 6: 867. https://doi.org/10.3390/math10060867
APA StyleMakarova, I., Balashova, D., Molchanov, S., & Yarovaya, E. (2022). Branching Random Walks with Two Types of Particles on Multidimensional Lattices. Mathematics, 10(6), 867. https://doi.org/10.3390/math10060867






