Abstract
The performance of constrained multi-objective differential evolution algorithms (CMOEAs) is mainly determined by constraint handling techniques (CHTs) and their generation strategies. To realize the adaptive adjustment of CHTs and generation strategies, an adaptive constrained multi-objective differential evolution algorithm based on the state–action–reward–state–action (SARSA) approach (ACMODE) is introduced in the current study. In the proposed algorithm, the suitable CHT and the appropriate generation strategy can be automatically selected via a SARSA method. The performance of the proposed algorithm is compared with four other famous CMOEAs on five test suites. Experimental results show that the overall performance of the ACMODE is the best among all competitors, and the proposed algorithm is capable of selecting an appropriate CHT and a suitable generation strategy to solve a particular type of constrained multi-objective optimization problems.
Keywords:
constrained multi-objective optimization; evolutionary computation; reinforcement learning; SARSA method MSC:
68Txx
1. Introduction
Constrained multi-objective optimization problems (CMOPs) are commonly found in the field of engineering optimization, such as robot’s design optimization [1], compressed-air station scheduling problem [2] and scheduling optimization of microgrid [3]. To effectively solve CMOPs, various improved CMOEAs have been proposed. For example, Wang et al. [4] proposed a cooperative multi-objective evolutionary algorithm with a propulsive population (CMOEA-PP) to achieve a tradeoff among the diversity, the convergence, and the feasibility in different evolutionary stages. Datta et al. [5] combined the evolutionary multi-objective optimization method with the penalty function method, and proposed a bi-objective hybrid constrained optimization algorithm (HyCon) to deal with CMOPs. Yuan et al. [6] proposed an indicator-based evolutionary algorithm to prevent the population from falling into local areas. Cui et al. [7] proposed an adaptive constraint handling technique (CHT), which can adaptively select suitable CHT from three state-of-the-art CHTs via the Q-learning method.
Although various CMOEAs have been proposed to carry out adaptation selection of CHTs, their search strategies are generally constant during the entire evolutionary process. Therefore, it may not be effective when solving different types of CMOPs. To alleviate the above issues, an adaptive constraint multi-objective differential evolution algorithm based on SARSA method (named as ACMODE) is proposed. In the ACMODE, three commonly used CHTs are selected and the SARSA [8] is utilized to select appropriate CHTs during different stages of the evolution. Moreover, two-generation strategies are chosen in differential evolution (DE), and the SARSA method is used to select appropriate generation strategies in the next iteration. Simulation experiments with four other CMOEAs are carried out on five constrained multi-objective test suites, and the results show that the ACMODE is more competitive than the four other CMOEAs.
The main contribution of this work is to realize the adaptive adjustment of CHTs and generation strategies in the ACMODE. Three CHTs and two DE’s generation strategies are integrated into the proposed algorithm. The simulation results show that the appropriate CHT and generation strategy can be self-adaptively selected from CHT and generation strategy pools to solve a particular type of CMOPs during the entire evolutionary process. Therefore, ACMODE can integrate the advantages of different CHTs and generation strategies when solving different CMOPs.
The rest of this paper is arranged as follows. Section 2 reviews the related works. Section 3 briefly introduces some basic concepts. The details of the proposed algorithm are presented in Section 4. Subsequently, the experimental results and analyses are shown in Section 5. Some discussions are provided in Section 6. Section 7 draws some conclusions.
2. Literature Review
2.1. Constrained Multi-Objective Evolutionary Algorithms
Recently, a large number of CMOEAs have been proposed to solve CMOPs. For example, Yu et al. [9] proposed a corner point-based algorithm, which has two stages: in the first stage, corner points are quickly found, and in the second stage, a new diversity and convergence strategy is used to approach the real Pareto front. In [10], CMOPs can be divided into three types according to the relationship between the constrained Pareto-optimal front and unconstrained Pareto front. By considering potential problem types, a new CHT was proposed to solve CMOPs. Fan et al. [11] introduced a novel framework, in which the entire search process is divided into push stage and pull stage. Constraints have not been considered in the push stage, while an improved epsilon-constraint method is used in the pull phase. To improve the search performance of MOEAs, a local search mechanism [12] was proposed, which can contain constraint information and does not need to explicitly calculate gradient information. Liu et al. [13] developed an indicator-based CMOEA framework, in which indicator-based MOEAs and CHTs are effectively combined to solve CMOPs. In [14], a coevolutionary framework was proposed to solve CMOPs via using two different populations. A two-phase framework (ToP) was proposed in Ref. [15]. In the ToP, a CMOP was transformed into constrained single-objective optimization problems for locating promising regions in the first phase, and a specific and efficient CMOEA was employed to find feasible solutions in the second stage. In addition, a dual-stage dual-population evolutionary algorithm [16] was proposed recently. The whole search process was divided into exploration and exploitation, and two populations evolved with and without considering the constraints. Based on the DE [17], a new DE variant named IMDE [18] was proposed, which used infeasible solutions to guide mutation operators and applied multiple combinations of mutation strategies and control parameters to enhance the search performance. Yu et al. [19] proposed a dynamic selection preference-assisted constrained multiobjective differential evolutionary algorithm (DSPCMDE). In DSPCMDE, the selection preference of each individual changes from objective functions to constraint function as the evolutionary process. To balance feasibility, convergence and distribution, Yang et al. [20] proposed a multi objective differential evolutionary algorithm based on partition selection (MODE-PS). In MODE-PS, a CMOP is divided into several subproblems by objective space to keep the distribution. Each subspace saves one feasible solution to a feasible solution set to maintain the feasibility of the subspaces. Once there are feasible solutions in one subspace, the individual selection strategy is changed from constraint search to non-constraint search to accelerate the convergence. Lin et al. [21] proposed a multi-objective differential evolution with dynamic hybrid constraint handling mechanism (MODE-DCH) to tackle CMOPs. In the MODE-DCH, the different search models combined with different CHTs are used. In addition, Xiao et al. [22] proposed a new mutation mechanism. In this mechanism, DE mutation operator and Gaussian mutation operator are used to deal with infeasible solutions and feasible solutions respectively. Wang et al. [23] proposed a cooperative differential evolution framework (CCMODE) in which the mutation operator is used to guide the infeasible individuals to move to the feasible region.
2.2. Self-Adaptive Evolutionary Algorithms
No strategy can perform best on all types of CMOPs due to No Free Lunch [24]. To integrate the advantage of different strategies, many self-adaptive constrained multi-objective evolutionary algorithms have been introduced. Based on the improved epsilon-constraint method, Yang et al. [25] proposed a multi-objective differential evolutionary algorithm named MODE-SaE. In MODE-SaE, the global search and local search can be self-adaptively adjusted by self-switching parameters of the search engine to balance the convergence and distribution. In [26], a CMOP was decomposed into multiple subproblems. Each subproblem has a subpopulation in a subregion. The appropriate CHT can be adaptively selected in each subregion. Based on decomposition and the DE, Liu and Bi [27] presented an adaptive ε-constraint MOEA to make full use of the information of infeasible solutions. They also proposed an adaptive DE mutation strategy to increase search efficiency and avoid falling into the local optimum. In [28], an adaptive search operator scheme was introduced. When a search operator hits a difficult patch in the search space, the scheme “reacts” to that by potentially calling upon a different search operator. Zhang et al. [29] proposed a constrained multi-objective optimization algorithm based on adaptive ε-truncation (ε-T-CMOA) to further improve the distribution and convergence of the obtained solutions. In [30], an adaptive repair approach was proposed to improve the efficiency of constraint handling in non-dominance. Repairing was carried out on the solutions that dominate all feasible solutions or have the smallest constraint violation.
3. Basic Concepts
3.1. Constrained Multi-Objective Optimization Problem
CMOPs can be mathematically defined as follows:
where x is the D-dimensional decision vector; f(x) is an objective vector containing m objectives; is the jth inequality constraint and p denotes the number of inequality constraints; is the (j-p)th equality constraint and has (q-p) equality constraints; O is the decision space.
The constraint violation degree of the solution x can be computed as:
where δ is the tolerance value of equality constraints and is usually set as a small positive value. The overall constraint violation degree of the solution x can be calculated as follows:
For Equation (3), the solution x is a feasible solution when C(x) = 0. On the contrary, it is an infeasible solution.
3.2. Concepts in Multi-Objective Optimization Problem
Basic concepts in multi-objective optimization are represented as follows [31]:
Definition 1
(Dominance relation). If there are two vectors u and v in the minimization optimization problem, and , then is said to dominate v, denoted as .
Definition 2
(Pareto optimal set). For a solution , if and only if there is no other solution x such that , it is called a Pareto optimal solution of a CMOP. All the Pareto optimal solutions form the Pareto set (PS), defined as .
Definition 3
(Pareto front). The Pareto front can be referred to .
3.3. Constraint Handling Strategies
The CHTs adopted in our proposed algorithm are self-adaptive penalty (SP), constrained-domination principle (CDP) and adaptive tradeoff model (ATM).
3.3.1. SP
SP [32] is a representative way to solve CMOPs which penalizes the infeasible individual with a penalty function. It has two main components: the distance value and the penalty function. SP can be defined as follows:
where ln(x) is the n-th distance value; bn(x) is the n-th penalty value; C(x) is the degree of constrained violation, ; is the normalized objective function value; rf is feasible rate of the population; Then, the population is sorted based on the m fitness functions M1, M2…, Mm via the nondominated sorting.
3.3.2. CDP
CDP [33] proposed by Deb is a simple and efficient technology to select individuals, which compares pairwise individuals based on the following rules:
- Any feasible solution is preferred to any infeasible solution.
- For two feasible solutions, the Pareto non-dominant individual is preferred.
- For two infeasible solutions, the one with a smaller degree of constraint violation is preferred.
3.3.3. ATM
Based on the feasibility ratio of the current population, ATM [34] divides the evolutionary process into three situations:
- The infeasible situation: The constraint violation is considered as an additional objective. The nondominated sorting is applied, and then half of the individuals with fewer constraint violations in the first layer are sorted in the offspring population, then deleted from the population. The same operation is performed on the remaining individuals until the number of offspring reaches population size.
- The semi-feasible situation: Similar to SP, ATM uses a new function, which is calculated as follows:
- The feasible situation: Nondominated sorting is used to select individuals.
3.4. Performance Metric
In the present work, two widely used performance metrics are employed: the inverted generational distance (IGD) and the hypervolume (HV).
3.4.1. IGD
IGD [35] is calculated as:
where H represents the PF approximation; PF* is a set of solutions obtained by evolutionary algorithms, which is uniformly distributed along the true PF; d (z*, H) is the minimum Euclidean distance between individual z* in PF* and H, |PF*| denotes the number of points in PF*. The algorithm with a smaller IGD value has better performance [36]. Generally, IGD can simultaneously evaluate the convergence and diversity of PF.
3.4.2. HV
HV [37] can be defined as follows:
where L is the Lebesgue measure; represents a solution in H; and denotes a worst point dominated by all the Pareto optimal solutions. A larger HV means a better Pareto front set in both the convergence and the diversity [36].
3.5. Basics of DE
Differential evolution algorithm [38] is a simple and efficient meta-heuristic search algorithm. Its main operator steps are as follows:
3.5.1. Generation Strategy
Two commonly seen generation strategies are as follows:
“DE/rand-to-best/1/bin”:
“DE/current-to-rand/1”:
where is the ith individual in the Gth generation; indices r1, r2, and r3, which are all different from i and are randomly generated from 1 to NP (population size). The scale factor is F, which is used to scale differential vectors. represents the best individual in the Gth generation. Rj is a random number, which ranges from 0 to 1; CR is crossover probability; jrand is an integer randomly generated within [1, D]. It is worth noting that the binomial crossover is not implemented in “DE/current-to-rand/1”. The information of the best individual is employed in “DE/rand-to-best/1/bin”, so it is able to enhance the convergence. While the diversity can be maintained in “DE/current-to-rand/1”, since other randomly selected individuals are learned.
3.5.2. Selection
After the generation strategy, the selection operation is performed to select the good solutions as the parents for the next generation, which can be defined as follows:
where is the selected solution that can be used in next generation.
4. Proposed Algorithm
Different CHTs and generation strategies have significant effects on the performance of CMOEAs. To further improve the performance, an adaptive constrained multi-objective differential evolution algorithm (ACMODE) is proposed in the present study. When solving different types of CMOPs in the ACMODE, suitable CHT and generation strategies can be adaptively selected during the whole evolutionary process.
The main operators in the ACMODE are as follows:
4.1. Adaptive Constraint Handling Technology
Different CHTs are suitable for solving different properties of CMOPs, thus the adaptation of CHTs is proposed in the current work. Three commonly used CHTs (SP [32], CDP [33] and ATM [34]) are selected and the SARSA method is used to realize the adaptation of these three different CHTs. To evaluate the performance of each CHT, an improved IGD is given as follows [39]:
where is selected from all achieved PF approximations.
The pseudocode of the proposed adaptive CHT method is described in Algorithm 1. The action space can be defined as AC = [SP, CDP, ATM], the state space can be expressed as SV = [excellent, medium, poor], and the value of reward RC is [1, 0, −1] [40]. The form of the Q-table is shown in Table 1:

Table 1.
The form of Q-table.
In lines 1 to 2, according to AC, the number of individuals choosing each CHT can be determined. Therefore, mIGD value can be calculated by Equation (12). In lines 3 to 6, the maximum mIGD value represents the individual choosing this CHT in the “poor” state and its reward is −1; the middle mIGD value indicates the state is “medium” and its reward is 0; and the reward of “excellent” CHT is 1. State s′ is used to predict action a′ and then update the Q-table. Finally, action chain AC is updated.
| Algorithm 1: Adaptive Constraint Handling Technique | |
| Input: the state vector SV and the reward chain RC | |
| Output: action chain AC | |
| 1 | Determine the number of individuals selecting each CHT via AC; |
| 2 | Calculate mIGD value according to Equation (12). |
| 3 | Obtain the s′ and r according to mIGD value, and update SV and RC; |
| 4 | Use ε-greedy method to predict individual action a′ according to s′; |
| 5 | Update Q-table: ; |
| 6 | Update action chain AC; |
4.2. Adaptive Generation Strategy
Different generation strategies play distinct roles in the search process. “DE/current-to-rand/1” has good exploration and search ability, while “DE/rand-to-best/1/bin” possesses good local search capability and its convergence speed is faster than “DE/rand/1”. Consequently, two-generation strategies are applied in the proposed algorithm. The process of adaptive generation strategy is as follows:
Step 1: initialize the state s0 for each individual and the corresponding Q-table. Set a as the action selected by the individual in the initial state using the ε-greedy method.
Step 2: perform the current action a in the current state s. According to the generation strategy chain GC, the number of individuals selecting each generation strategy can be determined. The mIGD value can be calculated by Equation (12).
Step 3: the minimum mIGD value represents that the individual choosing this generation strategy is in an “excellent” state, and its reward is 1. While the reward of “poor” generation strategy is 1. The new state and the corresponding reward can be obtained.
Step 4: according to s′, a new action a′ is selected.
Step 5: update the Q-table: .
Step 6: s = s′; a = a′.
Step 7: update GC.
4.3. Overall Implementation of the Proposed Algorithm
The proposed algorithm ACMODE mainly includes two stages, namely initialization and self-adaptation. The pseudocode of our proposed algorithm is described in Algorithm 2. Lines 1 to 2 are the initialization operator. Firstly, the population is randomly generated. Then, the state vector AV and GV, the action chain AC and GC and the reward chain RC and GRC are also initialized. Lines 3–9 realize the adaption of CHTs and the adaption of generation strategies. Finally, feasible solutions are selected to enter in the external archive B.
| Algorithm 2: ACMODE | |
| Input: Gmax: the maximum number of iterations | |
| Output: final solution set P | |
| 1 | Initialize population ; |
| 2 | Initialize the external archive B, Q-table, the state vector AV and GV, the action chain AC and GC and the reward chain RC and GRC; |
| 3 | for G=1: Gmax do |
| 4 | Each individual selects a F value from the set {0.6, 0.8, 1.0}; |
| 5 | Each individual selects a CR value from the set {0.1, 0.2, 1.0}; |
| 6 | Implement the adaptation of generation strategies according to Section 4.2; |
| 7 | Implement the adaptation of CHTs according to algorithm 1; |
| 8 | Save the feasible solutions at the first level of non-dominated sorting to B; |
| 9 | end for |
| 10 | Output final solution set P according to B. |
5. Experimental Studies
To evaluate the performance of the ACMODE algorithm, it was compared with four other CMOEAs, which are ACHT-CMODE [7], AGS-CMODE, MOEA/D-CDP [41] and ANSGAIII [42]. In addition, two nonparametric statistical tests, the Wilcoxon rank sum test [43] and the Friedman test [44], are employed to analyze the search performances of all comparison algorithms. “+”, “−” and “=”, respectively, indicate that the performance of the comparison algorithm is superior, inferior or similar to that of the ACMODE.
5.1. Benchmark Test Functions and Parameter Settings
All experiments are performed on five benchmark test suites, which are CF [45], LIR-CMOP [46], NCTP [47], MW [48] and DAS-CMOP [49]. CF has 10 CMOPs, LIR-CMOP has 14 test functions, NCTP has 18 test functions, MW has 14 test functions and DAS-CMOP has nine test functions. Two comprehensive performance indicators (IGD and HV) are used to evaluate the algorithm’s performance. For all compared algorithms, run times are set to be 30 on each function, the maximum number of iterations is set to be 500, and the population size is set to be 100. Furthermore, the parameter settings of other comparison algorithms are consistent with the original literature.
5.2. Comparison Results
5.2.1. Comparison Results on CF Test Suite
For the CF test suite, Table 2 and Table 3 give the comparison results of ACMODE and its comparison algorithms in terms of IGD and HV, respectively. Note that IGD and HV can be only used to calculate feasible solutions. The best results are in bold.

Table 2.
IGD results of all comparison algorithms on CF test suite.

Table 3.
HV results of all comparison algorithms on CF test suite.
As shown in Table 2, the results obtained by Wilcoxon’s rank sum test reveal that ACMODE is significantly better than ACHT-CMODE in nine test functions. There is no significant difference between ACMODE and ACHT-CMODE on CF4. In addition, ACMODE performs better than AGS-CMODE in five test functions. ACMODE is similar to AGS-CMODE in five test functions. For the rest of the competitors, MOEA/D-CDP and ANSGAIII are, respectively, worse than ACMODE in nine test functions. ACMODE is similar to MOEA/D-CDP and ANSGAIII in one test function, respectively. The results shown in Table 2 indicate that ACMODE is the best one among all compared algorithms with respect to IGD. The superior performance of the ACMODE is mainly because that appropriate generation strategy and CHT can be adaptively selected in the ACMODE at different stages of evolution.
It can be observed from Table 3 that ACHT-CMODE is outperformed by ACMODE in eight test functions. Moreover, there is no significant difference between ACMODE and ACHT-CMODE on CF9 and CF10. ACMODE performs significantly better than AGS-CMODE in seven test functions. The performance of ACMODE is similar to that of AGS-CMODE on CF2, CF7 and CF10. Furthermore, MOEA/D-CDP and ANSGAIII are significantly surpassed by ACMODE in all test functions. According to the results shown in Table 3, ACMODE is superior to the other four competitors in terms of HV. The superiority of ACMODE is mainly due to the adaptation of generation strategies and CHTs. The true PFs of CF8 and CF10 are disconnected and hindered by several large infeasible regions. This brings challenges to the CMOEAs. MOEA/D-CDP and ANSGAIII are unable to find feasible solutions. However, the experimental results show that the adaptive adjustment of CHTs and generation strategies is beneficial to pass through the infeasible region and then approach the feasible parts.
5.2.2. Comparison Results on LIR-CMOP Test Suite
For LIR-CMOP test suite, Table 4 and Table 5 list the results of all comparison algorithms in terms of IGD and HV, respectively. The best results are in bold.

Table 4.
IGD results of all comparison algorithms on LIR-CMOP test suite.

Table 5.
HV results of all comparison algorithms on LIR-CMOP test suite.
Based on the results obtained by Wilcoxon’s rank sum test in Table 4, we can observe that ACMODE significantly outperforms ACHT-CMODE in all 14 test functions. ACMODE performs better than AGS-CMODE in ten test functions and is similar to AGS-CMODE in four test functions. AGS-CMODE carries out the adaptation of generation strategies, and only one constraint handling method (i.e., CDP) is used. However, ACMODE simultaneously realizes the adaptive adjustment of CHTs and generation strategies. Compared with MOEA/D-CDP, ACMODE shows the similar performance on LIR-CMOP4 and LIR-CMOP6. ACMODE is significantly better than MOEA/D-CDP in 12 test functions. However, ACMODE is outperformed by MOEA/D-CDP on LIR-CMOP14. In addition, ANSGAIII is significantly worse than ACMODE in 12 test functions. The performance of the ACMODE is similar to that of ANSGAIII on LIR-CMOP4 and LIR-CMOP6. These experimental results demonstrate that the ACMODE outperforms all the compared algorithms. The effectiveness of the ACMODE can be attributed to the adaptation of CHTs and generation strategies.
When the solutions obtained by the algorithm are all Pareto dominated by the reference points, the HV value is zero. The reference points of other comparison algorithms are consistent with the original literature [7,41,42]. From the results regarding HV shown in Table 5, ACHT-CMODE performs significantly worse than ACMODE on all 14 test functions. In fact, LIR-CMOP5-LIR-CMOP14 exists within the infeasible barriers when approximating the true PF. ACMODE is more likely to choose “DE/rand-to-best/1/bin”, which has a better exploration ability. Therefore, ACMODE is able to pass through the infeasible region and find high-quality solutions. ACMODE is superior to AGS-CMODE in 11 test functions, and there is no significant difference between ACMODE and AGS-CMODE on LIR-CMOP4, LIR-CMOP9 and LIR-CMOP12. For the rest of compared algorithms, MOEA/D-CDP and ANSGAIII are, respectively, worse than ACMODE in 12 test functions. The performance of ACMODE is similar to that of MOEA/D-CDP and ANSGAIII in two test functions, respectively. ACMODE particularly stands out among all the comparison algorithms because its CHTs and generation strategies can be automatically selected at different evolutionary stages for different CMOPs.
5.2.3. Comparison Results on NCTP Test Suite
For the NCTP test suite, Table 6 and Table 7 give the comparison results of ACMODE and its comparison algorithms in terms of IGD and HV, respectively. The best results are in bold.

Table 6.
IGD results of all comparison algorithms on NCTP test suite.

Table 7.
HV results of all comparison algorithms on NCTP test suite.
According to the results obtained by Wilcoxon’s rank sum test in Table 6, ACHT-CMODE is better than the proposed algorithm ACMODE on NCTP2, NCTP4 and NCTP5. However, it is inferior to ACMODE in 14 test functions. ACMODE is similar to ACHT-CMODE on NCTP1. The main reason is that ACHT-CMODE realizes the adaptation selection of CHTs, and its search strategies are generally constant during the entire evolutionary process. In addition, ACMODE performs better than AGS-CMODE in 12 test functions. AGS-CMODE is better than the proposed algorithm on NCTP1, NCTP2, NCTP13 and NCTP14. There is no significant difference between AGS-CMODE and ACMODE on NCTP4 and NCTP5. For the rest of the competitors, MOEA/D-CDP performs worse than ACMODE in 16 test functions. MOEA/D-CDP and ACMODE have similar performance on NCTP1 and NCTP2. Additionally, ANSGAIII is significantly surpassed by ACMODE in all test functions. The results shown in Table 6 indicate that ACMODE is the best one among all compared algorithms. The reason may be that appropriate generation strategies and CHTs can be automatically selected at different stages of evolution for different types of CMOPs.
The results shown in Table 7 reveal that ACMODE performs better than ACHT-CMODE in 12 test functions, but ACMODE is surpassed by ACHT-CMODE on NCTP7, NCTP8 and NCTP13. ACMODE is superior to AGS-CMODE in eight test functions. However, AGS-CMODE outperforms ACMODE on NCTP7, NCTP8 and NCTP13. There is no significant difference between AGS-CMODE and ACMODE in seven test functions. The results demonstrate that both the adaptive CHT and the adaptation of generation strategy play an important role in improving the performance of CMOEAs. For the rest of compared algorithms, ACMODE is surpassed by MOEA/D-CDP on NCTP7 and NCTP8. MOEA/D-CDP performs worse than ACMODE in eight test functions. ACMODE and MOEA/D-CDP have no significant difference in eight test functions. Furthermore, ACMODE performs better than ANSGAIII in 11 test functions. ACMODE is significantly outperformed by ANSGAIII on NCTP3, NCTP5 and NCTP6. In addition, there is no significant difference between ACMODE and ANSGAIII in four test functions. Overall, ACMODE is capable of providing better feasible PF regarding convergence and diversity in most test functions.
5.2.4. Comparison Results on MW Test Suite
For the MW test suite, Table 8 and Table 9 give the comparison results of ACMODE and its comparison algorithms in terms of IGD and HV, respectively. The best results are in bold.

Table 8.
IGD results of all comparison algorithms on MW test suite.

Table 9.
HV results of all comparison algorithms on MW test suite.
As can be shown in Table 8, the performance of ACHT-CMODE is better than that of ACMODE on MW4 and MW14. However, it is inferior to ACMODE in 11 test functions. The performance of ACMODE is similar to that of ACHT-CMODE on MW9. In addition, ACMODE performs better than AGS-CMODE in 12 test functions. There is no significant difference between AGS-CMODE and ACMODE on MW4 and MW9. ACHT-CMODE realizes the adaption of CHTs, and AGS-CMODE realizes the adaption of generation strategies. However, the performance of ACMODE is better than that of these two algorithms. Its performance is improved by the adaptive adjustment of CHTs and generation strategies. For the rest of the competitors, MOEA/D-CDP performs worse than ACMODE in eight test functions. MOEA/D-CDP and ACMODE have similar performance on MW8 and MW12. MOEA/D-CDP outperforms ACMODE in four test functions. Additionally, ANSGAIII is significantly surpassed by ACMODE in 12 test functions. ANSGAIII performs better than ACMODE on MW13 and MW14. The results shown in Table 8 indicate that the performance of ACMODE is the best among all compared algorithms.
It can be observed from Table 9 that ACHT-CMODE is surpassed by ACMODE in eight test functions. There is no significant difference between ACHT-CMODE and ACMODE in six test functions. ACMODE is superior to AGS-CMODE in nine test functions. ACMODE and AGS-CMODE have no significant difference in five test functions. Table 9 also shows that ACMODE is surpassed by MOEA/D-CDP on MW4 and MW13. MOEA/D-CDP performs worse than ACMODE in six test functions. There is no significant difference between MOEA/D-CDP and ACMODE in six test functions. Furthermore, ACMODE performs better than ANSGAIII in 12 test functions and is significantly outperformed by ANSGAIII on MW14. ACMODE and ANSGAIII have similar performances on MW13. MOEA/D-CDP and ANSGAIII are unable to find the feasible solutions on MW1. This is because MW1 has a disconnected constrained PF with narrow feasible regions. However, the proposed algorithm can automatically select suitable CHT and generation strategies to solve different types of CMOPs.
5.2.5. Comparison Results on DAS-CMOP Test Suite
For DAS-CMOP test suite, Table 10 and Table 11 give the comparison results of ACMODE and its comparison algorithms in terms of IGD and HV, respectively. The best results are in bold.

Table 10.
IGD results of all comparison algorithms on DAS-CMOP test suite.

Table 11.
HV results of all comparison algorithms on DAS-CMOP test suite.
It can be observed from Table 10 that ACHT-CMODE performs better than ACMODE on DAS-CMOP7, but it is inferior to ACMODE in eight test functions. ACMODE performs better than AGS-CMODE in eight test functions. There is no significant difference between AGS-CMODE and ACMODE on DAS-CMOP9. ACMODE is significantly better than MOEA/D-CDP in five test functions. However, ACMODE is outperformed by MOEA/D-CDP in four test functions. In addition, ANSGAIII is significantly worse than ACMODE in six test functions. ANSGAIII performs better than ACMODE in three test functions. These experimental results demonstrate that the ACMODE outperforms all the compared algorithms.
The results shown in Table 11 reveal that ACMODE performs better than ACHT-CMODE in six test functions, but ACMODE is surpassed by ACHT-CMODE on DAS-CMOP7. ACMODE and ACHT-CMODE have no significant difference on DAS-CMOP3 and DAS-CMOP5. ACMODE is superior to AGS-CMODE in seven test functions. There is no significant difference between AGS-CMODE and ACMODE on DAS-CMOP3 and DAS-CMOP9. Table 11 also indicates that ACMODE is surpassed by MOEA/D-CDP on DAS-CMOP3, DAS-CMOP4, and DAS-CMOP7. MOEA/D-CDP performs worse than ACMODE in five test functions. Furthermore, ACMODE performs better than ANSGAIII in six test functions and is significantly outperformed by ANSGAIII on DAS-CMOP3, DAS-CMOP7 and DAS-CMOP8.
5.2.6. Overall Comparison Results on All Test Suites
In this section, the overall performance of ACMODE on all 65 test functions is evaluated by the Friedman test [44]. The average rankings of HV and IGD of all comparison algorithms are shown in Figure 1. A smaller average ranking value denotes a better performance. For the IGD values, the experimental results demonstrate that the proposed algorithm ranks first among all the comparison algorithms. The overall performance of ACMODE is the best in terms of HV. It can be concluded that the overall performance of ACMODE is better than that of the other four algorithms. This is because ACMODE can choose the CHT and generation strategy with the best performance during different stages of the search process.
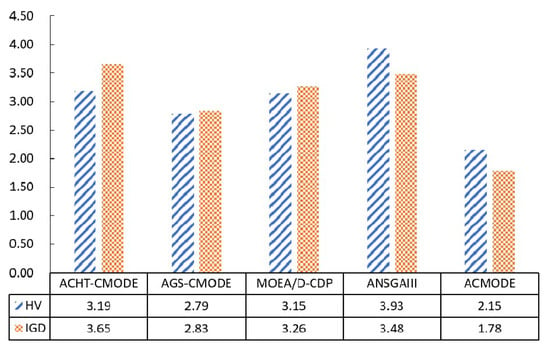
Figure 1.
Performance rankings of all comparison algorithms.
5.3. Experimental Analysis
5.3.1. The Effectiveness of Adaptive Constraint Handling Technology
In ACMODE, three widely used CHTs are selected to realize the adaptation of CHTs. In order to further verify the effectiveness of the proposed adaptive constraint handling technology, the evolution curves of CHTs in two test functions (CF6 and NCTP11) are presented in this experiment.
Figure 2 depicts the number of individuals of each CHT during the entire evolutionary process. In this section, three variants are investigated by adopting different CHTs. To be specific, only “ATM” is used in ACMODE-ATM, only “CDP” is used in ACMODE-CDP, and only “SP” is used in ACMODE-SP. The experimental results of these three variants on CF6 and NCTP11 are summarized in Table 12. The best results are in bold.
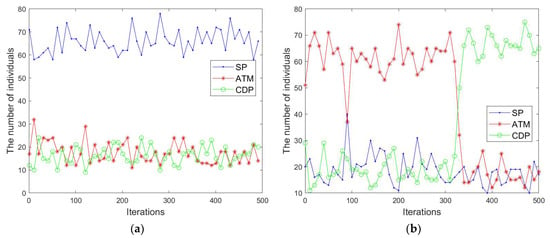
Figure 2.
The number of individuals of CHTs changes during the whole evolutionary process. (a) CH6, (b) NCTP11.

Table 12.
IGD and HV results of three variants on CF6 and NCTP11.
Table 12 shows that ACMODE-SP obtains the best results on CF6. The results achieved by the other two variants have no significant difference. It can be observed from Figure 2a that “SP” is always in the dominant position during the entire evolutionary process, while other two CHTs play similar roles. This confirms that ACMODE allocates more computing resources to a better CHT. Table 12 reveals that ACMODE-CDP and ACMODE-ATM, respectively, get the best results in terms of IGD and HV on NCTP11. The performance of ACMODE-SP is the worst one among the three variants. Figure 2b indicates that “SP” is relatively stable during the whole evolutionary process. “ATM” plays an important role at the early and middle stages of evolution, while “CDP” is mainly used in ACMODE at the later stage of evolution. It can be seen from Figure 2 that the resources allocated to these three CHTs change in real time during evolution. It can be concluded that appropriate CHTs can be adaptively selected according to different types of CMOPs in different evolutionary periods.
5.3.2. The Effectiveness of Adaptive Generation Strategy
To further validate the effectiveness of the proposed adaptive generation strategy, the evolution curves of generation strategies in two test functions (CF8 and LIR-CMOP9) are presented in this experiment.
Figure 3 shows that the number of the two-generation strategies changes during evolution. In this section, two variants are investigated by adopting different generation strategies. To be specific, only “DE/rand-to-best/1/bin” is used in ACMODE-best, and only “DE/current-to-rand/1” is used in ACMODE-current. The experimental results of these two variants on CF5 and LIR-CMOP9 are summarized in Table 13. The best results are in bold.
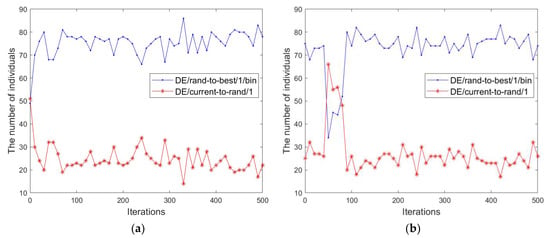
Figure 3.
The number of individuals of two generation strategies changes during the whole evolutionary process. (a) CH5, (b) LIR-CMOP9.

Table 13.
IGD and HV results of two variants on CF5 and LIR-CMOP9.
The results shown in Table 13 reveal that ACMODE-best performs better than ACMODE-current on CF5. As shown in Figure 3a, “DE/rand-to-best/1/bin” has good performance during the whole evolutionary process. ACMODE allocates more computing resources to “DE/rand-to-best/1/bin”. This is consistent with the results shown in Table 13. Table 13 also demonstrates that ACMODE-best is slightly superior to ACMODE-current on LIR-CMOP9. It can be seen from Figure 3b that “DE/rand-to-best/1/bin” plays an important role at the very early stage, while “DE/current-to-rand/1” also displays good performance at the early stage. However, as evolution progresses, more computing resources are allocated to “DE/rand-to-best/1/bin” at later evolutionary stages. Figure 3 also indicates that the ACMODE can effectively allocate computing resources to generation strategies. It can be concluded that the ACMODE can adaptively select appropriate generation strategies at different evolutionary stages.
5.3.3. Visual Comparison on PF approximation
To testify the performance of the proposed algorithm in the objective space, three test functions (LIR-CMOP3, NCTP9 and MW8) are selected to provide the PF approximations obtained by ACMODE and its competitors. The results are given in Figure 4.
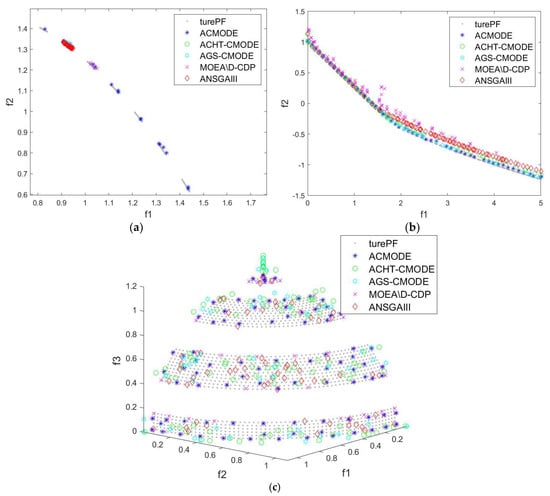
Figure 4.
PF approximation of all compared algorithms. (a) LIR-CMOP3, (b) NCTP9, (c) MW8.
It can be observed from Figure 4a that the true PF of LIR-CMOP3 is discontinuous. LIR-CMOP3 exists infeasible barriers on the way to the true PF, which prevents algorithms from converging towards the true PF. Figure 4a also depicts that ACHT-CMODE, AGS-CMODE, MOEA/D-CDP and ANSGAIII only obtain part of the true PF. However, ACMODE is capable of passing through the infeasible region barriers to uniformly cover the true PF. Therefore, ACMODE performs better than the other four CMOEAs on LIR-CMOP3. Figure 4b shows that AGS-CMODE and ACHT-CMODE are slightly inferior to ACMODE on NCTP9. The final solutions obtained by MOEA/D-CDP are far away from the true PF. However, the solutions obtained by the proposed ACMODE are very close and evenly distributed to the whole true PF. It is worth noting that MW8 has three objectives. Figure 4c indicates that the final solutions obtained by ACHT-CMODE and AGS-CMODE are far away from the true PF. Moreover, MOEA/D-CDP and ANSGAIII are slightly inferior to ACMODE. The PF approximation obtained by ACMODE is evenly distributed and is very close to the true PF. therefore, it can be concluded that selecting a suitable CHT and generation strategies is effective and important in ACMODE.
5.3.4. Parameter Analysis
The probability ε is mainly used to balance the exploration and exploitation [50]. Therefore, the ε value plays a certain role in the ACMODE. The ε value in the specific algorithm is generally obtained by trial. In this experiment, all 65 test functions used in Section 5.2 are selected to investigate the sensitivity of ε. Moreover, ε is selected from the set {0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9}.
Figure 5 provides the performance rankings of HV in terms of different ε values. A smaller average ranking value denotes better performance. It can be seen from Figure 5 that the overall performance of the algorithm is the best when ε = 0.5. Therefore, ε is set to 0.5 in the proposed algorithm.
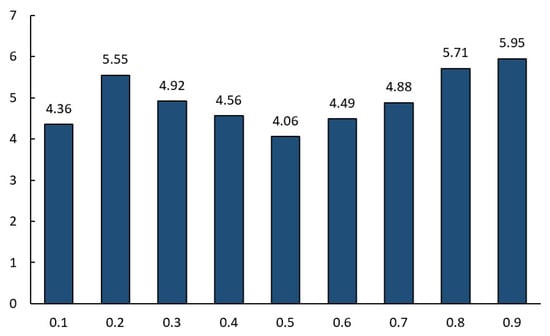
Figure 5.
Performance ranking of HV with different ε values.
6. Discussion
From the above experimental comparisons and analyses, it can be seen that the overall performance of the proposed algorithm is better than that of four compared algorithms on five test suites. Specifically, the following results can be obtained.
- Compared with the AGS-CMODE, the experimental results show that using adaptive CHTs can assist the proposed algorithm in improving its performance on CMOPs. Moreover, using an adaptive generation strategy can help enhance the performance of the proposed algorithm when compared with the ACHT-CMODE. Therefore, it can be concluded that adaptive CHT and generation strategy is useful for ACOMDE to solve different types of CMOPs.
- MOEA/D-CDP works well on the CMOPs with a low feasibility ratio, and ANSGAIII is a self-adaptive evolutionary algorithm, in which reference points can adaptively update. Compared with these two algorithms, although they are effective on some specific CMOPs, the proposed algorithm outperforms them on most functions.
- The effectiveness of the proposed algorithm is also analyzed. The results demonstrate that the computational resources can be self-adaptively allocated to different CHTs and DE’s generation strategies via the SARSA method during the entire evolutionary process.
However, ACMODE does not work very well when solving some DAS-CMOP series test problems with the difficulty of feasibility, convergence and diversity at the same time. The main reason may be that the existing CHTs and generation strategies may not enable the proposed algorithm to find feasible solutions. Moreover, the adaptive process may waste some computational resources, thus the efficiency of learning method is important.
7. Conclusions
CHTs and generation strategies significantly affect the performance of CMOEAs. In the present work, an adaptive constrained multi-objective differential evolution algorithm based on state–action–reward–state–action approach (ACMODE) is introduced to implement adaptation of CHTs and generation strategies, which can be automatically selected via a SARSA method. The performance of the ACMODE is compared with four other CMOEAs on five test suites, and the experimental results demonstrate that ACMODE is competitive in handling CMOPs. The main reason is that the ACMODE can adaptively select the appropriate CHT and generation strategy at different evolutionary stages when solving different types of CMOPs. Finally, the effectiveness of the introduced components of ACMODE is also demonstrated. Although adaptive adjustment of CHTs and generation strategies have been carried out in a current study, the selected CHT and generation strategy also have a great influence on the performance of the proposed algorithm. In future work, we will explore more novel CHTs and generation strategies with good performance, and incorporated them into ACMODE to solve CMOPs. Moreover, we will apply ACMODE to real-world problems to further confirm its effectiveness.
Author Contributions
Methodology: C.C., Q.L., Q.F.; writing—original draft: C.C., Q.L., Q.F.; writing—review and editing: Q.L., Q.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the National Natural Science Foundation of China (No. 61603244, 71904116), the National Social Science Fund of China (No. 18BGL103), and Shanghai Science and Technology Commission (No. 19DZ1209600, No. 18DZ1201500).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The original version of this paper was presented at the 16th International Conference on Bio-inspired Computing: Theories and Applications (BIC-TA 2021), December 2021. This paper was recommended for publication in revised form by the BIC-TA 2021 conference committees.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maminov, A.; Posypkin, M. Constrained Multi-objective Robot’s Design Optimization. In Proceedings of the 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg, Russia, 27–30 January 2020; pp. 1992–1995. [Google Scholar]
- Liu, J.; Yang, Y.; Tan, S.; Wang, H. Application of Constrained Multi-objective Evolutionary Algorithm in a Compressed-air Station Scheduling Problem. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 2023–2028. [Google Scholar]
- Li, B.; Wang, J.; Xia, N. Dynamic Optimal Scheduling of Microgrid Based on ε constraint multi-objective Biogeography-based Optimization Algorithm. In Proceedings of the 2020 5th International Conference on Automation, Control and Robotics Engineering (CACRE), Dalian, China, 19–20 September 2020; pp. 389–393. [Google Scholar]
- Wang, J.; Li, Y.; Zhang, Q.; Zhang, Z.; Gao, S. Cooperative Multiobjective Evolutionary Algorithm With Propulsive Population for Constrained Multiobjective Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2021, 1–16. [Google Scholar] [CrossRef]
- Datta, R.; Deb, K.; Segev, A. A bi-objective hybrid constrained optimization (HyCon) method using a multi-objective and penalty function approach. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia-San Sebastián, Spain, 5–8 June 2017; pp. 317–324. [Google Scholar]
- Yuan, J.; Liu, H.L.; Ong, Y.S.; He, Z. Indicator-based Evolutionary Algorithm for Solving Constrained Multi-objective Optimization Problems. IEEE Trans. Evol. Comput. 2021, 1. [Google Scholar] [CrossRef]
- Cui, C.X.; Fan, Q.Q. Constrained Multi-objective Differential Evolutionary Algorithm with Adaptive Constraint Handling Technique. World Sci. Res. J. 2021, 7, 322–339. [Google Scholar] [CrossRef]
- Richard, S.S.; Andrew, G.B. Temporal-Difference Learning. In Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; pp. 133–160. [Google Scholar]
- Yu, X.B.; Lu, Y.Q. A corner point-based algorithm to solve constrained multi-objective optimization problems. Appl. Intell. 2018, 48, 3019–3037. [Google Scholar] [CrossRef]
- Xiang, Y.; Yang, X.W.; Huang, H.; Wang, J.H. Balancing Constraints and Objectives by Considering Problem Types in Constrained Multiobjective Optimization. IEEE Trans. Cybern. 2021, 1–14. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.J.; Cai, X.Y.; Li, H.; Wei, C.M.; Zhang, Q.F.; Deb, K.; Goodman, E. Push and pull search for solving constrained multi-objective optimization problems. Swarm Evol. Comput. 2019, 44, 665–679. [Google Scholar] [CrossRef] [Green Version]
- Uribe, L.; Lara, A.; Deb, K.; Schutze, O. A new gradient free local search mechanism for constrained multi-objective optimization problems. Swarm Evol. Comput. 2021, 67, 100938. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, Y.; Wang, B.C. Indicator-Based Constrained Multiobjective Evolutionary Algorithms. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 5414–5426. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.; Xiao, J.; Zhang, X.; Jin, Y. A Coevolutionary Framework for Constrained Multiobjective Optimization Problems. IEEE Trans. Evol. Comput. 2021, 25, 102–116. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, Y. Handling Constrained Multiobjective Optimization Problems With Constraints in Both the Decision and Objective Spaces. IEEE Trans. Evol. Comput. 2019, 23, 870–884. [Google Scholar] [CrossRef]
- Ming, M.; Wang, R.; Ishibuchi, H.; Zhang, T. A Novel Dual-Stage Dual-Population Evolutionary Algorithm for Constrained Multi-Objective Optimization. IEEE Trans. Evol. Comput. 2021, 1. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Xu, B.; Duan, W.; Zhang, H.F.; Li, Z.Q. Differential evolution with infeasible-guiding mutation operators for constrained multi-objective optimization. Appl. Intell. 2020, 50, 4459–4481. [Google Scholar] [CrossRef]
- Yu, K.; Liang, J.; Qu, B.; Luo, Y.; Yue, C. Dynamic Selection Preference-Assisted Constrained Multiobjective Differential Evolution. IEEE Trans. Syst. Man Cybern. Syst. 2021, 1–12. [Google Scholar] [CrossRef]
- Yang, Y.K.; Liu, J.C.; Tan, S.B. A partition-based constrained multi-objective evolutionary algorithm. Swarm Evol. Comput. 2021, 66, 100940. [Google Scholar] [CrossRef]
- Lin, Y.; Du, W.; Du, W. Multi-objective differential evolution with dynamic hybrid constraint handling mechanism. Soft Comput. 2019, 23, 4341–4355. [Google Scholar] [CrossRef]
- Yu, X.B.; Yu, X.R.; Lu, Y.Q.; Yen, G.G.; Cai, M. Differential evolution mutation operators for constrained multi-objective optimization. Appl. Soft Comput. 2018, 67, 452–466. [Google Scholar] [CrossRef]
- Wang, J.; Liang, G.; Zhang, J. Cooperative Differential Evolution Framework for Constrained Multiobjective Optimization. IEEE Trans. Cybern. 2019, 49, 2060–2072. [Google Scholar] [CrossRef]
- Moniz, N.; Monteiro, H. No Free Lunch in imbalanced learning. Knowl.-Based Syst. 2021, 227, 107222. [Google Scholar] [CrossRef]
- Yang, Y.K.; Liu, J.C.; Tan, S.B.; Wang, H.H. A multi-objective differential evolutionary algorithm for constrained multi-objective optimization problems with low feasible ratio. Appl. Soft Comput. 2019, 80, 42–56. [Google Scholar] [CrossRef]
- Yang, N.; Liu, H.L. Adaptively Allocating Constraint-Handling Techniques for Constrained Multi-objective Optimization Problems. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2159032. [Google Scholar] [CrossRef]
- Liu, B.J.; Bi, X.J. Adaptive ε-Constraint Multi-Objective Evolutionary Algorithm Based on Decomposition and Differential Evolution. IEEE Access 2021, 9, 17596–17609. [Google Scholar] [CrossRef]
- Mashwani, W.K.; Salhi, A.; Yeniay, O.; Jan, M.A.; Khanum, R.A. Hybrid adaptive evolutionary algorithm based on decomposition. Appl. Soft Comput. 2017, 57, 363–378. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Bi, X.J.; Wang, Y.J. Adaptive Truncation technique for Constrained Multi-Objective Optimization. Ksii Trans. Internet Inf. Syst. 2019, 13, 5489–5511. [Google Scholar] [CrossRef]
- Samanipour, F.; Jelovica, J. Adaptive repair method for constraint handling in multi-objective genetic algorithm based on relationship between constraints and variables. Appl. Soft Comput. 2020, 90, 106143. [Google Scholar] [CrossRef]
- Fan, Q.; Zhang, Y.; Li, N. An Autoselection Strategy of Multiobjective Evolutionary Algorithms Based on Performance Indicator and Its Application. IEEE Trans. Autom. Sci. Eng. 2021, 1–15. [Google Scholar] [CrossRef]
- Woldesenbet, Y.G.; Yen, G.G.; Tessema, B.G. Constraint Handling in Multiobjective Evolutionary Optimization. IEEE Trans. Evol. Comput. 2009, 13, 514–525. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Cai, Z.; Zhou, Y.; Zeng, W. An Adaptive Tradeoff Model for Constrained Evolutionary Optimization. IEEE Trans. Evol. Comput. 2008, 12, 80–92. [Google Scholar] [CrossRef]
- Bosman, P.A.N.; Thierens, D. The balance between proximity and diversity in multiobjective evolutionary algorithms. IEEE Trans. Evol. Comput. 2003, 7, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Liu, H.-L.; He, Z. A constrained multi-objective evolutionary algorithm using valuable infeasible solutions. Swarm Evol. Comput. 2022, 68, 101020. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef] [Green Version]
- Fan, Q.; Yan, X.; Zhang, Y.; Zhu, C. A Variable Search Space Strategy Based on Sequential Trust Region Determination Technique. IEEE Trans. Cybern. 2021, 51, 2712–2724. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.Q.; Wang, W.L.; Yan, X.F. Multi-objective differential evolution with performance-metric-based self-adaptive mutation operator for chemical and qbiochemical dynamic optimization problems. Appl. Soft Comput. 2017, 59, 33–44. [Google Scholar] [CrossRef]
- Shahrabi, J.; Adibi, M.A.; Mahootchi, M. A reinforcement learning approach to parameter estimation in dynamic job shop scheduling. Comput. Ind. Eng. 2017, 110, 75–82. [Google Scholar] [CrossRef]
- Jan, M.A.; Khanum, R.A. A study of two penalty-parameterless constraint handling techniques in the framework of MOEA/D. Appl. Soft Comput. 2013, 13, 128–148. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Friedman, M. The Use of Ranks to Avoid the Assumption of Normality Implicit in the Analysis of Variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, A.; Zhao, S.; Suganthan, P.N.; Tiwari, S. Multiobjective optimization Test Instances for the CEC 2009 Special Session and Competition. Mech. Eng. 2008, 264, 1–30. [Google Scholar]
- Fan, Z.; Fang, Y.; Li, W.; Cai, X.; Wei, C.; Goodman, E. MOEA/D with angle-based constrained dominance principle for constrained multi-objective optimization problems. Appl. Soft Comput. J. 2018, 74, 621–633. [Google Scholar] [CrossRef] [Green Version]
- Li, J.P.; Wang, Y.; Yang, S.; Cai, Z. A comparative study of constraint-handling techniques in evolutionary constrained multiobjective optimization. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 4175–4182. [Google Scholar]
- Ma, Z.; Wang, Y. Evolutionary Constrained Multiobjective Optimization: Test Suite Construction and Performance Comparisons. IEEE Trans. Evol. Comput. 2019, 23, 972–986. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.J.; Cai, X.Y.; Li, H.; Wei, C.M.; Zhang, Q.F.; Deb, K.; Goodman, E. Difficulty Adjustable and Scalable Constrained Multiobjective Test Problem Toolkit. Evol. Comput. 2020, 28, 339–378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Cao, B.; Li, H. Improving ant colony optimization algorithm with epsilon greedy and Levy flight. Complex Intell. Syst. 2021, 7, 1711–1722. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).