Abstract
DNA has evolved as a cutting-edge medium for digital information storage due to its extremely high density and durable preservation to accommodate the data explosion. However, the strings of DNA are prone to errors during the hybridization process. In addition, DNA synthesis and sequences come with a cost that depends on the number of nucleotides present. An efficient model to store a large amount of data in a small number of nucleotides is essential, and it must control the hybridization errors among the base pairs. In this paper, a novel computational model is presented to design large DNA libraries of oligonucleotides. It is established by integrating a neural network (NN) with combinatorial biological constraints, including constant GC-content and satisfying Hamming distance and reverse-complement constraints. We develop a simple and efficient implementation of NNs to produce the optimal DNA codes, which opens the door to applying neural networks for DNA-based data storage. Further, the combinatorial bio-constraints are introduced to improve the lower bounds and to avoid the occurrence of errors in the DNA codes. Our goal is to compute large DNA codes in shorter sequences, which should avoid non-specific hybridization errors by satisfying the bio-constrained coding. The proposed model yields a significant improvement in the DNA library by explicitly constructing larger codes than the prior published codes.
MSC:
68U35
1. Introduction
The exponential increase in big data demands high density and capacity storage. Inspired by nature, DNA (deoxyribonucleic acid) has various applicable features for digital data storage. DNA comprises four bases: adenine (A), guanine (G), cytosine (C), and thymine (T), collectively called nucleotides. DNA data storage has three key steps [1,2,3,4,5,6,7]: (i) Digital data are converted into binary data, which are encoded into DNA strands with quaternary alphabet (A, C, T, and G) strings/sequences that are called DNA codes or codewords. (ii) These strands are synthesized (data writing) into oligonucleotides by a DNA synthesizer, and the data are stored. (iii) DNA strands are decoded by DNA sequencing (data reading) to retrieve the data. These key steps come under the big umbrella of DNA computing, in which DNA data storage is partially based on information technology (IT) and biotechnology (BT). In IT, data encoding and decoding techniques are employed, comprising computational and mathematical models. In BT, DNA synthesis, storage, and sequencing are carried out with base pairs (A, C, G, and T) in a DNA molecule. It is essential for any DNA computing model to select the DNA molecules and code them efficiently to attain maximum storage density [8].
In the DNA data storage system, various coding techniques, i.e., biological constraint/bio-constraint coding [9] and error correction coding [5], are presented to overcome the different ambiguities. In the literature, GC-content [3], no-run-length [10], reverse-complement () constraint [11], and Hamming distance () have been found as major biological constraints coding for DNA synthesis and sequencing errors. For any DNA sequence n, the GC-content is the ratio of the sum of bases content to the total number of bases for sequence length. It is close to 50% in each DNA codeword [12]. No-run-length is the avoidance of repetition of the same quaternary (q-ary) alphabet. Similarly, for the constraint, the reverse sequence , complement sequence , and reverse-complement sequence are , for which For instance, in a given DNA sequence TTCAGGA, the reverse is ATGACGT, the complement is AAGTCCT, and the reverse-complement is TACTGCA. and denote the maximum number of codewords in a DNA code satisfying two constraints (GC-content and ) and satisfying three constraints (GC-content, constraint and ), respectively. DNA libraries satisfying these bio-constraints will have a certain application to DNA computing, particularly DNA data storage [3,10].
A DNA sequence is read through a particular hybridization process in which two complementary single-stranded DNA molecules are combined to form a single-stranded molecule via base pairing. If any sequence in DNA codewords is identical to its reverse-complement, non-specific hybridization will occur, which causes the leading errors in retrieving information [2]. To avoid these, the authors utilized stochastic-based optimization algorithms and neural networks [13,14,15,16,17]. The algorithms in [13,17] were introduced to improve the lower bounds of DNA codes by different iterations and parameters.
Recently, a deep learning model (DLM) was introduced with three different next-generation sequences for DNA information storage [14]. Their DLM utilized four gated recurrent unit (GRU) neural networks grouped into two sets, which took sequences from 5′ to 3′ or from 3′ to 5′. GRUs with two gates have been adopted with a feed-forward neural network (FFNN) to predict the sequence during the hybridization process. The excessive number of hidden nodes and the model’s reliance on an FFNN exacerbate the DLM training. Despite this issue, it initiated an acceptive idea to bring neural networks for DNA data storage. This milestone has motivated us to implement a neural network on DNA codes to provide a novel coding scheme for high-density storage. In [15], a DeepMod system was proposed that integrates the recurrent neural network and long short-term memory (LSTM) models to perceive the DNA codes from various Oxford Nanopore sequences. Likewise, a convolutional neural network was embedded for the generation of DNA bases to achieve high-density storage. It employed a DNA-mapping method consisting of GC-content and homopolymer length constraints to design the DNA codebook [16]. Their work inspired us to seek a model that generalizes the DNA codewords as much as possible with the artificial neural network. However, the neural network (NN) with a fixed number of nodes, i.e., LSTM including forwarding pass, is not well-studied for DNA sequence input. Apart from non-specific hybridization, it is essential for DNA code development to detect the error source to avoid insertion, deletion, and substitution errors with DNA coding bio-constraints [4,5,12]. Several existing studies have been conducted to address these problems with DNA codewords. However, the literature that satisfies the GC-content, Hamming distance, and RC constraints is cited here.
In 2004, DNA codes with GC-content were extensively presented in [18]. It reported the upper and lower bounds on DNA code size with GC-content and Hamming distance to construct the DNA codewords. In a polymerase chain reaction (PCR), a DNA code with huge GC-content (say, >60%) caused the insertion and deletion errors. Thus, it is necessary to consider the GC-content for the stability of DNA sequences by avoiding computation errors. In 2017, a study pioneered by Erlich [3] delivered a seminal work on DNA data storage by proposing a fountain code with GC-content (45–55%) and a minimum Hamming distance (d). They achieved 1.57 net information density; however, they still faced errors in GC-content which propagated severe errors, including mismatches, deletions, and insertions, during the decoding process. In addition, no theoretical lower or upper bounds were presented for those constraints.
In 2018, ref. [10] proposed a novel altruistic algorithm with lower bounds to generate constraint-based stable DNA codes. It also used constant GC-content and minimum Hamming distance and reported an improved number of DNA codewords. However, the storage efficiency was not sufficiently considered for density-based DNA data storage. In 2020, the author [17] proposed a damping multi-verse optimizer algorithm to design the DNA coding sets by constructing the GC-content with no-run-length constraints. Their results revealed 4–16% more improved DNA coding than that of [10], which suggests that the increase in constraints can improve the codes for high-density DNA data storage. In 2021, our previous paper [12] extended the work [10] by proposing a novel algorithm to construct the DNA coding sets with improved lower bounds. The proposed algorithm was applied with GC-content and no-run-length constraints and achieved 30% better lower bounds. However, besides the insertion and deletion errors in DNA codes, another issue of secondary structures (SS) occurs during the reading process [19]. The SS is a base pairing contact of a single-strand sequence that folds back on itself, as presented in [11] (Figure 1). Any DNA sequence with an SS shape will consume the extra resources and energy to be unfolded, which slows the chemical reaction immensely. Therefore, DNA needs to be free from the SS shape before reading DNA sequences in the wet lab. There are few studies on eliminating this severe issue. The author in [11,20] introduced the RC constraint to overcome the SS issue. They subjected the GC-content and RC-content together to improve the DNA coding sets. Their studies furnish the basic idea of combinatorial constraints to generate DNA codes with minimum errors. Although the literature mentioned above [10,11,12,17,20] received high storage DNA code sets and coding rates, these studies do not provide a sufficient method to design higher DNA codes in the shorter sequences that must satisfy the biological constraints, which is enormously important for a stable density-based DNA storage system.
This paper introduces a more efficient coding technique with a novel computational model that is based on biologically inspired computing because it uses a neural network (NN) with biological constraints to obtain a high-density-based DNA data storage. In the proposed model, LSTM as an NN with a forward pass is utilized to open a new door in the NN for DNA code construction. Firstly, the binary data are converted into premiere DNA bases by using the [3] scheme. Then, the yielded premiere DNA strings are passed through the NN model with the forward passing mechanism. A particular criterion trains the activation functions to randomly generate DNA codes. If those DNA codes pass that criterion, we term them optimal DNA codes. Then, the combinatorial constraints are utilized to concatenate these optimal DNA codes. The combinatorial constraints, including GC-content and RC constraint with Hamming distance, are computed to generate a DNA library that is used to store the digital information, for which different propositions and theorems are constructed in the Magma program and proved in this paper. GC-content and Hamming distance are computed, and results are obtained with improved lower bounds. Meanwhile, the RC constraint with Hamming distance is constructed to avoid secondary structure, and it is concatenated with GC to generate the DNA library with the best-known codes. These codes are generated by Magma with different inequalities. These inequalities are based on the previous studies that are used for the comparison of our results. Furthermore, the results are analyzed by the coding rate formula, which helps us to evaluate the data storage density in DNA media.
In general, there are two goals to be delivered for high-density-based DNA data storage with the following features:
- To improve the net information density by storing a large amount of digital data in shorter DNA sequences.
- To construct the DNA codes that satisfy the combinatorial bio-constraints to overcome the reading errors.
In this scenario, these goals are accomplished by the following significant contributions:
- A novel computational model based on the LSTM neural network with a forward pass is proposed to generate the optimal DNA codes from the premiere DNA bases. To the best of our knowledge, such a model has not been studied in the prior studies.
- The combinatorial bio-constraints, including GC-content, RC constraint, and Hamming distance, are constructed for optimal DNA codes to avoid non-specific hybridization by overcoming sequencing errors and secondary structures.
- The results receive many DNA coding sets satisfying the bio-constraints and significantly improving the DNA coding rates compared to the existing studies.
The structure of the rest of the paper is as follows: Section 2 delivers the prior work about deep neural network and combinatorial constraints for DNA data storage. Section 3 presents the preliminaries and notations, Section 4 introduces the proposed model, Section 5 elaborates on the results, and Section 6 concludes this work.
2. Literature Review
This section is divided into two subsections to emphasize our paper’s contributions based on neural networks for DNA codes and DNA coding with combinatorial constraints.
2.1. Deep Neural Networks for DNA Codes
DNA computing has successfully impacted human life due to well-known computation tools based on machine learning and the deep learning community. With the rapid generation of digital data, efficient and effective deep learning architectures (DLAs) have been constructed to compute big data [21]. DLA has been approved in a variety of domains with significant accuracies and predictions. In this article, we consider applying the deep neural network based on DLA. Recurrent neural networks (RNNs) provide the connection between the nodes to form a directed graph along a temporal sequence. The graph exhibits a short-term memory that allows RNNs to remember information from the previous state to the next state [22]. Long short-term memory (LSTM) is a variant of RNN that efficiently learns the long-term dependencies. It has three gates: input, output, and the forget gate. An LSTM unit has a node or cell that accounts for the values over particular time intervals while the rest of the gates regulate the information [23,24].
Various deep neural networks have been applied with different methods and models in various natural computing studies. In 2015, a novel method was proposed for the transformation of DNA sequences into numerical sequences. This method was based on a pulse-coupled neural network and Huffman coding, which used triplet codes to encode the different lengths of DNA sequences [25]. Another study also attempted to encode the data with that method, but it found that encoded sequences are compressed at a close distance, making the results less informative [26]. Although numerous studies have been conducted with deep neural networks for natural computing, deep neural networks are still new models for the DNA data storage system. For instance, in 2021, a GRU (gated recurrent unit)-based deep learning model was presented for DNA information storage with next-generation sequence prediction [14]. Similarly, the author proposed a DeepMod system that integrates the RNN and LSTM models to perceive the DNA codes from various Oxford Nanopore sequences. While RNNs are employed to capture the Nanopore sequencing, LSTM overcomes the vanishing gradient issues in the training of RNNs. The proposed system collectively achieves better DNA codes from the given sequences compared to others [15]. In addition, in [16], the problem of DNA synthesis cost was addressed by delivering a high-density-based DNA data storage system. To achieve a high storage density, convolutional neural networks were embedded to generate the DNA bases. It employed a DNA-mapping method that consisted of GC-content and homopolymer length constraints to design the DNA codebook. It was reported that the proposed scheme efficiently stored and retrieved the information from the DNA storage system with the integration of a deep neural network with the DNA mapping method. These studies provide the motivation for the integrational system of deep neural networks with DNA coding and combinatorial bio-constraints.
2.2. DNA Coding with Combinatorial Bio-Constraints
In DNA synthesizing and sequencing, various errors occur, which are combated with different coding techniques. For instance, error correction coding and bio-constraint coding are mainly used in DNA-based information storage systems [27]. Bio-constraint coding has been practically applied in mass data storage, i.e., magnetic and optical data recording [28]. There are different types of DNA constraint coding reported in the existing literature. Researchers [2,29,30] have formulized single constraints and/or combined the constraints to attain the targeted results by preventing DNA sequence (DNA code) errors.
G. M. Church delivered a pivotal work on DNA data storage by converting 8-bit ASCII (0 to A or C and 1 to G or T) into DNA bases. It pondered the GC-content constraint and the homopolymer run-length constraint by disallowing a run-length greater than 3. It was a groundbreaking step toward storing the digital information into DNA, but it was plagued by huge errors and a lack of competency [7]. N. Goldman presented a different method by compressing the raw data into DNA sequencing with differential coding and a Huffman coding scheme. It employed the run-length constraint of at most 1 and achieved an effective coding rate. It suggested considering the GC-content for better constraint satisfaction [6]. Similarly, R. N. Grass combined the different constraints to deliver an error-correcting scheme. It used Reed–Solomon codes for error control [5]. In comparison, M. Blawat offered a seminal study for DNA data storage by proposing a forward error-correction mechanism. It provided the codewords (codes) that avoided deletion and substitution errors by utilizing the GC-content constraint [4]. Y. Erlich and D. Zielinski proposed another benchmark study by designing the fountain code that considered the GC-content and run-length for DNA synthesis and sequencing. Their study significantly achieved better coding rates compared to existing work; however, in the decoding process, it found error propagation in the information retrieval stage [3]. W. Song and Y. Wang also conducted research on DNA data storage by presenting a mathematical method for DNA code generation by preserving GC-content and Hamming distance constraints [9,27]. D. Limbachiya constructed an altruistic algorithm to create DNA codewords of a specific length. The algorithm also formalized the Hamming distance for each code to satisfy the constraints [10]. In our previous work, a novel algorithm was developed to generate the DNA codes. The obtained DNA codes’ errors have been corrected to a limited extent with GC-content and no-run-length constraints [12].
In conjunction with GC-content, no-run-length, and Hamming distance, a few inspiring and influential constraint studies deal with the reverse-complement constraint. In 2005, Oliver D. King reported the theoretical lower and upper bounds for the maximum size of DNA codes. The report created the codes with the minimum Hamming distance and reverse-complement of any code with the least distance. It stated that obtained DNA codes were larger than ever [18]. In 2010, A. Niema accommodated Oliver D. King’s bounds to design DNA codewords with GC-content, the Hamming distance, and the reverse-complement RC constraint by avoiding non-specific hybridizations. They employed RC constraint to handle the searching of codes related to bases with 0 and 1 points. It obtained many new codes for DNA data storage [20]. In 2021, Benerjee K.G. exhibited the families of those DNA codes which avoid secondary structures. It combined the RC constraint with homopolymers’ run-lengths to construct the dissimilar DNA codes [11].
The prior work on bio-constrained coding established an idea of combinatorial constraints with different mathematical methods and formulations. These studies achieved many DNA codes in their particular methods. However, we have found that the desired DNA codes are still capable of improving the lower and upper bounds for the generation of high-density-based DNA codes. As we discuss a few studies on deep neural networks that impact constructing DNA codes, in this paper, we propose a novel model that integrates a deep neural network with combinatorial constraints to design DNA codewords.
3. Preliminaries and Notations
According to fundamental bio-constraints (Section 1), we design the oligos as sequence α for . If , the alphabet at the position in the sequence α is presented as . Thus, a sequence will be generated. In the same way, let another sequence , be possible if the Hamming distance [31] between both sequences , denoted , satisfies the following:
Apart from sequences must satisfy the GC-content and reverse-complement constraints (Section 3) to produce the DNA library . Hereafter, oligos are denoted by Greek letters, and other notations are a generic set ξ of sequences . Here, we need to provide the definition of the DNA library [31].
Definition 1.
A set of DNA bases {A,C,G,T} with n-mer oligos ξ that satisfies the constant GC constraint, reverse-complement constraint, and Hamming distance constraint is called a DNA code/codeword which collectively forms a DNA library .
If a DNA library is indicated by the number of K-constrained sequences of strings initiated with a non-zero symbol , Shannon’s relationship [32] can be written as a recurrent relationship:
If the number of codes n increases, the increase exponentially by the following:
where is a constant and is an exponential growth factor which is a real root of
In order to store the digital data in the nucleotide, this expression leads to defining the DNA data density [32].
Definition 2.
The maximum number of digital data bits (b) stored per nucleotide (nt) is termed as data density, denoted byand defined:
In high-density-based DNA storage, there is a probability of secondary structures. In experiments, the Nussinov–Jacobson (NJ) algorithm is employed to predict the secondary structures approximately [33]. During the chemical reaction, a DNA sequence releases the energy to attain stability after forming secondary structures. Thus, this form can be calculated by a DNA property called free energy . This energy relies on the sequence pair , where and the pair releases its energy, which is termed as interaction energy . Note that between sequence and in any pair will be independent of other sequence pairs. In the NJ algorithm, the interaction energies depend on the selected sequence pairs as non-positive values, while, for the independent interaction energies, the assumption for the NJ algorithm with minimum free energy for a DNA sequence is for particular conditions and for [34].
4. Proposed Model
In this paper, the concept of a neural network is embedded with the combinatory constraints to design the DNA codes of nucleotides that preserve the GC-content, Hamming distance , and RC constraints. The proposed model is built on the three layers listed below:
- Transform the digital data into the sequence of bases (A, C, G, and T).
- Encode the DNA bases into optimal DNA codes.
- Create the bio-constraint codes for the DNA library construction.
This paper’s model novelty is based on layers 2 and 3. In contrast, the first layer is described in prior literature [3], in which, firstly, a digital data file is compressed into binary format. In our case, we compressed an image (cat.jpg) file into a binary file. Next, the binary file is preprocessed with different segments. Furthermore, it reiterates 2 computation processes: the Luby transform and screening. In the Luby transform, different bases are sets for fountain codes, while screening translates the binary droplet to a DNA sequence by converting (00, 01, 10, and 11) to (A, C, G, and T), respectively. Thereafter, we will term these codes premiere codes ξ .
After encoding, bio-constraints are applied to screen the sequences. However, in layer 2, we intend to apply the following neural network (NN) over the encoded premiere codes ξ to generate optimal DNA codes for high-density storage. The 3rd layer introduces the bio-constrained coding to overcome the errors and construct the DNA library . The comprehensive details of these layers (2 and 3) are given in the following subsections. The model diagram for the integration of NN with DNA coding constraints is illustrated in Figure 1.
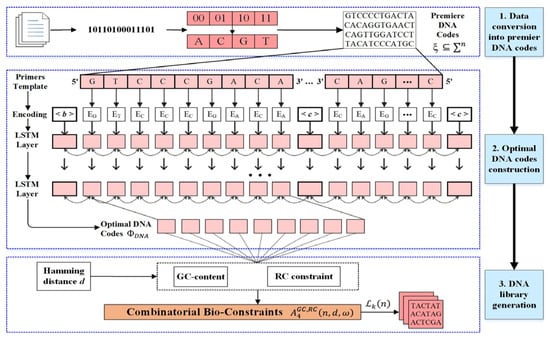
Figure 1.
The proposed computational model with NN and combinatorial bio-constraints for DNA data storage.
4.1. NN-Based DNA Codes
The encoded premiere DNA codes ξ are moved through the NN model to obtain the optimal DNA codes . This model is based on 4 layers (encodings, 2 LSTM layers, and forward pass). In this neural network, 128 LSTM units have been considered, while the amount of hidden units is 4 times greater than that of the LSTM units and the dropout rate is set to 0.5 to avoid the overfitting issue. This rate will result in a 50% decrease in the number of neurons in the repetition oligonucleotides. It creates weight = 0 if a code is in a forward pass for a single iteration. During the training process, the trainable parameter is automatically set to false to prevent weight updates. The model is trained on forward and reverse input sequences to append the DNA codes, which must have different oligos in front of each other. In this paper, various primer templates are created from the ξ with length 9 bases to make model learning efficient. The learning sequences are essential to attain the DNA codewords, avoiding identical bases. A sequence , learned from one layer, is concatenated to another layer according to the forward pass mechanism. In the encoding layer, two single-stranded sequences are concatenated by inserting a particular connector token, which serves as an ending token also. In addition, another special token is appended at the beginning of the sequence. Each encoded base is indexed and fed through the LSTM layers. These layers are double stacked, and the unique tokens are transferred through the dense layers. Each sequence in these layers interacts with two-headed arrows to present the bi-directional LSTM for readability. All sequence nodes are initiated from 0 and updated based on the next nucleotide’s information. The hidden LSTM nodes predict the potential patterns and the forget gates update all nucleotides in the given DNA sequence. In the last layer, the final sequence updating is passed through the forward pass of LSTM to identify the forward-base DNA code .
To construct the NN model that permits the constant flow of sequences through self-connected units, each oligonucleotide is protected with a self-linear unit . The input gate unit is responsible for protecting the linear unit from the other irrelevant units’ connection. Next, the critical unit, a memory cell, is designed for each DNA sequence with a linear unit to stop connecting with different DNA sequences. The memory cell of unit is indicated by , with the current net sequence with achieving the input from the multiplicative unit, which is considered the output gate in the LSTM model. The activation of the input gate and output gate with iteration time is indicated by and , respectively, which can be defined [23]:
where
where
where stands for the number of the weight matrix and is the activation of an arbitrary unit .
These activation functions enable the network to learn the complex features of each DNA sequence at the input gate and output gate . Although there are other weights and vector formulas for the LSTM gates [35,36], we omit them in this paper. However, we generalize the above activation functions to architect the forward pass for the final output. These functions learn the DNA bases to satisfy the following criteria for primer design.
- The DNA primer length is generally 15–30 nt [6]. The best length for PCR amplification primers is usually 20 nt; we also train our model at this limit.
- The length of repeated bases in a primer is generally ≤4 nt [5]. The consecutive appearance of any particular base makes the unstable DNA structure. We set consecutive base lengths ≤ 3 nt.
- The GC ratio of the primers should be 45–55% [3]. The bases A and T are linked by 2 hydrogen bonds, and C and G bases are connected by 3 hydrogen bonds (see Figure 6 [37]). We also consider the GC-content to be 45–55% in this work.
If the primer does not satisfy the above criteria, we alter one base from one primer. For example, if a primer does not satisfy the condition with the sequence AGGTCATC, we alter the first base ‘A’ with ‘T’, because they have a connected hydrogen bond between them, and reconfirm the criterion, while, if the primer meets the criteria, the premiere DNA codes ξ are trained to the multiplicative units. The j-th memory cell block , which found the input from multiplicative units and , will have a v-th unit of a memory cell block for a net input for time :
The internal state and output activation of the v-th memory for a time with memory cell block will be:
The final net input for the index , which ranges for output units and ranges of the final activation of output with are:
where
Note that each memory cell has its weight w for the final net input The DNA sequence is updated with the latest bases to design the DNA library. Finally, the LSTM cell determines the output by assigning these updates to the output gate . The computes the final output activation that is passed through the cell as a final optimal DNA code .
4.2. Combinatorial Constraints
This section deliberates the coding method to map the optimal DNA codes with sequence length to the DNA library with sequence length that satisfies the combinatorial constraints (). The basic idea is to combine or concatenate the optimal sequences of length to the sequence of length by constructing adjacency relations. For instance, if and are sequences with length n, then is the concatenation of Since the prescribed parameters of and to guarantee the sequence α is optimal are met, it is necessary that will be an optimal sequence, if , where indicates the sequence which must have 3 symbols of .
The constant GC-content can be presented analogously as for the if all DNA codewords in have similar melting temperatures and each code desires to be . The following are the upper and lower bound constraints for the DNA library construction. Proposition 1 is based on upper bounds with modified variables for the Hamming distance d, while the original proposition [18] considered only the number of sequences n. Due to new variables, the proof is presented with new codes for this work.
Proposition 1.
For the sequenceshaving the number of codewords, with constraintandfor the upper bound,
Proof.
Say that if there are 3 codewords having GC-content there will be some position where none of the words has C or G; thus, 2 of 3 words should agree in that position. Hence, and if , then 2 codewords will be and In contrast, if there are 4 codewords and none of the codes is agreed at any position , then all 4 nucleotides will occur in each position of . Thus, the average GC-content will be which is based on , and 3 codewords with will be , and Similarly, if there are 2 codewords and no agreement in any position, there can be 4 codes according to the pigeonhole principle. Thus, the average GC-content will be for and 4 codewords will be , and □
From this proposition, Theorem 1 is derived by considering the code length to generate the improved DNA coding sets. In contrast, Theorem 2 is an explicit condition for Hamming distance with constant GC-content to produce the DNA coding sets which satisfy both constraints.
Theorem 1.
A code with lengthcan be smaller than a code with lengthwith a minimum Hamming distance ofand.
Proof.
In the case of Equation (13), the sequence for words with length , and GC-content , there will be position where ⌈⌉ codewords have C nucleotide, or, at some position, it will be G. Otherwise, the average GC-content can be less than . Considering those codewords and deleting position can generate and GC-content codes with minimum In contrast, Equation (14) is analogous, which only differs with GC-content for some position where generates A’s or T’s. □
The inequalities in Equations (13) and (14) are applied to achieve the upper bounds on with , or conditions. Similarly, different bounds can also be obtained by varying different orders; for instance, at constant , Equation (13) can still be used after and Equation (14) after .
Theorem 2.
For the maximum code lengthwith minimum distancefor the GC-contentin lower bounds,
Proof.
By Equation (15), the numerator provides the total codewords with GC-content . The denominator yields the codewords with distance for a sequence α, while denotes the lower bounds, which give the codewords of a sequence β with GC-content ω that must satisfy the . □
Apart from the GC-content, a reverse-complement constraint is integrated with this paper since we are employing the NJ algorithm for interaction energies (Section 2) to control free energy for the secondary structures. To unfold the secondary structures before reading, let us consider a set of codewords, Any DNA code ξ in DNA codebook with length is constructed by defining a bijective map φ between the quinary alphabet and , and then the net code rate (, is number of DNA coding set, and is number of sequence length) is, in this case, times of code. The bounds on free energy DNA code ξ are presented in Proposition 2 to determine the secondary structure in a DNA sequence.
Proposition 2.
For all DNA sequencesandin DNA code ξ , the free energy
From this proposition, the free energy reduces for DNA sequences over ξ. Hence, any DNA sequence or in ξ will avoid secondary structures. In the above coding sets, with length , Now, from this proposition, we need to provide Theorems 3 and 4 to construct the model with which we avoid the secondary structure from any sequence.
Theorem 3.
Any DNA sequence or with length in ξ is free from the secondary structure if the stem length is more than 1 and minimum Hamming distance
Proof.
Note that in any DNA sequence, if there is a secondary structure of stem length, then there will be 2 disjoint sub-sequences (α and β) with length and there is . The result will be contrapositive, such as if a DNA sequence frees from an SC (secondary-complement) sub-sequence with length , then it will be freed from a secondary structure with a stem length of more than one. □
Theorem 4.
For any DNA codethe codeword over ξ, will be () if , wherein .
Proof.
DNA code length and size follow the complement of DNA sequence in RC constraints for a given codeword over ξ, Similarly, note that and . Hence, we have with minimum Hamming distance for the RC constraint. The results will follow the distance property of □
After constructing Propositions 1 and 2 for the upper and lower bounds’ improvement and avoiding the secondary structure, respectively, we present the combinatorial constraints by utilizing Proposition 3 [20]. This proposition leads to Theorems 5 and 6, improving the lower bounds of k-constraint length and avoiding particular errors from the number of sequences with errors r.
Proposition 3.
Suppose the bounds overare concatenated withandconstraints with the Hamming distanceforand. We have 2 cases:
Ifis even,
Ifis odd,
Proof.
For any set of codewords with length , if their complements in any subset replace all integers, the GC-content will be maintained due to the existence of a Hamming distance between each codeword of α and β. However, the reverse or reverse-complement and Hamming distance between the codewords are not maintained generally. Subsequentially, if is even, we can replace codeword by its complements to generate a new codeword with the first coordination, and then for all codewords and . In contrast, if is odd, we can replace codeword by its complements to generate a new codeword with the first coordination, and then for all codewords and [20]. □
Theorem 5.
The code with combinatorial constraint is optimal for maximum code lengthand minimum distancefor the GC-contentin lower bounds if and
Proof.
By Theorem 2, Similarly, by Proposition 3 (16), , and Theorem 4.5 of [38], . In this argument, the set of all binary words for does not have palindromes for odd Hamming weight , while the reverse of odd word weight is still odd weight when is even, so words are distributed into pairs , wherein each word from each pair indicates that . Thus, the product lower bounds for the Hamming distance between 2 separated words of odd weight should be at least 2; then, the inequality determines the Halving bound, □
The lower bounds with deletion or substitution errors ε and with are not tight enough to generate the DNA library for high-density data storage. We can improve the lower bounds of the maximum number of sequences without errors by constructing the redundancy of explicit DNA codes with by considering Shannon’s relationship [32] (Equation (2)). The purpose of Theorem 6 is to improve the lower bounds of sequences without errors ; for which, the lower bounds with deletion and substitution errors ε are considered with fixed numbers of errors.
Theorem 6.
Letbe positive integers withand. Suppose that. Then the redundancy of improved lower bounds is
Proof.
For a sequence , we consider the sequence in the way of descending lexicographic order. Each sequence contains discrete code, so each sequence of length occurs at most times. Hence, the number of equivalence classes is exactly the number of odd weights with runs. This number is known to be (see [39,40], page 360).
This expression for is inconvenient to work with, so we assign a lower bound on . W.L.O.G., we consider that for , where and with weight of discrete codes,
while the number of equivalence classes with repetitions is
where, in this expression, gives the number of choices of these discrete codes, and counts the remaining sequences as repetitions of the K discrete ones. Since , when , we have
It follows that is increasing in ; hence,
The Equation (18) is larger than Equation (19) w.r.t. discrete codes in each given sequence k:
Hence,
Now, let be an error-correcting code. According to the pigeonhole principle, the sequence size is least for a class , which indicates . Therefore,
Let and
We noted that while is a coding set, at this point, we use the lexicographic order to assign the indices,
We suppose that is a code of minimum Hamming distance at least ; otherwise, if there are two codewords in that have the Hamming distance at most , then both concerned codewords in can be confusable. Thus, by deleting the length of ε suffixes, the concerned codes will be different in . Thus, by using the Hamming bound on which is same as , we have
By combining the Equations (20) and (21), we have
Hence,
In this paper, biologically constrained quaternary codes are pondered to use DNA primers economically. The pseudo-code of Algorithm 1 is utilized to generate the DNA library which is based on the optimal DNA codes designed by a neural network. This algorithm produces the codes that satisfy the GC-content , reverse constraint, and Hamming distance using the quaternary encoding.
| Algorithm 1. Proposed algorithm to construct DNA library |
| Input: Premiere DNA codes ξ , optimal DNA codes , GC-content , code length , Hamming distance , and reverse constraint; |
| Output: DNA library
|
| return: DNA library for DNA data storage. |
5. Result Evaluations
This section elaborates on the improved lower bounds and DNA coding sets obtained by the proposed model of NN and combinatorial bio-constraints. Figure 2 illustrates a random sample of forward and reverse primers for the optimal DNA codes received after the NN implementation. These random DNA sequences were programmed in the Magma program [41] with different sequence lengths and a minimum Hamming distance. The aforementioned propositions and theorems were considered for program construction. As a result, we received files with different lower bounds of DNA codes, satisfying the combinatorial bio-constraints for particular and . The codes in the files were calculated in the Tables format. In addition, Figure 3 illustrates the numerical analysis by considering the coding rate and storage density of lower bounds given in these tables. Figure 3’s analyses were drawn by using the Prism program.

Figure 2.
A sample of received primers for the optimal DNA codes.
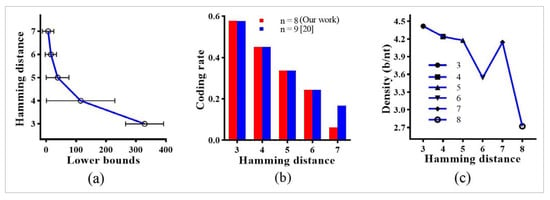
Figure 3.
Lower bounds acquired by coding constraints with : (a) The CI mean with lower and upper bounds of coding constraints with for . (b) The coding rate comparison between lower bounds is obtained by for our work () and that of [20] . (c) The storage density with our DNA codes for to and .
Table 1 and Table 2 present the lower bounds obtained by our model of GC-content ω and with the NN. In each row, the upper entries in Table 1 are directly taken from [10], while the upper entries in Table 2 belong to [17]. The lower entries are used to compare our outputs with existing studies. The superscript represents improved lower bounds and indicates the decreased lower bounds, while the rest of the other bounds have almost the same lower bounds as compared to [10] and [17], respectively.

Table 1.
Comparison of our lower bounds with [10] for .

Table 2.
Comparison of our lower bounds with [17] for .
In Table 1, the lower bounds are based on GC-content ω and by deriving Proposition 1 and Theorem 1, and they are compared with Table 1 of [10], which uses the and inequalities to construct the DNA codes. We have compared our proposed model’s results with [10] by considering the GC-content ω and with NN. As a comparison, 51% of bounds are improved, 5% have decreased, and 44% are almost the same lower bounds as in [10].
Similarly, in Table 2, the lower bounds are based on RC constraint and by deriving Proposition 1 and Theorem 2 and are compared with the Table 7 of the study [17], which considers the and inequalities to design the DNA codes. In comparison, 64% of bounds are improved in our work, while 11% have decreased and 25% are almost the same as the lower bounds of [17]. However, the limitations of these bounds can be further improved by constructing new theorems or modifying Proposition 1 by varying the values of n and ω.
Apart from the lower bound improvements for the given constraints, the coding rates , is the sequence length number, and L is the total number of lower bounds in a sequence) have also been improved in a shorter sequence . For instance, ref. [10] reported when , while our work reports the same coding rate (0.3034) with a shorter sequence when . Similarly, ref. [17] obtained when ; in contrast, this work receives this coding rate (0.4857) when . The reported improved lower bounds have a better influence on the DNA library generation, indicating the proposed model’s effectiveness for DNA code construction.
Regardless of this improvement, the 95% confidence interval () mean (Figure 3a) of received bounds presents a breakthrough coding for DNA data storage in DNA computing. The bigger the interval, the more significant the development of coding for DNA data storage. As the purpose of individual RC constraints is to avoid the secondary structures in the DNA sequences, the RC constraints are not concerned with generating the lower bounds separately. However, the studies [11,13,18,20] motivate the idea of integrating the RC constraint with GC-content and Hamming distance in an assembled format to design new DNA coding sets. Taking advantage of their work, we generalize the RC constraint with Proposition 3 and Theorems 5 and 6 to generate the new DNA codes.
Table 3 is the collection of lower bounds with combinatorial constraints. Each column has upper and lower entries; the former is taken from the Table 8 of the study [20], and the latter is attained by our proposed computational model. The bold entries indicate the outperformed bounds of our proposed model over [20]. Likewise, the coding rates are compared in Figure 3b for of our lower bounds with of [20]. Our model designs the codes with almost the same with sequences. In addition, the underlined entries indicate the best-known codes of this work that have nine bounds total. In [20], Tables 8 and 9 present the best-achieved bounds which satisfy the GC-content, Hamming distance, and RC constraints; we only compare our results with Table 8 due to its particular inequalities (i.e., ). As Table 1 and Table 2 are also based on these inequalities, we focus on a particular inequality in this paper for all the results.

Table 3.
Comparison of our lower bounds with [20] for .
The new lower bounds delivered by this work are better than the prior work. For instance, for and , the size of our DNA codes is 22% greater than that of [20]. In another scenario, if we consider all the sequences at , the new improved DNA codes are still 36% better than [20]. These significant improvements are based on our proposed computational model that integrates a neural network with combinatorial bio-constraints. In addition, the size of these DNA codes is still capable of increasing as that of the best-known codes for the highest storage density. The storage density with our DNA codes for to and is given in Figure 3c. The high storage density is received in lower Hamming distance, which is also based on the DNA coding sets of each sequence length. For the given particular lower bounds in Figure 3c, the highest density of 4.41 is attained for
Furthermore, the improvements of these lower bounds for any sequence length pioneer the DNA coding rates. A general analysis of Table 3 indicates that the same coding rate (R) is found in 73% of lower bounds with shorter sequences. For example, ref. [20] received when and , while this work acquires the same coding rate (0.2673) when and . Similarly, in another example, when and , ref. [20] reported a 0.4874 coding rate; in contrast, this work delivers with the number of sequence lengths at the same Hamming distance. In the case of best-known codes (bold underlined entries), our coding rate is better than [20], with a shorter sequence , i.e., , and , while this work reports when .
Thus, these analytical results present that the shorter sequences can achieve the same DNA storage density as the longer sequences. The improved lower bounds in various coding sets indicate the reduction in insertion and deletion errors in the DNA sequences, which enables the proposed computational model to avoid the non-specific hybridization process. In addition, Table 4 presents the DNA library satisfying the constraints when n = 10 and d = 7, as in Table 3. The satisfaction of combinatorial constraints over the optimal DNA codes from the NN’s output collaborated to improve the lower bounds of DNA coding sets, which emphasizes our proposed computational model.

Table 4.
DNA coding sets for DNA library retrieved when and .
6. Conclusions
An exciting research challenge in DNA data storage systems is to explore improved lower bounds by avoiding non-specific errors to generate high-density-based storage, which could store a large amount of information in a shorter sequence. In this paper, a novel computational model is offered to construct an extensive DNA library of oligonucleotides. It is accomplished by presenting a three-layer model that integrates a neural network (LSTM) and combinatorial bio-constraints, including GC-content, Hamming distance, and reverse-complement constraints. We derive the recursive expression in propositions and theorems to attain all possible large DNA coding sets by satisfying combinatorial constraints.
All DNA codewords in Table 1 and Table 2 satisfy the GC-content and Hamming distance constraints and improve 51% and 64% of lower bounds compared to [10] and [17], respectively. The lower bounds presented in Table 3 are single error-correcting codes based on the concatenation constraints, while the underlined bounds exhibit the DNA sequences that have avoided secondary structures. Furthermore, the improvements in the lower bounds directly impact the coding rate. For example, results in Section 3 report that the shorter sequences can achieve the same DNA storage density as the longer sequences. It is concluded that the proposed computational model can store a large amount of data in a small number of DNA nucleotides that can improve the data density and reduce the DNA synthesis and sequence cost for a DNA-based data storage system.
In our results, there are still lower bounds that need to be improved by mutation strategies for high-density data storage. Similarly, the insertion and deletion errors can be further controlled by experimenting with the application-oriented bio-constraints, i.e., run-length constraints [42].
Author Contributions
Conceptualization, A.R., Q.J. and Y.W.; methodology, A.R.; software, A.R.; validation, A.R., Q.J. and Y.W.; formal analysis, Q.J., Y.W. and Q.Q.; investigation, Q.J., Y.W. and Q.Q.; resources, Q.J.; writing—original draft preparation, A.R.; writing—review and editing, A.R. and Y.W.; visualization, A.R.; supervision, Q.J.; project administration, Q.J.; funding acquisition, Q.J., Q.Q. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Key Research and Development Program of China under fund numbers 2021YFF1200100, 2021YFF1200104, and 2020YFA0909100.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and codes used in this work are available at https://github.com/abdul-rasool/Coding-constraints-for-DNA-data-storage (accessed on 28 February 2021).
Acknowledgments
The authors would like to thank all the anonymous reviewers for their insightful comments and constructive suggestions that have obviously upgraded the quality of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, M.; Wu, J.; Dai, J.; Jiang, Q.; Qu, Q.; Huang, X.; Wang, Y. A self-contained and self-explanatory DNA storage system. Sci. Rep. 2021, 11, 18063. [Google Scholar] [CrossRef] [PubMed]
- Yazdi, S.M.H.T.; Gabrys, R.; Milenkovic, O. Portable and Error-Free DNA-Based Data Storage. Sci. Rep. 2017, 7, 5011. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erlich, Y.; Zielinski, D. DNA Fountain enables a robust and efficient storage architecture. Science 2017, 355, 950–953. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blawat, M.; Gaedke, K.; Hütter, I.; Chen, X.-M.; Turczyk, B.; Inverso, S.; Pruitt, B.W.; Church, G.M. Forward Error Correction for DNA Data Storage. Procedia Comput. Sci. 2016, 80, 1011–1022. [Google Scholar] [CrossRef] [Green Version]
- Grass, R.N.; Heckel, R.; Puddu, M.; Paunescu, D.; Stark, W.J. Robust Chemical Preservation of Digital Information on DNA in Silica with Error-Correcting Codes. Angew. Chem. Int. Ed. 2015, 54, 2552–2555. [Google Scholar] [CrossRef]
- Goldman, N.; Bertone, P.; Chen, S.; Dessimoz, C.; LeProust, E.M.; Sipos, B.; Birney, E. Towards practical, high-capacity, low-maintenance information storage in synthesized DNA. Nature 2013, 494, 77–80. [Google Scholar] [CrossRef] [Green Version]
- Church, G.M.; Gao, Y.; Kosuri, S. Next-Generation Digital Information Storage in DNA. Science 2012, 337, 1628. [Google Scholar] [CrossRef] [Green Version]
- Yan, S.; Wong, K.-C. Future DNA computing device and accompanied tool stack: Towards high-throughput computation. Future Gener. Comput. Syst. 2021, 117, 111–124. [Google Scholar] [CrossRef]
- Wang, Y.; Noor-A-Rahim, M.; Gunawan, E.; Guan, Y.L.; Poh, C.L. Construction of Bio-Constrained Code for DNA Data Storage. IEEE Commun. Lett. 2019, 23, 963–966. [Google Scholar] [CrossRef]
- Limbachiya, D.; Gupta, M.K.; Aggarwal, V. Family of Constrained Codes for Archival DNA Data Storage. IEEE Commun. Lett. 2018, 22, 1972–1975. [Google Scholar] [CrossRef]
- Benerjee, K.G.; Banerjee, A. On DNA Codes With Multiple Constraints. IEEE Commun. Lett. 2021, 25, 365–368. [Google Scholar] [CrossRef]
- Rasool, A.; Qu, Q.; Jiang, Q.; Wang, Y. A Strategy-Based Optimization Algorithm to Design Codes for DNA Data Storage System. In Algorithms and Architectures for Parallel Processing; Springer International Publishing: Xiamen, China, 2022; pp. 284–299. [Google Scholar]
- Chee, Y.M.; Ling, S. Improved lower bounds for constant GC-content DNA codes. IEEE Trans. Inf. Theory 2008, 54, 391–394. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.X.; Yordanov, B.; Gaunt, A.; Wang, M.X.; Dai, P.; Chen, Y.J.; Zhang, K.; Fang, J.Z.; Dalchau, N.; Li, J.M.; et al. A deep learning model for predicting next-generation sequencing depth from DNA sequence. Nat. Commun. 2021, 12, 4387. [Google Scholar] [CrossRef]
- Liu, Q.; Fang, L.; Yu, G.; Wang, D.; Xiao, C.-L.; Wang, K. Detection of DNA base modifications by deep recurrent neural network on Oxford Nanopore sequencing data. Nat. Commun. 2019, 10, 2449. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Wu, J.; Huang, B.; Liu, Y. High-density information storage and random access scheme using synthetic DNA. 3 Biotech 2021, 11, 328. [Google Scholar] [CrossRef]
- Cao, B.; Li, X.; Zhang, X.; Wang, B.; Zhang, Q.; Wei, X. Designing Uncorrelated Address Constrain for DNA Storage by DMVO Algorithm. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 1. [Google Scholar] [CrossRef]
- King, O.D. Bounds for DNA codes with constant GC-content. Electron. J. Comb. 2003, 10, R33. [Google Scholar] [CrossRef]
- Milenkovic, O.; Kashyap, N. On the design of codes for DNA computing. In Coding and Cryptography; Ytrehus, O., Ed.; Springer: Berlin, Heidelberg, Germany, 2006; Volume 3969, pp. 100–119. [Google Scholar]
- Aboluion, N.; Smith, D.H.; Perkins, S. Linear and nonlinear constructions of DNA codes with Hamming distance d, constant GC-content and a reverse-complement constraint. Discret. Math. 2012, 312, 1062–1075. [Google Scholar] [CrossRef] [Green Version]
- Koumakis, L. Deep learning models in genomics; are we there yet? Comput. Struct. Biotechnol. J. 2020, 18, 1466–1473. [Google Scholar] [CrossRef]
- Montana, D.J.; Davis, L. Training Feedforward Neural Networks Using Genetic Algorithms. In Proceedings of the Eleventh International Joint Conference on Artificial Intelligence, Detroit, MI, USA, 20–25 August 1989. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Muzammal, M.; Nasrulin, B. Renovating blockchain with distributed databases: An open source system. Future Gener. Comput. Syst. 2019, 90, 105–117. [Google Scholar] [CrossRef]
- Jin, X.; Nie, R.; Zhou, D.; Yao, S.; Chen, Y.; Yu, J.; Wang, Q. A novel DNA sequence similarity calculation based on simplified pulse-coupled neural network and Huffman coding. Phys. A Stat. Mech. Its Appl. 2016, 461, 325–338. [Google Scholar] [CrossRef]
- Deng, L.; Wu, H.; Liu, X.; Liu, H. DeepD2V: A Novel Deep Learning-Based Framework for Predicting Transcription Factor Binding Sites from Combined DNA Sequence. Int. J. Mol. Sci. 2021, 22, 5521. [Google Scholar] [CrossRef]
- Song, W.; Cai, K.; Zhang, M.; Yuen, C. Codes with Run-Length and GC-Content Constraints for DNA-Based Data Storage. IEEE Commun. Lett. 2018, 22, 2004–2007. [Google Scholar] [CrossRef]
- Siegel, P. Codes for Mass Data Storage Systems (Second Edition) (K. H. Schouhamer Immink; 2004) [Book review]. IEEE Trans. Inf. Theory 2006, 52, 5614–5616. [Google Scholar] [CrossRef]
- Félix, B. On the embedding capacity of DNA strands under substitution, insertion, and deletion mutations. In Proceedings of the International Society for Optics and Photonics, San Jose, CA, USA, 17–21 January 2010. [Google Scholar]
- Heckel, R.; Shomorony, I.; Ramchandran, K.; David, N. Fundamental limits of DNA storage systems. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 3130–3134. [Google Scholar]
- Tulpan, D.; Smith, D.H.; Montemanni, R. Thermodynamic Post-Processing versus GC-Content Pre-Processing for DNA Codes Satisfying the Hamming Distance and Reverse-Complement Constraints. IEEE-ACM Trans. Comput. Biol. Bioinform. 2014, 11, 441–452. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Nussinov, R.; Jacobson, A.B. Fast algorithm for predicting the secondary structure of single-stranded rna. Proc. Natl. Acad. Sci. USA 1980, 77, 6309–6313. [Google Scholar] [CrossRef] [Green Version]
- Peter Clote, R.B. Computational Molecular Biology: An Introduction; Wiley Series in Mathematical and Computational Biology; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Wu, Y.T.; Yuan, M.; Dong, S.P.; Lin, L.; Liu, Y.Q. Remaining useful life estimation of engineered systems using vanilla LSTM neural networks. Neurocomputing 2018, 275, 167–179. [Google Scholar] [CrossRef]
- Rasool, A.; Jiang, Q.; Qu, Q.; Ji, C. WRS: A Novel Word-embedding Method for Real-time Sentiment with Integrated LSTM-CNN Model. In Proceedings of the 2021 IEEE International Conference on Real-time Computing and Robotics (RCAR), Xining, China, 15–19 July 2021; pp. 590–595. [Google Scholar]
- Harding, S.E.; Channell, G.; Phillips-Jones, M.K. The discovery of hydrogen bonds in DNA and a re-evaluation of the 1948 Creeth two-chain model for its structure. Biochem. Soc. Trans. 2018, 46, 1171–1182. [Google Scholar] [CrossRef] [Green Version]
- Marathe, A.; Condon, A.; Corn, R.M. On Combinatorial DNA Word Design. J. Comput. Biol. A J. Comput. Mol. Cell Biol. 2001, 83, 201–219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Charalambides, C.A. Enumerative Combinatorics, CRC Press Series on Discrete Mathematics and Its Applications; Chapman & Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Wei, H.; Schwartz, M. Improved Coding over Sets for DNA-Based Data Storage. IEEE Trans. Inf. Theory 2021, 68, 118–129. [Google Scholar] [CrossRef]
- Cannon, J.; Bosma, W.; Fieker, C.; Steel, A.K. Handbook of Magma Functions. 2011. Available online: https://www.math.uzh.ch/sepp/magma-2.20.4-cr/HandbookVolume09 (accessed on 16 July 2021).
- Paluncic, F.; Abdel-Ghaffar, K.A.S.; Ferreira, H.C.; Clarke, W.A. A Multiple Insertion/Deletion Correcting Code for Run-Length Limited Sequences. IEEE Trans. Inf. Theory 2012, 58, 1809–1824. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).