1. Introduction
We consider the determination of optimal damping for the vibrating structure which is represented by a linear vibrational system described by
where
M and
K (called mass and stiffness, respectively) are real, symmetric positive definite matrices of order
n. The damping matrix is defined as
where matrices
and
correspond to internal and external damping, respectively. Internal damping can be modelled as
or
In Equation (
3), we assume that the internal damping is a small multiple of the critical damping, while (
4) corresponds to the so-called Rayleigh damping. Both cases are important and widely used in literature (see, e.g., books [
1,
2] or papers [
3,
4,
5]) and they are interesting from a modeling point of view since the matrix that simultaneously diagonalizes matrices
M and
K, diagonalizes the internal damping matrix as well. In the
Section 2.1 we give formulas for internal damping matrices in the modal coordinates. Moreover, analysis of the influence of different internal damping matrices is given in [
6].
From the optimization point of view, we are more interested in the external viscous damping which can be modeled as
where
is the viscosity and
describes a geometry of the corresponding damping position for
. Throughout this paper, we will refer to the pair
as a damper. Typically, the system has very few dampers compared to the full dimension [
1,
2,
7], which means that
. This is also the standard assumption all works from [
3,
4,
8,
9], where more details on the structure of internal and external damping can be found. For the full derivation of the problem and the solution and modeling procedure, we refer the reader to [
2]. The model of linear vibrational system (
1) corresponds to the quadratic eigenvalue problem
The damping optimization problem, in general, can be stated as follows: determine the “best” damping matrix D which insures optimal evanescence of each component of x. In practice, one can usually influence only the external damping. Therefore, the problem is to determine the optimal external damping matrix , which minimizes the total average energy of the system.
In order to optimize the external damping matrix from (
5), we need to optimize the damping viscosities
and the damping positions
such that the chosen optimization criterion is minimal. There exists several optimization criteria for this problem. One criterion is the so-called spectral abscissa criterion. This criterion requires that the maximal real part of the eigenvalues of the quadratic eigenvalue problem (
6) are minimized (see, e.g., [
10,
11]).
In this paper, we will use a criterion based on the total average energy of the considered system. Detailed overview of the optimization criteria can be found in [
2,
12]. This criterion considers minimization of the total energy of the system (as a sum of kinetic and potential energy) averaged over all initial states of the unit total energy and a given frequency range. This criterion is equivalent to finding viscosities for which the trace of the solution of a certain Lyapunov equation involving the linearization of the quadratic eigenvalue problem (
6) is minimal. Details about this linearization and the construction of the Lyapunov equation are given in
Section 2.1. This criterion has many benefits and it was investigated widely in the last two decades. More details can be found, e.g., in [
3,
5,
8,
9,
13,
14,
15]. Moreover, this criterion can be extended to the case where we consider Multiple-Input Multiple-Output systems that appear in the control theory in many applications, e.g., in paper [
16] authors consider mixed control performance measure that includes also the total average energy into account.
In practice we optimize the geometry of considered vibrating structures such as
n-mass oscillators or shear frame vibrating structures, for more details see, e.g., [
2,
6,
8,
11,
17]. However, since the optimization of damping positions is a very hard problem, in this work we will concentrate only on the optimization of viscosities. This can be then applied for different damping positions or it can be used within the algorithm that optimizes damping positions, but we also emphasize that such algorithms are typically heuristic algorithms, see, e.g., [
15]. Moreover, the objective function (which is in our case the total average energy) that needs to be minimized is a non-convex function that includes viscosity parameters and damping positions. Therefore, minimization of such objective function requires the evaluation of objective function a large number of times. Thus, directly applying the standard method requires
operations for each run, irrespective of the number of dampers. For the case of a small number of dampers
k, which is typical in applications [
2,
7], we propose a fast method that requires
operations for each run.
In this paper, matrices are denoted by uppercase Greek or Roman letters, vectors are denoted by lowercase Roman letters, and scalars are denoted by lowercase Greek letters. As in Matlab, function is used twofold: when A is a matrix, denotes the vectors of A’s diagonal elements. When is a vector, and denote the square diagonal matrix with elements of a on its diagonal.
This paper is organized as follows: in
Section 2 we describe the standard approach which uses linearization and minimizes trace of the solution of the respective Lyapunov equation. An overview of the existing
solution methods is presented in
Section 2.1. A new approach, which uses complex symmetric linearization and reduces the problem to a sequence of
k eigenvalue problems of complex symmetric diagonal-plus-rank-one (CSymDPR1) matrices, is presented in
Section 2.2. Here,
k is the number of dampers from (
5). This approach uses fast multiplication of linked Cauchy-like matrices and needs
operations in each optimization step. This makes the optimization using the new approach an order of magnitude faster than the standard approach if the number of dampers is small,
. Several large examples and some timings are given in
Section 3. Discussion of our results and algorithms is presented in
Section 4 and the conclusions are given in
Section 5.
2. Methods
In this section, we describe solution methods for finding the optimal damping of the linear vibrational system (
1) based on minimization of total average energy. First, we describe a linearization of the system (
1), which yields a linearization of the quadratic eigenvalue problem (
6). The linearization is performed by changing the basis and the linearized problem is further reduced to an eigenvalue problem of a simpler matrix. Of course, the corresponding quadratic eigenvalue problem can be solved by maintaining the second-order structure [
18,
19]. Although such approaches result in methods that works with matrices of dimension
n instead of our approach that uses matrices of dimension
, they still require
operations in each optimization step and can have numerical issues in some cases. Further, the linearization of the system is necessary for efficient calculation of total average energy [
2,
12].
In
Section 2.1, we present an existing direct approach (see, e.g., [
2,
4]), where each iteration of optimization requires
operations. In
Section 2.2, we describe the novel fast method which requires
operations in each optimization step, thus outperforming the standard method in the case of a small number of dampers.
For a structured system, the problem (
1) was considered in [
8,
9] where the authors proposed dimension reduction to accelerate the optimization process. However, to be efficient, dimension reduction requires a specific structure, so this approach cannot be applied efficiently in a general setting.
By symmetric linearization we transform quadratic eigenvalue problem (
6) to the generalized eigenvalue problem (GEVP) (see, e.g., [
20])
Let
be the generalized eigenvalue decomposition of the pair
. Since the calculation of matrices
and
does not depend on the damping matrix
D, they can be calculated prior to the optimization procedure.
Both choices of
, from (
3) and from (
4) imply that
is diagonal in the
-basis. More precisely,
if
is defined by (
3), and
if
is defined by (
4).
The external damping matrix, , is a low-rank matrix of rank k which depends on the number, positions, and the structure of dampers. For example, if all dampers are grounded and l is a vector of indices of damping positions, then is zero except for .
In the basis
problem (
7) reduces to GEVP
and in the basis
we have the hyperbolic generalized eigenvalue problem
Now, we can write the linearized system in the so-called modal coordinates. By simple transformation, (
11) is equivalent to the eigenvalue problem for the matrix
Let
where parameter
s determines the number of eigenfrequencies of the system which need to be damped (for more details, see, e.g., [
2,
5,
8]).
It can be shown (see, e.g., [
2,
4,
12]) that the criterion based on the minimzation of the total average energy of the considered system is equivalent to
where
is the solution of the Lyapunov equation
For the external damping matrix
defined by (
5), the problem is to determine optimal damping positions and damping viscosities such that
is minimal. This is a demanding problem, both, from the computational point of view and the point of optimization of damping positions. The main reason lies in the fact that the criterion of total average energy has many local minima, so we usually need to optimize viscosity parameters for many different damping positions.
2.1. Standard Methods
The Lyapunov Equation (
14) with structured matrices
and
G from (
12) and (
13), respectively, can be solved by iterative methods such as ADI method [
21,
22] used in [
5] or the sign function method [
23,
24] used in [
14]. Here, we are considering only direct methods due to simplicity of implementation, numerical stability in all cases, and ease of estimating computational complexity.
Standard direct methods calculate the solution of the Lyapunov Equation (
14) by using the Schur form, for example, Hammarling algorithm [
25,
26] and Bartels-Stewart algorithm [
27]. The computation of Schur form requires
operations, so these algorithms are
solutions. The algorithms are implemented in the SLICOT library [
28] and are used in Matlab. The timings for some examples are given in
Section 3.
2.2. Fast Method
In this section, we present our novel
method, where
k is the number of dampers. In our approach, instead of using the Schur form to solve (
14), we use diagonalization of the matrix
from (
12), where the external damping matrix
is defined by (
5). The eigenvalue problem for the matrix
is reduced to
k eigenvalue problems for the complex symmetric diagonal-plus-rank-one (CSymDPR1) matrices,
k being the number of dampers. Each of those EVPs can be efficiently solved in
operations. It is important that updating of the eigenvectors can also be performed using
operations, due to Cauchy-like structure of eigenvector matrices. In this way, after preparatory steps from
Section 2.1 and
Section 2.2.3 below, which require
operations, each computation of
, where
is from (
14), requires only
operations. This makes trace optimization considerably faster for the case when the number of dampers is small, which is the case prevalent in practice. If the number of dampers grows towards
n, our algorithm will require
operations for each iteration, as does the standard approach.
The section is organized as follows. In
Section 2.2.1, we present existing results about Cauchy-like matrices and their fast multiplication. In
Section 2.2.2 we develop an efficient
method for the solution of the CSymDPR1 eigenvalue problem. In
Section 2.2.3, we describe the reduction to the CSymDPR1 eigenvalue problems. In
Section 2.2.4, we develop a fast
algorithm for the final trace computation, based on the fast multiplication of Cauchy-like matrices.
2.2.1. Cauchy-like Matrices
A Cauchy-like matrix
is the matrix which satisfies the Sylvester-type displacement equation (see, e.g., [
29])
where
Here the vectors x and y and the matrices P and Q are called the generators of C.
For example, the standard Cauchy matrix with real vectors x and y is equal to , where . Clearly, given generators, all elements of a Cauchy-like matrix can be computed on operations.
For multiplication by Cauchy-like matrices, we have the following results.
Given
Cauchy-like matrix
A and
n-dimensional vector
v, the product
can be computed in
operations [
29] (Lemma 2.2).
Given two linked Cauchy-like matrices,
and
where
the product
is a Cauchy-like matrix
where
and
[
29] (Lemma 2.3), that is,
C satisfies the displacement equation
This generators of C can be computed in operations.
2.2.2. Eigenvalue Decomposition of CSymDPR1 Matrix
Let
A be an
CSymDPR1 matrix,
where
is a diagonal matrix,
is a vector, and
is a real scalar. Here
.
Without loss of generality, we assume that
A is irreducible, that is,
If for some i, then the diagonal element is an eigenvalue whose corresponding eigenvector is the i-th canonical vector, and if , then is an eigenvalue of the matrix A.
Let
be the eigenvalue decomposition of
A, where
are the eigenvalues and
is a matrix whose columns are the corresponding eigenvectors. Notice that the eigenvector matrix of a complex symmetric matrix satisfies the relation
.
The eigenvalue problem for
A can be solved by any of the standard methods (see [
30] and the references therein). However, due to the special structure of
A, we can use the following approach (see [
31,
32] (Section 8.5.3)): the eigenvalues of
A are the zeros of the secular equation
and the corresponding eigenvectors are given by
It is important to notice that
V is a Cauchy-like matrix,
Equation (
18) can, for example, be solved by the secular equation solver from the package MPSolve package [
33,
34].
If
A is real, the eigenvalues interlace the diagonal elements of
and can be computed highly accurately by bisection [
35]. In this case, orthogonality of computed eigenvectors follows from the accuracy of computed
s. In the complex symmetric case, there is no interlacing, but orthogonality is not an issue, so we developed a version of the Rayleigh quotient iteration.
Standard Rayleigh quotient iteration (RQI) is as follows [
36]: given starting
x repeat
Then,
. In our case
is again a CSymDPR1 matrix which is computed in
operations.
For real symmetric or Hermitian matrices, RQI converges quadratically to the absolutely largest eigenvalue. In the complex symmetric case, the convergence of RQI is slow and it is better to use the Modified Rayleigh Quotient Iteration (MRQI) which is as follows: given starting
x repeat
MRQI method converges quadratically [
36,
37].
For a CSymDPR1 matrix, having in mind the eigenvector formulas (
19), we further modify the method as follows: given starting
x repeat
This modification showed very good convergence properties in all our large damping problems.
Once
has converged to an eigenvalue, this eigenvalue can be deflated [
38] (Section 7.2). In particular, if for some
we have computed eigenvalues
of
A, then we can compute the remaining
eigenvalues
as eigenvalues of the
CSymDPR1 matrix
where
and
In our implementation, the first steps use RQI from (
21) and, after that, MRQI from (
23) is used until convergence.
The operation count to compute all eigenvalues of
A is
, construction of generators for the eigenvector matrix
V from (
20) takes
operations (computing
), and the reconstruction of
V from its generators, if needed, takes another
operations. This amounts to
operations to compute the complete eigenvalue decomposition of
A.
2.2.3. Reduction to CSymDPR1 Eigenproblems
Let
and
Q denote the solution of the hyperbolic GEVP
where
and
are defined by (
8)–(
11), such that
Due to the sparse structure of the eigenvalue problem from Equation (
26), the matrices
Q and
are computed by solving
n hyperbolic GEVPs of dimension 2: for
,
and all other elements of
Q and
are zero. For example, if
and
are given by (
3) and (
9), respectively, then
where
and ı is the imaginary unit.
The problem (
26) is equal to the problem (
11), but without external damping. Instead of solving the generalized eigenvalue proglem (
11), or the unsymmetric eigenvalue problem (
12), we compute the eigenvalue decomposition of the complex symmetric diagonal-plus-low-rank matrix
which is then used to solve (
14).
Assume, for example, that there is only one damper with viscosity
positioned at the mass
l. Instead of solving (
11), we compute the eigenvalue decomposition of the CSymDPR1 matrix
where
. In the case of
k dampers, the procedure is repeated. For example, in the case of two dampers we need to solve the eigenvalue problem for the matrix
We start by computing the eigenvalue decomposition of the matrix
Then, the eigenvalue decomposition of the matrix
is computed as
Since all involved matrices are complex symmetric, we have
From Equation (
20), it follows that
and
are Cauchy-like matrices,
where elements of the vectors
and
are reciprocals of the norms of the un-normalized eigenvectors
from Equation (
19). The matrices
and
are linked, so according to Equation (
16),
is a Cauchy-like matrix,
Using Equation (
34), the expression for
P further simplifies to
. This procedure is easily generalized to
dampers. The computation of
,
P and
Q requires
operations.
2.2.4. Trace Computation
Let
be given by (
29) and let
be its eigenvalue decomposition computed with the method from
Section 2.2.2. Then
S is a Cauchy-like matrix defined by
for some
satisfying
, where
k is the number of dampers.
Let
denote the element-wise conjugated matrix
. Inserting the eigenvalue decomposition of
into the Lyapunov Equation (
14) gives
Premultiplying Equation (
36) by
, postmultiplying by
and setting
, gives a displacement equation
Here
Y is a Cauchy-like matrix,
. Notice that
is not an actual matrix multiplication – due to the special form of
G from (
13), this is just a selection of columns of
. Generating full
Y, if needed, requires
operations.
To finish the computation, we need to compute
. Set
. Then
The matrices
S and
Y are linked Cauchy-like matrices, so, according to Equation (
16), the matrix
Z is a Cauchy-like matrix
where
Computating
requires
operations (see
Section 2.2.2).
Finally,
from (
38) is computed by using scalar products or respective columns of the matrices
S and
Z:
Computation of columns of
requires
operations, computation of columns of
Z requires
operations, and computation of scalar products requires
operations.
2.2.5. Algorithms
In this section, we give pseudocodes of algorithms that comprise our method. Algorithm 1 is the function that changes the basis of the symmetric linearization of the given vibrational system to obtain a diagonal-plus-low-rank matrix.
| Algorithm 1 Change of basis. |
functionChangeOfBasis() | ▹ Input is the vibrational system (1)–(4). |
compute matrices and from ( 8) | ▹ Use any of the standard methods, . |
| ▹ See (9) and (10), . |
compute matrices Q and from ( 27) | ▹ See also (28), |
return , Q, | |
end function | |
Algorithm 2 computes the eigenvalue decomposition of the CSymDPR1 matrix
A from (
17). The computed eigenvalues are diagonal elements of the diagonal matrix
and the eigenvector matrix
V is returned as a Cauchy-like matrix (
20).
| Algorithm 2 Eigenvalue decomposition of a CSymDPR1 matrix. |
functionEigen() | ▹ Input is the CSymDPR1 matrix from (17). |
for do | ▹ operations. |
choose starting vector x | |
for do | ▹ Repeat 4 times. |
compute and new x using ( 21) | ▹ Rayleigh Quotient Iteration. |
end for | |
repeat | |
compute and new x using ( 22) | ▹ Modified RQI. |
until convergence | |
| |
deflate using ( 24) and ( 25) | |
end for | |
set | ▹ See (20). |
return , V | |
end function | |
Given the geometries
and the viscosities
of external dampers from (
5), Algorithm 3 computes
from (
38), where
is defined by (
36).
| Algorithm 3 Trace computation. |
functionTraceX() | ▹ Inputs are from Algorithm 1, (5) and (13). |
factor | |
compute | |
| ▹ Algorithm 2, . |
for do | ▹ operations. |
factor | |
compute | ▹ See (33). |
| ▹ Algorithm 2, . |
| ▹ Multiplication of Cauchy-like matrices, see (35). |
end for | |
| ▹ See (37). |
| ▹ See (39) and (40). |
| ▹ See (41). |
return | |
end function | |
Finally, optimal viscosities
with fixed geometries
from (
5) are computed by Algorithm 4.
| Algorithm 4 Optimization of viscosities. |
functionOptimize() | |
use computed by Algorithm 1 | |
choose geometries of dampers | ▹ See (5). |
choose matrix G | ▹ See (13). |
define | |
| ▹ Use standard software. |
return | |
end function | |
2.2.6. Accuracy
Generally speaking, analyzing the accuracy of the solution
X of the Lyapunov Equation (
14), which is a special form of the Sylvester equation, is a complex task. The solution
X is usually computed with a small relative residual, but can at the same time have a large backward error [
39] (Chapter 16).
Let us analyze all four steps of the proposed method.
The first step is solving the GEVP (
8). Perturbation bounds and accuracy of the computed solution is given by the standard results from [
32] (Section 8.7.2) and [
40], and depends on the spectral condition number of the positive definite matrix
. In addition, small changes in elements of
K and
M, cause small changes in eigenvalues
[
2]. In some cases, (
8) can be computed with high relative accuracy [
41], but this is generally not needed for standard structures. The spectral condition numbers
for our examples are displayed in
Section 3.
The second step is solving hyperbolic GEVP (
26). If
is defined by (
9) for small
, then all elements of the matrices
Q and
from (
27) are computed using (
28) with very high accuracy.
The third step is solution of a sequence of CSymDPR1 eigenvalue problems (
31)–(
33). The perturbation theory for a general eigenvalue problem is given by the Bauer-Fike Theorem [
32]. It is expected that the errors in the computed eigenvalue decomposition (
33) is governed by the quantity
, where
is the machine precision. Due to (
34),
is computed in
operations. Maximal
over all matrices
,
and
S encountered during computations (
31)–(
33) is displayed in
Section 3.
The final step is the trace computation from
Section 2.2.4. Let
Y and
Z denote the exact matrices and
and
denote the computed matrices from (
37) and (
39), respectively. Although the complete error analysis is very tedious, from (
37) we expect that
Combining Equations (
39) and (
40), we expect that
where
3. Examples
In this section, we present three examples of vibrating structures that are represented by an
n-mass oscillator. The size of the problem is
for the “small” example,
for the “large” example, and
for the “homogeneous” example with more homogeneous masses. We compare our algorithm with the
algorithm from [
8]. The computations are performed on an Intel i7-8700K CPU running at 3.70 GHz with 12 cores.
Let us describe the large example. The small example has the same structure, we just use an
n-mass oscillator with a smaller number of masses. The code used to generate both examples is available in the file
src/GenerateExamples.jl in the GitHub repository [
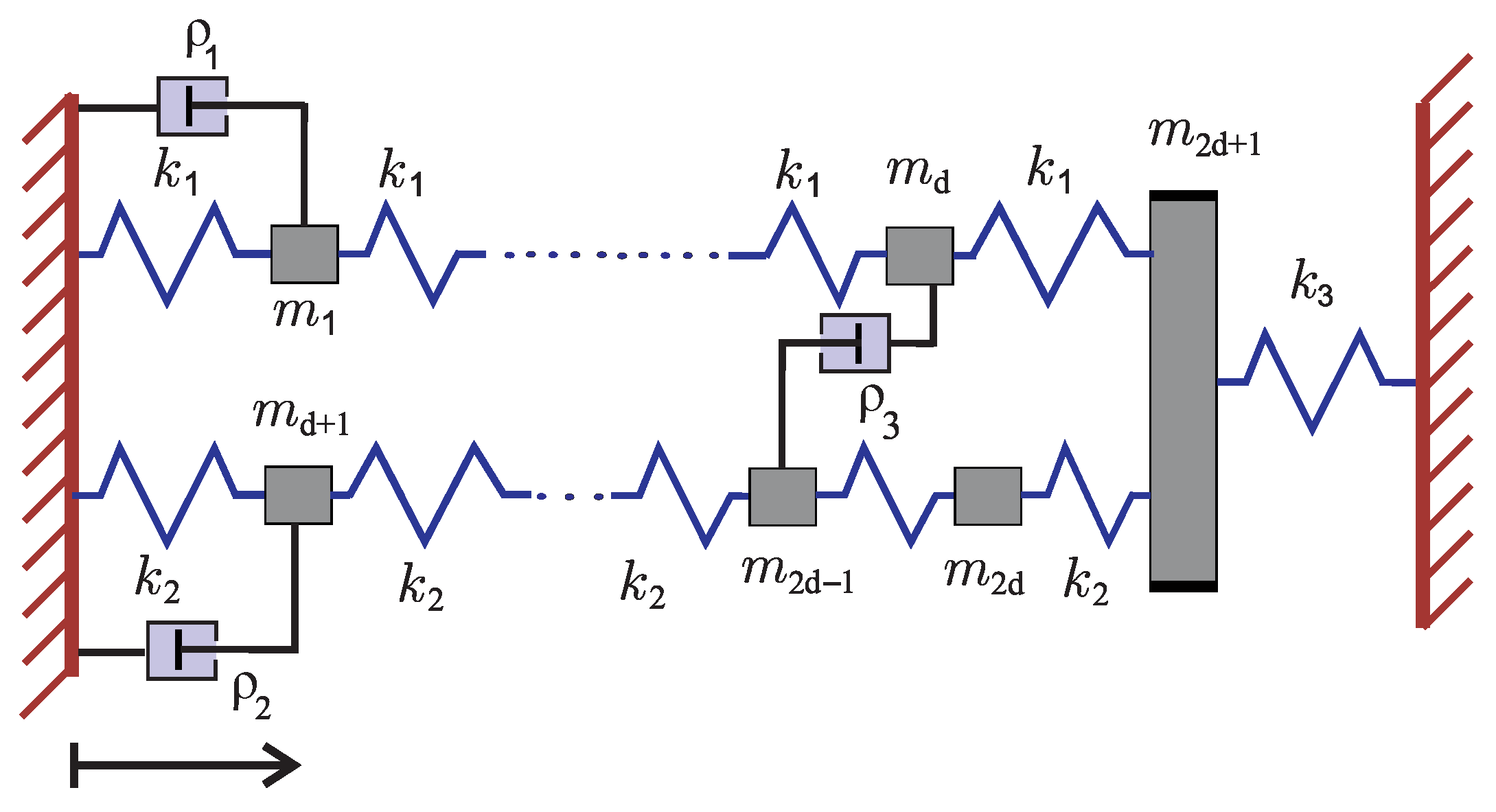
42]. We consider the mechanical system shown in
Figure 1. Similar examples were considered in [
3,
5,
8,
9,
13,
15]. In all our examples the mass oscillator contains two rows of
d masses that are grounded from one side, while on the other side masses are connected to one mass which is then grounded. Therefore, we consider
masses and
springs, while the system has three dampers of different viscosities
,
and
. However, we include several different configurations since system dimension
n and parameters that determine system configuration are changed as we will describe below.
For configuration given by
Figure 1, one can derive the system of differential equations that describe the behavior of displacements from equilibrium for each mass separately. In particular, for each mass one can write an equation that follows Newton’s law and describes displacement for corresponding mass. For that purpose, one should take into account that the elastic force from the neighboring springs is negatively proportional to the relative displacement and forces that arise due to the damping effects. This can be written in the matrix form using Equation (
1) (see, e.g, [
2]). We obtain the mass matrix
and the stiffness matrix
where
We consider the following configuration:
for
and
masses and the internal damping
determined by (
3) for
. As shown in
Figure 1, we consider three dampers. The first two dampers are grounded, while the third damper connects two rows of masses. This means that external damping is determined by (
5) with
where
corresponds to the
i-th canonical vector.
Here, we would like to emphasize that in general one needs to determine indices , , and corresponding viscosities and such that the total average energy is minimal. As we mentioned in the introduction, here we do not consider optimization of damping positions since our main aim was to accelerate the calculation of objective function. Thus, here we fix damping positions and optimize viscosities as we state below.
In particular, here we present results for only one configuration
. We would like to damp the 27 smallest eigenfrequencies of the system, that is, the matrix
G is defined by (
13) with
.
In the homogeneous example
,
, where the first thousand masses are
, the next thousand masses are
, the last mass is
, and
In this example we choose
in Equation (
13). The code used to generate the homogeneous example is available in the file
src/GenerateExamples.jl in the GitHub repository [
42].
Our problems and solutions are described in
Table 1. The timings for the standard method computed using Matlab and our new method using Julia [
43] are given in
Table 2 and
Table 3, respectively. In
Table 2 and
Table 3, comparison is made between Matlab and Julia. Julia is known to be faster than Matlab since the functions are pre-compiled before execution. In this case we are using Matlab’s built-in function
lyap(), which uses pre-compiled routines from the SLICOT library [
28]. Even more, Matlab’s implementation of the SLICOT library in a multithreading environment is more than twice faster as Julia’s, so the comparison between the standard algorithm and our method is fair. To see the influence of the number of dampers, the times for single trace computation and complete optimization for 3, 4, and 5 dampers are given in
Table 4. In
Table 5, we display the norm of residuals of the computed solution
X of the Lyapunov Equation (
36). We also display the maximal relative errors between minimal trace and optimal viscosities computed by our method from
Section 2.2 and the standard method from
Section 2.1 (see also [
8]), where solutions of (
14) with
given by (
12), are computed using Matlab’s function
lyap().
4. Discussion
Comparing
Table 2 and
Table 3, we see that the speedup of our method over the standard method grows with dimension (more precisely: 2.24, 4.03, and 4.8, computed by adjusting the number of trace computations). From
Table 2 we see that the computation times for the standard method for both, individual eigenvalue computations and optimization procedure, are proportional to
. Also, the computation times in
Table 3 for both, individual eigenvalue decomposition from the column
Eigen and trace computation from the column
TraceX, are clearly proportional to
. This confirms the fact that our method is asymptotically an order of magnitude faster than the standard direct method in the typical case when the number of dampers is small.
Timings from
Table 4 show that the duration of computation is indeed linearly proportional to the number of dampers, as predicted by the analysis.
The condition numbers
in
Table 5 govern the overall accuracy of the computation. The maximal condition numbers of all eigenvector matrices
S and
from (
32) and (
33) which appear during the entire optimization process are smaller than
, so our method does not introduce extra errors. Maximal relative residuals of the computed solutions of the Lyapunov Equation (
14) with
from (
29) over the entire optimization process, displayed in the third column of
Table 5, are very small. This behavior is expected according to the analysis from
Section 2.2.6. Maximal relative errors between optimal traces and optimal viscosities computed by our method and the standard method, shown in the fourth column of
Table 5, are small enough, which demonstrates that our method is comparable in accuracy to the standard one.
5. Conclusions
The proposed direct algorithm, based on the fast algorithm for the solution of the eigenvalue problems for CSymDPR1 matrices and fast multiplication of Cauchy-like matrices, is simple, stable, and outperforms the standard direct counterpart, especially when the size of the problem n is large and the number of dampers k is small. It is also easy to implement in Julia’s multithreading environment.
After the initial eigenvalue decomposition of the linearized problem, our algorithm computes optimal viscosities for each choice of external dampers in operations. Hence, if the number of dampers is small, the subsequent optimization is the order of magnitude faster than in the standard approach, while maintaining accuracy.
Future work may include a more detailed analysis of the new method and development of the eigenvalue decomposition algorithm for block complex symmetric diagonal-plus-low-rank matrices, which could treat all k dampers simultaneously and, thus, be even faster.