Abstract
Proof, a key topic in advanced mathematics, also forms an essential part of the formal learning experience at all levels of education. The reason is that the argumentation involved calls for pondering ideas in depth, organizing knowledge, and comparing different points of view. Geometry, characterized by the interaction between the visual appearance of geometric elements and the conceptual understanding of their meaning required to generate precise explanations, is one of the foremost areas for research on proof and argumentation. In this qualitative analysis of the arguments formulated by participants in an extracurricular mathematics stimulus program, we categorized students’ replies on the grounds of reasoning styles, representations used, and levels of generality. The problems were proposed in a lesson on a quotient set based on the similarity among triangles created with Geogebra and the responses were gathered through a Google form. By means a content analysis, the results inform about the reasoning style, the scope of the argumentation, and the representation used. The findings show that neither reasoning styles nor the representations used conditioned the level of generality, although higher levels of argumentation were favored by harmonic and analytical reasoning and the use of algebraic representations.
MSC:
97C70; 97G50; 97U99; 97C99
1. Introduction
International acknowledgment of the importance of proof in learning mathematics has inspired considerable research, although certain questions such as the extent of students’ aptitude for geometric proof and reasoning have yet to be answered [1,2]. Students have been observed to feel no need for proof or to be able to distinguish verification from explanation or proof [3]. This heightens the difficulties they encounter in higher education, with its emphasis on structured criteria such as rigor and logic [4].
Above and beyond the role of argumentation as a formal mathematical requirement, in mathematics education it is instrumental in learning [5] and explanation [6], for formulating arguments entails pondering ideas, organizing knowledge, and comparing different points of view [7]. This study consequently focused on argumentation in mathematics education, understood as the mathematical arguments generated by students and teachers in mathematics classrooms [8].
Geometry is a key area for researching proof and argumentation in primary and secondary school students [9]. More specifically, geometric transformations have been shown to be important for the recognition of similar figures [10]. By exploring the properties of shapes and their images using geometric transformations, students learn to justify and prove their arguments and to establish interconnections with algebra [8].
Spatial reasoning calls for “the mental manipulation of visual stimuli to transform spatial into other visual forms by thinking analytically about the structural features of spatial forms” [11] (p. 78). In other words, geometric reasoning is characterized by the interaction between the visual and the conceptual [12]. In many geometric proof problems, students find it difficult to make the verbal–symbolic/graphic–visual connection [13,14]. Reasoning styles or approaches that may prove helpful in algebra may hinder the construction of geometric proofs [15,16]. Proofs explicitly based on visual reasoning are often deemed explanatory, whereas, with scant exceptions, purely algebraic proofs are not [17]. This is because representation, on whose correct choice the use of symbols and furtherance of reasoning depend, plays different roles in algebra and geometry [18].
For those reasons, encouraging the use of different types of representation (verbal and symbolic notation among them) in argumentation has been highlighted as one of the principles of proof problem design [19]. The aim is to identify teaching characteristics that generate in students a need for proof beyond what the educator requires and assess their ability to do so [20]. Failure in that respect is an acknowledged weakness of other more traditional approaches to proof teaching [21,22].
Any number of empirical studies (including [23,24,25]) suggest that dynamic geometry software (DGS) or environments (DGEs) favor the development of deductive reasoning. Despite the use in recent years of proof assistant software and evidence of its benefits for learning to solve proof problems, however, its utility for classroom mathematics teaching has not been firmly established [26,27]. In the context of geometric transformations and the use of different types of representation, Geogebra accommodates constructs that can be dynamically altered by dragging separate objects, affording the program huge potential for proof and visualization in geometric problems [28,29,30]. Drag functions are ideal for solving proof problems with dynamic geometry software: building and validating figures, dragging to find properties, formulating conjectures and validating the properties and conjectures identified, and proving conjectures deductively [31]. Students taught receiving instruction on the definitions and congruency properties of triangles may find it easier to master deductive strategies in proof tasks [32]. The dragging function integrated in dynamic geometry software can be used to analyze the properties conserved on the grounds of similarity such as the Pythagorean theorem or to verify conjectures around triangles of different dimensions [33]. Moving figures and dragging one of the vertices to form a complete family has enormous potential, although whether or not students perceive the meaning of invariability or the many advantages involved remains unclear [34]. One potential advantage is the definition of a boundary case between condition-compliant and -noncompliant examples, which is crucial to generalizing conjectures [35]. That not all cases can be verified, even with dynamic geometry software, may encourage students to broach problems more deductively [7]. The possible simultaneous use of algebraic expressions with graphic representations may favor the formulation of more complete proofs [36].
Overall, proof problems require students to “do mathematics”, the highest level in the cognitive demand model (above memorization, procedures without connections, or procedures with connections) [37]. The greater complexity involved calls upon students to engage in more intensive thinking, making such problems more of a challenge and contributing to student enrichment [38]. Beyond the rigor demanded by the respective community, some generic proofs are more transparent than others. The appropriate choice of tasks and the demand for rigor and evidence consequently continue to be open questions [39], as is the transition from empirical proof to completely deductive proof [40,41]. Consideration should be given with respect to the degree of generality students attribute to their arguments, for they must be aware not only that the examples used constitute empirical evidence, but also that they must identify a general structure from such examples. For an argument to be sufficiently general and deemed a valid proof, it must hold for all the cases in a given domain [2].
In light of the foregoing ideas on proof in geometry, we believe argumentation must be analyzed on the grounds of the following three considerations: students’ reasoning style, representations in the justifications, and level of generality.
More summarily, this study aims to identify whether certain reasoning styles and representations favor generalized justifications. We determine whether they justify all possible cases or allude to particular situations which, a priori, may be drawn from visual perception. Concretely, we propose the following goals:
- Analyze students’ reasoning style and their willingness to use visual or analytical processes in proofs must be determined;
- Detect the role of representation in the justifications put forward by students;
- Organize the level of generality shown by the student in their arguments.
With this endeavor, we hope to furnish information on teaching tasks and processes that may favor the manipulation of and interconnection between different types of representation and improve students’ spatial reasoning [42,43].
In pursuit of these aims, we delivered a lesson on differently represented geometric proof problems and introduced a new way to characterize similar triangles. The resulting analysis of reasoning styles and representations used by secondary school students in their arguments sought to reply to calls for information in recent research on mathematics education practice. A number of authors have contended that students can gain an understanding of ideas associated with geometric transformations by deploying dynamic geometry environments (DGEs) [1,44] and using representations to justify their thinking [45,46]. The role of visualization or algebra in geometric reasoning was also explored [42,47].
2. Theoretical Framework
Many studies have endorsed the importance and utility of proof in mathematics education, which continues to be deemed a topic meriting further research [2]. That notwithstanding, no consensus has been reached on the consistent theoretical framework for mathematical reasoning deemed necessary by some authors [48].
Here by proof we mean “a connected sequence of assertions for or against a mathematical claim” [49] (p. 291). Related terms sometimes used include explanation, justification, and argumentation [4,22,50]. They differ in nuance, however, regarding (for instance) the degree of conviction and rigor, which depends on the community at issue [51]. Argumentation is nonetheless often found in a broader context of mathematical activity described with terms such as proof or reasoning, which may entail exploring examples or particular instances, formulating or refining conjectures, and putting forward arguments to establish such conjectures as proofs or using them as elements of proofs [20]. One criterion for an argument to be deemed a proof is that it must use statements, types of reasoning and of representation generally accepted in the classroom community’s conceptual environment [49]. Here, the context was a secondary school lesson in which the primary aim was to encourage proof as an aid to understanding [26].
The three elements around which we organized our study are described below. The second requirement is that reasoning styles and the representations used by students to support their arguments are consistent with the elements proposed by Stylianides et al. [20], to which we added the third criterion, the scope of argumentation/level of generality.
2.1. Reasoning Styles
Reasoning styles were classified as per Krutetskii [52] into analytical, geometric, and harmonic, depending on the procedure used to solve the problems and in keeping with a study by Hadamard, Menchinskaya, Poincaré, Richardson, and Walter [53].
- Analytical: where the logical–verbal dimension prevails over the visual–pictorial component. Scantly developed spatial concepts, inability to use visual support to solve problems, and no need felt for such support;
- Geometric: where the pictorial–visual dimension prevails over the logical–verbal component. Well-developed spatial concepts, and ability to use and acceptance of visual support as necessary for problem solving;
- Harmonic: where the logical–verbal and visual–pictorial components are in balance. Well-developed spatial concepts.
In Krutetskii’s studies with 34 mathematically talented students, 23 exhibited harmonic reasoning. In geometric instruction, teaching practice associated with argumentation encourages connections with other branches of mathematics and coordinates perceptual with numerical or symbolic skills [1,45,54,55]. Research has nonetheless revealed student preference for logical–verbal over visual processing [53], which is observed in fewer students [56].
Studies geared to characterizing high mathematical performance have shown mathematically talented students’ scant willingness to use visual methods [57,58,59]. Others have nonetheless found a positive relationship between visualization and effective mathematics problem solving [60,61,62,63].
A third group of researchers have reported that the preference for a given type of argument may not be found consistently across different contexts. Liu [64] concluded that students may deploy deductive reasoning in one area while finding visual illustration or the use of examples more convincing in others. Half of the 476 eighth-grade students participating in Liu’s study acknowledged that proving special cases did not suffice for argumentation to be deemed generally applicable, although most were unaware of the advantages of symbolic expressions for representing the general case. Other studies have identified the effect of other factors in students’ preference for one type of argumentation or another, including mathematical aptitude [65], beliefs [41], or the establishment of inter-representational relationships [66].
2.2. Representation
In proof, students’ argumentations may entail inductive, algebraic, visual, or perceptual reasoning defined on the grounds of how conclusions are drawn [67]. In inductive reasoning, conclusions are based on the veracity of certain cases; in algebraic reasoning, on a symbolically represented general case; in visual reasoning, on a geometric image; and in perceptual reasoning, on a known context. Therefore, the type of representation plays a significant role in students’ proofs. Gulkilik et al. [18] concluded that their ability to use algebraic representations and relate them to visual and verbal representations was important when transitioning from inductive to deductive arguments. Beitlich et al. [68], in turn, showed that students who spent time revising pictorial representations exhibited greater understanding when solving problems with pictures than with symbolic or verbal elements. The students participating in Healy and Hoyles’ study [69] found arguments involving symbols more difficult to follow than those using words, which they deemed clearer. Research by Liu [64] revealed visually, verbally, numerically, or symbolically represented examples to be the type of evidence of choice to support argument validity.
In this study, we deemed mathematical representations to be visible or tangible elements that code, represent, or integrate mathematical ideas [70]. They include diagrams, number lines, specific objects or manipulatives, physical models, written words, mathematical expressions, formulas and equations, and computer screen depictions, among others.
As the efficiency of a given type of representation depends on the associated task [71], several should be used with geometric notions to help students synopsize and convey their ideas [46]. Rodríguez and Gutiérrez [72] showed that DGE helped students identify and check their conjectures empirically, but did not prove to be more helpful than paper and pencil when building informal arguments in geometric proof problems. Other studies revealed that students found it difficult to draw the connection between properties or definitions and visual representations [73,74]. Surveys on problems using two-dimensional representations of three-dimensional geometric forms concluded that, when more than one-step reasoning is required, “either spatial visualization or property-based spatial analytical reasoning (…) these two skills have to be harmonised” [42] (p. 235). The degree of generality attributed by students to the representation used must be borne in mind in this process, for it may either further or hinder their ability to grasp the general characteristics of an idea or result [39].
2.3. Scope of Argumentation
We define the scope of argumentation as the level of generality involved in a proof. Generality is expressed with more or less sophistication depending on the degree of contraction of the semiotic media used [75] and may exist at different levels depending on the individual, for what is symbolic and abstract for one may be specific for another [76]. A generic argument entails explaining the reason why a statement about an object characteristic of its class is true [77]. Generic examples, which have attracted particular attention in the literature on proofs [40], may serve to transition from empirical to deductive proofs [78]. Mason and Prim [79] associated the idea “generic example” with the representative characteristic of the respective class. In that vein, a model for representing triangles that stresses the representative role of a class in terms of its properties is described below.
In mathematics, generalization may be divided into two main categories, empirical and theoretical. This study focused on empirical generalization, in which the basic process consists in detecting a feature or property common to two or more objects or situations based on perception and then defining those features as generally present in all the respective objects or situations [80]. Although deductive generalization often stems from empirical cases, mathematical generalization is not always based on such instances, for it may arise from changes in the way a given mathematical problem is posed. In generalization, the operators and sequence of operations identified that are common to specific cases are extended to the general case [81]. In the inductive reasoning model [82], the transition from working with specific cases to generalizing for all cases prior to the proof entails several steps: (1) working with specifics, (2) organizing specific cases, (3) seeking and predicting, (4) formulating conjectures, (5) justifying conjectures, (6) generalizing, and (7) proving or formally validating.
This study analyzed students’ reasoning styles, representations, and generalizations as they solved geometric proof problems. The subsequent qualitative analysis of the findings aimed to furnish information on the scope of generality in the arguments used in the various reasoning styles and representations.
3. Methodology
3.1. Subjects and Problems
In this descriptive qualitative study, data were gathered on the occasion of a lesson forming part of a program for stimulating mathematical talent. The program, whose lessons were delivered on Saturdays outside classroom hours, was designed to enlarge on curricular and extracurricular content. The students participating were selected intentionally from different schools in the southeast of Spain on the grounds of their high performance, willingness, and proven aptitude to undertake non-routine mathematical tasks. Those characteristics were closely aligned with research conducted to date in the field, such as the ability to think harmonically, generalize, and flexibly use different types of representation [52,83,84].
The lesson at issue was attended by 34 students enrolled in the program. Due to the circumstances imposed by the COVID-19 pandemic, it was delivered virtually on the Google Meet platform. The sample for this study is composed of 34 14- to 16-year-old students who took part in the program, but only 21 voluntarily sent in their replies to a questionnaire on a Google form. The lesson was delivered by two teachers who were also the head researchers for this study, posing the tasks both verbally (accompanied by slides) and written into a Google form. Although some features of proofs had been addressed previously, the content involved in this lesson had not been explicitly dealt with in any earlier session.
The data used for analysis consisted in the transcription of the video recording of the lesson, including chat interventions, and the students’ replies to a questionnaire that contained five problems (see Appendix A). The problems were designed based on two criteria: (a) the representations used to solve the problem; and (b) gradually increasing complexity. After the problems were validated with the cooperation of two enrichment program teachers, they were structured as follows: problems 1 and 2 familiarized students with proof based on their knowledge of right triangles and in-plane movement. Problems 3, 4, and 5 addressed an unknown property posed as a more cognitively demanding proof problem [37].
Problem 1 was posed using pictorial and algebraic representation, while problem 2 was posed verbally only. Problems 3 and 4 were supplemented with Geogebra manipulatives and problem 5 used Geogebra to represent the equivalence class of triangles (Figure 1) in which all similar triangles were represented by a single member of the class (on the grounds of similarity-determined equivalence). In that space, each point on the plane represented a class of triangles, and argumentations built for the representative were generalized to the entire class. The description of a property in any triangle in the equivalence class was generalized to all similar triangles. The outcome was a higher level of generality in the reasoning drawn from visual descriptions. Geogebra, which is a common resource within the program, was used in twofold ways: firstly, to show the construction of the equivalence class and how to manipulate it; secondly, a modeled resource of the equivalence class was provided to the students, so they were able to manipulate Geogebra to check, analyze, synthesize, and argument about the required questions.
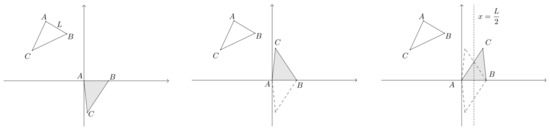
Figure 1.
Construction of the equivalence class of triangles. Each triangle is identified to a point C.
The replies were sent in sequentially after the students completed each problem. The forms accommodated written answers, pictures of their drawings, and Geogebra constructs. After all the individual responses were handed in, they were discussed collectively by some of the students, with the teachers acting as moderators.
Lesson Components and Sequence
The table below summarizes lesson components and sequence under four headings: problem stage, stage targets, description, and timing (Table 1).

Table 1.
Lesson components and sequence.
3.2. Analysis of Questionnaires
The unit of analysis for each student was established as their answer to each problem on the questionnaire and their participation during the pooling session. The three topics defined earlier were analyzed in each case: reasoning styles, level of generality, and representations used by students to support their arguments.
Reasoning style categories based on the Krutetskii [52] definitions were adapted to problem particulars.
- Geometric (visual): prevalence of the pictorial–visual component. Argumentation is supported by visual elements only, alluding exclusively to visually perceived equality of areas or lengths.
- Analytical: prevalence of the logical–verbal component. Argumentation is supported by algebraic expressions, deduction of properties, or the use of theorems.
- Harmonic: even balance between the two components. Argumentation is supported by the connection between visualization and analytical reasoning, alluding to area equality in the graphics to deduce algebraic expressions and vice-versa.
The scope of argumentation was characterized on the grounds of three deductive model stages [82]: particular, sets (of cases), and generalization.
- Particular: argumentation focused on a specific case, with allusion to no other.
- Set: argumentation with allusion to a given set of elements.
- Generalization: generalized argumentation valid for all cases.
Representations were categorized under the following headings, borrowed from Goldin [70].
- Verbal: use of natural language only.
- Algebraic: use of symbolic notation and algebraic expressions.
- Pictorial: use of resources such as drawings, diagrams, and graphics, including manipulation with Geogebra.
4. Results
An initial overview of the most significant elements of group behavior as a whole in each problem is followed by a qualitative review of the connection between reasoning style and generalization.
4.1. Overall Data
Table 2, Table 3, Table 4, Table 5 and Table 6 summarize the categories observed for each topic, citing only the students who answered each problem.

Table 2.
Answers to Problem 1.

Table 3.
Answers to Problem 2.

Table 4.
Answers to Problem 3.

Table 5.
Answers to Problem 4.

Table 6.
Answers to Problem 5.
Harmonic reasoning styles were observed in problem 1 only, the only one of the five formulated with both graphic and algebraic representations. All but four of the students formulated generally valid arguments applicable to all possible cases. Verbal representation predominated in their answers, usually in conjunction with algebraic notation.
Students’ answers to problem 2 were very uniform, with visual reasoning, general argumentation, and verbal representation (occasionally with algebraic symbols) prevailing.
As (interestingly) students’ replies to problem 3 were based on counter examples, the level of generality in their arguments could not be established. Pictorial representation predominated.
Many fewer students answered problem 4 than the preceding three, with analytical reasoning, the highest scope of argumentation, and verbal and pictorial representation prevailing.
All the replies to likewise scantly answered problem 5 involved visual reasoning and verbal representation. The scope of argumentation included allusions to given sets of elements as well as to overall generality.
On the whole, visual reasoning prevailed except in problem 4, where analytical reasoning predominated. Students who reasoned analytically in that problem nonetheless used visual reasoning in others. The inference derived from the overall findings was that the use of multiple representations to pose problems appeared to favor the connection between verbal and algebraic arguments in students reasoning harmonically. The type of representation used in the problem itself was not a determinant for any given reasoning style, however, each student exhibited different styles depending on the nature of the problem [64].
In problems 1, 2, and 4, most students’ argumentations drew from all the cases involved to reach a given level of generality. Problem 3 was solved in most cases with a counter example, with only two replies referring to a specific set of cases. In problem 5, the number of students who generalized was the same as the number who reasoned for a specific set of cases. The inference was that students generalized, irrespective of reasoning style or the ability to put forward formal proofs, by applying their arguments to the general case [81]. They nonetheless experienced difficulty in encompassing all the examples or generalizing what they perceived when building certain examples with Geogebra representations [34,39].
Verbal representations were predominantly used to complete arguments. Problem 1 prompted the largest proportion of algebraic representations, observed in conjunction with harmonic reasoning. Despite the lack of visual support in its formulation, problem 3 favored pictorial representations because students replied with a drawing depicting a counter example. Again, the inference was that the demands involved in solving a given problem had a greater impact than the representation used in the problem formulation on the way argumentation was represented [71]. That notwithstanding, although reasoning style did not determine a preference for the type of representation, all the students deploying harmonic reasoning combined algebraic with verbal or pictorial representations [42].
4.2. Reasoning Styles
4.2.1. Harmonic Reasoning
This type of reasoning was observed in only five students (S2, S3, S5, S13, and S18) and in problem 1 only. In their arguments, all five combined prior visual work that entailed identifying equal areas with the use of algebraic expressions.
S5, for instance, alluded to the position of the triangles, but supported his argument on equality with the respective equations.
S5: This is the proof of the Pythagorean theorem. If the triangles are subtracted from the large square, the result is an area of c2. If the position of the triangles changes, two squares would be left, a2 and b2, which means that c2 = (a + b)2 − 2ab and a2 + b2 = (a + b)2 − 2ab and, therefore, that c2 = a2 + b2.
S2, in turn, simplified the algebraic expressions deduced after calculating the areas of the four right triangles (Figure 2).

Figure 2.
Student S2’s answer to problem 1.
All the students using harmonic reasoning in problem 1 recognized the proof to refer to the Pythagorean theorem and formulated generalized arguments. Except for student S3, whose reasoning made no allusion to generality, harmonic reasoning was associated with that scope of argumentation and reinforced by the use of symbolic expressions, more broadly applicable than the specific pictorial representation used.
In her (pronouns indicating gender have been assigned randomly to protect students’ anonymity) arguments, S13 alluded explicitly to generalization, although she mentioned the role of graphic representation when deducing the formula:
S13: This proof is for the Pythagorean theorem. You know that because the formula represented is the sum of a + b squared. a and b form triangles because if you formulate an equation with them, you get c2 = (a + b)2 + (a × b + a × b + a × b + a × b)/2. If you simplify that equation, the result is a2 + b2.
Yes, it would be graphic proof because you can see from the drawing that the Pythagorean theorem holds. And you can also derive the formula from the graphic representation. Because in the end all you vary is their length. In other words, in the end [it doesn’t matter] whether the length is larger or smaller in the drawing, it will always be a + b and the area will be a times b divided by 2 and in the end you get the same result.
Some students represented their visual arguments with algebraic expressions, supplementing verbal discourse with symbolic representation:
S18: I think this is the proof of the Pythagorean theorem. I think it’s a proof first of all because if you find for the whole square you get a2 + b2 + 2ab and if you subtract the four right triangles from the square what should remain is the area of the central square, a2 + b2 + 2ab – 4 × ab/2 = a2 + b2, so c is the area of the square. And since the two squares have the same area when you remove the right triangles, which together sum the same area as the ones in the first square, what we have is that the sum of the areas of the squares with sides a and b is the same as the area of the square with side c in the first square, so again a2 + b2 + 2ab.
The behavior observed for the students who deployed harmonic reasoning denotes their willingness to use different strategies depending on the demands of the problem broached. S3 failed to reply to the other questions, whereas S2, S5, and S13 exhibited visual reasoning in the other problems, and S18 exhibited visual reasoning in problems 2 and 5 and analytical reasoning in problem 4.
4.2.2. Visual Reasoning
Visual reasoning was the style most frequently observed throughout the experiment. Students using that style based their arguments on their visual skills [85], particularly to recognize spatial relationships and positioning in objects after they were moved:
S4: When you rotate or move (the triangle) the angles remain unaffected so it continues to be a right triangle to which you can apply the Pythagorean theorem. Thanks to symmetry and homotheties it’s the same for similar triangles. The shape (angles) goes unchanged, except that the result is a larger or smaller mirror image.
The scope of argumentation differed in students using visual representation depending on the problem involved. Only two (S1 and S10) focused their arguments on specific cases without alluding to any other. In problem 2, S1, for instance, depicted movement in a particular triangle without arguing that the same properties would be applicable to any triangle (Figure 3).
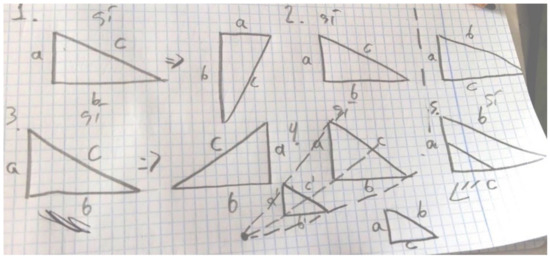
Figure 3.
Student S1’s particular case-based answer to problem 2.
Four other students (S5, S8, S13, and S18) used visual reasoning in conjunction with generalization for a given set of elements. In such cases, these students recognized the property by type of triangle as well as the general applicability of the property to a set of objects. They nonetheless did not argue on the grounds of generality but confined their description to the properties perceived with the manipulation of the examples, using the Geogebra drag function [34]. The argument and Figure 4 transcribed below, for instance, is the mere description of the student’s observations:
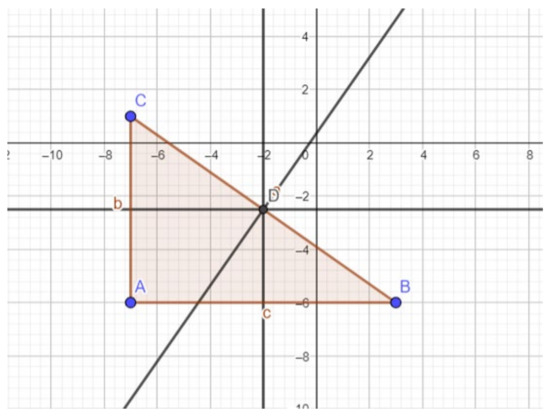
Figure 4.
Student S8’s drawing for the manipulative construction of the circumcenter.
S8: Yes, they intersect at the circumcenter, which is the point where all perpendicular bisectors for all sides of the triangle intersect. In right triangles that point is located on the hypotenuse; in obtuse triangles outside the triangle and in equilateral tringles inside it (inner point).
In contrast, in most of the answers involving visual reasoning, the arguments used to justify the generalization of the properties referred explicitly to their validity for any case or to properties known to be applicable:
S6: It holds in all [cases] because as long as the triangle has a right angle, it holds. It doesn’t matter if it’s moved or the sides are larger or smaller (Figure 5).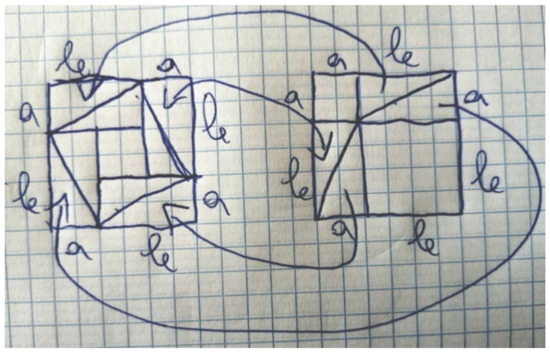 Figure 5. Student S6’s drawing for her argument around the Pythagorean theorem.
Figure 5. Student S6’s drawing for her argument around the Pythagorean theorem.
S19: Yes, because the triangle is always the same (and therefore always has a right angle which is why the Pythagorean theorem holds), except that the position changes.
Visual reasoning was not associated with any single type of representation. As in the other reasoning styles, verbal representation prevailed, although generalization was also represented algebraically and pictorially. In some cases, pictorial representation itself afforded a synoptic description of students’ reasoning, when they identified area equality, for instance.
In contrast to harmonic reasoning, in visual reasoning symbolic representation was used only to supplement some of the properties identified:
S11: It also holds after applying symmetry because the symmetric triangle would have the same angles and sides as the original, but in different positions.
It also holds after homotheties because if all the sides are multiplied times the same number, the squares [of those products] would comply. If m is the number times which they are multiplied, then m2(a2 + b2) = m2 × c2. If you then divide both sides of the equation by m2 you get the same equation.
4.2.3. Analytical Reasoning
This reasoning style was detected primarily in problem 4, where students based their arguments on the deduction or use of known properties, with no allusion to visual perception. Student S4, for instance, used this type of reasoning in problems 3 and 4 both, where he deduced the necessary properties:
S4: The perpendicular bisectors are a straight line where all the points are at an equal distance from both edges. Each bisector is therefore consistent with the definition. If all the points are at the same distance from both ends on the bisectors, there must be one point that’s at the same distance from all three points and that point would have to be on the three bisectors.
S4: The three bisectors intersect at a point that must be at the same distance from a, b and c. Since the circumcenter is the circumference formed with the points on the triangle, it has to be at that point.
Analytical reasoning was associated exclusively with arguments valid for the general case, with no reference to particular situations. S16 stressed that validity for all cases did not depend on the initial triangle for which the property was described:
S16: Yes, because it doesn’t matter what the triangle is like because since the point is at the same distance from all the vertices you’ll always be able to draw a circle that touches them all.
Although students worked manipulatively with Geogebra, representation was verbal only and their arguments were not associated with any other type of representation:
S11: Yes, it’s true, because like a classmate said, the perpendicular bisector for a is at the same distance from vertex a as from vertex b; the bisector for b is at the same distance from vertex b as from c and the bisector for c is at the same distance from c as from a. In that case, the point where the three bisectors intersect is at the same distance from all the vertices, and that distance is the radius of the circumcenter.
These findings appear to relate analytical reasoning to generalization and verbal representation. Irrespective of whether they worked with manipulative graphic representations, having to provide general arguments dissuaded them from using graphic representations.
4.3. Equivalence Class-Based Reasoning
Our perception was that students found working with equivalence class representation a challenge. On the one hand, only eight students replied to problem 5, four of whom reasoned solely on the grounds of a given set of elements, confining their arguments to a description of their observations around right triangles:
S13: Yes, for all right triangles the circumcenter would be on the hypotenuse. That is so because the perpendicular bisector for one leg is parallel to the other leg, and vice-versa. And they intersect at the midpoint of the leg where they form as well as at the midpoint of the hypotenuse, and the bisector for the hypotenuse, like the bisectors for the legs, springs from its midpoint.
Despite their use of visual reasoning supported with the manipulative representations observed, four students (S4, S9, S15, and S18), identified the examples as class representatives, extending the validity of the argument only to the set represented. Such considerations reveal the potential of equivalence class representation for arguing the general case, as may be perceived in some sample replies:
S13: There are infinite equilateral triangles, but they’re all similar.
S13: Yes, but it’s easier to prove than in all cases of right triangles that the circumcenter is on one side. It’s harder to prove than when the circumcenter is on one side, that it’s a right triangle.
S4: If the circumcenter is on one side, that means the point is equidistant from the edges of the triangle. It has to be a right triangle then, because if it were an acute triangle it would be inside and if it were an obtuse triangle, it would be outside it.
Another point worth highlighting is the use of the equivalence class built with Geogebra to confirm conjectures or formulate counter examples. This group of students used their constructs as an item for discussion during the pooling session. The following excerpt shows how one student formulated an erroneous argument because he used a property based on particular instances. When a classmate described an explicit counter example, he admitted that his initial argumentation was not valid:
S4: The perpendicular bisector is a straight line where all the points are at an equal distance from both edges of the segment. Therefore if we take the three bisectors there must necessarily be in all triangles a point that’s at the same distance from a as it is from b and c, in other words, the three vertices. The bisectors for legs ab, ac and ca will pass through that point. And it’s there they’ll intersect and it has to be inside because otherwise it wouldn’t be at the same distance from the three points.
R1: (…) Does anyone think otherwise?
S13: I don’t fully agree. Because when I uploaded it to Geogebra I found that when a right triangle is involved, the perpendicular bisector for one leg is parallel to the other leg and the same happens with the other leg. And the bisector for the hypotenuse intersects the square formed by the legs and the bisectors diagonally. And if the triangle is obtuse, it would start to shorten… and the point would lie outside. That would contradict what S4 said because the point where all the points are at the same distance doesn’t have to lie inside the triangle. In an obtuse triangle that point would be outside the triangle.
S4: What can I say? (…) You’ve convinced me.
Although the aim of the study was not to explore the functions of proof, the students were observed to understand the use of Geogebra as a tool to validate conjectures or check properties, while distinguishing it from formal proof. The foregoing example of the student who used Geogebra to counter the validity of her own argumentation is a case in point:
S13: Well… If the triangle is acute, the circumcenter lies inside it. And when it’s obtuse, outside.
R1: And why would that be?
S13: I’d have to think about that.
R1: If when you see in Geogebra that when it moves it falls outside, would that be a valid proof for you?
S13: It would be evidence, but not proof.
5. Discussion and Conclusions
In this study, we explored the effect of reasoning styles and the representations used in argumentation on the level of generality of the justifications put forward by students in proof problems. Analysis of the answers to a questionnaire designed for that purpose furnished information on three elements: students’ capacity to prove and reason geometrically [1]; the role of representation in guiding reasoning [18]; and the validity of proof for the general case, here termed the scope of the argumentation [2]. Three key takeaways can be identified.
Firstly, reasoning style alone was not observed to determine the level of generality, although harmonic and analytical reasoning proved to be more favorable than visual reasoning to generalized argumentation. In the lesson discussed here, the students built on a variety of reasoning styles, especially visual and analytical, to generalize their arguments. More precisely, those who deployed analytical reasoning or who combined harmonic reasoning with the use of algebraic expressions formulated arguments with a high level of generality. In contrast, the scope of argumentation was narrower in students who reasoned visually, whose justifications were confined to the description of the specific properties of a particular case or the set analyzed. Argumentation based on visual reasoning is more demanding cognitively, for generalizing what is perceived in visual scenarios may mean that reliable routines, such as those that can be applied in algebraic procedures, may not always be at hand [86].
The recommendation ensuing from these considerations is to favor the transition from visual to harmonic reasoning. One aim would be to establish a connection between the visual work performed to identify properties or perceive regularities and the construction of general arguments based on deduction or algebraic expressions. A second would be to highlight the advantages of that strategy for validating the general case [64]. Given that students exhibit different reasoning styles depending on the demands of the problem at hand, we contend that teaching approaches favoring the connection between visual arguments and algebraic expressions enhance the efficacy of students’ spatial reasoning [42,43].
The second takeaway from this study is that the type of representation was not found to be the sole determinant for the level of generality, although the use of algebraic representations favored the formulation of more general justifications.
The type of representation used to initially pose a problem had no clear effect on students’ use or otherwise of that specific style. Although the presence of both pictorial and algebraic representations favored the use of harmonic reasoning, the demands inherent in the problem had a greater impact on reasoning style than its formulation [64].
Moreover, students tended to use verbal representation to support their arguments, particularly when comparing different perspectives. That may infer that they deemed words to afford clearer explanations than other types of representation [70]. Their occasional use of Geogebra in their images or constructions, graphically supplementing their arguments, denoted a fuller understanding of the problem [68].
In this study, analytical reasoning was present in conjunction with verbal representation only, although the students involved used drawings in other instances, such as when suggesting counter examples. Here again, students deploying different types of representation in their arguments were observed to be more prone to supplement pictorial and algebraic features with multiple types of representation, including algebraic expressions, pictorial items, and Geogebra-mediated manipulative constructs [13,14].
The final idea that may be gleaned from this survey is that the use of representation systems based on items representative of whole sets may favor the transition from perceptive to general.
The students were introduced to the use of equivalence classes as a system for representing triangles. Although the problem posed constituted a challenge, some students’ answers supported the hypothesis that arguments deriving from the visual perception of a particular case can be generalized. With the use of Geogebra in the equivalence class model, such representations could be manipulated via geometric transformations, making visualization easier and enhancing the understanding of some features of triangles [44].
Despite the complexity attributable to the cognitively demanding nature of the problem [37], some students who reasoned visually from the equivalence class model were observed to put forward more general arguments. That model might consequently be a way of transitioning from empirical to deductive work [40,41].
Summarizing, we underline our three main results:
- Harmonic and analytical reasoning proved to be more favorable than visual reasoning to generalized argumentation
- The type of representation was not found to be the sole determinant for the level of generality
- The use of representation systems based on items representative of whole sets may favor the transition from perceptive to general
We are aware that the present findings, based on a small sample and certain specific problems, narrowly limit the scope for drawing general conclusions. We nonetheless deem them to be indicative of the role of reasoning styles and representations in students’ ability to generalize when engaging in geometric proof and reasoning [1]. Moreover, in order to improve and support this result, we plan new implementations in different contexts and with different students’ profiles.
Author Contributions
Conceptualization, R.R.-U.; methodology, R.R.-U. and J.F.R.-H.; software, J.F.R.-H.; investigation, R.R.-U. and J.F.R.-H.; writing—original draft preparation, R.R.-U.; writing—review and editing, J.F.R.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the research group of Didactic of Mathematics Numerical Thinking, FQM-193 of 3rd Andalusian Research Plan (PAIDI).
Institutional Review Board Statement
Ethical review and approval were waived for this study due to its anonymized nature. The activities were revised and authorized by the respective teachers. The parents were informed prior to the study that their children could be included in research studies.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Acknowledgments
This work was supported by Spanish national R + D + I projects PID2020-117395RB-I00 and PID2020-113601GB-I00, financed by the State Research Agency (SRA) from Spain.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Questionnaire:
- Problem 1: What is being proven in the Figure A1 below?
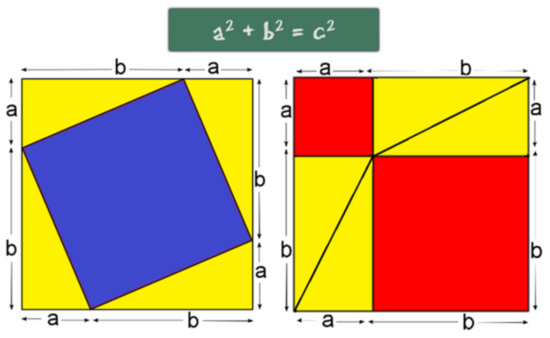
Figure A1.
Visual proof.
- Problem 2: If the Pythagorean theorem holds in a right triangle:
- Does it hold if the triangle is rotated?
- If it is translated?
- If it is symmetrically transformed?
- If it is homothetically transformed?
- Would it hold in a similar triangle?
- Problem 3: Is the following statement true? Explain your answer.
The three perpendicular bisectors in a triangle intersect on a point inside the triangle.
- Problem 4: Is the following statement true? Explain your answer.
The three perpendicular bisectors of a triangle intersect at the circumcenter.
- Problem 5: Is the following statement true? Explain your answer.
If the circumcenter lies on one of the three sides, the triangle is a right triangle.
References
- Jones, K.; Tzekaki, M. Research on the teaching and learning of geometry. In The Second Handbook of Research on the Psychology of Mathematics Education: The Journey Continues; Gutiérrez, Á., Leder, G.C., Boero, P., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2016; pp. 109–149. [Google Scholar]
- Stylianides, A.J.; Harel, G. Advances in Mathematics Education Research on Proof and Proving: An International Perspective; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Jones, K. Issues in the Teaching and Learning of Geometry. In Aspects of Teaching Secondary Mathematics. Perspectives on Practice; Haggarty, L., Ed.; Routledge Falmer: London, UK, 2002; pp. 121–139. [Google Scholar]
- Meyer, M.; Schnell, S. What counts as a “good” argument in school?—How teachers grade students’ mathematical arguments. Educ. Stud. Math. 2020, 105, 35–51. [Google Scholar] [CrossRef]
- Rocha, H. Mathematical proof: From mathematics to school mathematics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2019, 377, 20180045. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lange, M. Aspects of mathematical explanation: Symmetry, unity, and salience. Philos. Rev. 2014, 123, 485–531. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, B.B.; Hershkowitz, R.; Prusak, N. Argumentation and mathematics. In Educational Dialogues: Understanding and Promoting Productive Interaction; Howe, C., Littleton, K., Eds.; Routledge: London, UK, 2010; pp. 115–141. [Google Scholar]
- Sriraman, B.; Umland, K. Argumentation in Mathematics Education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: London, UK, 2014; pp. 46–48. [Google Scholar]
- Campbell, T.G.; Boyle, J.D.; King, S. Proof and argumentation in K-12 mathematics: A review of conceptions, content, and support. Int. J. Math. Educ. Sci. 2020, 51, 754–774. [Google Scholar] [CrossRef]
- Common Core State Standards Initiative. Common Core State Standards for Mathematics; National Governors Association Center for Best Practices and the Council of Chief State School Officers: Washington, DC, USA, 2010. [Google Scholar]
- Mulligan, J.; Woolcott, G.; Mitchelmore, M.; Davis, B. Connecting mathematics learning through spatial reasoning. Math. Educ. Res. J. 2018, 30, 77–87. [Google Scholar] [CrossRef]
- Duval, R. Understanding the Mathematical Way of Thinking: The Registers of Semiotic Representations; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Alcock, L.; Weber, K. Undergraduates’ example use in proof production: Purposes and effectiveness. Investig. Math. Learn. 2010, 3, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Zazkis, D.; Weber, K.; Mejía-Ramos, J.P. Bridging the gap between graphical arguments and verbal symbolic proofs in a real analysis context. Educ. Stud. Math. 2016, 93, 155–173. [Google Scholar] [CrossRef]
- Pedemonte, B. How can the relationship between argumentation and proof be analysed? Educ. Stud. Math. 2007, 66, 23–41. [Google Scholar] [CrossRef]
- Pedemonte, B. Argumentation and algebraic proof. ZDM—Int. J. Math. Educ. 2008, 40, 385–400. [Google Scholar] [CrossRef]
- Bartlo, J.R. Why Ask Why: An Exploration of the Role of Proof in the Mathematics Classroom. Ph.D. Thesis, Portland State University, Portland, OR, USA, 2013. [Google Scholar]
- Gulkilik, H.; Kaplan, H.A.; Emul, N. Investigating the relationship between argumentation and proof from a representational perspective. Int. J. Math. Teach. Learn. 2019, 20, 131–148. [Google Scholar]
- Lin, F.-L.; Yang, K.-L.; Lee, K.-H.; Tabach, M.; Stylianides, G. Principles for task design for conjecturing and proving. In Proof and Proving in Mathematics Education, New ICMI Study Series 15; Hanna, G., de Villiers, M., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 305–325. [Google Scholar]
- Stylianides, A.J.; Bieda, K.N.; Morselli, F. Proof and argumentation in mathematics education. In The Second Handbook of Research on the Psychology of Mathematics Education; Gutiérrez, A., Leder, G.C., Boero, P., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2016; pp. 315–351. [Google Scholar]
- Balacheff, N. The benefits and limits of social interaction: The case of teaching mathematical proof. In Mathematical Knowledge: Its Growth through Teaching; Bishop, A., Mellin-Olsen, S., Van Dormolen, J., Eds.; Kluwer: Dordrecht, The Netherlands, 1991; Volume 186, pp. 175–192. [Google Scholar]
- Schwarz, B. Argumentation and learning. In Argumentation and Education; Muller Mirza, N., Perret-Clermont, A., Eds.; Springer: New York, NY, USA, 2009; pp. 91–126. [Google Scholar]
- Healy, L.; Hoyles, C. Software tools for geometric problem solving: Potentials and pitfalls. Int. J. Comput. Math. Learn. 2001, 6, 235–256. [Google Scholar] [CrossRef]
- Mariotti, M.A. Justifying and proving in the Cabri environment. Int. J. Comput. Math. Learn. 2001, 6, 257–281. [Google Scholar] [CrossRef]
- Marrades, R.; Gutierrez, A. Proofs produced by secondary school students learning geometry in a dynamic computer environment. Educ. Stud. Math. 2000, 44, 87–125. [Google Scholar] [CrossRef]
- Hanna, G. Challenges to the importance of proof. Learn. Math. 1995, 15, 42–49. [Google Scholar]
- Hanna, G. Mathematical proof, argumentation, and reasoning. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: London, UK, 2014; pp. 561–566. [Google Scholar]
- Aksoy, Y.; Bayazit, İ.; Soybaş, D. The Effects of GeoGebra in Conjectures and Proofs. In Proceedings of the First North American GeoGebra Conference, Ithaca, NY, USA, 1 April 2010–31 March 2011; Geogebra-NA: Ithaca, NY, USA, 2010; pp. 190–195. [Google Scholar]
- Hohenwarter, M.; Fuchs, K. Combination of Dynamic Geometry, Algebra and Calculus in the Software System GeoGebra. In Computer Algebra Systems and Dynamic Geometry Systems in Mathematics Teaching Conference; Darwish, D., Ed.; 2004; pp. 1–6. Available online: https://www.researchgate.net/publication/228398347_Combination_of_dynamic_geometry_algebra_and_calculus_in_the_software_system_GeoGebra (accessed on 6 February 2022).
- Widder, M.; Berman, A.; Koichu, B. Action strategies in spatial geometry problem solving supported by dynamic geometry software. In Proceedings of the 42nd conference of the International Group for the Psychology of Mathematics Education, Umeå, Sweden, 3–8 July 2018; Bergqwist, E., Österholm, M., Granberg, C., Sumpter, L., Eds.; PME: Umea, Sweden, 2018; Volume 4, pp. 435–442. [Google Scholar]
- Gutiérrez, A. Aspectos metodológicos de la investigación sobre aprendizaje de la demostración mediante exploraciones con software de geometría dinámica. In Actas del IX Simposio de la Sociedad Española de Investigación en Educación Matemática; Maz, A., Gómez, B., Torralbo, M., Eds.; SEIEM: Córdoba, Spain, 2005; pp. 27–44. [Google Scholar]
- Tsujiyama, Y.; Yui, K. Using examples of unsuccessful arguments to facilitate students’ reflection on their processes of proving. In Advances in Mathematics Education Research on Proof and Proving: An International Perspective; Stylianides, A.J., Harel, G.H., Eds.; Springer: Cham, Switzerland, 2018; pp. 269–281. [Google Scholar]
- Subtil, M.; Domingos, A. The instrumental genesis in the demonstration of the pythagorean theorem. In Proceedings of the 42nd Conference of the International Group for the Psychology of Mathematics Education, Umeå, Sweden, 3–8 July 2018; Bergqwist, E., Österholm, M., Granberg, C., Sumpter, L., Eds.; PME: Umea, Sweden, 2018; Volume 5, p. 164. [Google Scholar]
- Battista, M.T. Representations and cognitive objects in modern school geometry. In Research on Technology and the Teaching and Learning of Mathematics; Blume, G., Heid, M.K., Eds.; Information Age Publishing: Charlotte, NC, USA, 2008; Volume 2, pp. 341–362. [Google Scholar]
- Komatsu, K. How do students generalize a conjecture through proving?: The importance of boundary cases between example and counterexample. In Proceedings of the 35th Conference of the International Group for the Psychology of Mathematics Education, Ankara, Turkey, 10–15 July 2011; Ubuz, B., Ed.; PME: Ankara, Turkey, 2011; Volume 3, pp. 89–96. [Google Scholar]
- Knuth, E. Teachers conceptions of proof in the context of secondary school mathematics. J. Res. Math. Educ. 2002, 5, 61–88. [Google Scholar]
- Benedicto, C.; Gutierrez, A.; Jaime, A. Analysis of Mathematically Gifted Students’ Answers to Cognitively Demanding School Tasks. In Proceedings of the 42nd Conference of the International Group for the Psychology of Mathematics Education, Umeå, Sweden, 3–8 July 2018; Bergqwist, E., Österholm, M., Granberg, C., Sumpter, L., Eds.; PME: Umea, Sweden, 2018; Volume 5, p. 18. [Google Scholar]
- National Council of Teachers of Mathematicas. Principles to Actions; NCTM: Reston, VA, USA, 2014. [Google Scholar]
- Zaslavsky, O. Genericity, conviction, and conventions: Examples that prove and examples that don’t prove. In Advances in Mathematics Education Research on Proof and Proving: An International Perspective; Stylianides, A.J., Harel, G., Eds.; Springer: Cham, Switzerland, 2018; pp. 283–298. [Google Scholar]
- Dogan, M.F.; Williams-Pierce, C. The role of generic examples in teachers’ proving activities. Educ. Stud. Math. 2021, 106, 133–150. [Google Scholar] [CrossRef]
- Rott, B. Inductive and deductive justification of knowledge: Epistemological beliefs and critical thinking at the beginning of studying mathematics. Educ. Stud. Math. 2021, 106, 117–132. [Google Scholar] [CrossRef]
- Fujita, T.; Kondo, Y.; Kumakura, H.; Kunimune, S.; Jones, K. Spatial reasoning skills about 2D representations of 3D geometrical shapes in grades 4 to 9. Math. Educ. Res. J. 2020, 32, 235–255. [Google Scholar] [CrossRef]
- Lowrie, T.; Logan, T.; Hegarty, M. The influence of spatial visualization training on students’ spatial reasoning and mathematics performance. J. Cogn. Dev. 2019, 20, 729–751. [Google Scholar] [CrossRef]
- Uygun, T. An inquiry-based design research for teaching geometric transformations by developing mathematical practices in dynamic geometry environment. Math. Educ. Res. J. 2020, 32, 523–549. [Google Scholar] [CrossRef]
- Seah, R.T.K.; Horne, M. The influence of spatial reasoning on analysing about measurement situations. Math. Educ. Res. J. 2020, 32, 365–386. [Google Scholar] [CrossRef]
- Subramaniam, K. Representational coherence in instruction as a means of enhancing students’ access to mathematics. In Proceedings of the 43rd Conference of the International Group for the Psychology of Mathematics Education, Pretoria, South Africa, 7–12 July 2019; Graven, M., Venkat, H., Essien, A., Vale, P., Eds.; PME: Pretoria, South Africa, 2019; Volume 1, pp. 33–52. [Google Scholar]
- Resnick, I.; Harris, D.; Logan, T.; Lowrie, T. The relation between mathematics achievement and spatial reasoning. Math. Educ. Res. J. 2020, 32, 171–174. [Google Scholar] [CrossRef]
- Kollosche, D. Styles of reasoning for mathematics education. Educ. Stud. Math. 2021, 107, 471–486. [Google Scholar] [CrossRef]
- Stylianides, A.J. Proof and proving in school mathematics. J. Res. Math. Educ. 2007, 38, 289–321. [Google Scholar]
- Mariotti, M.A. Proof and proving in mathematics education. In Handbook of Research on the Psychology of Mathematics Education: Past, Present and Future; Gutiérrez, A., Boero, P., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2006; pp. 173–204. [Google Scholar]
- Harel, G.; Sowder, L. Students’ proof schemes: Results from exploratory studies. In Research in Collegiate Mathematics Education III; Schoenfeld, A., Kaput, J., Dubinsky, E., Eds.; Mathematical Association of America: Washington, DC, USA, 1998; pp. 234–283. [Google Scholar]
- Krutetskii, V.A. The psychology of Mathematical Abilities in Schoolchildren; University of Chicago Press: Chicago, IL, USA, 1976. [Google Scholar]
- Lean, G.; Clements, M.A. Spatial ability, visual imagery, and mathematical performance. Educ. Stud. Math. 1981, 12, 267–299. [Google Scholar] [CrossRef]
- Rivera, F.D. Teaching and Learning Patterns in School Mathematics: Psychological and Pedagogical Considerations; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Cheah, U.H.; Herbst, P.G.; Ludwig, M.; Richard, P.R.; Scaglia, S. Topic study group no. 13: Teaching and learning of Geometry—Secondary Level. In Proceedings of the 13th ICME, Hamburg, Germany, 24–31 July 2017; Kaiser, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 435–438. [Google Scholar]
- Presmeg, N.C. Visualisation and mathematical giftedness. Educ. Stud. Math. 1986, 17, 297–311. [Google Scholar] [CrossRef]
- Lee, K.; Ko, E.; Song, S. The analysis of activity that gifted students construct definition of regular polyhedra. In Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education, Seoul, Korea, 8–13 July 2007; Wo, J.H., Lew, H.C., Park, K.S., Seo, D.Y., Eds.; PME: Seoul, Korea, 2007; Volume 3, pp. 153–160. [Google Scholar]
- Neria, D.; Amit, M. Talented middle school students’ strategies and reasoning in solving analytic reasoning problems. In Proceedings of the 34th Conference of the International Group for the Psychology of Mathematics Education, Belo Horizonte, Brazil, 18–23 July 2010; Pinto, M.M., Pinto, F., Kawasaki, T.F., Eds.; PME: Belo Horizonte, Brazil, 2010; Volume 3, pp. 321–328. [Google Scholar]
- Ryu, H.; Chong, Y.; Song, S. Mathematically gifted students’ spatial visualization ability of solid figures. In Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education, Seoul, Korea, 8–13 July 2007; Wo, J.H., Lew, H.C., Park, K.S., Seo, D.Y., Eds.; PME: Seoul, Korea, 2007; Volume 4, pp. 137–144. [Google Scholar]
- Gruessing, M. Spatial abilities and mathematics achievement among elementary school children. In Proceedings of the 35th Conference of the International Group for the Psychology of Mathematics Education, Ankara, Turkey, 10–15 July 2011; Ubuz, B., Ed.; PME: Ankara, Turkey, 2011; Volume 1, p. 306. [Google Scholar]
- Rabab’h, B.; Veloo, A. Spatial visualization as mediating between mathematics learning strategy and mathematics achievement among 8th grade students. Int. Educ. Stud. 2015, 8, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Rivera, F.D. Towards a Visually-Oriented School Mathematics Curriculum; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Van Garderen, D. Spatial visualization, visual imagery, and mathematical problem solving of students with varying abilities. J. Learn. Disabil. 2006, 39, 496–506. [Google Scholar] [CrossRef]
- Liu, Y. Aspects of Mathematical Arguments that Influence Eighth Grade Students’ Judgment of their Validity. Ph.D. Thesis, Ohio State University, Columbus, OH, USA, 2013. [Google Scholar]
- Laamena, C.M.; Nusantara, T.; Irawan, E.B.; Muksar, M. Analysis of the Students’ Argumentation based on the level of Ability: Study on the Process of Mathematical Proof. J. Phys. Conf. Ser. 2018, 1028, 012156. [Google Scholar] [CrossRef]
- Seah, R.; Horne, M. The construction and validation of a geometric reasoning test item to support the development of learning progression. Math. Educ. Res. J. 2020, 32, 607–628. [Google Scholar] [CrossRef]
- Sukirwan; Darhim; Herman, T.; Prahmana, R.C.I. The students’ mathematical argumentation in geometry. J. Phys. Conf. Ser. 2018, 943, 012026. [Google Scholar]
- Beitlich, J.T.; Obsteiner, A.; Reiss, K. How do secondary school students make use of different representation formats in heuristic worked examples? An analysis of eye movements. In Proceedings of the 39th Conference of the International Group for the Psychology of Mathematics Education, Hobart, Australia, 13–18 July 2015; Beswick, K., Muir, T., Fielding-Wells, J., Eds.; PME: Hobart, Australia, 2015; pp. 97–104. [Google Scholar]
- Healy, L.; Hoyles, C. A study of proof conceptions in Algebra. J. Res. Math. Educ. 2000, 31, 396–428. [Google Scholar] [CrossRef]
- Goldin, G.A. Mathematical representations. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: London, UK, 2014; pp. 409–413. [Google Scholar]
- Dreyfus, H.L. Intelligence without representation–Merleau-Ponty’s critique of mental representation the relevance of phenomenology to scientific explanation. Phenomenol. Cogn. Sci. 2002, 1, 367–383. [Google Scholar] [CrossRef]
- Rodriguez, F.; Gutiérrez, A. Analysis of proofs produced by university mathematics students, and the influence of using Cabri software. In Proceedings of the 30th Conference of the International Group for the Psychology of Mathematics Education, Prague, Czech Republic, 16–21 July 2006; Novotná, J., Moraová, H., Krátká, M., Stehlíková, N., Eds.; PME: Prague, Czech Republic, 2006; Volume 4, pp. 433–440. [Google Scholar]
- Haj-Yahya, A.; Hershkowitz, R. When visual and verbal representations meet-The case of geometrical figures. In Proceedings of the 37th Conference of the International Group for the Psychology of Mathematics Education, Kil, Germany, 28 July–2 August 20; Lindmeier, A.M., Heinze, A., Eds.; PME: Kil, Germany, 2013; Volume 2, pp. 409–416. [Google Scholar]
- Jones, K.; Fujita, T.; Kunimune, S. Representations and reasoning in 3-D geometry in lower secondary school. In Proceedings of the 36th Conference of the International Group for the Psychology of Mathematics Education, Taipei, Taiwan, 18–22 July 2011; Tso, T., Ed.; PME: Taipei, Taiwan, 2012; Volume 2, pp. 339–346. [Google Scholar]
- Ayala-Altamirano, C.; Molina, M. El proceso de generalización y la generalización en acto. Un estudio de casos. PNA 2021, 15, 211–241. [Google Scholar] [CrossRef]
- Mason, J. Expressing Generality and Roots of Algebra. In Approaches to Algebra, Perspectives for Research and Teaching; Bernarz, N., Kieran, C., Lee, L., Eds.; Springer: Dordrecht, The Netherlands, 1996; pp. 65–86. [Google Scholar]
- Balacheff, N. Aspects of proof in pupils’ practice of school mathematics. In Mathematics, Teachers and Children; Pimm, D., Ed.; Hodder and Stoughton: London, UK, 1988; pp. 216–235. [Google Scholar]
- Fiallo, J.; Gutiérrez, A. Analysis of the cognitive unity or rupture between conjecture and proof when learning to prove on a grade 10 trigonometry course. Educ. Stud. Math. 2017, 96, 145–167. [Google Scholar] [CrossRef]
- Mason, J.; Pimm, D. Generic examples: Seeing the general in the particular. Educ. Stud. Math. 1984, 15, 277–287. [Google Scholar] [CrossRef]
- Manouchehri, A.; Sriraman, B. Mathematical Cognition: In Secondary Years [13–18] Part 1. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: London, UK, 2014; pp. 505–520. [Google Scholar]
- Swafford, J.O.; Langrall, C.W. Grade 6 students’ preinstructional use of equations to describe and represent problem situations. J. Res. Math. Educ. 2000, 31, 89–112. [Google Scholar] [CrossRef]
- Torres, M.D.; Moreno, A.; Cañadas, M.C. Generalization Process by Second Grade Students. Mathematics 2021, 9, 1109. [Google Scholar] [CrossRef]
- Greenes, C. Identifying the Gifted Student in Mathematics. Arith. Teach. 1981, 28, 14–17. [Google Scholar] [CrossRef]
- Miller, R.C. Discovering Mathematical Talent; Office of Educational Research and Improvement: Washington, DC, USA, 1990. [Google Scholar]
- Del Grande, J.J. Spatial sense. Arith. Teach. 1990, 37, 14–20. [Google Scholar] [CrossRef]
- Arcavi, A. The role of visual representations in the learning of mathematics. Educ. Stud. Math. 2003, 52, 215–241. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).