Abstract
This study is concerned with dynamical investigation, electrical circuit realization, and emulation of a fractional three-echelon supply chain system. In the financial realm, long-term memory effects play important roles. On the other hand, most financial systems are uncertain with unknown nonlinear dynamics. However, most studies on nonlinear supply chains neither consider the fractional calculus nor take advantage of state-of-the-art emulation methods. These issues motivated the current study. A fractional-order chaotic three-echelon supply chain system is studied. At first, the system’s dynamic is studied through Lyapunov exponent and bifurcation diagrams. It is shown that a slight deferent in some parameters of the system can dramatically change the behavior of the system. Then, a real-time analog circuit is designed and implemented to investigate the system’s chaotic behavior. This way, the system’s chaotic attractors are empirically demonstrated. Finally, emulation and interpolation of the fractional-order chaotic system using the Gaussian process have been studied, and its luminous results have been presented.
1. Introduction
Supply chains are nonlinear dynamical systems triggered by various uncertain factors such as customer demands [1,2,3,4,5,6]. In recent years, several studies have been devoted to understanding the mechanism of supply chain systems [7,8,9]. A supply chain’s goal is to meet consumer needs in the right place, at the right time, and at the right service level, while requiring the least amount of money [10,11]. Because of rising customer expectations and fierce competition in global markets, business enterprises have always tried to achieve the best operation by managing their supply chain networks [12]. Although the success of supply chains depends on various factors, including transportation fleets, machinery, and equipment, the effectiveness of such systems is primarily determined by the quality of management decisions [13,14,15]. However, uncertainties in such systems make their control and management demanding tasks [16,17,18].
Since management and control of financial systems play a vital role in human life, this field of study has recently received extensive attention [19,20,21,22,23,24,25,26,27,28,29,30,31,32]. Due to the complexity of today’s financial systems, applying state-of-the-art control techniques to them will be beneficial [33]. However, the identification and prediction of nonlinear systems always play key roles in their control [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. The more we know about the dynamical behavior of real-world financial systems, the more reliable results can be provided by management’s decisions [50]. Actually, to move towards the best management decisions, we should enhance our understanding of systems and processes. Although many techniques are proposed for the regulation and synchronization of these systems, by taking advantage of control theory, some important matters are entirely ignored in this field of study. For instance, where chaos occurs, and which parameters can change the behavior of the three-echelon supply chain system, are yet to be studied.
On the other hand, most of the time we have limited observations of financial systems, and available data are noisy [51,52]. Hence, to be able to forecast and interpolate these systems, strong emulation and regression methods are required [53]. The Gaussian process (GP) is one of the best emulation and regression methods for nonlinear systems [54,55]. Nonetheless, to the best of our knowledge, there is no study in the literature investigating the GP for a three-echelon supply chain system. Motivated by this, in the last part of the current study, we have investigated the application of GP to a three-echelon supply chain system.
The remainder of this paper is arranged as follows: In Section 2, the governing equations of the fractional-order supply chain are presented, and its dynamical behavior is illustrated. In Section 3, to investigate the behavior of the nonlinear system empirically, an electrical circuit of the system is performed. In Section 4, GP is presented and applied for emulation and regression of the system. Finally, concluding remarks are presented in Section 5.
2. Literature Review
In Reference [56], various classes that have been proposed for modeling the dynamics of supply chains have been studied. In that study, all approaches were categorized as follows: discrete event models, discrete-time difference models, continuous-time differential equation models, and classical operational methods. Additionally, from another point of view, modeling of supply chains can be classified based on the deterministic and stochastic properties. In Reference [57], models of supply chains are classified as: deterministic models, where all the parameters are known; stochastic models, where at least one parameter is unknown, but follows a probabilistic distribution; economic game-theoretic models; and models based on simulation, which evaluate the performance of various supply chain strategies. The vast majority of these models are steady-state models based on average performance, or steady-state static models. In Table 1, some important studies on modeling, control, and investigation of supply chains are presented.

Table 1.
Some important studies on nonlinear supply chains.
Up to now, many scholars have attempted to model supply chain networks (see Table 1). Additionally, in the literature, there are some useful studies that assess and propose simulation (dynamic) models of supply chains. For instance, the specialized program anyLogistix, built based on a simulation model, does an excellent job of modeling supply chains of varying complexity (see [68,69,70]). Among the models presented for supply chain networks, the nonlinear model proposed by Anne et al. [58] has attracted a lot of attention. That model considers a nonlinear supply chain model that takes into account safety stock, information distortion, and retailer order fulfillment. Nonetheless, there is still room for modeling and investigation of these systems. For instance, since long memory of systems is important in supply chain systems, the application of fractional calculus can bring about luminous results for these systems. In comparison with integer-order derivatives, fractional ones have benefits in describing the long memory of systems.
Motivated by the issues and possible directions in Table 1, in the current study we investigate a fractional-order model. The effects of various parameters, including fractional derivatives, are studied on the nonlinear dynamics of the system. To realize the chaotic behavior of the system, a real-time analog circuit is designed and implemented.
Last but not least, from a management point of view, we want to design control strategies or manage supply chains as efficiently as possible, even if we have limited data from these systems. In this condition, rare data cannot work well for management purposes, and this is an obstacle in the management of these systems. In the last part of the current study, we want to propose a method to tackle this issue. One interesting way provided in the literature for other systems (no supply chains) is to use surrogate modeling approaches. Using surrogate methods, we can predict the behavior of the system even in unseen conditions. There are many surrogate models in the literature, and each has its advantages and disadvantages. Among all surrogate models, GP is known as one of the best methods when data are rare, which is the case in some supply chains. Motivated by this, the current study as a pioneer uses GP for surrogate modeling of fractional order supply chain systems.
3. Fractional-Order Three-Echelon Supply Chain
Inspired by [58], we investigate a fractional-order supply chain system as follows
where denotes fractional derivative. The parameters of the model are listed in Table 2.

Table 2.
Parameters of the systems as well their definition and value.
Figure 1 and Figure 2 show the chaotic attractors of the proposed system. In the current study, MATLAB 2021b has been used for numerical simulation. The initial conditions are considered as . As demonstrated in these figures, the proposed system acts chaotically in this condition.
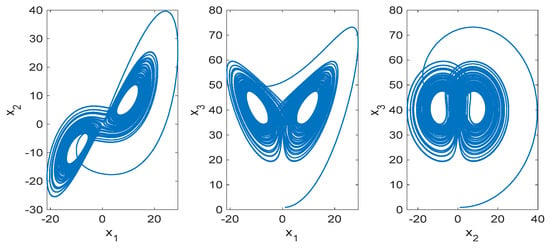
Figure 1.
2D phase diagram of the proposed fractional-order system.
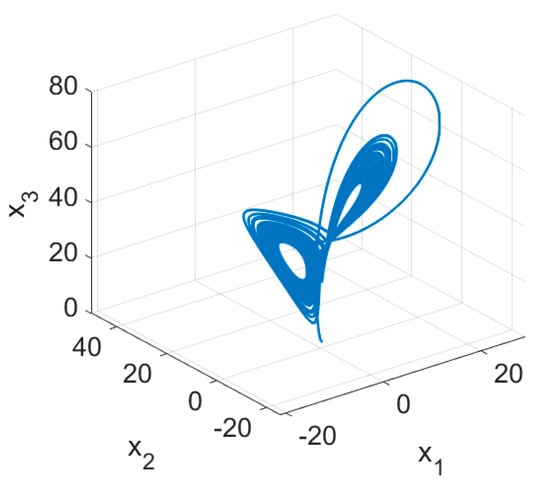
Figure 2.
3D phase diagram of the proposed fractional-order system.
Lyapunov exponents and bifurcation diagrams are used to better understand the impact of variable-order derivatives and various parameters on the behavior of the system. The Lyapunov exponents of the system are shown in Figure 3, indicating that the system is chaotic. In addition, the effects of the variable derivative on the behavior of the system are seen in Figure 3. The system enters chaos for , according to the bifurcation diagram in Figure 4.
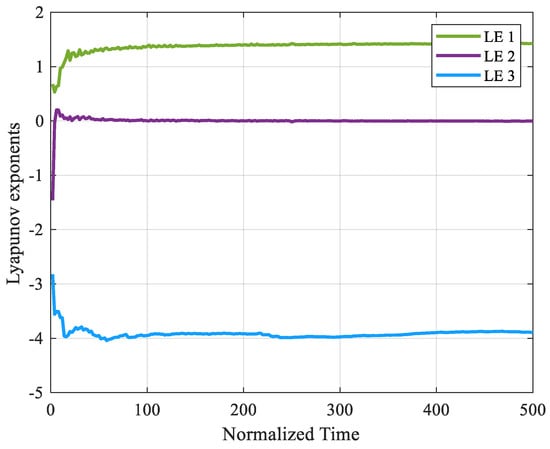
Figure 3.
Lyapunov exponents of proposed fractional-order system.
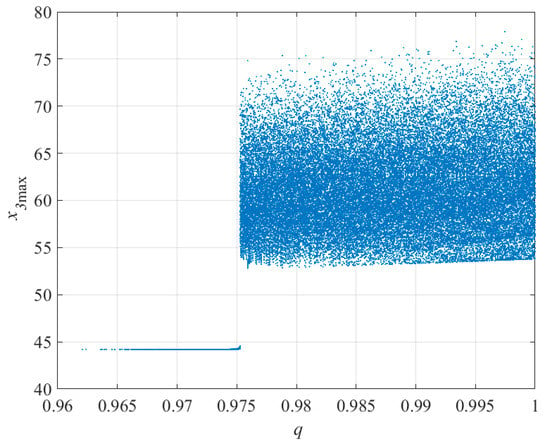
Figure 4.
Bifurcation diagram of proposed fractional-order system by changing fractional-order derivative ().
Figure 5 shows the bifurcation diagram by changing the value of parameter m. As illustrated, when m ∈ [5.42, 21.15]∪[23.12, 27.77], the system acts chaotically. As shown in the bifurcation diagram, parameter m considerably affects the behavior of the system.
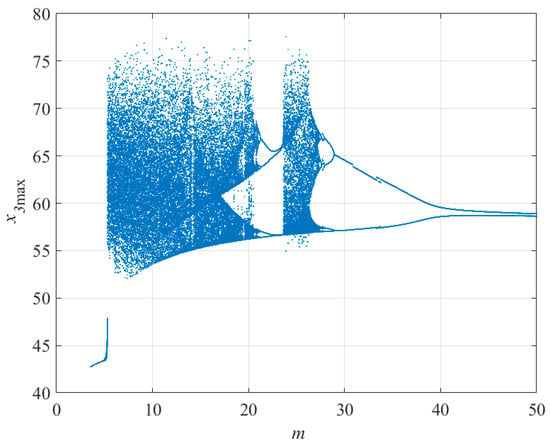
Figure 5.
Bifurcation diagram of proposed fractional-order system by changing parameter .
To investigate the effects of all parameters on the behavior of the system, we have continued extracting different bifurcation diagrams. Figure 6 illustrates the bifurcation diagram by changing the value of parameter n. As demonstrated, when the value of n is between 2.81 and 13.87, the system acts chaotically. The bifurcation relating to parameter r is displayed in Figure 7. As shown in this figure, in this situation the system exhibits antimonotonicity phenomenon for r ∈ [24.20, 93.14]∪[107.27, 123.292], which means that the chaotic and periodic orbits are created and annihilated.
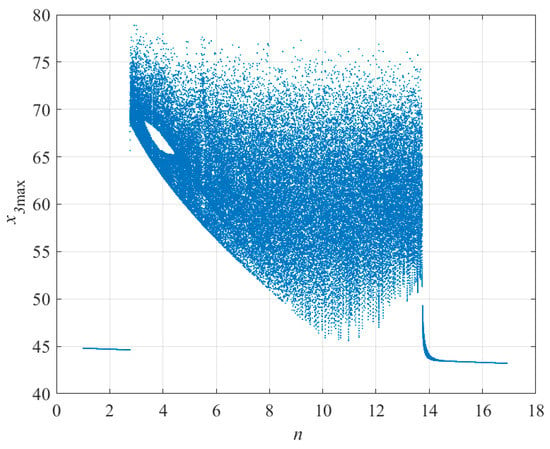
Figure 6.
Bifurcation diagram of the proposed fractional-order system by changing parameter n.
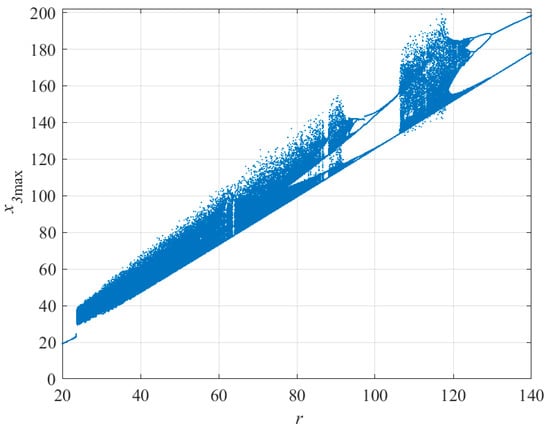
Figure 7.
Bifurcation diagram of the proposed fractional-order system by changing parameter r.
Remark 1.
There is no ground truth to be compared with both integer and fractional models, but when we use the fractional-order model without any doubt, it will act better, since this model has one more degree of freedom in comparison with the integer one. Additionally, in the fractional-order model, when the fractional-order derivative approaches1, it acts like the integer one. Therefore, in summary, the fractional-order model has more degrees of freedom and is better than the integer one, and in some cases, the integer one can provide the same results as the fractional-order model.
4. Electrical Circuit
Here, we dealt with the realization of the fractional integrator of the chain system In [71], Ahmat et al. designed the Bode plot approximation chart in the frequency domain with maximum error of 2 and 3 dB. Following this approach, we realized the approximation transfer function of at 1 dB approximation error in the frequency domain. According to Reference [72], we can obtain:
A circuit design where resistors and capacitors are connected in parallel was proposed in Reference [73] to realize fractional calculus. When , the fractional-order chain circuit unit is as shown in Figure 8.
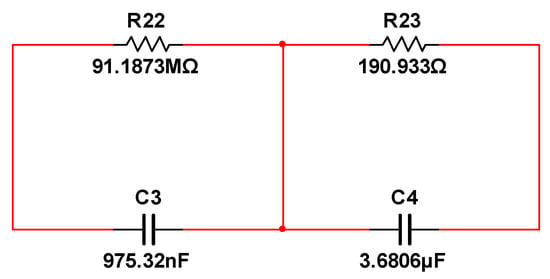
Figure 8.
The fractional-order chain circuit unit.
By using Electronics Workbench’s MultiSIM Software, we selected LF353D as the amplifier and AD633JN as the multiplier to design the fractional-order circuits. In order to restrict the change in state variables to the operating voltage of the analog circuit, the state variables are reduced by 20 times, i.e., . As a result, the new chain system can be rewritten as:
The schematic circuit of the fractional-order chain system is demonstrated by Figure 9.
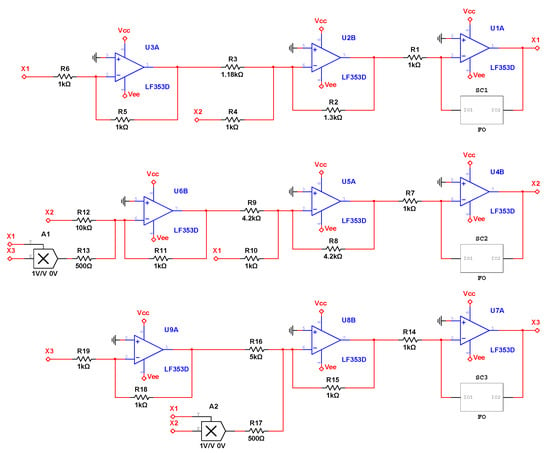
Figure 9.
The schematic circuit of the fractional-order chain system.
The circuit equation is as follows:
The input supplies are: Vcc = +9 V, and Vee = −9 V. The values of the electronic components in Figure 4 are chosen to match the known parameters of the system:
R1 = R4 = R5 = R6 = R7 = R10 = R11 = R13 = R14 = R15 = R17 = R18 = R19 = 1 kΩ, R2 = 1.3 kΩ, R3 = 1.18 kΩ, R8 = R9 = 4.2 kΩ, R12 = 10 kΩ, R16 = 5 kΩ.
The proposed circuit is drawn using Electronic Work Bench (EWB). Figure 10 shows the obtained phase portraits in (X1, X2)-plane, (X1, X3)-plane, and (X2, X3)-plane, respectively.
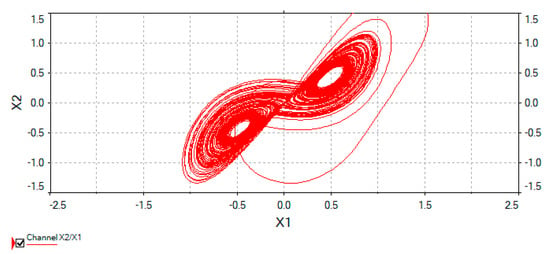
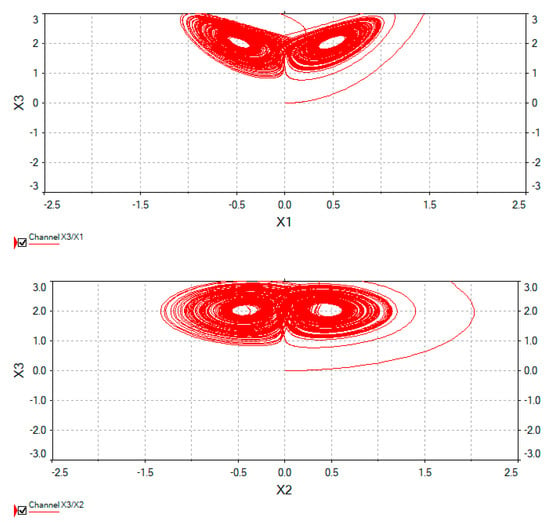
Figure 10.
The phase portraits of circuit of the fractional-order chain system.
5. GP for Regression and Emulation
Mathematical models have been extensively used in science and technology fields to visualize complex dynamic processes. However, accurate models are frequently so complex that they necessitate a considerable amount of computing time or other resources to function. Therefore, emulators have recently attracted a lot of attention. Emulators are known as techniques that focus on creating a mathematical description of the systems and processes. Emulators generally try to use available data, either noisy or not, to provide metamodels for processes. GP is among the most widely used methods for developing emulators [74,75,76]. We use GP to create an emulator for the three-echelon supply chain system in the current study. In fact, the aim is to create a metamodel based on GP and available noisy data.
Consider the following input–output relationship as a single realization of the random process:
where the inputs in the training data are denoted by . The predetermined set of basis functions is presented by . Additionally, indicate unknown coefficients of these bases. ξ(x) indicates a zero-mean GP, with the following parametric covariance function:
where stands for the process variance, and is the correlation function. The Gaussian correlation function, which is given by the following formula, is the most widely utilized correlation function.
in which and are hyperparameters and to be estimated based on the available data. Additionally, and are the scale parameters.
To determine hyperparameters and , we can apply maximum likelihood estimation (MLE) or cross-validation (CV). Additionally, Bayes’ rule can be applied to find the posterior distributions in the cases where there is prior knowledge about the value of hyperparameters. Herein, we consider a constant process means (i.e., ) and employ MLE to determine hyperparameters [77,78,79].
MLE necessitates the maximization of the multivariate Gaussian likelihood function, which is given by
where represents the natural logarithm, R indicates the correlation matrix, and each element of it is given by where . Additionally, 1 represents an vector of ones. By putting the partial derivatives with respect to and equal to zero, we reach
Simply replacing these obtained values into Equation (7) and removing the constants results in:
and by numerically minimizing the above equation, one may determine . To minimize , several global optimization methodologies have been used [80,81,82]. However, among all of them, gradient-based optimization approaches are most common because of their ease of use and improved computational efficiency [83,84]. To achieve global optimality, the optimization is performed numerous times with different beginning guesses.
After calculating hyperparameters, we will finally be able to obtain the mean and variance of the prediction probability distribution at any through the following formula:
In which indicates the vector of outputs in the training data and is an vector with i-th element Additionally, and is the covariance matrix at which its th element is given by . F is the matrix with element for and .
Numerical Results of Emulation and Regression
Herein, we apply the presented GP in order to estimate and interpolate the chaotic fractional three-echelon supply chain system. In fact, we suppose there are only some noisy data due to limitations, thus for management purposes, finding the noiseless states in each time step is essential.
Figure 11 demonstrates the results of the GP. As depicted by this figure, the findings closely match the real value of the fractional-order chaotic system. To summarize, the GP plays two key roles: (1) removing noises that are generated during the process and while data are collected; (2) interpolating data, which provides a noiseless time series of the results based on the noisy available data for all passed time units.
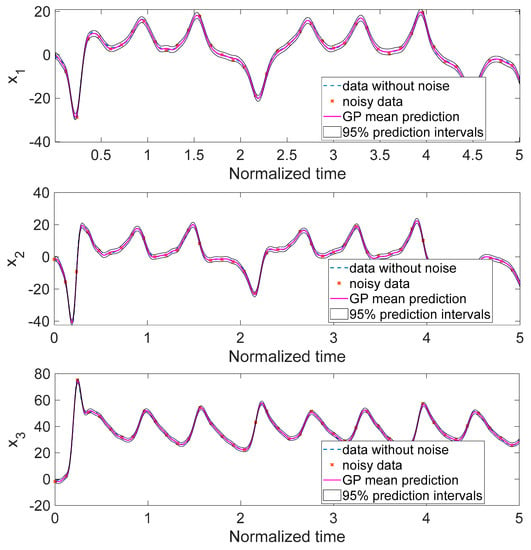
Figure 11.
The results of interpolation of chaotic fractional three-echelon supply chain system using GP regression.
6. Conclusions
In the current research, dynamical behaviors, chaos realization, as well as emulation and regression of a fractional three-echelon supply chain, were studied. At first, through Lyapunov exponent and bifurcation diagrams, the presence of chaos within the system was verified, and was is demonstrated that a slight deferent in some system parameters can considerably change the behavior of the system. Then, a real-time analog circuit was designed, and the chaotic attractors of the system were empirically demonstrated. Lastly, due to the advantages of metamodeling, GP, which is a strong candidate for metamodeling and emulation when data are rare, is employed for regression and interpolation of the three-echelon supply chain system. The results of the GP emulation clearly confirm that, by utilizing GP, we can extract accurate information about unknown points of the system’s time series, which is an important concern in supply chains. Another advantage of GP is the uncertainty bound that it provides (see the prediction interval in Figure 11). GP provides the bound of uncertainty for the points that have been estimated, which can be considered as a level for accuracy for management applications. Consequently, the output of the GP emulator can be used as a reliable source for management and control purposes, which are considered as a direction of future study by the authors.
Author Contributions
Conceptualization, Q.D., H.J., O.A.A., M.O.A. and W.-H.H.; methodology, Q.D., H.J., O.A.A., M.O.A. and W.-H.H.; software, Q.D., H.J., O.A.A., M.O.A. and W.-H.H.; validation, Q.D., H.J., O.A.A., M.O.A. and W.-H.H.; formal analysis, Q.D., H.J., O.A.A., M.O.A. and W.-H.H.; investigation, Q.D., H.J., O.A.A., M.O.A. and W.-H.H.; writing—original draft preparation, Q.D., H.J., O.A.A., M.O.A. and W.-H.H.; writing—review and editing, Q.D., H.J., O.A.A., M.O.A. and W.-H.H.; supervision, Q.D., H.J., O.A.A., M.O.A. and W.-H.H. All authors have read and agreed to the published version of the manuscript.
Funding
The Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, Saudi Arabia has funded this project, under grant No. (FP-152-43). This work was supported by the Hunan Provincial Department of Education Scientific Research Outstanding Youth Project (Grant No.: 20B093), the Hunan Philosophy and Social Science Foundation Project (Grant No.: 20JD008) and the Natural Science Foundation of China (Grant No.: 71873045).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Min, H.; Zhou, G. Supply chain modeling: Past, present and future. Comput. Ind. Eng. 2002, 43, 231–249. [Google Scholar] [CrossRef]
- Guo, Z.; Ma, J. Dynamics and implications on a cooperative advertising model in the supply chain. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 198–212. [Google Scholar] [CrossRef]
- Di Giacomo, L.; Patrizi, G. Dynamic nonlinear modelization of operational supply chain systems. J. Glob. Optim. 2006, 34, 503–534. [Google Scholar] [CrossRef]
- Wang, B.; Jahanshahi, H.; Volos, C.; Bekiros, S.; Yusuf, A.; Agarwal, P.; Aly, A. Control of a symmetric chaotic supply chain system using a new fixed-time super-twisting sliding mode technique subject to control input limitations. Symmetry 2021, 13, 1257. [Google Scholar] [CrossRef]
- Liu, Z.; Jahanshahi, H.; Gómez-Aguilar, J.F.; Fernandez-Anaya, G.; Torres-Jiménez, J.; Aly, A.A.; Aljuaid, A.M. Fuzzy adaptive control technique for a new fractional-order supply chain system. Phys. Scripta 2021, 96, 124017. [Google Scholar] [CrossRef]
- Liu, Z.; Jahanshahi, H.; Volos, C.; Bekiros, S.; He, S.; Alassafi, M.O.; Ahmad, A.M. Distributed Consensus Tracking Control of Chaotic Multi-Agent Supply Chain Network: A New Fault-Tolerant, Finite-Time, and Chatter-Free Approach. Entropy 2021, 24, 33. [Google Scholar] [CrossRef]
- Chilmon, B.; Tipi, N.S. Modelling and simulation considerations for an end-to-end supply chain system. Comput. Ind. Eng. 2020, 150, 106870. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q. Coordination mechanisms of supply chain systems. Eur. J. Oper. Res. 2007, 179, 1–16. [Google Scholar] [CrossRef]
- Sarimveis, H.; Patrinos, P.; Tarantilis, C.D.; Kiranoudis, C.T. Dynamic modeling and control of supply chain systems: A review. Comput. Oper. Res. 2008, 35, 3530–3561. [Google Scholar] [CrossRef]
- Alvarado, U.Y.; Kotzab, H. Supply chain management: The integration of logistics in marketing. Ind. Mark. Manag. 2001, 30, 183–198. [Google Scholar] [CrossRef]
- Zokaei, K.; Hines, P. Achieving consumer focus in supply chains. Int. J. Phys. Distrib. Logist. Manag. 2007, 37, 223. [Google Scholar] [CrossRef]
- Simchi-Levi, D.; Kaminsky, P.; Simchi-Levi, E.; Shankar, R. Designing and Managing the Supply Chain: Concepts, Strategies and Case Studies; Tata McGraw-Hill Education: New York, NY, USA, 2008. [Google Scholar]
- Nunes, L.J.R.; Causer, T.P.; Ciolkosz, D. Biomass for energy: A review on supply chain management models. Renew. Sustain. Energy Rev. 2020, 120, 109658. [Google Scholar] [CrossRef]
- Panfilova, E.; Dzenzeliuk, N.; Domnina, O.; Morgunova, N.; Zatsarinnaya, E. The impact of cost allocation on key decisions of supply chain participants. Int. J. Supply Chain. Manag. 2020, 9, 552–558. [Google Scholar]
- Halldorsson, A.; Kotzab, H.; Mikkola, J.H.; Skjøtt-Larsen, T. Complementary theories to supply chain management. Supply Chain. Manag. Int. J. 2007, 12, 284–296. [Google Scholar] [CrossRef]
- Peng, H.; Shen, N.; Liao, H.; Xue, H.; Wang, Q. Uncertainty factors, methods, and solutions of closed-loop supply chain—A review for current situation and future prospects. J. Clean. Prod. 2020, 254, 120032. [Google Scholar] [CrossRef]
- Sato, Y.; Tse, Y.K.; Tan, K.H. Managers’ risk perception of supply chain uncertainties. Ind. Manag. Data Syst. 2020, 120, 1617–1634. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Sallam, K.; Elhoseny, M. A novel decision-making model for sustainable supply chain finance under uncertainty environment. J. Clean. Prod. 2020, 269, 122324. [Google Scholar] [CrossRef]
- Shi, J.; He, K.; Fang, H. Chaos, Hopf bifurcation and control of a fractional-order delay financial system. Math. Comput. Simul. 2021, 194, 348–364. [Google Scholar] [CrossRef]
- Cao, Y. Chaotic synchronization based on fractional order calculus financial system. Chaos Solitons Fractals 2020, 130, 109410. [Google Scholar] [CrossRef]
- Zhou, S.-S.; Jahanshahi, H.; Din, Q.; Bekiros, S.; Alcaraz, R.; Alassafi, M.O.; Alsaadi, F.E.; Chu, Y.-M. Discrete-time macroeconomic system: Bifurcation analysis and synchronization using fuzzy-based activation feedback control. Chaos Solitons Fractals 2021, 142, 110378. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Sajjadi, S.S.; Bekiros, S.; Aly, A.A. On the development of variable-order fractional hyperchaotic economic system with a nonlinear model predictive controller. Chaos Solitons Fractals 2021, 144, 110698. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Bekiros, S.; Zambrano-Serrano, E.; Orozco-López, O.; Lahmiri, S.; Jahanshahi, H.; Aly, A.A. Artificial macro-economics: A chaotic discrete-time fractional-order laboratory model. Chaos Solitons Fractals. 2021, 145, 110776. [Google Scholar] [CrossRef]
- Ding, Q.; Jahanshahi, H.; Wang, Y.; Bekiros, S.; Alassafi, M.O. Optimal Reinforcement Learning-Based Control Algorithm for a Class of Nonlinear Macroeconomic Systems. Mathematics 2022, 10, 499. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Wei, Z.; Alcaraz, R.; Bekiros, S. A financial hyperchaotic system with coexisting attractors: Dynamic investigation, entropy analysis, control and synchronization. Chaos Solitons Fractals 2019, 126, 66–77. [Google Scholar] [CrossRef]
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- Soradi-Zeid, S.; Jahanshahi, H.; Yousefpour, A.; Bekiros, S. King algorithm: A novel optimization approach based on variable-order fractional calculus with application in chaotic financial systems. Chaos Solitons Fractals 2020, 132, 109569. [Google Scholar] [CrossRef]
- Wang, S.; Bekiros, S.; Yousefpour, A.; He, S.; Castillo, O.; Jahanshahi, H. Synchronization of fractional time-delayed financial system using a novel type-2 fuzzy active control method. Chaos Solitons Fractals 2020, 136, 109768. [Google Scholar] [CrossRef]
- Chen, S.-B.; Jahanshahi, H.; Abba, O.A.; Solís-Pérez, J.E.; Bekiros, S.; Gómez-Aguilar, J.F.; Yousefpour, A.; Chu, Y.-M. The effect of market confidence on a financial system from the perspective of fractional calculus: Numerical investigation and circuit realization. Chaos Solitons Fractals 2020, 140, 110223. [Google Scholar] [CrossRef]
- Wang, B.; Jahanshahi, H.; Bekiros, S.; Chu, Y.-M.; Gomez-Aguilar, J.F.; Alsaadi, F.E.; Alassafi, M.O. Tracking control and stabilization of a fractional financial risk system using novel active finite-time fault-tolerant controls. Fractals 2021, 29, 2150155–2150177. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Jahanshahi, H.; Bekiros, S.; Bezzina, F.; Chu, Y.-M.; Aly, A.A. Deep recurrent neural networks with finite-time terminal sliding mode control for a chaotic fractional-order financial system with market confidence. Chaos Solitons Fractals 2021, 146, 110881. [Google Scholar] [CrossRef]
- Bekiros, S.; Jahanshahi, H.; Bezzina, F.; Aly, A.A. A novel fuzzy mixed H2/H∞ optimal controller for hyperchaotic financial systems. Chaos Solitons Fractals 2021, 146, 110878. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, S.; Xie, Y.; Gui, W.; Tang, Z.; Ma, T.; Niyoyita, J.P. Learning local Gabor pattern-based discriminative dictionary of froth images for flotation process working condition monitoring. IEEE Trans. Ind. Inform. 2020, 17, 4437–4448. [Google Scholar] [CrossRef]
- Liu, J.; He, J.; Xie, Y.; Gui, W.; Tang, Z.; Ma, T.; Niyoyita, J.P. Illumination-invariant flotation froth color measuring via Wasserstein distance-based CycleGAN with structure-preserving constraint. IEEE Trans. Cybern. 2021, 51, 839–852. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, J.; Tang, Z.; Gui, W.; Xie, Y.; He, J.; Niyoyita, J.P. Toward flotation process operation-state identification via statistical modeling of biologically inspired Gabor filtering responses. IEEE Trans. Cybern. 2019, 50, 4242–4255. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Zheng, J.; Wang, X.; Zeng, Z.; Peng, X. Generating Any Number of Initial Offset-boosted Coexisting Chua’s Double-scroll Attractors via Piecewise-nonlinear Memristor. IEEE Trans. Ind. Electron. 2021, 69, 7202–7212. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, J.; Wang, X.; Zeng, Z.; Peng, X. A novel nonideal flux-controlled memristor model for generating arbitrary multi-double-scroll and multi-double-wing attractors. Int. J. Bifurc. Chaos 2021, 31, 2150086. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, J.; Wang, X.; Zeng, Z. A novel no-equilibrium HR neuron model with hidden homogeneous extreme multistability. Chaos Solitons Fractals 2021, 145, 110761. [Google Scholar] [CrossRef]
- Kosari, A.; Jahanshahi, H.; Razavi, S.A. An optimal fuzzy PID control approach for docking maneuver of two spacecraft: Orientational motion. Eng. Sci. Technol. Int. J. 2017, 20, 293–309. [Google Scholar] [CrossRef] [Green Version]
- Kosari, A.; Jahanshahi, H.; Razavi, S.A. Optimal FPID control approach for a docking maneuver of two spacecraft: Translational motion. J. Aerosp. Eng. 2017, 30, 04017011. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Sari, N.N.; Pham, V.-T.; Alsaadi, F.E.; Hayat, T. Optimal adaptive higher order controllers subject to sliding modes for a carrier system. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418782097. [Google Scholar] [CrossRef]
- Jahanshahi, H. Smooth control of HIV/AIDS infection using a robust adaptive scheme with decoupled sliding mode supervision. Eur. Phys. J. Spec. Top. 2018, 227, 707–718. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Shahriari-Kahkeshi, M.; Alcaraz, R.; Wang, X.; Singh, V.P.; Pham, V.-T. Entropy analysis and neural network-based adaptive control of a non-equilibrium four-dimensional chaotic system with hidden attractors. Entropy 2019, 21, 156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, B.; Jahanshahi, H.; Volos, C.; Bekiros, S.; Khan, M.A.; Agarwal, P.; Aly, A. A new RBF neural network-based fault-tolerant active control for fractional time-delayed systems. Electronics 2021, 10, 1501. [Google Scholar] [CrossRef]
- Li, J.-F.; Jahanshahi, H.; Kacar, S.; Chu, Y.-M.; Gómez-Aguilar, J.F.; Alotaibi, N.D.; Alharbi, K.H. On the variable-order fractional memristor oscillator: Data security applications and synchronization using a type-2 fuzzy disturbance observer-based robust control. Chaos Solitons Fractals 2021, 145, 110681. [Google Scholar] [CrossRef]
- Wang, H.; Jahanshahi, H.; Wang, M.-K.; Bekiros, S.; Liu, J.; Aly, A.A. A Caputo–Fabrizio Fractional-Order Model of HIV/AIDS with a Treatment Compartment: Sensitivity Analysis and Optimal Control Strategies. Entropy 2021, 23, 610. [Google Scholar] [CrossRef]
- Wang, B.; Jahanshahi, H.; Dutta, H.; Zambrano-Serrano, E.; Grebenyuk, V.; Bekiros, S.; Aly, A.A. Incorporating fast and intelligent control technique into ecology: A Chebyshev neural network-based terminal sliding mode approach for fractional chaotic ecological systems. Ecol. Complex. 2021, 47, 100943. [Google Scholar] [CrossRef]
- Wang, B.; Derbeli, M.; Barambones, O.; Yousefpour, A.; Jahanshahi, H.; Bekiros, S.; Aly, A.A. Experimental validation of disturbance observer-based adaptive terminal sliding mode control subject to control input limitations for SISO and MIMO systems. Eur. J. Control. 2021, 63, 151–163. [Google Scholar] [CrossRef]
- Wang, B.; Liu, J.; Alassafi, M.O.; Alsaadi, F.E.; Jahanshahi, H.; Bekiros, S. Intelligent parameter identification and prediction of variable time fractional derivative and application in a symmetric chaotic financial system. Chaos Solitons Fractals 2021, 154, 111590. [Google Scholar] [CrossRef]
- Bensaïda, A. Noisy chaos in intraday financial data: Evidence from the American index. Appl. Math. Comput. 2014, 226, 258–265. [Google Scholar] [CrossRef]
- Magdon-Ismail, M.; Nicholson, A.; Abu-Mostafa, Y.S. Financial markets: Very noisy information processing. Proc. IEEE 1998, 86, 2184–2195. [Google Scholar] [CrossRef]
- Abdulkadir, S.J.; Yong, S.-P. Unscented Kalman Filter for Noisy Multivariate Financial Time-Series Data; Springer: Berlin/Heidelberg, Germany, 2013; pp. 87–96. [Google Scholar]
- Wang, J.; Hertzmann, A.; Fleet, D.J. Gaussian process dynamical models. In Advances in Neural Information Processing Systems; University of Toronto: Toronto, ON, Canada, 2005; Volume 18, Available online: http://www.dgp.toronto.edu/~jmwang/gpdm/nips05final.pdf (accessed on 18 December 2021).
- Oyebamiji, O.K.; Wilkinson, D.J.; Jayathilake, P.G.; Curtis, T.P.; Rushton, S.P.; Li, B.; Gupta, P. Gaussian process emulation of an individual-based model simulation of microbial communities. J. Comput. Sci. 2017, 22, 69–84. [Google Scholar] [CrossRef]
- Riddalls, C.E.; Bennett, S.; Tipi, N.S. Modelling the dynamics of supply chains. Int. J. Syst. Sci. 2000, 31, 969–976. [Google Scholar] [CrossRef]
- Beamon, B.M. Supply chain design and analysis: Models and methods. Int. J. Prod. Econ. 1998, 55, 281–294. [Google Scholar] [CrossRef]
- Anne, K.R.; Chedjou, J.C.; Kyamakya, K. Bifurcation analysis and synchronisation issues in a three-echelon supply chain. Int. J. Logist. Res. Appl. 2009, 12, 347–362. [Google Scholar] [CrossRef]
- Anne, K.R.; Chedjou, J.C.; Bhagavatula, S.K.; Kyamakya, K. Modeling of a Three-Echelon Supply Chain: Stability Analysis and Synchronization Issues. 2008. Available online: https://www.researchgate.net/profile/Koteswara-Rao-Anne/publication/267224704_Modeling_of_a_Three-Echelon_Supply_Chain_Stability_Analysis_and_Synchronization_Issues/links/546b1ee80cf20dedafd3f287/Modeling-of-a-Three-Echelon-Supply-Chain-Stability-Analysis-and-Synchronization-Issues.pdf (accessed on 18 December 2021).
- Helo, P.T. Dynamic modelling of surge effect and capacity limitation in supply chains. Int. J. Prod. Res. 2000, 38, 4521–4533. [Google Scholar] [CrossRef]
- Cuong, T.N.; Kim, H.-S.; Nguyen, D.A.; You, S.-S. Nonlinear analysis and active management of production-distribution in nonlinear supply chain model using sliding mode control theory. Appl. Math. Model. 2021, 97, 418–437. [Google Scholar] [CrossRef]
- Yan, L.; Liu, J.; Xu, F.; Teo, K.L.; Lai, M. Control and synchronization of hyperchaos in digital manufacturing supply chain. Appl. Math. Comput. 2021, 391, 125646. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, D. Simulation-based optimization on control strategies of three-echelon inventory in hybrid supply chain with order uncertainty. IEEE Access 2018, 6, 54215–54223. [Google Scholar] [CrossRef]
- Mondal, S. A new supply chain model and its synchronization behaviour. Chaos Solitons Fractals 2019, 123, 140–148. [Google Scholar] [CrossRef]
- Han, W.; Wang, J. The impact of cooperation mechanism on the chaotic behaviours in nonlinear supply chains. Eur. J. Ind. Eng. 2015, 9, 595–612. [Google Scholar] [CrossRef]
- Sadeghi, J.; Mousavi, S.M.; Niaki, S.T.A.; Sadeghi, S. Optimizing a bi-objective inventory model of a three-echelon supply chain using a tuned hybrid bat algorithm. Transp. Res. Part E Logist. Transp. Rev. 2014, 70, 274–292. [Google Scholar] [CrossRef]
- Wang, K.-J.; Lee, C.H. A revised ant algorithm for solving location–allocation problem with risky demand in a multi-echelon supply chain network. Appl. Soft Comput. 2015, 32, 311–332. [Google Scholar] [CrossRef]
- d’Apice, C.; Göttlich, S.; Herty, M.; Piccoli, B. Modeling, Simulation, and Optimization of Supply Chains: A Continuous Approach; SIAM: Philadelphia, PN, USA, 2010. [Google Scholar]
- Towill, D.R.; Naim, M.M.; Wikner, J. Industrial dynamics simulation models in the design of supply chains. Int. J. Phys. Distrib. Logist. Manag. 1992, 22, 3–13. [Google Scholar] [CrossRef]
- Barykin, S.Y.; Bochkarev, A.A.; Kalinina, O.V.; Yadykin, V.K. Concept for a supply chain digital twin. Int. J. Math. Eng. Manag. Sci. 2020, 5, 1498–1515. [Google Scholar] [CrossRef]
- Ahmad, W.M.; Sprott, J.C. Chaos in fractional-order autonomous nonlinear systems. Chaos Solitons Fractals 2003, 16, 339–351. [Google Scholar] [CrossRef] [Green Version]
- Cuomo, K.M.; Oppenheim, A.V. Circuit implementation of synchronized chaos with applications to communications. Phys. Rev. Lett. 1993, 71, 65. [Google Scholar] [CrossRef]
- Zhe, X.; Chong-Xin, L. Realization of fractional-order Liu chaotic system by a new circuit unit. Chin. Phys. B 2008, 17, 4033. [Google Scholar] [CrossRef]
- von Rohr, A.; Neumann-Brosig, M.; Trimpe, S. Probabilistic Robust Linear Quadratic Regulators with Gaussian Processes. In Proceedings of the 3rd Conference on Learning for Dynamics and Control, Online, 6 August 2021; pp. 324–335. [Google Scholar]
- Kontoudis, G.P.; Stilwell, D.J. Decentralized nested Gaussian processes for multi-robot systems. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May 2021; pp. 8881–8887. [Google Scholar]
- Briffa, R.; Capozziello, S.; Said, J.L.; Mifsud, J.; Saridakis, E.N. Constraining teleparallel gravity through Gaussian processes. Class. Quantum Gravity 2021, 38, 055007. [Google Scholar] [CrossRef]
- Plumlee, M.; Apley, D.W. Lifted Brownian kriging models. Technometrics 2017, 59, 165–177. [Google Scholar] [CrossRef]
- Bilionis, I.; Zabaras, N. Multi-output local Gaussian process regression: Applications to uncertainty quantification. J. Comput. Phys. 2011, 231, 5718–5746. [Google Scholar] [CrossRef]
- Nguyen-Tuong, D.; Seeger, M.; Peters, J. Model learning with local gaussian process regression. Adv. Robot. 2009, 23, 2015–2034. [Google Scholar] [CrossRef] [Green Version]
- Toal, D.J.J.; Bressloff, N.W.; Keane, A.J.; Holden, C.M.E. The development of a hybridized particle swarm for kriging hyperparameter tuning. Eng. Optim. 2011, 43, 675–699. [Google Scholar] [CrossRef]
- Alamaniotis, M.; Ikonomopoulos, A.; Tsoukalas, L.H. A Pareto optimization approach of a Gaussian process ensemble for short-term load forecasting. In Proceedings of the 2011 16th International Conference on Intelligent System Applications to Power Systems, Hersonissos, Greece, 25–28 September 2011; pp. 1–6. [Google Scholar]
- Toal, D.J.J.; Bressloff, N.W.; Keane, A.J. Kriging hyperparameter tuning strategies. AIAA J. 2008, 46, 1240–1252. [Google Scholar] [CrossRef]
- Chu, W.; Ghahramani, Z. Preference learning with Gaussian processes. In Proceedings of the ICML’05: Proceedings of the 22nd International Conference on Machine Learning, New York, NY, USA, 7–11 August 2005; pp. 137–144. [Google Scholar]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian processes using pseudo-inputs. Adv. Neural Inf. Proces Syst. 2006, 18, 1257. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).