The Least Squares Homotopy Perturbation Method for Systems of Differential Equations with Application to a Blood Flow Model
Abstract
:1. Introduction
2. The Least Squares Homotopy Perturbation Method
3. Numerical Application
3.1. The Case and
- First-term approximations:
- Second-term approximations:
- Third-term approximations:
- Second-term approximations:
- Third-term approximations:
3.2. The Case and
- First-term approximations:
- Second-term approximations:
- Third-term approximations:
- Second-term approximations:
- Third-term approximations:
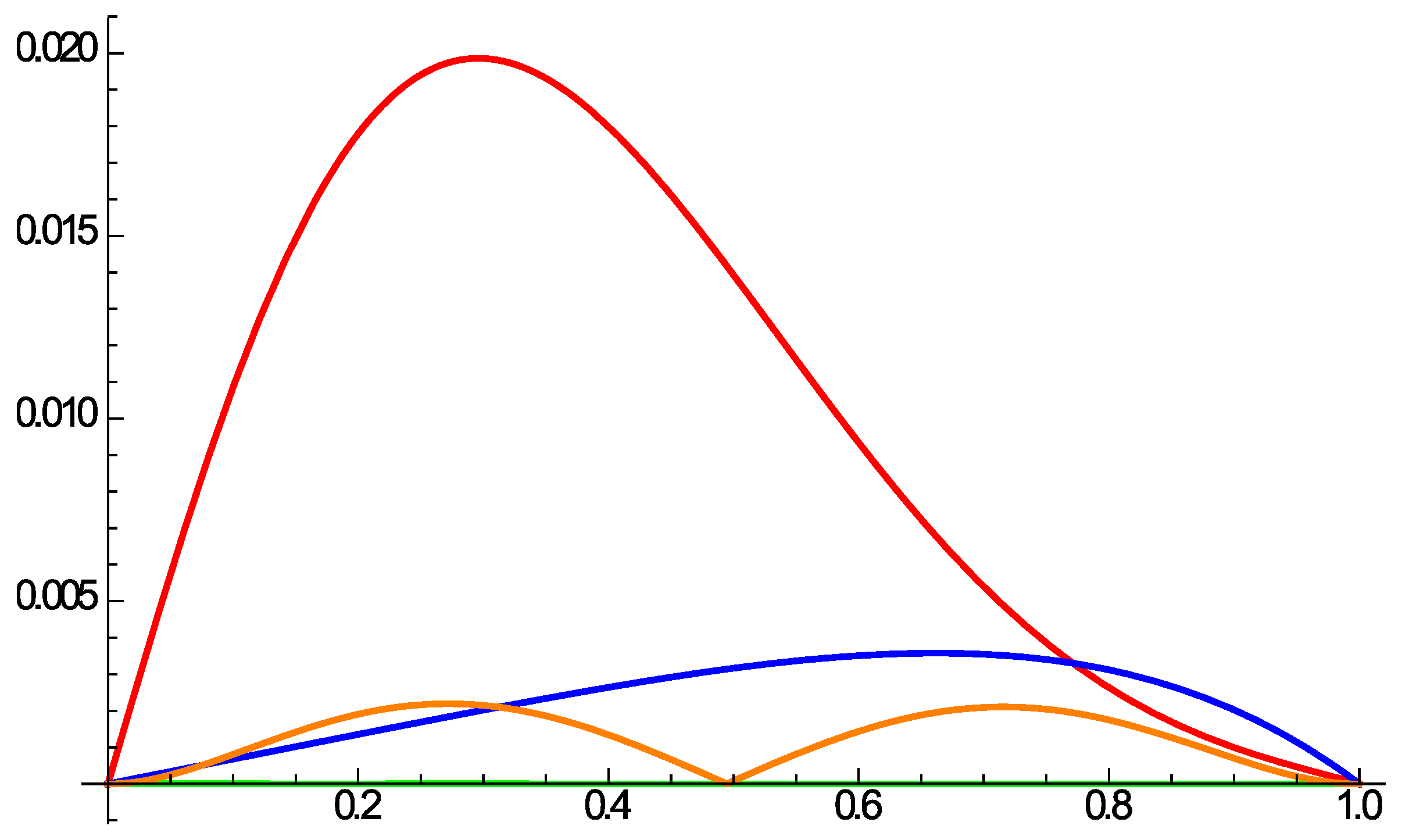
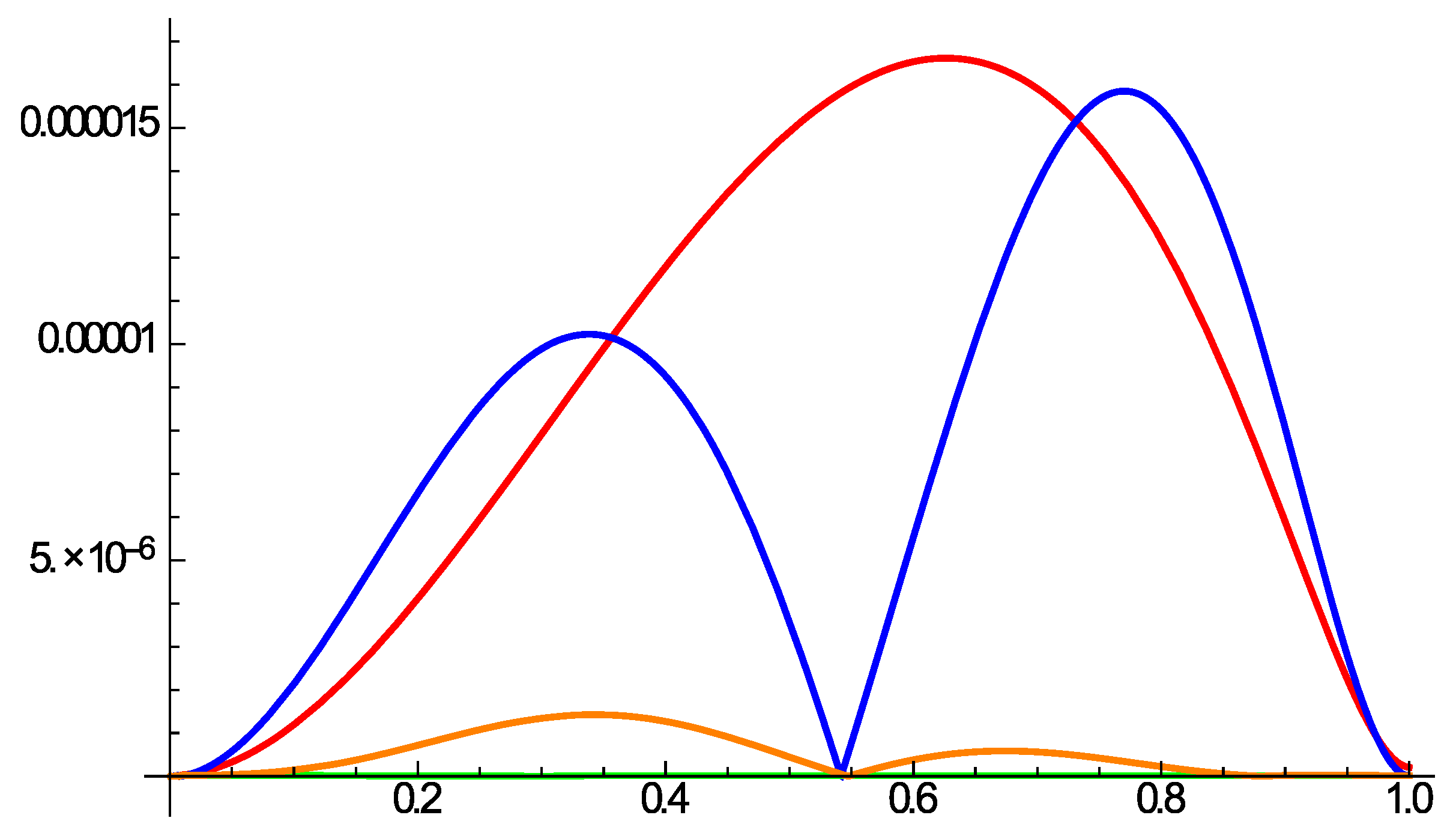
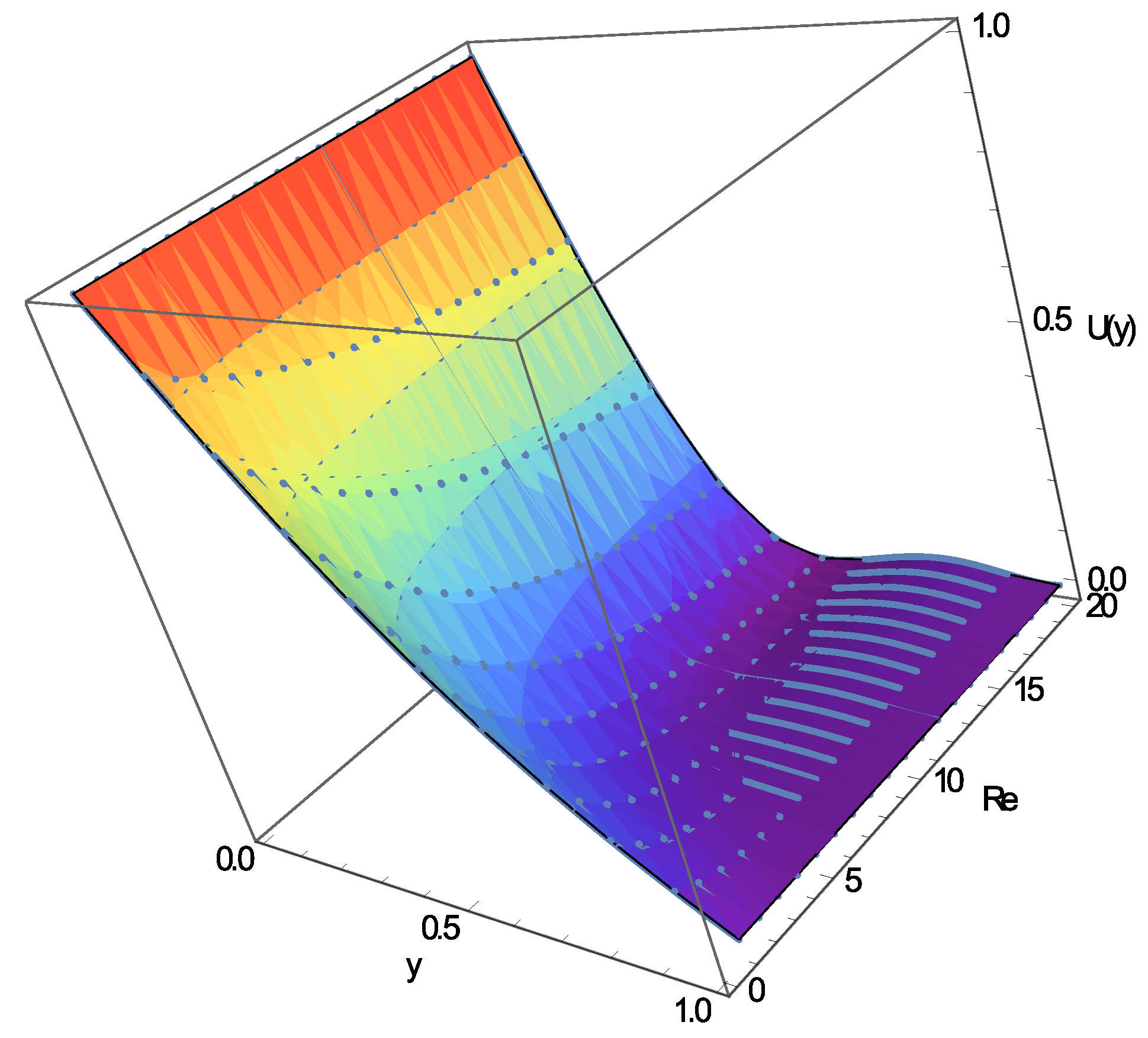
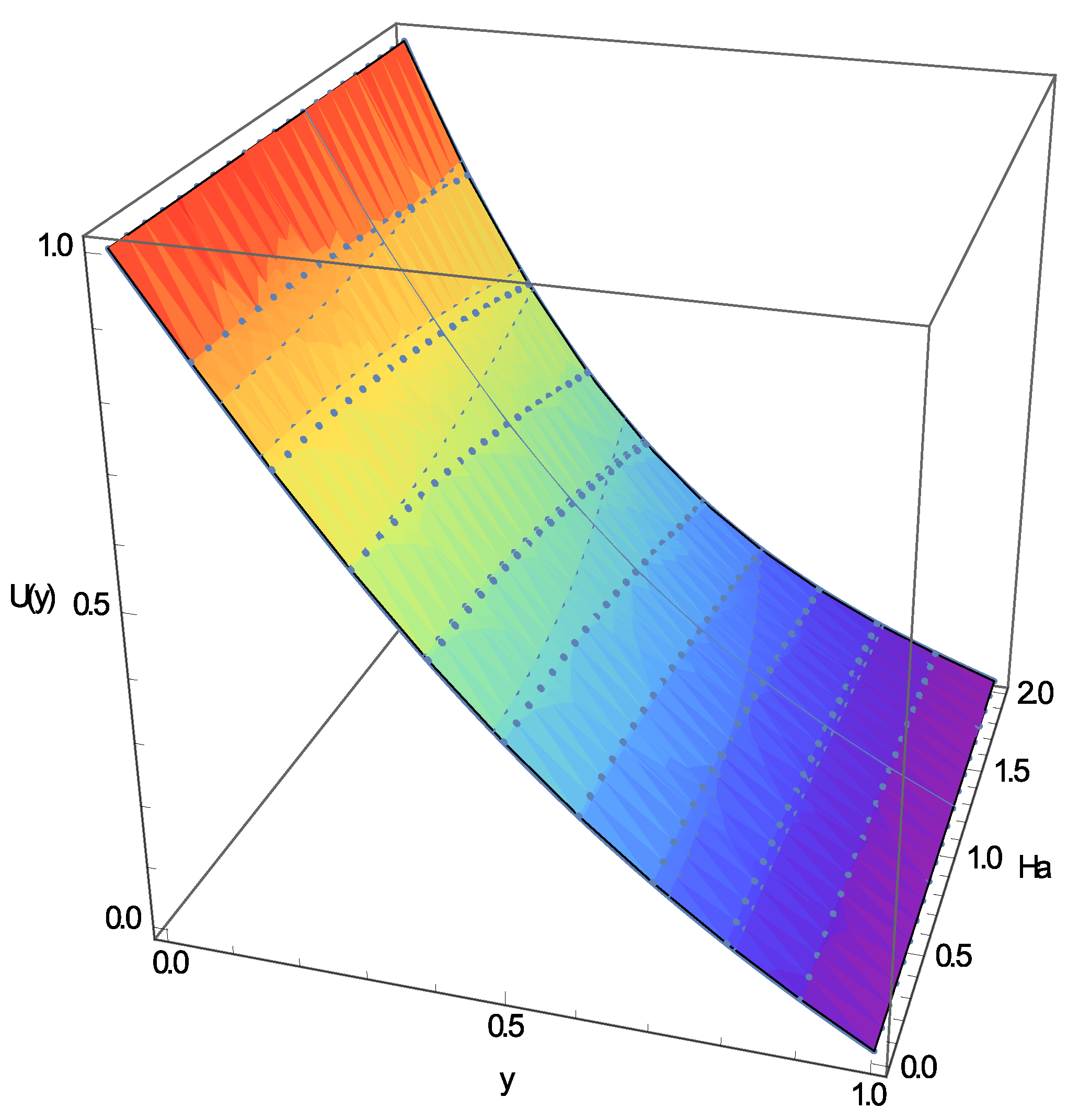
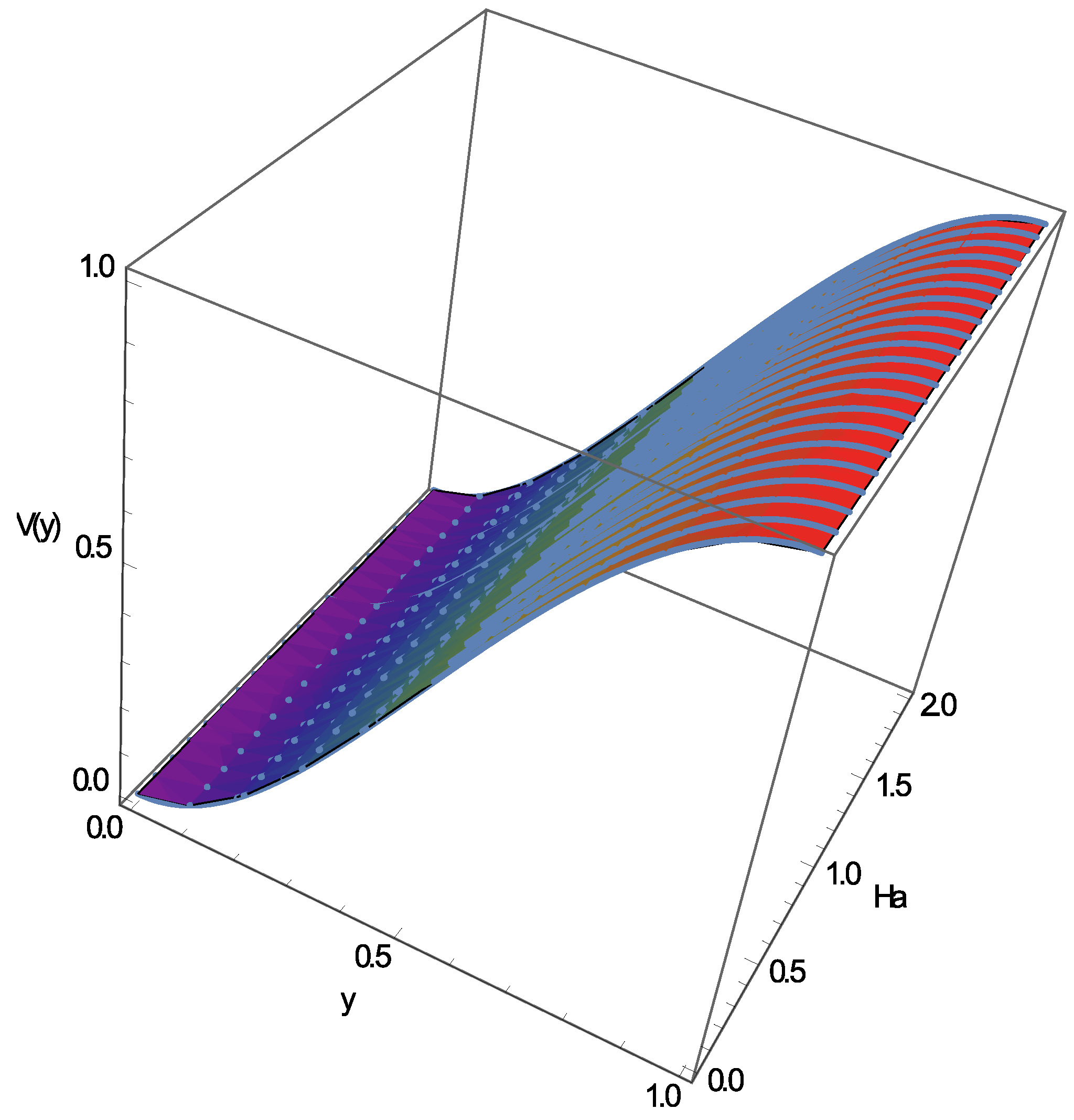
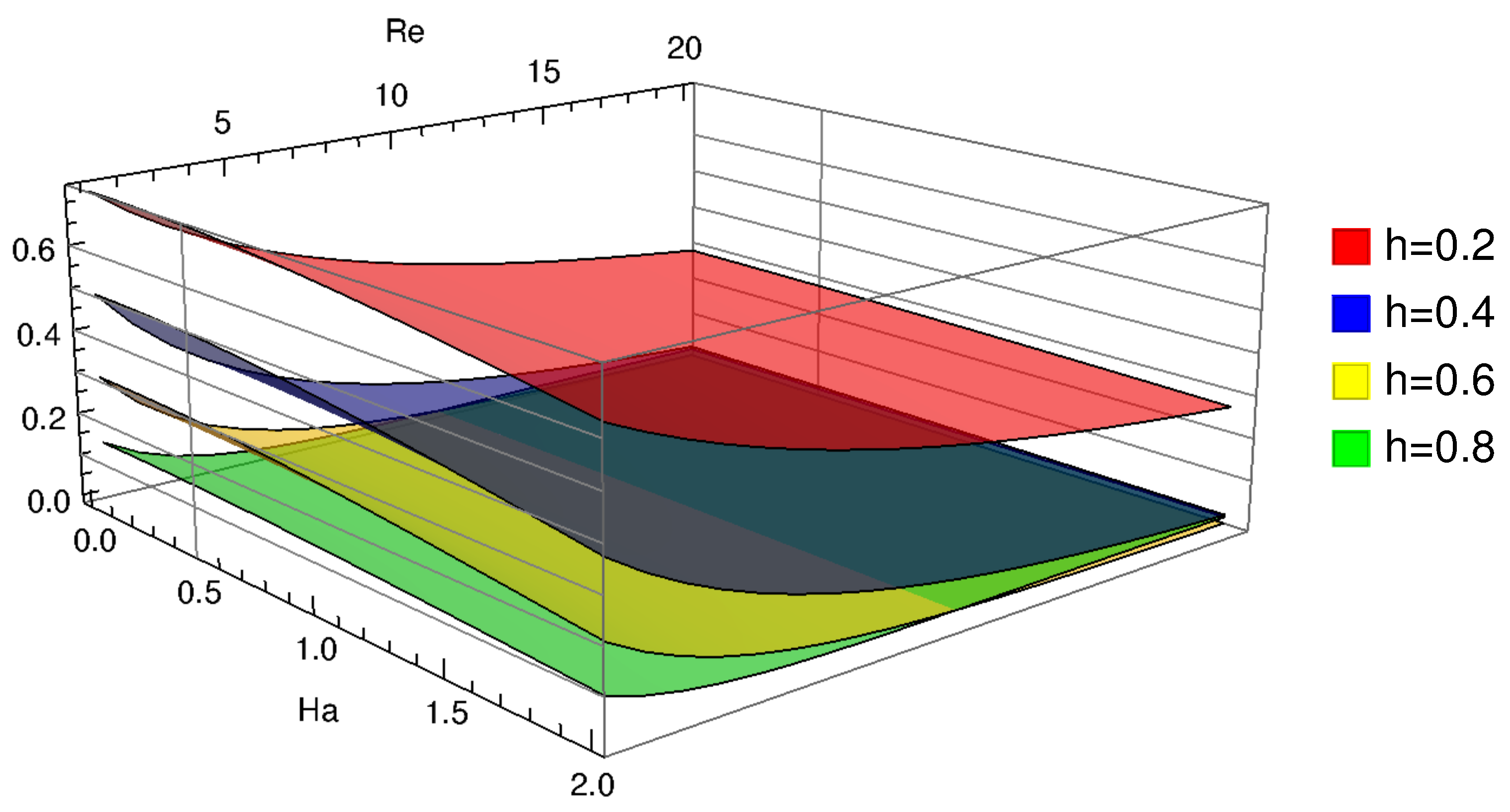
4. Discussion of the Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Bota, C.; Caruntu, B. Approximate analytical solutions of nonlinear differential equations using the Least Squares Homotopy Perturbation Method. J. Math. Anal. Appl. 2017, 448, 401–408. [Google Scholar] [CrossRef]
- Bota, C.; Caruntu, B.; Lazureanu, C. The Least Squares Homotopy Perturbation Method for boundary value problems. Appl. Comput. Math. 2017, 16, 39–47. [Google Scholar]
- Qayyum, M.; Oscar, I. Least Square Homotopy Perturbation Method for Ordinary Differential Equations. J. Math. 2021, 2021, 7059194. [Google Scholar] [CrossRef]
- Thabet, H.; Kendre, S. Modified least squares homotopy perturbation method for solving fractional partial differential equations. Malaya J. Mat. 2018, 6, 420–427. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Koundal, R.; Shehzad, S.A. Generalized least square homotopy perturbation solution of fractional telegraph equations. Comput. Appl. Math. 2019, 38, 184. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, Z.; Li, L.; Zhou, C. Least-Squares Residual Power Series Method for the Time-Fractional Differential Equations. Complexity 2019, 2019, 6159024. [Google Scholar] [CrossRef]
- Das, P.; Rana, S. Theoretical prospects of fractional order weakly singular Volterra Integro differential equations and their approximations with convergence analysis. Math. Methods Appl. Sci. 2021, 44, 9419–9440. [Google Scholar] [CrossRef]
- Kumar, R.; Koundal, R.; Shehzad, S.A. Modified homotopy perturbation approach for the system of fractional partial differential equations: A utility of fractional Wronskian. Math. Methods Appl. Sci. 2022, 45, 809–826. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals 2005, 26, 695–700. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method, a kind of nonlinear analytical technique. Some examples. Int. J. Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- Parsa, A.B.; Rashidi, M.M.; Beg, O.A.; Sardi, S.M. Semi-computational simulation of magneto-hemodynamic flow in a semi-porous channel using optimal homotopy and differential transform methods. Comput. Biol. Med. 2013, 43, 1142–1153. [Google Scholar] [CrossRef] [PubMed]
- Adomian, G.A. Review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 1998, 135, 501–544. [Google Scholar] [CrossRef] [Green Version]
- Marinca, V.; Herisanu, N.; Bota, C. An optimal homotopy asymptotic method applied to the steady flow of a fourth-grade fluid past a porous plate. Appl. Math. Lett. 2009, 22, 245–251. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, V.P. A Theoretical Model for Blood Flow in Small Vessels. Int. J. Appl. Appl. Math. 2007, 2, 51–65. [Google Scholar]
- Wang, C.Y.; Bassingthwaighte, J.B. Blood Flow in Small Curved Tubes. J. Biomech. Eng. 2003, 125, 910–913. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bali, R.; Awasthi, U. Mathematical model of Blood Flow in Small Blood Vessel in the Presence of Magnetic Field. Appl. Math. 2001, 2, 264–269. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, T.; Nagayama, Y.; Tamura, M. A blood-oxygenation-dependent increase in blood viscosity due to a static magnetic field. Phys. Med. Biol. 2004, 49, 3267. [Google Scholar] [CrossRef] [PubMed]
- Alshare, A.; Tashtoush, B.; El-Khalil, H.H. Computational Modeling of Non-Newtonian Blood Flow Through Stenosed Arteries in the Presence of Magnetic Field. J. Biomech. Eng. 2013, 135, 1145–1153. [Google Scholar] [CrossRef]
- Weng, H.C. Hydrodynamic Modeling of Targeted Magnetic-Particle Delivery in a Blood Vessel. J. Biomech. Eng. 2013, 135, 034504. [Google Scholar] [CrossRef] [PubMed]
- Mekheimer, K.S. Peristaltic flow of blood under effect of a magnetic field in a non-uniform channels. Appl. Math. Comput. 2004, 153, 763–777. [Google Scholar] [CrossRef]
- Tenforde, T.S. Magnetically induced electric fields and currents in the circulatory system. Prog. Biophys. Mol. Biol. 2005, 87, 279–288. [Google Scholar] [CrossRef] [PubMed]
- Bhatti, M.M.; Zeeshan, A.; Bashir, F.; Sait, S.M.; Ellahi, R. Sinusoidal motion of small particles through a Darcy-Brinkman-Forchheimer microchannel filled with non-Newtonian fluid under electro-osmotic forces. J. Taibah Univ. Sci. 2021, 15, 514–529. [Google Scholar] [CrossRef]
- Rostami, S.; Ellahi, R.; Oztop, H.F.; Goldanlou, A.S. A study on the effect of magnetic field and the sinusoidal boundary condition on free convective heat transfer of non-Newtonian power-law fluid in a square enclosure with two constant-temperature obstacles using lattice Boltzmann method. J. Therm. Anal. Calorim. 2021, 144, 2557–2573. [Google Scholar] [CrossRef]
- Khan, A.S.; Xu, H.Y.; Khan, W. Magnetohydrodynamic Hybrid Nanofluid Flow Past an Exponentially Stretching Sheet with Slip Conditions. Mathematics 2021, 9, 3291. [Google Scholar] [CrossRef]
- Rehman, A.; Salleh, Z. Influence of Marangoni Convection on Magnetohydrodynamic Viscous Dissipation and Heat Transfer on Hybrid Nanofluids in a Rotating System among Two Surfaces. Mathematics 2021, 9, 2242. [Google Scholar] [CrossRef]
- Ali, B.; Naqvi, R.A.; Haider, A.; Hussain, D.; Hussain, S. Finite Element Study of MHD Impacts on the Rotating Flow of Casson Nanofluid with the Double Diffusion Cattaneo—Christov Heat Flux Model. Mathematics 2020, 8, 1555. [Google Scholar] [CrossRef]
- Ryu, J.; Hu, X.; Shadden, S.C. A Coupled Lumped-Parameter and Distributed Network Model for Cerebral Pulse-Wave Hemodynamics. J. Biomech. Eng. 2015, 137, 101009. [Google Scholar] [CrossRef] [Green Version]
- Srinivasacharya, D.; Rao, G.M. Mathematical model for blood flow through a bifurcated artery using couple stress fluid. Math. Biosci. 2016, 278, 37–47. [Google Scholar] [CrossRef]
- Sinha, A. MHD flow and heat transfer of a third order fluid in a porous channel with stretching wall: Application to hemodynamics. Alex. Eng. J. 2015, 54, 1243–1252. [Google Scholar] [CrossRef] [Green Version]
- Zaman, A.; Ali, N.; Sajid, M. Numerical simulation of pulsatile flow of blood in a porous-saturated overlapping stenosed artery. Math. Comput. Simul. 2017, 134, 1–16. [Google Scholar] [CrossRef]
- Caruntu, B.; Bota, C.; Bundau, O. Analytical simulation of magneto-hemodynamic flow in a semi-porous channel using the Polynomial Least Squares Method. ITM Web Conf. 2019, 29, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Skalak, F.M.; Wang, C.Y. On the non-unique solutions of laminar flow through a porous tube or channel. SIAM J. Appl. Math. 1978, 34, 535–544. [Google Scholar] [CrossRef]
- Quaile, J.P.; Levy, E.K. Laminar flow in a porous tube with suction. Int. J. Heat Mass Transf. 1975, 97, 223–243. [Google Scholar] [CrossRef]
- Evans, E.A.; Skalak, R. Mechanics and Thermodynamics of Biomembranes. In Elsevier Biomedical; Hue, L., Van de Werve, G., Eds.; Elsevier Biomedical: Amsterdam, NY, USA, 1981; 464p. [Google Scholar]

| y | |||||||
|---|---|---|---|---|---|---|---|
| 0.1 | |||||||
| 0.2 | |||||||
| 0.3 | |||||||
| 0.4 | |||||||
| 0.5 | |||||||
| 0.6 | |||||||
| 0.7 | |||||||
| 0.8 | |||||||
| 0.9 |
| y | |||||||
|---|---|---|---|---|---|---|---|
| 0.1 | |||||||
| 0.2 | |||||||
| 0.3 | |||||||
| 0.4 | |||||||
| 0.5 | |||||||
| 0.6 | |||||||
| 0.7 | |||||||
| 0.8 | |||||||
| 0.9 |
| y | |||||||
|---|---|---|---|---|---|---|---|
| 0.1 | |||||||
| 0.2 | |||||||
| 0.3 | |||||||
| 0.4 | |||||||
| 0.5 | |||||||
| 0.6 | |||||||
| 0.7 | |||||||
| 0.8 | |||||||
| 0.9 |
| y | |||||||
|---|---|---|---|---|---|---|---|
| 0.1 | |||||||
| 0.2 | |||||||
| 0.3 | |||||||
| 0.4 | |||||||
| 0.5 | |||||||
| 0.6 | |||||||
| 0.7 | |||||||
| 0.8 | |||||||
| 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paşca, M.S.; Bundău, O.; Juratoni, A.; Căruntu, B. The Least Squares Homotopy Perturbation Method for Systems of Differential Equations with Application to a Blood Flow Model. Mathematics 2022, 10, 546. https://doi.org/10.3390/math10040546
Paşca MS, Bundău O, Juratoni A, Căruntu B. The Least Squares Homotopy Perturbation Method for Systems of Differential Equations with Application to a Blood Flow Model. Mathematics. 2022; 10(4):546. https://doi.org/10.3390/math10040546
Chicago/Turabian StylePaşca, Mădălina Sofia, Olivia Bundău, Adina Juratoni, and Bogdan Căruntu. 2022. "The Least Squares Homotopy Perturbation Method for Systems of Differential Equations with Application to a Blood Flow Model" Mathematics 10, no. 4: 546. https://doi.org/10.3390/math10040546
APA StylePaşca, M. S., Bundău, O., Juratoni, A., & Căruntu, B. (2022). The Least Squares Homotopy Perturbation Method for Systems of Differential Equations with Application to a Blood Flow Model. Mathematics, 10(4), 546. https://doi.org/10.3390/math10040546







