Relationship between the Mandelbrot Algorithm and the Platonic Solids
Abstract
1. Introduction
2. The Algebra of Tricomplex Numbers
2.1. Definitions and Basics
2.2. Idempotent Representations of a Tricomplex Number
3. Geometrical Characterizations
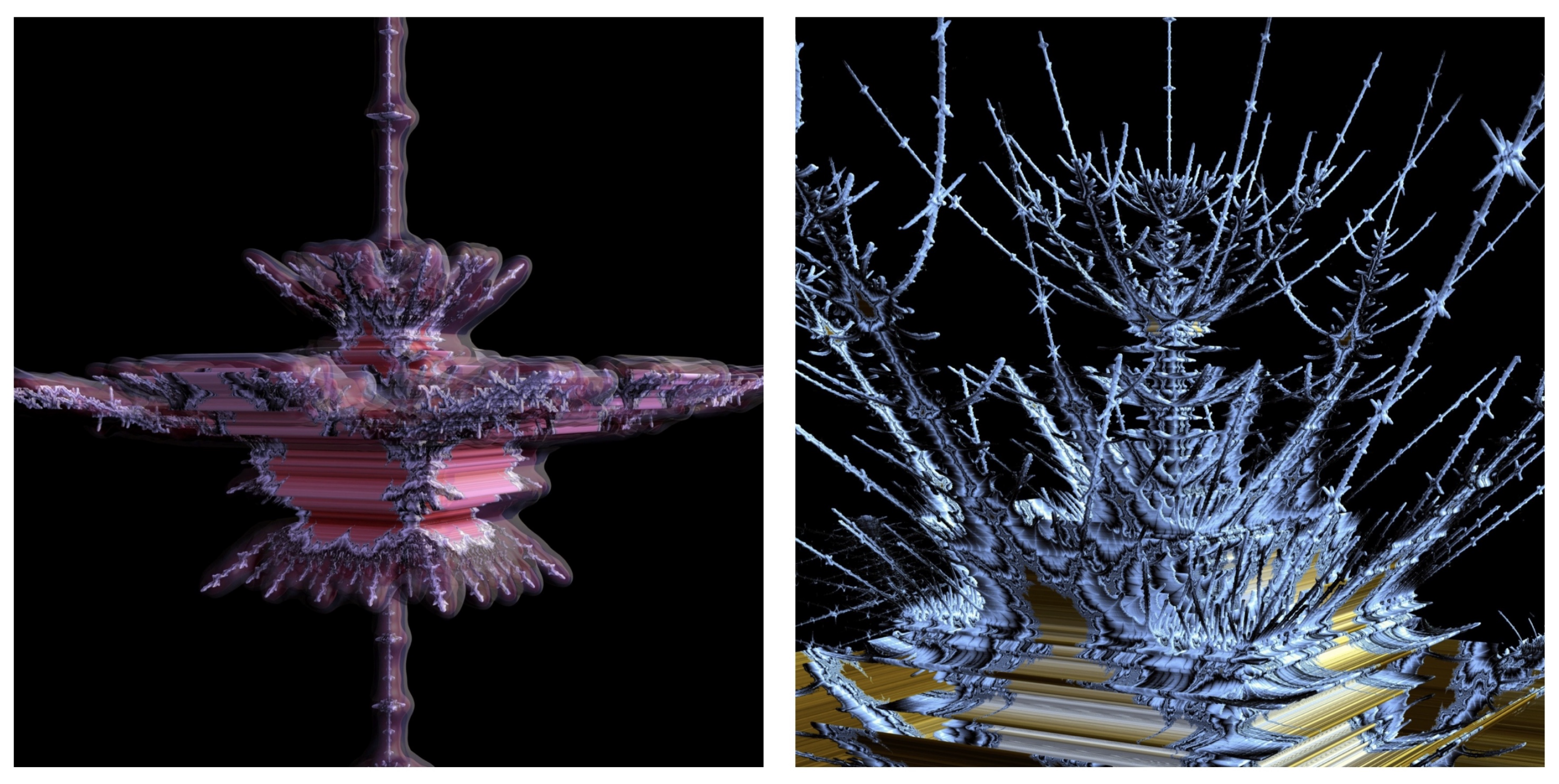
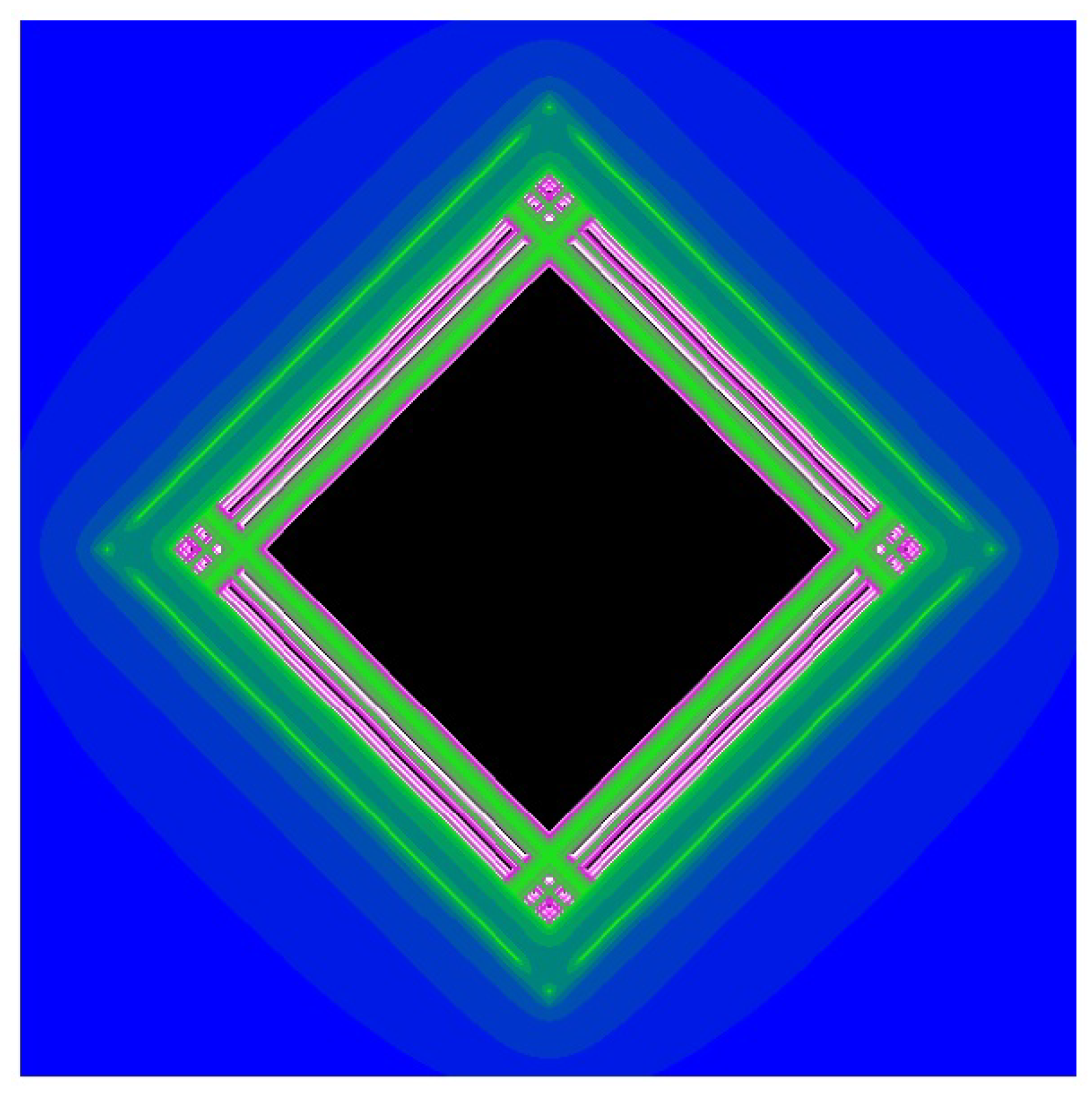
3.1. The Tricomplex Mandelbrot Set
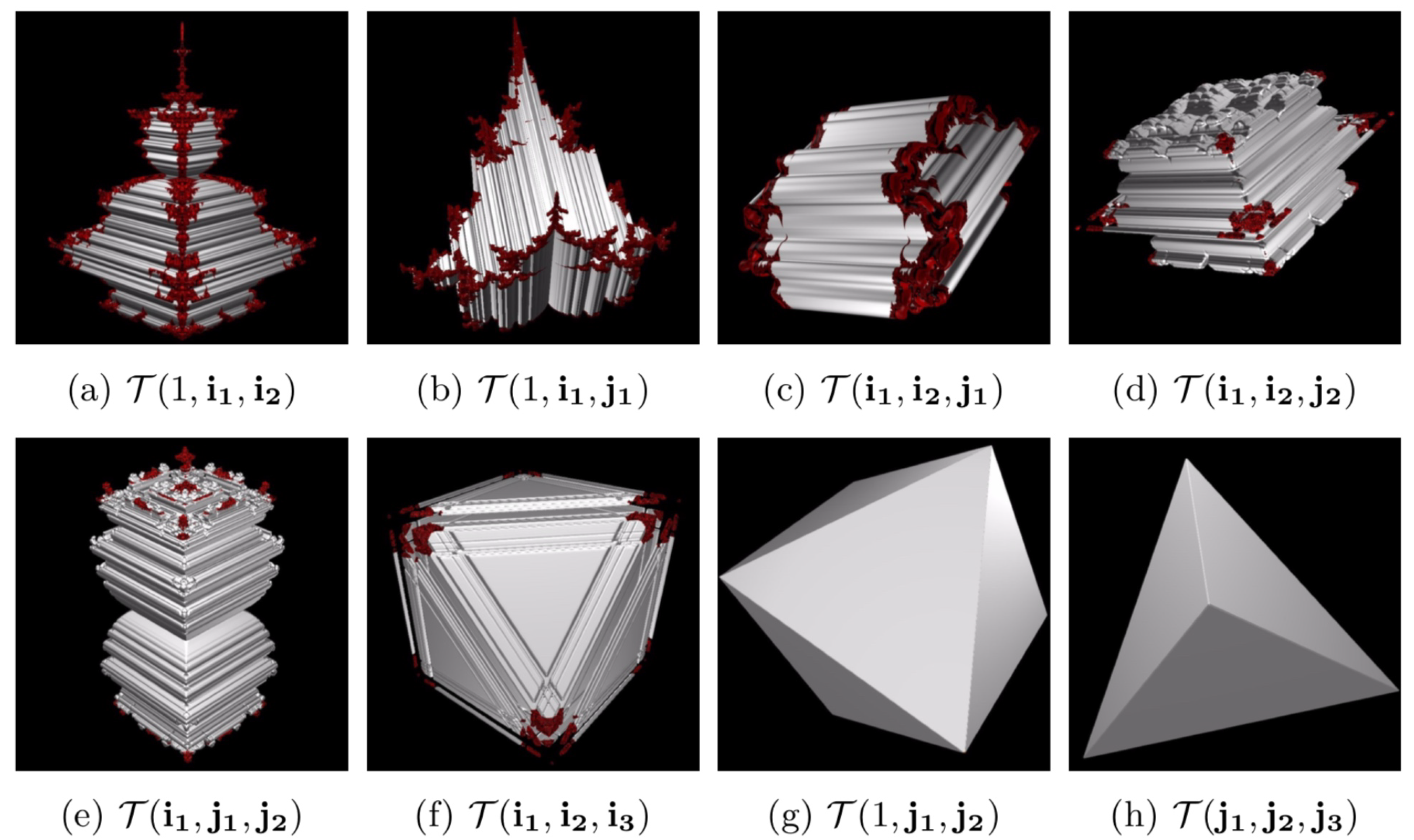
3.2. Characterizations of the Principal 3D Slices
4. The Cube and the Stellated Octahedron
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bedding, S.; Briggs, K. Iteration of Quaternion Maps. Int. J. Bifurc. Chaos 1995, 5, 877–881. [Google Scholar] [CrossRef]
- Brouillette, G.; Rochon, D. Characterization of the Principal 3D Slices Related to the Multicomplex Mandelbrot Set. Adv. Appl. Clifford Algebr. 2019, 29, 39. [Google Scholar] [CrossRef]
- Dang, Y.; Kauffman, L.H.; Sandin, D.J. Hypercomplex Iterations: Distance Estimation and Higher Dimensional Fractals; World Scientific: Singapore, 2002. [Google Scholar]
- Garant-Pelletier, V.; Rochon, D. On a generalized Fatou-Julia theorem in multicomplex spaces. Fractals 2009, 17, 241–255. [Google Scholar] [CrossRef]
- Katunin, A. A Concise Introduction to Hypercomplex Fractals; CRC Press (Taylor & Francis Group): Boca Raton, FL, USA, 2017. [Google Scholar]
- Norton, A. Generation and Display of Geometric Fractals in 3-D. Comput. Graph. 1982, 16, 61–67. [Google Scholar] [CrossRef]
- Rochon, D. A generalized Mandelbrot set for bicomplex numbers. Fractals 2000, 8, 355–368. [Google Scholar] [CrossRef]
- Senn, P. The Mandelbrot set for binary numbers. Am. J. Phys. 1990, 58, 1018. [Google Scholar] [CrossRef]
- Wang, X.Y.; Song, W.J. The generalized M–J sets for bicomplex numbers. Nonlinear Dyn. 2013, 72, 17–26. [Google Scholar] [CrossRef]
- Wang, X.Y.; Sun, Y.Y. The general quaternionic M–J sets on the mapping z ← zα + c (α ∈ N). Comput. Math. Appl. 2007, 53, 1718–1732. [Google Scholar] [CrossRef]
- Barrallo, J. Expanding the Mandelbrot Set into Higher Dimensions. In Bridges 2010: Mathematics, Music, Art, Architecture, Culture; The Bridges Organisation: Kansas, MO, USA, 2010. [Google Scholar]
- Fishback, P.E.; Horton, M.D. Quadratic dynamics in matrix rings: Tales of ternary number systems. Fractals 2005, 13, 147–156. [Google Scholar] [CrossRef]
- Garg, A.; Agrawal, A.; Negi, A. Construction of 3D Mandelbrot Set and Julia Set. Int. J. Comput. Appl. 2014, 85, 32–36. [Google Scholar]
- Rochon, D. On a generalized Fatou-Julia theorem. Fractals 2003, 11, 213–219. [Google Scholar] [CrossRef]
- Parisé, P.O.; Rochon, D. Tricomplex dynamical systems generated by polynomials of odd degree. Fractals 2017, 25, 1750026. [Google Scholar] [CrossRef]
- Parisé, P.O.; Ransford, T.; Rochon, D. Tricomplex dynamical systems generated by polynomials of even degree. Chaotic Model. Simul. 2017, 1, 37–48. [Google Scholar]
- Parisé, P.O.; Rochon, D. A Study of Dynamics of the Tricomplex Polynomial ηp + c. Nonlinear Dyn. 2015, 82, 157–171. [Google Scholar] [CrossRef]
- Brouillette, G. Classification des Coupes Tridimensionnelles Principales des Multibrots Multicomplexes. Master’s Thesis, Université du Québec à Trois-Rivières, Trois-Rivières, QC, Canada, 2019. [Google Scholar]
- Daintith, J. A Dictionary of Chemistry, 6th ed.; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Domokos, G.; Jerolmack, D.; Kun, F.; Török, J. Plato’s cube and the natural geometry of fragmentation. Proc. Natl. Acad. Sci. USA 2020, 117, 18178–18185. [Google Scholar] [CrossRef]
- Tang, M.; Liang, Y.; Lu, X.; Miao, X.; Jiang, L.; Liu, J.; Bian, L.; Wang, S.; Wu, L.; Liu, Z. Molecular-strain engineering of double-walled tetrahedra. Chem 2021, 7, 2160–2174. [Google Scholar] [CrossRef]
- Segre, C. The real representation of complex elements and hyperalgebraic entities. Math. Ann. 1892, 40, 413–467. (In Italian) [Google Scholar] [CrossRef]
- Price, G.B. An Introduction to Multicomplex Spaces and Functions; M. Dekker: New York, NY, USA, 1991. [Google Scholar]
- Luna-Elizarraras, M.E.; Shapiro, M.; Struppa, D.C.; Vajiac, A. Bicomplex Holomorphic Functions: The Algebra, Geometry and Analysis of Bicomplex Numbers; Frontiers in Mathematics; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Rochon, D. Sur une Généralisation des Nombres Complexes: Les Tétranombres. Master’s Thesis, Université de Montréal, Montréal, QC, Canada, 1997. [Google Scholar]
- Rochon, D. A Bloch constant for hyperholomorphic functions. Complex Var. 2001, 44, 85–201. [Google Scholar] [CrossRef]
- Rochon, D.; Shapiro, M. On algebraic properties of bicomplex and hyperbolic numbers. Anal. Univ. Oradea, Fasc. Math 2004, 11, 110. [Google Scholar]
- Cockle, J. On certain functions resembling quaternions, and on a new imaginary in algebra. Lond. Edinburg Dublin Philos. Mag. J. Sci. 1848, 33, 435–439. [Google Scholar] [CrossRef]
- Cockle, J. On a new imaginary in algebra. Lond. Edinburg Dublin Philos. Mag. J. Sci. 1849, 34, 37–47. [Google Scholar] [CrossRef]
- Cockle, J. On the symbols of algebra, and on the theory of tessarines. Lond. Edinburg Dublin Philos. Mag. J. Sci. 1849, 34, 406–410. [Google Scholar] [CrossRef][Green Version]
- Cockle, J. On impossible equations, on impossible quantities, and on tessarines. Lond. Edinburg Dublin Philos. Mag. J. Sci. 1850, 37, 281–283. [Google Scholar] [CrossRef][Green Version]
- Sobczyk, G. The Hyperbolic Number Plane. Coll. Math. J. 1995, 26, 268–280. [Google Scholar] [CrossRef]
- Struppa, D.C.; Vajiac, A.; Vajiac, M.B. Holomorphy in Multicomplex Spaces. In Spectral Theory, Mathematical System Theory, Evolution Equations, Differential and Difference Equations; Springer: Berlin/Heidelberg, Germany, 2012; pp. 617–634. [Google Scholar]
- Vajiac, A.; Vajiac, M.B. Multicomplex hyperfunctions. Complex Var. Elliptic Equ. 2012, 57, 751–762. [Google Scholar] [CrossRef]
- Vallières, A. Dynamique Tricomplexe et Solides de Platon. Master’s Thesis, Université du Québec à Trois-Rivières, Trois-Rivières, QC, Canada, 2021. [Google Scholar]
- Garant-Pelletier, V. Ensembles de Mandelbrot et de Julia Classiques, Généralisés aux Espaces Multicomplexes et Théorème de Fatou-Julia Généralisé. Master’s Thesis, Université du Québec à Trois-Rivières, Trois-Rivières, QC, Canada, 2011. [Google Scholar]
- Matteau, C.; Rochon, D. The Inverse Iteration Method for Julia Sets in the 3-Dimensional Space. Chaos Solitons Fractals 2015, 75, 272–280. [Google Scholar] [CrossRef][Green Version]
- Carleson, L.; Gamelin, T.W. Complex Dynamics, 1st ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Shapiro, M.; Struppa, D.C.; Vajiac, A.; Vajiac, M.B. Hyperbolic numbers and their functions. Anal. Univ. Oradea 2012, 19, 265–283. [Google Scholar]
- Metzler, W. The “mystery” of the quadratic Mandelbrot set. Am. J. Phys. 1994, 62, 813–814. [Google Scholar] [CrossRef]
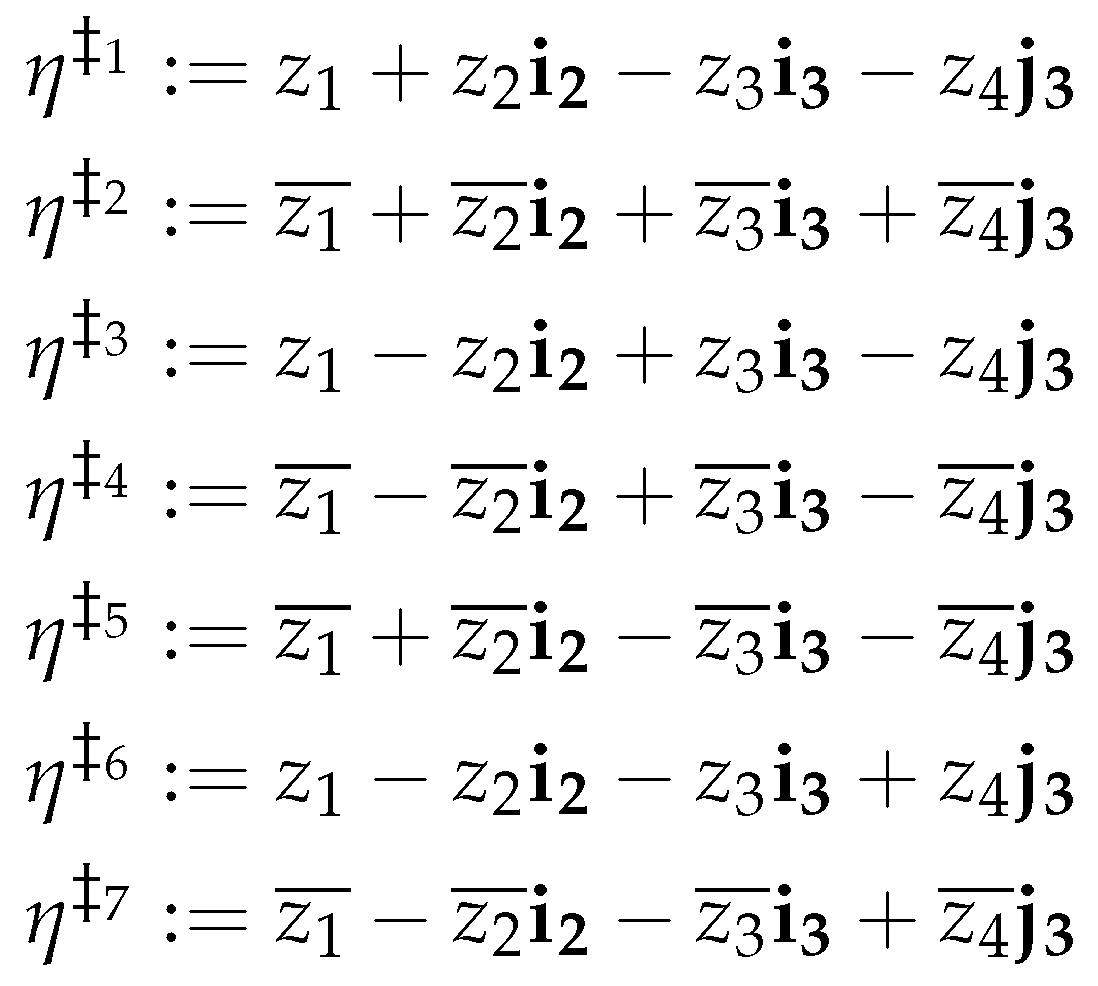



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallières, A.; Rochon, D. Relationship between the Mandelbrot Algorithm and the Platonic Solids. Mathematics 2022, 10, 482. https://doi.org/10.3390/math10030482
Vallières A, Rochon D. Relationship between the Mandelbrot Algorithm and the Platonic Solids. Mathematics. 2022; 10(3):482. https://doi.org/10.3390/math10030482
Chicago/Turabian StyleVallières, André, and Dominic Rochon. 2022. "Relationship between the Mandelbrot Algorithm and the Platonic Solids" Mathematics 10, no. 3: 482. https://doi.org/10.3390/math10030482
APA StyleVallières, A., & Rochon, D. (2022). Relationship between the Mandelbrot Algorithm and the Platonic Solids. Mathematics, 10(3), 482. https://doi.org/10.3390/math10030482






