The Sehgal’s Fixed Point Result in the Framework of ρ-Space

Abstract

In this paper, we prove a fixed point theorem of Sehgal type (see Sehgal, V.M., Proc Amer Math Soc 23: 631–634, 1969) in a more general setting of $\rho$-space (see Secelean, N.A. and Wardowski, D., Results Math, 72: 919–935, 2017). In this way, we can find, as particular cases, some results of Sehgal type in metric, b-metric and rectangular b-metric spaces.

1. Introduction

In 1969 Sehgal [1] proved a fixed point theorem for mappings with a contractive iterate at a point, which generalized the Banach contraction principle as follows: if T is a continuous self-map on a complete metric space $(X,\mathrm{d})$ and $\lambda \in (0,1)$ such that, for each $x\in X$, there exists $N=N\left(x\right)\in \mathbb{N}$ such that

$$\mathrm{d}(T^{N}x,T^{N}y)\le \lambda \mathrm{d}(x,y),\forall y\in X,$$

(1)

then T has a unique fixed point that is approximated by $\left(T^{n}x\right)$ for all $x\in X$.

Following Sehgal’s idea, many authors improved this result by eliminating the continuity condition and generalizing the right-hand side of (1) or extending the space where the function T is defined (see [2,3,4,5,6,7,8] and the references given there).

In [8] Mitrovi et al. investigated the general case when, given some map $T:X\to X$ and $\lambda \in (0,1)$, we have the following property: for every two elements $x,y$ in a complete metric space $(X,\mathrm{d})$, there exists $N=N(x,y)$ such that

$$\mathrm{d}(T^{N}x,T^{N}y)\le \lambda \mathrm{d}(x,y).$$

Using a counterexample, they showed that, in this case, T does not necessarily have a fixed point.

Our purpose in this paper is to improve the fixed point theorem of Sehgal in a more general setting. Thus, some existing results in the current literature on this topic can be obtained as particular cases from our main result stated as Theorem 1.

2. Preliminaries

The concept of dislocated metric was introduced by Hitzler and Seda in [9]. Very recently, Alghamdi et al. [10] generalized dislocated metric spaces and introduced the notion of dislocated b-metric space (b-metric-like space). In 2000, Branciari [11] defined rectangular metric space (RMS for short). This concept is interesting because RMS does not necessarily have a compatible topology. Next, combining the notions of b-metric space and RMS, George et al. [12] defined rectangular b-metric spaces (R-bMS for short). Recently, Golhare and Aage [13] introduced the notion of the dislocated rectangular b-metric.

For our purpose we will provide a new notion, in which a weaker version of the symmetry condition will suffice.

Definition 1.

Let X be a nonempty set and $d:X\times X\to [0,\infty )$ a mapping. We consider the following conditions for some $s\ge 1$ and every $x,y,z\in X$:

(d1) $d(x,y)=0\Rightarrow x=y$;

(d1${}^{\prime }$) $d(x,x)=0$;

(d2) if $\left(x_n\right)\subset X$, one has $[{lim}_{n}d(x_n,x)=d(x,x)\iff {lim}_{n}d(x,x_n)=d(x,x)]$;

(d3) $d(x,z)\le s\left[d\right(x,y)+d(y,z\left)\right]$;

(d4) $d(x,y)\le s\left[d\right(x,u)+d(u,v)+d(v,y\left)\right]$ for all $u,v\in X\backslash \{x,y\}$, $u\ne v$.

If d satisfies (d1), (d2), (d3), then the pair $(X,d)$ is called a weak dislocated b-metric space with constant s and, if $s=1$, it is called aweak dislocated metric space. We say that $(X,d)$ is aweak dislocated rectangular b-metric spacewith constant s whenever the axioms (d1), (d2), (d4) hold. If $(X,d)$ satisfies, additionally, (d1${}^{\prime }$), they are called aweak b-metric space, weak metric space, and a weak rectangular metric space, respectively.

Remark 1.

Let X be a nonempty set and $d:X\times X\to [0,\infty )$ be a function. If $m:=inf\left\{d\right(x,y):x,y\in X,x\ne y\}>0$ and $M:=sup\left\{d\right(x,y):x,y\in X\}<\infty$, then d satisfies (d4) for $s=max\{1,\frac{M}{3m}\}$.

Proof. 

Choose $x,y\in X$ and $u,v\in X\backslash \{x,y\}$, $u\ne v$. The assertion follows immediately from the inequalities

$$d(x,y)\le M\le s·3m\le s\left[d\right(x,u)+d(u,v)+d(v,y\left)\right].$$

□

Example 1.

Let us consider $X=[0,\infty )$ and the mapping $d:X\times X\to [0,\infty )$ defined by

$$d(x,y)=\left\{\begin{array}{cc}x,& \mathrm{if}x=y,\hfill \\ {(x-y)}^2+x,& \mathrm{if}x>y,\hfill \\ {(x-y)}^4+y,& \mathrm{if}x<y.\hfill \end{array}\right.$$

Then $(X,d)$ is a weak dislocated b-metric space with the constant $s=8$. Moreover, d is asymmetric and $d(x,x)\ne 0$ for all $x>0$.

Proof. 

Clearly, (d1) holds.

To prove (d2), consider a sequence $\left(x_n\right)$ in X and $x\in X$.

Suppose that ${lim}_{n}d(x_n,x)=d(x,x)$. Then, for every $\epsilon >0$ there exists $N\in \mathbb{N}$ such that $|d(x_n,x)-d(x,x)|<\epsilon$ for all $n\ge N$. One has

$$|d(x_n,x)-d(x,x)|=d(x_n,x)-x=\left\{\begin{array}{cc}0,& \mathrm{if}x=x_n,\hfill \\ {(x_n-x)}^2+x_n-x,& \mathrm{if}x<x_n,\hfill \\ {(x_n-x)}^4,& \mathrm{if}x>x_n\hfill \end{array}\right.$$

and so

$$|d(x_n,x)-d(x,x)|<\epsilon \iff \left\{\begin{array}{c}(x_n-x)(x_n-x+1)<\epsilon \mathrm{or}\hfill \\ {(x_n-x)}^4<\epsilon \hfill \end{array}\right.$$

for all $n\ge \mathrm{N}$. It follows that

$$\underset{n}{lim}d(x_n,x)=d(x,x)\iff |x_n-x|\to 0.$$

(2)

Analogously, one can prove that

$$\underset{n}{lim}d(x,x_n)=d(x,x)\iff |x_n-x|\to 0.$$

(3)

Next, from ${(a+b)}^2\le 2(a^2+b^2)$ we obtain ${(a+b)}^4\le 4{(a^2+b^2)}^2\le 8(a^4+b^4)$. Therefore a trivial verification shows that (d3) holds. □

Remark 2.

1. The symmetry of the function d implies condition (d2), the converse implication is not generally true, as it follows from the previous example.

2. Obviously, the following implications hold: weak (dislocated) metric space ⇒ weak (dislocated) b-metric space ⇒ weak (dislocated) rectangular b-metric space.

Definition 2.

Let $(X,d)$ be a weak dislocated rectangular b-metric space. We say that a sequence $\left(x_n\right)\subset X$convergesto some $x\in X$ if $d(x_n,x)\to d(x,x)$. We denote this by $x_n\to x$.

In particular, if $(X,d)$ is a weak rectangular b-metric space, then $x_n\to x$ if $d(x_n,x)\to 0$.

Definition 3.

We say that the sequence $\left(x_n\right)$ in a weak rectangular metric space $(X,d)$ isCauchyif $d(x_n,x_m)\underset{n,m}{⟶}0$.

$(X,d)$ is calledcompleteif every Cauchy sequence converges to some $x\in X$.

Samet [14] showed, using a counterexample, that, in an RMS convergence does not imply Cauchyness and the function d is not necessarily continuous. In a complete RMS every Cauchy sequence of distinct points has a unique limit (see ([15], Lemma 1.10), ([16], Proposition 3.4)).

Strong $\rho$-Metric Spaces

Motivated by the notion of $\rho \text{-}$space introduced by Secelean and Wardowski in [17], we present a notion of strong $\rho \text{-}$metric spaces.

Let X be a non-empty set and a function $\rho :X\times X\backslash \Delta \to \mathbb{R}$, where $\Delta :=\left\{(x,x):x\in X\right\}$.

We say that a sequence $\left(x_n\right)\subset X$ backward (respectively forward) ρ-converges to some $x\in X$ whenever, for each $\epsilon >0$, there exists $n_{\epsilon }>0$ such that, for every $n\ge n_{\epsilon }$, we have

$$x_n\ne x\Rightarrow \rho (x,x_n)<-\epsilon (\mathrm{resp}.\rho (x_n,x)<-\epsilon ).$$

We denote $x_n\to x$ or ${lim}_n{x}_n=x$ as usually.

Throughout the paper we will use only backward $\rho$-convergence, therefore, for simplicity, we will omit “backward”.

Remark 3.

$1^0$. If, in the above setting, $\left(x_n\right)\subset X$ is stationary (i.e., there exist $x\in X$ and $N\in \mathbb{N}$ such that $x_n=x$ for all $n\ge N$), then it converges to x. Additionally, if $\left(x_n\right)$ is such that $x_n\ne x$ for all n greater than some $N\in \mathbb{N}$, then

$$x_n\to x\iff \rho (x,x_n)\to -\infty .$$

(4)

$2^0$. If the set $A=\{k\in \mathbb{N}:x_k\ne x\}$ is infinite and $\rho (x,x_k)\underset{k\in A}{⟶}-\infty$, then $x_n\to x$.

For the following we will need a stronger version of the $\rho$-metric concept.

Definition 4.

We say that ρ is astrong $\rho$-metricand $(X,\rho )$ is astrong $\rho$-space($s\rho$-space for short) if, for every two convergent sequences $\left(x_n\right)$, $\left(y_n\right)$ in X, $x_n\ne y_n$ for all n, such that ${lim}_n\rho (x_n,y_n)=-\infty$, one has ${lim}_n{x}_n={lim}_n{y}_n$.

Example 2.

If $\alpha >0$, then the function $\rho :\mathbb{R}\times \mathbb{R}\backslash \Delta \to \mathbb{R}$ given by

$$\rho (x,y)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{x-y},}\hfill & \mathrm{if}y>x\hfill \\ {\displaystyle \frac{\alpha }{y-x},}\hfill & \mathrm{if}y<x\hfill \end{array}\right.$$

is a strong ρ-metric on $\mathbb{R}$ which is asymmetric provided $\alpha \ne 1$.

Proof. 

Let us consider the sequences $\left(x_n\right)$, $\left(y_n\right)$ in $\mathbb{R}$ such that $x_n\ne y_n$ for all n, $x_n\to x$, $y_n\to y$ with respect to $\rho$ and $\rho (x_n,y_n)\to -\infty$.

Then it is obvious that $|x_n-x|\to 0$, $|y_n-y|\to 0$ and $|x_n-y_n|\to 0$ (in Euclidean metric). Hence $x=y$. □

Remark 4.

In an $s\rho$-space every convergent sequence has a unique limit, so it is a ρ-space (as it is defined in [17]).

Proof. 

Assume that $\left(y_n\right)$ is a convergent sequence and $x,y$ are its two limits, $x\ne y_n\ne y$ for all $n\in \mathbb{N}$. Then, considering the constant sequence $x_n=x$, $n=1,2,\dots$, one has ${lim}_n{x}_n=x$ and ${lim}_n\rho (x_n,y_n)={lim}_n\rho (x,y_n)=-\infty$. Therefore, by the assumption, $x={lim}_n{x}_n={lim}_n{y}_n=y$. □

Definition 5.

Let$(X,\rho )$be an$s\rho$-space. A sequence$\left(x_n\right)\subset X$of distinct elements is said to be$\rho$-forward-Cauchywhenever

$$\rho (x_n,x_{n+p})\underset{n,p}{⟶}-\infty .$$

We say that $(X,\rho )$ isforward-completeif every ρ-forward-Cauchy sequence ρ-converges. An analogous definition can be formulated forbackward-completeness.

Numerous examples of $s\rho$-spaces can be given (see [17]). For this purpose, we denote by $\mathcal{F}$ the family of all mappings $F:(0,\infty )\to \mathbb{R}$ such that

$$\forall \left(x_n\right)\subset (0,\infty ),F\left(x_n\right)\to -\infty \iff x_n\to 0.$$

(5)

Note that, if there exists $\epsilon >0$ such that a function $F:(0,\infty )\to \mathbb{R}$ is increasing on $(0,\epsilon )$, then $F\in \mathcal{F}$ if and only if $infF=-\infty$ (according to ([18], Remark 3.1)).

Few examples of such functions can be found in [18,19].

Example 3.

If $(X,d)$ is a weak b-metric space, then $\rho (x,y):=F\left(d(x,y)\right)$ for all $x\ne y$, is an $s\rho$-space. In particular, if d is a weak (standard) metric, then ρ is a strong ρ-metric. Thus, for $x,y\in X$, $x\ne y$, the functions $\rho (x,y):=lnd(x,y)$, $\rho (x,y):=-d{(x,y)}^{-\alpha }$, $\alpha >0$, $\rho (x,y):=d(x,y)-d{(x,y)}^{-1}$, $\rho (x,y):={[1-e^{d(x,y)}]}^{-1}$, $\rho (x,y):=lnd(x,y)+d(x,y)$, $\rho (x,y):=ln\left(\frac{d(x,y)}{3}+sind(x,y)\right)$, $\rho (x,y):=tan\left(\frac{\pi x}{x+1}+\frac{\pi }{2}\right)$ are just few examples of strong ρ-metrics (notice that, since $x\ne y\Rightarrow d(x,y)>0$, the composition $F\circ d$ is well defined).

Furthermore, if $(X,d)$ is complete, then $(X,\rho )$ is complete, as well.

In the following we give an example of $s\rho$-space obtained from a weak dislocated b-metric space. An $s\rho$-space coming from a weak dislocated rectangular metric space can be found in Example 7.

Example 4.

Let us consider the weak dislocated b-metric space $(X,d)$ given in Example 1, a function $F\in \mathcal{F}$ and define $\rho :X\times X\backslash \Delta \to \mathbb{R}$, $\rho (x,y)=F\left(\left|d\right(x,y)-d(x,x\left)\right|\right)$ for all $x,y\in X$, $x\ne y$. Then $(X,\rho )$ is an $s\rho$-space. Furthermore, $(X,\rho )$ is both ρ-forward and ρ-backward complete.

Proof. 

Let us consider $\left(x_n\right),\left(y_n\right)\subset X$ such that $x_n\ne y_n$ for every n, and ${lim}_n\rho (x_n,y_n)=-\infty$. Then

$$|d(x_n,y_n)-d(x_n,x_n)|=|d(x_n,y_n)-x_n|=\left\{\begin{array}{cc}{(x_n-y_n)}^2,\hfill & \mathrm{if}{x}_n>y_n\hfill \\ {(x_n-y_n)}^4+y_n-x_n,\hfill & \mathrm{if}{x}_n<y_n.\hfill \end{array}\right.$$

Hence

$$\underset{n}{lim}\rho (x_n,y_n)=-\infty \iff \underset{n}{lim}|x_n-y_n|=0.$$

(6)

Let $x\in X,{lim}_n\rho (x,x_n)=d(x,x)$. Then, from (3), it follows that $x_n\to x$ (in Euclidean metric) so, using (6), one has $y_n\to x$ (in Euclidean metric). Using, again, (3) we obtain ${lim}_{n}d(x,y_n)=d(x,x)$, so ${lim}_n{x}_n={lim}_n{y}_n$.

Thus $\rho$ is a strong $\rho$-metric.

In order to prove the completeness, let $\left(x_n\right)$ be a $\rho$-forward Cauchy sequence. Then $x_n\ne x_m$ for every $n\ne m$ and, as before, one has

$$\rho (x_n,x_{n+p})\underset{n,p}{⟶}-\infty \iff \underset{n,p}{lim}|d(x_n,x_{n+1})-x_n|=0.$$

Thus $\left(x_n\right)$ is a Cauchy sequence with respect to Euclidean metrics, hence, there is $x\in X$ such that $|x_n-x|\to 0$. From (3), it follows that $\rho (x,x_n)\to -\infty$ so $\left(x_n\right)$ $\rho$-converges to x.

Analogously we can show that $(X,\rho )$ is backward complete. □

Example 5.

Let $(X,d)$ be a weak rectangular b-metric space such that every convergent sequence has a unique limit and $F\in \mathcal{F}$. Then $\rho :=F\circ d$ is a strong ρ-metric on X. If $(X,d)$ is complete, then $(X,\rho )$ is complete as well.

Proof. 

Clearly, for a sequence $\left(x_n\right)$ one has $x_n\stackrel{\rho }{⟶}x$, $x\in X$, if and only if $d(x,x_n)\to 0$.

Let $\left(x_n\right),\left(y_n\right)\subset X$, $x,y\in X$, $x_n\ne y_n$ for all n, and assume that $x_n\stackrel{\rho }{⟶}x$, $y_n\stackrel{\rho }{⟶}y$ and ${lim}_n\rho (x_n,y_n)=-\infty$. Then

$$\underset{n}{lim}d(x,x_n)=\underset{n}{lim}d(y,y_n)=\underset{n}{lim}d(x_n,y_n)=0.$$

Two cases can occur.

Case I: There exists $N\in \mathbb{N}$ such that $x_n=x$ for all $n\ge N$. Since ${lim}_{n}d(x_n,y_n)=0={lim}_{n}d(x,y_n)$, we deduce that ${lim}_n{y}_n=x$. Thus, by the uniqueness of the limit of $\left(y_n\right)$, it follows that $x=y$.

Case II: $x_n\ne x$ and $y_n\ne y$ for all n. In this case we have

$$d(x,y)\le s[d(x,x_n)+d(x_n,y_n)+d(y_n,y)]\underset{n\to \infty }{⟶}0,$$

so $x=y$.

Case III: When $\left(y_n\right)$ is stationary we proceed as in the first case. □

3. Results

Let $(X,\rho )$ be a strong $\rho$-space and $T:X\to X$ be a mapping. We say that T is a Picard operator (P.O. for short) if it has a unique fixed point $\xi \in X$ and $\left(T^{n}x\right)$ converges to $\xi$ for every $x\in X$, where we denote by $T^n$ the n-fold composition of T.

Definition 6.

For a mapping $T:X\to X$ and $x_0\in X$, theorbitof T starting at the point $x_0$ is the set $\mathcal{O}(T,x_0)=\{x_0,T{x}_0,T^2{x}_0,\cdots \}.$

The $s\rho$-space X isforward-T-orbitally completestarting at $x_0$ if every ρ-forward-Cauchy sequence of the distinct elements of the form ${\left(T^{n_k}{x}_0\right)}_k$ converges in X.

Let $\Psi$ denote the family of all non-decreasing maps $\psi :(-\infty ,\mu )\to \mathbb{R}$ such that ${\psi }^n\left(t\right)\to -\infty$ for all $t\in (-\infty ,\mu )$, where $\mu >{sup}_{x\ne y\in X}\rho (x,y)$. We adopt the convention that $\mu >\infty$ means $\mu =\infty$.

Remark 5.

1^o If $\psi \in \Psi$, then $\psi \left(t\right)<t$ for all $t\in (-\infty ,\mu )$.

2^o ([17], Lemma 2.1) If $\psi :(-\infty ,\mu )\to \mathbb{R}$, $\mu \in \mathbb{R}$, is a non-decreasing and upper semi-continuous mapping with $\psi \left(t\right)<t$ for all $t<\mu$, then $\psi \in \Psi$.

Proof. 

$1^0$ If there is $t_0\in (-\infty ,\mu )$ such that $\psi \left(t_0\right)\ge t_0$, then ${\psi }^2\left(t_0\right)\ge \psi \left(t_0\right)\ge t_0$ and, inductively, ${\psi }^n\left(t_0\right)\ge t_0$ for all $n\in \mathbb{N}$. This contradicts ${\psi }^n\left(t_0\right)\to -\infty$.

$2^0$ Set $t\in (-\infty ,\mu )$. We will show that ${lim}_n{\psi }^n\left(t\right)=-\infty$. Since ${\psi }^{n+1}\left(t\right)<{\psi }^n\left(t\right)$, for every $n\in \mathbb{N}$, the sequence $\left({\psi }^n\left(t\right)\right)$ is decreasing so it has a limit $l\in [-\infty ,\mu )$. If $l\in \mathbb{R}$, then $l\le {lim\; sup}_{t\to l}\psi \left(t\right)\le \psi \left(l\right)$ which is a contradiction. So $l=-\infty$. □

Notice that the previous remark offers a variety of mappings in the family $\Psi$, such as those having the form $\psi \left(t\right)=t-f\left(t\right)$, where f is a non-increasing, positive and continuous function.

Theorem 1.

Let $(X,\rho )$ be an $s\rho$-space and T a self mapping on X. Assume that the following conditions hold:

$\left(\alpha \right)$ there exists $\psi \in \Psi$ such that, for each $x\in X$, there is a positive integer $N=N\left(x\right)$ such that

$$\rho (T^{N}x,T^{N}y)\le \psi \left(\rho (x,y)\right)$$

(7)

for all $y\in X$ with $T^{N}x\ne T^{N}y$;

$\left(\beta \right)$ there exists $x_0\in X$ such that $M:={sup}_n\{\rho (x_0,T^n{x}_0):x_0\ne T^n{x}_0\}<\infty$;

$\left(\gamma \right)$ the space $(X,\rho )$ is ρ-forward-T-orbitally complete starting at $x_0$.

Then T is a P.O.

Proof. 

We will construct a successively approximation sequence for the fixed point of T.

Let us consider $x_0$ from $\left(\beta \right)$ and denote $N_1=N\left(x_0\right)$. Next, for each $k=1,2,\dots$, let

$$x_k:=T^{N_k}{x}_{k-1}=T^{{\sigma }_k}{x}_0,\mathrm{where}{N}_k=N\left(x_{k-1}\right),{\sigma }_k:=N_1+N_2+\cdots +N_k.$$

(8)

Denote $A:=\{(p,q)\in \mathbb{N}:x_p\ne x_q\}$.

If the set A is finite, then $\left(x_k\right)$ is stationary, hence, according to Remark 3, it is convergent.

Assume that A is infinite and we will prove that $\left(x_k\right)$ is $\rho$-forward-Cauchy.

For this purpose, choose $(k,p)\in A$, $k<p$, and let $\sigma :=N_{k+1}+\cdots +N_p$. Then, by (7) and (8), Remark 3 and hypothesis, one has

$$\rho (x_k,x_p)=\rho (T^{N_k}{x}_{k-1},T^{N_k+\sigma }{x}_{k-1})\le \psi \left(\rho (x_{k-1},T^{\sigma }{x}_{k-1})\right)$$

$$=\psi \left(\rho (T^{N_{k-1}}{x}_{k-2},T^{N_{k-1}+\sigma }{x}_{k-2})\right)\le {\psi }^2\left(\rho (x_{k-2},T^{\sigma }{x}_{k-2})\right)\le \dots$$

$$\le {\psi }^k\left(\rho (x_0,T^{\sigma }{x}_0)\right)\le {\psi }^k\left(M\right)\underset{\begin{array}{c}k,p\to \infty \\ (k,p)\in A\end{array}}{⟶}-\infty ,$$

hence the sequence $\left(x_k\right)$ is $\rho$-forward-Cauchy. Thus, $\left(x_k\right)$ is convergent. In both cases we denote by $\xi \in X$ its limit. We intend to prove that $\xi$ is the unique fixed point for T. For this, we first show that $\xi$ is a fixed point for $T^N$, where $N=N\left(\xi \right)$.

Set $B:=\{k\in \mathbb{N}:T^N\xi \ne T^N{x}_k\}$. If B is finite, then the sequence $\left(T^N{x}_k\right)$ is stationary, so it converges to $T^N\xi$.

Let us suppose that B is infinite. Then, using Remark 3, we have for $k\in B$

$$\rho (T^N\xi ,T^N{x}_k)\le \psi \left(\rho (\xi ,x_k)\right)<\rho (\xi ,x_k)\underset{\begin{array}{c}k\to \infty \\ k\in B\end{array}}{⟶}-\infty ,$$

so

$$\underset{k}{lim}{T}^N{x}_k=T^N\xi .$$

(9)

Two cases can occur:

Case I. If there is $k_0\in \mathbb{N}$ such that $T^N{x}_{k_0}=x_{k_0}$, then $\xi :=x_{k_0}$ is a fixed point for $T^N$.

Case II. Assume that $T^N{x}_k\ne x_k$ for all $k\ge 1$. Then

$$\rho (x_k,T^N{x}_k)=\rho (T^{N_k}{x}_{k-1},T^{N_k}{T}^N{x}_{k-1})\le \psi \left(\rho (x_{k-1},T^N{x}_{k-1})\right)\le \dots$$

$$\le {\psi }^k\left(\rho (x_0,T^N{x}_0)\right)\underset{k}{⟶}-\infty ,$$

hence

$$\underset{k}{lim}\rho (x_k,T^N{x}_k)=-\infty .$$

(10)

Since ${lim}_k{x}_k=\xi$, using (10) and Definition 4, it follows that ${lim}_k{T}^N{x}_k={lim}_k{x}_k=\xi$ which, together to (9), implies $T^N\xi =\xi$.

Consequently, in either case, $T^N$ has a fixed point. We now prove that $\xi$ is the unique fixed point of $T^N$. Indeed, if we suppose that $\eta$ is another fixed point of $T^N$, $\xi \ne \eta$, then one obtains

$$\rho (\xi ,\eta )=\rho (T^N\xi ,T^N\eta )\le \psi \left(\rho (\xi ,\eta )\right)<\rho (\xi ,\eta ),$$

a contradiction.

Next, from the equality $T^{N}T\xi =T{T}^N\xi =T\xi$ we deduce that $T\xi$ is a fixed point for $T^N$ hence, by the uniqueness, $T\xi =\xi$ assuring that $\xi$ is a fixed point for T. Since every fixed point of T is also a fixed point for $T^N$, the uniqueness follows.

It remains to prove that the sequence $\left(T^{n}x\right)$ converges to $\xi$ for all $x\in X$.

Let any $x\in X$. If there is $n_0\in \mathbb{N}$ such that $T^{n_0}x=\xi$, then $\left(T^{n}x\right)$ is stationary, hence it converges to $\xi$. Suppose that $T^{n}x\ne \xi$ for all $n\in \mathbb{N}$. Then, for every $n>N$, one can find $q\in \mathbb{N}$, $r\in \{0,1,\dots ,N-1\}$ such that $n=qN+r$. One has

$$\rho (\xi ,T^{n}x)=\rho (T^N\xi ,T^{qN+r}x)\le \psi \left(\rho (\xi ,T^{(q-1)N+r}x)\right)\le \dots$$

$$\le {\psi }^q\left(\rho (\xi ,T^{r}x)\right)\le {\psi }^q\left(\lambda \right)\to -\infty ,$$

where $\lambda :=max\{\rho (\xi ,T^{r}x):r=0,1,\dots ,N-1\}$.

Consequently, $\xi ={lim}_n{T}^{n}x$ completing the proof. □

Here are two examples to support the validity of Theorem 1.

Example 6.

Let $X=[0,\infty )$, $d:X\times X\to [0,+\infty )$ be defined by

$$d(x,y)=\left\{\begin{array}{cc}\frac{1}{2}(x-y),\hfill & x\ge y\hfill \\ \frac{1}{4}(y-x),\hfill & x<y.\hfill \end{array}\right.$$

Moreover, for every $x,y\in X$, $x\ne y$, we set $\rho (x,y)=lnd(x,y)$, $Tx=\frac{x}{2+x}$ and $\psi \left(t\right)=t-ln\lambda$ for $t\in \mathbb{R}$, where $\lambda \in (1,\infty )$. Then

(1) d is a weak (asymmetric) $b-$metric and $(X,\rho )$ is an $s\rho$-metric space;

(2) T is a P.O.

Proof. 

(1) From definition it follows that d satisfies axioms (d1) and (d2) (see Definition 1). Obviously, we have the following inequalities:

$$\frac{1}{2}(x-z)=\frac{1}{2}(x-y+y-z)\le \frac{1}{2}|x-y|+\frac{1}{2}|y-z|\le |x-y|+|y-z|$$

(11)

and

$$\frac{1}{4}(z-x)=\frac{1}{4}(z-y+y-x)\le \frac{1}{4}|z-y|+\frac{1}{4}|y-x|\le \frac{1}{2}|z-y|+\frac{1}{2}|y-x|.$$

(12)

Relation (11) assure that (d3) holds for $s=2$, such case includes three subcases: (i) $y>x>z$; (ii) $x>y>z$; (iii) $x>z>y$. Similarly, (12) contains the other three subcases: (i) $x<z<y$; (ii) $y<x<z$; (iii) $x<y<z$.

Combining these inequalities, we obtain $d(x,z)\le s\left[d\right(x,y)+d(y,z\left)\right]$ for all $x,y,z\in X$ with $s=2$.

The fact that $(X,\rho )$ is an $s\rho$-metric space follows from Example 3.

(2) We intend to apply Theorem 1. First observe that, from Remark 5, $2^0$, one has $\psi \in \Psi$. Obviously, T is increasing and it is easy to prove that

$$T^{n}x=\frac{x}{2^n+(2^n-1)x}\forall x\in X.$$

(13)

For every $x,y\in X$ with $x\ne y$ and $N\in \mathbb{N}$, we have

$$\rho (T^{N}x,T^{N}y)=ln\left(d(T^{N}x,T^{N}y)\right)$$

$$=\left\{\begin{array}{cc}{\displaystyle ln\frac{x-y}{2^{N+1}\left(1+(1-2^{-N})x\right)\left(1+(1-2^{-N})y\right)},}\hfill & x>y\hfill \\ {\displaystyle ln\frac{y-x}{2^{N+2}\left(1+(1-2^{-N})x\right)\left(1+(1-2^{-N})y\right)},}\hfill & x<y\hfill \end{array}\right.$$

and

$$\psi \left(\rho (x,y)\right)=\rho (x,y)-ln\lambda =lnd(x,y)-ln\lambda =\left\{\begin{array}{cc}{\displaystyle ln\frac{x-y}{2\lambda },}\hfill & x>y\hfill \\ {\displaystyle ln\frac{y-x}{4\lambda },}\hfill & x<y.\hfill \end{array}\right.$$

Since

$$\left(1+(1-2^{-N})x\right)\left(1+(1-2^{-N})y\right)>1,\forall x\ne y\in X,$$

we deduce that, for $N\ge {log}_2\lambda$, one has

$$\frac{1}{2^{N+1}\left(1+(1-2^{-N})x\right)\left(1+(1-2^{-N})y\right)}\le \frac{1}{2\lambda },\mathrm{if}x>y$$

$$\frac{1}{2^{N+2}\left(1+(1-2^{-N})x\right)\left(1+(1-2^{-N})y\right)}\le \frac{1}{4\lambda },\mathrm{if}x<y.$$

By the above, we obtain

$$\rho (T^{N}x,T^{N}y)\le \psi \left(\rho (x,y)\right).$$

Hence, for each x we can find an integer $N\ge {log}_2\lambda$ such that (7) is satisfied.

In order to prove that $(X,\rho )$ is forward-T-orbitally complete starting at some $x_0>0$ it suffices to observe that, by (13), every sequence of positive numbers $x_{n_k}:=T^{n_k}{x}_0$ converges to 0 with respect to Euclidean metrics. Therefore ${\displaystyle \rho (0,x_{n_k})=ln\frac{T^{n_k}{x}_0}{4}\underset{k}{⟶}-\infty }$ meaning that $\left(x_{n_k}\right)$$\rho$-converges to 0.

Next, notice that ${\displaystyle d(x_0,T^n{x}_0)=d(x_0,x_n)=\frac{x_0-x_n}{2}<x_0}$ for every $n\in \mathbb{N}$ proving that ${sup}_n\{\rho (x_0,T^n{x}_0):T^n{x}_0\ne x_0\}<\infty$.

Therefore, all the assumptions of Theorem 1 are satisfied, consequently T is a P.O. (its fixed point being $\xi =0$). □

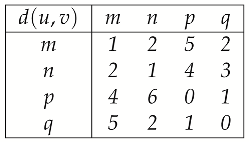
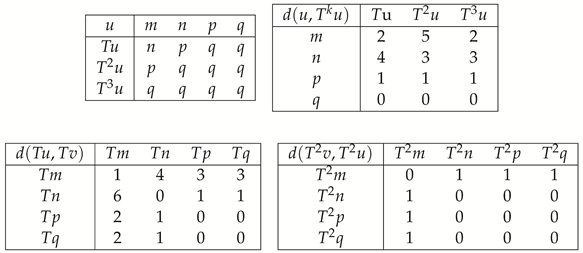
Example 7.

Let $X=\{m,n,p,q\}$ where $m,n,p,q$ are distinct and let $d:X\times X\to [0,\infty )$ be defined by

Define $T:X\to X$ by $Tm=n$, $Tn=p$, $Tp=q$, $Tq=q$. Then d is a weak dislocated rectangular $b-$metric with $s=2$ and T is a P.O.

Proof. 

By Remark 1, it is easy to check that d satisfies the axioms of Definition 1.

Next, a simple computation gives

Take $\rho (u,v):=lnd(u,v)+d(u,v)$ for $u,v\in X$ with $d(u,v)\ne 0$, and $\psi :(-\infty ,7)\to \mathbb{R}$, $\psi \left(t\right):=t-1$.

By Remark 5 we deduce that $\psi \in \Psi$. It is easy to check that $(X,\rho )$ is an $s\rho$-space.

In the following, we need to verify that T satisfies the assumptions provided in Theorem 1.

Clearly, X being bounded, one has ${sup}_n\{d(u,T^{n}u):u\ne T^{n}u\}<\infty$ for every $u\in X$, so condition $\left(\beta \right)$ is verified. Additionally, it is obvious that T is $\rho -$forward-T-orbitally complete starting at any $u\in X$, which assures that T satisfies $\left(\gamma \right)$.

Next, we need to prove that T satisfies the contraction assumption $\left(\alpha \right)$ of Theorem 1.

A trivial verification shows that, for each $u\in X=\{m,n,p,q\}$, there exists $N=2$ such that

$$\rho (T^{2}u,T^{2}v)=lnd(T^{2}u,T^{2}v)+d(T^{2}u,T^{2}v)=1$$

$$\le \psi \left(\rho \right(u,v\left)\right)=lnd(u,v)+d(u,v)-1$$

for all $v\in X$ with $T^{2}u\ne T^{2}v$.

Therefore, according to Theorem 1, T is a P.O., its fixed point being q. □

In the following some consequences in weak (rectangular) b-metric spaces are deduced.

Let us denote by $\Phi$ the class of comparison functions, i.e., those non-decreasing maps $\phi :(0,\infty )\to (0,\infty )$, such that ${\phi }^n\left(t\right)\underset{n}{⟶}0$ for all $t>0$. If $(X,d)$ is a (dislocated) b-metric space with constant $s\ge 1$, a comparison function $\phi \in \Phi$ such that

$$\underset{t\to \infty }{lim}\left(t-s\phi \left(t\right)\right)=\infty$$

(14)

is called a strict comparison function.

Corollary 1.

Let $(X,d)$ be a complete weak b-metric space, a mapping $T:X\to X$ and $\phi \in \Phi$. Assume that, for each $x\in X$, there exists $N=N\left(x\right)\in \mathbb{N}$ such that the following conditions are satisfied

$\left(i\right)d(T^{N}x,T^{N}y)\le \phi \left(d(x,y)\right),\forall y\in Xsuch thatTy\ne Tx.$

$\left(ii\right)\exists x_0\in Xsuch that{sup}_n\{d(x_0,T^n{x}_0):x_0\ne T^n{x}_0\}<\infty .$

Then T is a P.O.

Furthermore, if φ is a strict comparison function, then condition $\left(ii\right)$ can be dropped.

Proof. 

Define $\rho (x,y):=lnd(x,y)$ for all $x\ne y\in X$, and $\psi :\mathbb{R}\to \mathbb{R}$, $\psi \left(t\right):=ln\phi \left(e^t\right)$. Then $\rho$ is a strong forward-complete $\rho$-metric. Clearly, $\psi$ is non-decreasing and we have ${\psi }^n\left(t\right)=ln{\phi }^n\left(e^t\right)$ for all $n\in \mathbb{N}$, $t\in \mathbb{R}$. Thus, since $\phi \in \Phi$, one has ${\phi }^n\left(e^t\right)\to 0$ so ${\psi }^n\left(t\right)\to -\infty$. Consequently, $\psi \in \Psi$.

Relation (7) now follows from $\left(i\right)$ by applying the logarithm function.

From hypothesis $\left(ii\right)$, we deduce that ${sup}_n\{\rho (x_0,T^n{x}_0):x_0\ne T^n{x}_0\}<\infty$.

Now we can apply Theorem 1.

For the second part, we will prove that, for each $x\in X$, ${sup}_{n}d(x,T^{n}x)<\infty$.

Let any $x\in X$ and $N=N\left(x\right)$. We consider the nontrivial case $d(x,T^{n}x)\ne 0$ for all n. Set $\lambda :=max\{d(x,T^{i}x):i=1,\dots ,N\}$.

If $n\in \mathbb{N}$, $n\ge N$, there are $k\in \mathbb{N}$, $r\in \{0,1,\dots ,N-1\}$ such that $n=kN+r$.

We fix $r\in \{0,\dots ,N-1\}$ and define the sequence $\left(u_k\right)$ as follows

$$u_0:=d(x,T^{r}x),\dots ,u_k:=d(x,T^{kN+r}x),\mathrm{for}k=1,2,\dots$$

For our purpose, it is enough to show that $\left(u_k\right)$ is bounded.

By (14) one can find $\mu >\lambda$ such that

$$t-s\phi \left(t\right)>s\lambda ,\forall t>\mu .$$

(15)

We now proceed by induction. Clearly $u_0<\mu$. Assume that $u_0,u_1,\dots ,u_{k-1}\in (0,\mu )$ for some $k\in \mathbb{N}$ and prove that $u_k<\mu$. Suppose, contrary to our claim, that $u_k\ge \mu$. Then $u_{k-1}<u_k$ and from $\left(i\right)$, the triangle inequality (d2) and the monotonicity of $\phi$, we get

$$u_k=d(x,T^{kN+r}x)\le s[d(x,T^{N}x)+d(T^{N}x,T^N{T}^{(k-1)N+r}x)]$$

$$\le s[\lambda +\phi \left(d(x,T^{(k-1)N+r}x)\right)]=s\lambda +s\phi \left(u_{k-1}\right)\le s\lambda +s\phi \left(u_k\right),$$

so

$$u_k-s\phi \left(u_k\right)\le s\lambda$$

contradicting (15). □

Remark 6.

If, in the previous corollary, we consider $\phi \left(t\right):=\lambda t$, where $\lambda \in (0,1/s)$, then φ is a strict comparison function and condition $\left(i\right)$ becomes

$$d(T^{N}x,T^{N}y)\le \lambda d(x,y).$$

In this case, condition $\left(ii\right)$ can be dropped. Thus, we obtain ([2], Theorem 3.2).

We mention that, in this particular case, using a similar argument as in ([7], Lemma 1.6) one obtains the boundedness of the set $\{d(x,T^{n}x):n=1,2,\dots \}$ for every $x\in X$ even when $\lambda \in (0,1)$. Thus, by this result we get ([7], Theorem 2.1) in the framework of complete dislocated b-metric space.

Corollary 2.

Let $(X,d)$ be a complete weak rectangular b-metric space and a mapping $T:X\to X$ which satisfies (7) for $\rho :=F\circ d$ and $\psi \in \Psi$, where $F\in \mathcal{F}$. If F is upper bounded or $(X,d)$ is bounded and F is nondecreasing, then T is a P.O.

In particular, assume that there exist $\alpha ,\beta ,\tau \in (0,\infty )$, $\beta <e$, such that, for each $x\in X$, there exists $N=N\left(x\right)\in \mathbb{N}$ such that one of the following conditions are satisfied for all $y\in X$ with $Ty\ne Tx$:

$$d(T^{N}x,T^{N}y)\le \beta e^{\frac{-1}{d(x,y)}};$$

(16)

or

$${\displaystyle d(T^{N}x,T^{N}y)\le \frac{\alpha d(x,y)}{\alpha +\tau d(x,y)};}$$

(17)

or

$$d(T^{N}x,T^{N}y)\le ln\left(2-e^{-d(x,y)}\right).$$

(18)

Then T is a P.O.

Proof. 

First, observe that, by hypothesis, $\rho =F\circ d$ is upper bounded, hence condition $\left(\beta \right)$ of Theorem 1 is obviously verified.

Next, note that (16) follows from (7) taking

$$\rho (x,y)=\frac{-1}{d(x,y)},\psi \left(t\right)=\frac{-1}{\beta e^t}\forall x,y\in X,x\ne y,\forall t\in \mathbb{R}$$

and (17) is equivalent to (7) if we write

$$\rho (x,y)=\frac{-\alpha }{d(x,y)},\psi \left(t\right)=t-\tau \forall x,y\in X,x\ne y,\forall t\in \mathbb{R}.$$

Likewise, (17) is equivalent to (7) if we consider

$$\rho (x,y)=\frac{1}{1-e^{d(x,y)}},\psi \left(t\right)=t-1,\forall x,y\in X,x\ne y,\forall t\in \mathbb{R}.$$

Since in all cases $\rho (x,y)<0$ for every $x,y\in X$, $x\ne y$, the conclusion now follows from Theorem 1. □

Notice that a variety of examples can be obtained as in the previous corollaries if we consider strong $\rho$-metrics of the form $F\circ d$, $F\in \mathcal{F}$, and functions $\psi \in \Psi$.

4. Conclusions

We define the concept of strong $\rho$-space and we prove a fixed point result for a self-mapping on such a space which satisfies a Sehgal type contractive condition. This is a general framework and some known results studied in the literature can be obtained as particular cases of our work. Some illustrative examples including one in a weak dislocated b-metric space are given. Results analogous to those in our fixed point theorem can be deduced in other generalized spaces.