A Dynamic Analysis of Randomly Oriented Functionally Graded Carbon Nanotubes/Fiber-Reinforced Composite Laminated Shells with Different Geometries
Abstract
:1. Introduction
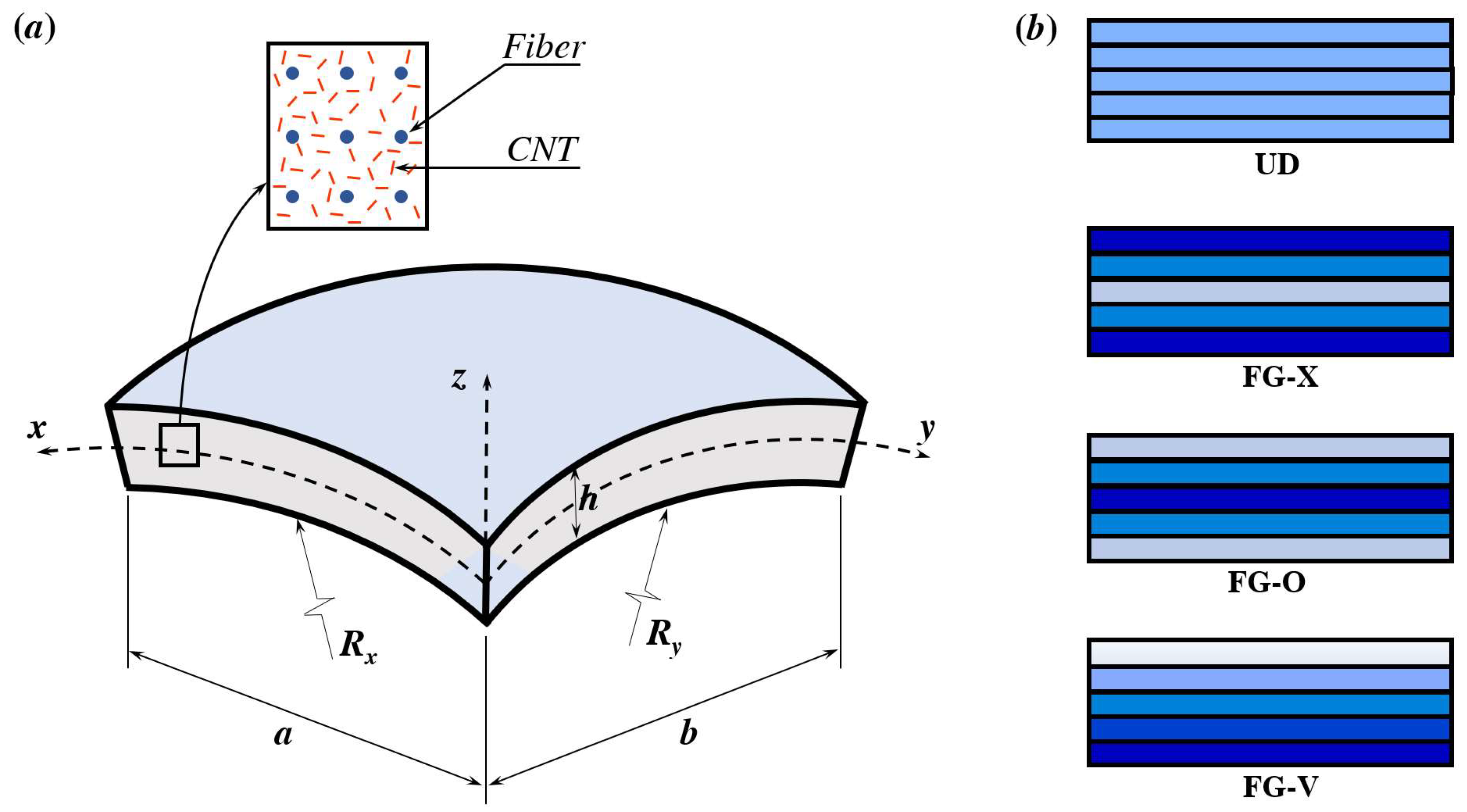
2. Material and Geometrical Modeling
2.1. Mechanical Properties and Geometrics
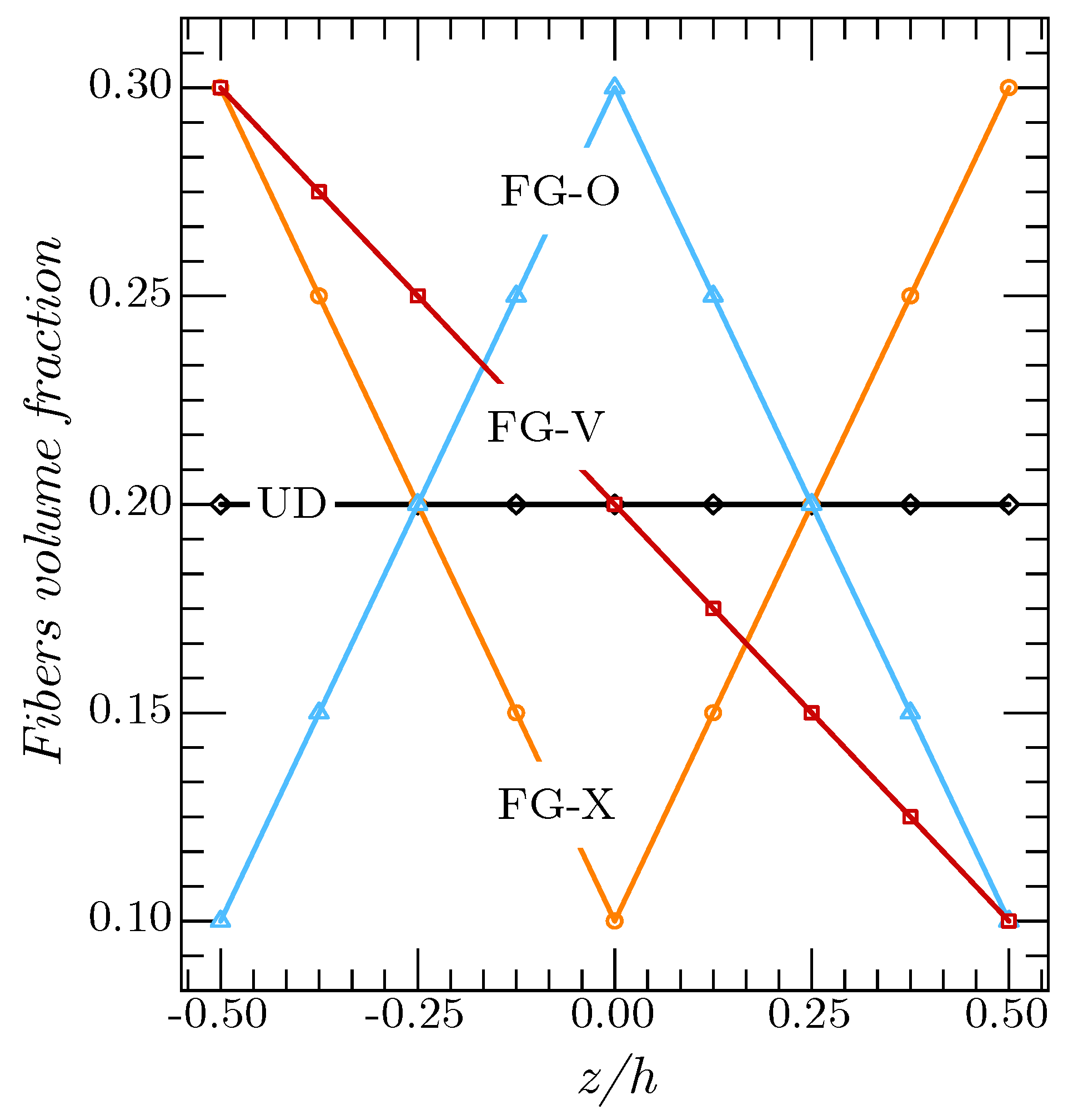
2.2. Volume Fraction of the Reinforcement Fibers
3. Mathematical Formulations
4. Variational Statements
5. Analytical Solution
6. Results and Discussions
6.1. Verification Analysis
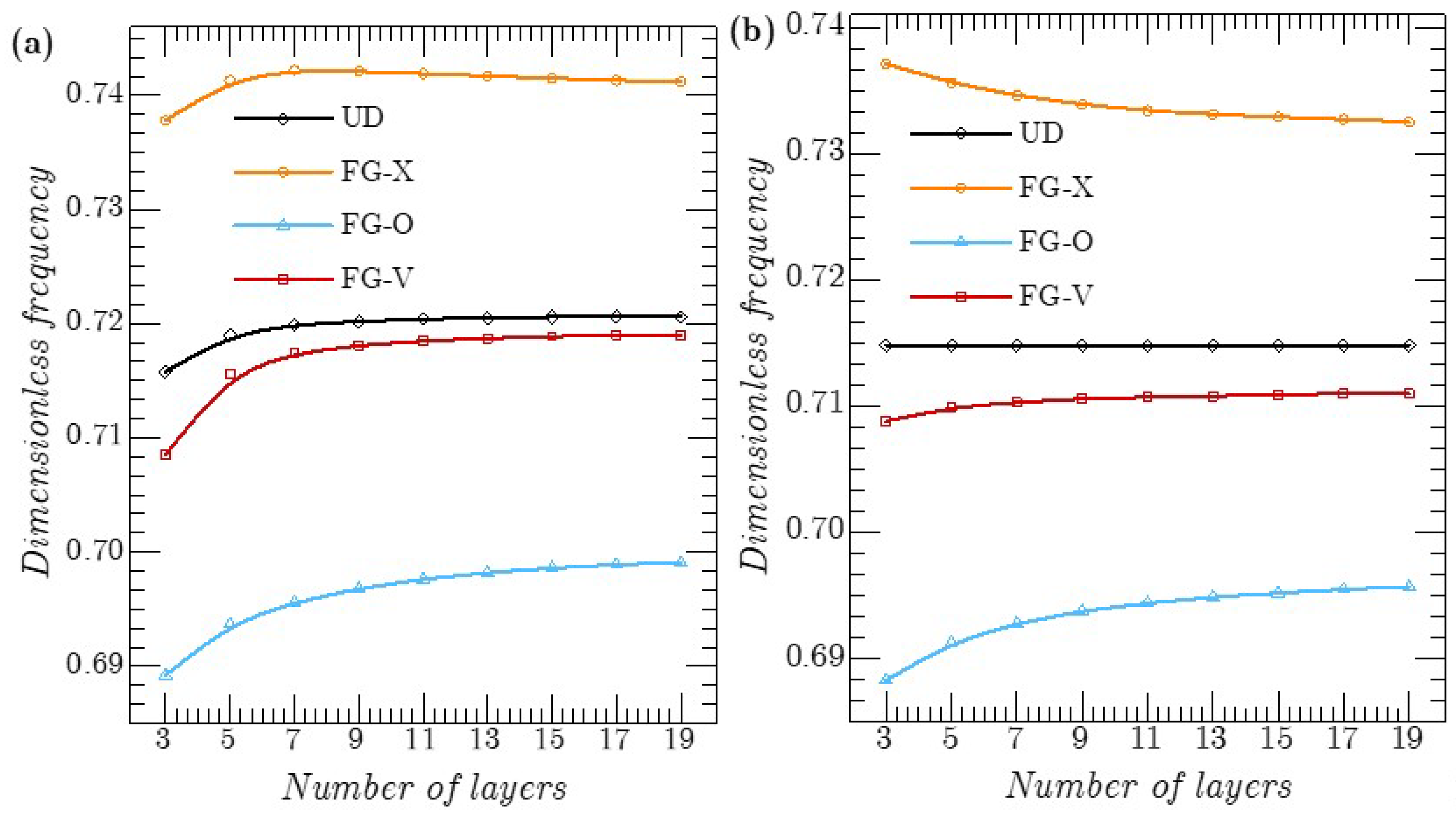
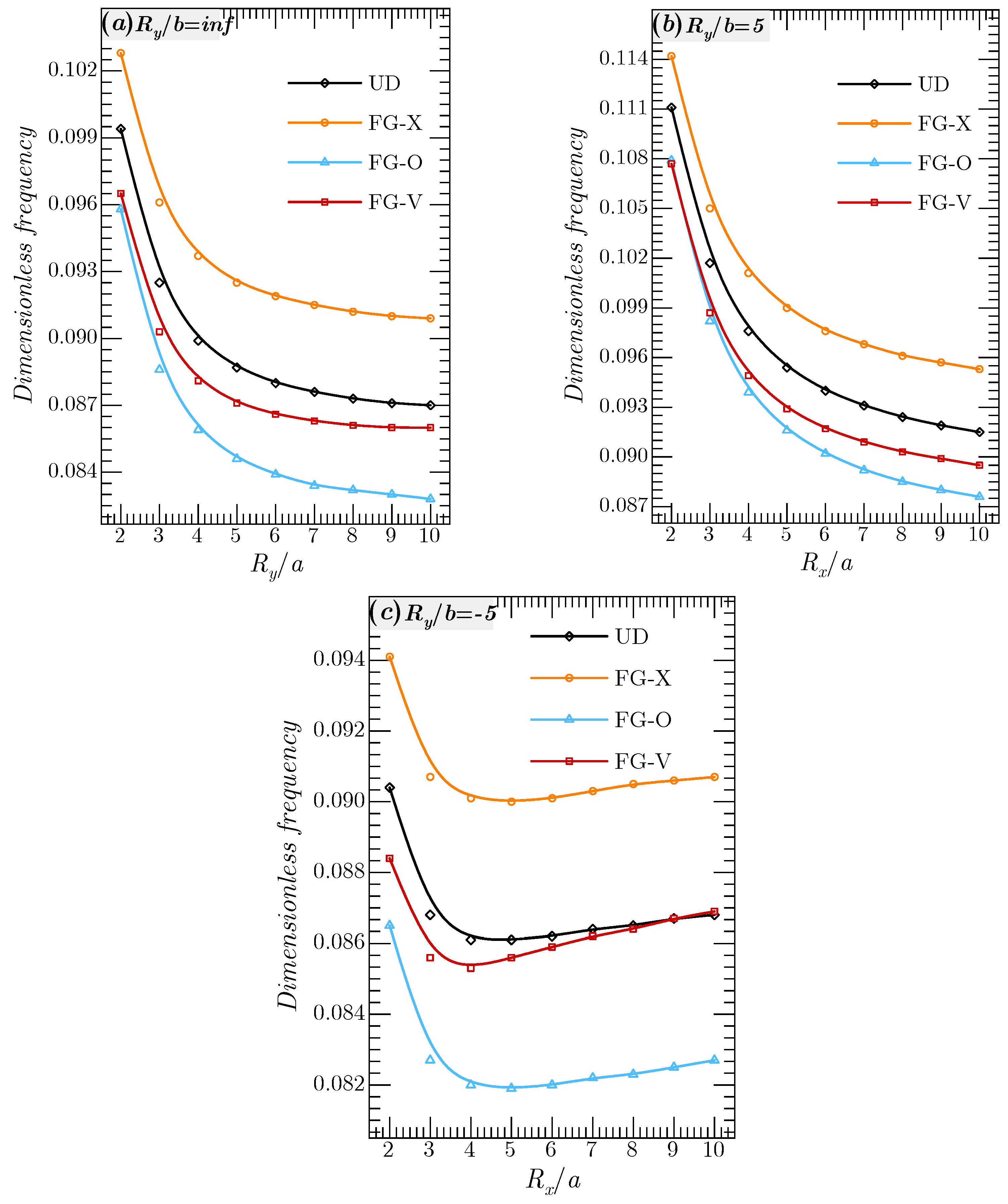
6.2. Parametric Stud
7. Conclusions
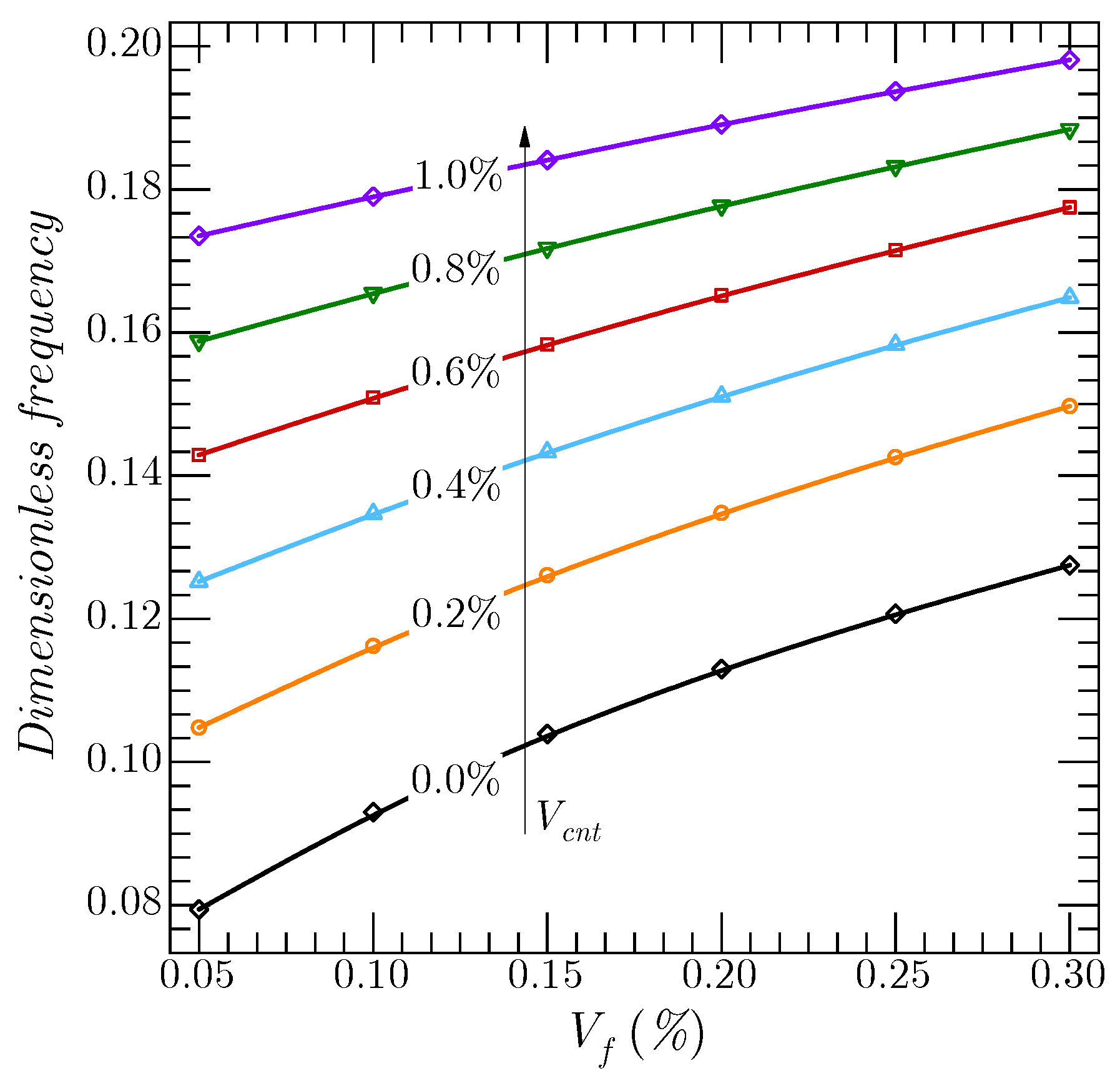
- It seems that the dimensionless frequencies increased for an increased volume fraction of CNTs/fibers because of a global augmentation in the stiffness of the CNTs/F-RC laminated shell;
- Because of the considerable reinforcement in the superior and inferior layers, the distribution pattern of FG-X fibers produced the highest values of frequencies;
- The variation of the geometric parameters such as aspect ratio, thickness ratio, and radii of curvature had a significant effect on the vibration response of the proposed structure;
- The analytical solution proposed in this work could represent valid benchmarks for engineers and researchers for the purposes of the practical design of shell structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Daikh, A.A.; Houari MS, A.; Eltaher, M.A. A novel nonlocal strain gradient Quasi-3D bending analysis of sigmoid functionally graded sandwich nanoplates. Compos. Struct. 2021, 262, 113347. [Google Scholar] [CrossRef]
- Mohamed, N.; Mohamed, S.A.; Eltaher, M.A. Buckling and post-buckling behaviors of higher order carbon nanotubes using energy-equivalent model. Eng. Comput. 2021, 37, 2823–2836. [Google Scholar] [CrossRef]
- Zuo, Y.T.; Liu, H.J. Fractal approach to mechanical and electrical properties of graphene/sic composites. Facta Univ. Ser. Mech. Eng. 2021, 19, 271–284. [Google Scholar] [CrossRef]
- He, C.H.; Liu, S.H.; Liu, C.; Mohammad-Sedighi, H. A novel bond stress-slip model for 3-D printed concretes. Discret. Contin. Dyn. Syst.-S 2021, 14, 3459–3478. [Google Scholar] [CrossRef]
- Ji, F.Y.; He, C.H.; Zhang, J.J.; He, J.H. A fractal Boussinesq equation for nonlinear transverse vibration of a nanofiber-reinforced concrete pillar. Appl. Math. Model. 2020, 82, 437–448. [Google Scholar] [CrossRef]
- Boutahar, Y.; Lebaal, N.; Bassir, D. A Refined Theory for Bending Vibratory Analysis of Thick Functionally Graded Beams. Mathematics 2021, 9, 1422. [Google Scholar] [CrossRef]
- Shen, H.S.; Zhang, C.L. Thermal buckling and postbuckling behavior of functionally graded carbon nanotube-reinforced composite plates. Mater. Des. 2010, 31, 3403–3411. [Google Scholar] [CrossRef]
- Zhu, P.; Lei, Z.X.; Liew, K.M. Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos. Struct. 2012, 94, 1450–1460. [Google Scholar] [CrossRef]
- Alibeigloo, A. Three-dimensional thermoelasticity solution of functionally graded carbon nanotube reinforced composite plate embedded in piezoelectric sensor and actuator layers. Compos. Struct. 2014, 118, 482–495. [Google Scholar] [CrossRef]
- Liew, K.M.; Lei, Z.X.; Zhang, L.W. Mechanical analysis of functionally graded carbon nanotube reinforced composites: A review. Compos. Struct. 2015, 120, 90–97. [Google Scholar] [CrossRef]
- Zhang, L.W.; Lei, Z.X.; Liew, K.M. Computation of vibration solution for functionally graded carbon nanotube-reinforced composite thick plates resting on elastic foundations using the element-free IMLS-Ritz method. Appl. Math. Comput. 2015, 256, 488–504. [Google Scholar] [CrossRef]
- Phung-Van, P.; Thanh, C.L.; Nguyen-Xuan, H.; Abdel-Wahab, M. Nonlinear transient isogeometric analysis of FG-CNTRC nanoplates in thermal environments. Compos. Struct. 2018, 201, 882–892. [Google Scholar] [CrossRef]
- Daikh, A.A.; Drai, A.; Houari MS, A.; Eltaher, M.A. Static analysis of multilayer nonlocal strain gradient nanobeam reinforced by carbon nanotubes. Steel Compos. Struct. 2020, 36, 643–656. [Google Scholar] [CrossRef]
- He, X.T.; Yang, Z.X.; Li, Y.H.; Li, X.; Sun, J.Y. Application of multi-parameter perturbation method to functionally-graded, thin, circular piezoelectric plates. Mathematics 2020, 8, 342. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Li, C.; Wang, C.; Lai, J.W.; Cheong, K.H. A simple-FSDT-based isogeometric method for piezoelectric functionally graded plates. Mathematics 2020, 8, 2177. [Google Scholar] [CrossRef]
- Li, Y.D.; Tang, Z.C.; Fu, Z.J. Generalized Finite Difference Method for Plate Bending Analysis of Functionally Graded Materials. Mathematics 2020, 8, 1940. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari MS, A.; Belarbi, M.O.; Chakraverty, S.; Eltaher, M.A. Analysis of axially temperature-dependent functionally graded carbon nanotube reinforced composite plates. Eng. Comput. 2021, 2021, 1–22. [Google Scholar] [CrossRef]
- Esen, I.; Daikh, A.A.; Eltaher, M.A. Dynamic response of nonlocal strain gradient FG nanobeam reinforced by carbon nanotubes under moving point load. Eur. Phys. J. Plus 2021, 136, 458. [Google Scholar] [CrossRef]
- Karamanli, A.; Vo, T.P. Finite element model for carbon nanotube-reinforced and graphene nanoplatelet-reinforced composite beams. Compos. Struct. 2021, 264, 113739. [Google Scholar] [CrossRef]
- Karamanli, A.; Aydogdu, M. Vibration behaviors of two-directional carbon nanotube reinforced functionally graded composite plates. Compos. Struct. 2021, 262, 113639. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari MS, A.; Belarbi, M.O.; Mohamed, S.A.; Eltaher, M.A. Static and dynamic stability responses of multilayer functionally graded carbon nanotubes reinforced composite nanoplates via quasi 3D nonlocal strain gradient theory. Def. Technol. 2021, in press. [CrossRef]
- Daikh, A.A.; Houari MS, A.; Karami, B.; Eltaher, M.A.; Dimitri, R.; Tornabene, F. Buckling Analysis of CNTRC Curved Sandwich Nanobeams in Thermal Environment. Appl. Sci. 2021, 11, 3250. [Google Scholar] [CrossRef]
- Rostami, R.; Mohammadimehr, M. Dynamic stability and bifurcation analysis of sandwich plate with considering FG core and FG-CNTRC face sheets. J. Sandw. Struct. Mater. 2021, 23, 2296–2325. [Google Scholar] [CrossRef]
- Khadir, A.I.; Daikh, A.A.; Eltaher, M.A. Novel four-unknowns quasi 3D theory for bending, buckling and free vibration of functionally graded carbon nanotubes reinforced composite laminated nanoplates. Adv. Nano Res. 2021, 11, 621–640. [Google Scholar] [CrossRef]
- Babaei, H. On frequency response of FG-CNT reinforced composite pipes in thermally pre/post buckled configurations. Compos. Struct. 2021, 276, 114467. [Google Scholar] [CrossRef]
- Duc, N.D.; Minh, P.P. Free vibration analysis of cracked FG CNTRC plates using phase field theory. Aerosp. Sci. Technol. 2021, 112, 106654. [Google Scholar] [CrossRef]
- Adhikari, B.; Singh, B.N. A Coupled Mori–Tanaka model and FEM RVE approach for the geometrical nonlinear dynamic response of the FG-CNTRC plate based on a novel shear strain function using isogeometric finite element procedure. Compos. Struct. 2022, 280, 114947. [Google Scholar] [CrossRef]
- Shen, H.S. Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments, Part I: Axially-loaded shells. Compos. Struct. 2011, 93, 2096–2108. [Google Scholar] [CrossRef]
- Shen, H.S. Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments, Part II: Pressure-loaded shells. Compos. Struct. 2011, 93, 2496–2503. [Google Scholar] [CrossRef]
- Aragh, B.S.; Barati, A.N.; Hedayati, H. Eshelby–Mori–Tanaka approach for vibrational behavior of continuously graded carbon nanotube-reinforced cylindrical panels. Compos. Part B Eng. 2012, 43, 1943–1954. [Google Scholar] [CrossRef]
- Shen, H.S. Torsional postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments. Compos. Struct. 2014, 116, 477–488. [Google Scholar] [CrossRef]
- Mirzaei, M.; Kiani, Y. Snap-through phenomenon in a thermally postbuckled temperature dependent sandwich beam with FG-CNTRC face sheets. Compos. Struct. 2015, 134, 1004–1013. [Google Scholar] [CrossRef]
- Thomas, B.; Roy, T. Vibration analysis of functionally graded carbon nanotube-reinforced composite shell structures. Acta Mech. 2016, 227, 581–599. [Google Scholar] [CrossRef]
- Pouresmaeeli, S.; Fazelzadeh, S. Frequency analysis of doubly curved functionally graded carbon nanotube-reinforced composite panels. Acta Mech. 2016, 227, 2765–2794. [Google Scholar] [CrossRef]
- Shojaee, M.; Setoodeh, A.R.; Malekzadeh, P. Vibration of functionally graded CNTs-reinforced skewed cylindrical panels using a transformed differential quadrature method. Acta Mech. 2017, 228, 2691–2711. [Google Scholar] [CrossRef]
- Tohidi, H.; Hosseini-Hashemi, S.H.; Maghsoudpour, A. Nonlinear size-dependent dynamic buckling analysis of embedded micro cylindrical shells reinforced with agglomerated CNTs using strain gradient theory. Microsyst. Technol. 2017, 23, 5727–5744. [Google Scholar] [CrossRef]
- Avramov, K.V.; Chernobryvko, M.; Uspensky, B.; Seitkazenova, K.K.; Myrzaliyev, D. Self-sustained vibrations of functionally graded carbon nanotubes-reinforced composite cylindrical shells in supersonic flow. Nonlinear Dyn. 2019, 98, 1853–1876. [Google Scholar] [CrossRef]
- Aminipour, H.; Janghorban, M.; Civalek, O. Analysis of functionally graded doubly-curved shells with different materials via higher order shear deformation theory. Compos. Struct. 2020, 251, 112645. [Google Scholar] [CrossRef]
- Ahmadi, H.; Bayat, A.; Duc, N.D. Nonlinear forced vibrations analysis of imperfect stiffened FG doubly curved shallow shell in thermal environment using multiple scales method. Compos. Struct. 2021, 256, 113090. [Google Scholar] [CrossRef]
- Babaei, H.; Kiani, Y.; Eslami, M.R. Vibrational behavior of thermally pre-/post-buckled FG-CNTRC beams on a nonlinear elastic foundation: A two-step perturbation technique. Acta Mech. 2021, 232, 3897–3915. [Google Scholar] [CrossRef]
- Chakraborty, S.; Dey, T. Non-linear stability analysis of CNT reinforced composite cylindrical shell panel subjected to thermomechanical loading. Compos. Struct. 2021, 255, 112995. [Google Scholar] [CrossRef]
- Chakraborty, S.; Dey, T.; Kumar, R. Instability characteristics of damped CNT reinforced laminated shell panels subjected to in-plane excitations and thermal loading. Structures 2021, 34, 2936–2949. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, L.; Bolandi, S.Y.; Habibi, M. On the vibrations of the non-polynomial viscoelastic composite open-type shell under residual stresses. Compos. Struct. 2021, 263, 113599. [Google Scholar] [CrossRef]
- Fares, M.E.; Elmarghany, M.K.; Atta, D.; Salem, M.G. An improved layerwise formulation for free vibrations of multilayered FG truncated conical shells reinforced by carbon nanotubes. Compos. Struct. 2021, 275, 114372. [Google Scholar] [CrossRef]
- Fu, T.; Wu, X.; Xiao, Z.; Chen, Z. Dynamic instability analysis of FG-CNTRC laminated conical shells surrounded by elastic foundations within FSDT. Eur. J. Mech.-A/Solids 2021, 85, 104139. [Google Scholar] [CrossRef]
- Yadav, A.; Amabili, M.; Panda, S.K.; Dey, T.; Kumar, R. Nonlinear damped vibrations of three-phase CNT-FRC circular cylindrical shell. Compos. Struct. 2021, 255, 112939. [Google Scholar] [CrossRef]
- Mohammadi, H.; Setoodeh, A.R.; Vassilopoulos, A.P. Isogeometric Kirchhoff–Love shell patches in free and forced vibration of sinusoidally corrugated FG carbon nanotube-reinforced composite panels. Thin-Walled Struct. 2022, 171, 108707. [Google Scholar] [CrossRef]
- Cong, P.H.; Trung, V.D.; Khoa, N.D.; Duc, N.D. Vibration and nonlinear dynamic response of temperature-dependent FG-CNTRC laminated double curved shallow shell with positive and negative Poisson’s ratio. Thin-Walled Struct. 2022, 171, 108713. [Google Scholar] [CrossRef]
- Babaei, H. Free vibration and snap-through instability of FG-CNTRC shallow arches supported on nonlinear elastic foundation. Appl. Math. Comput. 2022, 413, 126606. [Google Scholar] [CrossRef]
- Yengejeh, S.I.; Kazemi, S.A.; Öchsner, A. Carbon nanotubes as reinforcement in composites: A review of the analytical, numerical and experimental approaches. Comput. Mater. Sci. 2017, 136, 85–101. [Google Scholar] [CrossRef]
- Shahmohammadi, M.A.; Azhari, M.; Saadatpour, M.M.; Salehipour, H.; Civalek, Ö. Dynamic instability analysis of general shells reinforced with polymeric matrix and carbon fibers using a coupled IG-SFSM formulation. Compos. Struct. 2021, 263, 113720. [Google Scholar] [CrossRef]
- Mehrabadi, S.J.; Aragh, B.S.; Khoshkhahesh, V.; Taherpour, A. Mechanical buckling of nanocomposite rectangular plate reinforced by aligned and straight single-walled carbon nanotubes. Compos. Part B Eng. 2012, 43, 2031–2040. [Google Scholar] [CrossRef]
- Alijani, F.; Amabili, M.; Karagiozis, K.; Bakhtiari-Nejad, F. Nonlinear vibrations of functionally graded doubly curved shallow shells. J. Sound Vib. 2011, 330, 1432–1454. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded shallow shells according to a 2D higher-order deformation theory. Compos. Struct. 2008, 84, 132–146. [Google Scholar] [CrossRef]
- Chorfi, S.M.; Houmat, A. Non-linear free vibration of a functionally graded doubly-curved shallow shell of elliptical plan-form. Compos. Struct. 2010, 92, 2573–2581. [Google Scholar] [CrossRef]
- Trinh, M.C.; Kim, S.E. A three variable refined shear deformation theory for porous functionally graded doubly curved shell analysis. Aerosp. Sci. Technol. 2019, 94, 105356. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Linear static response of nanocomposite plates and shells reinforced by agglomerated carbon nanotubes. Compos. Part B Eng. 2017, 115, 449–476. [Google Scholar] [CrossRef]
- Bowles, D.E.; Tompkins, S.S. Prediction of coefficients of thermal expansion for unidirectional composites. J. Compos. Mater. 1989, 23, 370–388. [Google Scholar] [CrossRef]



| 271 | 88 | 17 | 1089 | 442 |
| BCs. | Boundaries Parallel to the x-Axis | Boundaries Parallel to the y-Axis |
|---|---|---|
| Simply supported (S) | ||
| Clamped (C) |
| BCs. | ||
|---|---|---|
| SSSS | ||
| CCCC | ||
| CSCS | ||
| CCSS | ||
| CSSS | ||
| CCCS | ||
| Alijani [53] | Matsunaga [54] | Chorfi [55] | Trinh [56] | Present | ||||
|---|---|---|---|---|---|---|---|---|
| Plate | 0 | 0 | 0 | 0.0597 | 0.0588 | 0.0577 | 0.0577 | 0.0577 |
| 0.5 | 0.0506 | 0.0492 | 0.0490 | 0.0490 | 0.0490 | |||
| 1 | 0.0456 | 0.0430 | 0.0442 | 0.0442 | 0.0442 | |||
| 4 | 0.0396 | 0.0381 | 0.0383 | 0.0381 | 0.0380 | |||
| 10 | 0.0380 | 0.0364 | 0.0366 | 0.0364 | 0.0363 | |||
| Spherical | 0.5 | 0.5 | 0 | 0.0779 | 0.0751 | 0.0762 | 0.0761 | 0.0753 |
| 0.5 | 0.0676 | 0.0657 | 0.0664 | 0.0662 | 0.0653 | |||
| 1 | 0.0617 | 0.0601 | 0.0607 | 0.0605 | 0.0595 | |||
| 4 | 0.0519 | 0.0503 | 0.0509 | 0.0506 | 0.0496 | |||
| 10 | 0.0482 | 0.0464 | 0.0471 | 0.0467 | 0.0459 | |||
| Cylindrical | 0.5 | 0 | 0 | 0.0648 | 0.0622 | 0.0629 | 0.0628 | 0.0622 |
| 0.5 | 0.0553 | 0.0535 | 0.0540 | 0.0538 | 0.0533 | |||
| 1 | 0.0501 | 0.0485 | 0.0490 | 0.0488 | 0.0482 | |||
| 4 | 0.0430 | 0.0413 | 0.0419 | 0.0416 | 0.0410 | |||
| 10 | 0.0408 | 0.0390 | 0.0395 | 0.0392 | 0.0387 | |||
| Hyperbolic–paraboloidal | 0.5 | −0.5 | 0 | 0.0597 | 0.0563 | 0.0580 | 0.0577 | 0.0563 |
| 0.5 | 0.0506 | 0.0479 | 0.0493 | 0.0490 | 0.0478 | |||
| 1 | 0.0456 | 0.0432 | 0.0445 | 0.0442 | 0.0431 | |||
| 4 | 0.0396 | 0.0372 | 0.0385 | 0.0381 | 0.0371 | |||
| 10 | 0.0380 | 0.0355 | 0.0368 | 0.0364 | 0.0354 |
| N | UD | FG-X | FG-O | FG-V | |||
|---|---|---|---|---|---|---|---|
| Plate | inf | inf | 3 | 0.1896 | 0.1862 | 0.1750 | 0.1779 |
| 7 | 0.1900 | 0.1840 | 0.1734 | 0.1783 | |||
| 11 | 0.1900 | 0.1927 | 0.1823 | 0.1881 | |||
| 15 | 0.1901 | 0.2040 | 0.1934 | 0.1984 | |||
| 19 | 0.1901 | 0.1976 | 0.1821 | 0.1893 | |||
| Cylindrical shell | 5 | inf | 3 | 0.1917 | 0.1883 | 0.1778 | 0.1789 |
| 7 | 0.1921 | 0.1862 | 0.1762 | 0.1792 | |||
| 11 | 0.1922 | 0.1948 | 0.1848 | 0.1888 | |||
| 15 | 0.1922 | 0.2059 | 0.1959 | 0.1988 | |||
| 19 | 0.1922 | 0.1997 | 0.1844 | 0.1899 | |||
| Spherical shell | 5 | 5 | 3 | 0.1986 | 0.1953 | 0.1856 | 0.1855 |
| 7 | 0.1991 | 0.1933 | 0.1842 | 0.1854 | |||
| 11 | 0.1992 | 0.2016 | 0.1924 | 0.1947 | |||
| 15 | 0.1992 | 0.2125 | 0.2031 | 0.2041 | |||
| 19 | 0.1992 | 0.2064 | 0.1917 | 0.1955 | |||
| Elliptical–paraboloid shell | 5 | 7.5 | 3 | 0.1959 | 0.1925 | 0.1825 | 0.1828 |
| 7 | 0.1964 | 0.1905 | 0.1811 | 0.1829 | |||
| 11 | 0.1964 | 0.1989 | 0.1894 | 0.1923 | |||
| 15 | 0.1964 | 0.2098 | 0.2003 | 0.2019 | |||
| 19 | 0.1964 | 0.2038 | 0.1888 | 0.1932 | |||
| Hyperbolic–paraboloidal shell | 5 | −5 | 3 | 0.1888 | 0.1855 | 0.1744 | 0.1769 |
| 7 | 0.1892 | 0.1834 | 0.1728 | 0.1776 | |||
| 11 | 0.1893 | 0.1920 | 0.1816 | 0.1873 | |||
| 15 | 0.1893 | 0.2032 | 0.1927 | 0.1975 | |||
| 19 | 0.1893 | 0.1969 | 0.1814 | 0.1885 |
| N | UD | FG-X | FG-O | FG-V | |||
|---|---|---|---|---|---|---|---|
| Plate | inf | inf | 3 | 0.1894 | 0.1858 | 0.1748 | 0.1776 |
| 7 | 0.1894 | 0.1834 | 0.1735 | 0.1773 | |||
| 11 | 0.1894 | 0.1919 | 0.1818 | 0.1868 | |||
| 15 | 0.1894 | 0.2029 | 0.1928 | 0.1968 | |||
| 19 | 0.1894 | 0.1967 | 0.1817 | 0.1879 | |||
| Cylindrical shell | 5 | inf | 3 | 0.1913 | 0.1877 | 0.1771 | 0.1790 |
| 7 | 0.1913 | 0.1854 | 0.1754 | 0.1787 | |||
| 11 | 0.1913 | 0.1937 | 0.1840 | 0.1881 | |||
| 15 | 0.1913 | 0.2046 | 0.1948 | 0.1979 | |||
| 19 | 0.1913 | 0.1985 | 0.1838 | 0.1891 | |||
| Spherical shell | 5 | 5 | 3 | 0.1979 | 0.1941 | 0.1841 | 0.1855 |
| 7 | 0.1979 | 0.1916 | 0.1822 | 0.1849 | |||
| 11 | 0.1979 | 0.1995 | 0.1901 | 0.1939 | |||
| 15 | 0.1979 | 0.2102 | 0.2007 | 0.2035 | |||
| 19 | 0.1979 | 0.2048 | 0.1906 | 0.1955 | |||
| Elliptical–paraboloid shell | 5 | 7.5 | 3 | 0.1953 | 0.1915 | 0.1813 | 0.1829 |
| 7 | 0.1953 | 0.1891 | 0.1795 | 0.1824 | |||
| 11 | 0.1953 | 0.1972 | 0.1877 | 0.1916 | |||
| 15 | 0.1953 | 0.2079 | 0.1983 | 0.2012 | |||
| 19 | 0.1953 | 0.2023 | 0.1879 | 0.1929 | |||
| Hyperbolic–paraboloidal shell | 5 | −5 | 3 | 0.1887 | 0.1852 | 0.1743 | 0.1768 |
| 7 | 0.1887 | 0.1831 | 0.1728 | 0.1768 | |||
| 11 | 0.1887 | 0.1917 | 0.1817 | 0.1864 | |||
| 15 | 0.1887 | 0.2026 | 0.1926 | 0.1960 | |||
| 19 | 0.1887 | 0.1959 | 0.1810 | 0.1867 |
| Type of Shells | Fiber Distribution Pattern | ||||
|---|---|---|---|---|---|
| FRC UD | FRC FG-X | FRC FG-O | FRC FG-V | ||
| Plate | 0.0% | 0.1176 | 0.1288 | 0.1033 | 0.1140 |
| 0.2% | 0.1387 | 0.1508 | 0.1246 | 0.1358 | |
| 0.4% | 0.1543 | 0.1658 | 0.1414 | 0.1521 | |
| 0.6% | 0.1676 | 0.1781 | 0.1560 | 0.1659 | |
| 0.8% | 0.1794 | 0.1888 | 0.1691 | 0.1780 | |
| 1.0% | 0.1900 | 0.1984 | 0.1811 | 0.1891 | |
| Cylindrical shell | 0.0% | 0.1181 | 0.1292 | 0.1039 | 0.1140 |
| 0.2% | 0.1398 | 0.1517 | 0.1258 | 0.1358 | |
| 0.4% | 0.1557 | 0.1671 | 0.1430 | 0.1522 | |
| 0.6% | 0.1693 | 0.1797 | 0.1578 | 0.1661 | |
| 0.8% | 0.1813 | 0.1906 | 0.1712 | 0.1785 | |
| 1.0% | 0.1922 | 0.2004 | 0.1834 | 0.1896 | |
| Spherical shell | 0.0% | 0.1200 | 0.1310 | 0.1062 | 0.1163 |
| 0.2% | 0.1434 | 0.1551 | 0.1298 | 0.1389 | |
| 0.4% | 0.1605 | 0.1715 | 0.1481 | 0.1561 | |
| 0.6% | 0.1749 | 0.1850 | 0.1639 | 0.1707 | |
| 0.8% | 0.1877 | 0.1967 | 0.1779 | 0.1836 | |
| 1.0% | 0.1992 | 0.2071 | 0.1907 | 0.1953 | |
| Elliptical–paraboloid shell | 0.0% | 0.1193 | 0.1303 | 0.1053 | 0.1154 |
| 0.2% | 0.1419 | 0.1538 | 0.1283 | 0.1377 | |
| 0.4% | 0.1586 | 0.1698 | 0.1461 | 0.1545 | |
| 0.6% | 0.1727 | 0.1829 | 0.1615 | 0.1688 | |
| 0.8% | 0.1852 | 0.1943 | 0.1753 | 0.1815 | |
| 1.0% | 0.1964 | 0.2045 | 0.1878 | 0.1929 | |
| Hyperbolic–paraboloidal shell | 0.0% | 0.1171 | 0.1283 | 0.1029 | 0.1125 |
| 0.2% | 0.1382 | 0.1502 | 0.1241 | 0.1348 | |
| 0.4% | 0.1537 | 0.1651 | 0.1408 | 0.1511 | |
| 0.6% | 0.1669 | 0.1774 | 0.1554 | 0.1649 | |
| 0.8% | 0.1786 | 0.1888 | 0.1684 | 0.1771 | |
| 1.0% | 0.1893 | 0.1976 | 0.1804 | 0.1881 | |
| Type of Shells | Fiber Distribution Pattern | ||||
|---|---|---|---|---|---|
| FRC UD | FRC FG-X | FRC FG-O | FRC FG-V | ||
| Plate | 5% | 0.1735 | 0.1735 | 0.1735 | 0.1735 |
| 10% | 0.1765 | 0.1790 | 0.1740 | 0.1765 | |
| 20% | 0.1822 | 0.1891 | 0.1751 | 0.18158 | |
| 30% | 0.1875 | 0.1982 | 0.1760 | 0.1859 | |
| Cylindrical shell | 5% | 0.1758 | 0.1758 | 0.1758 | 0.1758 |
| 10% | 0.1788 | 0.1812 | 0.1763 | 0.1782 | |
| 20% | 0.1844 | 0.1912 | 0.1774 | 0.1823 | |
| 30% | 0.1897 | 0.2002 | 0.1784 | 0.1860 | |
| Spherical shell | 5% | 0.1831 | 0.1831 | 0.1831 | 0.1831 |
| 10% | 0.1861 | 0.1884 | 0.1837 | 0.1850 | |
| 20% | 0.1916 | 0.1982 | 0.1848 | 0.1883 | |
| 30% | 0.1968 | 0.2069 | 0.1859 | 0.1912 | |
| Elliptical–paraboloid shell | 5% | 0.1802 | 0.1802 | 0.1802 | 0.1802 |
| 10% | 0.1832 | 0.1856 | 0.1808 | 0.1822 | |
| 20% | 0.1888 | 0.1954 | 0.1819 | 0.1858 | |
| 30% | 0.1940 | 0.2042 | 0.1829 | 0.1890 | |
| Hyperbolic–paraboloidal shell | 0.0% | 0.1728 | 0.1728 | 0.1728 | 0.1728 |
| 0.2% | 0.1758 | 0.1783 | 0.1733 | 0.1757 | |
| 0.8% | 0.1815 | 0.1884 | 0.1743 | 0.1808 | |
| 1.0% | 0.1868 | 0.1974 | 0.1753 | 0.1850 | |
| Type of Shells | BCs. | Fiber Distribution Pattern | |||
|---|---|---|---|---|---|
| FRC UD | FRC FG-X | FRC FG-O | FRC FG-V | ||
| Plate | SSSS | 0.1900 | 0.1984 | 0.1811 | 0.1891 |
| CCCC | 0.3599 | 0.3778 | 0.3398 | 0.3572 | |
| CCSS | 0.2978 | 0.3162 | 0.2767 | 0.2950 | |
| CSCS | 0.3409 | 0.3567 | 0.3237 | 0.3389 | |
| CSSS | 0.2821 | 0.2989 | 0.2634 | 0.2797 | |
| CCCS | 0.2386 | 0.2581 | 0.2155 | 0.2353 | |
| Cylindrical shell | SSSS | 0.1922 | 0.2004 | 0.1834 | 0.1896 |
| CCCC | 0.3661 | 0.3839 | 0.3461 | 0.3633 | |
| CCSS | 0.3053 | 0.3235 | 0.2844 | 0.3023 | |
| CSCS | 0.3449 | 0.3607 | 0.3277 | 0.3421 | |
| CSSS | 0.2866 | 0.3033 | 0.2681 | 0.2837 | |
| CCCS | 0.2484 | 0.2676 | 0.2258 | 0.2452 | |
| Spherical shell | SSSS | 0.1992 | 0.2071 | 0.1907 | 0.1953 |
| CCCC | 0.3729 | 0.3904 | 0.3533 | 0.3706 | |
| CCSS | 0.3083 | 0.3264 | 0.2877 | 0.3042 | |
| CSCS | 0.3501 | 0.3656 | 0.3332 | 0.3470 | |
| CSSS | 0.2911 | 0.3075 | 0.2729 | 0.2868 | |
| CCCS | 0.2611 | 0.2794 | 0.2398 | 0.2584 | |
| Elliptical–paraboloid shell | SSSS | 0.1964 | 0.2045 | 0.1878 | 0.1929 |
| CCCC | 0.3694 | 0.3871 | 0.3496 | 0.3669 | |
| CCSS | 0.3069 | 0.3251 | 0.2862 | 0.3032 | |
| CSCS | 0.3476 | 0.3632 | 0.3305 | 0.3446 | |
| CSSS | 0.2892 | 0.3057 | 0.2708 | 0.2853 | |
| CCCS | 0.2546 | 0.2734 | 0.2327 | 0.2517 | |
| Hyperbolic–paraboloidal shell | SSSS | 0.1893 | 0.1976 | 0.1804 | 0.1881 |
| CCCC | 0.3703 | 0.3879 | 0.3506 | 0.3671 | |
| CCSS | 0.3056 | 0.3238 | 0.2848 | 0.3038 | |
| CSCS | 0.3469 | 0.3625 | 0.3298 | 0.3443 | |
| CSSS | 0.2865 | 0.3031 | 0.2680 | 0.2851 | |
| CCCS | 0.2566 | 0.2752 | 0.2349 | 0.2532 | |
| Type of Shells | a/h | ||||
|---|---|---|---|---|---|
| 5 | 10 | 20 | 30 | ||
| Plate | 0.5 | 1.4689 | 0.4559 | 0.1231 | 0.0556 |
| 1 | 0.7077 | 0.1984 | 0.0513 | 0.0230 | |
| 2 | 0.5230 | 0.1437 | 0.0369 | 0.0165 | |
| 3 | 0.4952 | 0.1358 | 0.0348 | 0.0156 | |
| Cylindrical shell | 0.5 | 1.4715 | 0.4587 | 0.1260 | 0.0584 |
| 1 | 0.7092 | 0.2004 | 0.0535 | 0.0251 | |
| 2 | 0.5226 | 0.1440 | 0.0374 | 0.0170 | |
| 3 | 0.4944 | 0.1356 | 0.0350 | 0.0157 | |
| Spherical shell | 0.5 | 1.4749 | 0.4620 | 0.1294 | 0.0617 |
| 1 | 0.7164 | 0.2071 | 0.0597 | 0.0307 | |
| 2 | 0.5276 | 0.1486 | 0.0417 | 0.0210 | |
| 3 | 0.4973 | 0.1383 | 0.0375 | 0.0181 | |
| Elliptical–paraboloid shell | 0.5 | 1.4741 | 0.4609 | 0.1282 | 0.0605 |
| 1 | 0.7137 | 0.2045 | 0.0572 | 0.0286 | |
| 2 | 0.5255 | 0.1466 | 0.0399 | 0.0193 | |
| 3 | 0.4960 | 0.1371 | 0.0363 | 0.0170 | |
| Hyperbolic–paraboloidal shell | 0.5 | 1.4652 | 0.4552 | 0.1235 | 0.0562 |
| 1 | 0.7049 | 0.1976 | 0.0511 | 0.0229 | |
| 2 | 0.5219 | 0.1438 | 0.0374 | 0.0170 | |
| 3 | 0.4947 | 0.1361 | 0.0354 | 0.0162 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melaibari, A.; Daikh, A.A.; Basha, M.; Wagih, A.; Othman, R.; Almitani, K.H.; Hamed, M.A.; Abdelrahman, A.; Eltaher, M.A. A Dynamic Analysis of Randomly Oriented Functionally Graded Carbon Nanotubes/Fiber-Reinforced Composite Laminated Shells with Different Geometries. Mathematics 2022, 10, 408. https://doi.org/10.3390/math10030408
Melaibari A, Daikh AA, Basha M, Wagih A, Othman R, Almitani KH, Hamed MA, Abdelrahman A, Eltaher MA. A Dynamic Analysis of Randomly Oriented Functionally Graded Carbon Nanotubes/Fiber-Reinforced Composite Laminated Shells with Different Geometries. Mathematics. 2022; 10(3):408. https://doi.org/10.3390/math10030408
Chicago/Turabian StyleMelaibari, Ammar, Ahmed Amine Daikh, Muhammad Basha, Ahmed Wagih, Ramzi Othman, Khalid H. Almitani, Mostafa A. Hamed, Alaa Abdelrahman, and Mohamed A. Eltaher. 2022. "A Dynamic Analysis of Randomly Oriented Functionally Graded Carbon Nanotubes/Fiber-Reinforced Composite Laminated Shells with Different Geometries" Mathematics 10, no. 3: 408. https://doi.org/10.3390/math10030408
APA StyleMelaibari, A., Daikh, A. A., Basha, M., Wagih, A., Othman, R., Almitani, K. H., Hamed, M. A., Abdelrahman, A., & Eltaher, M. A. (2022). A Dynamic Analysis of Randomly Oriented Functionally Graded Carbon Nanotubes/Fiber-Reinforced Composite Laminated Shells with Different Geometries. Mathematics, 10(3), 408. https://doi.org/10.3390/math10030408






