Abstract
We introduce a generalized adjacency matrix in order to distinguish cospectral graphs. Our reasoning is motivated by the work of Johnson and Newman and properties of p-adic numbers. Using a polynomial time algorithm, we comment on computer experiments with which we can distinguish cospectral (non-isomorphic) graphs.
MSC:
05C60; 68R05
1. Introduction and Motivation
Two undirected graphs are called isomorphic if between their vertex sets there exists a one-to-one correspondence such that any pair of vertices is adjacent in one graph if, and only if, the corresponding pair of vertices is adjacent in the other graph. The graph isomorphism problem is to decide whether two given graphs are isomorphic or not. Recently, Babai [1] found a quasi-polynomial algorithm; nevertheless, the graph isomorphism problem is not known to be solvable in polynomial time in general (nor to be NP-complete). For subfamilies, however, there exist fast algorithms, e.g., for the easy case of trees [2] as well as for the much more advanced case of circulant graphs by Muzychuk et al. [3] (by using Schur ring theory). In both examples, the corresponding algorithms run indeed in polynomial time.
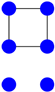
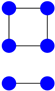
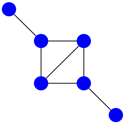
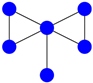
Obviously, if two graphs are isomorphic, they need to have the same number of vertices, edges, connected components, degree sequence, etc. Moreover, their adjacency matrices have to be equal up to permutations of the rows (or columns), hence their spectrum (of eigenvalues counting multiplicities) is identical. Unfortunately, one cannot distinguish two non-isomorphic graphs by their spectra in general; the least example (with respect to the number of vertices) is given by the following graphs:
Both adjacency matrices have the same characteristic polynomial ; however, the graphs are not isomorphic since one graph is connected and the other one is not. Note that here and in the sequel we define the characteristic polynomial of a matrix A by .
Two non-isomorphic graphs having an identical spectrum are said to be cospectral (or isospectral); we shall use the same word as well for the adjacency matrices associated with these graphs. For an enumeration of such pairs of cospectral graphs, we refer to [4] and for a construction to [5].
Already in 1980, Johnson and Newman [6] suggested to use a generalized adjacency matrix in order to distinguish non-isomorphic graphs. For these “algebraic accidents”, as they have called cospectral graphs, they have replaced the numbers 1 and 0 in the entries of the classical adjacency matrices (standing for ‘adjacent’, resp. ‘not adjacent’) by formal quantities x and y. It is not difficult to see that it is no restriction to normalize , and then the generalized adjacency matrices are
in place of the classical adjacency matrices of the given graphs and , respectively; here, J denotes the matrix and each of whose entries is equal to 1. With this simple but ingenious idea Johnson and Newman [6] were able to prove that the generalized adjacency matrices are cospectral for all x if, and only if, the classical adjacency matrices of the graphs, and those of their complements are cospectral. We shall call such a generalized adjacency matrix the Johnson–Newman adjacency matrix. For the above example of a pair of cospectral graphs (in Figure 1 and Figure 2), the Johnson–Newman adjacency matrices are given by
(resp. permutations thereof). The associated characteristic polynomials of these Johnson–Newman adjacency matrices and are different:
Consequently, the underlying graphs are non-isomorphic. Unfortunately, this idea has limits (as was already noted by Johnson and Newman [6]; see also page 4 below). For further information on this topic, we refer to [7,8,9,10,11].
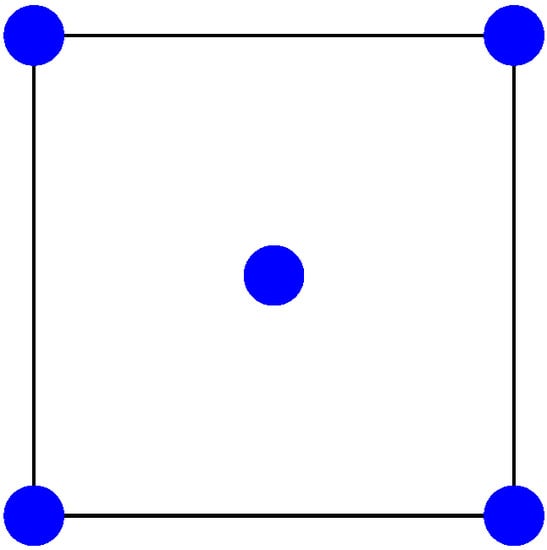
Figure 1.
plus an isolated vertex.
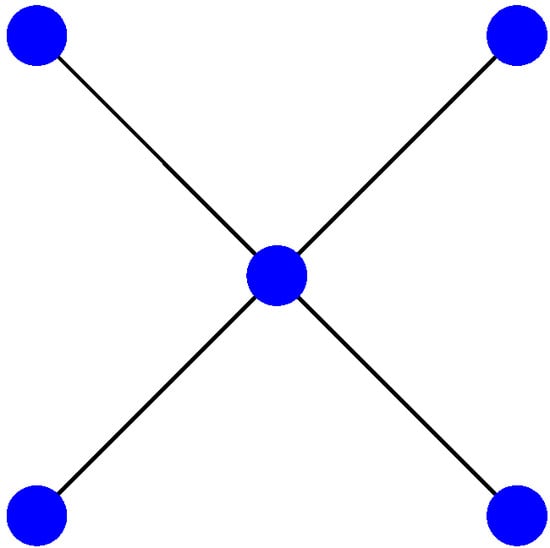
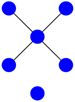
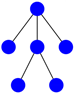
Figure 2.
The star with five vertices.
In this note, we propose another, though not unrelated, approach for distinguishing cospectral graphs and matrices, respectively. In the sequel, we assume that every graph is undirected and simple (i.e., without multiple edge and without loop).
2. p-Adic Numbers
Given a prime number p, the set of p-adic numbers is the completion of the field ℚ of rational numbers with respect to the p-adic absolute value on ℚ, defined by
where
(as follows from the unique prime factorization ). Hence, an integer has a small p-adic absolute value if it is divisible by a high power of p.
It is not difficult to see that is a complete field with respect to the continuation of the p-adic absolute value. A p-adic number is called a p-adic integer if . The set of p-adic integers constitute a commutative ring and one can represent its elements by power series in p, namely
p-adic numbers have been introduced by Hensel in the 1890s; for the basic properties, we refer to [12].
Our first aim is to extend a theorem of Johnson and Newman [6] about cospectral graphs from the field ℝ of real numbers to a p-adic field .
Theorem 1.
Let and be two graphs, each of which on n vertices and denoted by their associated Johnson–Newman adjacency matrices. For every prime number p, there exists a computable p-adic number , depending only on the number of vertices n, such that the respective characteristic polynomials and are identical in x if, and only if,
Our proof is following the original one; only the p-adic topology makes a difference: For , let
Then, and are not identical if, and only if, there exists an index j such that
is not identically vanishing (as a function of x). We observe that is a polynomial in x of degree at most (as follows from Leibniz’s representation theorem of determinants). Moreover, its largest coefficient is bounded by a function , depending only on n and j (namely, bounded by by Hadamard’s inequality). Taking into account the concept of Newton polygons, the p-adic absolute value of the roots of any polynomial over is ruled by the slopes of the associated polygon, hence any p-adic number of sufficiently large p-adic value will yield
unless and are identical. This implies the result of the theorem.
The only difference in our reasoning is the bound for the zeros of for which Johnson and Newman suggest 1 plus the largest of the absolute values of the coefficients (as follows from a straightforward application of Rouché’s theorem from complex analysis), which gives
(see [13]). In the p-adic context, the concept of Newton polygons serves as a substitute (see [12]). We should mention that there is no practical benefit of the p-adic version of the theorem of Johnson and Newman since, with the characteristic polynomials of the Johnson–Newman adjacency graphs, their difference is also defined over , and hence the p-adic counterpart is equal to this very polynomial. The challenging question is whether this polynomial vanishes identically or not.
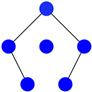
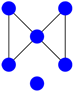
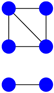
Concerning their result, Johnson and Newman [6] remarked that an application of the test embodied in (their) Theorem 1 to the seven cospectral pairs listed in [14] distinguishes six of them. The undistinguished pair is given by Figure 3 and Figure 4 below:
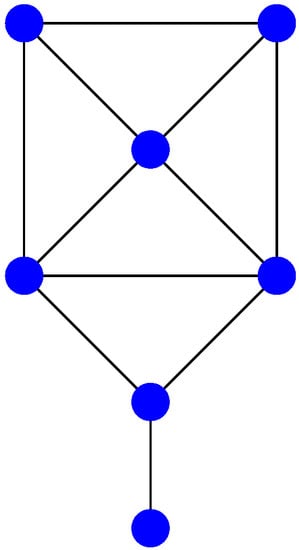
Figure 3.
The first cospectral graph with seven vertices.
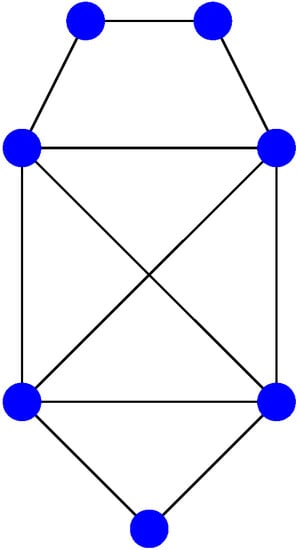
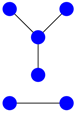
Figure 4.
The second cospectral graph with seven vertices.
In fact, the authors of [6] have overlooked another graph cospectral to this, namely Figure 5 above (see [14]). The latter three graphs all have the characteristic polynomial
A trio of three cospectral graphs is just an example of how large a set of cospectral graph can be. In fact, Harary et al. [14] showed that, for any positive integer m, there exists an integer n such that there are m cospectral graphs with n vertices.
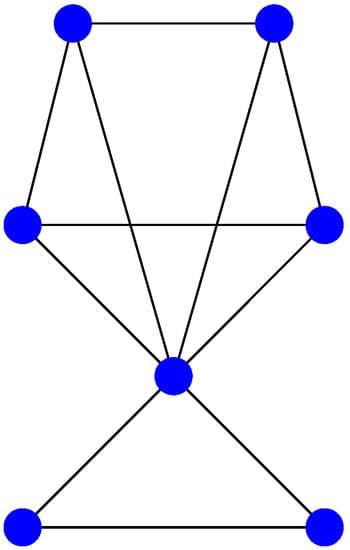
Figure 5.
The third cospectral graph with seven vertices.
3. A New Approach
The advantage of the idea of Johnson and Newman to replace the zeros in the adjacency matrices by a variable is its simplicity; however, examples show the limitations of this approach. Another related idea could be to replace an entry with some explicit number that is related to the configuration around the missing edge in the graph. Recalling that integers which are divisible by a large power of a prime number p have a small p-adic value, which means that they are close to zero in the p-adic topology, one may try to use p-adic integers here.
Of course, there are many ways to generalize the concept of adjacency matrix by replacing the zero entries with p-adic numbers carrying graph theoretical information. After some computer experiments, we suggest the following replacements:
Given a graph G with vertex set and associated adjacency matrix , we define the generalized adjacency matrix by setting and
where is the number of paths of length from i to j (or vice versa), where an edge is added between i and j if there is none (or ). Here, a path is defined to contain no repeated vertex (see [15]). Moreover, by definition, every entry is a polynomial in p.
Then, obviously, . The question is what can be achieved by this generalized adjacency matrix. Note that the generalized adjacency matrix B is not identical with the formal series for the classical adjacency matrix , i.e.,
We illustrate the definition from above with the most simple example of a pair of cospectral graphs from the introduction (given by Figure 1 and Figure 2). Their classical adjacency matrices are given by
These lead to the following generalized adjacency matrices
The characteristic polynomials of these generalized adjacency matrices and are given by
and
respectively. These two characteristic polynomials agree modulo p. Since their difference is
it follows that the underlying graphs are not isomorphic.
In addition, for the three cospectral graphs behind Figure 3, Figure 4 and Figure 5, the characteristic polynomials differ pairwise. In order to see this, we introduce the notion of a signature to any given generalized adjacency matrix B. This signature, denoted as , is defined by the degrees of the polynomials in p appearing as the coefficients of in the associated characteristic polynomial ; if the coefficient of is vanishing, we define .
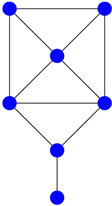
For example, the generalized adjacency matrix associated with the graph of Figure 3 is given by
We observe that the associated signature is given by . In addition, for the other two cospectral graphs, we obtain the signatures and (see Appendix A for the characteristic polynomials of the generalized adjacency matrices). Since these signatures are pairwise different, the underlying three copsectral graphs are pairwise non-isomorphic.
4. Further Examples on Six and Sixteen Vertices
There are five pairs of cospectral graphs on six vertices (see [4]). In the sequel, we list them, their classical adjacency matrices and the associated signature defined in the previous section.
Since the signatures in all these examples (in Table 1) are different, there is no pair of isomorphic graphs among them.

Table 1.
All cospectral graphs with six vertices.
We conclude our computer experiments by another example of a pair of cospectral graphs on a comparably large number of vertices, namely by the graph product and the Shrikhande graph (Shrikhande [16] showed that the graph named after him plays a special role in the classification of strongly regular graphs.) (which both appear to be Cayley graphs of the same group ).
Probably, the easiest way to distinguish these 6-regular graphs on 16 vertices is by considering the neighbourhood of an arbitrary vertex (consisting of the adjacent vertices and the edges in between). For , the neighbourhood is the disjoint union of two circles , each of which are on three vertices, while, for the Shrikhande graph, the neighbourhood is a circle on six vertices (as illustrated in the coloured Figure 6 and Figure 7).
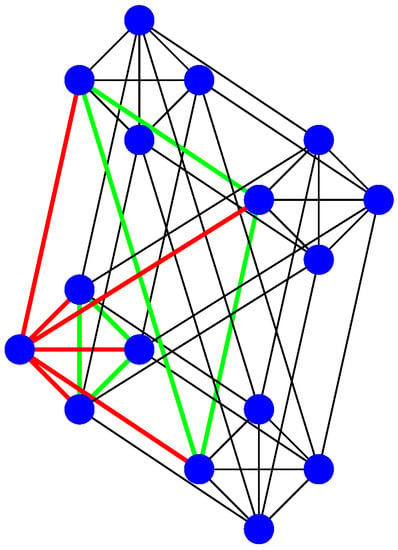
Figure 6.
.
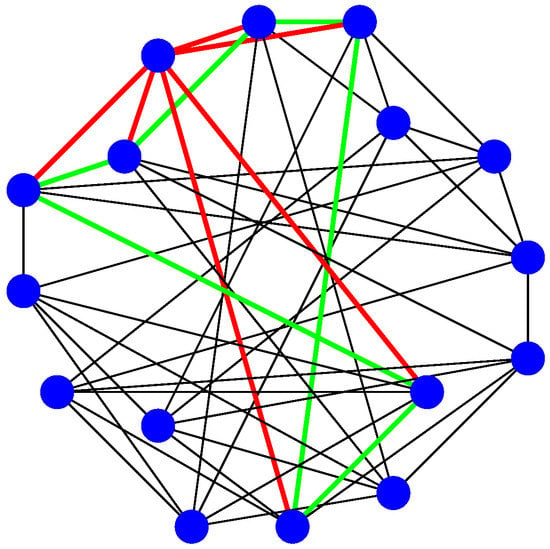
Figure 7.
Shrikhande graph.
The signatures of these two graphs are the same and equal to
Consequently, the signature does not allow for distinguishing these cospectral graphs (which is probably related to the fact that they arise as Cayley graphs from the same group); the generalized adjacency matrix, however, is doing the job: the difference between the respective characteristic polynomials of this pair is of the form
where is a polynomial in the variable p of degree d, and is explicitly given in Appendix B.
5. A (Probably) Polynomial Time-Algorithm and Concluding Remarks
Our computer experiments were realized with a (probably) polynomial time algorithm.
In the Algorithm 1,
- The set L is the collection of all permutations of a set consisting of e 1’s and 0s;
- The set M is the collection of all matrices having v vertices and e edges;
- The set C is the collection of classes of cospectral graphs (up to isomorphism);
- The set P is the set of characteristic polynomials which are correspondence with C.
The outline of each step in Algorithm 1:
- Step 1–2: Setting all parameters;
- Step 3: Construct all matrices having v vertices and e edges;
- Step 4: Classify a cospectral graph;
- Step 5: Return all classes of a cospectral graph.
| Algorithm 1 Find cospectral graph: |
|
Source code (Mathematica) 1 (Find cospectral graph).
list[v_,e_]:=(
A={};
For[i=1,i<=e,i++,AppendTo[A,1]];
For[i=e+1,i<=v∗(v-1)/2,i++,AppendTo[A,0]];
Return[A])
genmat[v_,e_]:=(
mattemp={};
permu=Permutations[list[v,e]];
For[k=1,k<=Length[permu],k++,
xtemp=permu[[k]];
M=Insert[Insert[xtemp~Internal`PartitionRagged~Range[v-1,1,-1]
~Flatten~{2},0,{1,1}],{0},v]//PadLeft;
M2=M+Transpose[M];
AppendTo[mattemp,M2]];
Return[mattemp])
cospec[v_,e_]:=(
allmatrices=genmat[v,e];
characteristic=SplitBy[SortBy[Table[
{i,CharacteristicPolynomial[allmatrices[[i]],$\lambda$]},
{i,1,Length[allmatrices]}],Last],Last];
data={};
For[i=1,i<=Length[characteristic],i++,AppendTo[data,Flatten[
Transpose[Drop[characteristic[[i]],{},{2}]]]]];
cospectral={};
For[i=1,i<=Length[characteristic],i++,
some=data[[i]];
matrixlist=Table[allmatrices[[some[[i]]]],{i,1,Length[some]}];
If[Length[matrixlist]==1,
AppendTo[cospectral,matrixlist],
temp={matrixlist[[1]]};
For[j=2,j<=Length[matrixlist],j++,
check=0;
For[k=1,k<=Length[temp],k++,
If[IsomorphicGraphQ[AdjacencyGraph[matrixlist[[j]]],
AdjacencyGraph[temp[[k]]]],
check=check+2;
Break[]]];
If[check==0,
AppendTo[temp,matrixlist[[j]]]]];
AppendTo[cospectral,temp]]];
For[i=1,i<=Length[cospectral],i++,
If[Length[cospectral[[i]]]!=1,
Print[cospectral[[i]]]]])
The example (for and ) of the above algorithm is shown in Appendix C.
Source code (Mathematica) 2 (Generalize Matrix).
pathlength[A_,i_,j_,l_]:=Length[FindPath[AdjacencyGraph[A],i,j,{l},All]]
entry[A_,i_,j_]:=Sum[pathlength[A,i,j,l]p^(l-1),{l,1,Length[A]}]
mat[A_]:=Table[Table[entry[A,i,j],{i,1,Length[A]}],{j,1,Length[A]}]
charac[A_]:=CharacteristicPolynomial[mat[A],$\lambda$]
Of course, it is not essential for our approach that p is a prime number; however, we found the p-adic way of thinking that p-adic integers (resp. p-adic power series) with only large exponents are p-adically close to zero rather useful.
The number of cospectral graphs is exploding with an increasing number of vertices, although their proportion within the set of all graphs is probably tending to zero (see [4]). Thus, we had to stop our computer experiments at some point, but we are quite optimistic that our algorithm allows for distinguishing many cospectral graphs in (probably) polynomial time.
6. Conclusions
We introduce a generalized adjacency matrix in Section 3 to distinguish some cospectral graphs. These were shown in Section 3 and Section 4. Furthermore, an algorithm (which may be improved) for computer programming is presented in Section 5. Unfortunately, we could not prove that our approach is successful for all cospectral graphs or at least for certain families. We invite the dear reader to continue our studies.
Author Contributions
Conceptualization, J.S. and J.T.; methodology, S.W., J.S. and J.T.; software, S.W.; validation, S.W., J.S. and J.T.; formal analysis, J.S.; investigation, S.W., J.S. and J.T.; writing—original draft preparation, J.S.; writing—review and editing, S.W., J.S. and J.T.; visualization, J.T.; supervision, J.S.; project administration, J.T.; funding acquisition, J.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research Council of Thailand (NRCT) and Walailak University Grant No. NRCT5-RSA63019-06 (2563NRCT322800).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the anonymous referee for his or her valuable comments and corrections.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Figure 3.
Table A1.
Figure 3.
| Original Adjacency Matrix | Graph | Signature |
|---|---|---|
 |
Its generalized characteristic polynomial is

Table A2.
Figure 4.
Table A2.
Figure 4.
| Original Adjacency Matrix | Graph | Signature |
|---|---|---|
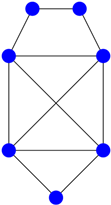 |
Its generalized characteristic polynomial is

Table A3.
Figure 5.
Table A3.
Figure 5.
| Original Adjacency Matrix | Graph | Signature |
|---|---|---|
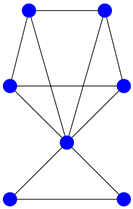 |
Its generalized characteristic polynomial is
Appendix B
Below we provide the polynomial (appearing in Section 3):
Appendix C
We note an example from the algorithm (Algorithm 1) in Section 5 with six vertices and four edges ().
In the setting, the number of elements in the set M (which is equal to L (in the beginning)) is . Then, the set
and
(the order is important) where


Table A4.
All classes of cospectral graphs with six vertices and four edges.
Table A4.
All classes of cospectral graphs with six vertices and four edges.
| Class | Characteristic Polynomial | Graph | |
| 1 | 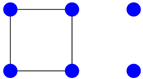 | 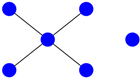 | |
| 2 |  | ||
| 3 |  | 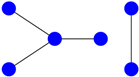 | |
| 4 | 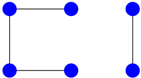 | ||
| 5 | 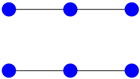 | ||
| 6 | 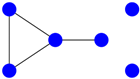 | ||
| 7 | 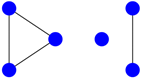 | ||
Using the generalized matrix in Section 4, the graphs and are non-isomorphic. Thus, the graphs are and .
References
- Babai, L. Group, graphs, algorithms: The graph isomorphism problem. In Proceedings of the International Congress of Mathematicians, Rio de Janeiro, Brazil, 1–9 August 2018. [Google Scholar]
- Busacker, R.G.; Saaty, T.L. Finite Graphs and Networks; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Muzychuk, M.; Klin, M.; Pöschel, R. The isomorphism problem for circulant graphs via Schur ring theory. Codes Assoc. Schemes 1999, 56, 241–264. [Google Scholar]
- Haemers, W.H.; Spence, E. Enumeration of cospectral graphs. Eur. J. Comb. 2004, 25, 199–211. [Google Scholar] [CrossRef]
- Mönius, K. Constructions of isospectral circulant graphs. Elem. Math. 2020, 75, 45–57. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.; Newman, M. A Note on Cospectral Graphs. J. Comb. Theory 1980, 28, 96–103. [Google Scholar] [CrossRef]
- van Dam, E.R.; Haemers, W.H.; Koolen, J.H. Cospectral graphs and the generalized adjacency matrix. Linear Algebra Appl. 2007, 423, 33–41. [Google Scholar] [CrossRef]
- van Dam, E.R.; Haemers, W.H. Developments on spectral characterizations of graphs. Discrete Math. 2009, 309, 576–586. [Google Scholar] [CrossRef]
- van Dam, E.R.; Haemers, W.H. Which graphs are determined by their spectrum? Linear Algebra Appl. 2003, 373, 241–272. [Google Scholar] [CrossRef]
- Wang, W. A simple arithmetic criterion for graphs being determined by their generalized spectra. J. Comb. Theory Ser. B 2017, 122, 438–451. [Google Scholar] [CrossRef]
- Wang, W.; Xu, C.-X. A sufficient condition for a family of graphs being determined by their generalized spectra. Eur. J. Comb. 2005, 27, 826–840. [Google Scholar] [CrossRef]
- Koblitz, N. p-adic Numbers, p-adic Analysis, and Zeta-Functions, 2nd ed.; Springer: New York, NY, USA, 1984. [Google Scholar]
- Prasolov, V. Polynomials; Springer: New York, NY, USA, 2004. [Google Scholar]
- Harary, F.; King, C.; Mowshowitz, A.; Read, R. Cospectral graphs and digraphs. Bull. Lond. Math. Soc. 1971, 3, 321–328. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Shrikhande, S.S. The uniqueness of the L2 association scheme. Ann. Math. Stat. 1959, 30, 781–798. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).