Swarm-Inspired Computing to Solve Binary Optimization Problems: A Backward Q-Learning Binarization Scheme Selector

Abstract

In recent years, continuous metaheuristics have been a trend in solving binary-based combinatorial problems due to their good results. However, to use this type of metaheuristics, it is necessary to adapt them to work in binary environments, and in general, this adaptation is not trivial. The method proposed in this work evaluates the use of reinforcement learning techniques in the binarization process. Specifically, the backward Q-learning technique is explored to choose binarization schemes intelligently. This allows any continuous metaheuristic to be adapted to binary environments. The illustrated results are competitive, thus providing a novel option to address different complex problems in the industry.

1. Introduction

The resolution of real problems can be approached through mathematical modeling to find a solution with an optimization algorithm [1]; under this scheme, it is increasingly common for different industries to solve combinatorial problems for their normal operation to minimize costs and times, as well as maximize profits. Such is the case of the forestry industry [2], flight planning for unmanned aircraft [3], or the detection of cracks in pavements [4]. Combinatorial problems are mostly NP-hard, which makes it difficult to find solutions with polynomial-time algorithms [5], which is why the use of intelligent optimization algorithms, mainly metaheuristics (MHs) [6], have considerably supported the growth of combinatorial problem solving; through their search processes, they manage to intelligently explore the search space, finding quasi-optimal solutions in reasonable computational times.

MHs are general-purpose algorithms widely used to solve optimization problems. Talbi in [7] indicated that metaheuristics can be classified according to how they perform the search process. Single-solution metaheuristics transform a single solution during the search process. Some classic examples of this type of metaheuristics are simulated annealing [8] and tabu search [9]. On the other hand, population-based metaheuristics are a set of solutions that are evolved as the optimization process progresses. Some classic examples of this type of metaheuristics are particle swarm optimization [10], cuckoo search [11], and the generic algorithm [12]. In the literature, population-based metaheuristics are more widely used than single-solution metaheuristics.

The no-free-lunch (NFL) theorem [13] tells us that there is no optimization algorithm that is good at all optimization problems. This theorem motivates researchers to keep developing new innovative algorithms. Thanks to this theorem, new metaheuristics have been created with very good performance. These good metaheuristics are grey wolf optimization [14], the whale optimization algorithm [15], and the sine–cosine algorithm (SCA) [16].

The grey wolf optimizer has been used for example in feature selection [17], training neural networks [18], optimizing support vector machines [19], designing and tuning controllers [20], economic dispatch problems [21], robotics and path planning [22], and scheduling [23].

The whale optimization algorithm has been used for example in optimal power flow problem [24], the economic dispatch problem [25], the electric vehicle charging station locating problem [26], image segmentation [27], feature selection [28], drug toxicity prediction [29], and $C{O}_2$ emissions prediction and forecasting [30].

The sine–cosine algorithm has been used for example in the trajectory controller problem [31], feature selection [32], power management [33], network integration [34], engineering problems [35], and Image processing [36].

The grey wolf optimizer, sine–cosine algorithm, and whale optimization algorithm have been developed to perform in continuous domains; however, there are a small number of techniques that are capable of operating in binary and continuous domains, as is the case of genetic algorithms [37] and some variations of ant colony optimization (ACO) [38]. However, they have not been able to obtain the performance obtained by continuous metaheuristic techniques that use an operator capable of transforming their continuous solutions to binary space. In recent years, there has been an increase in the literature on new and novel binarization operators, such as those based on machine learning, specifically clustering techniques such as K-means [39] and DB-scan [40], based on reinforcement learning, such as Q-learning [41] and SARSA [42], among other inspirations, such as quantum [43], logical operators [44], crossovers [45], and percentiles [46]. Among the most-common and -used operators is the two-step operator, which consists of normalizing the continuous values through a transfer function (Step 1) to be subsequently binarized an approximation rule, finally obtaining a value of 0 or 1 (Step 2) [47]. In this context, it is necessary to continue the search for new variations of binarization techniques, since it has been proven that they directly influence the performance of the MHs [48,49,50,51,52].

In this work, we propose a new intelligent operator using a binarization scheme selection (BSS) capable of adapting any continuous MHs to work in the binary domain. BSS is based on the two-step technique, where employing an intelligent operator, the transfer function, and the binarization rules to be used are chosen; this scheme was first proposed in [53]. BSS has been previously used with reinforcement learning techniques within the machine learning umbrella: Q-learning and SARSA; in this case, a new intelligent operator called backward Q-learning (BQSA) [54] is presented, which is a combination between Q-learning and SARSA, updating the Q-values by SARSA and in a delayed way with Q-learning. On the other hand, the set of schemes of this proposal is more extensive, going from 40 possible combinations to 80. All of the above points to the need to investigate hybrid methods to improve the algorithm’s performance. The contributions made as a result of this work are presented below:

• The implementation of a BSS, as a binarization operator capable of operating in any continuous MH.
• The use of the BQSA as an smart operator in BSS.
• A larger set of transfer functions obtained from the literature, which generates an increase from 40 to 80 possible binarization schemes to be used.

Experimental tests were carried out against multiple state-of-the-art binarization strategies that solve the set covering problem. Among the results obtained, there are considerably competitive performances for the proposed work, but not having statistically significant differences, although the difference with static versions is validated. In these quantitative comparisons, we can observe differences in the convergence behavior between the 80 and 40 actions versions, as well as the balance between exploration and exploitation.

The rest of the paper is structured as follows: Section 2 presents the work related to metaheuristic techniques, machine learning, and their hybridization. Section 3 presents the proposal for the incorporation of the BQSA in BSS, while in Section 4, its implementation is validated with the results obtained and the respective statistical tests, ending with the analysis and conclusions in Section 5.

2. Related Work

In the following subsections, we present some of the concepts necessary to internalize the work.

2.1. Reinforcement Learning

Machine learning (ML) aims to analyze data in the search of patterns and to develop predictions obtaining future results [55]; when decomposing ML, we can find four main types (Figure 1): supervised, unsupervised, semi-supervised, and reinforcement learning (RL). In RL, an agent receives a set of instructions, actions, or guidelines with which it will then make its own decisions based on a process of reward and penalty to guide the agent toward the optimal solution to the problem.

Figure 1. Machine learning classification.

Under this basis, an RL agent is constituted by four sub-elements: policy; value function; reward function; the environment model; however, the latter is usually optional [56]. As a definition of these elements, we give the following:

• A policy defines the agent’s behavior at each instant of time, i.e., it is a mapping from the set of perceived states to the set of actions to be performed when the agent is in those states.
• The value function allows the agent to maximize the sum of total rewards in the long run. It calculates the value of a state–action pair as the total amount of rewards that the agent can expect to accumulate in the future, starting from the state it is in. Thus, the agent selects the action based on value judgments. Indeed, while the reward determines the immediate and intrinsic desirability of a state–action pair, the value indicates the long-term desirability of a state–action pair considering likely future state–action pairs and their rewards.
• A reward function represents the agent’s goal, i.e., it translates each perceived state–action pair into a single number. In other words, a reward indicates the intrinsic desirability of that state–action pair. It is a way of communicating to the agent what the agent wants to obtain, but not how to achieve it.
• An environment model is intended to reproduce the behavior of the environment, i.e., the model that directs the agent to the next state and the subsequent reward based on the current state–action pair. The environment model is not always available and is therefore an optional element.

Among the existing RL classifications, we find the temporal difference techniques [57], where the Q-learning (QL) algorithm is the most popular for its contributions in several areas [58]. Still, there are other algorithms, such as SARSA [59] and the BQSA [54], which are variations of QL, but have obtained different performances for different problems.

2.2. Q-Learning

Among the algorithms present in RL, we find the QL algorithm first proposed in [60], which provides agents with the ability to learn to act optimally without the need to build domain maps. Having several possible s states, where from the “environment”, we obtain the current s in which the agent interacts and performs decisions. The agent has a set of possible actions which affect the reward and the next state. Once an action is performed, the state changes. When changing state, the agent receives a reward for the decision made. Where the rewards received by the agent consequently generate learning in the agent. To solve the problem, the agent learns the best course of action it can take, which has a maximum cumulative reward. The sequence of actions from the first state to the terminal state is called an episode. The transition of states is given by the Equation (1).

$$Q_{new}(s_t,a_t)=(1-\alpha )·Q_{old}(s_t,a_t)+\alpha ·[r_n+\gamma ·maxQ(s_{t+1},a_{t+1})]$$

(1)

where $Q_{new}(s_t,a_t)$ is nominating the reward of the action taken in state $s_t$ and $r_n$ is the reward received when action $a_t$ is taken, $maxQ(s_{t+1},a_{t+1})$ is the maximum value of the action for the next state, the value of $\alpha$ must be $0<\alpha \le 1$ and corresponds to the learning factor. On the other hand, the value of $\gamma$ must be $0\le \gamma \le 1$ and corresponds to the discount factor. If $\gamma$ reaches the value of 0, only the immediate reward will be considered, while as it approaches 1, the future reward receives greater emphasis relative to the immediate reward. QL is algorithmically presented with the following Algorithm 1:

Algorithm 1 Q-learning.

1: Initialize$Q(s,a)$   2: for each episode do   3:     Initialize state s   4:     while $s\ne s_{terminal}$ do   5:         Choose action a from state s   6:         Take action a   7:         Observe reward r   8:         Observe next state $s^{\prime }$   9:         Update $Q(s,a)$ using Equation (1) 10:       $s\leftarrow s^{\prime }$ 11:     end while 12: end for

2.3. State-Action-Reward-State-Action

This is a method of RL that uses generalized policy iteration patterns, which consists of two processes that are performed simultaneously and interact with each other, where one performs the value function with the current policy, and at the same time, the other one improves the current policy. These two processes complement each other in each iteration, but each one does not need to be completed before the next one begins.

The learning agent learns the current value function derived from the policy currently in use. To understand how it works, the first step is to learn an action-value function instead of a state-value function. In particular, for the on-policy method, we must estimate $Q_{\pi }(s,a)$ for the current policy $\pi$ and all states s and actions a.

To understand the algorithm, let us consider the transitions as a pair of values, state–action to state–action, where the values of the state–action pairs are learned. These cases are identical: both are Markov chains with a rewarding process. The theorems that ensure convergence of state values also apply to the corresponding algorithm for action values, with Equation (2).

$$Q_{new}(s_t,a_t)=(1-\alpha )·Q_{old}(s_t,a_t)+\alpha ·[r_n+\gamma ·(s_{t+1},a_{t+1})]$$

(2)

After each transition the state is updated, until a terminal state is reached. When a state $s_{t+1}$ is terminal then $Q(s_{t+1}$, $a_{t+1})$ is defined as zero. Each transition process is composed of five events: $s_t,a_t,r_{t+1},s_{t+1},a_{t+1}$ (State-Action-Reward-State-Action), giving the name to the SARSA algorithm. The following is the Algorithm 2:

Algorithm 2 SARSA.

1: Initialize$Q(s,a)$   2: for each episode do   3:     Initialize state s   4:     Choose action a from state s   5:     while $s\ne s_{terminal}$ do   6:         Take action a   7:         Observe reward r   8:         Observe next state $s^{\prime }$   9:         Choose next action $a^{\prime }$ from next state $s^{\prime }$ 10:       Update $Q(s,a)$ using Equation (2) 11:       $s\leftarrow s^{\prime }$ 12:       $a\leftarrow a^{\prime }$ 13:     end while 14: end for

2.4. Backward Q-Learning

Backward Q-learning is another RL technique, although its name is similar to QL, it is not an ordinary Q-function update function (Equation (1)), this time, a backward update is added, hence the name backward Q-learning.

In this structure, action is directly affected, while the policy is indirectly affected. As the agent increases interaction with the environment, the agent’s precise knowledge also increases. Due to its structure, the agent can improve the learning speed, balance the explore–exploit dilemma and converge to the global minimum by using those previous states, actions, and information in an episode. Then, it is recorded that agents went through states, chose actions, and acquired rewards in an episode, and then this information will be used to update the Q-function again.

When the agent reaches the target state in the current episode, the produced data is used to update the Q-function backward. For example, state $s_0$ is defined as an initial state, and state $s_n$ is defined as a terminal state. The agent updates the Q-function N times from the initial state $s_0$ to the terminal state $s_n$ in an episode thanks to the recorded events: “s, a, r, s”. Therefore, we redefine Equation (1) of a step as:

$$\begin{array}{c}\hfill Q_{new}(s_t^i,a_t^i)⟵(1-\alpha )·Q(s_t^i,a_t^i)+\alpha ·[r_{t+1}^i+\gamma ·ma{x}_{a}Q(s_{t+1}^i,a_{t+1}^i)]\end{array}$$

(3)

where $i=1,2,\cdots ,N$ is the number of times the Q-function will be updated in the current episode. In turn, the agent simultaneously records the four events in $M^i$, represented mathematically with the Equation (4):

$$\begin{array}{c}\hfill M^i⟵s_t^i,a_t^i,r_t^i,s_{t+1}^i\end{array}$$

(4)

Once the agent reaches the terminal state, the agent will backward update the Q-function based on the information obtained from Equation (4) as follows (Equation (5)).

$$\begin{array}{c}\hfill Q_{new}(s_t^j,a_t^j)⟵(1-\alpha )·Q(s_t^j,a_t^j)+{\alpha }_b·[r_{t+1}^j+{\gamma }_b·maxQ(s_{t+1}^j,a_{t+1}^j)]\end{array}$$

(5)

where $j=N,N-1,N-2,\cdots ,1$, ${\alpha }_b$ and ${\gamma }_b$ are the learning and discount factors respectively for the backward update of Q-function. Algorithm 3 is added for a better understanding of the above.

Algorithm 3 Backward Q-learning.

1: Initialize arbitrarily all $Q(s,a)$, M and set $\alpha$ and $\gamma$   2: for each episode do   3:     Choose initialize state $s_t$   4:     Choose an action $a_t$ from state $s_t$   5:     while $N\ge 1$ do   6:         for each step in the episode do   7:              Execute the select action $a_t^i$ to the environment   8:              Observe reward $r_{t+1}$   9:              Observe new state $s_{t+1}^i$ 10:              Choose an action $a_{t+1}^i$ from state $s_{t+1}^i$ 11:              Record the four events in $M^i⟵s_t^i,a_t^i,r_t^i,s_{t+1}^i$ 12:              Update $Q(s_t^i,a_t^i)$ using the Equation (3) 13:              $s_t^i\leftarrow s_{t+1}^i$ 14:              $a_t^i\leftarrow a_{t+1}^i$ 15:              $i\leftarrow i+1$ 16:         end for 17:     end while 18:     for $j=N$ to 1 do 19:         Backward update $Q(s_t^j,a_t^j)$ using Equation (5) 20:     end for 21:     Initialize all M values 22: end for

2.5. Metaheuristics

MHs are used to solve optimization problems, which can be considered a strategy that guides and modifies other heuristics to produce solutions beyond those normally generated in a search for local optimality [61]. Blum and Roli [6] mention two main components of any metaheuristic algorithm, which are: diversification and intensification, also known as exploration and exploitation. Exploration means generating diverse solutions to explore the search space on a global scale, while exploitation is to focus the search on a local region, knowing that a good solution is found in this neighborhood. Global optimization can be achieved with a good combination of these two main components, as a good balance while selecting the best solutions will improve the convergence rate of the algorithms. Choosing the best solutions can ensure that the solutions converge to the optimum. At the same time, diversification through randomization allows the search from the local optimum to the whole search space, causing the diversity of the solutions to grow.

The great advantage of MHs is that they are able to generate near-optimal solutions in reduced computational times as opposed to exact methods and, in addition, they are able to adapt to the problem in contrast to heuristic methods [7].

A high percentage of MHs are nature-based; this is mainly because their development is based on some abstraction of nature. The existing taxonomy can be defined in various ways and in various sections of the MH if one wanted to dissect; at first, they can be classified as those based on the trajectory or based on population. A popular classification can be those presented by [62,63], decomposing the population-based ones into 4 main categories: physics-based, human-based, evolutionary-based and swarm-based (Figure 2). Furthermore, the taxonomy presented in [64] deepens in the main components that conform to these algorithms: the solution evaluation, parameters, encoding, initialization of the agents or the population, management of the population, operators, and finally, local search.

Figure 2. Nature-inspired metaheuristics.

Along this regard, and going deeper into the metaheuristic components and behavior, a metaheuristic can be represented algorithmically as a triple nested cycle. The first cycle corresponds to the iterations performed during the optimization process, the second cycle corresponds to the solutions obtained from the agents and finally, the third cycle corresponds to the dimensions associated with the problem. It is necessary to mention that within the third cycle, there is a $\Delta$ that is characteristic of each MH. In the Algorithm 4 the above mentioned is presented.

Algorithm 4 Discrete general scheme of metaheuristics.

1: Random initialization 2: for$iteration\left(t\right)$do 3:     for $solution\left(i\right)$ do 4:         for $dimension\left(d\right)$ do 5:            $X_{i,d}^{t+1}=X_{i,d}^t+\Delta$ 6:         end for 7:     end for 8: end for

2.6. Hybridizations

Hybridizations between MHs and other approaches have been thoroughly studied in the literature, among these approaches is ML including RL. Various authors propose taxonomies and types of interactions such as [65,66,67,68]. Optimization and ML approaches according to Song et al. [65] interact in four ways:

• Optimization supports ML.
• The ML supports the optimization.
• ML supports ML.
• Optimization supports optimization.

Interaction number 2 is also structured in the classification presented in [66,67], where the way it supports ML is at the problem level, replacing, for example, objective functions or constraints that are costly; at a low level, i.e., in the components or operators of the MH; and finally at a high level, where ML techniques can be used to choose between different MHs or components of an MH.

2.7. Binarization

As mentioned above, a high percentage of population-based metaheuristics are continuous in nature. Therefore, they are not suitable for solving binary optimization problems directly. Due to this reason, an adaptation to the context of the 0 and 1 domain is necessary. The two-step sequential mechanism and the BSS used in other works are detailed below [41,42].

Two-Step

Within the literature, the transfer from continuous to binary through the two-step mechanism is one of the most common. Its characteristic name is due to its sequential mechanism, where the first step consists of transferring from the reals to a bounded interval through transfer functions, i.e., $[0,1]$, then in the second step, by means of binarization rules, the bounded interval is transformed to a value of $\{0,1\}$. In the last few years, several transfer functions have been presented, among the most common ones are the S and V type functions [49], others exist such as the X [69,70], Z [71], U [72,73], Q [74], in the literature we can find versions that change during the iterative process by means of a decreasing parameter [75,76,77,78]

2.8. Binarization Scheme Selector

As mentioned in Section 1, other works proposed the idea of combining RL with MHs, following the framework proposed by Talbi et al. in [66,67], being born from this combination an intelligent selector based on the two-step technique mentioned above, called BSS. The breakthrough of this smart selector is that it is able to learn autonomously through trial and error which transfer function (first step) and binarization rule (second step) best fit in the binarization when obtaining the solutions of the optimization process. In the proposals [42], there are S-type and V-type transfer functions, and as binarization rules there are standard, static, complement, elitist and elitist roulette, resulting in a total of 40 possible combinations, combinations that the intelligent selector is able to determine which one to use in each iteration. Figure 3 shows in general how the BSS is applied, and the Algorithm 5 explains the operation of the BSS.

Algorithm 5 Binarization scheme selector.

1: Initialize a random swarm   2: Initialize Q-table   3: for$iteration\left(t\right)$do   4:     Select action $a_t$ for $s_t$ from the Q-table   5:     for $solution\left(i\right)$ do   6:         for $dimension\left(d\right)$ do   7:            $X_{i,d}^{t+1}⟵X_{i,d}^t+\Delta \left(a_t\right)$   8:         end for   9:     end for 10:     Get immediate reward $r_t$ 11:     Get the maximum Q-value for the next state $s_{t+1}$ 12:     Update Q-table using Equation (1) or Equation (2) 13:     Update the current state $s_t⟵s_{t+1}$ 14: end for

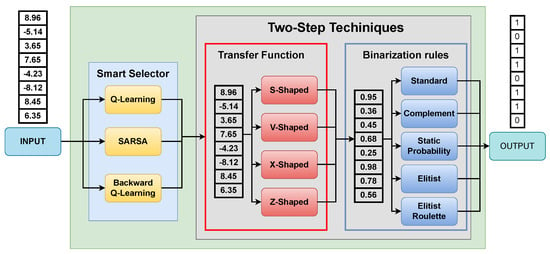
Figure 3. Binarization scheme selector.

3. The Proposal: Binarization Scheme Selector

As mentioned above, this work proposes to apply and integrate a new intelligent operator called the BQSA [54] integrated into the BSS. This time, it is necessary to modify the original BSS operation related to the way the BQSA operates, i.e., memory. We detail the modification in question in the Algorithm 6. Algorithm 6 is very similar to Algorithm 5 except for some differences, which are highlighted in black (Lines 14–17). First, we initialize the Q-table, M (where the events are recorded), N (the number of times the Q-function will be updated), and randomly the swarm. Then, at each iteration, a binarization scheme for the “exploration” or “exploitation” state is selected from the Q-table and then applied. Subsequently, we obtain the reward by applying the binarization scheme to then update the Q-values in the Q-table. Finally, as explained in Section 2.4, we record the four events $(s_t^i,a_t^i,r_t^i,s_{t+1}^i)$, once the iterations reach the same value as N, we start to perform the backward update of the Q-table.

Algorithm 6 Binarization scheme selector modified.

1: Initialize a random swarm   2: Initialize Q-table, M and N   3: for$iteration\left(t\right)$do   4:       Select action $a_t$ for $s_t$ from the Q-table   5:       for $solution\left(i\right)$ do   6:           for $dimension\left(d\right)$ do   7:              $X_{i,d}^{t+1}⟵X_{i,d}^t+\Delta \left(a_t\right)$   8:           end for   9:       end for 10:       Get immediate reward $r_t$ 11:       Get the maximum Q-value for the next state $s_{t+1}$ 12:       Update Q-table using Equation (3) 13:       Update the current state $s_t⟵s_{t+1}$ 14:       Record the four events in M 15:       if $t=N$ then 16:           Backward update Q-table using Equation (5) 17:       end if 18: end for

Another modification made to the BSS is the number of transfer functions with which it operates; in its original version, it has implemented eight functions in total, four transfer functions type S-shaped [49] and V-shaped [79] (see Figure 4a,b). The new ones added are the so-called X-shaped [69,70] and Z-shaped [71,80] types. Figure 4c,d and Table 1 show the details of the new transfer functions and the originals.

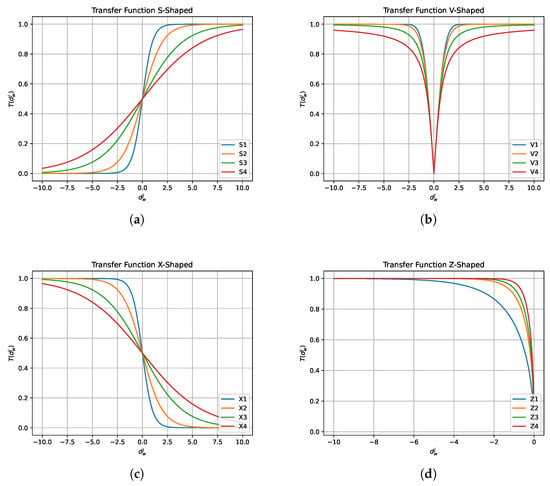
Figure 4. Transfer functions. (a) S-shaped; (b) V-shaped; (c) X-shaped; (d) Z-shaped.

Table 1. Transfer functions.

Transfer Functions
S-Shaped [49]		V-Shaped [49,79]		X-Shaped [69,70]		Z-Shaped [71,80]
Name	Equation	Name	Equation	Name	Equation	Name	Equation
S1	$T\left(d_w^j\right)=\frac{1}{1+e^{-2d_w^j}}$	V1	$T\left(d_w^j\right)=\left|erf\left(\frac{\sqrt{\pi }}{2}{d}_w^j\right)\right|$	X1	$T\left(d_w^j\right)=\frac{1}{1+e^{2d_w^j}}$	Z1	$T\left(d_w^j\right)=\sqrt{1-2^{d_w^j}}$
S2	$T\left(d_w^j\right)=\frac{1}{1+e^{-d_w^j}}$	V2	$T\left(d_w^j\right)=\left|tanh\left(d_w^j\right)\right|$	X2	$T\left(d_w^j\right)=\frac{1}{1+e^{d_w^j}}$	Z2	$T\left(d_w^j\right)=\sqrt{1-5^{d_w^j}}$
S3	$T\left(d_w^j\right)=\frac{1}{1+e^{\frac{-d_w^j}{2}}}$	V3	$T\left(d_w^j\right)=\left|\frac{d_w^j}{\sqrt{1+{\left(d_w^j\right)}^2}}\right|$	X3	$T\left(d_w^j\right)=\frac{1}{1+e^{\frac{d_w^j}{2}}}$	Z3	$T\left(d_w^j\right)=\sqrt{1-8^{d_w^j}}$
S4	$T\left(d_w^j\right)=\frac{1}{1+e^{\frac{-d_w^j}{3}}}$	V4	$T\left(d_w^j\right)=\left|\frac{2}{\pi }arctan\left(\frac{\pi }{2}{d}_w^j\right)\right|$	X4	$T\left(d_w^j\right)=\frac{1}{1+e^{\frac{d_w^j}{3}}}$	Z4	$T\left(d_w^j\right)=\sqrt{1-{20}^{d_w^j}}$

4. Experimental Results

To validate the performance of our proposal, a comparison of eight different versions of GWO, SCA, and WOA was carried out. Three of these versions incorporate BQSA, QL, and SARSA, where 80 binarization schemes were selected (80aBQSA, 80aQL, 80aSA). The other three versions of the final refer to incorporating BQSA, QL, and SARSA, where 40 binarization schemes were selected (40aBQSA,40aQL,40aSA). Finally, the last two use fixed binarization schemes. Regarding the binarization schemes and versions, it is necessary to mention that the schemes or also called actions are composed of the multiplication of the $\{TransferFunctions\times BinarizationRules\}$; in this case, we have four families of transfer functions with 4 functions each, 16 in total and 5 binarization rules: $16\times 5=80$. Regarding the versions mentioned and performed, 40aQL and 40aSA are the original versions of 40 actions (families S and V) applied to QL [41] and SARSA [42], respectively, in order to see the performance of our proposal, we replicated QL and SARSA, but this time in 80 actions and BQSA in both 40 and 80 actions. Finally, the versions in the middle, the first, BCL, uses the V4-Elitist [48]. The second, called MIR, uses the V4-Complement [49].

The benchmark instances of the set covering problem solved are those proposed in Beasley’s OR-Library [81]. In particular, we solved 45 instances delivered in this library.

The programming language used in the construction of the algorithms was Python 3.7, and it was executed with the free services of Google Colaboratory [82]. The results were stored and processed from databases provided by the Google Cloud Platform. The authors at [48] suggest making 40,000 calls to the objective function. To this end, we used 40 individuals from the population and 1000 iterations for all GWO, SCA, and WOA execution instances. 31 independent executions were performed for each executed instance. All parameters used for GWO, SCA, WOA, BQSA, QL, and SARSA are detailed in Table 2.

Table 2. Parameters’ setting.

Parameter	Value
Independent runs	31
Number of populations	40
Number of iterations	1000
parameter a of SCA	2
parameter a of GWO	decreases linearly from 2 to 0
parameter a of WOA	decreases linearly from 2 to 0
parameter b of WOA	1
parameter $\alpha$ of backward Q-learning, Q-learning and SARSA	0.1
parameter $\gamma$ of backward Q-learning, Q-learning and SARSA	0.4
parameter N of backward Q-learning	10

The results obtained from the experimentation process are summarized in the Table 3, Table 4 and Table 5, where the results are presented for each of the eight versions, and the 45 benchmark instances, wherein the first row the names of the versions are presented, in the second row, the titles that go as follows, the first column names the OR-Library instances used (Inst.), the second column the optimal value known for each of these instances (Opt.), while the following columns are titled in three columns the best result obtained in the 31 independent runs (Best), the average of these 31 runs (Avg), and finally the relative percentage deviation (RPD), which is defined in Equation (6). While in the last row, each column’s average results are presented to facilitate the comparison between versions.

$$\mathrm{RPD}=\frac{100·\left(Best-Opt\right)}{Opt}.$$

(6)

Table 3. Comparison of the metaheuristics’ GWO.

		80aBQSA			80aQL			80aSA			BCL			MIR			40aBQSA			40aQL			40aSA
Inst.	Opt.	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD
41	429	430.0	459.26	0.23	429.0	454.23	0.0	430.0	451.68	0.23	431.0	437.32	0.47	431.00	436.81	0.47	431.0	453.32	0.47	430.0	460.71	0.23	430.0	453.65	0.23
42	512	515.0	587.26	0.59	515.0	596.87	0.59	515.0	595.58	0.59	526.0	540.58	2.73	540.00	551.26	5.47	524.0	605.48	2.34	516.0	588.23	0.78	521.0	593.45	1.76
43	516	516.0	610.68	0.0	518.0	594.0	0.39	519.0	604.06	0.58	519.0	535.84	0.58	535.00	550.26	3.68	517.0	577.97	0.19	518.0	593.35	0.39	518.0	587.42	0.39
44	494	499.0	548.48	1.01	497.0	567.19	0.61	502.0	544.61	1.62	503.0	520.35	1.82	513.00	524.45	3.85	505.0	604.94	2.23	498.0	553.19	0.81	505.0	549.1	2.23
45	512	516.0	601.06	0.78	517.0	563.39	0.98	517.0	626.94	0.98	523.0	533.84	2.15	532.00	551.39	3.91	517.0	581.42	0.98	519.0	616.81	1.37	521.0	627.71	1.76
46	560	565.0	727.42	0.89	565.0	659.61	0.89	563.0	654.68	0.54	570.0	583.58	1.79	576.00	586.03	2.86	563.0	668.71	0.54	564.0	639.61	0.71	565.0	649.32	0.89
47	430	431.0	477.87	0.23	433.0	477.23	0.7	433.0	475.03	0.7	434.0	441.77	0.93	438.00	447.58	1.86	434.0	487.45	0.93	434.0	504.16	0.93	435.0	469.26	1.16
48	492	497.0	613.81	1.02	494.0	586.58	0.41	495.0	578.06	0.61	499.0	509.84	1.42	506.00	515.13	2.85	495.0	649.65	0.61	494.0	580.81	0.41	495.0	563.97	0.61
49	641	655.0	715.0	2.18	652.0	821.19	1.72	655.0	765.55	2.18	656.0	680.61	2.34	679.00	693.06	5.93	658.0	803.84	2.65	650.0	740.9	1.4	653.0	789.32	1.87
410	514	518.0	594.16	0.78	515.0	570.16	0.19	514.0	565.61	0.0	520.0	532.68	1.17	526.00	532.74	2.33	517.0	617.74	0.58	519.0	575.84	0.97	514.0	623.52	0.0
51	253	255.0	304.84	0.79	256.0	293.35	1.19	256.0	278.87	1.19	259.0	268.23	2.37	262.00	268.26	3.56	254.0	297.84	0.4	258.0	284.87	1.98	257.0	305.55	1.58
52	302	318.0	385.42	5.3	311.0	402.19	2.98	315.0	371.9	4.3	320.0	330.19	5.96	326.00	335.39	7.95	316.0	407.97	4.64	319.0	410.35	5.63	320.0	387.71	5.96
53	226	229.0	258.45	1.33	228.0	258.87	0.88	229.0	276.29	1.33	229.0	235.55	1.33	232.00	236.32	2.65	228.0	254.39	0.88	229.0	273.29	1.33	228.0	263.35	0.88
54	242	245.0	275.45	1.24	244.0	295.45	0.83	244.0	287.32	0.83	244.0	251.55	0.83	250.00	254.68	3.31	244.0	281.84	0.83	245.0	291.58	1.24	244.0	283.23	0.83
55	211	211.0	231.26	0.0	212.0	243.0	0.47	212.0	226.94	0.47	212.0	216.74	0.47	216.00	219.32	2.37	212.0	236.39	0.47	213.0	243.32	0.95	212.0	250.06	0.47
56	213	215.0	257.81	0.94	213.0	268.26	0.0	215.0	260.03	0.94	216.0	226.77	1.41	222.00	230.03	4.23	215.0	235.32	0.94	213.0	255.81	0.0	213.0	252.39	0.0
57	293	299.0	345.39	2.05	296.0	366.71	1.02	296.0	323.68	1.02	299.0	310.84	2.05	306.00	314.29	4.44	295.0	348.23	0.68	297.0	352.48	1.37	298.0	353.81	1.71
58	288	290.0	363.42	0.69	290.0	344.42	0.69	289.0	349.58	0.35	290.0	298.77	0.69	297.00	302.97	3.12	290.0	329.71	0.69	291.0	363.0	1.04	288.0	354.03	0.0
59	279	279.0	328.19	0.0	280.0	328.71	0.36	281.0	332.35	0.72	281.0	288.39	0.72	285.00	293.71	2.15	281.0	326.58	0.72	282.0	334.58	1.08	281.0	344.23	0.72
510	265	267.0	314.29	0.75	266.0	306.61	0.38	266.0	292.03	0.38	269.0	276.81	1.51	277.00	282.16	4.53	267.0	329.9	0.75	269.0	314.42	1.51	267.0	294.06	0.75
61	138	140.0	221.13	1.45	141.0	214.23	2.17	141.0	200.84	2.17	140.0	146.94	1.45	144.00	149.10	4.35	141.0	206.32	2.17	140.0	251.58	1.45	141.0	227.68	2.17
62	146	146.0	250.48	0.0	147.0	259.45	0.68	146.0	309.68	0.0	147.0	154.32	0.68	155.00	161.23	6.16	148.0	284.77	1.37	148.0	263.23	1.37	146.0	333.58	0.0
63	145	146.0	227.71	0.69	145.0	250.77	0.0	147.0	236.35	1.38	145.0	152.03	0.0	148.00	154.32	2.07	148.0	317.84	2.07	148.0	303.65	2.07	146.0	207.94	0.69
64	131	131.0	170.29	0.0	131.0	175.42	0.0	131.0	169.0	0.0	131.0	136.23	0.0	134.00	136.26	2.29	131.0	194.45	0.0	131.0	191.42	0.0	131.0	150.77	0.0
65	161	162.0	243.74	0.62	162.0	256.42	0.62	161.0	293.06	0.0	167.0	175.13	3.73	175.00	184.61	8.70	162.0	232.42	0.62	165.0	375.19	2.48	162.0	300.71	0.62
a1	253	259.0	512.84	2.37	260.0	362.1	2.77	259.0	516.1	2.37	262.0	267.0	3.56	265.00	279.84	4.74	260.0	393.71	2.77	261.0	531.97	3.16	257.0	429.0	1.58
a2	252	257.0	447.1	1.98	254.0	375.1	0.79	255.0	400.32	1.19	262.0	271.52	3.97	275.00	283.13	9.13	258.0	392.29	2.38	259.0	431.26	2.78	258.0	377.13	2.38
a3	232	238.0	382.26	2.59	238.0	336.84	2.59	239.0	435.61	3.02	238.0	248.16	2.59	246.00	257.84	6.03	238.0	446.06	2.59	241.0	384.0	3.88	240.0	378.71	3.45
a4	234	237.0	382.42	1.28	236.0	347.77	0.85	238.0	361.52	1.71	238.0	250.94	1.71	250.00	263.19	6.84	238.0	337.45	1.71	239.0	400.58	2.14	236.0	376.97	0.85
a5	236	239.0	411.9	1.27	241.0	418.52	2.12	239.0	408.26	1.27	244.0	250.0	3.39	253.00	261.84	7.20	240.0	320.77	1.69	239.0	388.42	1.27	240.0	409.52	1.69
b1	69	69.0	274.94	0.0	69.0	365.39	0.0	69.0	229.23	0.0	69.0	72.26	0.0	75.00	89.94	8.70	69.0	298.9	0.0	69.0	394.29	0.0	69.0	259.0	0.0
b2	76	76.0	335.13	0.0	76.0	317.61	0.0	76.0	354.13	0.0	76.0	80.71	0.0	86.00	97.87	13.16	76.0	372.13	0.0	76.0	359.19	0.0	76.0	351.35	0.0
b3	80	80.0	308.52	0.0	80.0	427.65	0.0	81.0	540.23	1.25	81.0	83.97	1.25	89.00	107.29	11.25	81.0	474.84	1.25	81.0	430.97	1.25	80.0	327.55	0.0
b4	79	79.0	421.42	0.0	79.0	274.13	0.0	79.0	241.16	0.0	81.0	84.16	2.53	93.00	105.90	17.72	79.0	372.74	0.0	79.0	391.84	0.0	79.0	330.48	0.0
b5	72	72.0	278.87	0.0	72.0	287.81	0.0	72.0	226.16	0.0	73.0	74.77	1.39	81.00	93.32	12.50	72.0	351.39	0.0	72.0	233.65	0.0	72.0	345.94	0.0
c1	227	233.0	590.16	2.64	232.0	662.94	2.2	233.0	422.9	2.64	239.0	249.26	5.29	258.00	270.35	13.66	236.0	523.0	3.96	232.0	369.84	2.2	234.0	524.23	3.08
c2	219	226.0	548.97	3.2	227.0	500.68	3.65	225.0	597.06	2.74	228.0	239.52	4.11	252.00	267.19	15.07	226.0	472.77	3.2	224.0	577.1	2.28	227.0	395.52	3.65
c3	243	248.0	615.35	2.06	248.0	563.9	2.06	246.0	649.55	1.23	252.0	260.94	3.7	279.00	294.81	14.81	247.0	642.42	1.65	247.0	477.35	1.65	252.0	701.87	3.7
c4	219	223.0	409.97	1.83	222.0	628.97	1.37	222.0	510.97	1.37	228.0	237.32	4.11	250.00	263.61	14.16	224.0	435.61	2.28	224.0	655.0	2.28	225.0	683.84	2.74
c5	215	221.0	413.29	2.79	219.0	406.39	1.86	222.0	524.71	3.26	222.0	230.68	3.26	243.00	259.06	13.02	220.0	555.68	2.33	220.0	484.0	2.33	219.0	376.16	1.86
d1	60	60.0	476.16	0.0	60.0	588.71	0.0	60.0	427.19	0.0	61.0	64.65	1.67	83.00	104.32	38.33	61.0	586.23	1.67	60.0	451.45	0.0	60.0	644.55	0.0
d2	66	66.0	618.74	0.0	67.0	782.61	1.52	66.0	492.77	0.0	66.0	68.9	0.0	87.00	124.68	31.82	66.0	760.16	0.0	66.0	457.26	0.0	66.0	403.0	0.0
d3	72	72.0	513.06	0.0	73.0	435.58	1.39	73.0	526.16	1.39	75.0	77.81	4.17	106.00	130.84	47.22	74.0	509.84	2.78	74.0	702.23	2.78	73.0	492.77	1.39
d4	62	62.0	580.35	0.0	62.0	468.81	0.0	62.0	349.45	0.0	62.0	65.35	0.0	90.00	111.87	45.16	62.0	392.16	0.0	62.0	429.32	0.0	62.0	400.03	0.0
d5	61	61.0	470.55	0.0	61.0	530.77	0.0	61.0	302.35	0.0	61.0	64.68	0.0	85.00	109.42	39.34	61.0	492.52	0.0	61.0	475.19	0.0	61.0	481.68	0.0
		256.73	424.55	1.01	256.29	427.48	0.93	256.64	413.01	1.03	258.84	267.28	1.9	270.02	281.95	10.33	257.36	432.56	1.31	257.24	430.83	1.32	257.27	420.11	1.19

Table 4. Comparison of the metaheuristics SCA.

		80aBQSA			80aQL			80aSA			BCL			MIR			40aBQSA			40aQL			40aSA
Inst.	Opt.	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD
41	429	432.0	519.1	0.7	432.0	509.48	0.7	432.0	516.06	0.7	505.0	606.16	17.72	679.00	716.90	58.28	432.0	556.19	0.7	430.0	556.97	0.23	432.0	547.9	0.7
42	512	524.0	724.42	2.34	525.0	698.1	2.54	527.0	687.68	2.93	600.0	785.13	17.19	1060.00	1211.42	107.03	522.0	745.97	1.95	522.0	700.52	1.95	522.0	690.52	1.95
43	516	522.0	714.23	1.16	522.0	652.61	1.16	521.0	688.39	0.97	589.0	794.94	14.15	1185.00	1295.61	129.65	521.0	747.32	0.97	522.0	758.26	1.16	520.0	797.32	0.78
44	494	496.0	631.87	0.4	503.0	647.03	1.82	502.0	688.19	1.62	564.0	728.87	14.17	962.00	1051.61	94.74	502.0	651.48	1.62	503.0	630.29	1.82	504.0	624.0	2.02
45	512	521.0	674.45	1.76	524.0	713.45	2.34	523.0	649.32	2.15	615.0	815.74	20.12	1126.00	1222.71	119.92	521.0	816.1	1.76	522.0	718.19	1.95	519.0	703.84	1.37
46	560	565.0	799.65	0.89	565.0	823.35	0.89	566.0	902.16	1.07	638.0	867.52	13.93	1331.00	1485.23	137.68	566.0	807.35	1.07	567.0	941.9	1.25	563.0	840.39	0.54
47	430	433.0	600.58	0.7	435.0	564.52	1.16	433.0	585.74	0.7	491.0	645.19	14.19	877.00	946.10	103.95	435.0	589.13	1.16	435.0	615.23	1.16	434.0	591.52	0.93
48	492	495.0	744.42	0.61	496.0	730.84	0.81	493.0	659.77	0.2	577.0	798.84	17.28	1119.00	1257.00	127.44	501.0	731.84	1.83	496.0	721.19	0.81	496.0	721.39	0.81
49	641	659.0	1063.13	2.81	665.0	975.23	3.74	665.0	870.68	3.74	766.0	995.9	19.5	1535.00	1695.74	139.47	664.0	1005.97	3.59	667.0	937.52	4.06	663.0	1013.55	3.43
410	514	518.0	695.0	0.78	519.0	633.26	0.97	517.0	640.97	0.58	576.0	778.9	12.06	1104.00	1210.84	114.79	520.0	758.1	1.17	517.0	747.87	0.58	517.0	716.74	0.58
51	253	258.0	362.94	1.98	258.0	344.71	1.98	258.0	380.45	1.98	302.0	383.0	19.37	568.00	625.13	124.51	254.0	395.58	0.4	258.0	368.23	1.98	258.0	344.23	1.98
52	302	317.0	453.03	4.97	320.0	522.61	5.96	319.0	503.29	5.63	356.0	475.77	17.88	748.00	919.45	147.68	315.0	473.48	4.3	319.0	556.19	5.63	317.0	514.45	4.97
53	226	229.0	296.42	1.33	229.0	335.87	1.33	230.0	288.32	1.77	265.0	346.87	17.26	498.00	561.35	120.35	229.0	345.81	1.33	229.0	368.16	1.33	229.0	324.35	1.33
54	242	247.0	306.68	2.07	246.0	367.58	1.65	246.0	345.77	1.65	281.0	356.9	16.12	534.00	590.90	120.66	247.0	355.74	2.07	247.0	383.58	2.07	246.0	368.97	1.65
55	211	213.0	255.84	0.95	213.0	274.16	0.95	212.0	275.87	0.47	224.0	318.19	6.16	411.00	438.87	94.79	212.0	295.13	0.47	213.0	276.55	0.95	213.0	261.32	0.95
56	213	216.0	334.32	1.41	217.0	315.35	1.88	218.0	291.23	2.35	242.0	347.13	13.62	472.00	539.23	121.60	217.0	321.52	1.88	218.0	320.74	2.35	217.0	315.16	1.88
57	293	299.0	412.84	2.05	300.0	437.23	2.39	297.0	400.48	1.37	345.0	464.58	17.75	643.00	717.23	119.45	298.0	424.81	1.71	299.0	393.03	2.05	298.0	442.9	1.71
58	288	289.0	389.81	0.35	291.0	460.68	1.04	292.0	444.23	1.39	350.0	447.45	21.53	650.00	739.77	125.69	290.0	397.45	0.69	291.0	407.81	1.04	291.0	413.26	1.04
59	279	281.0	381.13	0.72	282.0	369.0	1.08	281.0	371.77	0.72	313.0	424.77	12.19	682.00	751.87	144.44	282.0	423.16	1.08	280.0	412.03	0.36	282.0	391.87	1.08
510	265	267.0	382.03	0.75	270.0	366.39	1.89	267.0	339.32	0.75	305.0	419.77	15.09	621.00	673.71	134.34	267.0	396.48	0.75	270.0	358.77	1.89	268.0	380.77	1.13
61	138	141.0	315.9	2.17	141.0	322.23	2.17	140.0	273.39	1.45	171.0	267.29	23.91	669.00	834.23	384.78	141.0	305.87	2.17	142.0	382.58	2.9	140.0	303.29	1.45
62	146	149.0	427.74	2.05	149.0	502.29	2.05	149.0	423.16	2.05	188.0	327.42	28.77	1086.00	1199.00	643.84	147.0	535.26	0.68	148.0	596.23	1.37	147.0	399.26	0.68
63	145	147.0	414.48	1.38	147.0	404.71	1.38	147.0	418.26	1.38	158.0	308.23	8.97	1057.00	1147.90	628.97	145.0	360.0	0.0	147.0	463.26	1.38	146.0	432.77	0.69
64	131	131.0	266.19	0.0	131.0	264.55	0.0	132.0	301.32	0.76	159.0	299.71	21.37	623.00	729.03	375.57	131.0	333.58	0.0	131.0	297.81	0.0	131.0	234.87	0.0
65	161	162.0	352.06	0.62	166.0	432.0	3.11	165.0	491.65	2.48	190.0	307.39	18.01	1000.00	1177.03	521.12	164.0	502.0	1.86	165.0	455.39	2.48	165.0	542.16	2.48
a1	253	260.0	529.81	2.77	261.0	475.48	3.16	259.0	471.35	2.37	272.0	368.97	7.51	1127.00	1343.65	345.45	261.0	647.52	3.16	260.0	728.74	2.77	260.0	604.06	2.77
a2	252	259.0	495.61	2.78	259.0	475.52	2.78	259.0	513.74	2.78	290.0	415.94	15.08	1129.00	1238.03	348.02	260.0	589.71	3.17	261.0	587.32	3.57	260.0	611.32	3.17
a3	232	240.0	511.1	3.45	239.0	510.9	3.02	238.0	534.1	2.59	261.0	341.61	12.5	1067.00	1189.39	359.91	240.0	576.03	3.45	239.0	502.9	3.02	240.0	539.52	3.45
a4	234	237.0	467.19	1.28	239.0	484.32	2.14	237.0	541.97	1.28	274.0	391.55	17.09	1095.00	1158.55	367.95	238.0	527.52	1.71	238.0	587.13	1.71	240.0	592.39	2.56
a5	236	240.0	478.87	1.69	241.0	540.39	2.12	239.0	416.74	1.27	276.0	368.9	16.95	1082.00	1178.23	358.47	241.0	545.29	2.12	240.0	544.39	1.69	242.0	556.39	2.54
b1	69	69.0	391.0	0.0	69.0	482.0	0.0	69.0	521.74	0.0	76.0	132.94	10.14	1323.00	1436.32	1817.39	69.0	657.61	0.0	69.0	480.26	0.0	69.0	403.77	0.0
b2	76	76.0	451.0	0.0	76.0	511.1	0.0	76.0	419.61	0.0	88.0	143.58	15.79	1364.00	1445.39	1694.74	76.0	464.74	0.0	76.0	365.42	0.0	76.0	611.19	0.0
b3	80	81.0	525.61	1.25	80.0	741.58	0.0	81.0	836.71	1.25	87.0	136.9	8.75	1670.00	1843.23	1987.50	81.0	551.48	1.25	81.0	772.94	1.25	81.0	612.32	1.25
b4	79	80.0	680.13	1.27	80.0	651.84	1.27	80.0	743.68	1.27	88.0	147.35	11.39	88.00	1604.94	11.39	80.0	813.19	1.27	80.0	685.35	1.27	79.0	716.52	0.0
b5	72	72.0	458.94	0.0	72.0	359.42	0.0	72.0	444.74	0.0	72.0	126.97	0.0	1401.00	1480.29	1845.83	72.0	505.1	0.0	72.0	626.61	0.0	72.0	408.32	0.0
c1	227	235.0	756.94	3.52	235.0	626.35	3.52	236.0	678.97	3.96	285.0	346.42	25.55	1508.00	1608.61	564.32	235.0	785.61	3.52	235.0	628.84	3.52	235.0	698.16	3.52
c2	219	227.0	700.84	3.65	229.0	778.68	4.57	227.0	792.39	3.65	259.0	318.06	18.26	1637.00	1783.68	647.49	228.0	628.45	4.11	227.0	745.61	3.65	227.0	859.77	3.65
c3	243	251.0	956.19	3.29	249.0	777.87	2.47	249.0	871.1	2.47	279.0	354.42	14.81	268.00	2063.45	10.29	250.0	815.42	2.88	249.0	675.77	2.47	247.0	954.26	1.65
c4	219	226.0	574.94	3.2	226.0	751.42	3.2	225.0	824.29	2.74	243.0	314.1	10.96	1657.00	1773.26	656.62	226.0	751.97	3.2	223.0	947.58	1.83	226.0	871.52	3.2
c5	215	221.0	564.94	2.79	219.0	783.71	1.86	220.0	717.29	2.33	242.0	306.48	12.56	1537.00	1684.84	614.88	221.0	586.48	2.79	221.0	755.45	2.79	221.0	629.35	2.79
d1	60	60.0	538.9	0.0	61.0	603.55	1.67	61.0	752.42	1.67	69.0	122.19	15.0	1979.00	2093.84	3198.33	61.0	661.58	1.67	61.0	717.1	1.67	61.0	932.45	1.67
d2	66	67.0	493.48	1.52	67.0	746.97	1.52	67.0	700.97	1.52	72.0	125.03	9.09	72.00	2284.97	9.09	67.0	737.39	1.52	67.0	966.06	1.52	67.0	943.58	1.52
d3	72	74.0	908.77	2.78	73.0	803.97	1.39	74.0	686.32	2.78	81.0	145.74	12.5	2369.00	2583.81	3190.28	74.0	1094.16	2.78	74.0	755.16	2.78	74.0	759.26	2.78
d4	62	62.0	789.42	0.0	62.0	913.58	0.0	62.0	1025.77	0.0	68.0	114.52	9.68	1929.00	2126.94	3011.29	62.0	779.32	0.0	62.0	753.48	0.0	62.0	727.16	0.0
d5	61	61.0	467.71	0.0	61.0	723.52	0.0	61.0	600.03	0.0	77.0	122.55	26.23	1945.00	2114.74	3088.52	61.0	755.94	0.0	61.0	745.94	0.0	61.0	1048.45	0.0
		257.98	539.1	1.56	258.76	564.65	1.77	258.31	567.36	1.66	293.98	403.46	15.29	1055.27	1283.87	645.97	258.36	594.44	1.64	258.53	598.67	1.74	258.18	599.92	1.61

Table 5. Comparison of the metaheuristics’ WOA.

		80aBQSA			80aQL			80aSA			BCL			MIR			40aBQSA			40aQL			40aSA
Inst.	Opt.	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD	Best	Avg	RPD
41	429	430.0	619.9	0.23	431.0	781.87	0.47	430.0	610.0	0.23	489.00	607.55	13.99	638.00	715.87	48.72	430.0	771.06	0.23	430.0	799.29	0.23	431.0	655.35	0.47
42	512	523.0	930.13	2.15	522.0	839.19	1.95	519.0	872.87	1.37	679.00	852.94	32.62	1079.00	1181.94	110.74	521.0	1198.97	1.76	521.0	1113.26	1.76	520.0	1338.45	1.56
43	516	520.0	1031.16	0.78	519.0	912.03	0.58	520.0	979.13	0.78	739.00	884.48	43.22	1222.00	1293.61	136.82	520.0	922.0	0.78	520.0	1140.23	0.78	519.0	1233.65	0.58
44	494	502.0	927.19	1.62	500.0	789.13	1.21	503.0	776.26	1.82	596.00	779.06	20.65	954.00	1052.03	93.12	501.0	860.71	1.42	503.0	1197.19	1.82	501.0	1142.29	1.42
45	512	519.0	902.65	1.37	517.0	913.68	0.98	520.0	1032.16	1.56	755.00	874.68	47.46	1067.00	1204.13	108.40	521.0	1306.61	1.76	520.0	1150.58	1.56	522.0	933.42	1.95
46	560	561.0	1011.32	0.18	565.0	1007.32	0.89	564.0	1028.68	0.71	815.00	981.26	45.54	1389.00	1483.13	148.04	563.0	1526.55	0.54	568.0	1551.68	1.43	564.0	1511.35	0.71
47	430	431.0	608.39	0.23	433.0	710.55	0.7	434.0	645.0	0.93	570.00	682.42	32.56	854.00	931.84	98.60	430.0	845.58	0.0	434.0	846.32	0.93	434.0	959.9	0.93
48	492	493.0	775.16	0.2	496.0	950.55	0.81	497.0	836.39	1.02	713.00	875.42	44.92	1148.00	1236.16	133.33	494.0	1315.0	0.41	494.0	1046.0	0.41	496.0	1348.87	0.81
49	641	667.0	1494.29	4.06	659.0	1297.0	2.81	664.0	1422.0	3.59	922.00	1141.55	43.84	1532.00	1706.10	139.00	660.0	1487.42	2.96	662.0	1388.1	3.28	655.0	1731.65	2.18
410	514	516.0	736.0	0.39	515.0	825.61	0.19	517.0	812.45	0.58	696.00	847.00	35.41	1046.00	1180.97	103.50	515.0	1028.45	0.19	516.0	1308.87	0.39	518.0	1029.84	0.78
51	253	257.0	411.06	1.58	259.0	418.9	2.37	259.0	473.1	2.37	347.00	411.10	37.15	543.00	614.74	114.62	259.0	628.61	2.37	259.0	794.48	2.37	257.0	524.94	1.58
52	302	314.0	865.26	3.97	314.0	617.1	3.97	316.0	628.74	4.64	468.00	577.35	54.97	762.00	913.61	152.32	316.0	799.58	4.64	315.0	890.71	4.3	319.0	576.48	5.63
53	226	228.0	354.0	0.88	228.0	410.39	0.88	229.0	325.48	1.33	313.00	377.84	38.50	506.00	558.06	123.89	229.0	584.16	1.33	230.0	485.39	1.77	229.0	585.13	1.33
54	242	246.0	563.68	1.65	246.0	503.58	1.65	247.0	405.26	2.07	318.00	394.97	31.40	540.00	580.19	123.14	246.0	521.84	1.65	245.0	488.68	1.24	245.0	486.0	1.24
55	211	212.0	276.71	0.47	212.0	356.87	0.47	213.0	355.42	0.95	294.00	339.65	39.34	397.00	427.84	88.15	212.0	353.9	0.47	212.0	371.77	0.47	212.0	377.13	0.47
56	213	214.0	409.74	0.47	213.0	369.68	0.0	214.0	335.81	0.47	334.00	389.71	56.81	507.00	544.58	138.03	215.0	537.84	0.94	214.0	447.68	0.47	215.0	497.68	0.94
57	293	299.0	598.74	2.05	297.0	538.74	1.37	298.0	548.81	1.71	387.00	504.06	32.08	642.00	710.52	119.11	296.0	630.32	1.02	298.0	716.65	1.71	296.0	711.65	1.02
58	288	290.0	586.06	0.69	290.0	534.9	0.69	290.0	395.81	0.69	399.00	497.35	38.54	663.00	745.32	130.21	292.0	730.55	1.39	289.0	664.45	0.35	289.0	747.26	0.35
59	279	281.0	547.35	0.72	282.0	602.74	1.08	281.0	562.42	0.72	404.00	497.03	44.80	673.00	740.35	141.22	281.0	732.61	0.72	282.0	611.52	1.08	282.0	808.23	1.08
510	265	268.0	378.84	1.13	267.0	461.35	0.75	266.0	402.58	0.38	390.00	470.13	47.17	594.00	669.58	124.15	268.0	575.19	1.13	265.0	626.94	0.0	268.0	488.77	1.13
61	138	140.0	370.35	1.45	140.0	480.94	1.45	140.0	654.55	1.45	283.00	403.26	105.07	736.00	836.52	433.33	140.0	563.29	1.45	141.0	426.16	2.17	140.0	643.42	1.45
62	146	148.0	647.06	1.37	146.0	603.32	0.0	146.0	619.52	0.0	320.00	561.77	119.18	1100.00	1211.81	653.42	146.0	1416.06	0.0	147.0	1215.68	0.68	149.0	779.55	2.05
63	145	148.0	677.55	2.07	145.0	479.03	0.0	147.0	696.0	1.38	337.00	537.19	132.41	912.00	1125.97	528.97	147.0	613.13	1.38	146.0	635.19	0.69	148.0	864.1	2.07
64	131	131.0	275.23	0.0	132.0	308.0	0.76	131.0	376.81	0.0	246.00	366.19	87.79	652.00	722.42	397.71	131.0	558.03	0.0	131.0	618.52	0.0	131.0	648.03	0.0
65	161	165.0	580.74	2.48	162.0	842.87	0.62	162.0	652.77	0.62	357.00	531.74	121.74	1020.00	1155.81	533.54	164.0	867.58	1.86	162.0	722.35	0.62	161.0	1129.45	0.0
a1	253	257.0	823.84	1.58	260.0	785.84	2.77	260.0	800.94	2.77	455.00	662.71	79.84	1243.00	1352.03	391.30	259.0	1343.55	2.37	258.0	815.19	1.98	260.0	1253.45	2.77
a2	252	259.0	629.03	2.78	259.0	886.87	2.78	263.0	910.58	4.37	452.00	651.16	79.37	1150.00	1241.00	356.35	260.0	1299.87	3.17	260.0	915.65	3.17	260.0	961.58	3.17
a3	232	240.0	975.58	3.45	239.0	608.71	3.02	239.0	582.29	3.02	436.00	601.58	87.93	1066.00	1185.84	359.48	240.0	944.13	3.45	239.0	1108.71	3.02	242.0	738.16	4.31
a4	234	238.0	933.68	1.71	237.0	794.77	1.28	237.0	672.42	1.28	467.00	595.97	99.57	1080.00	1161.45	361.54	238.0	873.48	1.71	239.0	942.06	2.14	238.0	888.84	1.71
a5	236	240.0	874.26	1.69	241.0	800.0	2.12	240.0	702.77	1.69	447.00	618.65	89.41	1139.00	1191.23	382.63	240.0	766.81	1.69	240.0	730.26	1.69	241.0	1070.1	2.12
b1	69	69.0	555.74	0.0	69.0	1085.1	0.0	69.0	890.42	0.0	309.00	561.94	347.83	1344.00	1441.68	1847.83	70.0	888.68	1.45	69.0	1107.26	0.0	69.0	1284.52	0.0
b2	76	76.0	822.32	0.0	76.0	630.23	0.0	76.0	548.48	0.0	337.00	547.39	343.42	1265.00	1426.32	1564.47	76.0	941.77	0.0	76.0	1094.9	0.0	76.0	614.1	0.0
b3	80	81.0	1164.97	1.25	80.0	912.77	0.0	80.0	648.65	0.0	378.00	689.84	372.50	1737.00	1848.74	2071.25	81.0	1419.9	1.25	81.0	1199.71	1.25	81.0	1361.23	1.25
b4	79	80.0	411.94	1.27	79.0	978.26	0.0	79.0	1268.35	0.0	334.00	631.39	322.78	1514.00	1644.03	1816.46	79.0	1225.81	0.0	79.0	1315.84	0.0	80.0	1663.42	1.27
b5	72	72.0	834.58	0.0	72.0	785.74	0.0	72.0	959.45	0.0	299.00	541.81	315.28	1372.00	1467.52	1805.56	72.0	1201.84	0.0	72.0	1254.29	0.0	72.0	1196.68	0.0
c1	227	236.0	1010.42	3.96	234.0	812.35	3.08	233.0	794.55	2.64	523.00	717.65	130.40	1488.00	1610.13	555.51	234.0	1689.23	3.08	234.0	1309.52	3.08	231.0	1117.84	1.76
c2	219	227.0	585.32	3.65	224.0	1061.39	2.28	226.0	1099.06	3.2	474.00	737.55	116.44	1654.00	1779.23	655.25	224.0	1564.39	2.28	225.0	1233.94	2.74	226.0	1772.81	3.2
c3	243	249.0	1307.13	2.47	252.0	1560.45	3.7	248.0	1298.35	2.06	629.00	919.10	158.85	1970.00	2126.94	710.70	248.0	1523.48	2.06	245.0	1516.65	0.82	248.0	1504.32	2.06
c4	219	227.0	816.48	3.65	226.0	1105.35	3.2	225.0	1148.52	2.74	570.00	769.13	160.27	1582.00	1734.13	622.37	226.0	1546.39	3.2	226.0	1067.32	3.2	226.0	1092.32	3.2
c5	215	221.0	1011.97	2.79	220.0	894.19	2.33	221.0	918.71	2.79	496.00	754.65	130.70	1541.00	1686.84	616.74	221.0	1284.48	2.79	217.0	1012.68	0.93	221.0	1099.65	2.79
d1	60	60.0	850.03	0.0	60.0	918.32	0.0	61.0	951.23	1.67	419.00	801.39	598.33	1950.00	2080.39	3150.00	60.0	1278.58	0.0	60.0	1213.19	0.0	60.0	1157.81	0.0
d2	66	67.0	1092.65	1.52	66.0	1271.84	0.0	67.0	799.77	1.52	480.00	806.10	627.27	2261.00	2333.68	3325.76	66.0	1320.65	0.0	67.0	2011.74	1.52	67.0	1672.32	1.52
d3	72	73.0	889.16	1.39	73.0	647.81	1.39	72.0	1528.39	0.0	506.00	880.23	602.78	2445.00	2581.48	3295.83	73.0	1705.74	1.39	73.0	1883.68	1.39	73.0	2095.32	1.39
d4	62	62.0	1370.87	0.0	62.0	1464.52	0.0	62.0	1201.81	0.0	312.00	755.48	403.23	2025.00	2107.97	3166.13	62.0	2044.81	0.0	62.0	1884.16	0.0	62.0	1449.16	0.0
d5	61	61.0	895.29	0.0	61.0	750.81	0.0	61.0	1044.03	0.0	344.00	792.87	463.93	1930.00	2093.29	3063.93	61.0	1708.77	0.0	61.0	1649.65	0.0	61.0	1081.1	0.0
		257.73	765.2	1.45	257.33	784.68	1.21	257.73	782.6	1.36	463.07	653.83	152.83	1176.27	1280.82	778.69	257.49	1065.5	1.34	257.49	1033.87	1.28	257.67	1040.61	1.43

4.1. Convergence and Exploration–Exploitation Charts

During the experimentation, several data from the optimization process were recorded, such as the fitness obtained in iteration and the diversity among individuals as presented in [41,42], in order to analyze their behavior during the iterations. A graphical representation is the convergence graphs shown in Figure 5, Figure 6 and Figure 7, where the X axis corresponds to the 1000 iterations, while the Y axis presents the best fitness obtained up to that iteration. The graphs correspond to the best runs for representative instances, and the fitness value found is recorded in the subtitle of each graph, while in the graph set title, the known optimum is presented in order to make a simpler comparison. Other representations are the exploration and exploration graphs, presented in Figure 8, Figure 9 and Figure 10, where on the X-axis, the iterations are presented while on the Y-axis, the exploration (XPL) and exploitation (XPLT) are displayed.

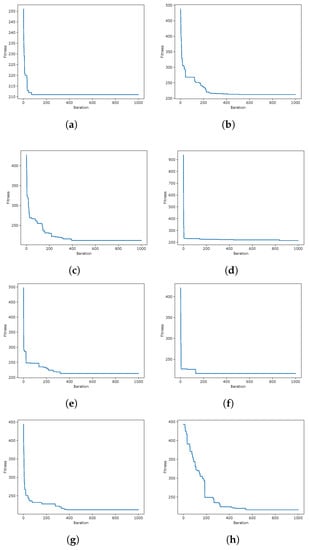
Figure 5. GWO instances coverage when resolving the scp55 instance of the SCP. Instance Optimum: 211. (a) 80aBQSA—fitness obtained 211—Instance 55; (b) 80aQL—fitness obtained 212—Instance 55 (c) 80aSA—fitness obtained 212—Instance 55; (d) 40aBQSA—fitness obtained 212—Instance 55; (e) 40aQL—fitness obtained 213—Instance 55; (f) 40aSA—fitness obtained 212—Instance 55; (g) BCL—fitness obtained 212—Instance 55; (h) MIR—fitness obtained 216—Instance 55.

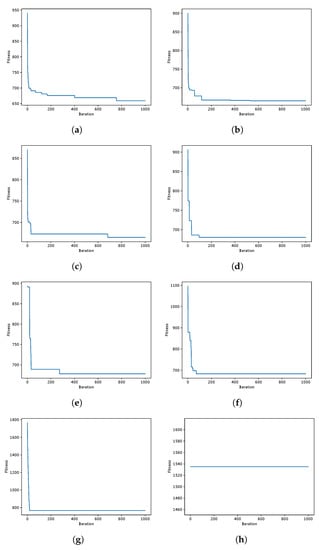
Figure 6. SCA instances coverage when resolving the scp49 instance of the SCP. Instance Optimum: 641. (a) 80aBQSA—fitness obtained 659—Instance 49; (b) 80aQL—fitness obtained 665—Instance 49; (c) 80aSA—fitness obtained 665—Instance 49; (d) 40aBQSA—fitness obtained 664—Instance 49; (e) 40aQL—fitness obtained 667—Instance 49; (f) 40aSA—fitness obtained 663—Instance 49; (g) BCL—fitness obtained 766—Instance 49; (h) MIR—fitness obtained 1535—Instance 49.

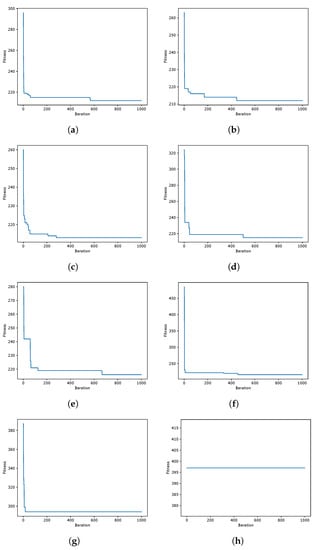
Figure 7. WOA instances coverage when resolving the scp55 instance of the SCP. Instance Optimum: 211. (a) 80aBQSA—fitness obtained 212—Instance 55; (b) 80aQL—fitness obtained 212—Instance 55; (c) 80aSA—fitness obtained 213—Instance 55; (d) 40aBQSA—fitness obtained 212—Instance 55; (e) 40aQL—fitness obtained 212—Instance 55; (f) 40aSA—fitness obtained 212—Instance 55; (g) BCL—fitness obtained 294—Instance 55; (h) MIR—fitness obtained 397—Instance 55.

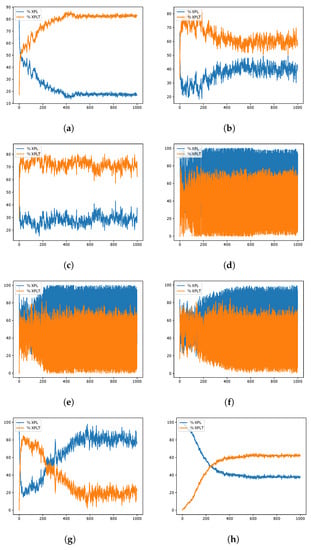
Figure 8. GWO instances exploration–exploitation percentages when resolving the scp51 instance of the SCP. Instance Optimum: 253. (a) 80aBQSA—fitness obtained 255; (b) 80aQL—fitness obtained 256; (c) 80aSA—fitness obtained 256; (d) 40aBQSA—fitness obtained 254; (e) 40aQL—fitness obtained 258; (f) 40aSA—fitness obtained 257; (g) BCL—fitness obtained 259; (h) MIR—fitness obtained 262.

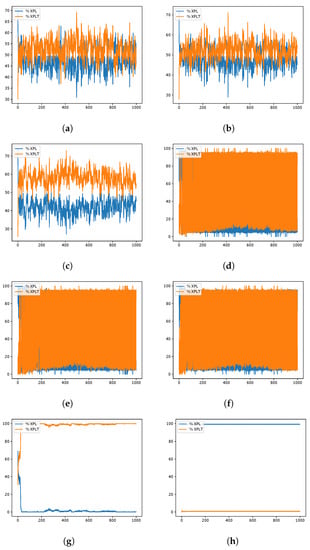
Figure 9. SCA instances exploration–exploitation percentages when resolving the scp51 instance of the SCP. Instance Optimum: 494. (a) 80aBQSA—fitness obtained 496; (b) 80aQL—fitness obtained 503; (c) 80aSA—fitness obtained 502; (d) 40aBQSA—fitness obtained 502; (e) 40aQL—fitness obtained 503; (f) 40aSA—fitness obtained 504; (g) BCL—fitness obtained 564; (h) MIR—fitness obtained 962.

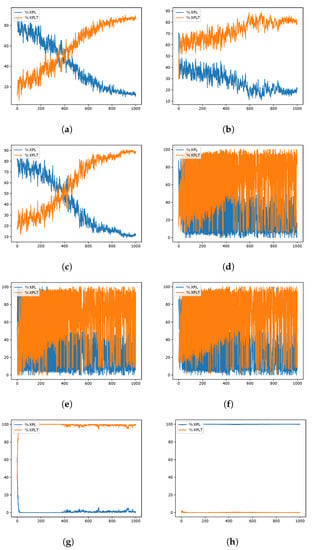
Figure 10. WOA instances exploration–exploitation percentages when resolving the scp41 instance of the SCP. Instance Optimum: 429. (a) 80aBQSA—fitness obtained 430; (b) 80aQL—fitness obtained 431; (c) 80aSA—fitness obtained 430; (d) 40aBQSA—fitness obtained 430; (e) 40aQL—fitness obtained 430; (f) 40aSA—fitness obtained 431; (g) BCL—fitness obtained 489; (h) MIR—fitness obtained 638.

4.2. Statistical Results

To validate the comparison between averages, it is necessary to define by means of the corresponding statistical test if the difference between the results is significant, for which we use the Wilcoxon–Mann–Whitney test [83], making a comparison between all the versions, with a significance level of 0.05, for each of the MH used, where these results are represented in Table 6, Table 7 and Table 8. These tables are structured as follows; the first column presents the techniques used, the following columns present the average p-values of the 45 instances compared with the version indicated in the column title; if the value of this comparison is greater than 0.05 it is presented as “$\ge$0.05”, when the comparison is against the same version the symbol “-” is presented and the values have been approximated to the second decimal place.

Table 6. Average p-value of GWO compared to others algorithm.

	80aBQSA	80aQL	80aSA	BCL	MIR	40aBQSA	40aQL	40aSA
80aBQSA	-	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05
80aQL	≥0.05	-	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05
80aSA	≥0.05	≥0.05	-	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05
BCL	≥0.05	≥0.05	≥0.05	-	0.02	≥0.05	≥0.05	≥0.05
MIR	≥0.05	≥0.05	≥0.05	≥0.05	-	≥0.05	≥0.05	≥0.05
40aBQSA	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05	-	≥0.05	≥0.05
40aQL	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05	-	≥0.05
40aSA	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05	≥0.05	-

Table 7. Average p-value of SCA compared to others algorithm.

	80aBQSA	80aQL	80aSA	BCL	MIR	40aBQSA	40aQL	40aSA
80aBQSA	-	≥0.05	≥0.05	≥0.05	0.00	≥0.05	≥0.05	≥0.05
80aQL	≥0.05	-	≥0.05	≥0.05	0.00	≥0.05	≥0.05	≥0.05
80aSA	≥0.05	≥0.05	-	≥0.05	0.00	≥0.05	≥0.05	≥0.05
BCL	≥0.05	≥0.05	≥0.05	-	0.00	≥0.05	≥0.05	≥0.05
MIR	≥0.05	≥0.05	≥0.05	≥0.05	-	≥0.05	≥0.05	≥0.05
40aBQSA	≥0.05	≥0.05	≥0.05	≥0.05	0.00	-	≥0.05	≥0.05
40aQL	≥0.05	≥0.05	≥0.05	≥0.05	0.00	≥0.05	-	≥0.05
40aSA	≥0.05	≥0.05	≥0.05	≥0.05	0.00	≥0.05	≥0.05	-

Table 8. Average p-value of WOA compared to others algorithm.

	80aBQSA	80aQL	80aSA	BCL	MIR	40aBQSA	40aQL	40aSA
80aBQSA	-	≥0.05	≥0.05	≥0.05	0.00	≥0.05	≥0.05	≥0.05
80aQL	≥0.05	-	≥0.05	≥0.05	0.00	≥0.05	≥0.05	≥0.05
80aSA	≥0.05	≥0.05	-	≥0.05	0.00	≥0.05	≥0.05	≥0.05
BCL	≥0.05	≥0.05	≥0.05	-	0.00	≥0.05	≥0.05	≥0.05
MIR	≥0.05	≥0.05	≥0.05	≥0.05	-	≥0.05	≥0.05	≥0.05
40aBQSA	≥0.05	≥0.05	≥0.05	≥0.05	0.01	-	≥0.05	≥0.05
40aQL	≥0.05	≥0.05	≥0.05	≥0.05	0.01	≥0.05	-	≥0.05
40aSA	≥0.05	≥0.05	≥0.05	≥0.05	0.00	≥0.05	≥0.05	-

5. Conclusions

The increase in computing capacity at more accessible costs has allowed the democratization of the use of machine learning, which has generated an increase in research in different areas, where we can see that every day, the use of these techniques is more common in both academia and industry. The use of machine learning in the improvement of the metaheuristics search process is a field in constant development, where several researches seek to validate the use of ML as a process improvement. The literature presents two explicit schemes for these hybridizations, the high-level ones, where we can observe the hyperheuristics, and the low-level ones, as is the case of this research, where the ML technique is a further operator of the MH.

In this paper, a new intelligent operator is presented in the use of binarization scheme selection (BSS), able to adapt any continuous MH to work in the binary domain. The main contributions are the implementation of a BSS capable of operating in any MH, using a new intelligent operator such as BQSA, and the increase of the possible actions of the intelligent operator from 40 to 80. The increase in these actions comes from the incorporation of two novel families that are rarely used in binarization schemes, such as Z-shaped and X-shaped.

The two-step binarization schemes are the most-used binarization methods in the literature [47], both for their versatility in programming and their low computational cost; for this, it is necessary to choose a transfer function (Step 1) and binarization rule (Step 2), but in the literature, there are many different ways to binarize, since there is a combinatorial problem between the options of Step 1 and Step 2, reaching the extreme of having infinite alternatives [75,78], having so many options, it is necessary to choose intelligently among all the possible options.

In the literature, to solve the problem of choosing the binarization scheme, in most cases, a combination that has presented good performance is chosen, while in some more exhaustive works, the combination is validated against an extensive experimental analysis, as is the case in [48,49], but these only confirm a good two-step combinatorial problem, for a given problem and instances, which is not necessarily replicable to other problems in the same domain. Under this context, an intelligent scheme was proposed in [41] to select among different actions (two-step combinatorics), where by means of QL, an action is chosen for each iteration, which is rewarded or penalized according to their performance, this being a hybridization where a machine learning technique supports metaheuristics. There are other works where BSS is used, which present different intelligent selectors such as QL [41] and SARSA [42], but always with the most-used set of 40 actions (8 choices of V-shaped and S-shaped transfer functions and five binarizations), which have presented diverse favorable performances, but in this work, besides replicating these experiments, we analyzed the performance of 80 actions (16 options of V-shaped, S-shaped, X-shaped, and Z-shaped transfer functions, and 5 binarizations), with the objective of validating that, by having a wider range of actions, the intelligent selector will be able to choose in a better way, avoiding biases by having reduced actions, besides directing the research so that the intelligent selector has more options to choose from.

In response to this proposal, an extensive set of experiments was carried out, which were detailed in Section 4, where eight different versions were compared between 3 MHs, solving 45 different instances of the set covering problem, all of them executed in 31 independent runs, in order to perform the respective statistical tests. The versions containing 80 actions (80aBQSA, 80aQL, and 80aSA) presented competitive performances, obtaining a similar average RPD and, in some cases, better, but having differences that were not significant in front of the respective statistical tests; therefore, we cannot conclude that they have a better performance compared to the versions with 40 actions (40aBQSA, 40aQL, and 40aSA), but for the MHs’ WOA and SCA, there were significant differences when compared to the static version MIR (v4-Complement), which had the worst performance of the eight versions. After analyzing the convergence plots, we can observe that, although the results are diverse, we can assume that the static schemes present early convergences, compared to the dynamic versions (40 and 80 actions), which is related to a good search process without getting trapped early in local optima. Along with this, the exploration and exploitation graphs give us a different perspective of the behavior during the search process, which gives us information on the diversity between individuals, as defined in [84]; from these graphs, we can conclude that the versions with 80 shares tend to have a more predominant tendency to exploit, On the other hand, we confirmed that the recommendations of the literature will not necessarily be applicable for any problem, as is the case of using the MIR combination, which was validated for another problem, confirming what is stated in the no-free-lunch theorem [13].

During the theoretical and experimental development of this work, new research questions have arisen, which remain as possible future works based on the work implemented in this paper, where we can highlight the need to advance in addressing the use of variable transfer functions [75,78]. This is in order to take advantage of the richness of being able to vary the transfer function under a continuous parameter, but which in turn generates a problem to solve, which is that BQSA, SARSA, QL, and other temporal difference techniques are defined to choose between a discrete set of actions, not allowing directly choosing actions in continuous domains. It is also necessary to study the influence of transfer functions against binarization rules, i.e., to use a variety of actions, either individual transfer functions or individual binarization rules. Along with answering the above questions, the option of evaluating other MHs in the literature in other binary domain problems is contemplated in order to confirm that the incorporation of reinforcement learning techniques generates the same effect on them. Another area to investigate is the behavior of this hybridization under smaller subsets in order to evaluate the impact of each of the combinatorics.