Abstract
This work presents the construction and implementation of a two-parameter exponentially fitted Taylor method suitable for solving ordinary differential equations that possess oscillatory or periodic behaviour. The methodology is based on a six-step algorithm discussed in the literature. We present the associated truncation error of the method and demonstrate its accuracy using two test cases. The method gave better results compared with its counterparts discussed in the literature.
MSC:
65L05; 65L06; 65L20
1. Introduction
One important and interesting class of initial value problems that often arise in practice consists of ordinary differential equations (ODEs), whose solutions are periodic or oscillate with known frequencies. Usually, classical numerical methods produce less accurate results when applied to such problems but they can be adapted to efficiently give better accuracy [1,2,3]. This adaptation is the core of the exponential fitting technique [3,4,5,6,7]. The adapted classical method is modified such that it is exact for the problem whose solution is a linear combination of
where K and P are integers. The adaptation of several classical methods for problems with the fitting space (1) has gained popularity in recent times [5,7,8,9,10,11,12,13]. However, very little has been performed in the construction of exponentially fitted methods for fitting space with multiple frequencies [3,6,14]. Authors in Refs. [15,16,17] constructed a Runge–Kutta-type method for the fitting space
In Ref. [6], a multiparameter exponentially fitted Numerov method for the space
for solving periodic problems with more than one frequency was proposed. This work is related to Refs. [6,12,18] and shall provide extension by the construction of a two-parameter exponentially fitted Taylor method for the fitting space
This work is justified by the fact that there are many problems whose solution lies within the fitting space (4).
2. Construction of Method
The general r-th-order Taylor scheme is given as
We set in (5) to obtain the classical fourth-order Taylor method (6)
to be fitted exponentially in this work. Following the six-step algorithm proposed in Ref. [3], the base method (6) is first written in a more general form as
and the associated linear difference operator is given as
where . Next, we determine the maximum value of M that makes the system
compatible. The system obtained from (8) is given as
and is compatible with . Solving (9) yields the coefficient of the well-known classical fourth-order Taylor method here referred to as S0. In order to fit (6) exponentially, a six-step algorithm requires that we obtain the expressions for and , defined, respectively, as
where
and
Now, the respective expressions for and are obtained as
where , the frequencies of oscillation, are real or imaginary. Considering the general fitting space (4) with , the algorithm gave rise to a two-parameter exponentially fitted variant of (6) referred to as EF2PT and characterized by:
- :
- The two-parameter exponentially fitted case with the set
3. Error Analysis: Local Truncation Error (LTE)
4. Convergence and Stability Analysis
Theorem 1
(Dahlquist Theorem). The necessary and sufficient conditions for a linear multistep method to be convergent are that it be consistent and zero-stable [19].
For exponentially fitted algorithms, the Dahlquist Theorem (1) also holds true; however, the concepts of consistency and stability have to be adapted since their coefficients are no longer constants.
Definition 1.
An exponentially fitted method is said to be of exponential order q if q is the maximum value of M, such that the algebraic system is compatible [3].
Definition 2.
A linear multistep method is said to be consistent if it has order [1].
Since our proposed method, EF2PT, is of order , the consistency requirement is satisfied. Hence, the constructed scheme is consistent.
Definition 3.
The method, EF2PT, is zero-stable if no root of the first characteristic polynomial has a modulus greater than one and if every root with modulus one is simple [20].
In order to establish the stability of EF2PT, we apply it to the test problems and obtain the stability function of the class of methods as
Definition 4.
A region of absolute stability is a region in the complex plane, throughout which . Any closed curve defined by is an absolute stability boundary. In addition, any interval of the real line is said to be the interval of absolute stability if the method is stable for all [1,19].
The absolute stability region for the method constructed in this work is given in Figure 1. It has an absolute stability interval of .
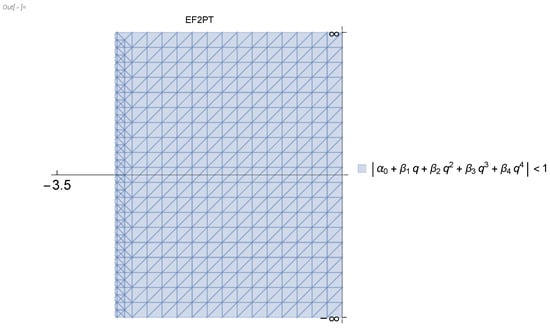
Figure 1.
Region of absolute stability for the constructed methods.
5. Numerical Results
Here, we demonstrate the performance of our method, referred to as EF2PT, using three standard test problems. We implement our method on these test problems and compare the obtained results with those of the classical Taylor, Runge–Kutta, Stomer and Numerov methods, which are methods proposed by the authors in Ref. [21], hereby referred to as Hollevoet-1, Hollevoet-2 and Hollevoet-3. A comparison with the method proposed in Ref. [6] was also carried out.
5.1. Problem 1
Consider the initial value problem given as
whose exact solution is
Problem (21) has two complex conjugate frequencies, which are and , and have been studied by Refs. [6,12,21]. Here, we solve this problem using a different steplength h on the interval , and the maximum absolute error for each steplength is obtained and presented in Figure 2.
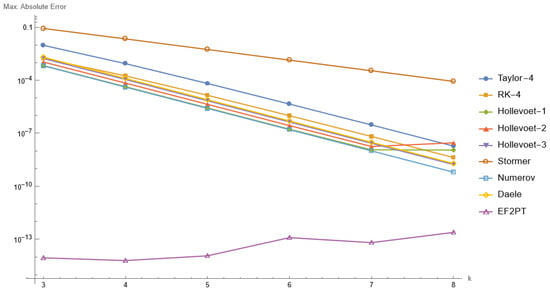
Figure 2.
Maximum absolute errors for Problem 1 as a function of the stepsize .
Our method performed better compared with the methods discussed in the literature, as seen in Figure 2.
5.2. Problem 2
Consider the equation
with exact solution
This problem was also solved using different stepsizes on the interval , although the solution lies outside the fitting space of our method; however, our method gave good results compared with its counterparts, as seen in Figure 3.
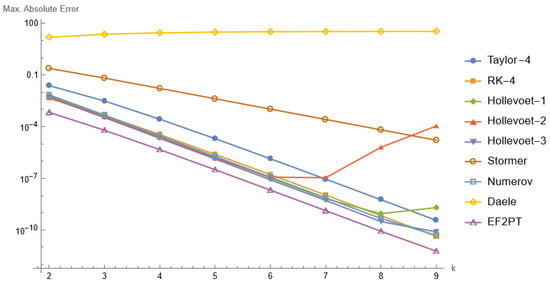
Figure 3.
Maximum absolute errors for Problem 2 as a function of the stepsize .
6. Conclusions
The two-parameter exponentially fitted Taylor method constructed in this work is of algebraic order four and is self-starting. Its local truncation error is of order five. Compared with its classical counterparts, the results obtained from the numerical example showed that the new method is suitable for solving periodic/oscillatory problems.
Author Contributions
Methodology, A.S.W.; Software, M.M.; Investigation, A.S.W.; Data curation, A.S.W.; Writing—original draft, A.S.W. and O.A.O.; Writing—review and editing, O.A.O.; Visualization, M.M.; Funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Institute of Software Development and Engineering, Innopolis University, Innopolis 420500, Russia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lambert, J.D. Computational Methods in ODEs; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Simos, T.E. An exponentially-fitted Runge–Kutta method for the numerical integration of initial-value problems with periodic or oscillating solutions. Comput. Phys. Commun. 1998, 115, 1–8. [Google Scholar] [CrossRef]
- Ixaru, L.; Vanden Berghe, G. Exponential Fitting: Mathematics and Its Applications; Kluwer Academic Publishers: Dordrecht, The Netherland, 2004. [Google Scholar]
- Liniger, W.S.; Willoughby, R.A. Efficient Integration methods for Stiff System of ODEs. SIAM J. Numerical Anal. 1970, 7, 47–65. [Google Scholar] [CrossRef]
- Berghe, G.V.; Daele, M.V. Exponentially-Fitted Stormer/Verlet methods. J. Numer. Anal. Ind. Appl. Math. (JNAIAM) 2006, 1, 241–255. [Google Scholar]
- Daele, M.V.; Hollevoet, D.; Berghe, G.V. Multiparameter exponentially-fitted methods applied to second-order boundary value problems. In Proceedings of the Seventh International Conference of Numerical Analysis and Applied Mathematics, Rethymno, Crete, Greece, 18–22 September 2009. [Google Scholar]
- Wusu, A.; Olabanjo, O.; Mazzara, M. Exponentially-Fitted Fourth-Derivative Single-Step Obrechkoff Method for Oscillatory/Periodic Problems. Mathematics 2022, 10, 2392. [Google Scholar] [CrossRef]
- Franco, J. Exponentially fitted explicit Runge–Kutta-Nystrom methods. J. Comput. Appl. Math. 2004, 167, 1–19. [Google Scholar] [CrossRef]
- Franco, J.M. An embedded pair of exponentially fitted explicit Runge–Kutta methods. J. Comput. Appl. Math. 2002, 149, 407–414. [Google Scholar] [CrossRef][Green Version]
- Avdelas, G.; Simos, T.E.; Vigo-Aguiar, J. An embedded exponentially-fitted Runge–Kutta method for the numerical solution of the Schrodinger equation and related periodic initial-value problems. Comput. Phys. Commun. 2000, 131, 52–67. [Google Scholar] [CrossRef]
- Van de Vyver, H. A Runge–Kutta-Nystrom pair for the numerical integration of perturbed oscillators. Comput. Phys. Commun 2005, 167, 129–142. [Google Scholar] [CrossRef]
- Wusu, A. A Two-parameter Family of Exponentially-fitted Obrechkoff Methods for Second-order Boundary Value Problems. J. Res. Rev. Sci. 2020, 7, 28–32. [Google Scholar] [CrossRef]
- Vanden Berghe, G.; Meyer, H.D.; Daele, M.V.; Hecke, T.V. Exponentially-fitted explicit Runge–Kutta methods. Comput. Phys. Commun. 1999, 123, 7–15. [Google Scholar] [CrossRef]
- Paternoster, B. Present state-of-the-art in exponential fitting. A contribution dedicated to Liviu Ixaru on their 70th birthday. Comput. Phys. Commun. 2012, 183, 2499–2512. [Google Scholar] [CrossRef]
- Calvo, M.; Franco, J.; Montijano, J.; Randez, L. Sixth–order symmetric and symplectic exponentially fitted modified runge-kutta methods of gauss type. Comput. Phys. Commun. 2008, 175, 732–744. [Google Scholar] [CrossRef]
- Calvo, M.; Franco, J.; Montijano, J.; Randez, L. Structure preservation of exponentially fitted runge-kutta methods. J. Comput. Appl. Math. 2008, 218, 421–434. [Google Scholar] [CrossRef]
- Calvo, M.; Franco, J.; Montijano, J.; Randez, L. Sixth-order symmetric and symplectic exponentially fitted runge–kutta methods of the gauss type. J. Comput. Appl. Math. 2009, 223, 387–398. [Google Scholar] [CrossRef]
- Vanden Berghe, G.; Van Daele, M. Exponentially-fitted numerov methods. J. Comput. Appl. Math. 2007, 200, 140–153. [Google Scholar] [CrossRef][Green Version]
- Butcher, J. Numerical Methods for Ordinary Differential Equations; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Lambert, J. Numerical Methods for Ordinary Differential Systems; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Hollevoet, D.; Van Daele, M.; Vanden Berghe, G. The optimal exponentially-fitted Numerov method for solving two-point boundary value problems. J. Comput. Appl. Math. 2009, 230, 260–269. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).