Nonlinear Vibration of Electrostatically Actuated Microbeam
Abstract
1. Introduction
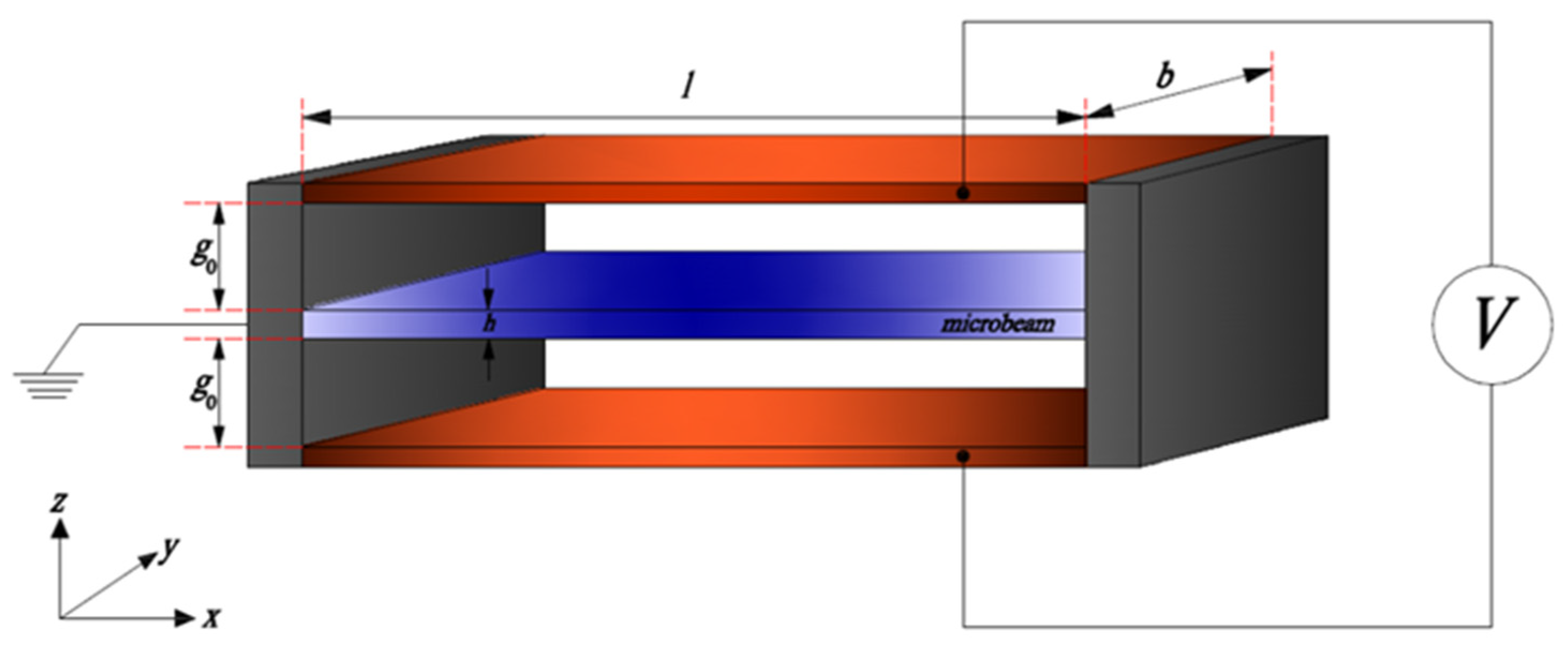
2. Nonlinear Vibration of an Electrostatically Actuated Microbeam
3. Application of the Global Residue Harmonic Balance Method (GRHBM)
3.1. Zero-Order GRHBM Approximation
3.2. First-Order GRHBM Approximation
3.3. Second-Order GRHBM Approximation
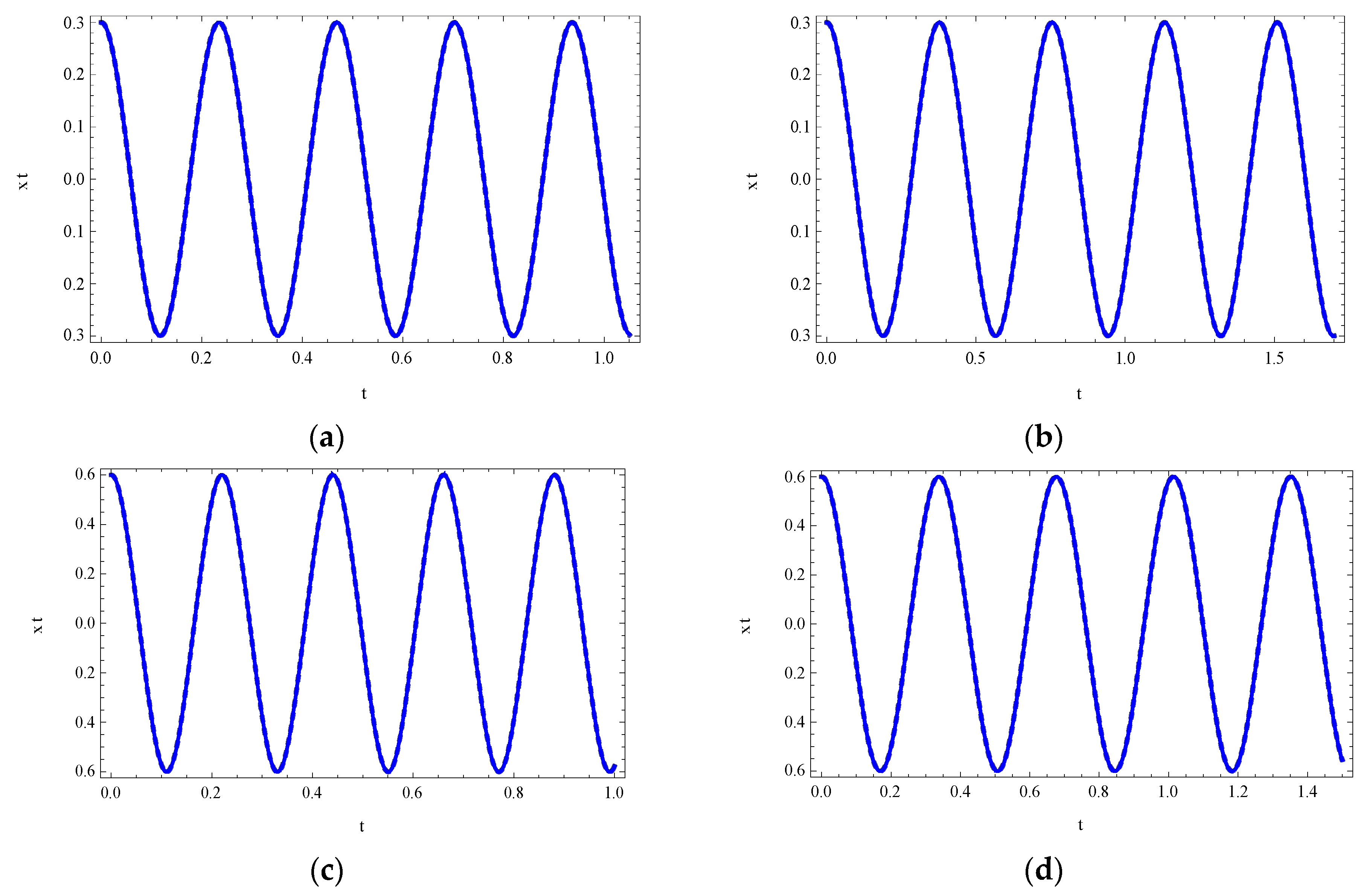
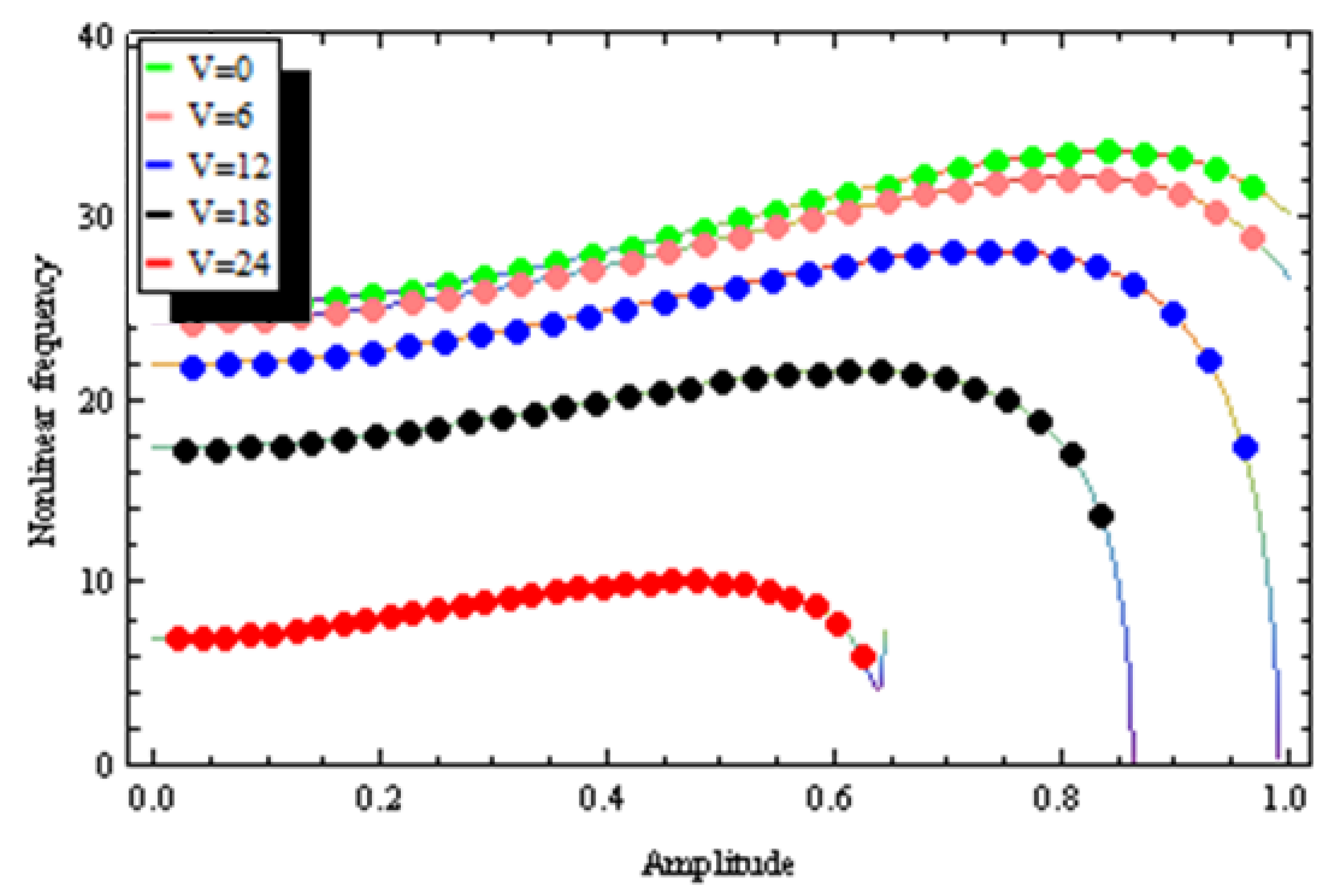
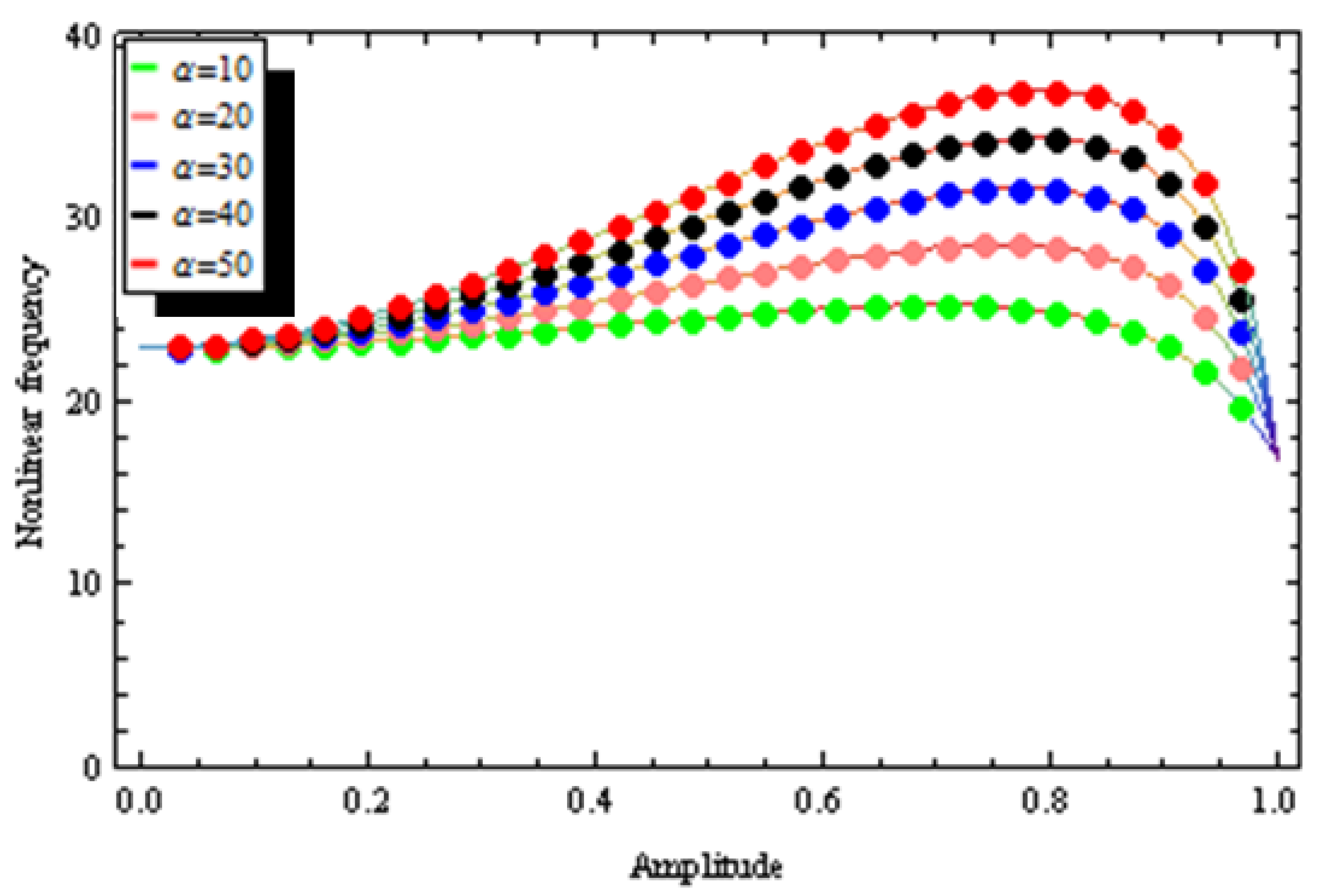
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Batra, R.C.; Porfiri, M.; Spinello, D. Electromechanical model of electrically actuated narrow microbeams. J. Microelectromech. Syst. 2006, 15, 1175–1189. [Google Scholar] [CrossRef]
- Sadeghzadeh, S.; Kabiri, A. Application of higher order Hamiltonian approach to the nonlinear vibration of micro electro mechanical systems. Lat. Am. J. Solids Struct. 2016, 13, 478–497. [Google Scholar] [CrossRef]
- Moghimi, Z.M.; Ahmadian, M.T. Vibrational analysis of electrostatically actuated microstructures considering nonlinear effects. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1664–1678. [Google Scholar] [CrossRef]
- Starosta, R.; Sypniewska-Kamińska, G.; Awrejcewicz, J. Quantifying non-linear dynamics of mass-springs in series oscillators via asymptotic approach. Mech. Syst. Signal Process. 2017, 89, 149–158. [Google Scholar] [CrossRef]
- Lee, S.; Ramadoss, R.; Buck, M.; Bright, V.M.; Gupta, K.C.; Lee, Y.C. Reliability testing of flexible printed circuit-based RF MEMS capacitive switches. Microelectron. Reliab. 2004, 44, 245–250. [Google Scholar] [CrossRef]
- Rhoads, J.F.; Shaw, S.W.; Turner, K.L. The nonlinear response of resonant micro-beam systems with purely-parametric electrostatic actuation. J. Micromech. Microeng. 2006, 16, 890–899. [Google Scholar] [CrossRef]
- Shishesaz, M.; Shirbani, M.M.; Sedighi, H.M.; Hajnayeb, A. Design and analytical modeling of magneto-electromechanical characteristics of a novel magneto-electroelastic vibration-based energy harvesting system. J. Sound Vib. 2018, 425, 149–169. [Google Scholar] [CrossRef]
- Shirbani, M.M.; Shishesaz, M.; Hajnayeb, A.; Sedighi, H.M. Coupled magneto-electro-mechanical lumped parameter model for a novel vibration-based magnetoelectro-elastic energy harvesting systems. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 90, 158–169. [Google Scholar] [CrossRef]
- Anjum, N.; He, J. Nonlinear dynamic analysis of vibratory behavior of a graphene nano/microelectromechanical system. Math. Methods Appl. Sci. 2020, 43. [Google Scholar] [CrossRef]
- He, J.-H.; Nurakhmetov, D.; Skrzypacz, P.; Wei, D. Dynamic pull-in for micro-electromechanical device with a current-carrying conductor. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1059–1066. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H. Analysis of nonlinear vibration of nano/microelectromechanical system switch induced by electromagnetic force under zero initial conditions. Alex. Eng. J. 2020, 59, 4343–4352. [Google Scholar] [CrossRef]
- Mohammadian, M. Application of the variational iteration method to nonlinear vibrations of nanobeams induced by the van der Waals force under different boundary conditions. Eur. Phys. J. Plus 2017, 132, 169–181. [Google Scholar] [CrossRef]
- Qian, Y.H.; Pan, J.L.; Qiang, Y.; Wang, J.S. The spreading residue harmonic balance method for studying the doubly clamped beam-type N/MEMS subjected to the van der Waals attraction. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1261–1271. [Google Scholar] [CrossRef]
- Mehdipour, I.; Ganji, D.D.; Mozaffari, M. Application of the energy balance method to nonlinear vibrating equations. Curr. Appl. Phys. 2010, 10, 104–112. [Google Scholar] [CrossRef]
- Bayat, M.; Pakar, I.; Bayat, M. On the large amplitude free vibrations of axially loaded Euler-Bernoulli beams. Steel Compos. Struct. 2013, 14, 73–83. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, J.; Wan, L. Application of the energy balance method to a nonlinear oscillator arising in the microelectromechanical system (MEMS). Curr. Appl. Phys. 2011, 11, 482–485. [Google Scholar] [CrossRef]
- Yazdi, M.K.; Khan, Y.; Madani, M.; Askari, H.; Saadatnia, Z.; Yildirim, A. Analytical solutions for autonomous conservative nonlinear oscillator. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 979–984. [Google Scholar] [CrossRef]
- Akbarzade, M.; Farshidianfar, A. Nonlinear dynamic analysis of an elastically restrained cantiliver tabered beam. J. Appl. Mech. Tech. Phys. 2017, 58, 556–565. [Google Scholar] [CrossRef]
- Khan, Y.; Wu, Q. Homotopy perturbation transform method for nonlinear equations using He’s polynomials. Comput. Math. Appl. 2011, 61, 1963–1967. [Google Scholar] [CrossRef]
- Bayat, M.; Pakara, I.; Bayat, M. Analytical study on the vibration frequencies of tapered beams. Lat. Am. J. Solids Struct. 2011, 8, 149–162. [Google Scholar] [CrossRef]
- Ganji, D.D. The application of He’s homotopy perturbation method to nonlinear equations arising in heat transfer. Phys. Lett. A 2006, 355, 337–341. [Google Scholar] [CrossRef]
- He, C.H.; El-Dib, Y.O. A heuristic review on the homotopy perturbation method for non-conservative oscillators. J. Low Freq. Noise Vib. Act. Control 2022, 41, 572–603. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. Homotopy perturbation method with three expansions for Helmholtz-Fangzhu oscillator. Int. J. Mod. Phys. B 2021, 35, 2150244. [Google Scholar] [CrossRef]
- Hosen, M.A.; Ismail, G.M.; Chowdhury, M.S.H.; Ali, M.Y. A modified harmonic balance method to obtain higher-order approximations to strongly nonlinear oscillators. J. Interdiscip. Math. 2020, 23, 1325–1345. [Google Scholar] [CrossRef]
- Dang, V.H.; Nguyen, D.A.; Le, M.Q.; Duong, T.H. Nonlinear vibration of nanobeams under electrostatic force based on the nonlocal strain gradient theory. Int. J. Mech. Mater. Des. 2020, 16, 289–308. [Google Scholar] [CrossRef]
- Hieu, D.V.; Thoa, N.T.K.; Duy, L.Q. Analysis of nonlinear oscillator arising in the microelectromechanical system by using the parameter expansion and equivalent linearization methods. Int. J. Eng. Technol. 2018, 7, 597–604. [Google Scholar] [CrossRef]
- He, J.H.; Anjum, N.; Skrzypacz, P.S. A variational principle for a nonlinear oscillator arising in the microelectromechanical system. J. Appl. Comput. Mech. 2021, 7, 78–83. [Google Scholar]
- Bayat, M.; Pakar, I. Nonlinear vibration of an electrostatically actuated microbeam. Lat. Am. J. Solids Struct. 2014, 11, 534–544. [Google Scholar] [CrossRef]
- Qian, Y.H.; Liu, W.K.; Shen, L.; Chen, S.P. Asymptotic analytical solutions of an electrostatically actuated microbeam base on homotopy analysis method. Int. J. Math. Comput. Sci. 2015, 1, 339–346. [Google Scholar]
- Qian, Y.H.; Ren, D.X.; Lai, S.K.; Chen, S.M. Analytical approximations to nonlinear vibration of an electrostatically actuated microbeam. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1947–1955. [Google Scholar] [CrossRef]
- Ismail, G.M.; Cveticanin, L. Higher order Hamiltonian approach for solving doubly clamped beam type N/MEMS subjected to the van der Waals attraction. Chin. J. Phys. 2021, 72, 69–77. [Google Scholar] [CrossRef]
- Ismail, G.M.; Abul-Ez, M.; Ahmad, H.; Farea, N.M. Analytical study of the vibrating double-sided quintic nonlinear nanotorsional actuator using higher-order Hamiltonian approach. J. Low Freq. Noise Vib. Act. Control 2022, 41, 269–271. [Google Scholar] [CrossRef]
- Hieu, D.V.; Hoa, N.T.; Duy, L.Q.; Thoa, N.T.K. Nonlinear vibration of an electrostatically actuated functionally graded microbeam under longitudinal magnetic field. J. Appl. Comput. Mech. 2021, 7, 1537–1549. [Google Scholar]
- Ju, P.; Xue, X. Global residue harmonic balance method to periodic solutions of a class of strongly nonlinear oscillators. Appl. Math. Model. 2014, 38, 6144–6152. [Google Scholar] [CrossRef]
- Ju, P.; Xue, X. Global residue harmonic balance method for large-amplitude oscillations of a nonlinear system. Appl. Math. Model. 2015, 39, 449–454. [Google Scholar] [CrossRef]
- Ju, P. Global residue harmonic balance method for a nonlinear oscillator with discontinuity. Appl. Math. Model. 2015, 39, 6738–6742. [Google Scholar] [CrossRef]
- Ju, P. Global residue harmonic balance method for Helmholtz-Duffing oscillator. Appl. Math. Model. 2015, 39, 2172–2179. [Google Scholar] [CrossRef]
- Mohammadian, M.; Akbarzade, M. Higher-order approximate analytical solutions to nonlinear oscillatory systems arising in engineering problems. Arch. Appl. Mech. 2017, 87, 1317–1332. [Google Scholar] [CrossRef]
- Mohammadian, M. Application of the global residue harmonic balance method for obtaining higher-order approximate solutions of a conservative system. Int. J. Comput. Appl. Math. 2017, 3, 2519–2532. [Google Scholar] [CrossRef]
- Bayat, M.; Pakar, I.; Emadi, A. Vibration of electrostatically actuated microbeam by means of homotopy perturbation method. Struct. Eng. Mech. 2013, 48, 823–883. [Google Scholar] [CrossRef]
- Mohammadian, M.; Shariati, M. Approximate analytical solutions to a conservative oscillator using global residue harmonic balance method. Chin. J. Phys. 2017, 55, 47–58. [Google Scholar] [CrossRef]
- Ismail, G.M.; Abul-Ez, M.; Farea, N.M.; Saad, N. Analytical approximations to nonlinear oscillation of nanoelectro-mechanical resonators. Eur. Phys. J. Plus 2019, 134, 47. [Google Scholar] [CrossRef]


| A | N | V | (Error %) | (Error %) | (Error %) | (Error %) | (Error %) | ||
|---|---|---|---|---|---|---|---|---|---|
| Constant Parameters | [2] | [16] | [28] | [30] | Present | [30] | |||
| 0.3 | 10 | 24 | 0 | 26.3669 | 26.3867 | 26.3644 | 26.8372 | 26.8372 | 26.8372 |
| (1.7837) | (1.7073) | (1.7933) | (0.0000) | (0.0000) | |||||
| 0.3 | 10 | 24 | 20 | 16.3547 | 16.3829 | 16.3556 | 16.6486 | 16.6486 | 16.6486 |
| (1.7970) | (1.6218) | (1.7914) | (0.0000) | (0.0000) | |||||
| 0.6 | 10 | 24 | 10 | 26.3562 | 26.5324 | 26.1671 | 28.5368 | 28.5378 | 28.5382 |
| (8.2789) | (7.5598) | (9.0614) | (0.0049) | (0.0014) | |||||
| 0.6 | 10 | 24 | 20 | 17.3013 | 17.5017 | 17.0940 | 18.5902 | 18.5902 | 18.5902 |
| (7.4497) | (6.2194) | (8.7528) | (0.0000) | (0.0000) | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismail, G.M.; Hosen, M.A.; Mohammadian, M.; El-Moshneb, M.M.; Bayat, M. Nonlinear Vibration of Electrostatically Actuated Microbeam. Mathematics 2022, 10, 4762. https://doi.org/10.3390/math10244762
Ismail GM, Hosen MA, Mohammadian M, El-Moshneb MM, Bayat M. Nonlinear Vibration of Electrostatically Actuated Microbeam. Mathematics. 2022; 10(24):4762. https://doi.org/10.3390/math10244762
Chicago/Turabian StyleIsmail, Gamal M., Md. Alal Hosen, Mostafa Mohammadian, Maha M. El-Moshneb, and Mahmoud Bayat. 2022. "Nonlinear Vibration of Electrostatically Actuated Microbeam" Mathematics 10, no. 24: 4762. https://doi.org/10.3390/math10244762
APA StyleIsmail, G. M., Hosen, M. A., Mohammadian, M., El-Moshneb, M. M., & Bayat, M. (2022). Nonlinear Vibration of Electrostatically Actuated Microbeam. Mathematics, 10(24), 4762. https://doi.org/10.3390/math10244762








