Metaheuristics in Business Model Development for Local Tourism Sustainability Enhancement

Abstract

This study focused on analyzing planning and scheduling services in the tourism industry. Because dealing with these issues necessitates consideration of several important factors and stakeholders in the tourism business, it is challenging to operate resources efficiently. The purpose of this research is to propose a novel approach that allows maximizing the profits of tourism-related service sectors while considering many real-life constraints, such as sequence-dependent travel time, tourist time windows, points of interest, and specific destination constraints. We test our mathematical model for solving first small-scale problems and then metaheuristics proposed for finding a solution for real-life size problems. Moreover, sensitivity analysis was used to analyze the case study’s worthiness when the total cost and the revenue factor were changed. A real case study from Thailand’s Khon Kaen and Kanchanaburi provinces were used to verify the proposed models. The results indicate that the proposed models can be applied to investment decisions and strategy development. Furthermore, the outputs of the proposed models (i.e., the mathematical and metaheuristics models) can be employed to enhance the sustainability of other supply chains.

1. Introduction

Tourism is an essential and growing hospitality sector. It is a vital industry that drives economic and social growth worldwide [1]. Consequently, connection and coordination are critical for the most effective utilization of the available resources within the tourism supply chain. In addition, the various stakeholders in the tourism industry’s supply chain must be considered. This approach promotes tourism sustainability, employment opportunities, and the equal distribution of direct and indirect benefits from businesses to local areas. Tourism is a major driver of economic growth in Thailand. It is a considerable contributor to the nation’s gross domestic product (GDP) and a major employer. In 2019, the tourism industry recorded a contribution of 21.9 percent to the country’s GDP and accounted for more than 16.2 percent of all employees before the COVID-19 pandemic [2]. As a result of the virus, there have recently been fewer international tourists visiting the country. When the pandemic subsides, a community’s tourism business can bounce back by addressing new and exciting visitor requirements.

An important tool for maintaining the tourism industry’s sustainable growth is sharing tourism revenues with local businesses. Sustainable development is development that satisfies present needs without causing future problems. It is a type of development in which a given society, economy, and environment must be interconnected and interdependent. Managing tourism profits within a given area can help communities achieve financial sustainability, allowing them to expand their existing businesses or invest in new projects such as food and beverage, agriculture, and market initiatives to support increasing numbers of tourists. Effective community tourism business plans or commercial models require coordination across the network supply chains of an area’s various tourism businesses. All tourism supply chain stakeholders, including lodgings, tourist attractions, souvenir stores, and restaurants, must collaborate to maximize the potential of a tourism benefit-sharing scheme.

Such a scheme covers a wide variety of activities, including private, group, event, and tourist destinations or points of interest (POIs). Tourists often choose points of interest based on personal preferences, such as goodwill, customer reviews, and their price ranges [3]. Due to the different things that any one location can offer, tourists require there to be a particular activity that can only be carried out in the one location. Depending on the location, tourists’ closing time and sightseeing time are limited for each activity. An itinerary’s completion time must fall within the traveler’s time window. Each tourism company offers a series of diverse activities to service every kind of need of each tourist, such as shopping, rest, eating, visiting, sleeping, etc.

This paper carried out a case study focusing on Thailand’s tourism industry. The study dealt with the service scheduling problem for tourists who visit multiple points of interest, interact with multiple companies, engage in multiple activities, and have multiple lengths of stay. This problem was therefore formulated as a multi-period and multi-visit service scheduling problem with a time window (MMSSPTW). The study aimed to maximize the profits of tourism-related service sectors while considering many real-life constraints, such as sequence-dependent travel time, tourist time windows, points of interest, and specific destination constraints. These aspects make a MMSSPTW a difficult issue to solve manually for optimality. To address this issue, a mixed-integer linear programming model (MILP) was devised to solve a small-sized problem, while metaheuristics approaches were developed to solve various practical problems. Applying the proposed models to various tourism businesses would assist in the time-consuming planning process, raw material preparation, supplier coordination, and resource optimization among different supply chain participants. The solutions obtained from these approaches (i.e., the profits of each tourism business) were used to determine the NPV, IRR, B/C ratio, and payback period using the sensitivity analysis method, which attempts to complement the growing demands of businesses in any given tourism supply chain with the capability of the service sectors, while maintaining maximum tourist satisfaction.

The remainder of the paper is organized as follows. Section 2 discusses the existing literature. Section 3 describes the problem framework and the mathematical model proposed to solve the problem. In Section 4, metaheuristics are developed. A case study and computational results are presented in Section 5. In Section 6, a sensitivity analysis is performed to validate the model. Finally, Section 7 provides the conclusion and future research directions.

2. Literature Review

Tourism supply chain management (TSCM) is an important topic of focus in the tourism industry, which defines the tourism supply chain as a network of tourism businesses engaged in a variety of operations, with the provision of tourism services/diverse product aspects also accounted for. These networks comprise many different people from the public and private sectors [4]. Components of TSCM include the suppliers of products and services for visitors, such as transportation firms, attraction providers, accommodation suppliers, travel agents, memento stores, and so on. In [5], the authors stated that for supply chain efficiency, it is essential for the many tourism service providers to coordinate and collaborate with one another. The tourism industry has two main characteristics: the supply side and the demand side. Firstly, tourism goods are multifaceted and blend commodities and services. These goods are varied and complex, comprising lodging, commuting, touring, eating, and purchasing [6]. Secondly, tourism demand is characterized by extreme unpredictability and fragility, and is sometimes more volatile than demand in other sectors.

To provide tourism services to visitors, tourism business owners must plan and schedule services. Efficient tourist sequencing to minimize lost opportunity time is thus one of the essential variables in boosting the profitability of tourism businesses. In this study, this problem was defined as a multi-period and multi-visit service scheduling problem with a time window (MMSSPTW) to maximize the total profits of tourism-related service sectors while considering many real-life constraints, such as sequence-dependent travel time, tourist time windows, points of interest, and specific destination constraints. To the best of our knowledge, there are currently no existing publications on MMSSPTWs. These problems are classified as service scheduling problems (SSP), which involve scheduling arriving customers who demand services across a finite time horizon [7].

Numerous studies on SSPs have been undertaken, with these focusing on various attributes, including customer preference, travel time, planning horizon, time windows, time duration, servicing capacity, and location constraints. These attributes may result in distinct SSP characteristics. The research conducted in [8] is one example of a problem-related investigation. In their investigation of a multi-period service scheduling problem, their study examined two factors: the total number of ahead-of-time periods and operators. The objective was to determine the duration of service for each customer. In 2020, the authors of [7] focused on a logistics service scheduling problem to enhance the overall job delivery time. Recently, [9] addressed the patient transportation problem using a stochastic mixed-integer program, considering the constraints of customers, vehicles, and real-time handling to dynamically update planned routes and schedules. A sensitivity analysis is an analysis of a project’s worthiness when factors change, regardless of whether they increase or decrease; it assesses whether the project is worth further investment [10] if any changes in factors affect the Benefit/Cost Ratio (B/C Ratio), Internal Rate of Return (IRR) or Net Present Value (NPV). Investment value analysis has been applied in many industrial sectors, including consumer products, the agro-food industry, technology, property and construction, services, finance, and resources [11]. The authors of [12] designed a model for machine tool selection through utilizing various methods. A sensitivity analysis was used in their research to demonstrate how the model results varied in response to alterations in the relative importance of cost-related, technical, operational, and quality-related factors. Therefore, our study applied sensitivity analysis to analyze the opportunity cost incurred by each tourism business operator in the study area.

Based on the literature just reviewed, mathematical programming, heuristics, and metaheuristics were determined to be the most prevalent methods used to solve SSPs. However, the mathematical model has limitations in terms of its computational time, and heuristics may need help finding the optimal solution. Therefore, the use of heuristics is appropriate for simple issue features and a few linked components. In contrast, complicated issues or real-world scenarios need the employment of a metaheuristic, since the primary benefit of metaheuristic approaches is their ability to achieve near-optimal answers in an acceptable amount of time.

Therefore, this paper used the hybridization of a differential evolution algorithm and variable neighborhood search algorithm (HDEVNS), and also the hybridization of a traditional genetic algorithm and k-variable moves algorithm (HGAKV), which were firstly developed for solving the SSP with large-scale instances in order to maximize the profits of service operations in the tourism industry. Differential evolution (DE) is a population-based search algorithm that Storn and Price [13] initially proposed. The DE mechanism’s merits include its simplicity and ease of implementation, making it extremely popular among academics and practitioners, yet it frequently becomes trapped in the local optimum [14]. Consequently, the original structure was required to improve its performance. Various studies have investigated the DE approach, and it has been used extensively in multiple problems, such as a workforce scheduling and routing problem in a sugarcane mill [15], a multi-trip vehicle routing problem with backhauls and a heterogeneous fleet in the beverage logistics industry [16], a large-scale global black-box optimization problem [17], a cyclical multiple parallel machine scheduling problem in sugarcane unloading systems [18], and an employee transportation problem [19,20]. The variable neighborhood search algorithm is a metaheuristic that uses the idea of neighborhood change, which has more than one type of neighborhood structure, to systematically explore the solution space [18,21]. A genetic algorithm (GA) is a model that replicates natural evolution to identify approaches that combine stochastic and directed search to achieve a balance between exploitation and exploration of the search area [22]. Holland [23] introduced the GA concept in 1975. The benefits of GAs are their rapid calculation and simplicity. As a result, in this study, integer encoding was used to solve this problem since it is a simple procedure for genetic algorithms [24]. Still, its disadvantage is that local search is insufficient to identify the optimal solution. This paper used the K-Variable moves algorithm (KV) to enhance the performance of the traditional GA. The KV is a local search strategy [18]. Despite the availability of newer algorithms, GA are still widely used, particularly when combined with another algorithm [25].

The main contributions of this paper are threefold. Firstly, to the best of our knowledge, the literature has yet to discuss MMSSPTWs, which involve several visits and periods. Furthermore, our work considers the time windows of tourists, points of interest, location restrictions, and sequence-dependent travel time. Secondly, even though the mathematical model has limitations in terms of its computational time, it is often used to solve other kinds of problems, such as scheduling [8], allocation [26], manufacturing [27,28,29], planning [30], and routing problems [31,32,33]. MMSSPTWs have never been solved using such a paradigm. In this study, the mathematical model derived from [5] was presented as a solution to the MMSSPTW. Lastly, DE and GAs have never been used to solve MMSSPTWs, despite their extensive use in solving a variety of issues, as evidenced by a literature review of studies conducted on tourism-related difficulties. This research employed DE, a GA, hybrid differential evolution (HDEVNS), and a hybrid genetic algorithm (HGAKV) to solve a realistic-sized MMSSPTW.

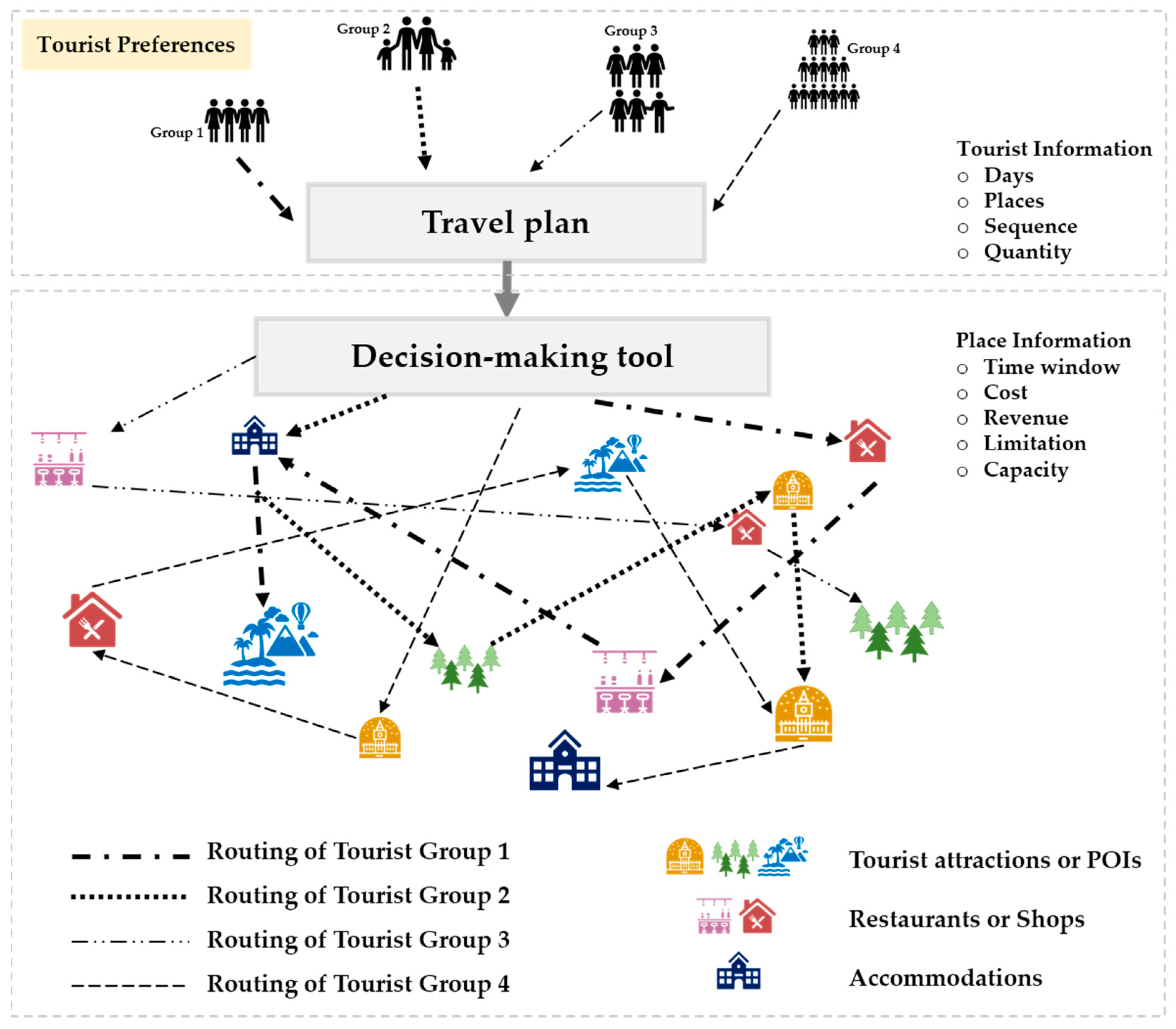
3. Problem Description and Mathematical Model

We analyzed a multi-period and multi-visit service scheduling problem with a time window (MMSSPTW) in the local tourism industry. The problem framework is illustrated in Figure 1. Each tourist group n has a specific activity, and each activity o can be selected or determined based on which activity in their itinerary a tourist chooses. Each business k has a limited capacity Q_k to serve tourists. Each group’s activities o are carried out in the time frame set by the tourist, such as the starting time, finishing time, earliest service time of activity j at the business k, and latest service time of activity j at the business k.

Figure 1. Illustration of the MMSSPTW.

The following assumptions were considered to develop a mathematical model:

• At time zero, all tourist groups and locations are available.
• Each location can only accommodate one tourist group at a time.
• Each activity has only one location constraint.
• Each tourist group visits only one location at a time.
• The tourists’ sightseeing time correlates.
• Activities and locations are assigned ahead of time, and no preemption of activities is permitted.
• Activities and locations are announced in advance, and there is a strict prohibition on any form of activity preemption; attendees are not permitted to disrupt ongoing activities until they have been completed.

Mathematical Model

This section describes the proposed MILP for the MMSSPTW. The indices, sets, parameters, and decision variables used in the MILP model are defined as follows.

Indices and sets:
i,p	Tourist group index;
N	Set of tourist groups;
j,l	Activity index;
Oi	Set of activities for tourist group i;
k,h	Business index;
K	Set of businesses.
Parameters:
$A_{kij}$	Sightseeing time of business k for activity Oij (unit: hour);
$T_{hk}$	Travel time between the business h to the business k (unit: hour);
$V$	Positive large number;
$M{R}_{kij}$	Tourist group i activity j performs at the business k;
$Q_k$	Maximum capacity of the business k (unit: person);
$D_i$	Number of tourists in group i (unit: person);
$B_i$	Starting time of tourist group i (unit: hour);
$U_i$	Finishing time of tourist group i (unit: hour);
$E_{kij}$	Earliest service time of business k for activities Oij (unit: hour);
$F_{kij}$	Latest service time of business k for at activities Oij (unit: hour);
$R{V}_{jk}$	The revenue (collection fee per visit) of business k for activities Oij (unit: THB/person);
$C{C}_{jk}$	The cost (staff cost, service cost and administration cost) of business k for activities Oij (unit: THB/person).
Decision variables:
$S{T}_{kij}$	Starting time of tourist group i activity j at the business k (unit: hour);
$C{T}_{kij}$	Completion time of tourist group i activity j at the business k (unit: hour);
$X_{kij}$	= 1, if tourist group i activity j is assigned at the business k; = 0, otherwise;
$Y_{kijpl}$	= 1, if tourist group i activity j precedes activity l at the business k; = 0, otherwise;
$W_{khij}$	= 1, if tourist group i activity j is processed at business k and activity j-1 at the business h; = 0, otherwise.
Objective function:
$MAX Z={\displaystyle \sum _{i\in N}^{}{\displaystyle \sum _{j\in O_i}^{}{\displaystyle \sum _{k\in K}^{}DE{M}_i\cdot (R{V}_{jk}-C{C}_{jk})\cdot X_{kij}}}}$		(1)
The objective function is used to maximize businesses’ profits with tourist satisfaction.
Subject to:
${\displaystyle \sum _{k\in K}^{}{X}_{kij}\le 1}$	$\forall i,j$	(2)
Equation (2) ensures that the activity is assigned to at least one business.
$S{T}_{kij} + C{T}_{kij} \le X_{kij}V$	$\forall i,j,k$	(3)
$C{T}_{kij } \ge S{T}_{kij}+A_{kij}-(1-X_{kij}) V$	$\forall i,j,k$	(4)
Equations (3) and (4) ensure that the amount of time between the starting and finishing times must at least equal the amount of time spent sightseeing at business k.
$S{T}_{kij} \ge C{T}_{kpl}- Y_{kijpl}V$	$\forall i,j,p\ne i,l,k$	(5)
$S{T}_{kpl} \ge C{T}_{kij}- (1-Y_{kijpl}) V$	$\forall i,j,p\ne i,l,k$	(6)
$Y_{kijpl}+Y_{kplij} \le 1$	$\forall i,j,p\ne i,l,k$	(7)
Equations (5)–(7) ensure that tourist i and activity j and tourist p and activity l cannot be carried out simultaneously at any business.
$M{R}_{kij}-X_{kij}\ge 0$	$\forall i,j,k$	(8)
${\displaystyle \sum _{i\in N}{\displaystyle \sum _{j\in O_i}{X}_{kij}\ge 0}}$	$\forall k$	(9)
Equations (8) and (9) guarantee the feasibility of the businesses that are demonstrated for any activity.
${\displaystyle \sum _{k\in K}^{}S{T}_{ki1 }\ge {\displaystyle \sum _{\begin{array}{l}k\in K\\ k>1\end{array}}^{}{W}_{k1i1}{T}_{1k}}}$	$\forall i$	(10)
${\displaystyle \sum _{k\in K}^{}S{T}_{kij }\ge {\displaystyle \sum _{\begin{array}{l}k\in K\\ k>1\end{array}}^{}C{T}_{ki(j-1)}+{\displaystyle \sum _{\begin{array}{l}k\in K\\ k>1\end{array}}^{}{\displaystyle \sum _{h\in K}^{}{T}_{hk}{W}_{khij}}}}}$	$\forall i,j>1$	(11)
Equations (10) and (11) are sequencing constraints that take travel time into account.
${\displaystyle \sum _{k\in K}^{}{\displaystyle \sum _{\begin{array}{l}h\in K\\ h>1\end{array}}^{}{W}_{khij}\le 1}}$	$\forall i,j>1$	(12)
${\displaystyle \sum _{k\in K}^{}{W}_{k1i1}}\le 1$	$\forall i$	(13)
Equations (12) and (13) guarantee that no action can include more than one of the businesses.
${\displaystyle \sum _{h\in K}^{}{W}_{khij}=X_{kij}}$	$\forall i,j,k$	(14)
${\displaystyle \sum _{k\in K}^{}{W}_{khij}\le {\displaystyle \sum _{k\in K}^{}{W}_{khi(j-1)}}}$	$\forall i,j>1,h$	(15)
Equations (14) and (15) ensure that each activity’s business is chosen from the available alternatives.
$D_i{X}_{kij}\le Q_k$	$\forall i,j,k$	(16)
Equation (16) ensures that the number of tourists is fewer than the limit of business k.
$B_i\le {\displaystyle \sum _{k\in K}^{}S{T}_{ki1}}$	$\forall i$	(17)
$U_i\ge {\displaystyle \sum _{k\in K}^{}C{T}_{kij}}$	$\forall i,j$	(18)
$E_{kij}{X}_{kij}\le S{T}_{kij}$	$\forall i,j,k$	(19)
$F_{kij}{X}_{kij}\ge C{T}_{kij}$	$\forall i,j,k$	(20)
Equations (17)–(20) ensure that the completion and starting times fall within the time windows of the business’s and the tourist group’s goals.
$S{T}_{kij},C{T}_{kij}\ge 0$	$\forall i,j,k$	(21)
$X_{kij},W_{khij},Y_{kijpl}\in \left\{0,1\right\}$	$\forall i,j,p,l,k$	(22)
Equation (21) is a continuous decision variable constraint, while Equation (22) is a binary decision variable constraint.

4. Development of Metaheuristics

When the size and complexity of problems grow too great for exact solution methods, metaheuristics are often used. This study used a metaheuristic employing a Genetic Algorithm (GA) and Differential Evolution (DE). To increase the exploitation and exploration capabilities of the search and control strategy, we designed a hybrid approach based on a GA (called HGAKV) and a hybrid based on DE (called HDEVNS). Exploration and exploitation are global and local searches from a latent perspective. The traditional DE and GA have strong global optimizing exploring capabilities. However, preserving motions to a local optimum still lacks exploitation potential. Therefore, the K-Variable moves algorithm (KV) and Variable Neighborhood Search algorithm (VNS) were introduced to increase our ability to search for the best solutions using the local search approach.

4.1. The Traditional Differential Evolution (DE) and Traditional Genetic Algorithm (GA)

4.1.1. The Traditional DE

Four processes comprise the DE algorithm: initial solution, mutation, recombination, and selection. X_ji,G represents the vector containing dimension (D) variables. The population size or the number of vectors utilized in a differential evolution iteration is determined by the number of samples in the population. The first iteration will generate a random population size, and each vector will be identical. Then, the vectors will be changed into mutant and trial vectors using mutation and recombination processes.

4.1.2. The Traditional GA

The overall structure of a GA includes operators comprising an initial solution, crossover, mutation, and selection. In this study, GA operators were utilized to deal with this issue, including weight mapping crossover (WMX), swapping mutation, and the elitism method for selection.

4.2. Hybrid Differential Evolution Algorithm with Variable Neighborhood Search Algorithm (HDEVNS)

In this study, a Variable Neighborhood Search algorithm (VNS) was employed to develop a hybrid with the DE algorithm. The VNS is a metaheuristic that uses the idea of neighborhood change, which has more than one type of neighborhood structure, to systematically explore the solution space. The conceptual properties of the neighborhood descend to local minima and escape from valleys that contain them. The insert and swap neighborhoods are two different neighborhood structures that were applied in this study. Swap or insert operators are random at any position in the sequence. In Algorithm 1, the VNS pseudocode is illustrated. N_k is the neighborhood structures (k = 1, 2, …, kmax). The collection of solutions inside the k^th neighborhood of s is represented by N_k(s), which is a solution set. A random solution, s′, is generated for each iteration using the N_k(s). A second solution, designated s″, is then produced via a local search for solution s′. If a solution is not produced, the procedures are repeated using the following neighborhood, k = k + 1. The old solution is updated, and the value of k is set to 1 if the new solution, s″, is superior to the previous one. The process continues until the termination condition is met.

Algorithm 1. Variable Neighborhood Search algorithm (VNS)
1	Initialize solution s
2	For k = 1 to kmax
3	Shaking: generate at random a starting solution s’ ∈ Nk(x)
4	Local search: apply a local search from the starting solution x′ using the base random neighborhood structure s″
	(optional) insert algorithm
	(optional) swap algorithm
5	Improve or not:
6	If s″ is better than s
7	s = s″
8	End If
9	Neighborhood change: k = k + 1
10	End for
11	Output: s

The structure of the hybrid DE algorithm with the VNS algorithm consists of an initial solution, mutation process (Equation (23)), recombination process (Equation (24)), and selection process (Equation (25)). The VNS algorithm was used after the crossover operator because we wanted to increase our chances of obtaining better results in the search area according to [5]. Algorithm 2 illustrates the pseudocode for the HDEVNS algorithm.

Algorithm 2. Hybrid Differential Evolution algorithm with Variable Neighborhood Search algorithm (HDEVNS)
1	Input: MMSSPTWdata, DE parameters (NP, CR, F)
2	Output: the best solution
3	Begin Generate the initial population of NP
4	while termination condition is not satisfied do
5	for i = 1 to NP //NP is the predefined number of population
6	Perform mutation process using Equation (23)
7	Perform recombination process using Equation (24)
8	Perform VNS algorithm
9	Evaluate objective value of vectors
10	Perform selection process using Equation (25)
11	Update best solution
12	end for
13	end while
14	end

4.2.1. Initial Solution

DE, an approach for solving some tourism problems, was used by Thumrongvut et al. [5]. They used two elements in each vector to denote the activity sequence and the place selection. The population number is the population size or the number of vectors, where each vector consists of the activity of a tourist group vector and a place vector. Firstly, each vector is a randomly generated real number equal to the number of activity counts. The vector’s dimension corresponds to the group’s serial number, and its sequence corresponds to the group’s activity number. Then, the decoding of each dimension sorts the rank order value (ROV) of each vector in ascending order so that it obtains the sequence of groups and activities to be operated. In addition, the place selection, or k selection (KS), is an alternative set in individual groups and activities. The internal KS number represents the serial number of the optional places, corresponding to the place selected by the matching activity sequence operation.

4.2.2. Mutation Process

The mutation process transforms the target vector into the mutant vector. Equation (23) is used in the generating process.

$$V_{ji,G+1}=X_{r1,G}+F(X_{r2,G}-X_{r3,G})$$

(23)

where V_ji,G+1 is called the mutant vector; i represents the vector number (i = 1, 2, …, NP); j is the position of a vector (j = 1, 2, …, D); F is a scaling factor, which is set as 0.8 [34]; r₁, r₂, and r₃ are the indices of randomly selected vectors.

4.2.3. Recombination Process

The recombination process transforms the mutant vector into the trial vector. Equation (24) is used in the recombination or crossover process. Each position value in a vector may correlate to a target or trial vector depending on the random number (Rand) generated for that position and compared to the crossover rate (CR), a preset parameter set to 0.8 in this study [34].

$$U_{ji,G+1}=\{\begin{array}{l}{V}_{ji,G+1} if (Rand(j)\le CR)\\ X_{ji,G} if (Rand(j)>CR)\end{array}$$

(24)

where X_ji,G is the target vector; U_ji,G+1 is the trial vector; V_ji,G+1 is the mutant vector.

4.2.4. Selection Process

The selection process is used to select the new target vector. We compared the current trial vector fitness function and the current target vector fitness function with the highest objective value selected for the next iteration (X_ji,G+1) using Equation (25).

$$X_{ji,G+1}=\{\begin{array}{l}{U}_{ji,G} if f(U_{ji,G+1})<f(X_{ji,G})\\ X_{ji,G} otherwise\end{array}$$

(25)

4.3. Hybrid Genetic Algorithm with K-Variable Moves Algorithm (HGAKV)

The KV algorithm is a local search-based heuristic that extends the swap method, in which k travels from one position to the next k positions until the final k in the chromosome arrives at the first k. We set the light and strong motion percentages to 20% and 80%, respectively. We used k = 20% in this study, which indicates that k should be the random number for transferring up to roughly 20% of the tourist groups. Figure 2 shows a KV example where k equals 3.

Figure 2. Example of KV algorithm.

The hybrid GA with KV algorithm structure consists of an initial solution, crossover operator, mutation operator, and selection using elitism. Because we wanted to eliminate duplicate algorithm solutions, we employed the KV algorithm instead of the mutation operator. This method considerably reduces computational time while producing superior results. The detailed HGAKA algorithm is shown in Algorithm 3.

Algorithm 3. Hybrid Genetic Algorithm with K-Variable moves algorithm (HGAKV)
1	Input: MMSSPTWdata, GA parameters (popSize, maxGen, pm, pc)
2	Output: the best solution
3	Begin t ← 0
	Generate the initial populations
	Evaluate objective value of populations
4	while t ≤ maxGen
5	Generate F(t) from P(t) by weight mapping crossover (WMX)
6	Generate F(t) from P(t) by swap mutation operation or KV algorithm
7	Evaluate objective value of F(t)
8	Select P(t+1) from P(t) and F(t) by elitist selection operation
9	t ← t + 1
10	end while
11	end

4.3.1. Initial Solution

The initial population is crucial for the GA since it directly affects the convergence rate of fitness values and the quality of solutions. The initial chromosomal population is generated randomly as an integer number based on the activity number in each chromosome, since the genetic algorithm’s conventional operators easily convey it. There are two elements to consider: the Activity sequence (AS) and the k selection (KS). Figure 3 displays an example of the encoding procedure. In the decoding procedure, chromosomes are decoded to evaluate fitness under the constraints of the multi-period and multi-visit service scheduling problem with a time window (MMSSPTW) and taking into account conditions such as the time windows of tourists and locations, sequence-dependent travel time, and destination restrictions. The operation can be described as follows.

Figure 3. Example of encoding procedure.

Step 1:

Construct a random initial solution based on the activity number in the chromosome, which is composed of the group numbers.

Step 2:

Consider the following tourist and location constraints:

• Examine the time window restrictions of existing tourists and locations.
• Evaluate the present capacity restrictions of the location.
• Update the sequence of group I in the set number population.
• Repeat until the sequence is completed.

Step 3:

Check the cumulative tourists in the location. If the operation locations are not in service, the defined sequence must be repaired, and then step 2 must be returned to.

Step 4:

Update capacity in locations.

Step 5:

Update the time window of tourists.

Step 6:

Evaluate fitness using the objective function.

Step 7:

Select the best solution.

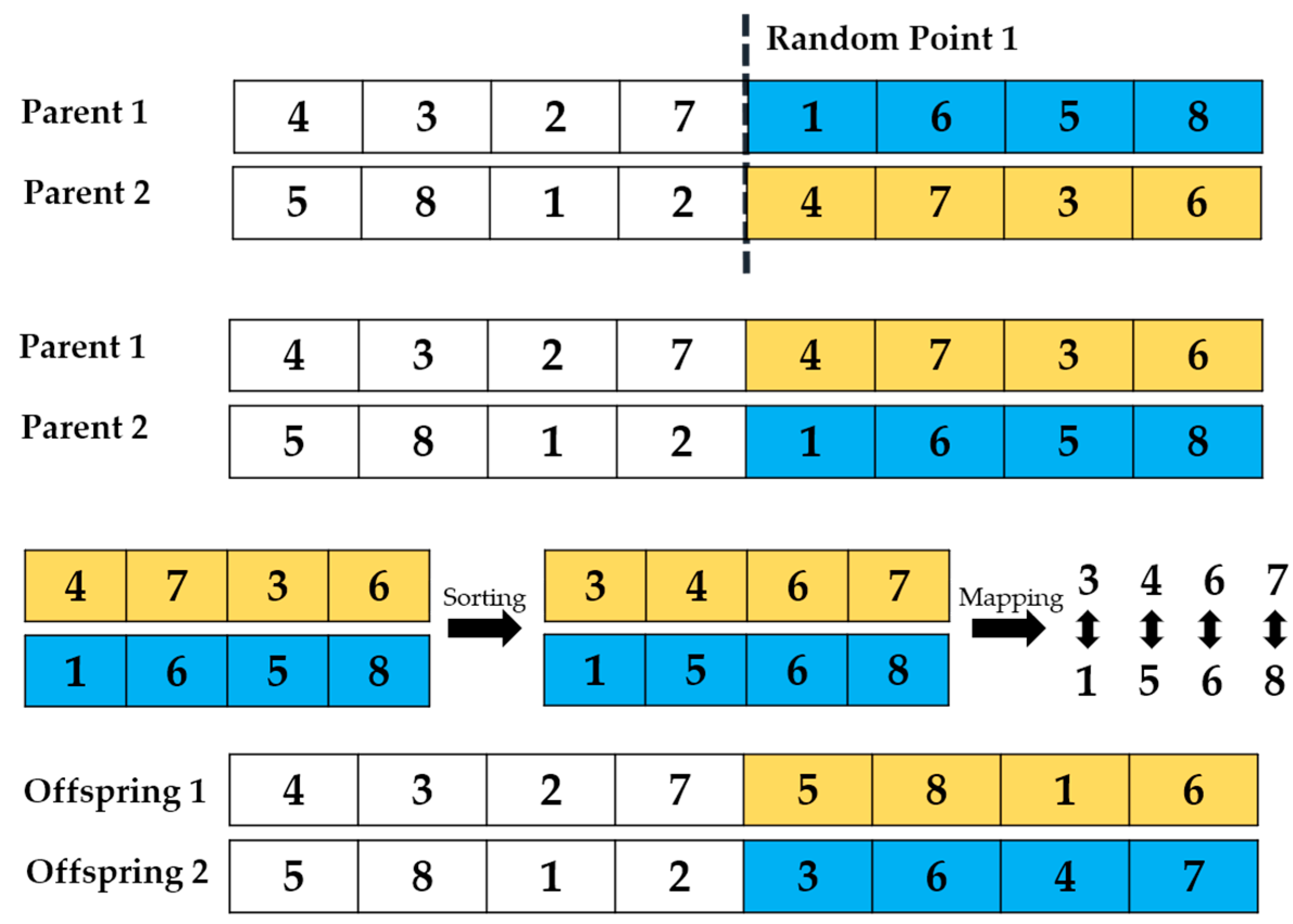
4.3.2. Crossover Operator

The crossover operator facilitates the transfer of genetic information across two chromosomes from one generation to the next. This study employed a precedence weight-mapping crossover (WMX) for the operation sequence. According to [24,25], the WMX has significant effects when used for crossover operations. The WMX determines a one cut-point randomly and then exchanges substrings between the parents for both the tourist group priority and activity tourism type. To avoid the repairing process after a crossover, the weight of the ascending number segment is mapped, and an offspring is formed through a mapping relationship, as shown in Figure 4.

Figure 4. Example of weight mapping crossover (WMX).

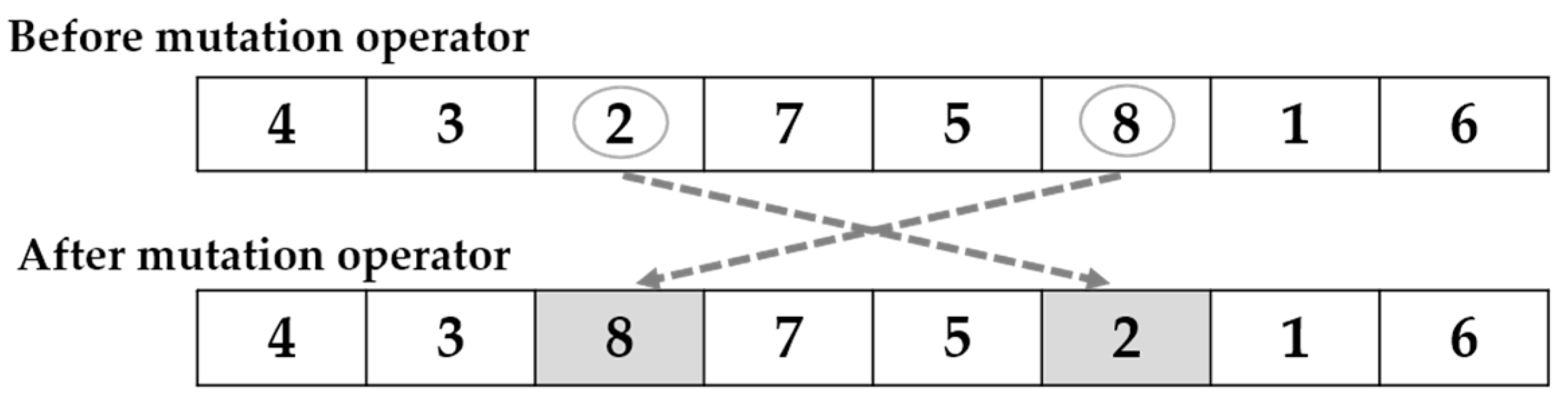
4.3.3. Mutation Operator

The mutation operator can expand the population’s variety by providing additional variability to avoid the local optima phenomenon. A swap mutation was applied in this study. A cut-point is selected randomly and assigned as a mutation point for two allele values in a string, similar to the crossover technique. If the random value from a uniform number falls within the mutation rate range, two allele values inside the chromosome will swap. Figure 5 shows an example of a swap mutation.

Figure 5. Example of swap mutation.

4.3.4. Selection Operator

The selection operation aims to develop a new population with greater fitness values than the current population. In this study, an elitism method was used, due its incredible effect on selection operation, according to [16]. A limited number of individuals with the highest fitness values are selected to continue to the next iteration in the elitist selection strategy.

4.4. Current Practice (CP)

Thailand’s tourism industry uses a constructive heuristic based on the first-come, first-served (FCFS) principle for scheduling travelers’ routes. FCFS is an inefficient method that leads to poor management practices in the tourism industry, negatively impacting income and tourist satisfaction. Due to significant constraints (such as time windows, location eligibility, and travel time between areas), the issue has become too complex for the authorities to resolve.

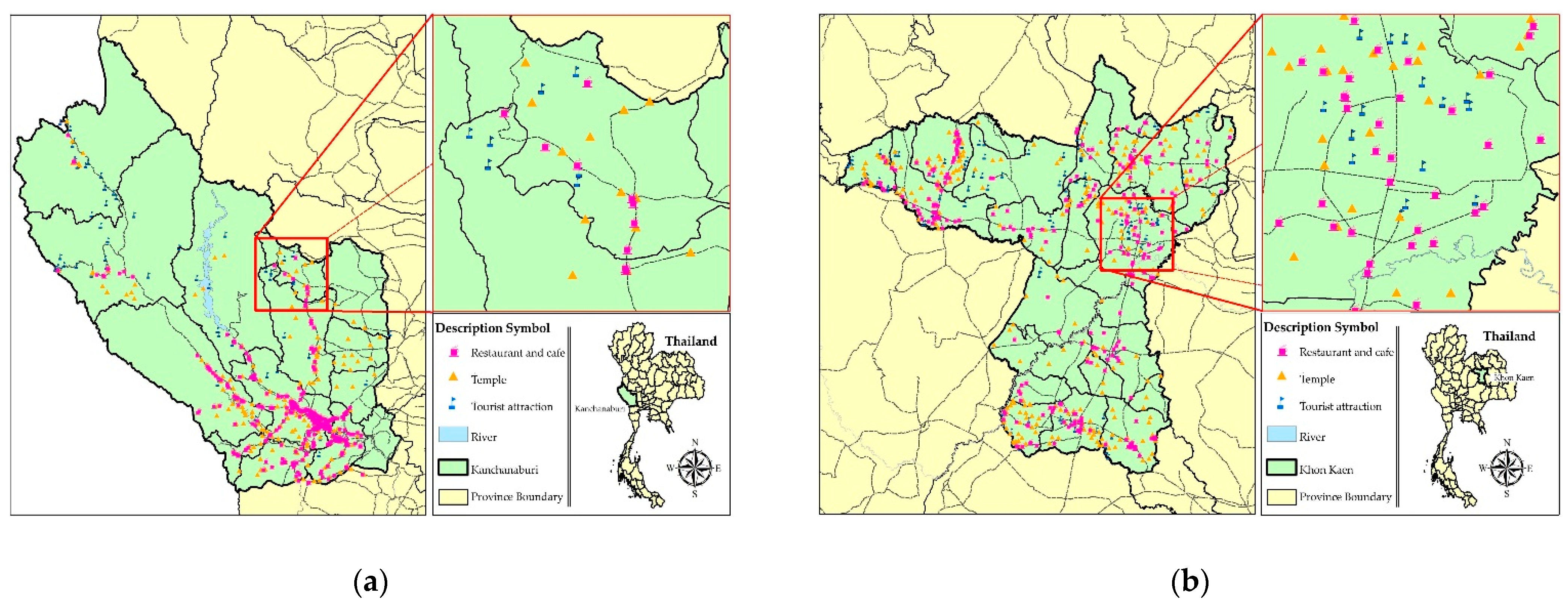
5. Case Study

In this paper, the issue under consideration was a real-life case study of a network supply chain of various tourism businesses. The Khon Kaen and Kanchanaburi provinces of northeastern and central Thailand were selected for the case study. Khon Kaen tourism is characterized by many tourism service providers, many cultural and historical sights, high-quality silk, leisure shopping, beautiful nature, and local cuisine, and various unique characteristics of the province. Likewise, Kanchanburi is a popular vacation spot for nature enthusiasts. As a place to unwind, the area allows visitors to view the water from the river’s banks, either inside a raft house or from a riverside restaurant. Along with witnessing stunning waterfalls, lush woods, and three of Thailand’s largest reservoirs, white water rafting, golf, and elephant trekking are activities popular with travelers. Furthermore, many people enjoy relaxing beside the river, which provides pleasant relief from the heat and congestion of the surrounding capital town.

Table 1 shows the details of the Khon Kaen tourists in each group and the value in parentheses is the business number. For example, as seen in Table 1, tourist group 1 had a sightseeing time (A_ijk) of 2.00 h for activity 1 at business no. 1, 1.00 h for activity 2 at business no. 7, 2.50 h for activity 3 at business no. 12, and 0.50 h for activity 4 at business no. 15. The group’s time window ([B_i, U_i]) was between 2.00 and 8.00 h. Each business had a limited capacity (Q_k) to serve tourists. The revenue (collection fee or income per visit per person) and various business costs (staff costs, service costs, and administration costs) (THB/person) of the businesses are shown in Table 2. As shown in Table 2, the case study featured four restuarants, two hotels, and nine tourist attractions or POIs. The travel time (T_hk) between any two points was not a symmetric function; the time between points k and h differed from the time between points h and k. In addition, the number of tourists in each group was 15, 30, 45, 10, 4, and 20 persons, respectively. Figure 6a,b show various businesses in the Khon Kaen and Kanchanaburi provinces, respectively.

Table 1. The sightseeing time and time windows of tourist groups (hour).

Group	Aijk				Bi	Ui
	j = 1	j = 2	j = 3	j = 4
1	2.00(1)	1.00(7)	2.50(12)	0.50(15)	2.00	8.00
2	7.00(5)	1.00(4)	2.00(11)	1.50(9)	0.00	14.00
3	1.50(10)	1.00(14)	1.50(3)	7.00(6)	0.00	18.00
4	2.50(8)	1.15(2)	2.50(12)	2.00(13)	2.00	12.00
5	1.50(7)	1.00(4)	2.50(8)	1.50(9)	1.50	8.00
6	1.50(2)	6.50(6)	2.50(8)	1.50(10)	0.00	15.00

Table 2. Characteristics of the businesses in Khon Kaen.

Business	Detail	Qk (Person)
1	Restaurant	50
2	Restaurant	70
3	Restaurant	30
4	Restaurant	50
5	Accommodation	500
6	Accommodation	300
7	Tourist attraction or POI	200
8	Tourist attraction or POI	50
9	Tourist attraction or POI	100
10	Tourist attraction or POI	60
11	Tourist attraction or POI	80
12	Tourist attraction or POI	90
13	Tourist attraction or POI	60
14	Tourist attraction or POI	150
15	Tourist attraction or POI	120

Figure 6. Locations of various businesses in Thailand’s central and northeastern regions: (a) Kanchanaburi province; (b) Khon Kaen province.

According to the data collected, restaurant income ranged between 70 and 250 THB per person, accommodation income ranged between 200 and 700 THB per person, and attraction income ranged between 10 and 200 THB per person. Therefore, if its service was fully utilized, a given business generated a certain amount of income per person, as shown in Table 3. Similarly, Table 4 presents the total costs, which were the proportions of the revenue of the restaurant, accommodation, and tourist attraction or POI businesses, which were 30–60%, 30–40%, and 30–60%, respectively.

Table 3. The revenue type of activity j for business k (THB/person).

RVjk	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	128.00	600.00	181.00	200.00	1249.00	1482.00	27.00	497.00	98.00	327.00	359.00	409.00	106.00	201.00	42.00
2	117.00	195.00	425.00	616.00	913.00	2399.00	55.00	136.00	53.00	207.00	138.00	179.00	455.00	381.00	376.00
3	288.00	381.00	550.00	698.00	3203.00	5455.00	139.00	253.00	267.00	98.00	116.00	482.00	83.00	441.00	231.00
4	389.00	593.00	144.00	116.00	6284.00	822.00	329.00	34.00	167.00	379.00	300.00	320.00	23.00	105.00	38.00

Table 4. The total cost type of activity j for business k (THB/person).

CCjk	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	76.80	240.00	63.35	60.00	374.70	592.80	10.80	149.10	34.30	147.15	179.50	163.60	47.70	120.60	23.10
2	70.20	78.00	148.75	184.80	273.90	959.60	22.00	40.80	18.55	93.15	69.00	71.60	204.75	228.60	206.80
3	172.80	152.40	192.50	209.40	960.90	2182.00	55.60	75.90	93.45	44.10	58.00	192.80	37.35	264.60	127.05
4	233.40	237.20	50.40	34.80	1885.20	328.80	131.60	10.20	58.45	170.55	150.00	128.00	10.35	63.00	20.90

Making a profit is the primary goal of any business in any industry, as it indicates that limited resources, such as humans, materials, and facilities, are being used to their full potential. The total profits of the businesses in the case study in Khon Kaen province were computed by multiplying their revenue by the number of customers minus the total costs by the number of customers. The profits of each business are shown in Table 5. The objective value aimed to maximize the total profits, which, for all the activities of all the tourist groups and businesses, was calculated to be 24,031.8 THB. When business owners increase their income through effective planning and management, increased profits and returns are obtained, contributing to better long-term stability.

Table 5. The profit each business obtained (THB).

Profit	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	960.00	1000.00	0.00	0.00	2988.00	0.00	40.80	174.00	0.00	1215.00	0.00	0.00	0.00	0.00	0.00
2	0.00	475.00	0.00	1972.00	0.00	3192.00	108.00	0.00	0.00	0.00	0.00	0.00	0.00	972.00	0.00
3	0.00	0.00	3375.00	0.00	0.00	0.00	0.00	374.40	0.00	0.00	648.00	510.00	0.00	0.00	0.00
4	0.00	0.00	0.00	0.00	0.00	3996.00	0.00	0.00	1161.60	456.00	0.00	0.00	0.00	0.00	414.00
SUM	960.00	1475.00	3375.00	1972.00	2988.00	7188.00	148.80	548.40	1161.60	1671.00	648.00	510.00	0.00	972.00	414.00
TOTAL	24,031.8

6. Computational Results

The proposed methods were coded in MATLAB software (R2021a), and the mathematical model was executed using LINGO (v.18) for MILP on an Intel^® Core™ i7-1165G7 processor 2.80 GHz, with 16.0 GB of RAM, running on Windows 10. The input and algorithm parameters were set according to the preliminary test, as summarized in Table 6. The experiments were tested with 20 randomly generated data sets, which comprised small sized problems (instance no. 1–5), medium sized problems (instance no. 6–12), and large sized problems (instance no. 13–20). All details of the test instances are shown in Table 7. The computational time of the mathematical model can be divided into two categories. For the first category, we ran LINGO until it discovered the optimal solution, and then reported the computational time. The second computational time was employed when LINGO could not identify the optimal solution within 28,800 s. At this point, we halted the process and reported the best solution obtained by LINGO within 28,800 s. Due to LINGO’s inability to find the optimal solution within the acceptable computing time for of the medium and large sized problems, the best and upper-bound solutions were used for comparison with the proposed methods.

Table 6. The input data and parameter values used in all proposed methods.

Detail	Parameter	Interval Values
Input data:
Travel time between locations (hour)	Thk	U [0.05–8.00]
Sightseeing time (hour)	Aijk	U [1.00–12.00]
Number of tourists in each group (person)	Di	U [2.00–50.00]
Servicing capacity (person)	Qk	U [2.00–100.00]
Earliest arrival time of activity for any business (hour)	Ekij	U [0.00–2.00]
Latest arrival time of activity for any business (hour)	Fkij	U [0.5–72.00]
Starting time (hour)	Bi	U [0.00–2.00]
Finishing time (hour)	Ui	U [0.05–72.00]
Costs of business (THB/person):  Restaurant;  Accommodation;  Attraction	CCjk	U [70–250]; U [200–3000]; U [10–300]
Revenue of business (THB/person):  Restaurant;  Accommodation;  Attraction	RVjk	U [100–700]; U [300–7000]; U [20–500]
Parameter values used in all proposed methods:
Mutation rate	pm	0.2
Crossover rate	pc	0.8
Number of population size	NP	25
Termination condition:  Small-size instances;  Medium-size instances;  Large-size instances	maxGen	300 iterations; 60 s; 120 s
Scaling factor	F	2
Crossover rate	CR	0.8

Table 7. Details of the problem instances.

Instance No.	Number of Locations (K)	Number of Tourists (i)	Number of Activities (j)	Total Number of Tourists (Person)
1	3	3	3	60
2	4	4	3	153
3	5	4	4	125
4	5	5	4	135
5	5	6	4	197
6	6	8	4	169
7	8	8	4	231
8	8	10	5	277
9	9	10	4	136
10	9	12	6	395
11	10	12	3	364
12	10	14	6	368
13	12	15	3	389
14	15	15	4	372
15	15	20	3	556
16	20	20	5	635
17	30	30	5	792
18	30	30	6	803
19	40	40	6	941
20	50	40	6	1085

All algorithms’ termination conditions were determined according to the problem size. The number of iterations was used as the stopping criteria for the small sized problems (set to be 300 iterations). In contrast, for the medium and large sized problems, the computational time was used, which was fixed to be 60 and 120 s, respectively. The experiment was repeated five times, and the average solution was reported. Computational results are shown in Table 8 and Figure 7. It can be seen that the mathematical model was able to find optimal solutions for instances no. 1 to 5, while for instances no. 6 to 12 and 13 to 20, the best objective was found and the upper bound solution was found during the limited computation time, respectively. The numerical experiment results show that our proposed HGAKV method outperformed the current practice, the traditional DE, the traditional GA, and the HDEVNS method. The results were statistically tested and are displayed in Table 9 using the Wilcoxon sign rank test with a 95% confidence interval, obtained using IBM SPSS Software (V.28). The statistical test indicates that the solutions obtained from the HGAKV method were significantly different at a p-value ≤ 0.05 compared to those obtained from all the proposed methods.

Table 8. Computational results of the problem instances.

Instance No.	Lingo V.18		Proposed Method					Comp. Time (s)
	Total Profit (THB)	Comp. Time (s)	Total Profit (THB)
			CP	DE	HDEVNS	GA	HGAKV	CP	DE	HDEVNS	GA	HGAKV
1	23,400.00	2.00	23,400.00	23,400.00	23,400.00	23,400.00	23,400.00	16.13	22.08	20.32	23.40	25.10
2	59,670.00	2.00	36,780.00	59,670.00	59,670.00	59,670.00	59,670.00	31.08	22.22	28.10	24.20	31.50
3	65,000.00	3.00	55,400.00	65,000.00	65,000.00	65,000.00	65,000.00	39.65	42.63	44.20	43.50	50.10
4	70,200.00	5.00	54,890.00	70,200.00	70,200.00	70,200.00	70,200.00	29.31	34.98	36.20	37.10	39.30
5	102,440.00	8.00	78,290.00	102,440.00	102,440.00	102,440.00	102,440.00	54.90	35.23	44.20	37.40	49.20
6	97,880.00 BOF	28,800.00	57,030.00	78,520.00	81,640.00	78,510.00	81,710.00	60.00	60.00	60.00	60.00	60.00
7	120,120.00 BOF	28,800.00	93,290.00	105,960.00	109,120.00	106,200.00	115,180.00	60.00	60.00	60.00	60.00	60.00
8	130,050.00 BOF	28,800.00	65,030.00	87,750.00	97,500.00	87,900.00	111,530.00	60.00	60.00	60.00	60.00	60.00
9	90,720.00 BOF	28,800.00	60,010.00	63,440.00	64,480.00	63,440.00	64,480.00	60.00	60.00	60.00	60.00	60.00
10	168,100.00 BOF	28,800.00	74,930.00	108,600.00	115,440.00	114,600.00	131,480.00	60.00	60.00	60.00	60.00	60.00
11	191,960.00 BOF	28,800.00	91,120.00	140,010.00	141,960.00	139,120.00	152,690.00	60.00	60.00	60.00	60.00	60.00
12	107,120.00 BOF	28,800.00	49,320.00	69,640.00	70,200.00	70,550.00	95,660.00	60.00	60.00	60.00	60.00	60.00
13	161,710.00 UB	28,800.00	83,380.00	149,370.00	150,540.00	148,910.00	155,490.00	120.00	120.00	120.00	120.00	120.00
14	193,440.00 UB	28,800.00	90,120.00	141,440.00	151,840.00	144,310.00	165,720.00	120.00	120.00	120.00	120.00	120.00
15	216,840.00 UB	28,800.00	113,900.00	185,640.00	197,730.00	189,930.00	200,100.00	120.00	120.00	120.00	120.00	120.00
16	302,750.00 UB	28,800.00	108,240.00	190,450.00	198,250.00	197,120.00	223,530.00	120.00	120.00	120.00	120.00	120.00
17	284,800.00 UB	28,800.00	122,370.00	206,700.00	231,400.00	226,500.00	242,370.00	120.00	120.00	120.00	120.00	120.00
18	226,340.00 UB	28,800.00	99,810.00	153,660.00	161,460.00	156,000.00	199,290.00	120.00	120.00	120.00	120.00	120.00
19	233,980.00 UB	28,800.00	132,080.00	204,360.00	189,540.00	200,900.00	221,880.00	120.00	120.00	120.00	120.00	120.00
20	366,300.00 UB	28,800.00	159,020.00	247,260.00	280,800.00	256,600.00	313,670.00	120.00	120.00	120.00	120.00	120.00

Note: ^BOF = Best Objective Found; ^UB = Upper Bound.

Figure 7. Scatter plot of the total profit obtained from Table 8.

Table 9. The p-value of the statistical test of differences of the solutions of the proposed method.

	DE	HDEVNS	GA	HGAKV
CP	0.001	0.001	0.001	0.001
DE	-	0.008	0.035	0.001
HDEVNS	-	-	0.011	0.001
GA	-	-	-	0.001

Based on the results shown in Table 8, the heuristic performance (HP) was measured by comparing the solution obtained from all the compared algorithms with the solution obtained from the mathematical model. Another factor examined in this study was the relative improvement (RI), which was compared to the total profit of the solution from all the algorithms.

$$HP(\%)=\frac{Solutio{n}_{a\lg }}{Solutio{n}_{MILP}}\times 100$$

(26)

$$RI(\%)=\frac{Solotio{n}_{a\lg }-Solotio{n}_{old}}{Solotio{n}_{a\lg }}\times 100$$

(27)

where

• Solution_MILP = the solution of the mixed integer linear programming;
• Solution_old = the solution of the current practice;
• Solution_alg = the solution of the current practice, DE, HDEVNS, GA, and HGAKV.

The HP of all the proposed methods was calculated using Equation (26), and the RI using Equation (27). As shown in Table 10, the HP revealed that the HGAKV obtained a near-optimal result, recording an average of 89.24%. The RI was compared to the total profit of the solution obtained using the current practice, DE, HDEVNS, GA, and HGAKV methods. As shown in Table 10, these algorithms had average RIs of 29.04%, 30.80%, 29.48%, and 35.20%, respectively. Additionally, the HGAKV improved the solution quality by 9.75%, 6.82%, and 8.62% with regard to the DE, GA, and HDEVNS, respectively.

Table 10. The heuristic performance and relative improvement of all proposed methods obtained from Table 8.

Instance No.	HP (%)					RI (%)				RI (%)
	The Proposed Methods Compared to the MILP					The Proposed Methods Compared to the CP Algorithm				The Proposed Methods Compared to the HGAKV Algorithm
	CP	DE	HDEVNS	GA	HGAKV	DE	HDEVNS	GA	HGAKV	DE	HDEVNS	GA
1	100.00	100.00	100.00	100.00	100.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
2	61.64	100.00	100.00	100.00	100.00	38.36	38.36	38.36	38.36	0.00	0.00	0.00
3	85.23	100.00	100.00	100.00	100.00	14.77	14.77	14.77	14.77	0.00	0.00	0.00
4	78.19	100.00	100.00	100.00	100.00	21.81	21.81	21.81	21.81	0.00	0.00	0.00
5	76.43	100.00	100.00	100.00	100.00	23.57	23.57	23.57	23.57	0.00	0.00	0.00
6	58.27	80.22	83.41	80.21	83.48	27.37	30.14	27.36	30.20	3.90	0.09	3.92
7	77.66	88.21	90.84	88.41	95.89	11.96	14.51	12.16	19.01	8.00	5.26	7.80
8	50.00	67.47	74.97	67.59	85.76	33.30	33.30	26.02	41.69	21.32	12.58	21.19
9	66.15	69.93	71.08	69.93	71.08	5.41	6.93	5.41	6.93	1.61	0.00	1.61
10	44.57	64.60	68.67	68.17	78.22	31.00	35.09	34.62	43.01	17.40	12.20	12.84
11	47.47	72.94	73.95	72.47	79.54	34.92	35.81	34.50	40.32	8.30	7.03	8.89
12	46.04	65.01	65.53	65.86	89.30	29.18	29.74	30.09	48.44	27.20	26.62	26.25
13	51.56	92.37	93.09	92.08	96.15	44.18	44.61	44.01	46.38	3.94	3.18	4.23
14	46.59	73.12	78.49	74.60	85.67	36.28	40.65	37.55	45.62	14.65	8.38	12.92
15	52.53	85.61	91.19	87.59	92.28	38.64	42.40	40.03	43.08	7.23	1.18	5.08
16	35.75	62.91	65.48	65.11	73.83	43.17	45.40	45.09	51.58	14.80	11.31	11.81
17	42.97	72.58	81.25	79.53	85.10	40.80	47.12	45.97	49.51	14.72	4.53	6.55
18	44.10	67.89	71.34	68.92	88.05	35.04	38.18	36.02	49.92	22.90	18.98	21.72
19	56.45	87.34	81.01	85.86	94.83	35.37	30.32	34.26	40.47	7.90	14.58	9.46
20	43.41	67.50	76.66	70.05	85.63	35.69	43.37	38.03	49.30	21.17	10.48	18.19
MAX	56.16	100.00	100.00	100.00	100.00	44.18	47.12	45.97	51.58	27.20	26.62	26.25
MIN	55.89	62.91	65.48	65.11	71.08	0.00	0.00	0.00	0.00	0.00	0.00	0.00
AVG	58.25	80.89	83.35	81.82	89.24	29.04	30.80	29.48	35.20	9.75	6.82	8.62

The hybrid algorithm (HGAKV)’s advantages are the combined advantages of extensive exploration in the search space, deriving from the GA algorithm, and high exploitation, deriving from the KV algorithm. Consequently, in most cases, the HGAKV produced the best solution, outperforming the other approaches and significantly improving a given company’s total profit. In contrast, the current practice approach recorded the lowest quality result among all the approaches.

Sensitivity Analyses

The profits of a tourism supply chain will increase if more demand is achieved, which is accomplished when available points of interest (restaurants, accommodation, shops, tourist attractions, etc.) can accommodate an increase in tourist demand. One way to increase the demand response is by decreasing the total costs of venues or by reducing the opportunity costs of businesses by planning and scheduling servicing effectiveness. Governments can boost a nation’s GDP and foreign exchange by investing in the tourism industry, which is economically significant for developing nations. Further, governments and the private sector must collaborate to develop profitable and sustainable growth plans. To encourage the participation of the private sector in financing, constructing, and managing infrastructure and other related development projects, a combination of policy reforms, institutional support, incentives, and financing modalities are used to foster public–private partnerships in the tourism industry. According to the references discussed above, an alternative to budgetary limitations enables the tourism industry to build assets and maximizes the use of private sector skills. The potential benefits of a public–private partnership for the private sector include, by the partnership’s very nature, risk sharing; a public–private partnership involves the sharing of project risks and cost reduction, which encourages private investment in tourism.

In sensitivity analysis approaches, the specific parameters of the objective function are given the most weight overall. The majority of these have a high to extremely high sensitivity. Sensitivity analysis determines how much the decision-making evaluation index changes when one or more uncertainties are changed. Through this, the degree to which the adjustments impact the achievement of the targeted outcomes is determined. Then, judgments about the plan’s capacity can be formed when the external environment changes negatively. In this study, sensitivity analysis was employed to analyze the case study’s worthiness when the total cost and the revenue factor were changed in terms of the NPV, IRR, B/C Ratio, and payback period. In the method, two parameters (revenue and cost) were varied simultaneously, but the range of variation was defined differently. The similar outcomes obtained show that the parameter sensitivity was able to be measured without the chosen method’s impacting the outcomes.

Table 11 presents the effects on a business’s profit when their revenue and costs were changed by 5% and 10%. The three examples shown are business no. 3, a restaurant, business no. 6, a hotel, and business no.10, a tourist attraction, with each business example having eight scenarios. For scenario 1 of business no. 3, increasing its revenue and costs by 5% was found to increase its profit by 5% (3543.75THB). Thus, profit was found to be significantly sensitive to changes in the revenue and cost values. Another way to formulate this is that the business’s profit was found to grow by 1% for every 1% increase in revenue and costs, or fall by 1% for every 1% decrease in revenue and cost (see scenario 4 of the restaurant). Similarly, in scenario 2, if the business’s revenue was increased by 5% and its costs were decreased by 5%, its profit was increased by 15% (3881.25THB). On the other hand, if its revenue was decreased by 5% and its costs were increased by 5%, its profit was decreased by 15% (scenario 3). Scenarios 5 to 8 for each business show the impact of changing the business’s revenue and costs by 10%. For example, scenario 7 of business no. 3 shows that decreasing its revenue by 10% and increasing its cost by 10% resulted in a 30% (3712.50THB) decrease in its profit. Consequently, profit was found to be likewise quite sensitive to shifts in these parameters. To state this another way, every 1% decrease in these parameters was found to result in a 3% decrease in profit, or every 1% increase in these parameters was found to result in a 3% gain in profit. Comparing the changed factors in the four scenarios found that the profits of each of the example businesses were more sensitive to changes that involved revenue increases, which lead to a positive objective value or increases in profits than to changes that involved revenue decreases. However, all changes were found to have a significant impact on profit.

Table 11. The effects of changing the parameters of the case study.

	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5	Scenario 6	Scenario 7	Scenario 8
	Revenue + 5%; Cost + 5%	Revenue + 5%; Cost − 5%	Revenue − 5%; Cost + 5%	Revenue − 5%; Cost − 5%	Revenue + 10%; Cost + 10%	Revenue + 10%; Cost − 10%	Revenue − 10%; Cost +10%	Revenue − 10%; Cost − 10%
Business no. 3: Restaurant
Revenue	157.50	157.50	142.5	142.5	165.00	165.00	135.00	135.00
Cost	78.75	71.25	78.75	71.25	82.50	67.50	82.50	67.5
Profit	3543.75	3881.25	2868.75	3206.25	3712.50	4387.50	2362.50	3037.50
% Change in profit	5.00%	15.00%	(15.00%)	(5.00%)	10.00%	30.00%	(30.00%)	(10.00%)
Business no. 6: Hotel
Revenue	652.05	652.05	589.95	589.95	683.10	683.10	558.90	558.90
Cost	391.23	353.97	391.23	353.97	409.86	335.34	409.86	335.34
Profit	7547.40	8625.60	5750.40	6828.60	7906.80	10,063.20	4312.80	6469.20
% Change in profit	5.00%	20.00%	(20.00%)	(5.00%)	10.00%	40.00%	(40.00%)	(10.00%)
Business no. 10: Attraction
Revenue	87.15	87.15	78.85	78.85	91.30	91.30	74.70	74.70
Cost	34.86	31.54	34.86	31.54	36.52	29.88	36.52	29.88
Profit	1754.55	1865.95	1476.05	1587.45	1838.10	2060.90	1281.10	1503.90
% Change in profit	5.00%	11.67%	(11.67%)	(5.00%)	10.00%	23.33%	(23.33%)	(10.00%)

Based on the sensitivity analysis, company owners or stakeholders may need to devise strategies to boost income and eliminate expenditures to ensure a business’s sustainability. In addition, the strength of sensitivity analysis is that it determines how changes in variables will affect a business’s profits, and this approach can also determine economic indicators. For example, the economic indicators of business no. 3 were as follows: its Net Present Value (NPV) was 13,542,512.92 THB, its Internal Rate of Return (IRR) was 59.44%, its Benefit/Cost Ratio (B/C Ratio) was 2.86 %, and its payback period was nine months, indicating that the case study was worth the investment. Since the NPV and the B/C Ratio values were greater than zero, the IRR was greater than the Minimum Attractive Rate of Return (MARR) (set to be 20%), and the payback period was faster than the target payback period.

7. Conclusions

This paper addresses a multi-period and multi-visit service scheduling problem with a time window (MMSSPTW) in local tourism businesses. The study intended to maximize the total profits of service operations in the tourism industry within service hours by considering the time windows of tourists and locations, sequence-dependent travel time, and destination restrictions. The proposed methods were developed to solve a real-world case study of a local tourism business network supply chain. This case study featured Khon Kaen and Kanchanaburi, Thailand. A mixed-integer linear programming model (MILP) was devised to solve the small-sized problems, while metaheuristics approaches were developed to obtain solutions for the practical problems. In the study, the DE, GA, HDEVNS, and HGAKV algorithms were employed.

Numerical results from these metaheuristics were investigated and compared to a set of constructed instances to illustrate the algorithms’ benefits in terms of their solution quality. For a significant number of instances and real-world issues, the HGAKV algorithm outperformed the DE, GA, and HDEVNS algorithms in terms of its solution quality under identical experimental conditions. The results obtained in the present work show the service schedule of each tourism business with the sequence of tourists, including the number of tourists, time duration, activity details, the time windows of tourists, and the tardiness time of a given location. The solution obtained from these approaches (i.e., the profit of each tourism business) was used to determine the NPV, IRR, B/C ratio, and payback period using the sensitivity analysis method, which attempts to complement the growing demands of businesses in a tourism supply chain with the capability of the service sectors while maintaining maximum tourist satisfaction.

In future research, we plan to consider multiple objective functions and vehicle conditions in transport modes. We believe that the proposed model can solve complicated combinatorial optimization problems in other industries (e.g., hospitality, hotel, transportation, and food and beverage industries). Although the proposed method is beneficial, additional work should be conducted to discover solutions by implementing other hybrid methods to compare the merits of other approaches in tackling issues of this nature.