Adaptive Fuzzy Command Filtered Finite-Time Tracking Control for Uncertain Nonlinear Multi-Agent Systems with Unknown Input Saturation and Unknown Control Directions
Abstract
1. Introduction
2. Problem Statement and Mathematical Preliminaries
2.1. Problem Statement
2.2. Mathematical Preliminaries
2.3. Fuzzy Logic Systems
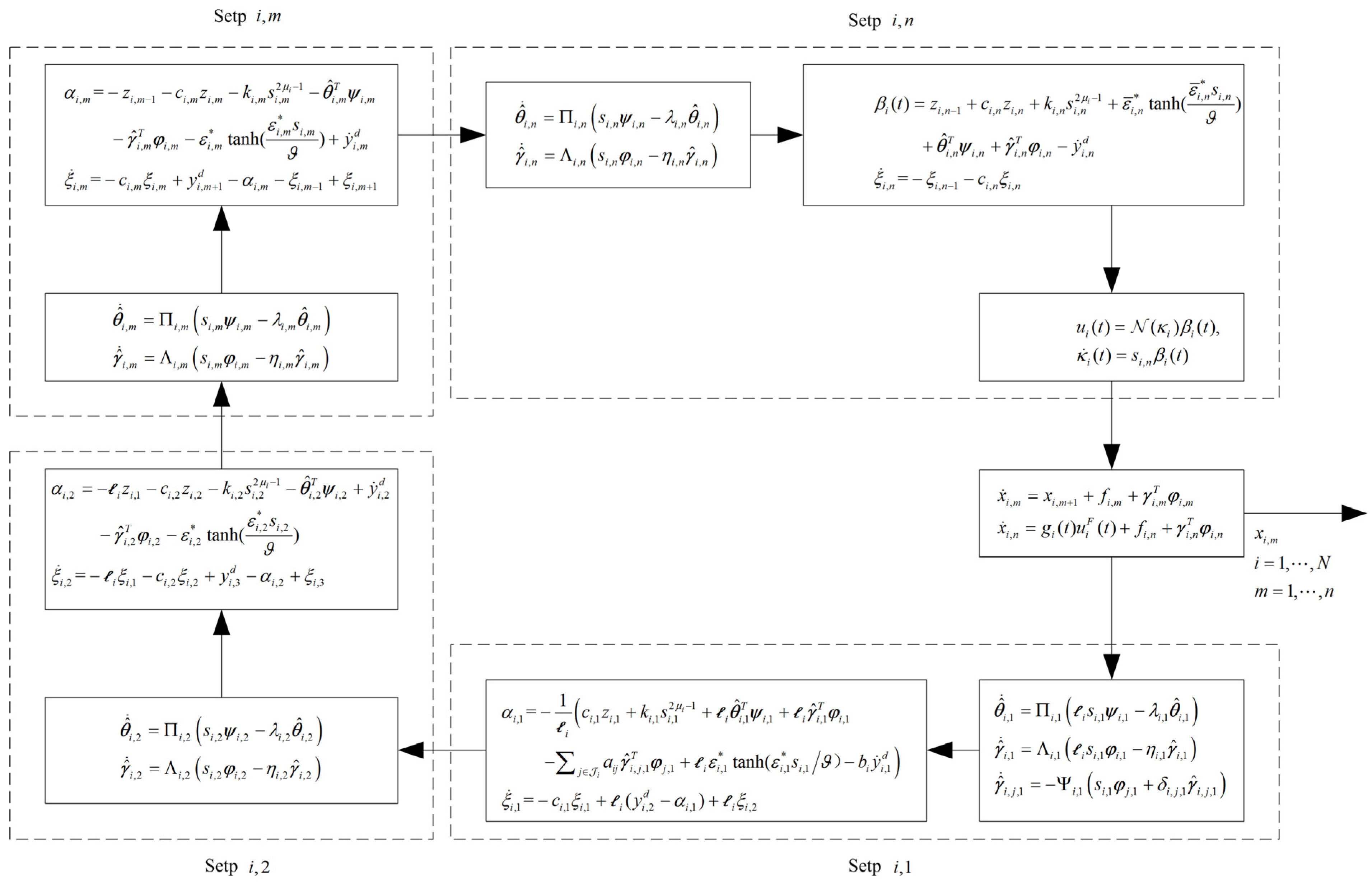
3. Main Results and Stability Analysis
3.1. Adaptive Fuzzy Finite-Time Consensus Control Law Design
3.2. Stability Analysis
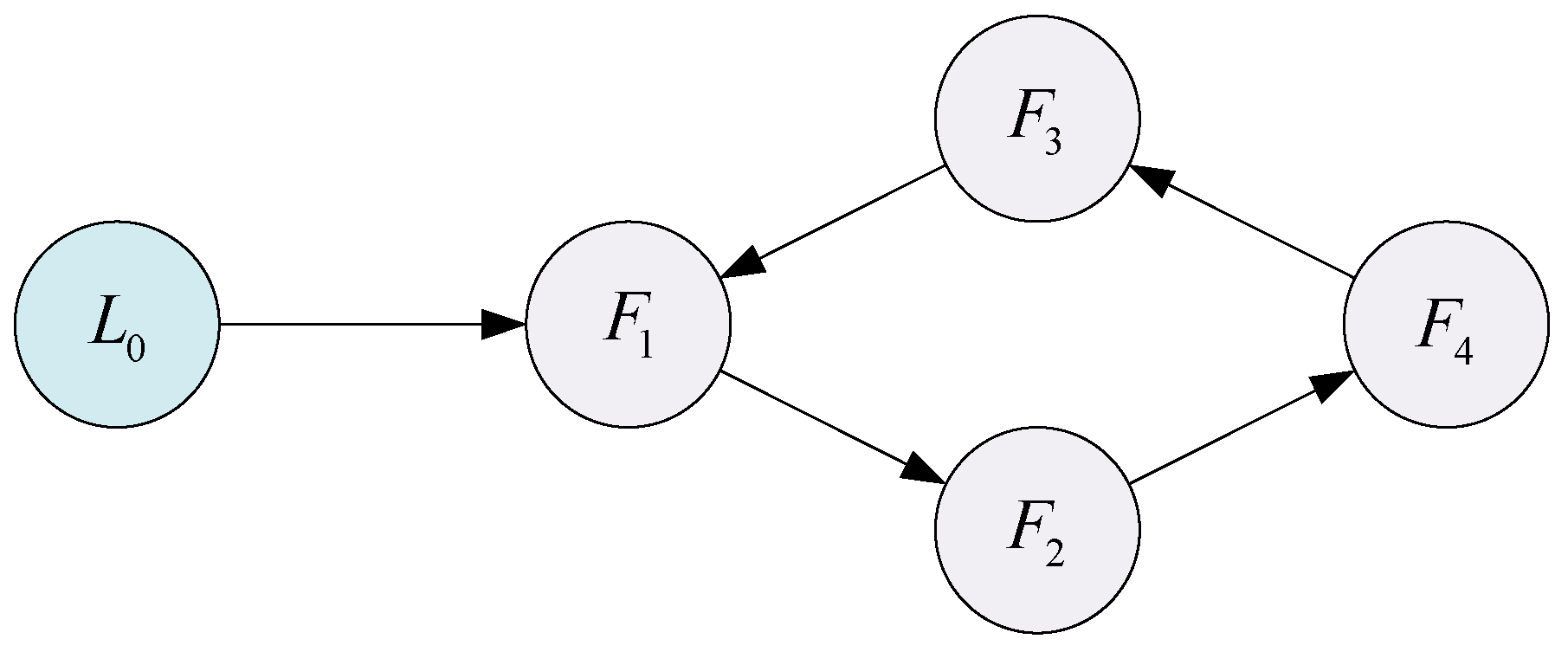
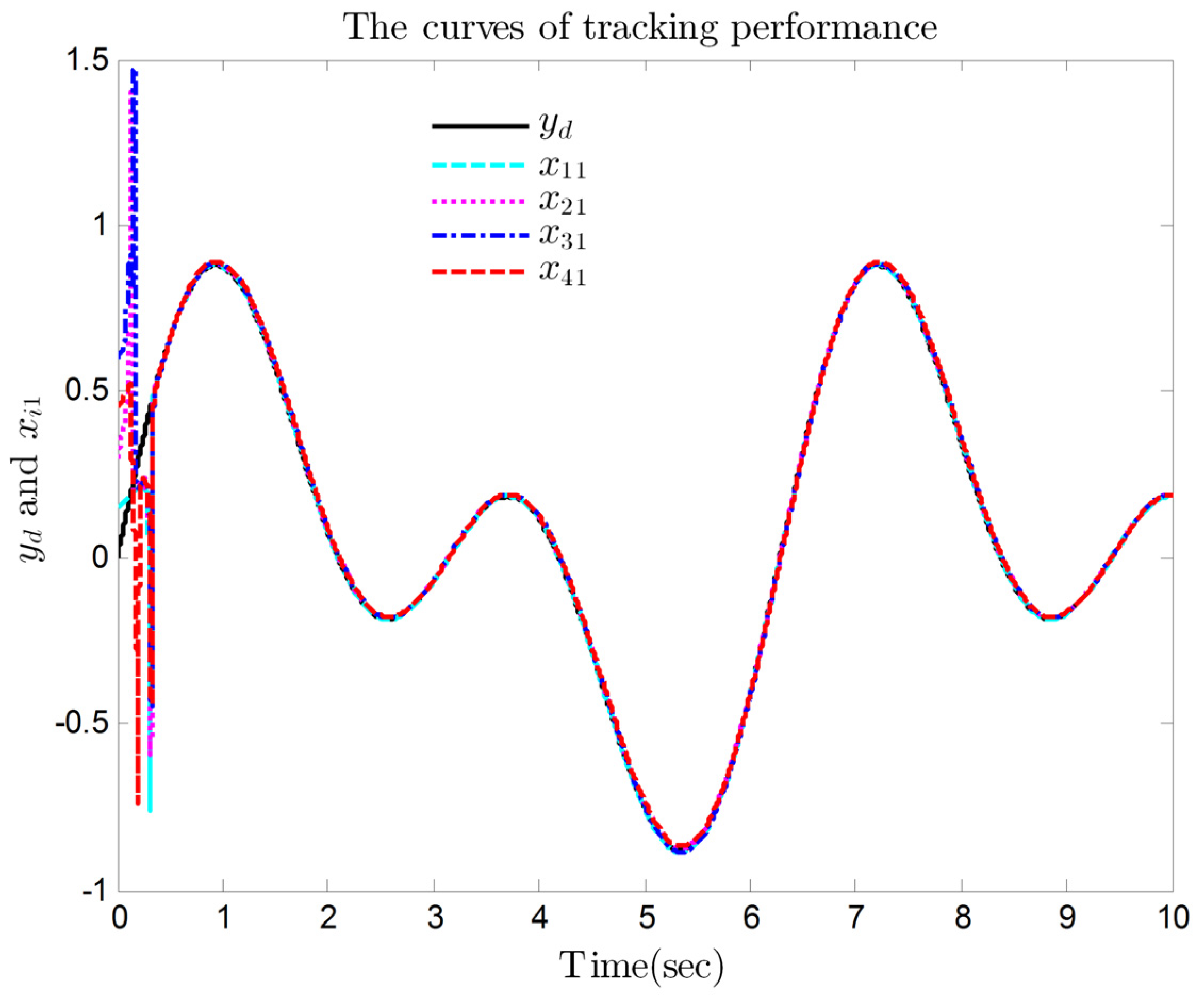
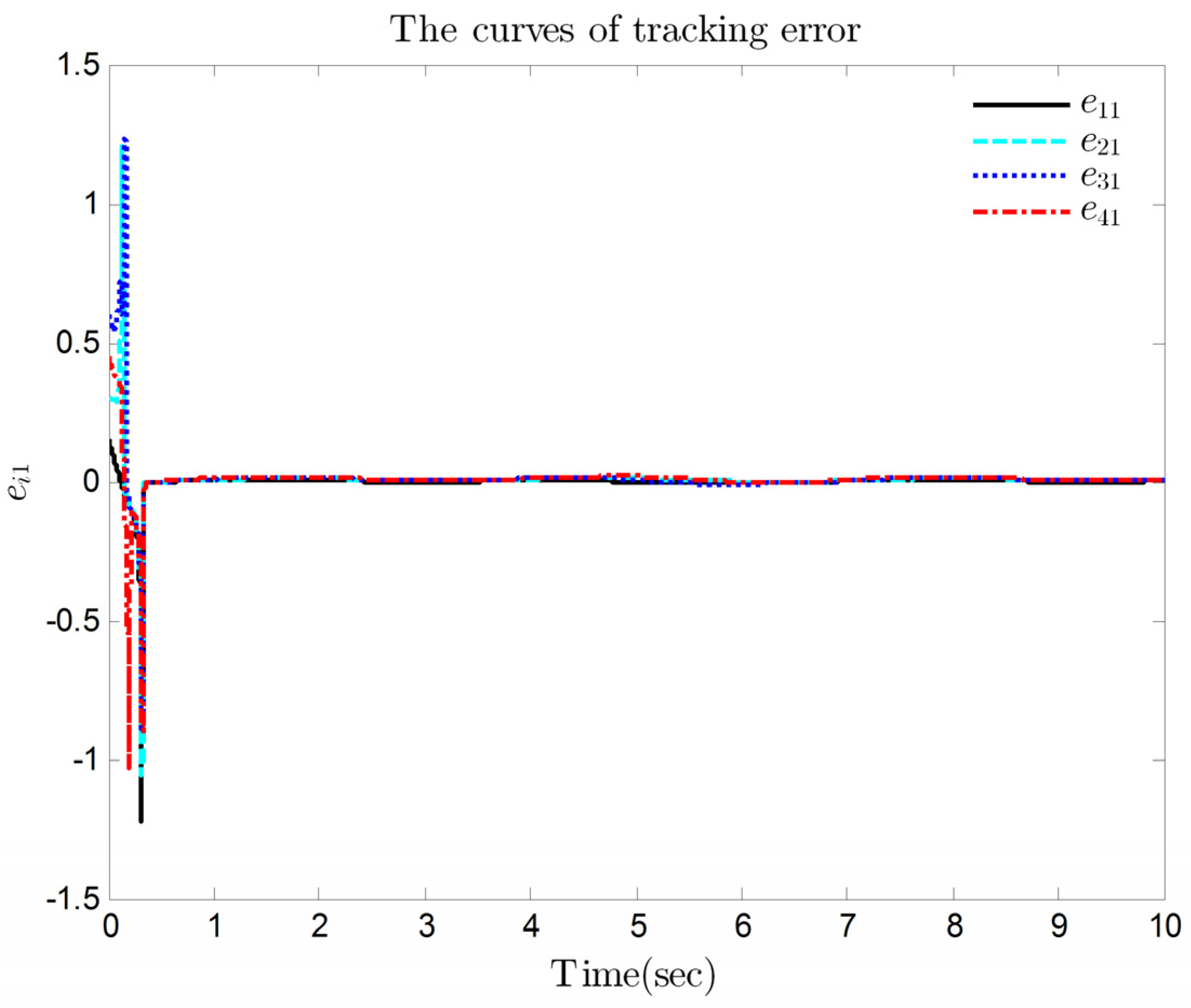
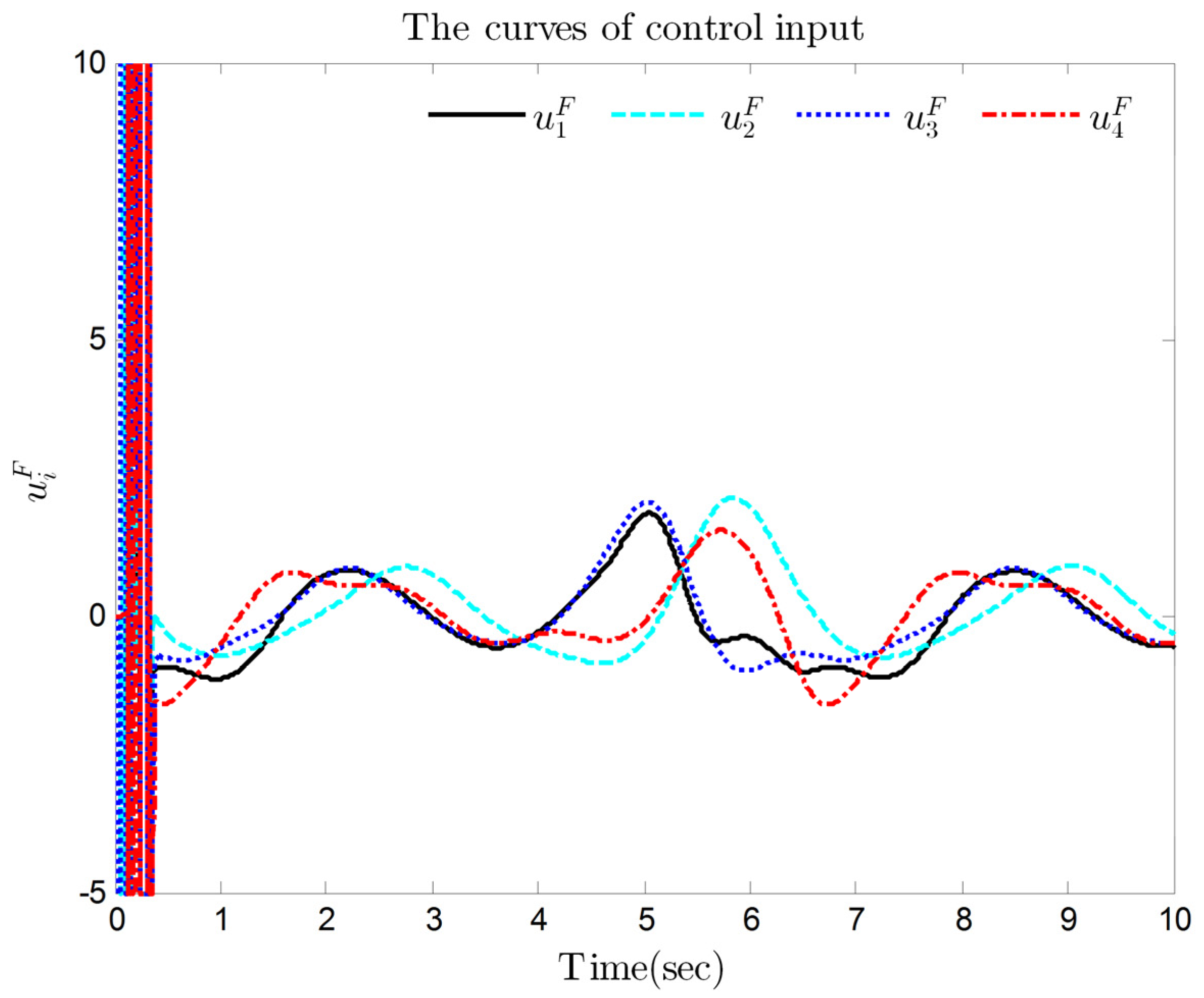
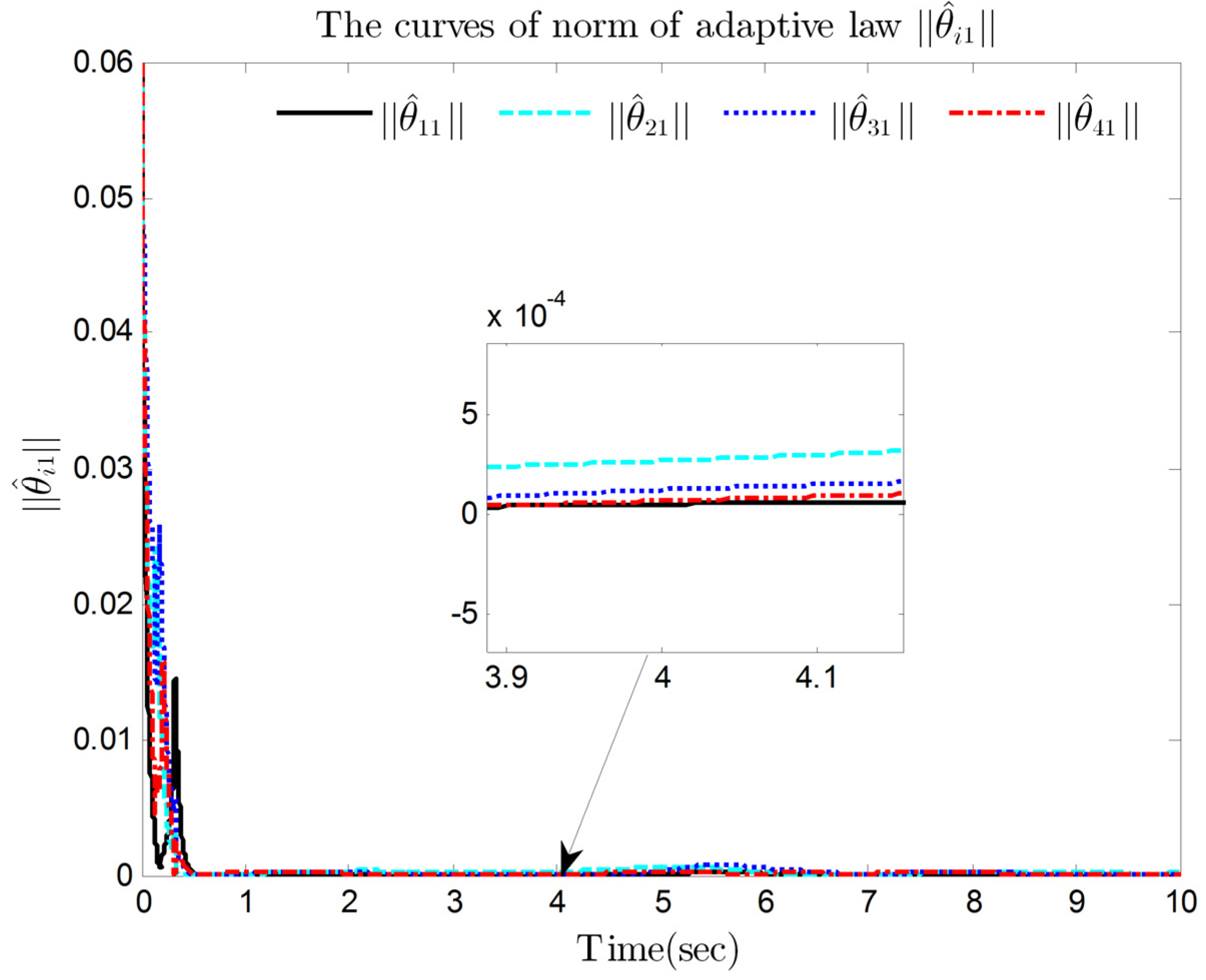
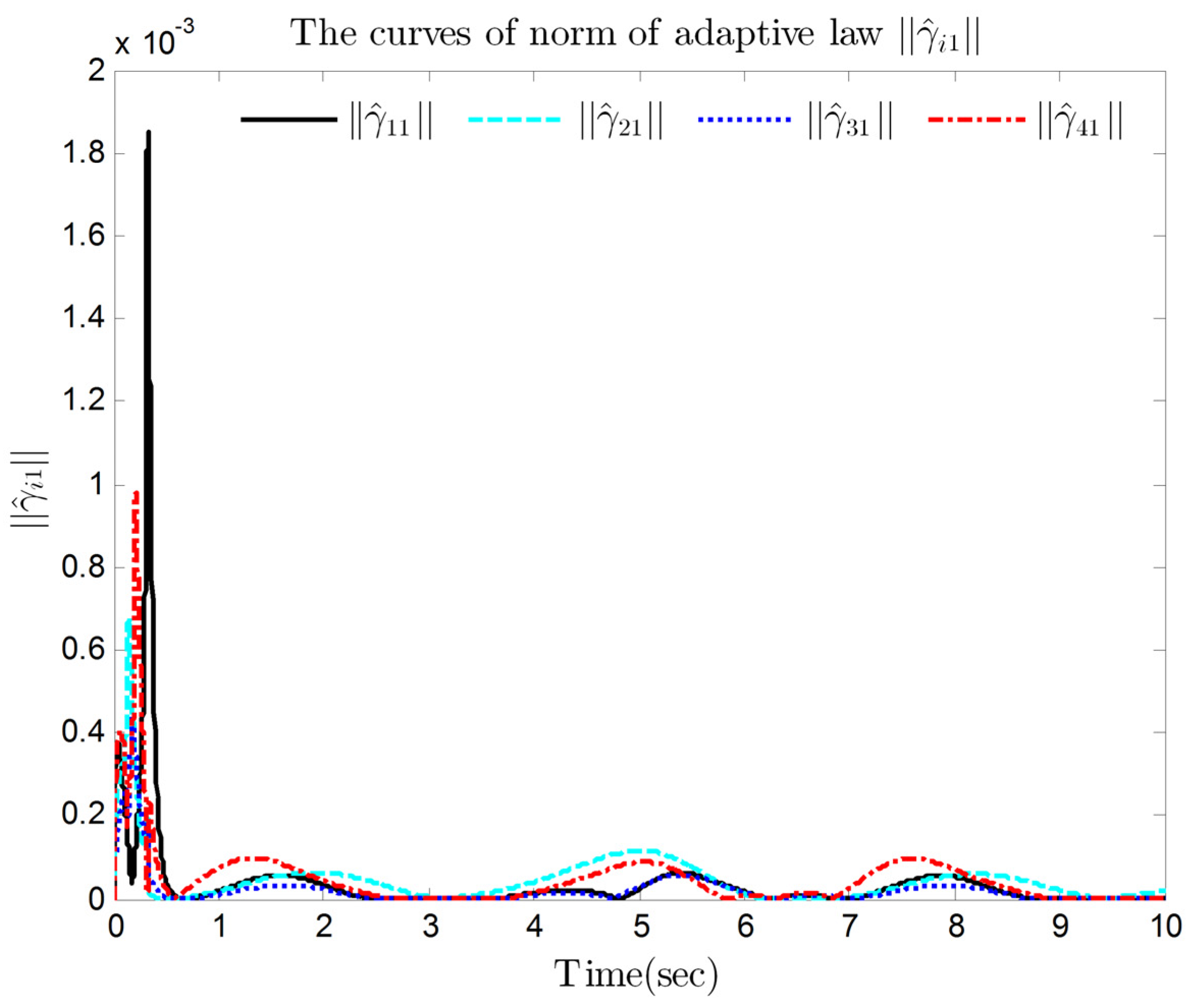
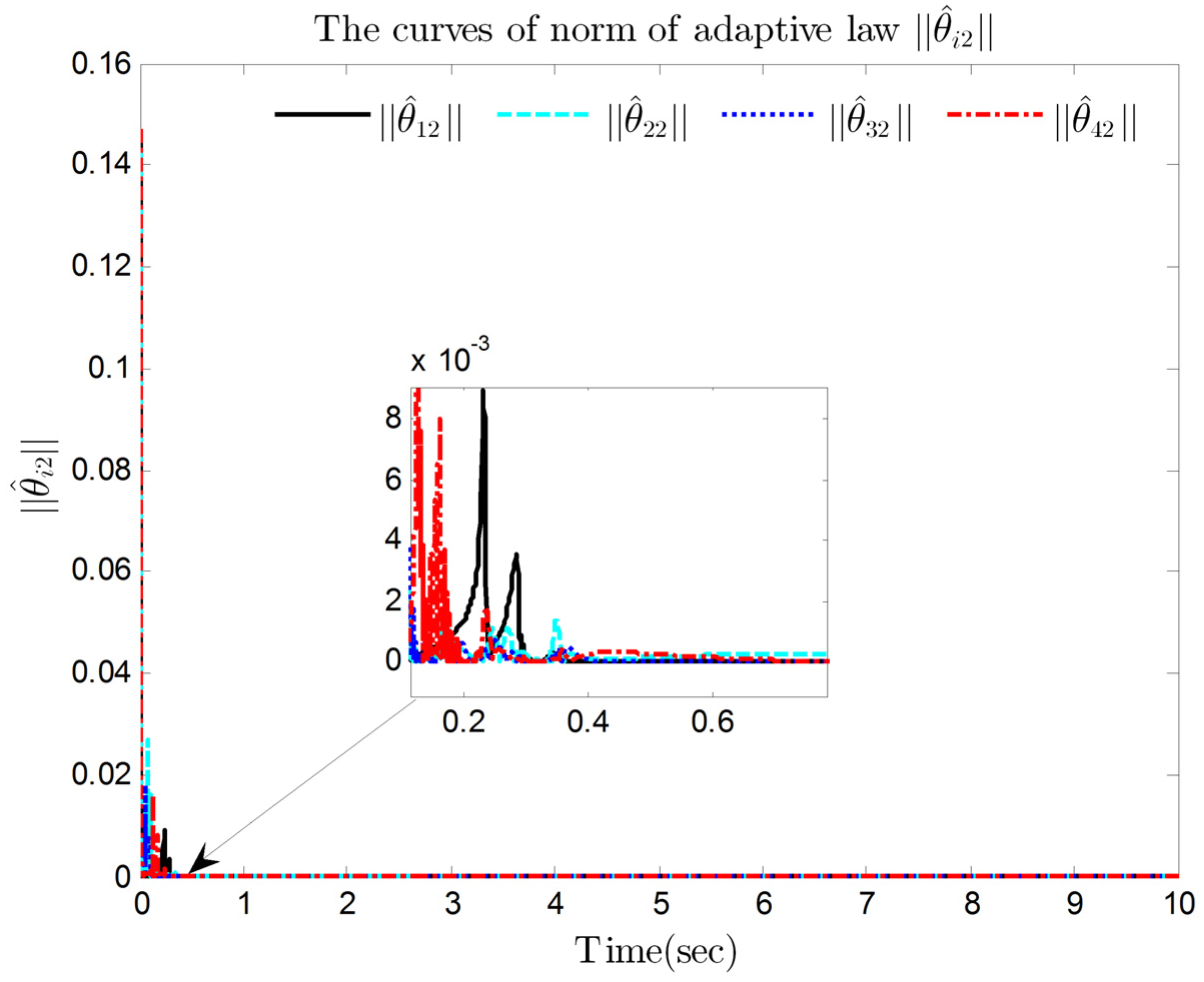
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
References
- Wang, B.; Chen, W.; Zhang, B.; Shi, P.; Zhang, H. A nonlinear observer-based approach to robust cooperative tracking for heterogeneous spacecraft attitude control and formation applications. IEEE Trans. Autom. Control 2022. [CrossRef]
- Li, Y.; Wu, Y.; He, S. Network-based leader-following formation control of second-order autonomous unmanned systems. J. Frankl. Inst. 2021, 358, 757–775. [Google Scholar] [CrossRef]
- Foderaro, G.; Zhu, P.; Wei, H.; Wettergren, T.A.; Ferrari, S. Distributed optimal control of sensor networks for dynamic target tracking. IEEE Trans. Control. Netw. Syst. 2018, 5, 142–153. [Google Scholar] [CrossRef]
- Zhang, P.; Xue, H.; Gao, S.; Zuo, X.; Zhang, J. Adaptive cooperative fault-tolerance tracking control for multi-agent system with hybrid actuator faults and multiple unknown control directions. Expert Syst. Appl. 2022, 197, 116711. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, Y. Distributed adaptive output-feedback tracking control of non-affine multi-agent systems with prescribed performance. J. Frankl. Inst. 2018, 355, 6087–6110. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, J.; Bai, C.; Li, J. Global iterative learning control based on fuzzy systems for nonlinear multi-agent systems with unknown dynamics. Inf. Sci. 2022, 587, 556–571. [Google Scholar] [CrossRef]
- Kaheni, M.; Usai, E.; Franceschelli, M. Resilient constrained optimization in multi-agent systems with improved guarantee on approximation bounds. IEEE Control. Lett. 2022, 6, 2659–2664. [Google Scholar] [CrossRef]
- Wen, G.; Zheng, W.X.; Wan, Y. Distributed robust optimization for networked agent systems with unknown nonlinearities. IEEE Trans. Autom. Control 2022. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, C.; Zhao, D.; Sun, B.; Li, Y. Event-triggered consensus control of continuous-time stochastic multi-agent systems. Automatica 2022, 137, 110022. [Google Scholar] [CrossRef]
- Qian, Y.-Y.; Liu, L.; Feng, G. Distributed event-triggered adaptive control for consensus of linear multi-agent systems with external disturbances. IEEE Trans. Cybern. 2020, 50, 2197–2208. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, Q.; Zhang, Y.; Liang, H. Fuzzy tracking control for nonlinear multi-agent systems with actuator faults and unknown control directions. Fuzzy Sets Syst. 2020, 385, 81–97. [Google Scholar] [CrossRef]
- Shamloo, N.F.; Kalat, A.A.; Chisci, L. Direct Adaptive Fuzzy Control of Nonlinear Descriptor Systems. Int. J. Fuzzy Syst. 2019, 21, 2588–2599. [Google Scholar] [CrossRef]
- Pan, T.-T.; Chang, X.-H.; Liu, Y. Robust Fuzzy Feedback Control for Nonlinear Systems With Input Quantization. IEEE Trans. Fuzzy Syst. 2022, 30, 4905–4914. [Google Scholar] [CrossRef]
- Zheng, S.; Shi, P.; Wang, S.; Shi, Y. Adaptive neural control for a class of nonlinear multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 763–776. [Google Scholar] [CrossRef]
- Wang, F.; Gao, Y.; Zhou, C.; Zong, Q. Disturbance observer-based backstepping formation control of multiple quadrotors with asymmetric output error constraints. Appl. Math. Comput. 2022, 415, 126693. [Google Scholar] [CrossRef]
- Wu, W.; Tong, S. Fixed-time adaptive fuzzy containment dynamic surface control for nonlinear multi-agent systems. IEEE Trans. Fuzzy Syst. 2022, 30, 5237–5248. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, X.; Deng, X.; Wen, G. Command-filter-based adaptive finite-time consensus control for nonlinear strict-feedback multi-agent systems with dynamic leader. Inf. Sci. 2021, 565, 17–31. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, X. Adaptive fuzzy tracking control of uncertain nonlinear multi-agent systems with unknown control directions and a dead-zone fault. Mathematics 2022, 10, 2655. [Google Scholar] [CrossRef]
- Nussbaum, R.D. Some remarks on a conjecture in parameter adaptive control. Syst. Control. Lett. 1983, 3, 243–246. [Google Scholar] [CrossRef]
- Kamalamiri, A.; Shahrokhi, M.; Mohit, M. Adaptive finite-time neural control of non-strict feedback systems subject to output constraint, unknown control direction, and input nonlinearities. Inf. Sci. 2020, 520, 271–291. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, C.; Ge, Y. Adaptive neural network dynamic surface control of uncertain strict-feedback nonlinear systems with unknown control direction and unknown actuator fault. J. Frankl. Inst. 2022, 359, 4054–4073. [Google Scholar] [CrossRef]
- Ma, J.; Xu, S.; Ma, Q.; Zhang, Z. Event-triggered adaptive neural network control for nonstrict-feedback nonlinear time-delay systems with unknown control directions. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4196–4205. [Google Scholar] [CrossRef]
- Cai, X.; Wang, C.; Wang, G.; Liang, D. Distributed consensus control for second-order nonlinear multi-agent systems with unknown control directions and position constraints. Neurocomputing 2018, 306, 61–67. [Google Scholar] [CrossRef]
- Fan, B.; Yang, Q.; Jagannathan, S.; Sun, Y. Output-constrained control of nonaffine multiagent systems with partially unknown control directions. IEEE Trans. Autom. Control 2019, 64, 3936–3942. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Cai, X. Consensus control of higher-order nonlinear multi-agent systems with unknown control directions. Neurocomputing 2019, 359, 122–129. [Google Scholar] [CrossRef]
- Ao, W.; Huang, J.; Xue, F. Adaptive leaderless consensus control of a class of strict-feedback nonlinear multi-agent systems with unknown control directions: A non-Nussbaum function based approach. J. Frankl. Inst. 2020, 357, 12180–12196. [Google Scholar] [CrossRef]
- Rezaee, H.; Abdollahi, F. Adaptive leaderless consensus control of strict-feedback nonlinear multiagent systems with unknown control directions. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6435–6444. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Liu, W.; Tong, S. Observer-based adaptive optimized control for stochastic nonlinear systems with input and state constraints. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7791–7805. [Google Scholar] [CrossRef]
- Zhang, W.; Wei, W. Disturbance-observer-based finite-time adaptive fuzzy control for non-triangular switched nonlinear systems with input saturation. Inf. Sci. 2021, 561, 152–167. [Google Scholar] [CrossRef]
- He, C.; Wu, J.; Dai, J.; Zhang, Z. Fixed-time adaptive neural tracking control of output constrained nonlinear pure-feedback system with input saturation. Neurocomputing 2021, 451, 125–137. [Google Scholar] [CrossRef]
- Li, P.; Jabbari, F.; Sun, X.-M. Containment control of multi-agent systems with input saturation and unknown leader inputs. Automatica 2021, 130, 109677. [Google Scholar] [CrossRef]
- Zhu, Z.-H.; Guan, Z.-H.; Hu, B.; Zhang, D.-X.; Cheng, X.-M.; Li, T. Semi-global bipartite consensus tracking of singular multi-agent systems with input saturation. Neurocomputing 2021, 432, 183–193. [Google Scholar] [CrossRef]
- Cheng, W.; Xue, H.; Liang, H.; Wang, W. Prescribed performance adaptive fuzzy control of stochastic nonlinear multi-agent systems with input hysteresis and saturation. Int. J. Fuzzy Syst. 2022, 24, 91–104. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, J.; Lin, C. Command filter based adaptive fuzzy bipartite output consensus tracking of nonlinear coopetition multi-agent systems with input saturation. ISA Trans. 2018, 80, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Hao, R.; Wang, H.; Zheng, W. Dynamic event-triggered adaptive command filtered control for nonlinear multi-agent systems with input saturation and disturbances. ISA Trans. 2022, 130, 104–120. [Google Scholar] [CrossRef]
- Wang, H.; Chen, B.; Liu, X.; Liu, K.; Lin, C. Robust adaptive fuzzy tracking control for pure-feedback stochastic nonlinear systems with input constraints. IEEE Trans. Cybern. 2013, 43, 2093–2104. [Google Scholar] [CrossRef]
- Wang, M.; Liu, X.; Shi, P. Adaptive neural control of pure-feedback nonlinear time-delay systems via dynamic surface technique. IEEE Trans. Syst. Man Cybern. Part B (Cybernetics) 2011, 41, 1681–1692. [Google Scholar] [CrossRef]
- Hu, J.; Feng, G. Distributed tracking control of leader–follower multi-agent systems under noisy measurement. Automatica 2010, 46, 1382–1387. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Liu, X.; Lin, C. Finite-time adaptive fuzzy tracking control design for nonlinear systems. IEEE Trans. Fuzzy Syst. 2018, 26, 1207–1216. [Google Scholar] [CrossRef]
- Deng, X.; Wang, J. Fuzzy-based adaptive dynamic surface control for a type of uncertain nonlinear system with unknown actuator faults. Mathematics 2022, 10, 1624. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Dong, W.; Yu, H. Observer and command-filter-based adaptive fuzzy output feedback control of uncertain nonlinear systems. IEEE Trans. Ind. Electron. 2015, 62, 5962–5970. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, X.; Huang, Y.; Wei, L. Adaptive Fuzzy Command Filtered Finite-Time Tracking Control for Uncertain Nonlinear Multi-Agent Systems with Unknown Input Saturation and Unknown Control Directions. Mathematics 2022, 10, 4656. https://doi.org/10.3390/math10244656
Deng X, Huang Y, Wei L. Adaptive Fuzzy Command Filtered Finite-Time Tracking Control for Uncertain Nonlinear Multi-Agent Systems with Unknown Input Saturation and Unknown Control Directions. Mathematics. 2022; 10(24):4656. https://doi.org/10.3390/math10244656
Chicago/Turabian StyleDeng, Xiongfeng, Yiqing Huang, and Lisheng Wei. 2022. "Adaptive Fuzzy Command Filtered Finite-Time Tracking Control for Uncertain Nonlinear Multi-Agent Systems with Unknown Input Saturation and Unknown Control Directions" Mathematics 10, no. 24: 4656. https://doi.org/10.3390/math10244656
APA StyleDeng, X., Huang, Y., & Wei, L. (2022). Adaptive Fuzzy Command Filtered Finite-Time Tracking Control for Uncertain Nonlinear Multi-Agent Systems with Unknown Input Saturation and Unknown Control Directions. Mathematics, 10(24), 4656. https://doi.org/10.3390/math10244656











