Two Analytical Techniques for Fractional Differential Equations with Harmonic Terms via the Riemann–Liouville Definition

Abstract

This paper considers a class of non-homogeneous fractional systems with harmonic terms by means of the Riemann–Liouville definition. Two different approaches are applied to obtain the dual solution of the studied class. The first approach uses the Laplace transform (LT) and the solution is given in terms of the Mittag-Leffler functions. The second approach avoids the LT and expresses the solution in terms of exponential and periodic functions which is analytic in the whole domain. The current methods determine the solution directly and efficiently. The results are applicable for other problems of higher order.

1. Introduction

The fractional calculus (FC) is a natural generalization of the classical calculus (CC). The FC is useful in studying physical phenomena of memory effects [1,2,3]. In [4,5,6,7,8], several models have been solved in view of FC. In addition, other interesting results for the FC applications are listed in [9,10,11,12,13,14]. In elementary physics, some problems have been reformulated and re-solved via the FC. For example, the projectile motion was analyzed in [15,16] via the Caputo fractional derivative (CFD), where the comparisons between their results and experimental data have been declared. The same problem has been solved via the Riemann–Liouville fractional derivative (RLFD) in [17]. Such models were introduced as second-order fractional initial value problems (second-order FIVPs).

For first-order fractional initial value problems (first-order FIVPs), an example has been presented recently in [18,19] in which the model of light absorption by the interstellar matter was solved. The Laplace transform (LT) was successfully applied in [19] to construct the exact solution. The same model has been solved via the RLFD by El-Zahar et al. [20]. However, they applied a series solution method and hence obtained the solution in a closed series form through avoiding the LT. This means that the approximate or the exact solution of a physical model mainly depends on the chosen method of solution [21,22,23,24,25,26,27,28,29,30,31,32,33].

This work aims to apply the RLFD to the following class:

$${}_{-\infty }^{RL}{D}_t^{\alpha }y\left(t\right)+{\omega }^{2}y\left(t\right)=acos(\Omega t)+bsin(\Omega t),D_t^{\alpha -1}y\left(0\right)=A,0<\alpha \le 1,$$

(1)

where $\alpha$ is the non-integer order of the RLFD, while a, b, $\omega$, $\Omega$, and A are constants. The class (1) seems simple, however, determining its exact solution is not an easy task as demonstrated later. It will be declared that class (1) has a dual solution. Two types of exact solutions are to be obtained for the current class. The first solution will be determined via Mittag-Leffler functions through the LT. Moreover, the second one avoids such functions, and instead, it uses exponential/trigonometric functions. It will be shown that the dual solution reduces to the corresponding results in [31] when b vanishes. Moreover, our solutions agree with those of ordinary derivatives as $\alpha \to 1$. Furthermore, characteristics of the dual solution will also be analyzed. The solution involving exponential/trigonometric functions has some advantages over the Mittag-Leffler one which will be demonstrated later.

The paper is organized as follows. In Section 2, some preliminaries and concepts in fractional calculus are presented. Section 3 is devoted to analyze the complementary and particular solutions of the governing equation. In addition, some theoretical results are obtained in this section. Moreover, Section 4 focuses on deriving the dual solution of the current system. The behavior and the properties of the obtained solution are discussed in Section 5. The paper is concluded in Section 6.

2. Preliminaries

The RLFD of order $\alpha \in {\mathbb{R}}_0^{+}$ of function $f:[c,d]\to \mathbb{R}(-\infty <c<d<\infty )$ is (see [1,2,3])

$${}_c^{RL}{D}_t^{\alpha }f\left(t\right)=\frac{1}{\Gamma \left(n-\alpha \right)}\frac{d^n}{d{t}^n}\left({\int }_c^t\frac{f\left(\tau \right)}{{\left(t-\tau \right)}^{\alpha -n+1}}d\tau \right),n=\left[\alpha \right]+1,t>c,$$

(2)

where $\left[\alpha \right]$ is the integral part of $\alpha$. As $c\to -\infty$ and for $t\in \mathbb{R}$, we have [30,31]

$$\begin{array}{cc}& {}_{-\infty }^{RL}{D}_t^{\alpha }{e}^{i\omega t}={\left(i\omega \right)}^{\alpha }{e}^{i\omega t},\hfill \\ & {}_{-\infty }^{RL}{D}_t^{\alpha }cos\left(\omega t\right)={\omega }^{\alpha }cos\left(\omega t+\frac{\alpha \pi }{2}\right),\hfill \\ & {}_{-\infty }^{RL}{D}_t^{\alpha }sin\left(\omega t\right)={\omega }^{\alpha }sin\left(\omega t+\frac{\alpha \pi }{2}\right).\hfill \end{array}$$

(3)

In [1,2,3], the LT of the RLFD (as $c\to 0$) is given by

$$\mathcal{L}\left[{}_0^{RL}{D}_t^{\alpha }y\left(t\right)\right]=s^{\alpha }Y\left(s\right)-\sum _{i=0}^{n-1}{s}^i{D}_t^{\alpha -i-1}y\left(0\right).$$

(4)

So, our paper considers the two RLFD operators ${}_{-\infty }^{RL}{D}_t^{\alpha }$ and ${}_0^{RL}{D}_t^{\alpha }$. The first operator is defined from $-\infty$ (as the initial point c) which will be used to construct the solution in terms of exponential and periodic functions with the help of the properties in Equation (3). The second operator is defined from $c=0$ and it allows to use the LT in Equation (4) and hence to obtain the solution via the Mittag-Leffler function.

The inverse LT of the following expression is expressed in terms of the Mittag-Leffler function as

$${\mathcal{L}}^{-1}\left(\frac{s^{\alpha -\mathrm{g}}}{s^{\alpha }+{\omega }^2}\right)=t^{\mathrm{g}-1}{E}_{\alpha ,\mathrm{g}}(-{\omega }^2{t}^{\alpha }),Re\left(s\right)>{\left|{\omega }^2\right|}^{\frac{1}{\alpha }},$$

(5)

where the Mittag-Leffler function of two parameters $E_{\alpha ,\mathrm{g}}\left(z\right)$ is defined as

$$E_{\alpha ,\mathrm{g}}\left(z\right)=\sum _{i=0}^{\infty }\frac{z^i}{\Gamma (\alpha i+\mathrm{g})},(\alpha >0,\mathrm{g}>0).$$

(6)

The definition (6) leads to

$$E_{\alpha ,1}\left(z\right)=E_{\alpha }\left(z\right),E_1\left(z\right)=e^z,E_{2,1}(-z^2)=cos\left(z\right),E_{2,2}(-z^2)=\frac{sinz}{z}.$$

(7)

The following expressions can be derived as special cases of Formula (5)

$$\begin{array}{ccc}& & {\mathcal{L}}^{-1}\left(\frac{s^{\alpha -1}}{s^{\alpha }+1}\right)=E_{\alpha }(-t^{\alpha }),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}& & {\mathcal{L}}^{-1}\left(\frac{1}{s^{\alpha }+{\omega }^2}\right)=t^{\alpha -1}{E}_{\alpha ,\alpha }(-{\omega }^2{t}^{\alpha }),Re\left(s\right)>{\left|{\omega }^2\right|}^{\frac{1}{\alpha }},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}& & {\mathcal{L}}^{-1}\left(\frac{s^{-1}}{s^{\alpha }+{\omega }^2}\right)=t^{\alpha }{E}_{\alpha ,\alpha +1}(-{\omega }^2{t}^{\alpha }),Re\left(s\right)>{\left|{\omega }^2\right|}^{\frac{1}{\alpha }}.\hfill \end{array}$$

(10)

3. Analysis

Theorem 1.

The complementary solution $y_c\left(t\right)$ is

$$y_c\left(t\right)=c_1\left(\alpha \right)e^{i\delta t},\delta =-i{\left(-{\omega }^2\right)}^{1/\alpha },$$

(11)

where $c_1\left(\alpha \right)$ is a constant.

Proof. 

The complementary solution $y_c\left(t\right)$ is the solution of the homogeneous part of Equation (1):

$${}_{-\infty }^{RL}{D}_t^{\alpha }{y}_c\left(t\right)+{\omega }^2{y}_c\left(t\right)=0.$$

(12)

In view of [31], the solution $y_c\left(t\right)$ takes the form:

$$y_c\left(t\right)=c_1\left(\alpha \right)e^{i\delta t},$$

(13)

where $c_1\left(\alpha \right)$ is a constant. The $\delta \left(\omega \right)$ can be determined by substituting (13) into (12), this yields

$$c_1\left(\alpha \right)\left[{\delta }^{\alpha }{e}^{i\frac{\pi \alpha }{2}}+{\omega }^2\right]e^{i\delta t}=0.$$

(14)

For the non-trivial solution $y_c\left(t\right)$, we restrict that $c_1\left(\alpha \right)\ne 0$, and hence, Equation (14) becomes

$${\left(\delta \left(\omega \right)e^{i\frac{\pi }{2}}\right)}^{\alpha }+{\omega }^2=0,$$

(15)

and this gives

$$\delta \left(\omega \right)=-i{\left(-{\omega }^2\right)}^{1/\alpha },y_c\left(t\right)=c_1\left(\alpha \right)e^{i\delta t}.$$

(16)

The constant $c_1\left(\alpha \right)$ will be determined later by applying the given initial condition. □

Theorem 2.

(The particular solution $y_p$) The solution $y_p\left(t\right)$ of Equation (1) is

$$y_p\left(t\right)={\rho }_1\left(\alpha \right)cos(\Omega t)+{\rho }_2\left(\alpha \right)sin(\Omega t),0<\alpha \le 1,$$

(17)

where

$${\rho }_1\left(\alpha \right)=\frac{a{\omega }^2+{\Omega }^{\alpha }\left(acos\left(\frac{\pi \alpha }{2}\right)-bsin\left(\frac{\pi \alpha }{2}\right)\right)}{{\omega }^4+{\Omega }^{2\alpha }+2{\omega }^2{\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)},{\rho }_2\left(\alpha \right)=\frac{b{\omega }^2+{\Omega }^{\alpha }\left(bcos\left(\frac{\pi \alpha }{2}\right)+asin\left(\frac{\pi \alpha }{2}\right)\right)}{{\omega }^4+{\Omega }^{2\alpha }+2{\omega }^2{\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)}.$$

(18)

Proof. 

In view of Equation (17), we have

$$\begin{array}{ccc}\hfill {}_{-\infty }^{RL}{D}_t^{\alpha }{y}_p& =& {\rho }_1\left(\alpha \right){}_{-\infty }^{RL}{D}_t^{\alpha }cos(\Omega t)+{\rho }_2\left(\alpha \right){}_{-\infty }^{RL}{D}_t^{\alpha }sin(\Omega t),\hfill \\ & =& {\Omega }^{\alpha }cos\left(\Omega t\right)\left({\rho }_1\left(\alpha \right)cos\left(\frac{\pi \alpha }{2}\right)+{\rho }_2\left(\alpha \right)sin\left(\frac{\pi \alpha }{2}\right)\right)+\hfill \\ & & {\Omega }^{\alpha }sin\left(\Omega t\right)\left({\rho }_2\left(\alpha \right)cos\left(\frac{\pi \alpha }{2}\right)-{\rho }_1\left(\alpha \right)sin\left(\frac{\pi \alpha }{2}\right)\right),\hfill \end{array}$$

(19)

and hence

$$\begin{array}{ccc}\hfill {}_{-\infty }^{RL}{D}_t^{\alpha }{y}_p+{\omega }^2{y}_p& =& \left[\left({\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)+{\omega }^2\right){\rho }_1\left(\alpha \right)+{\Omega }^{\alpha }sin\left(\frac{\pi \alpha }{2}\right){\rho }_2\left(\alpha \right)\right]cos\left(\Omega t\right)+\hfill \\ & & \left[\left({\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)+{\omega }^2\right){\rho }_2\left(\alpha \right)-{\Omega }^{\alpha }sin\left(\frac{\pi \alpha }{2}\right){\rho }_1\left(\alpha \right)\right]sin\left(\Omega t\right).\hfill \end{array}$$

(20)

The coefficients ${\rho }_1\left(\alpha \right)$ and ${\rho }_2\left(\alpha \right)$ can be obtained by solving the following coupled algebraic equations:

$$\begin{array}{cc}& \left({\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)+{\omega }^2\right){\rho }_1\left(\alpha \right)+{\Omega }^{\alpha }sin\left(\frac{\pi \alpha }{2}\right){\rho }_2\left(\alpha \right)=a,\hfill \\ \hfill & \left({\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)+{\omega }^2\right){\rho }_2\left(\alpha \right)-{\Omega }^{\alpha }sin\left(\frac{\pi \alpha }{2}\right){\rho }_1\left(\alpha \right)=b,\hfill \end{array}$$

(21)

and then,

$${\rho }_1\left(\alpha \right)=\frac{a{\omega }^2+{\Omega }^{\alpha }\left(acos\left(\frac{\pi \alpha }{2}\right)-bsin\left(\frac{\pi \alpha }{2}\right)\right)}{{\omega }^4+{\Omega }^{2\alpha }+2{\omega }^2{\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)},{\rho }_2\left(\alpha \right)=\frac{b{\omega }^2+{\Omega }^{\alpha }\left(bcos\left(\frac{\pi \alpha }{2}\right)+asin\left(\frac{\pi \alpha }{2}\right)\right)}{{\omega }^4+{\Omega }^{2\alpha }+2{\omega }^2{\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)}.$$

(22)

Inserting (22) into $y_p$ in (17) and simplifying, we obtain

$$y_p\left(t\right)=\frac{{\omega }^2\left[acos\left(\Omega t\right)+bsin\left(\Omega t\right)\right]+{\Omega }^{\alpha }\left[acos\left(\Omega t-\frac{\pi \alpha }{2}\right)+bsin\left(\Omega t-\frac{\pi \alpha }{2}\right)\right]}{{\omega }^4+{\Omega }^{2\alpha }+2{\omega }^2{\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)}.$$

(23)

This solution $y_p$ reduces to the corresponding one in [31] when $b=0$. It is also agrees with that reported in [30] at $b=0$ and $a=1$. □

Corollary 1.

The solution $y_p$ of the fractional differential equation (FDE):

$${}_{-\infty }^{RL}{D}_t^{\alpha }y\left(t\right)+{\omega }^{2}y\left(t\right)=bsin(\Omega t),0<\alpha \le 1,$$

(24)

is

$$y_p\left(t\right)=b\left[\frac{{\omega }^{2}sin\left(\Omega t\right)+{\Omega }^{\alpha }sin\left(\Omega t-\frac{\pi \alpha }{2}\right)}{{\omega }^4+{\Omega }^{2\alpha }+2{\omega }^2{\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)}\right].$$

(25)

Proof. 

On setting $a=0$ in Equation (23), we obtain Equation (25). Furthermore, the solution $y_p$ at $b=1$ becomes

$$y_p\left(t\right)=\frac{{\omega }^{2}sin\left(\Omega t\right)+{\Omega }^{\alpha }sin\left(\Omega t-\frac{\pi \alpha }{2}\right)}{{\omega }^4+{\Omega }^{2\alpha }+2{\omega }^2{\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)}.$$

(26)

This result coincides with that reported in [30]. □

Corollary 2.

The FDE:

$${}_{-\infty }^{RL}{D}_t^{\alpha }y\left(t\right)+{\omega }^{2}y\left(t\right)=acos(\Omega t),0<\alpha \le 1,$$

(27)

has the following solution $y_p\left(t\right)$:

$$y_p\left(t\right)=a\left[\frac{{\omega }^{2}cos\left(\Omega t\right)+{\Omega }^{\alpha }cos\left(\Omega t-\frac{\pi \alpha }{2}\right)}{{\omega }^4+{\Omega }^{2\alpha }+2{\omega }^2{\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)}\right].$$

(28)

Proof. 

Setting $b=0$ in Equation (23), we get Equation (28). Moreover, the particular solution at $a=1$ becomes

$$y_p\left(t\right)=\frac{{\omega }^{2}cos\left(\Omega t\right)+{\Omega }^{\alpha }cos\left(\Omega t-\frac{\pi \alpha }{2}\right)}{{\omega }^4+{\Omega }^{2\alpha }+2{\omega }^2{\Omega }^{\alpha }cos\left(\frac{\pi \alpha }{2}\right)}.$$

(29)

This result was reported in [31] (Equation (7)) using an operator approach. □

4. The Dual Solution

In this section, it is shown that a dual solution exists for the class (1).

4.1. First Solution: Mittag-Leffler Functions

Taking LT for Equation (1), then

$$s^{\alpha }Y\left(s\right)-D_t^{\alpha -1}y\left(0\right)+{\omega }^{2}Y\left(s\right)=\frac{as}{s^2+{\Omega }^2}+\frac{b\Omega }{s^2+{\Omega }^2},$$

(30)

which gives $Y\left(s\right)$ in the form:

$$Y\left(s\right)=\frac{A}{s^{\alpha }+{\omega }^2}+\frac{as}{(s^{\alpha }+{\omega }^2)(s^2+{\Omega }^2)}+\frac{b\Omega }{(s^{\alpha }+{\omega }^2)(s^2+{\Omega }^2)}.$$

(31)

The inversion reads

$$y\left(t\right)=A{\mathcal{L}}^{-1}\left(\frac{1}{s^{\alpha }+{\omega }^2}\right)+{\mathcal{L}}^{-1}\left[\frac{as}{(s^{\alpha }+{\omega }^2)(s^2+{\Omega }^2)}+\frac{b\Omega }{(s^{\alpha }+{\omega }^2)(s^2+{\Omega }^2)}\right],$$

(32)

or

$$y\left(t\right)=A{t}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{t}^{\alpha }\right)+a{\mathcal{L}}^{-1}\left(\frac{1}{s^{\alpha }+{\omega }^2}\right)*{\mathcal{L}}^{-1}\left(\frac{s}{s^2+{\Omega }^2}\right)+b{\mathcal{L}}^{-1}\left(\frac{1}{s^{\alpha }+{\omega }^2}\right)*{\mathcal{L}}^{-1}\left(\frac{\Omega }{s^2+{\Omega }^2}\right),$$

(33)

and thus,

$$\begin{array}{ccc}& & y\left(t\right)=A{t}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{t}^{\alpha }\right)+a{\int }_0^t{\tau }^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{\tau }^{\alpha }\right)cos\left[\Omega \left(t-\tau \right)\right]d\tau +\hfill \\ & & b{\int }_0^t{\tau }^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{\tau }^{\alpha }\right)sin\left[\Omega \left(t-\tau \right)\right]d\tau ,\hfill \end{array}$$

(34)

i.e.,

$$\begin{array}{ccc}& & y\left(t\right)=A{t}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{t}^{\alpha }\right)+acos\left(\Omega t\right){\int }_0^t{\tau }^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{\tau }^{\alpha }\right)cos\left(\Omega \tau \right)d\tau +\hfill \\ & & asin\left(\Omega t\right){\int }_0^t{\tau }^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{\tau }^{\alpha }\right)sin\left(\Omega \tau \right)d\tau +bsin\left(\Omega t\right){\int }_0^t{\tau }^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{\tau }^{\alpha }\right)cos\left(\Omega \tau \right)d\tau -\hfill \\ & & bcos\left(\Omega t\right){\int }_0^t{\tau }^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{\tau }^{\alpha }\right)sin\left(\Omega \tau \right)d\tau ,\hfill \end{array}$$

(35)

or

$$\begin{array}{ccc}& & y\left(t\right)=A{t}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{t}^{\alpha }\right)+\left[acos\left(\Omega t\right)+bsin\left(\Omega t\right)\right]{\int }_0^t{\tau }^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{\tau }^{\alpha }\right)cos\left(\Omega \tau \right)d\tau +\hfill \\ & & \left[asin\left(\Omega t\right)-bcos\left(\Omega t\right)\right]{\int }_0^t{\tau }^{\alpha -1}{E}_{\alpha ,\alpha }\left(-{\omega }^2{\tau }^{\alpha }\right)sin\left(\Omega \tau \right)d\tau .\hfill \end{array}$$

(36)

The case $\alpha \to 1$ gives

$$\begin{array}{ccc}& & y\left(t\right)=A{E}_{1,1}\left(-{\omega }^{2}t\right)+\left[asin\left(\Omega t\right)-bcos\left(\Omega t\right)\right]{\int }_0^t{E}_{1,1}\left(-{\omega }^2\tau \right)cos\left(\Omega \tau \right)d\tau +\hfill \\ & & \left[asin\left(\Omega t\right)-bcos\left(\Omega t\right)\right]{\int }_0^t{E}_{1,1}\left(-{\omega }^2\tau \right)sin\left(\Omega \tau \right)d\tau ,\hfill \end{array}$$

(37)

hence,

$$\begin{array}{ccc}& & y\left(t\right)=A{e}^{-{\omega }^{2}t}+\left[asin\left(\Omega t\right)-bcos\left(\Omega t\right)\right]{\int }_0^t{e}^{-{\omega }^2\tau }cos\left(\Omega \tau \right)d\tau +\hfill \\ & & \left[asin\left(\Omega t\right)-bcos\left(\Omega t\right)\right]{\int }_0^t{e}^{-{\omega }^2\tau }sin\left(\Omega \tau \right)d\tau .\hfill \end{array}$$

(38)

Therefore,

$$y\left(t\right)=\left(A-\frac{a{\omega }^2-b\Omega }{{\omega }^4+{\Omega }^2}\right)e^{-{\omega }^{2}t}+\frac{1}{{\omega }^4+{\Omega }^2}\left[(a{\omega }^2-b\Omega )cos\left(\Omega t\right)+(b{\omega }^2+a\Omega )sin\left(\Omega t\right)\right].$$

(39)

Equation (39) is a solution for class (1) with ordinary derivatives. In addition, Equation (36) gives the same result reported in [30] by setting $b=0$. The existence of $t^{\alpha -1}$ prevents the solution (36) to be analytic at $t=0$. However, an analytic solution $\forall t\ge 0$ exists by means of exponential/trigonometric functions.

4.2. Second Solution: Exponential/Trigonometric Functions

Based on the results of Section 3, the general solution of Equation (1) is

$$y\left(t\right)=c_1\left(\alpha \right)e^{i\delta t}+{\rho }_1\left(\alpha \right)cos(\Omega t)+{\rho }_2\left(\alpha \right)sin(\Omega t),$$

(40)

where ${\rho }_1\left(\alpha \right)$ and ${\rho }_2\left(\alpha \right)$ were already obtained by Theorem 2. We have from Equation (40) that

$$D_t^{\alpha -1}y\left(t\right)=c_1\left(\alpha \right){\left(i\delta \right)}^{\alpha -1}{e}^{i\delta t}+{\rho }_1{\Omega }^{\alpha -1}cos\left(\Omega t+\frac{\pi }{2}(\alpha -1)\right)+{\rho }_2{\Omega }^{\alpha -1}sin\left(\Omega t+\frac{\pi }{2}(\alpha -1)\right).$$

(41)

At $t=0$, we have

$$D_t^{\alpha -1}y\left(0\right)=c_1\left(\alpha \right){\left(i\delta \right)}^{\alpha -1}+{\rho }_1{\Omega }^{\alpha -1}cos\left(\frac{\pi \alpha }{2}-\frac{\pi }{2}\right)+{\rho }_2{\Omega }^{\alpha -1}sin\left(\frac{\pi \alpha }{2}-\frac{\pi }{2}\right),$$

(42)

i.e.,

$$D_t^{\alpha -1}y\left(0\right)=c_1\left(\alpha \right){\left(i\delta \right)}^{\alpha -1}+{\rho }_1{\Omega }^{\alpha -1}sin\left(\frac{\pi \alpha }{2}\right)-{\rho }_2{\Omega }^{\alpha -1}cos\left(\frac{\pi \alpha }{2}\right).$$

(43)

Utilizing the condition $D_t^{\alpha -1}y\left(0\right)=A$, we have

$$c_1\left(\alpha \right){\left(i\delta \right)}^{\alpha -1}+{\rho }_1{\Omega }^{\alpha -1}sin\left(\frac{\pi \alpha }{2}\right)-{\rho }_2{\Omega }^{\alpha -1}cos\left(\frac{\pi \alpha }{2}\right)=A.$$

(44)

Therefore,

$$c_1\left(\alpha \right)={\left(i\delta \right)}^{1-\alpha }\left[A-{\Omega }^{\alpha -1}\left({\rho }_{1}sin\left(\frac{\pi \alpha }{2}\right)-{\rho }_{2}cos\left(\frac{\pi \alpha }{2}\right)\right)\right].$$

(45)

Inserting $\delta$ in terms of $\omega$ gives

$$c_1\left(\alpha \right)={\left(-{\omega }^2\right)}^{\frac{1}{\alpha }-1}\left[A-{\Omega }^{\alpha -1}\left({\rho }_{1}sin\left(\frac{\pi \alpha }{2}\right)-{\rho }_{2}cos\left(\frac{\pi \alpha }{2}\right)\right)\right].$$

(46)

Thus,

$$y\left(t\right)={\left(-{\omega }^2\right)}^{\frac{1}{\alpha }-1}\left[A-{\Omega }^{\alpha -1}\left({\rho }_{1}sin\left(\frac{\pi \alpha }{2}\right)-{\rho }_{2}cos\left(\frac{\pi \alpha }{2}\right)\right)\right]e^{{\left(-{\omega }^2\right)}^{\frac{1}{\alpha }}t}+{\rho }_1\left(\alpha \right)cos(\Omega t)+{\rho }_2\left(\alpha \right)sin(\Omega t),$$

(47)

where ${\rho }_1\left(\alpha \right)$ and ${\rho }_2\left(\alpha \right)$ are given by Equations (18). Consider $\alpha \to 1$, then

$$y\left(t\right)=\left(A-{\left[{\rho }_1\right]}_{\alpha \to 1}\right)e^{-{\omega }^{2}t}+{\left[{\rho }_1\right]}_{\alpha \to 1}cos(\Omega t)+{\left[{\rho }_1\right]}_{\alpha \to 2}\left(\alpha \right)sin(\Omega t).$$

(48)

where

$${\left[{\rho }_1\right]}_{\alpha \to 1}=\frac{a{\omega }^2-b\Omega }{{\omega }^4+{\Omega }^2},{\left[{\rho }_2\right]}_{\alpha \to 1}=\frac{b{\omega }^2+a\Omega }{{\omega }^4+{\Omega }^2}.$$

(49)

Substituting (49) into (48), we get

$$y\left(t\right)=\left(A-\frac{a{\omega }^2-b\Omega }{{\omega }^4+{\Omega }^2}\right)e^{-{\omega }^{2}t}+\frac{1}{{\omega }^4+{\Omega }^2}\left[(a{\omega }^2-b\Omega )cos\left(\Omega t\right)+(b{\omega }^2+a\Omega )sin\left(\Omega t\right)\right].$$

(50)

This equation coincides with Equation (39). In addition, Equation (47) becomes the same result as that reported in [30] at $b=0$. Although Equation (47) is analytic $\forall t\ge 0$, it is real at certain values of $\alpha$, see [31].

Remark 1.

One of the main advantages of this work is that it generalizes the existing results in the literature [30,31] by addressing the additional sinusoidal term $bsin(\Omega t)$. In addition, the current analysis introduces a simple and a straightforward approach in contrast to the operator method [30] that was used to derive the solution at the special case $b=0$ of the present class. Moreover, the obtained dual solution in [31] can be recovered as a special case of our results. Furthermore, the current simple approach seems effective to determine the exact solution of a generalized class involving any finite number of sinusoidal terms. For example, the present analysis can be used to solve the following class with $2n$ harmonic terms:

$${}_{-\infty }^{RL}{D}_t^{\alpha }y\left(t\right)+{\omega }^{2}y\left(t\right)=\sum _{j=1}^n(a_{j}cos\left({\Omega }_{j}t\right)+b_{j}sin\left({\Omega }_{j}t\right)),D_t^{\alpha -1}y\left(0\right)=A,0<\alpha \le 1.$$

(51)

Therefore, the exact solution of this generalized class can be directly derived as a consequence of the current simple/effective approach if compared with the previous results in the literature [30,31].

5. Properties of Solutions

The solution (47) is real when ${\left(-{\omega }^2\right)}^{\frac{1}{\alpha }}\in \mathbb{R}$, i.e., if ${(-1)}^{\frac{1}{\alpha }}=ϵ\left(\mathrm{say}\right)\in \mathbb{R}$. Very recently, Ebaid and Al-Jeaid [31] proved the following theorem to specify those values of $\alpha$ at which $ϵ\in \mathbb{R}$.

Theorem 3

([31]). For $n,k\in {\mathbb{N}}^{+}$, $y\left(t\right)\in \mathbb{R}$ when $\alpha =\frac{2n-1}{2(k+n-1)}$ ($ϵ=1$) and $\alpha =\frac{2n-1}{2(k+n)-1}$ ($ϵ=-1$).

According to this theorem, the solution (47) is displayed in Figure 1, Figure 2, Figure 3 and Figure 4 at some selected values of $\alpha$. At such values, the periodicity/oscillatory of the solution appear in these figures. Moreover, as $\alpha \to 1$, the present fractional solution is identical to the ordinary one given by Equation (50), as can be observed in Figure 4. In addition, the impacts of A and $\Omega$ on the behavior of $y\left(t\right)$ are shown in Figure 5 and Figure 6.

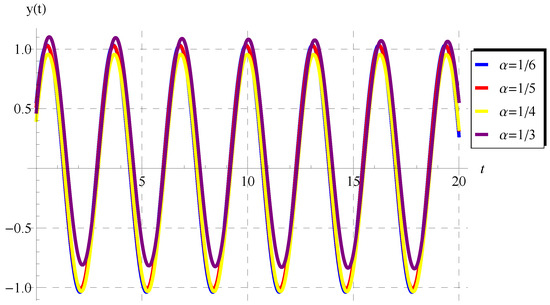
Figure 1. Graphs of the solution (47) at $a=1$, $b=1$, $A=2$, $\omega =\frac{1}{2}$, and $\Omega =2$ for $\alpha =\frac{1}{6},\frac{1}{5},\frac{1}{4},\frac{1}{3}$.

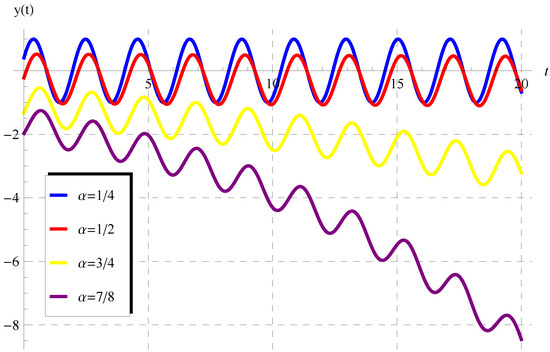
Figure 2. Graphs of the solution (47) at $a=1$, $b=1$, $A=2$, $\omega =\frac{1}{3}$, and $\Omega =3$ for $\alpha =\frac{1}{4},\frac{1}{2},\frac{3}{4},\frac{7}{8}$.

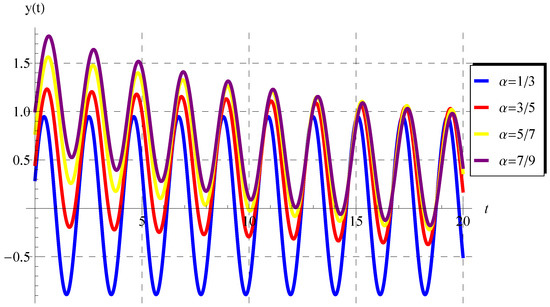
Figure 3. Graphs of the solution (47) at $a=1$, $b=1$, $A=2$, $\omega =\frac{1}{3}$, and $\Omega =3$ for $\alpha =\frac{1}{3},\frac{3}{5},\frac{5}{7},\frac{7}{9}$.

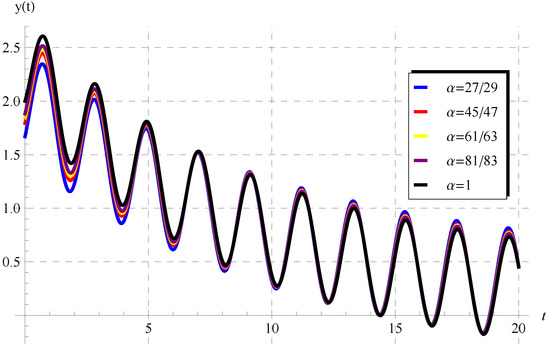
Figure 4. Graphs of the solution (47) at $a=1$, $b=1$, $A=2$, $\omega =\frac{1}{3}$, and $\Omega =3$ for $\alpha =\frac{27}{29},\frac{45}{47},\frac{61}{63},\frac{81}{83},1$.

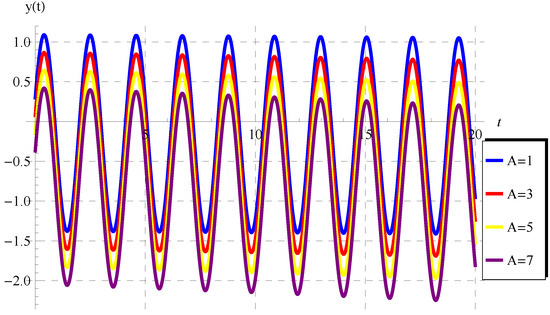
Figure 5. Graphs of the solution (47) at $\alpha =\frac{1}{2}$, $a=2$, $b=1$, $\omega =\frac{1}{3}$, and $\Omega =3$ for $A=1,3,5,7$.

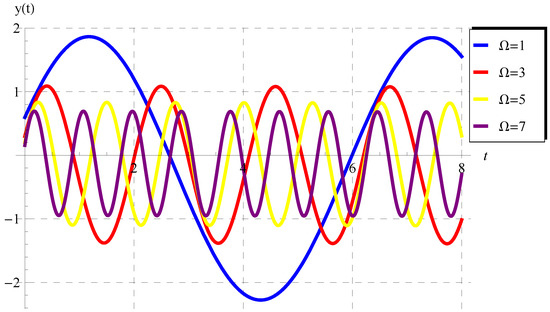
Figure 6. Graphs of the solution (47) at $\alpha =\frac{1}{2}$, $A=1$, $a=2$, $b=1$, and $\omega =\frac{1}{3}$ for $\Omega =1,3,5,7$.

6. Conclusions

In this paper, a class of oscillatory problems in engineering was analyzed. A dual solution for such a class was obtained. The LT method was applied to obtain the solution with the help of Mittag-Leffler functions, but this solution was not analytic at the initial time. In order to obtain an analytic solution in whole domain, a new approach was developed which gave the solution in terms of exponential/trigonometric functions. The latter solution was analytic everywhere and real at prescribed values for $\alpha$. Such values of $\alpha$ that admit real solutions were theoretically verified through several plots. The developed approach can be extended to solve other higher-order oscillatory problems in the FC, including more generalized fractional operators [32,33,34,35].