Reservoir Permeability Identification under Three-Phase Filtration Using a Priori Information on Wells
Abstract
1. Introduction
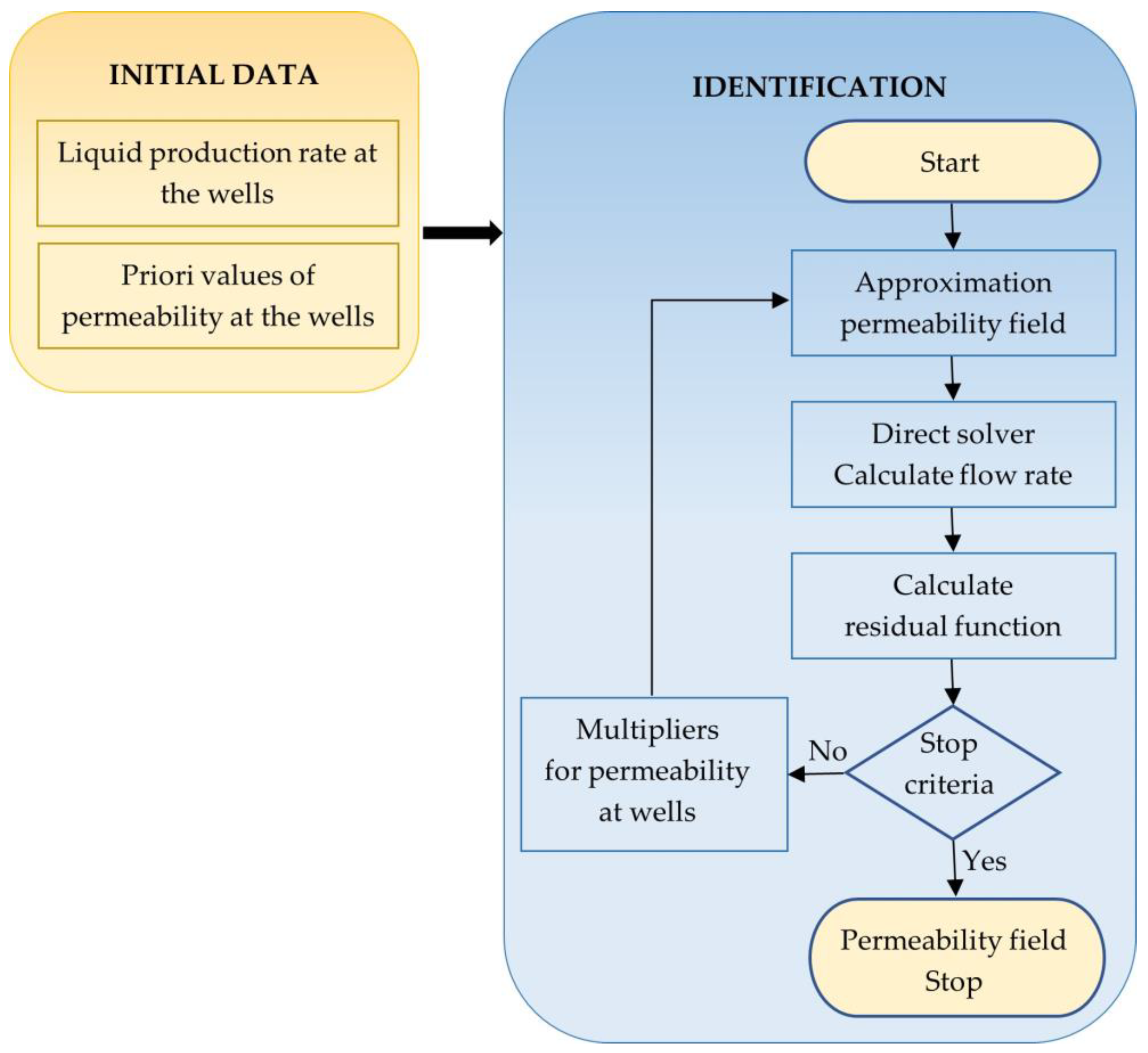
2. Methods
- The reservoir was layered, the values of permeability remained constant across the thickness for each layer in the j-th layer;
- The logarithm of the permeability of each layer was represented as a surface spline. A spline surface is a model of a thin plate bent under the action of external forces applied at some points (interpolation nodes). To construct a spline surface, it was necessary to solve the variational problem of finding the minimum free energy of the plate, which led to the following formula [34]:where , are the coordinates of the wells. The use of the logarithm of absolute permeability made it possible to obtain positive permeability values at any point of the reservoir. The coefficient was determined by solution of the system of equations:where represents the value of permeability at i-th wells in j-th layer;
- The value of permeability in the i-th well in the j-th layer was calculated by the formula , where is the unknown coefficient, and is the a priori value of .
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| boundary of the reservoir | |
| part of the boundary on which the boundary condition of the first kind is specified | |
| part of the boundary on which the boundary condition of the second kind is specified | |
| inflow boundary () | |
| sensitivity matrix | |
| formation volume factor of phase α | |
| g | gradient of the residual function |
| approximate matrix of second derivatives | |
| I | unit matrix |
| residual function | |
| absolute permeability | |
| relative permeability of phase α | |
| gas phase relative permeability of oil–gas system | |
| oil phase relative permeability of oil–gas system | |
| oil phase relative permeability of oil–water system | |
| water phase relative permeability of oil–water system | |
| length of the perforated zone of the i-th well | |
| total number of measurements for all wells | |
| number of measurements on i-th well | |
| number of wells | |
| outward unit normal to the boundary | |
| pressure | |
| bottom hole pressure of the i-th well | |
| time | |
| external sources and sinks of component α | |
| calculated values of the total liquid production rate | |
| measured values of the total liquid production rate | |
| radius of the i-th well | |
| drainage radius of the i-th well | |
| gas solubility | |
| saturation of phase α | |
| critical water saturation in the oil–water system | |
| volumetric velocity of phase α | |
| vector of identification parameters | |
| Dirac delta function at | |
| Marquardt parameter | |
| viscosity of phase α | |
| porosity | |
| Subscripts and Superscripts | |
| a—priori values; c—calculated values; G—gas component; g—gas phase; O—-oil component; o—oil phase; tr—true values; W—water component; w—water phase | |
Appendix A. The Method of the Simultaneous Solution for Black Oil Model
References
- Aitokhuehi, I.; Durlofsky, L.J. Optimizing the performance of smart wells in complex reservoirs using continuously updated geological models. J. Pet. Sci. Eng. 2005, 48, 254–264. [Google Scholar] [CrossRef]
- Jansen, J.-D.; Brouwer, R.; Douma, S.G. Closed loop reservoir management. In SPE Reservoir Simulation Symposium; Society of Petroleum Engineers: Richardson, TX, USA, 2009. [Google Scholar]
- Zhao, H.; Xu, L.; Guo, Z.; Liu, W.; Zhang, Q.; Ning, X.; Li, G.; Shi, L. A new and fast waterflooding optimization workflow based on INSIM-derived injection efficiency with a field application. J. Pet. Sci. Eng. 2019, 179, 1186–1200. [Google Scholar] [CrossRef]
- Zhu, M.; Yu, L.; Zhang, X.; Davarpanah, A. Application of Implicit Pressure-Explicit Saturation Method to Predict Filtrated Mud Saturation Impact on the Hydrocarbon Reservoirs Formation Damage. Mathematics 2020, 8, 1057. [Google Scholar] [CrossRef]
- Romm, E.S. Strukturnye Modeli Porovogo Prostranstva Gornyh Porod; Nedra: Moscow, Russia, 1985. (In Russian) [Google Scholar]
- Dakhnov, V.N. Geophysical Methods to Determine Reservoir Properties and Oil-and-Gas Saturation of Rocks; Nedra: Moscow, Russia, 1985. (In Russian) [Google Scholar]
- Matthews, C.S.; Russell, D.G. Pressure Buildup and Flow Tests in Wells; Society of Petroleum Engineers of AIME: New York, NY, USA, 1967; SPE Monograph Series; Volume 1. [Google Scholar]
- Bourdet, D. Well Test Analysis: The Use of Advanced Interpretation Models (Handbook of Petroleum Exploration and Production); Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Earlougher, R.C., Jr. Advances in Well Test Analysis, 11th Printing; Society of Petroleum Engineering of AIME (TX): Richardson, TX, USA, 2003. [Google Scholar]
- Sun, N.-Z. Inverse Problems in Groundwater Modeling; Kluwer Academic Publishers: Norwell, MA, USA, 1994. [Google Scholar]
- Carrera, J.; Newman, S.P. Estimation of Aquifer Parameters Under Transient and Steady State Conditions: 3. Application to Synthetic and Field Data. Water Resour. Res. 1986, 22, 228–242. [Google Scholar] [CrossRef]
- Yeh, W.W.-G. Review of parameter identification procedures in groundwater hydrology: The inverse problem. Water Resour. Res. 1986, 22, 95–108. [Google Scholar] [CrossRef]
- Oliver, D.; Reynolds, A.; Liu, N. Inverse Theory for Petroleum Reservoir Characterization and History Matching; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Oliver, D.S.; Chen, Y. Recent progress on reservoir history matching: A review. Comput. Geosci. 2011, 15, 185–221. [Google Scholar] [CrossRef]
- Shirangi, M.G.; Emerick, A.A. An improved TSVD-based Levenberg-Marquardt algorithm for history matching and comparison with Gauss-Newton. J. Pet. Sci. Eng. 2016, 143, 258–271. [Google Scholar] [CrossRef]
- Elesin, A.V.; Kadyrova, A.S. The Levenberg-Marquartd Method in the Problem of Identifying the Absolute Penetrability Coefficient of a Bed Under Conditions of Two-Phase Filtration. J. Eng. Phys. Thermophys. 2017, 90, 1362–1368. [Google Scholar] [CrossRef]
- Elesin, A.V.; Kadyrova, A.S. Using the Spline Function to Restore the Permeability Field under Three-Phase Flow Filtration. Lobachevskii J. Math. 2021, 42, 2109–2113. [Google Scholar] [CrossRef]
- Elesin, A.V.; Kadyrova, A.S.; Nikiforov, A.I. Identifying the permeability field of a three-dimensional layered bed with allowance for a priori information on wells under steady-state single-phase filtration conditions. J. Eng. Phys. Thermophys. 2021, 94, 587–591. [Google Scholar] [CrossRef]
- Gasca-Ortiz, T.; Domínguez-Mota, F.J.; Pantoja, D.A. Determination of Optimal Diffusion Coefficients in Lake Zirahuén through a Local Inverse Problem. Mathematics 2021, 9, 1695. [Google Scholar] [CrossRef]
- Aziz, K.; Settari, A. Petroleum Reservoir Simulation; Springer: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Barenblatt, G.I.; Entov, V.M.; Ryzhik, V.M. The Movement of Liquids and Gases in Natural Formations; Nedra: Moscow, Russia, 1984. (In Russian) [Google Scholar]
- Li, B.; Chen, Z.; Huan, G. Control volume function approximation methods and their applications to modeling porous media flow II: The black oil model. Adv. Water Resour. 2004, 27, 99–120. [Google Scholar] [CrossRef]
- Chen, Z.; Huan, G.; Ma, Y. Computational Methods for Multiphase Flows in Porous Media; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Zhang, R.H.; Zhang, L.H.; Luo, J.X.; Yang, Z.D.; Xu, M.Y. Numerical simulation of water flooding in natural fractured reservoirs based on control volume finite element method. J. Pet. Sci. Eng. 2016, 146, 1211–1225. [Google Scholar] [CrossRef]
- Jacquard, P.; Jain, C. Permeability distribution from field pressure data. Soc. Pet. Eng. J. 1965, 5, 281–294. [Google Scholar] [CrossRef]
- Emsellem, Y.; De Marsily, G. An automatic solution for the inverse problem. Water Resour. Res. 1971, 7, 1264–1283. [Google Scholar] [CrossRef]
- DiStefano, N.; Rath, A. An identification approach to subsurface hydrological systems. Water Resour. Res. 1975, 11, 1005–1012. [Google Scholar] [CrossRef]
- Yeh, W.W.-G.; Yoon, Y.S. Aquifer parameter identification with optimum dimension in parameterization. Water Resour. Res. 1981, 17, 664–672. [Google Scholar] [CrossRef]
- Yakowitz, S.; Noren, P. On the identification of inhomogeneous parameters in dynamic linear partial differential equations. J. Math. Anal. Appl. 1976, 53, 521–538. [Google Scholar] [CrossRef][Green Version]
- Makhlouf, E.M.; Chen, W.H.; Wasserman, M.L.; Seinfeld, J.H. A general history matching algorithm for three-phase, three-dimensional petroleum reservoirs. SPE Adv. Technol. Ser. 1993, 1, 83–91. [Google Scholar] [CrossRef]
- Garay, H.L.; Haimes, Y.Y.; Das, P. Distributed parameter identification of groundwater system by nonlinear estimation. J. Hydrol. 1976, 30, 47–61. [Google Scholar] [CrossRef]
- Clifton, P.M.; Newman, S.P. Effects of kriging and inverse modeling on conditional simulation of the Avra Valley aquifer in Southern Arizona. Water Resour. Res. 1982, 18, 1215–1234. [Google Scholar] [CrossRef]
- Wen, X.-H.; Lee, S.; Yu, T. Simultaneous integration of pressure, water cut, 1 and 4-D seismic data in geostatistical reservoir modeling. Math. Geol. 2006, 38, 301–325. [Google Scholar] [CrossRef]
- Harder, R.L.; Desmarais, R.N. Interpolation using surface splines. J. Aircr. 1972, 9, 189–191. [Google Scholar] [CrossRef]
- Tikhonov, A.N. Regularization of incorrectly formulated problems and the regularization method. Dokl. Akad. Nauk SSSR 1963, 151, 501–504. (In Russian) [Google Scholar]
- Stone, H.L. Estimation of three-phase relative permeability and residual data. J. Can. Pet. Technol. 1973, 12, 53–61. [Google Scholar] [CrossRef]
- Peaceman, D.W. Interpretation of well block pressures in numerical reservoir simulation. Soc. Pet. Eng. J. 1978, 18, 183–194. [Google Scholar] [CrossRef]
- Li, B.; Chen, Z.; Huan, G. Comparison of solution schemes for black oil reservoir simulations with unstructured grids. Comput. Methods Appl. Mech. Eng. 2004, 193, 319–355. [Google Scholar] [CrossRef]
- Dennis, J.E.; Schnabel, R.B. Numerical Methods for Unconstructed Optimization and Nonlinear Equations. Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- Golub, G.H.; Loan, C.F. Matrix Computations; Johns Hopkins University Press: London, UK; Baltimore, MD, USA, 1996. [Google Scholar]
- Elesin, A.V.; Kadyrova, A.S. Identification of the Permeability Field of a Three-Dimensional Reservoir with a Large Number of Wells under Three-Phase Fluid Flow. Lobachevskii J. Math. 2022, 43, 1088–1093. [Google Scholar] [CrossRef]


| p, MPa | |||
|---|---|---|---|
| 5 | 1.025 | 0.02 | 300 |
| 10 | 1.045 | 0.01 | 600 |
| 15 | 1.07 | 0.006 | 900 |
| 20 | 1.09 | 0.0045 | 1200 |
| 25 | 1.11 | 0.0035 | 1400 |
| 0.2 | 0.00 | 1.00 | 0.0 | 0.00 | 1.00 |
| 0.3 | 0.05 | 0.40 | 0.05 | 0.00 | 0.60 |
| 0.4 | 0.10 | 0.10 | 0.1 | 0.01 | 0.30 |
| 0.6 | 0.30 | 0.005 | 0.2 | 0.05 | 0.10 |
| 0.8 | 0.60 | 0.00 | 0.3 | 0.10 | 0.01 |
| 1.00 | 1.00 | 0.00 | 0.4 | 0.20 | 0.00 |
| 0.6 | 0.50 | 0.00 | |||
| 0.7 | 0.70 | 0.00 | |||
| 0.8 | 1.00 | 0.00 |
| 2.08 × 10−4 | 5.42 × 10−5 | 0.014 | 6 | |
| 0.00450 | 0.00428 | 1.593 | 11 | |
| 0.00454 | 0.00435 | 1.708 | 11 | |
| 0.00437 | 0.00388 | 1.355 | 11 | |
| 0.02179 | 0.02055 | 7.389 | 10 | |
| 0.02823 | 0.02273 | 4.095 | 13 | |
| 0.02144 | 0.01535 | 4.298 | 10 | |
| 0.04355 | 0.03958 | 15.127 | 11 | |
| 0.08357 | 0.04937 | 23.377 | 9 | |
| 0.04497 | 0.03683 | 14.607 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elesin, A.V.; Kadyrova, A.S.; Nikiforov, A.I.; Tsepaev, A.V. Reservoir Permeability Identification under Three-Phase Filtration Using a Priori Information on Wells. Mathematics 2022, 10, 4558. https://doi.org/10.3390/math10234558
Elesin AV, Kadyrova AS, Nikiforov AI, Tsepaev AV. Reservoir Permeability Identification under Three-Phase Filtration Using a Priori Information on Wells. Mathematics. 2022; 10(23):4558. https://doi.org/10.3390/math10234558
Chicago/Turabian StyleElesin, Andrey V., Alfiya Sh. Kadyrova, Anatoliy I. Nikiforov, and Aleksey V. Tsepaev. 2022. "Reservoir Permeability Identification under Three-Phase Filtration Using a Priori Information on Wells" Mathematics 10, no. 23: 4558. https://doi.org/10.3390/math10234558
APA StyleElesin, A. V., Kadyrova, A. S., Nikiforov, A. I., & Tsepaev, A. V. (2022). Reservoir Permeability Identification under Three-Phase Filtration Using a Priori Information on Wells. Mathematics, 10(23), 4558. https://doi.org/10.3390/math10234558





