A Fully Coupled Thermomechanical Phase Field Method for Modeling Cracks with Frictional Contact
Abstract
1. Introduction
2. Phase Field Method for Coupled Thermomechanical Problems
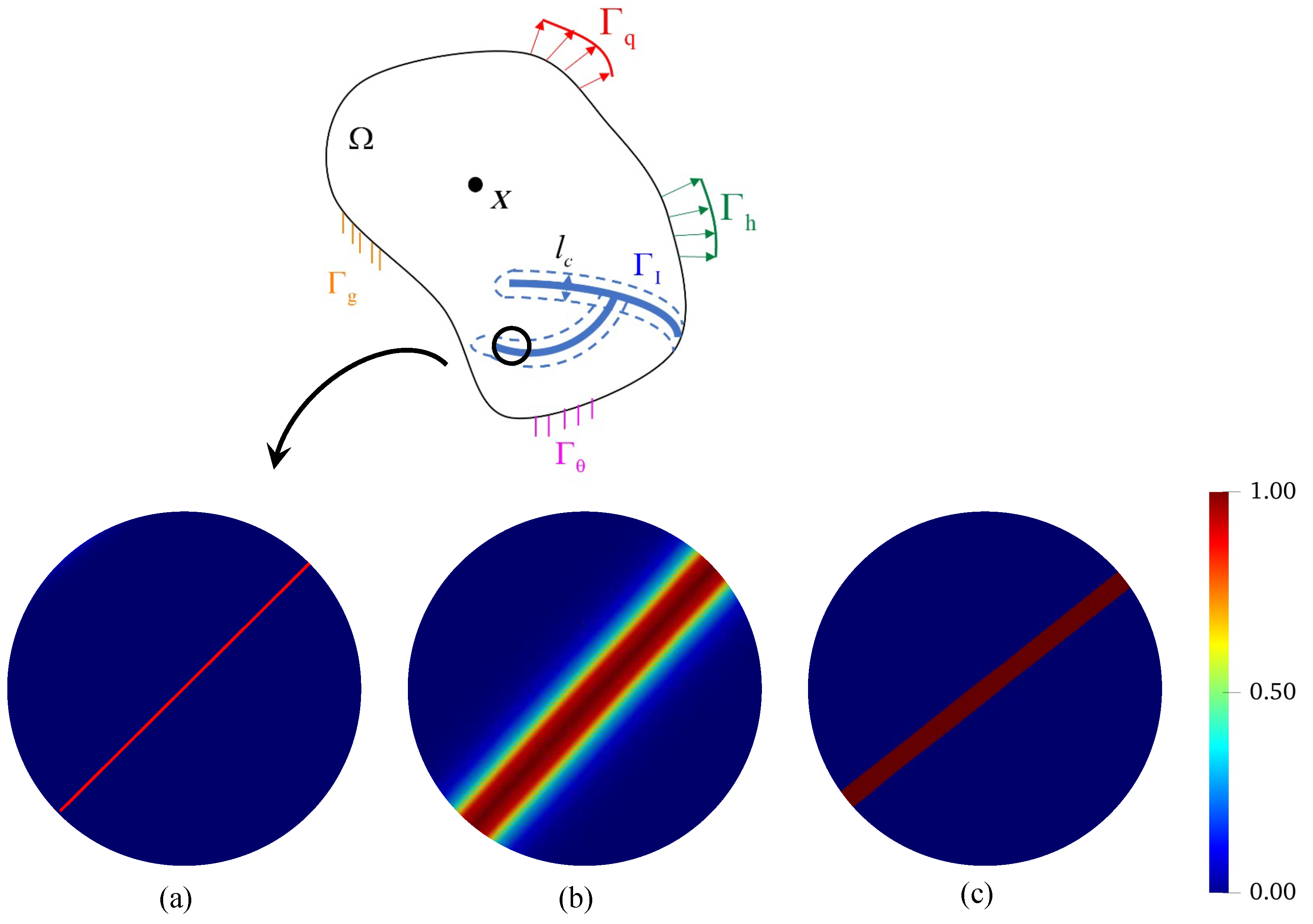
2.1. Regularized Variational Framework
2.2. Phase Field Approximation
3. Governing Equations and Corresponding Weak Forms
4. Stress Tensor and Thermal Conductivity Calculation for Different Contact Conditions
4.1. Stress Tensor Updates in the Phase Field Modeling
4.2. Thermal Conductivity Tensor Updates in Phase Field Modeling
Four Thermal Conductance Contact Models
5. Numerical Examples
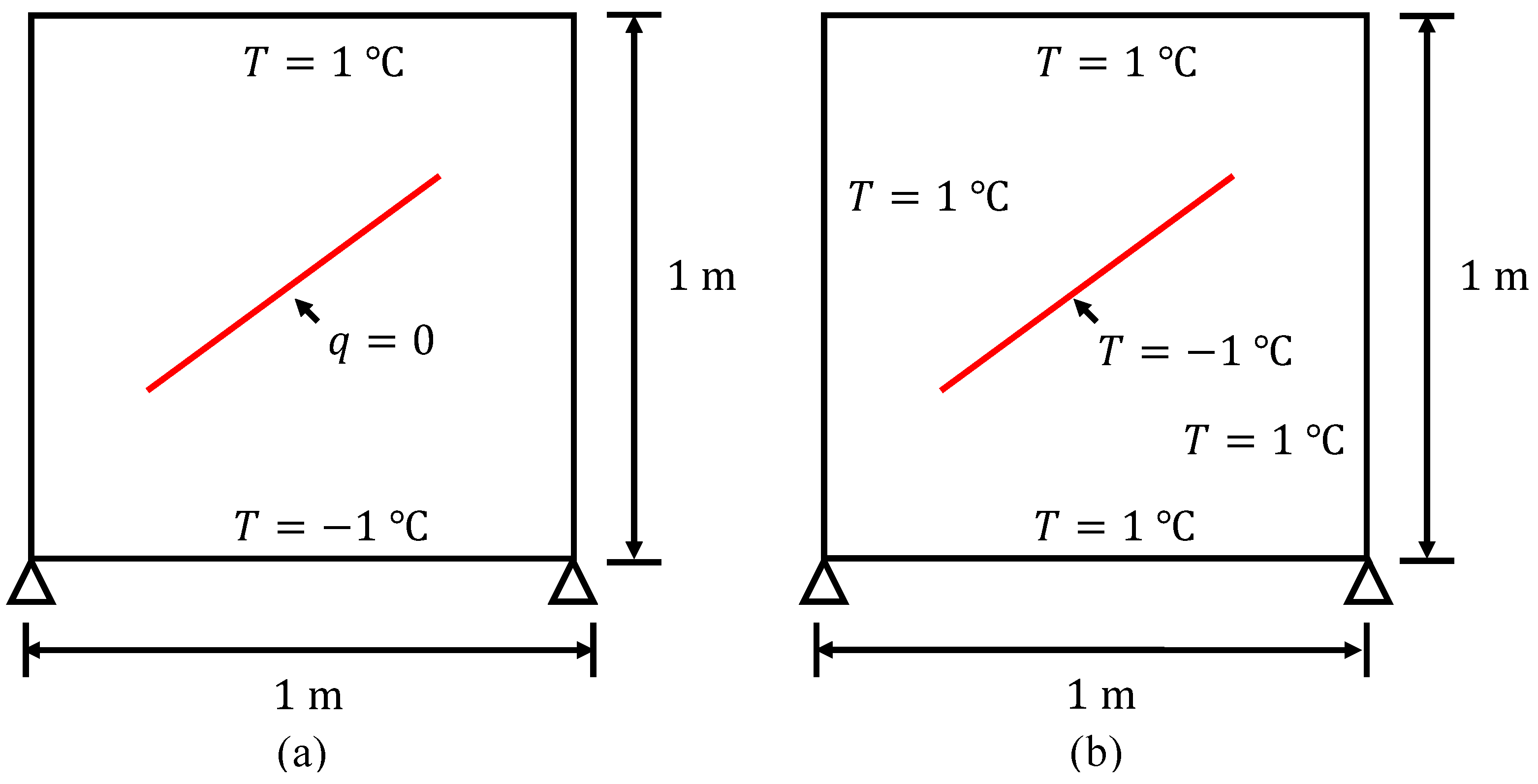
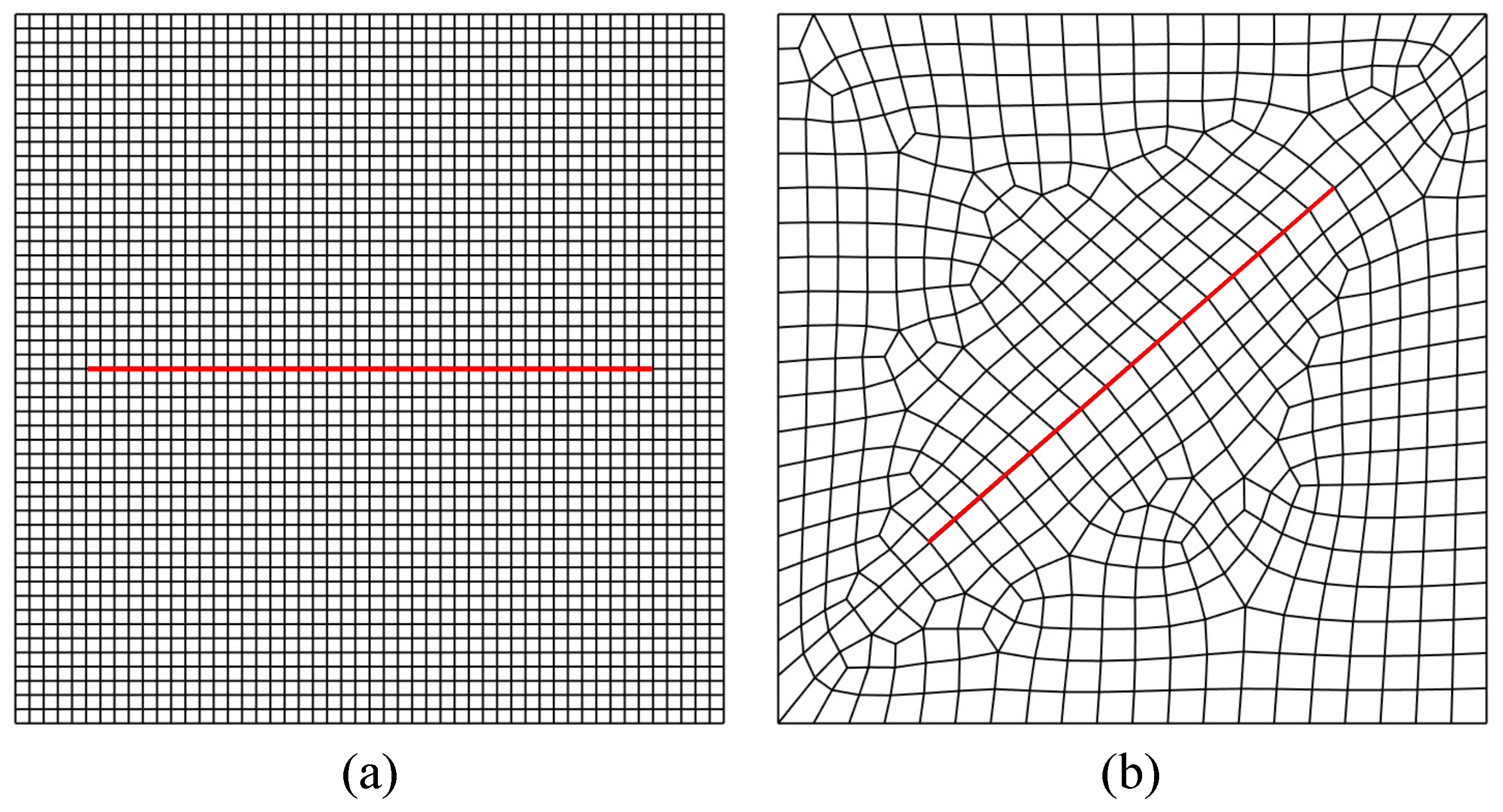
5.1. Square Plate with (a) Central Horizontal and (b) Inclined Cracks
5.2. Squared Domain with an Internal Slant Frictional Crack
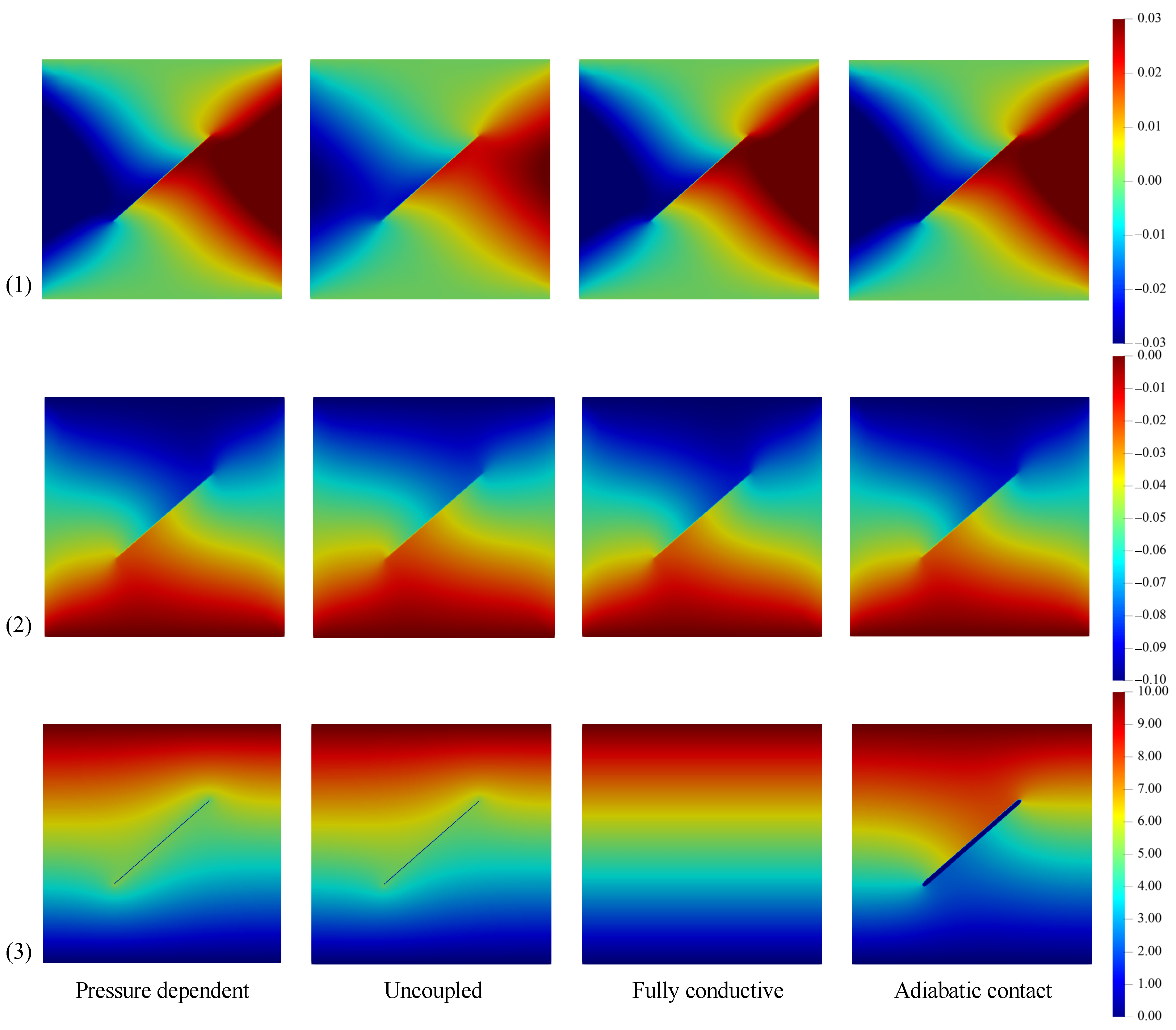
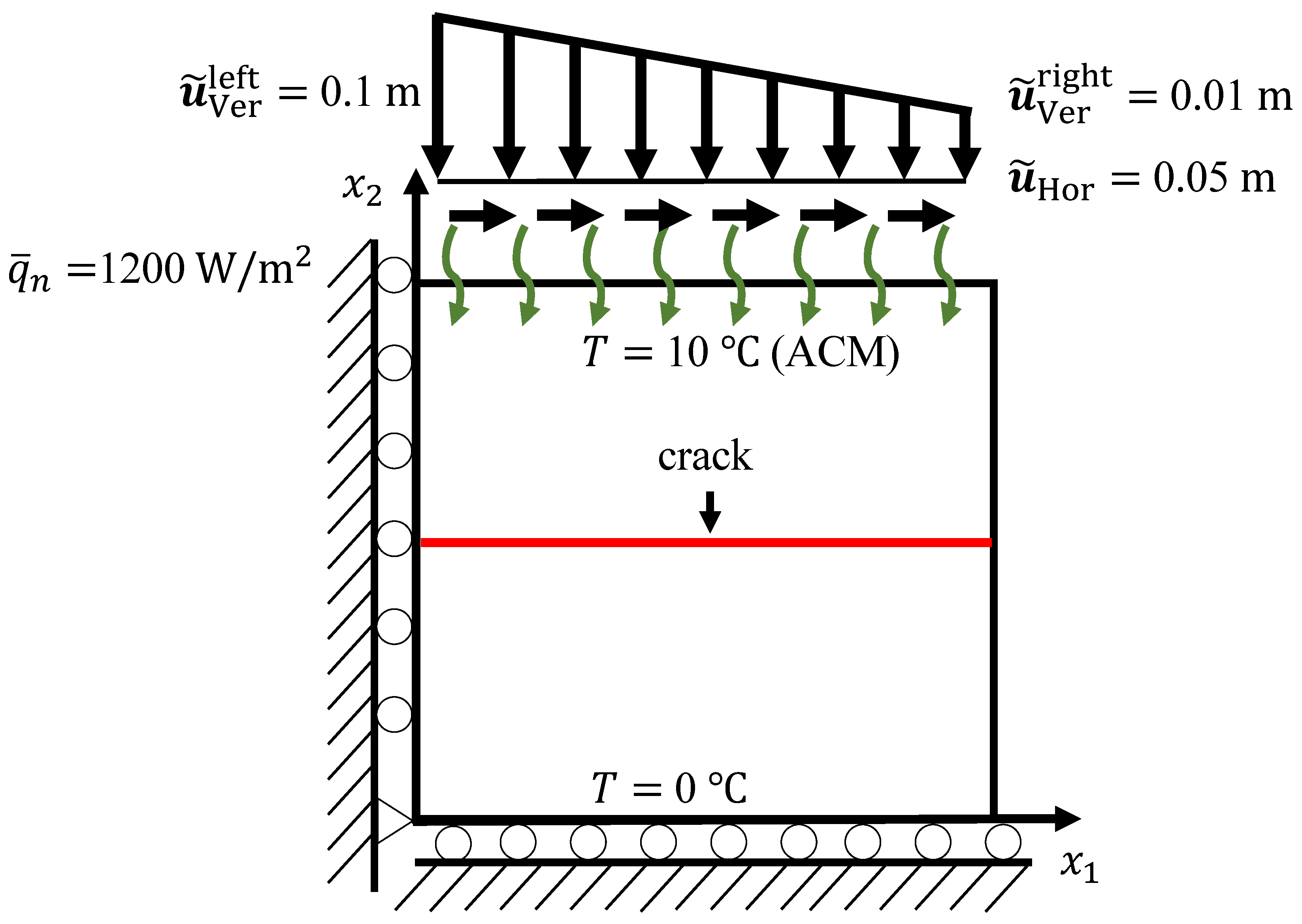
5.3. The Frictional Sliding Problem under Different Thermomechanical Coupled Conditions
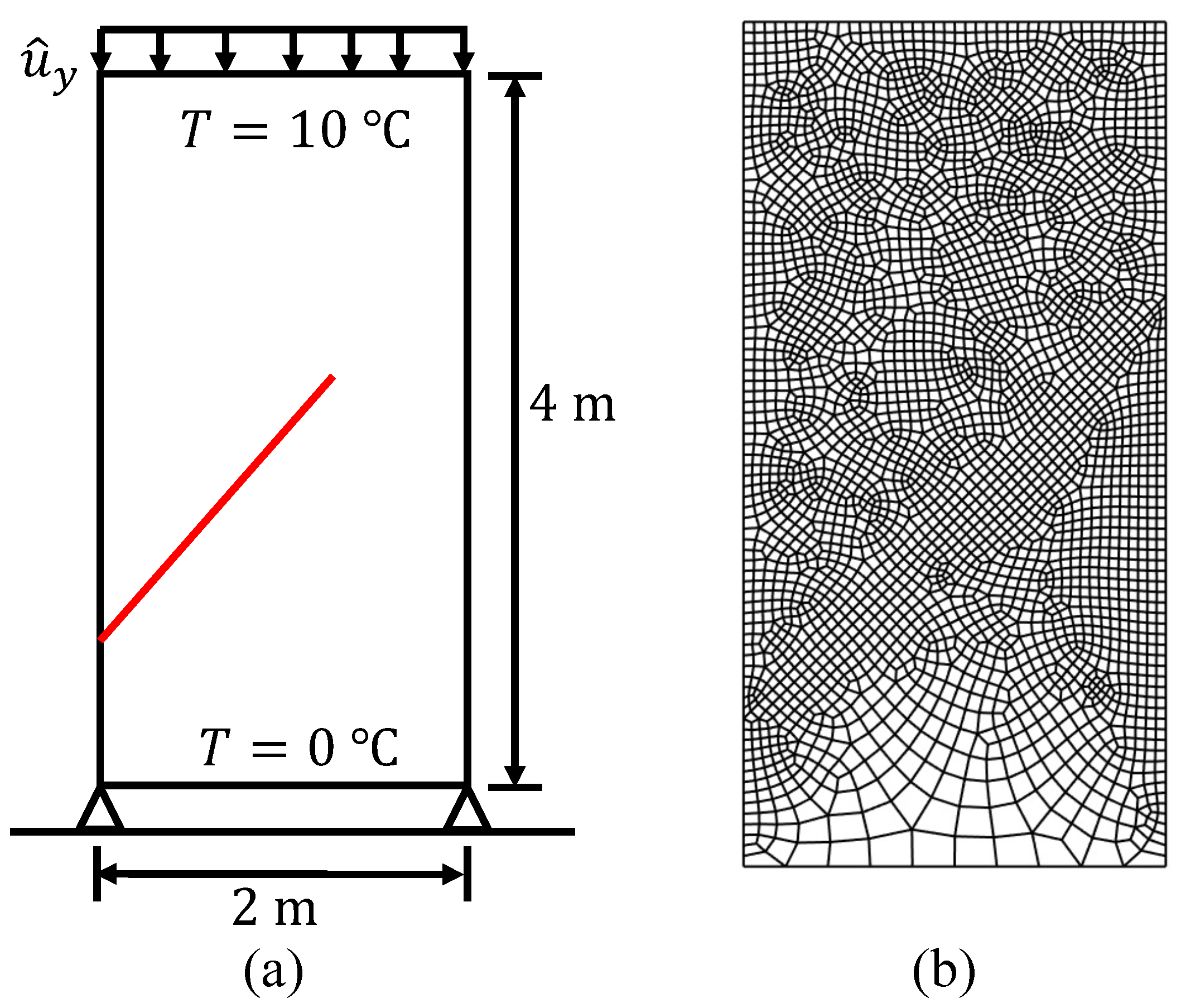
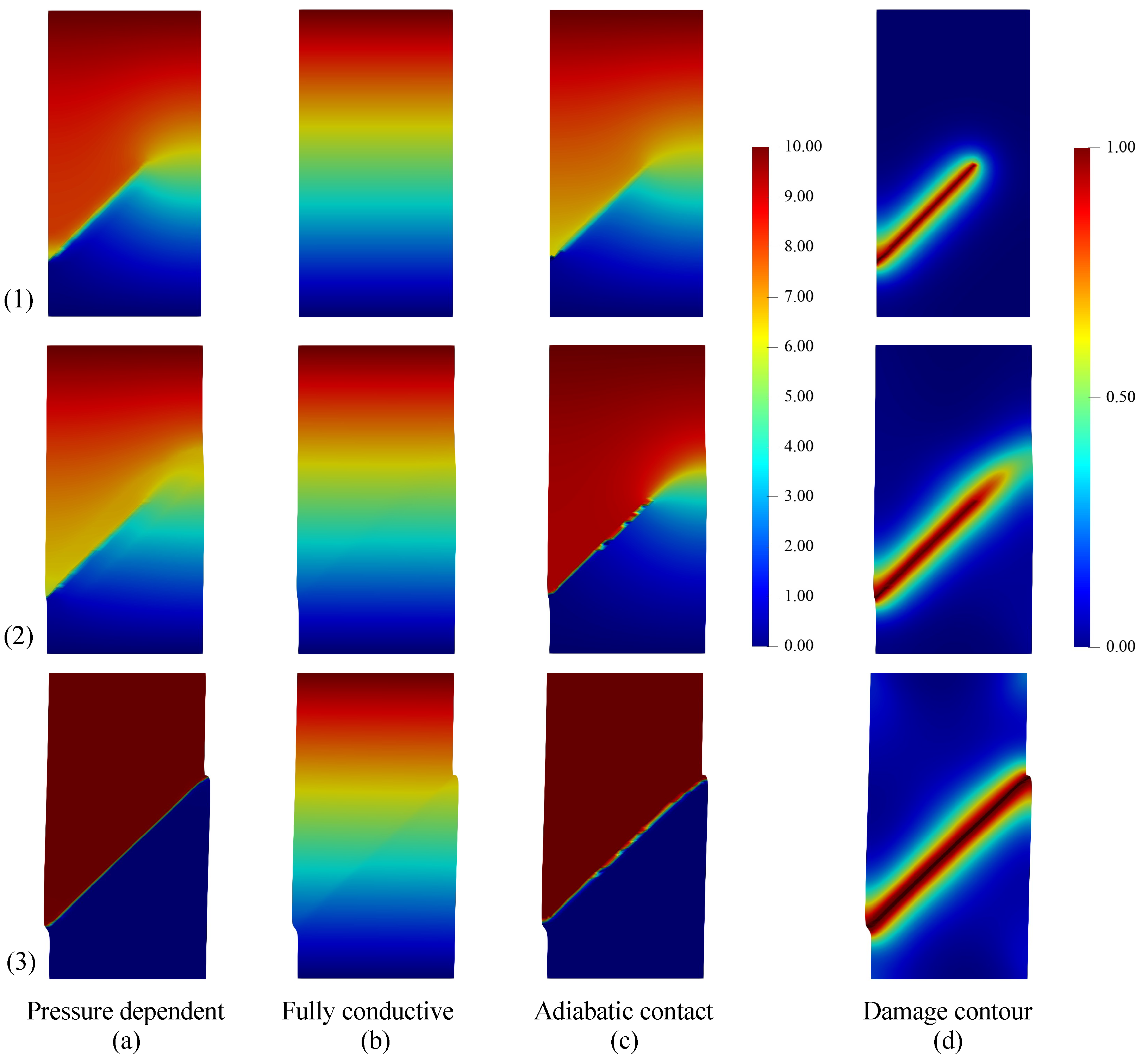
5.4. Propagation of an Inclined Crack in a Rectangular Plate
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
Nomenclature
| Symbol | Description | Unit |
| T | Temperature | |
| E | Young’s modulus | |
| k | Thermal conductivity | |
| Specific heat capacity | J/kgC | |
| Density | ||
| Heat conductivity | ||
| Thermal expansion coefficient | /C | |
| Coefficient of thermal contact conductivity | W/mC | |
| Vickers hardness | ||
| Heat flux on the contact surface | ||
| Critical stress | ||
| Softening stiffness. | ||
| Critical separation | m | |
| Chemical bonding conductance | ||
| Surface contact conductance | ||
| Gas conductance | ||
| Applied heat flux | ||
| Damage length parameter | ||
| Griffth’s critical energy | ||
| Strain energy history | ||
| Stored elastic energy | ||
| Fractured surface energy | ||
| Bulk energy density | ||
| Crack energy density |
Abbreviations
| Abbreviation | Description |
| PF | Phase Field |
| VMDG | Variational Multiscale Discontinuous Galerkin |
| FCM | Fully Coupled Model |
| ADM | Adiabatic Model |
| PDM | Pressure Dependent Model |
| UCM | Uncoupled Model |
References
- Chaboche, J.L. Development of continuum damage mechanics for elastic solids sustaining anisotropic and unilateral damage. Int. J. Damage Mech. 1993, 2, 311–329. [Google Scholar] [CrossRef]
- Seitz, A.; Wall, W.A.; Popp, A. Nitsche’s method for finite deformation thermomechanical contact problems. Comput. Mech. 2019, 63, 1091–1110. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Borden, M.J.; Verhoosel, C.V.; Scott, M.A.; Hughes, T.J.; Landis, C.M. A phase-field description of dynamic brittle fracture. Comput. Methods Appl. Mech. Eng. 2012, 217, 77–95. [Google Scholar] [CrossRef]
- Hansbo, P.; Lovadina, C.; Perugia, I.; Sangalli, G. A Lagrange multiplier method for the finite element solution of elliptic interface problems using non-matching meshes. Numer. Math. 2005, 100, 91–115. [Google Scholar] [CrossRef]
- Hirmand, M.; Vahab, M.; Khoei, A. An augmented Lagrangian contact formulation for frictional discontinuities with the extended finite element method. Finite Elem. Anal. Des. 2015, 107, 28–43. [Google Scholar] [CrossRef]
- Simo, J.C.; Laursen, T. An augmented Lagrangian treatment of contact problems involving friction. Comput. Struct. 1992, 42, 97–116. [Google Scholar] [CrossRef]
- Dittmann, M.; Franke, M.; Temizer, I.; Hesch, C. Isogeometric analysis and thermomechanical mortar contact problems. Comput. Methods Appl. Mech. Eng. 2014, 274, 192–212. [Google Scholar] [CrossRef]
- Cardiff, P.; Karač, A.; Ivanković, A. Development of a finite volume contact solver based on the penalty method. Comput. Mater. Sci. 2012, 64, 283–284. [Google Scholar] [CrossRef]
- Chouly, F.; Fabre, M.; Hild, P.; Mlika, R.; Pousin, J.; Renard, Y. An overview of recent results on Nitsche’s method for contact problems. In Geometrically Unfitted Finite Element Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2017; pp. 93–141. [Google Scholar]
- Wriggers, P.; Zavarise, G. A formulation for frictionless contact problems using a weak form introduced by Nitsche. Comput. Mech. 2008, 41, 407–420. [Google Scholar] [CrossRef]
- Arnold, D.N. An interior penalty finite element method with discontinuous elements. SIAM J. Numer. Anal. 1982, 19, 742–760. [Google Scholar] [CrossRef]
- Nitsche, J. Über ein Variationsprinzip zur Lösung von Dirichlet-Problemen bei Verwendung von Teilräumen, die keinen Randbedingungen unterworfen sind. Abh. Math. Semin. Univ. Hambg. 1971, 36, 9–15. [Google Scholar] [CrossRef]
- Sanders, J.D.; Laursen, T.A.; Puso, M.A. A Nitsche embedded mesh method. Comput. Mech. 2012, 49, 243–257. [Google Scholar] [CrossRef]
- Annavarapu, C.; Hautefeuille, M.; Dolbow, J.E. A robust Nitsche’s formulation for interface problems. Comput. Methods Appl. Mech. Eng. 2012, 225, 44–54. [Google Scholar] [CrossRef]
- Truster, T.J.; Chen, P.; Masud, A. Finite strain primal interface formulation with consistently evolving stabilization. Int. J. Numer. Methods Eng. 2015, 102, 278–315. [Google Scholar] [CrossRef]
- Masud, A.; Chen, P. Thermoelasticity at finite strains with weak and strong discontinuities. Comput. Methods Appl. Mech. Eng. 2019, 347, 1050–1084. [Google Scholar] [CrossRef]
- Francfort, G.A.; Marigo, J.J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Dolbow, J.; Moës, N.; Belytschko, T. An extended finite element method for modeling crack growth with frictional contact. Comput. Methods Appl. Mech. Eng. 2001, 190, 6825–6846. [Google Scholar] [CrossRef]
- Fries, T.P.; Belytschko, T. The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 2010, 84, 253–304. [Google Scholar] [CrossRef]
- Armero, F.; Garikipati, K. An analysis of strong discontinuities in multiplicative finite strain plasticity and their relation with the numerical simulation of strain localization in solids. Int. J. Solids Struct. 1996, 33, 2863–2885. [Google Scholar] [CrossRef]
- Oliver, J. Modelling strong discontinuities in solid mechanics via strain softening constitutive equations. Part 1: Fundamentals. Int. J. Numer. Methods Eng. 1996, 39, 3575–3600. [Google Scholar] [CrossRef]
- Armero, F.; Linder, C. New finite elements with embedded strong discontinuities in the finite deformation range. Comput. Methods Appl. Mech. Eng. 2008, 197, 3138–3170. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yvonnet, J.; Zhu, Q.Z.; Bornert, M.; Chateau, C. A phase field method to simulate crack nucleation and propagation in strongly heterogeneous materials from direct imaging of their microstructure. Eng. Fract. Mech. 2015, 139, 18–39. [Google Scholar] [CrossRef]
- Ehlers, W.; Luo, C. A phase-field approach embedded in the theory of porous media for the description of dynamic hydraulic fracturing. Comput. Methods Appl. Mech. Eng. 2017, 315, 348–368. [Google Scholar] [CrossRef]
- Paggi, M.; Reinoso, J. Revisiting the problem of a crack impinging on an interface: A modeling framework for the interaction between the phase field approach for brittle fracture and the interface cohesive zone model. Comput. Methods Appl. Mech. Eng. 2017, 321, 145–172. [Google Scholar] [CrossRef]
- Macek, W. Fracture surface formation of notched 2017A-T4 aluminium alloy under bending fatigue. Int. J. Fract. 2022, 234, 141–157. [Google Scholar] [CrossRef]
- Macek, W.; Branco, R.; Costa, J.D.; Trembacz, J. Fracture Surface Behavior of 34CrNiMo6 High-Strength Steel Bars with Blind Holes under Bending-Torsion Fatigue. Materials 2021, 15, 80. [Google Scholar] [CrossRef]
- Lanwer, J.P.; Höper, S.; Gietz, L.; Kowalsky, U.; Empelmann, M.; Dinkler, D. Fundamental Investigations of Bond Behaviour of High-Strength Micro Steel Fibres in Ultra-High Performance Concrete under Cyclic Tensile Loading. Materials 2021, 15, 120. [Google Scholar] [CrossRef]
- Griffith, A. The phenomena of rupture and flow in solids. In Proceedings of the First International Congress for Applied Mechanics, Delft, The Netherlands, 22–26 April 1924; pp. 53–63. [Google Scholar]
- Schneider, D.; Schoof, E.; Huang, Y.; Selzer, M.; Nestler, B. Phase-field modeling of crack propagation in multiphase systems. Comput. Methods Appl. Mech. Eng. 2016, 312, 186–195. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. The variational approach to fracture. J. Elast. 2008, 91, 5–148. [Google Scholar] [CrossRef]
- Ulmer, H.; Hofacker, M.; Miehe, C. Phase field modeling of brittle and ductile fracture. PAMM 2013, 13, 533–536. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. Phase-field modeling of ductile fracture. Comput. Mech. 2015, 55, 1017–1040. [Google Scholar] [CrossRef]
- Carrara, P.; Ambati, M.; Alessi, R.; De Lorenzis, L. A framework to model the fatigue behavior of brittle materials based on a variational phase-field approach. Comput. Methods Appl. Mech. Eng. 2020, 361, 112731. [Google Scholar] [CrossRef]
- Schreiber, C.; Kuhn, C.; Müller, R.; Zohdi, T. A phase field modeling approach of cyclic fatigue crack growth. Int. J. Fract. 2020, 225, 89–100. [Google Scholar] [CrossRef]
- Schreiber, C.; Müller, R.; Kuhn, C. Phase field simulation of fatigue crack propagation under complex load situations. Arch. Appl. Mech. 2021, 91, 563–577. [Google Scholar] [CrossRef]
- Seiler, M.; Linse, T.; Hantschke, P.; Kästner, M. An efficient phase-field model for fatigue fracture in ductile materials. Eng. Fract. Mech. 2020, 224, 106807. [Google Scholar] [CrossRef]
- Loew, P.J.; Poh, L.H.; Peters, B.; Beex, L.A. Accelerating fatigue simulations of a phase-field damage model for rubber. Comput. Methods Appl. Mech. Eng. 2020, 370, 113247. [Google Scholar] [CrossRef]
- Tan, Y.; He, Y.; Li, X.; Kang, G. A phase field model for fatigue fracture in piezoelectric solids: A residual controlled staggered scheme. Comput. Methods Appl. Mech. Eng. 2022, 399, 115459. [Google Scholar] [CrossRef]
- Schröder, J.; Pise, M.; Brands, D.; Gebuhr, G.; Anders, S. Phase-field modeling of fracture in high performance concrete during low-cycle fatigue: Numerical calibration and experimental validation. Comput. Methods Appl. Mech. Eng. 2022, 398, 115181. [Google Scholar] [CrossRef]
- Miehe, C.; Schaenzel, L.M.; Ulmer, H. Phase field modeling of fracture in multi-physics problems. Part I. Balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 449–485. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Schänzel, L.M.; Aldakheel, F. Phase field modeling of fracture in multi-physics problems. Part II. Coupled brittle-to-ductile failure criteria and crack propagation in thermo-elastic–plastic solids. Comput. Methods Appl. Mech. Eng. 2015, 294, 486–522. [Google Scholar] [CrossRef]
- Tangella, R.G.; Kumbhar, P.; Annabattula, R.K. Hybrid phase-field modeling of thermo-elastic crack propagation. Int. J. Comput. Methods Eng. Sci. Mech. 2022, 23, 29–44. [Google Scholar] [CrossRef]
- Fei, F.; Choo, J. A phase-field model of frictional shear fracture in geologic materials. Comput. Methods Appl. Mech. Eng. 2020, 369, 113265. [Google Scholar] [CrossRef]
- Fei, F.; Choo, J. A phase-field method for modeling cracks with frictional contact. Int. J. Numer. Methods Eng. 2020, 121, 740–762. [Google Scholar] [CrossRef]
- Nguyen, M.N.; Bui, T.Q.; Nguyen, N.T.; Truong, T.T. Simulation of dynamic and static thermoelastic fracture problems by extended nodal gradient finite elements. Int. J. Mech. Sci. 2017, 134, 370–386. [Google Scholar] [CrossRef]
- Wan, W.; Chen, P. Variational multiscale method for fully coupled thermomechanical interface contact and debonding problems. Int. J. Solids Struct. 2021, 210, 119–135. [Google Scholar] [CrossRef]
- Shahba, A.; Ghosh, S. Coupled phase field finite element model for crack propagation in elastic polycrystalline microstructures. Int. J. Fract. 2019, 219, 31–64. [Google Scholar] [CrossRef]
- Khoei, A.; Bahmani, B. Application of an enriched FEM technique in thermo-mechanical contact problems. Comput. Mech. 2018, 62, 1127–1154. [Google Scholar] [CrossRef]
- Duflot, M. The extended finite element method in thermoelastic fracture mechanics. Int. J. Numer. Methods Eng. 2008, 74, 827–847. [Google Scholar] [CrossRef]
- Amor, H.; Marigo, J.J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]





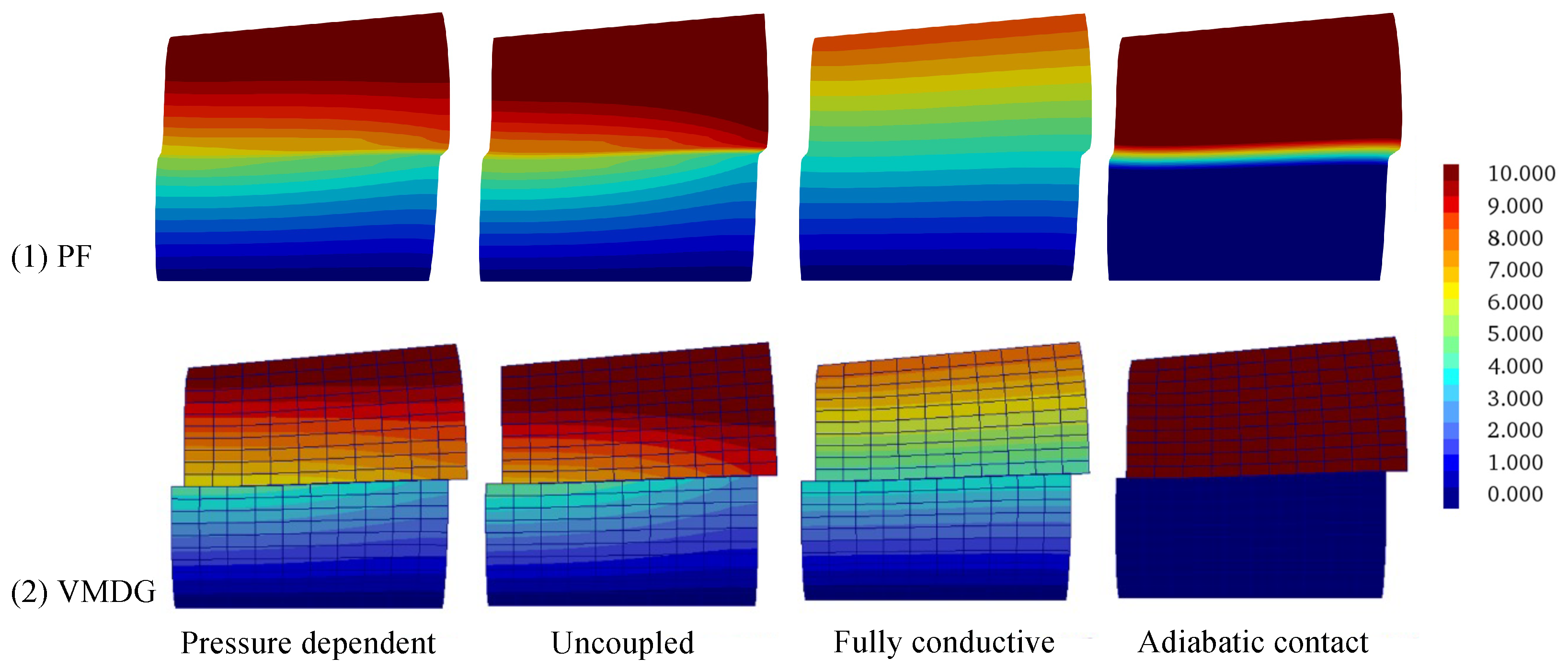
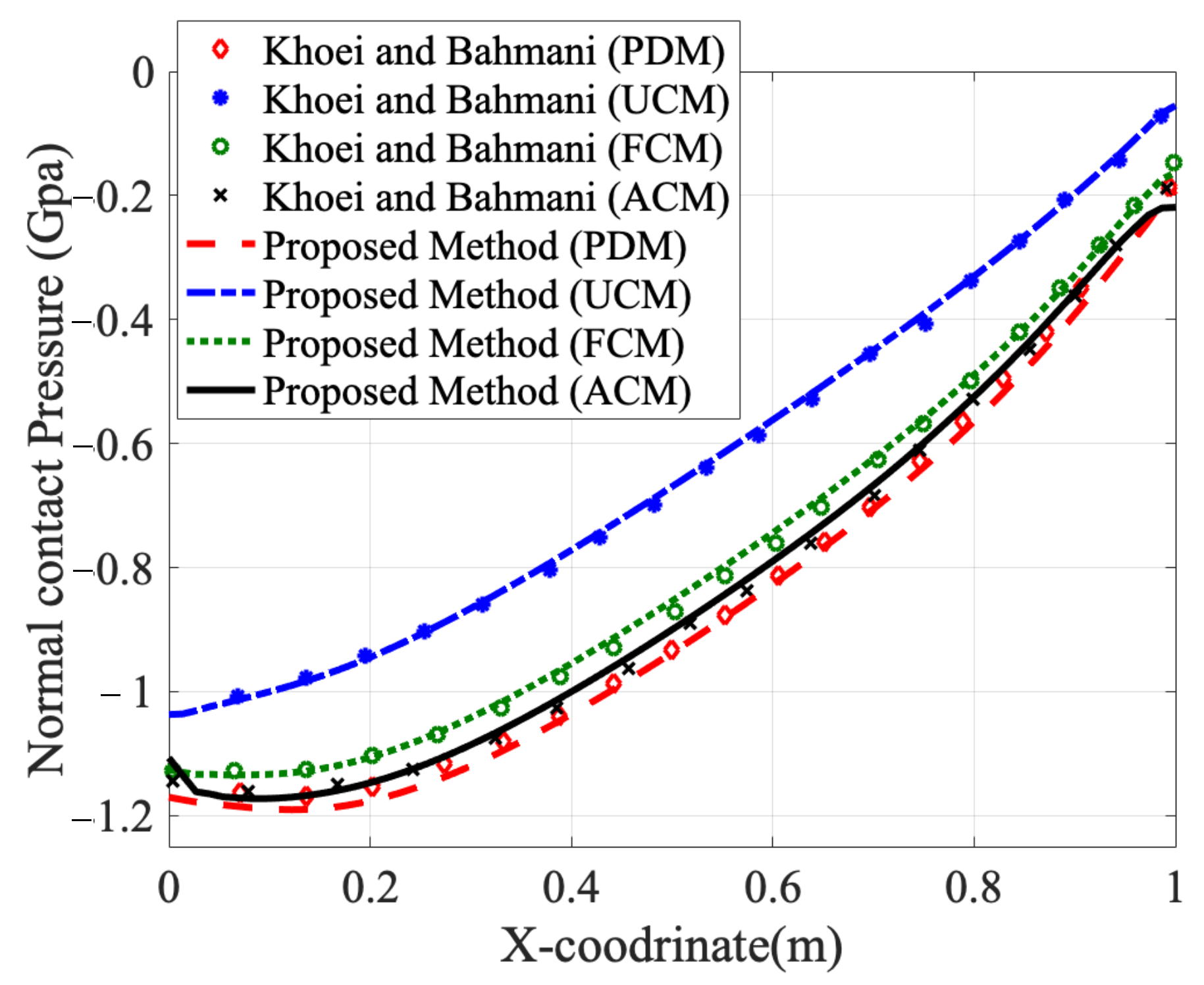
| Thermal Conductance Models | Thermal Expansion Coefficient | ||
|---|---|---|---|
| Pressure dependent model (PDM) | |||
| Uncoupled model (UCM) | |||
| Fully conductive model (FCM) | |||
| Adiabatic contact model (ACM) |
| Bulk Material | ||
|---|---|---|
| Young’s modulus | E | 10,000 MPa |
| Poisson’s ratio | 0.3 | |
| Density | ||
| Thermal expansion coefficient | ||
| Bulk thermal conductivity | ||
| Interface thermal conductivity (for adiabatic case) | ||
| Poisson’s ratio | |
| Young’s modulus | |
| Thermal conductivity | |
| Thermal conductance coefficient | |
| Vickers hardness | |
| Thermal constant | |
| Frictional coefficient |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, W.; Chen, P. A Fully Coupled Thermomechanical Phase Field Method for Modeling Cracks with Frictional Contact. Mathematics 2022, 10, 4416. https://doi.org/10.3390/math10234416
Wan W, Chen P. A Fully Coupled Thermomechanical Phase Field Method for Modeling Cracks with Frictional Contact. Mathematics. 2022; 10(23):4416. https://doi.org/10.3390/math10234416
Chicago/Turabian StyleWan, Wan, and Pinlei Chen. 2022. "A Fully Coupled Thermomechanical Phase Field Method for Modeling Cracks with Frictional Contact" Mathematics 10, no. 23: 4416. https://doi.org/10.3390/math10234416
APA StyleWan, W., & Chen, P. (2022). A Fully Coupled Thermomechanical Phase Field Method for Modeling Cracks with Frictional Contact. Mathematics, 10(23), 4416. https://doi.org/10.3390/math10234416






