Vectorized MATLAB Implementation of the Incremental Minimization Principle for Rate-Independent Dissipative Solids Using FEM: A Constitutive Model of Shape Memory Alloys
Abstract
1. Introduction
2. Constitutive Model of Shape Memory Alloys and Incremental Energy Problem Formulation
3. Numerical Implementation
3.1. Minimization Strategy
3.2. Details on Implementation in MATLAB

- Two nodes are constrained in all three directions (indicated by red circles);
- Nine nodes are constrained in two directions (indicated by violet circles);
- Twelve nodes are constrained in one direction (indicated by green circles).
4. Computational Examples
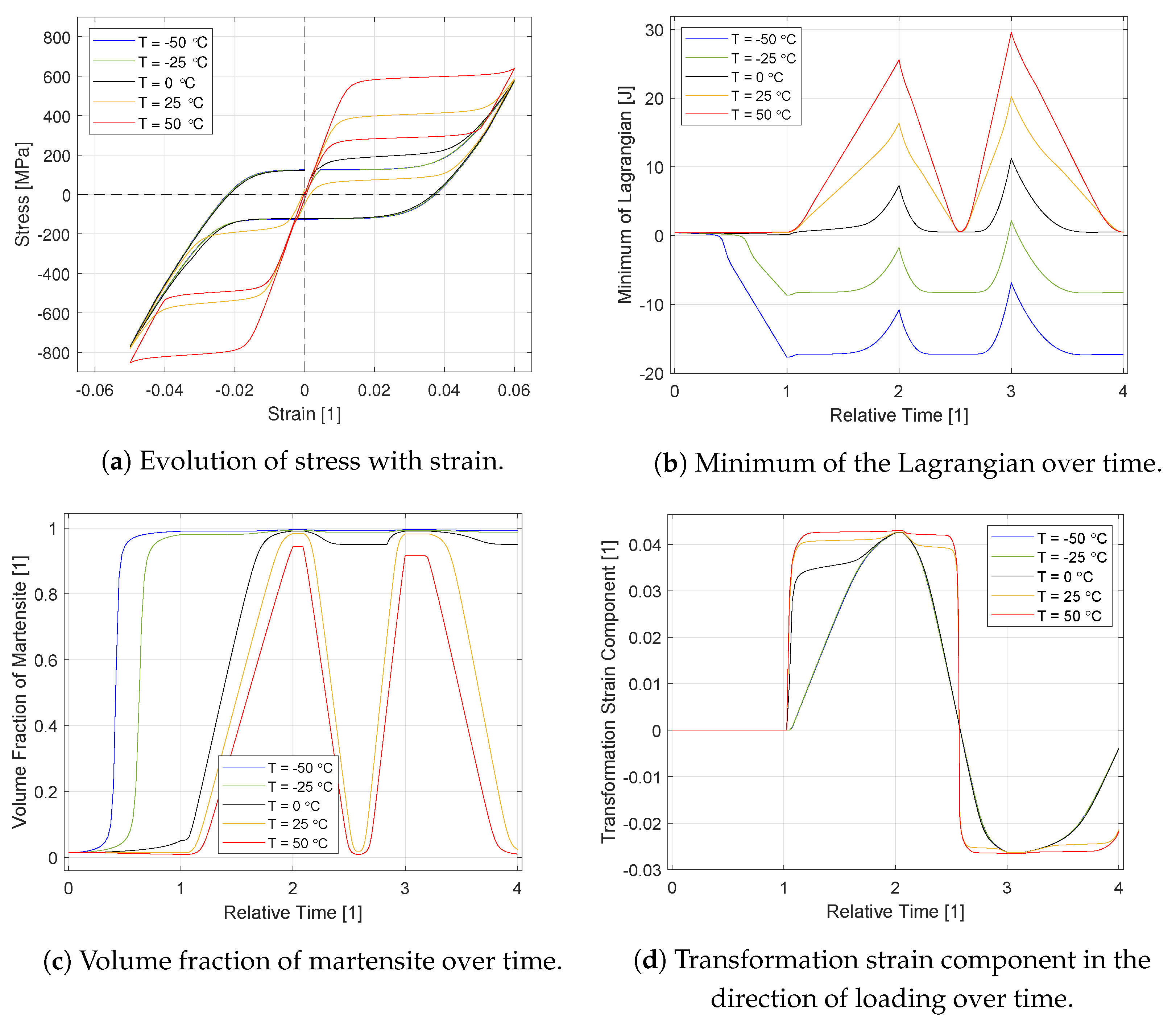
4.1. Example 1: Uniaxial Tension–Compression Tests at Different Temperatures
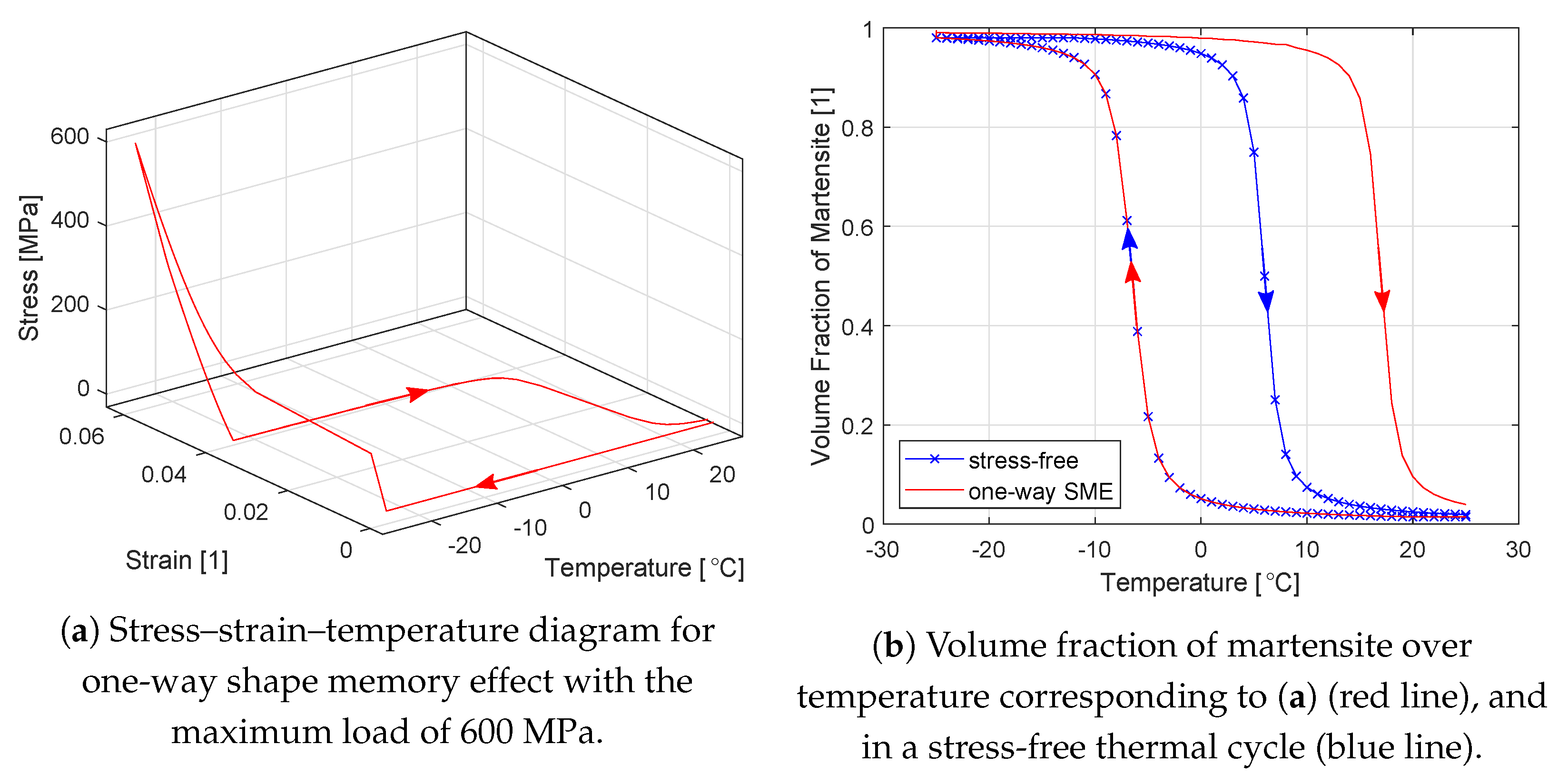
4.2. Example 2: One-Way Shape Memory Effect and Martensite Stabilization Effect
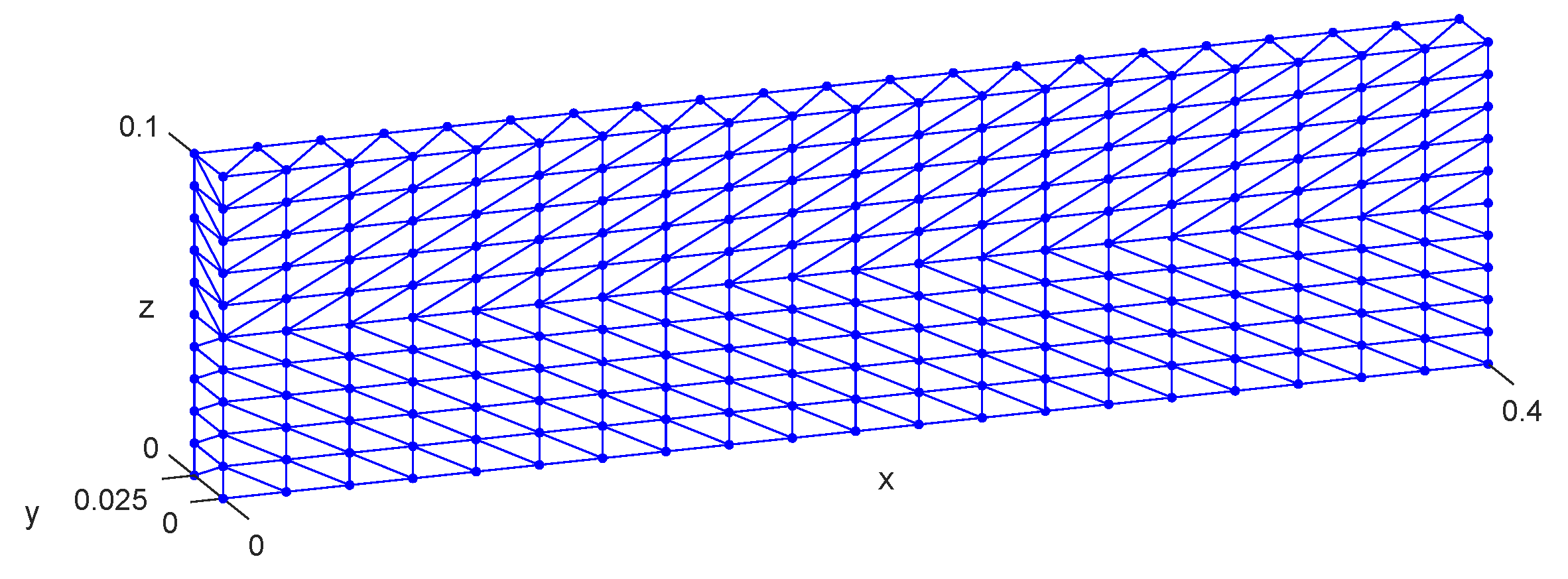
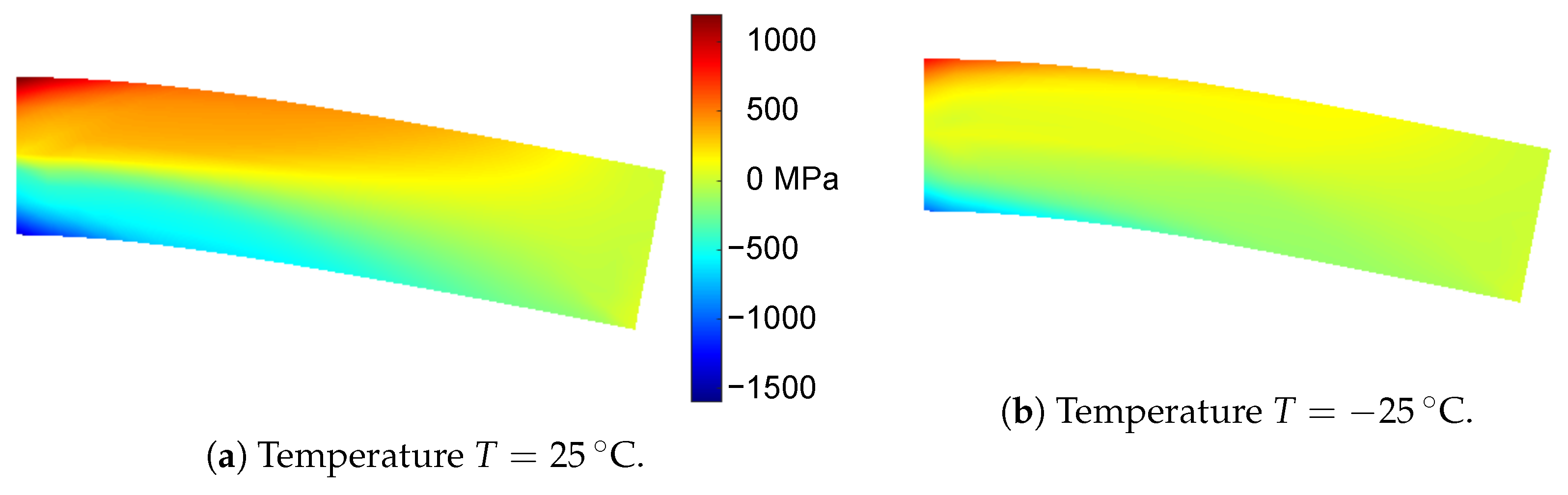
4.3. Example 3: Bending of a Shape Memory Alloy Beam
5. Conclusions and Future Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Treatment of Constraints for Employing Unconstrained Minimization Algorithms
Appendix B. Initiation of Internal Variables
Appendix C. Mesh Sensitivity Inspection
| Mesh Label | Nodes | Elements | DOFs Displacement | DOFs Int. Variables | DOFs Total |
|---|---|---|---|---|---|
| coarse | 288 | 720 | 698 | 4320 | 5018 |
| original | 462 | 1200 | 1129 | 7200 | 8329 |
| fine | 650 | 1728 | 1595 | 10,368 | 11,963 |
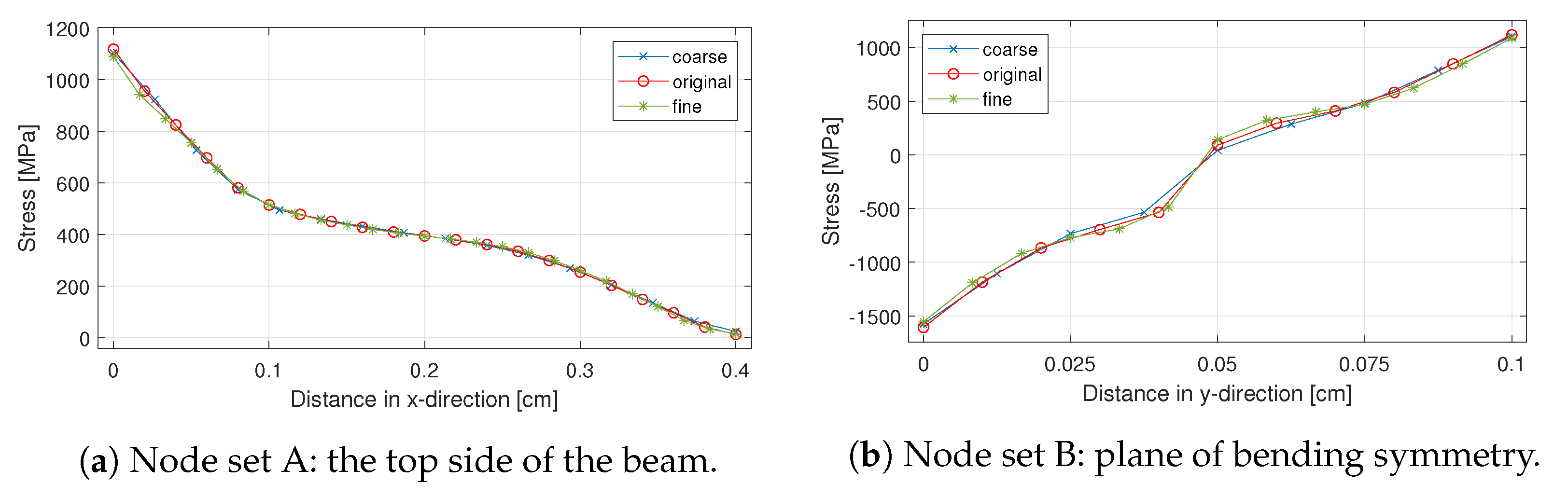
References
- Halphen, B.; Nguyen, Q.S. Sur les matériaux standard généralisés. J. Mec. 1975, 14, 39–63. [Google Scholar]
- Ziegler, H. An Introduction to Thermodynamics, 1st ed.; North-Holland Series in Applied Mathematics and Mechanics; North-Holland: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Germain, P.; Nguyen, Q.S.; Suquet, P. Continuum Thermodynamics. J. Appl. Mech. 1983, 50, 1010–1020. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Puzrin, A.M. A thermomechanical framework for constitutive models for rate-independent dissipative materials. Int. J. Plast. 2000, 16, 1017–1047. [Google Scholar] [CrossRef]
- Hackl, K.; Fischer, F.D. On the relation between the principle of maximum dissipation and inelastic evolution given by dissipation potentials. Proc. R. Soc. Lond. Ser. A 2008, 464, 117–132. [Google Scholar] [CrossRef]
- Petryk, H. Incremental energy minimization in dissipative solids. CR Mec. 2003, 331, 469–474. [Google Scholar] [CrossRef]
- Miehe, C. Strain-driven homogenization of inelastic microstructures and composites based on an incremental variational formulation. Internat. J. Numer. Methods Engrg. 2002, 55, 1285–1322. [Google Scholar] [CrossRef]
- Miehe, C. A multi-field incremental variational framework for gradient-extended standard dissipative solids. J. Mech. Phys. Solids 2011, 59, 898–923. [Google Scholar] [CrossRef]
- Mielke, A.; Roubíček, T. Rate-Independent Systems: Theory and Application; Applied Mathematical Sciences; Springer: New York, NY, USA, 2015. [Google Scholar]
- Owen, D.R.; Williams, W.O. On the concept of rate-independence. Quart. Appl. Math. 1968, 26, 321–329. [Google Scholar] [CrossRef]
- Moskovka, A.; Valdman, J. Fast MATLAB evaluation of nonlinear energies using FEM in 2D and 3D: Nodal elements. Appl. Math. Comput. 2022, 424, 127048. [Google Scholar] [CrossRef]
- Scalet, G.; Auricchio, F. Computational Methods for Elastoplasticity: An Overview of Conventional and Less-Conventional Approaches. Arch. Computat. Methods Eng. 2018, 25, 545–589. [Google Scholar] [CrossRef]
- Stupkiewicz, S.; Petryk, H. A robust model of pseudoelasticity in shape memory alloys. Int. J. Numer. Methods Eng. 2013, 93, 747–769. [Google Scholar] [CrossRef]
- Artioli, E.; Bisegna, P. An incremental energy minimization state update algorithm for 3D phenomenological internal-variable SMA constitutive models based on isotropic flow potentials. Int. J. Numer. Methods Eng. 2016, 105, 197–220. [Google Scholar] [CrossRef]
- Scalet, G.; Peigney, M. A robust and efficient radial return algorithm based on incremental energy minimization for the 3D Souza-Auricchio model for shape memory alloys. Eur. J. Mech. A Solids 2017, 61, 364–382. [Google Scholar] [CrossRef]
- Egner, H.; Skoczen, B.; Rys, M. Constitutive and numerical modeling of coupled dissipative phenomena in 316L stainless steel at cryogenic temperatures. Int. J. Plast. 2015, 64, 113–133. [Google Scholar] [CrossRef]
- Peigney, M.; Scalet, G.; Auricchio, F. A time-integration algorithm for a 3D constitutive model for SMAs including permanent inelasticity and degradation effects. Int. J. Numer. Methods Eng. 2018, 115, 1053–1082. [Google Scholar] [CrossRef]
- Einav, I.; Houlsby, G.T.; Nguyen, G.D. Coupled damage and plasticity models derived from energy and dissipation potentials. Int. J. Solids Struct. 2007, 44, 2487–2508. [Google Scholar] [CrossRef]
- Rahman, T.; Valdman, J. Fast MATLAB assembly of FEM matrices in 2D and 3D: Nodal elements. Appl. Math. Comput. 2013, 219, 7151–7158. [Google Scholar] [CrossRef]
- Anjam, I.; Valdman, J. Fast MATLAB assembly of FEM matrices in 2D and 3D: Edge elements. Appl. Math. Comput. 2015, 267, 252–263. [Google Scholar] [CrossRef]
- Cimrman, R.; Lukeš, V.; Rohan, E. Multiscale finite element calculations in Python using SfePy. Adv. Comput. Math. 2019, 45, 1897–1921. [Google Scholar] [CrossRef]
- Sedlák, P.; Frost, M.; Benešová, B.; Šittner, P.; Ben Zineb, T. Thermomechanical model for NiTi-based shape memory alloys including R-phase and material anisotropy under multi-axial loadings. Int. J. Plast. 2012, 39, 132–151. [Google Scholar] [CrossRef]
- Frost, M.; Benešová, B.; Sedlák, P. A microscopically motivated constitutive model for shape memory alloys: Formulation, analysis and computations. Math. Mech. Solids 2016, 21, 358–382. [Google Scholar] [CrossRef]
- Frost, M.; Sedlák, P.; Kadeřávek, L.; Heller, L.; Šittner, P. Modeling of mechanical response of NiTi shape memory alloy subjected to combined thermal and non-proportional mechanical loading: A case study on helical spring actuator. J. Intel. Mat. Syst. Str. 2016, 27, 1927–1938. [Google Scholar] [CrossRef]
- Frost, M.; Benešová, B.; Seiner, H.; Kružík, M.; Šittner, P.; Sedlák, P. Thermomechanical model for NiTi-based shape memory alloys covering macroscopic localization of martensitic transformation. Int. J. Solids Struct. 2021, 221, 117–129. [Google Scholar] [CrossRef]
- Benešová, B.; Frost, M.; Kadeřávek, L.; Roubíček, T.; Sedlák, P. An experimentallly-fitted thermodynamical constitutive model for polycrystalline shape memory alloys. Disc. Cont. Dynam. Syst. S 2021, 14, 3925–3952. [Google Scholar] [CrossRef]
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Elkhal Letaief, W.; Hassine, T.; Gamaoun, F.; Sarraj, R.; Ben Kahla, N. Coupled diffusion-mechanical model of NiTi alloys accounting for hydrogen diffusion and ageing. Int. J. Appl. Mech. 2020, 12, 2050039. [Google Scholar] [CrossRef]
- Wang, L.; Feng, P.; Xing, X.; Wu, Y.; Liu, Z. A one-dimensional constitutive model for NiTi shape memory alloys considering inelastic strains caused by the R-phase transformation. J. Alloy. Compd. 2021, 868, 159192. [Google Scholar] [CrossRef]
- Wang, L.; Feng, P.; Wu, Y.; Liu, Z. A Temperature-Dependent Model of Shape Memory Alloys Considering Tensile-Compressive Asymmetry and the Ratcheting Effect. Materials 2020, 13, 3116. [Google Scholar] [CrossRef]
- Zhu, X.; Chu, L.; Dui, G. Constitutive Modeling of Porous Shape Memory Alloys Using Gurson–Tvergaard–Needleman Model Under Isothermal Conditions. Int. J. Appl. Mech. 2020, 12, 2050038. [Google Scholar] [CrossRef]
- Adeodato, A.; Vignoli, L.L.; Paiva, A.; Monteiro, L.L.; Pacheco, P.M.; Savi, M.A. A Shape Memory Alloy Constitutive Model with Polynomial Phase Transformation Kinetics. Shap. Mem. Superelasticity 2022. [Google Scholar] [CrossRef]
- Jiang, D.; Xiao, Y. Modelling on grain size dependent thermomechanical response of superelastic NiTi shape memory alloy. Int. J. Solids Struct. 2021, 210, 170–182. [Google Scholar] [CrossRef]
- Auricchio, F.; Petrini, L. Improvements and algorithmical considerations on a recent three-dimensional model describing stress-induced solid phase transformations. Int. J. Numer. Methods Eng. 2002, 55, 1255–1284. [Google Scholar] [CrossRef]
- Ciarlet, P.G. The Finite Element Method for Elliptic Problems; Classics in Applied Mathematics; SIAM: Phiadelphia, PA, USA, 2002. [Google Scholar]
- Alberty, J.; Carstensen, C.; Funken, S.A.; Klose, R. Matlab Implementation of the Finite Element Method in Elasticity. Computing 2002, 69, 239–263. [Google Scholar] [CrossRef]
- Matonoha, C.; Moskovka, A.; Valdman, J. Minimization of p-Laplacian via the Finite Element Method in MATLAB. In International Conference on Large-Scale Scientific Computing, (LSSC 2021); Lecture Notes in Computer Science; Lirkov, I., Margenov, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; Volume 13127, pp. 533–540. [Google Scholar]
- Šittner, P.; Heller, L.; Pilch, J.; Sedlák, P.; Frost, M.; Chemisky, Y.; Duval, A.; Piotrowski, B.; Ben Zineb, T.; Patoor, E.; et al. Roundrobin SMA modeling. In ESOMAT 2009—The 8th European Symposium on Martensitic Transformations; Šittner, P., Heller, L., Paidar, V., Eds.; EDP Sciences: Ulis, France, 2009; p. 08001. [Google Scholar]
- Piao, M.; Otsuka, K.; Miyazaki, S.; Horikawa, H. Mechanism of the As temperature increase by pre-deformation in thermoelastic alloys. Mater. Trans. JIM 1993, 34, 919–929. [Google Scholar] [CrossRef]
- Liu, Y.; Favier, D. Stabilisation of martensite due to shear deformation via variant reorientation in polycrystalline NiTi. Acta Mater. 2000, 48, 3489–3499. [Google Scholar] [CrossRef]
- Belyaev, S.; Resnina, N.; Iaparova, E.; Ivanova, A.; Rakhimov, T.; Andreev, V. Influence of chemical composition of NiTi alloy on the martensitestabilization effect. J. Alloy. Compd. 2019, 787, 1365–1371. [Google Scholar] [CrossRef]
- Rao, Z.; Wang, X.; Leng, J.; Yan, Z.; Yan, X. Design methodology of the Ni50Ti50 shape memory alloy beam actuator: Heat treatment, training and numerical Simulation. Mater. Des. 2022, 217, 110615. [Google Scholar] [CrossRef]
- Viet, N.V.; Zaki, W.; Umer, R. Analytical investigation of an energy harvesting shape memory alloy piezoelectric beam. Arch. Appl. Mech. 2020, 90, 2715–2738. [Google Scholar] [CrossRef]
- Seigner, L.; Tshikwand, G.K.; Wendler, F.; Kohl, M. Bi-Directional Origami-Inspired SMA Folding Microactuator. Actuators 2021, 10, 181. [Google Scholar] [CrossRef]
- Eshghinejad, A.; Elahinia, M. Exact solution for bending of shape memory alloy beams. Mech. Adv. Mater. Struc. 2015, 22, 829–838. [Google Scholar] [CrossRef]
- Viet, N.V.; Zaki, W.; Moumni, Z. A model for shape memory alloy beams accounting for tensile compressive asymmetry. J. Intell. Mater. Syst. Struct. 2019, 30, 2697–2715. [Google Scholar] [CrossRef]
- Radi, E. Analytical modeling of the shape memory effect in SMA beams with rectangular cross section under reversed pure bending. J. Intell. Mater. Syst. Struct. 2021, 32, 2214–2230. [Google Scholar] [CrossRef]
- Sielenkämper, M.; Wulfinghoff, S. A thermomechanical finite strain shape memory alloy model and its application to bistable actuators. Acta Mech. 2022, 3059–3094, 233. [Google Scholar] [CrossRef]
- Kundu, A.; Banerjee, A. Coupled thermomechanical modelling of shape memory alloy structures undergoing large deformation. Int. J. Mech. Sci. 2022, 220, 107102. [Google Scholar] [CrossRef]
- Frost, M.; Sedlák, P.; Heller, L.; Kadeřávek, L.; Šittner, P. Experimental and computational study on phase transformations in superelastic NiTi snake-like spring. Smart Mater. Struct. 2018, 27, 095005. [Google Scholar] [CrossRef]
- Ostadrahimi, A.; Taheri-Behrooz, F.; Choi, E. Effect of Tension-Compression Asymmetry Response on the Bending of Prismatic Martensitic SMA Beams: Analytical and Experimental Study. Materials 2021, 14, 5415. [Google Scholar] [CrossRef]
- Mohd Jani, J.; Leary, M.; Subic, A. Designing shape memory alloy linear actuators: A review. J. Intell. Mater. Syst. Struct. 2017, 28, 1699–1718. [Google Scholar] [CrossRef]
- De Saxcé, G.; Feng, Z.Q. New inequality and functional for contact with friction: The implicit standard material approach. J. Struct. Mech. 1991, 19, 301–325. [Google Scholar] [CrossRef]
- Lahellec, N.; Suquet, P. On the effective behavior of nonlinear inelastic composites: I. Incremental variational principles. J. Mech. Phys. Solids 2007, 55, 1932–1963. [Google Scholar] [CrossRef]
- Blühdorn, J.; Gauger, N.R.; Kabel, M. AutoMat: Automatic differentiation for generalized standard materials on GPUs. Comput. Mech. 2022, 69, 589–613. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Drozdenko, D.; Knapek, M.; Kružík, M.; Máthis, K.; Švadlenka, K.; Valdman, J. Elastoplastic Deformations of Layered Structures. Milan J. Math. 2022. [Google Scholar] [CrossRef]


| Parameter | Value | Unit | Brief Description |
|---|---|---|---|
| K | 150 | GPa | Bulk modulus common to both phases. |
| GPa | Shear moduli of A and M. | ||
| k | 1 | Maximum transformation strain in tension. | |
| a | 1 | Asymmetry parameter. | |
| As, Af Ms, Mf Teq | 5,7 −5, −8 0 | C | Temperature parameters related to the direct phase transformation between A and M. |
| 100 | MPa | Reorientation stress of M at 25 C. | |
| MPa/C | Difference between specific entropies of M and A. | ||
| MPa | Parameter of regularization function r in [22]. | ||
| MPa | Parameter of reorientation-hardening function. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frost, M.; Valdman, J. Vectorized MATLAB Implementation of the Incremental Minimization Principle for Rate-Independent Dissipative Solids Using FEM: A Constitutive Model of Shape Memory Alloys. Mathematics 2022, 10, 4412. https://doi.org/10.3390/math10234412
Frost M, Valdman J. Vectorized MATLAB Implementation of the Incremental Minimization Principle for Rate-Independent Dissipative Solids Using FEM: A Constitutive Model of Shape Memory Alloys. Mathematics. 2022; 10(23):4412. https://doi.org/10.3390/math10234412
Chicago/Turabian StyleFrost, Miroslav, and Jan Valdman. 2022. "Vectorized MATLAB Implementation of the Incremental Minimization Principle for Rate-Independent Dissipative Solids Using FEM: A Constitutive Model of Shape Memory Alloys" Mathematics 10, no. 23: 4412. https://doi.org/10.3390/math10234412
APA StyleFrost, M., & Valdman, J. (2022). Vectorized MATLAB Implementation of the Incremental Minimization Principle for Rate-Independent Dissipative Solids Using FEM: A Constitutive Model of Shape Memory Alloys. Mathematics, 10(23), 4412. https://doi.org/10.3390/math10234412






