Estimating Value-at-Risk and Expected Shortfall: Do Polynomial Expansions Outperform Parametric Densities?

Abstract

We assess Value-at-Risk (VaR) and Expected Shortfall (ES) estimates assuming different models for the standardized returns: distributions based on polynomial expansions such as Cornish-Fisher and Gram-Charlier, and well-known parametric densities such as normal, skewed-t and Johnson. This paper aims to analyze whether models based on polynomial expansions outperform the parametric ones. We carry out the model performance comparison in two stages: first, with a backtesting analysis of VaR and ES; and second, using loss functions. Our backtesting results show that all distributions, except for normal ones, perform quite well in VaR and ES estimations. Regarding the loss function analysis, we conclude that polynomial expansions (specifically, the Cornish-Fisher one) usually outperform parametric densities in VaR estimation, but the latter (specifically, the Johnson density) slightly outperform the former in ES estimation; however, the gains of using one approach or the other are modest.

1. Introduction

In recent years, big events such as the great plunge in oil prices in 2015, the economic instability in Greece during 2009–2017, the China stock market turbulence in 2015–2016, Brexit in 2016 and the COVID-19 pandemic in 2020–2021, have caused important losses for investors; consequently, measuring risk properly has become a crucial task for researchers and practitioners in finance. Nowadays, two of the most used downside risk measures are the Value-at-Risk (VaR) and the Expected Shortfall (ES). Indeed, the Basel Committee on Banking Supervision (Basel III) imposes to financial institutions to meet some capital requirements based on VaR and ES estimates. If they are not properly estimated, it may lead to a sub-optimal capital allocation, affecting the profitability or stability of financial institutions. The VaR and the ES measure, respectively, the quantile and the expected return conditioning on returns being lower than its quantile. These two risk measures have received some criticism: desirable properties of a risk measure (among them, the coherence property) are formalized by [1] in a set of axioms, and VaR has been found not to be coherent because it does not satisfy the subadditivity property and, as a consequence, it might fail to appropriately account for risk concentrations, and diversification strategies might be negatively affected; VaR has also been criticized for not providing information beyond the quantile; regarding ES, it does not verify the elicitability condition, which means that there could be an issue with direct backtesting of ES estimates (see [2]), although some feasible approaches to backtesting ES have recently been proposed (see, among others, [3], using a linear approximation of ES based on VaRs at different coverage levels, and [4], using cumulative violations). In spite of this criticism, Var and ES are very informative about the tail shape of the asset returns distribution, and regulatory requirements have focused on them.

Both VaR and ES estimates are usually obtained by previously estimating, with maximum likelihood (ML) techniques, the parameters implied in a returns model with ARMA structure for the conditional mean of returns and GARCH-type models for their conditional variance, and assuming a particular distribution for the standardized errors, henceforth $Z_t$. The standard normal distribution has been the most frequent distribution assumed for $Z_t,$ but this assumption is often rejected in the empirical finance literature when modeling stock returns and other financial assets, even after controlling for volatility clustering effects. As a consequence, recent research has focused on the analysis of models that use generalizations of the normal distribution that are flexible enough to tackle with asymmetry and heavy tails, but that are also analytically tractable. Here we focus on two approaches which have been highly used in recent years to obtain generalizations of the normal distribution that might lead to more accurate daily estimates of VaR and ES: (i) use of polynomial expansions that allow to easily obtain more flexible models than the normal; (ii) use of parametric densities that encompass the normal. Our aim in this paper is to compare the performance of these two approaches, through the implementation of backtesting methods and loss functions. In principle, one could think that the flexibility inherent to polynomial expansions should lead to better estimates of VaR and ES, if the sample size is large enough. However, the parametric densities have been introduced to specifically address the departures from non-normality that are typical in financial data and, thus, they might yield better results than the polynomial expansions, with the sample sizes that are usual in econometric practice with financial series. This is precisely the kind of comparison that we are interested in; and, in order to perform a fair comparison between the two approaches, the order of the polynomial expansions that we will consider will lead to distributions with two parameters, and the parametric distributions that we will consider will have two shape parameters.

The polynomial expansions that we use here are the Cornish-Fisher (CF) and the Gram-Charlier (GC) expansions. Both expansions differ in their nature: CF is a transformation of the normal quantile function (see [5]), whereas GC is a transformation of the normal probability density function. The CF distribution that we consider here is obtained using a fourth-order expansion. In this way, a two-parameter distribution is obtained, and there is a simple relation between the two parameters and the skewness and kurtosis; this easy tractability comes from using the bijective property of the CF polynomial expansion, once the domain of variation is appropriately restricted (monotonicity condition), see [6]; if the monotonicity condition does not hold, then the ‘increasing rearrangement’ procedure of [7] can be used to restore monotonicity (an empirical application of this methodology can be seen in [8]). The GC expansions (see, e.g., [9]) are very flexible and analytically tractable since many densities can be expressed as the product of the standard normal probability density function times an infinite series of Hermite polynomials. In practice, truncated GC expansions (also known as Edgeworth- Sargan densities) have to be used (see [10] for the analysis of these densities with financial data), and this often implies negative densities over some interval of their domain. Several solutions have been proposed to handle this problem: (i) restricting the parameter space and then estimating the parameters by constrained ML, see [11]; (ii) using certain transformations in order to guarantee positivity of the expansion, see [12,13]; (iii) considering semi-nonparametric densities which are always positive by construction, and hence the parameters can be easily estimated by using ML instead of constrained ML, see [14,15,16]. In this work we use the third approach, and consider the standardized semi-nonparametric distribution of fourth order, which is a two-parameter distribution.

The parametric densities that we use here are two well-known two-parameter densities: the skewed-t density, introduced by [17] in financial econometrics; and one of the densities proposed in Johnson [18], which was analyzed by [19,20] in the context of modeling financial returns. The skewed-t density exploits the leptokurtosis property of the Student-t distribution, but also allows for asymmetries thanks to the introduction of an additional parameter. The idea behind Johnson’s approach to derive densities that encompass the normal is to consider random variables obtained by transforming a normal random variable with the inverse of a non-decreasing continuous function g; specifically, three different g functions have been proposed, leading to lognormal, unbounded and bounded distributions, although here we will consider exclusively the unbounded one, that is, $g\left(x\right)=$ sinh${}^{-1}(x)$.

The accuracy of VaR and ES estimates under the two approaches (polynomial expansions or parametric densities) is measured using backtesting techniques with rolling-window data. For backtesting VaR, we implement the traditional tests, i.e., the unconditional coverage test of [21] and the independence test of [22]. For backtesting ES, we use the robust unconditional and conditional coverage tests of [4], which focus on cumulative violations. Furthermore, different loss functions (see, e.g., [23]) are used in order to rank models that are not rejected with backtesting procedures.

The remainder of the paper is structured as follows. Section 2 describes the statistical specifications that are used for modeling returns, and how inference on VaR and ES is made with them. Section 3 describes the procedures that are used to assess the performance of the statistical models, namely, backtesting procedures for VaR and ES and loss functions. Section 4 describes the data and applies the different methods to study the performance through backtesting and loss functions. Section 5 concludes the paper with a summary of the main findings and contributions.

2. Statistical Models and Inference

2.1. General Framework

We assume that daily stock returns, $R_t$, satisfy that

$$R_t=\mu +{\sigma }_t{Z}_t,$$

(1)

where $\{Z_t\}$ are independent and identically distributed (iid) zero-mean unit-variance random variables, $\mu$ is a parameter and $\{{\sigma }_t\}$ follows a non-linear asymmetric GARCH (NGARCH) model, see e.g., [24], given by

$${\sigma }_t^2=b_0+b_1{\sigma }_t^2+b_2{(R_{t-1}-\mu -c{\sigma }_{t-1})}^2,$$

(2)

where $b_0$, $b_1$ and $b_2$ are positive parameters, and c is an additional parameter that captures the leverage effect. Note that $c>0$ implies that returns exhibit leverage effect, i.e., volatility increases more after negative shocks than after positive shocks of the same magnitude, whereas $c<0$ means that there is inverse leverage effect, i.e., volatility increases more after positive shocks than after negative shocks of the same magnitude. The NGARCH is reduced to the GARCH when $c=0$. In this paper we assume that $Z_t=$ v${}_Y^{-1/2}(Y_t-$m${}_Y)$, where $Y_t$ is random variable that is defined by means of a polynomial expansion or a parametric model, and we denote m${}_Y\equiv E(Y_t)$ and v${}_Y\equiv$ Var$(Y_t).$ The aim of our research is to compare the performance of densities based on polynomial expansions and densities based on parametric models; in order to make a fair comparison, both the polynomial expansions and the parametric models that we consider will be characterized by two parameters ${\psi }_1,$ ${\psi }_2$ that determine the skewness and the kurtosis of $Y_t$ in each case. Thus, hereafter the probability density function (pdf) and the cumulative distribution function (cdf) of $Y_t$ are denoted as $f_Y(·\mid {\psi }_1,{\psi }_2)$ and $F_Y(·\mid {\psi }_1,{\psi }_2)$, respectively.

Our analysis will focus on the performance of the models when estimating the value at risk (VaR) and the expected shortfall (ES) of returns. Given $\alpha \in (0,1),$ the $\alpha$-VaR and the $\alpha$-ES of $Y_t$ will be denoted as VaR${}_Y(\alpha \mid {\psi }_1,{\psi }_2)$ and ES${}_Y(\alpha \mid {\psi }_1,{\psi }_2)$, respectively, that is, VaR${}_Y(\alpha \mid {\psi }_1,{\psi }_2)=F_Y^{-1}(\alpha \mid {\psi }_1,{\psi }_2)$ and ES${}_Y(\alpha \mid {\psi }_1,{\psi }_2)=E(Y_t\mid Y_t\le$VaR${}_Y(\alpha \mid {\psi }_1,{\psi }_2)).$ Therefore, as $Y_t=$m${}_Y+\frac{{\mathrm{v}}_Y^{1/2}}{{\sigma }_t}(R_t-\mu ),$ it follows that the cdf, the pdf, the $\alpha$-VaR and the $\alpha$-ES of $R_t$ conditional on information up to period $t-1$ are:

$$F_t(r\mid {\mathcal{F}}_{t-1})=F_Y({\mathrm{m}}_Y+\frac{{\mathrm{v}}_Y^{1/2}}{{\sigma }_t}(r-\mu )\mid {\psi }_1,{\psi }_2),$$

(3)

$$f_t(r\mid {\mathcal{F}}_{t-1})=\frac{{\mathrm{v}}_Y^{1/2}}{{\sigma }_t}{f}_Y({\mathrm{m}}_Y+\frac{{\mathrm{v}}_Y^{1/2}}{{\sigma }_t}(r-\mu )\mid {\psi }_1,{\psi }_2),$$

(4)

$${\mathrm{VaR}}_t(\alpha \mid {\mathcal{F}}_{t-1})=\mu +\frac{{\sigma }_t}{{\mathrm{v}}_Y^{1/2}}({\mathrm{VaR}}_Y(\alpha \mid {\psi }_1,{\psi }_2)-{\mathrm{m}}_Y),$$

(5)

$${\mathrm{ES}}_t(\alpha \mid {\mathcal{F}}_{t-1})=\mu +\frac{{\sigma }_t}{{\mathrm{v}}_Y^{1/2}}({\mathrm{ES}}_Y(\alpha \mid {\psi }_1,{\psi }_2)-{\mathrm{m}}_Y).$$

(6)

Note that these expressions depend on seven parameters: the mean parameter $\mu ,$ the four parameters of the NGARCH model $b_0,$ $b_1,$ $b_2,$ $c,$ and the two shape parameters ${\psi }_1,$ ${\psi }_2$. These seven parameters can be estimated by Maximum Likelihood (ML), once the pdf $f_Y(·\mid {\psi }_1,{\psi }_2)$ is specified, and the corresponding mean and variance (m${}_Y,$ v${}_Y$) are found. Specifically, the estimates are found by maximizing

$$lnL(\mu ,b_0,b_1,b_2,c,{\psi }_1,{\psi }_2)={\sum }_{t=1}^T\left(\frac{1}{2}ln{\mathrm{v}}_Y-\frac{1}{2}ln{\sigma }_t^2+ln{f}_Y({\mathrm{m}}_Y+\frac{{\mathrm{v}}_Y^{1/2}}{{\sigma }_t}(R_t-\mu )\mid {\psi }_1,{\psi }_2)\right)$$

where ${\sigma }_t$ is given in (2). The optimization problem incorporates non-negativity restrictions on $b_0,$ $b_1$ and $b_2,$ the second-order stationarity restriction $b_2(1+c^2)+b_1<1,$ and the restrictions on ${\psi }_1$ and ${\psi }_2$ that are specified below in each case. Once the parameters of the model are estimated, VaR${}_t(\alpha \mid {\mathcal{F}}_{t-1})$ and ES${}_t(\alpha \mid {\mathcal{F}}_{t-1})$ are estimated using the expressions given in (5) and (6), but replacing the unknown parameters by their ML estimates. In the next two subsections we specify the distributions for $Y_t$ that we consider.

2.2. Distributions Based on Polynomial Expansions

2.2.1. Cornish-Fisher Expansion

We follow here the specification of the Cornish-Fisher expansion described in [25]. A random variable Y follows a two-parameter Cornish-Fisher distribution (a CF distribution, for short) with parameters ${\psi }_1$ and ${\psi }_2$ if

$$Y=a_0({\psi }_1,{\psi }_2)+a_1({\psi }_1,{\psi }_2)W+a_2({\psi }_1,{\psi }_2)W^2+a_3({\psi }_1,{\psi }_2)W^3,$$

(7)

where W is a standard normal random variable, ${\psi }_1,$${\psi }_2$ are parameters such that

$$\left|{\psi }_1\right|<6(\sqrt{2}-1)\approx 2.4853$$

and

$${\psi }_2\in \left[\frac{36+11{\psi }_1^2-\sqrt{{\psi }_1^4-216{\psi }_1^2+1296}}{9},\frac{36+11{\psi }_1^2+\sqrt{{\psi }_1^4-216{\psi }_1^2+1296}}{9}\right],$$

and we denote $a_0({\psi }_1,{\psi }_2)=-{\psi }_1/6,$$a_1({\psi }_1,{\psi }_2)=1-{\psi }_2/8+5{\psi }_1^2/36,$$a_2({\psi }_1,{\psi }_2)={\psi }_1/6$ and $a_3({\psi }_1,{\psi }_2)={\psi }_2/24-{\psi }_1^2/18$. For simplicity, hereafter we write $a_j$ instead of $a_j({\psi }_1,{\psi }_2)$. Note that the conditions on ${\psi }_1$ and ${\psi }_2$ are introduced to guarantee that the transformation from W to Y is one-to-one. As a consequence, if we denote $h(W)=a_0+a_{1}W+a_2{W}^2+a_3{W}^3,$ the relationship (7) implies that the cdf of Y is $F_Y(y\mid {\psi }_1,{\psi }_2)=\mathsf{\Phi }(h^{-1}(y)).$ The corresponding pdf is

$$f_Y(y\mid {\psi }_1,{\psi }_2)=\frac{\varphi (d(y,{\psi }_1,{\psi }_2))}{(\frac{{\psi }_2}{8}-\frac{{\psi }_1^2}{6})d{(y,{\psi }_1,{\psi }_2)}^2+\frac{{\psi }_1}{3}d(y,{\psi }_1,{\psi }_2)+1-\frac{{\psi }_2}{8}+\frac{5{\psi }_1^2}{36}}$$

where $\varphi (·)$ denotes the standard normal pdf,

$$d(y,{\psi }_1,{\psi }_2)\equiv -\frac{a_2}{3a_3}+\sqrt[3]{-\frac{q(y,{\psi }_1,{\psi }_2)}{2}+\sqrt{\Delta (y,{\psi }_1,{\psi }_2)}}+\sqrt[3]{-\frac{q(y,{\psi }_1,{\psi }_2)}{2}-\sqrt{\Delta (y,{\psi }_1,{\psi }_2)}},$$

$$q(y,{\psi }_1,{\psi }_2)\equiv \frac{2a_2^3-9a_1{a}_2{a}_3+27a_3^2(a_0-y)}{27a_3^3},\mathrm{and}$$

$$\Delta (y,{\psi }_1,{\psi }_2)\equiv \frac{q{(y,{\psi }_1,{\psi }_2)}^2}{4}+\frac{{(3a_1{a}_3-a_2^2)}^3}{729a_3^6}.$$

It also follows from (7) that m${}_Y=0$ and

$${\mathrm{v}}_Y=1+\frac{1}{96}{\psi }_2^2+\frac{25}{1296}{\psi }_1^4-\frac{1}{36}{\psi }_2{\psi }_1^2.$$

Additionally, the $\alpha$-VaR and the $\alpha$-ES of Y are:

$${\mathrm{VaR}}_Y(\alpha \mid {\psi }_1,{\psi }_2)=a_0+a_1{\mathsf{\Phi }}^{-1}(\alpha )+a_2{\mathsf{\Phi }}^{-1}{(\alpha )}^2+a_3{\mathsf{\Phi }}^{-1}{(\alpha )}^3,$$

$${\mathrm{ES}}_Y(\alpha \mid {\psi }_1,{\psi }_2)=a_0-\frac{a_1}{\alpha }\varphi ({\mathsf{\Phi }}^{-1}(\alpha ))+\frac{a_2}{\alpha }(\alpha -{\mathsf{\Phi }}^{-1}(\alpha )\varphi ({\mathsf{\Phi }}^{-1}(\alpha )))-\frac{a_3}{\alpha }(2+{\mathsf{\Phi }}^{-1}{(\alpha )}^2)\varphi ({\mathsf{\Phi }}^{-1}(\alpha )).$$

The latter expression follows because $E[Y\mid Y\le$VaR${}_Y(\alpha \mid {\psi }_1,{\psi }_2)]=$$E[h(W)\mid h(W)\le h({\mathsf{\Phi }}^{-1}(\alpha ))]=$$E[a_0+a_{1}W+a_2{W}^2+a_3{W}^3\mid W\le {\mathsf{\Phi }}^{-1}(\alpha )],$ and the truncated moments of a standard normal distribution are $E[W\mid W\le a]=$$-\varphi (a)/\mathsf{\Phi }(a),$$E[W^2\mid W\le a]=$$1-a\varphi (a)/\mathsf{\Phi }(a),$ and $E[W^3\mid W\le a]=$$-(2+a^2)\varphi (a)/\mathsf{\Phi }(a)$ (see e.g., [26]).

2.2.2. Gram-Charlier Expansion

We follow here the specification of the Gram-Charlier expansion described in [27]. A random variable Y follows a two-parameter Gram-Charlier distribution (a GC distribution, for short) with parameters ${\psi }_1$ and ${\psi }_2$ if its pdf is

$$f_Y(y\mid {\psi }_1,{\psi }_2)=\frac{\varphi (y)}{{\mathbf{v}}^{\prime }\mathbf{v}}{\left(1+{\psi }_1{H}_1(y)+{\psi }_2{H}_2(y)\right)}^2,$$

(8)

where we denote $\mathbf{v}={(1,{\psi }_1,{\psi }_2)}^{\prime }$, and ${\{H_k(·)\}}_{k=0}^{\infty }$ are the normalized Hermite polynomials, defined recursively as follows: $H_0(y)=1$, $H_1(y)=y$ and, for $k\ge 2,$

$$H_k(y)=\frac{y{H}_{k-1}(y)-\sqrt{k-1}{H}_{k-2}(y)}{\sqrt{k}}.$$

The corresponding cdf of Y is given by

$$F_Y(y\mid {\psi }_1,{\psi }_2)=\mathsf{\Phi }(y)-\varphi (y){\sum }_{k=1}^4\frac{{\gamma }_k({\psi }_1,{\psi }_2)}{\sqrt{k}}{H}_{k-1}(y),$$

(9)

where we denote ${\gamma }_1({\psi }_1,{\psi }_2)=2{\psi }_1(1+\sqrt{2}{\psi }_2)/{\mathbf{v}}^{\prime }\mathbf{v},$${\gamma }_2({\psi }_1,{\psi }_2)=\sqrt{2}({\psi }_1^2+2{\psi }_2^2+\sqrt{2}{\psi }_2)/{\mathbf{v}}^{\prime }\mathbf{v},$${\gamma }_3({\psi }_1,{\psi }_2)=2\sqrt{3}{\psi }_1{\psi }_2/{\mathbf{v}}^{\prime }\mathbf{v}$ and ${\gamma }_4({\psi }_1,{\psi }_2)=\sqrt{6}{\psi }_2^2/{\mathbf{v}}^{\prime }\mathbf{v}.$ For simplicity, hereafter we write ${\gamma }_j$ instead of ${\gamma }_j({\psi }_1,{\psi }_2)$. It also follows from (8) that m${}_Y={\gamma }_1$ and v${}_Y=\sqrt{2}{\gamma }_2+1-{\gamma }_1^2$. The $\alpha$-VaR of Y is

$${\mathrm{VaR}}_Y(\alpha \mid {\psi }_1,{\psi }_2)=F_Y^{-1}(\alpha \mid {\psi }_1,{\psi }_2),$$

where $F_Y(·)$ is given in (9); there is no closed-form expression for $F_Y^{-1}(·)$, but it can be computed numerically using the procedure described in [28]. Finally, the $\alpha$-ES of Y is

$${\mathrm{ES}}_Y(\alpha \mid {\psi }_1,{\psi }_2)=\frac{1}{\alpha }\mathsf{\Phi }\left({\mathrm{VaR}}_Y(\alpha \mid {\psi }_1,{\psi }_2)\right){\sum }_{k=1}^5{\eta }_k({\psi }_1,{\psi }_2)p_k({\mathrm{VaR}}_Y(\alpha \mid {\psi }_1,{\psi }_2)),$$

where ${\eta }_1({\psi }_1,{\psi }_2)=1-{\gamma }_2/\sqrt{2}+3{\gamma }_4/\sqrt{24},$${\eta }_2({\psi }_1,{\psi }_2)={\gamma }_1-3{\gamma }_3/\sqrt{6},$${\eta }_3({\psi }_1,{\psi }_2)={\gamma }_2/\sqrt{2}-6{\gamma }_4/\sqrt{24},$${\eta }_4({\psi }_1,{\psi }_2)={\gamma }_3/\sqrt{6},$${\eta }_5({\psi }_1,{\psi }_2)={\gamma }_4/\sqrt{24}$, $p_1(y)=-\varphi (y)/\mathsf{\Phi }(y),$$p_2(y)=1-y\varphi (y)/\mathsf{\Phi }(y),$ and $p_k(y)=(k-1)p_{k-2}(y)-y^{k-1}\varphi (y)/\mathsf{\Phi }(y)$ for $k\ge 3.$

2.3. Parametric Distributions

2.3.1. Skewed-t Distribution

There are several equivalent specifications of a skewed-t distribution; here we use the parameterization of [29]. A random variable Y follows a skewed-t distribution with parameter ${\psi }_1$ (skewness parameter) and ${\psi }_2$ (degrees of freedom), where ${\psi }_1\in \left(0,1\right)$ and ${\psi }_2>0$, if its pdf is

$$f_Y(y\mid {\psi }_1,{\psi }_2)=\left\{\begin{array}{cc}{f}_{{\psi }_2}(\frac{y}{2{\psi }_1})\hfill & \mathrm{if}y\le 0,\hfill \\ f_{{\psi }_2}(\frac{y}{2(1-{\psi }_1)})\hfill & \mathrm{if}y>0,\hfill \end{array}\right.$$

where $f_{{\psi }_2}(·)$ denotes the pdf of the Student-t distribution with ${\psi }_2$ degrees of freedom. The corresponding cdf is

$$F_Y(y\mid {\psi }_1,{\psi }_2)=\left\{\begin{array}{cc}2{\psi }_1{F}_{{\psi }_2}(\frac{y}{2{\psi }_1})\hfill & \mathrm{if}y\le 0,\hfill \\ 2(1-{\psi }_1)F_{{\psi }_2}(\frac{y}{2(1-{\psi }_1)})+(2{\psi }_1-1)\hfill & \mathrm{if}y>0,\hfill \end{array}\right.$$

where $F_{{\psi }_2}(·)$ denotes the cdf of the Student-t distribution with ${\psi }_2$ degrees of freedom. When ${\psi }_2>1$ the mean of Y is

$${\mathrm{m}}_Y=\frac{2\sqrt{{\psi }_2}(1-2{\psi }_1)\mathrm{\Gamma }(\frac{{\psi }_2-1}{2})}{\sqrt{\pi }\mathrm{\Gamma }(\frac{{\psi }_2}{2})}.$$

Additionally, if ${\psi }_2>2$ the variance of Y is

$${\mathrm{v}}_Y=\frac{4{\psi }_2(1-3{\psi }_1+3{\psi }_1^2)}{{\psi }_2-2}-{\mathrm{m}}_Y^2.$$

Note that the Student-t distribution is nested in this distribution when ${\psi }_1=1/2$. Also note that the pdf of $(Y-$m${}_Y)/$v${}_Y^{1/2}$ is the same as the pdf in Equation (10) of [17], after reparameterization. The $\alpha$-VaR of Y is

$${\mathrm{VaR}}_Y(\alpha \mid {\psi }_1,{\psi }_2)=\left\{\begin{array}{cc}2{\psi }_1{F}_{{\psi }_2}^{-1}(\frac{\alpha }{2{\psi }_1})\hfill & \mathrm{if}\alpha \le {\psi }_1,\hfill \\ -2(1-{\psi }_1)F_{{\psi }_2}^{-1}(\frac{1-\alpha }{2(1-{\psi }_1)})\hfill & \mathrm{if}\alpha >{\psi }_1.\hfill \end{array}\right.$$

Note that, by the symmetry of $f_{{\psi }_2}(·),$ it follows that $F_{{\psi }_2}^{-1}(\alpha )=-F_{{\psi }_2}^{-1}(1-\alpha )$ for $\alpha \in (0,1).$ Also note that there is no closed-form expression for $F_{{\psi }_2}^{-1}(·)$, but most programming languages include this function. Finally, the $\alpha$-ES of Y is

$${\mathrm{ES}}_Y(\alpha \mid {\psi }_1,{\psi }_2)=\left\{\begin{array}{c}-\frac{4{\psi }_2}{\alpha ({\psi }_2-1)}{\psi }_1^2{f}_{{\psi }_2}(F_{{\psi }_2}^{-1}(\frac{\alpha }{2{\psi }_1}))(1+\frac{F_{{\psi }_2}^{-1}{(\frac{\alpha }{2{\psi }_1})}^2}{{\psi }_2}),\mathrm{if}\alpha \le {\psi }_1,\hfill \\ -\frac{4{\psi }_2{(1-{\psi }_1)}^2}{\alpha ({\psi }_2-1)}\{f_{{\psi }_2}(F_{{\psi }_2}^{-1}(\frac{1-\alpha }{2(1-{\psi }_1)}))(1+\frac{F_{{\psi }_2}^{-1}{(\frac{1-\alpha }{2(1-{\psi }_1)})}^2}{{\psi }_2})-\frac{1-2{\psi }_1}{{(1-{\psi }_1)}^2}{f}_{{\psi }_2}(0)\},\mathrm{if}\alpha >{\psi }_1.\hfill \end{array}\right.$$

2.3.2. Johnson Distribution

We follow here the parameterization of the Johnson distribution described in [30]. A random variable Y follows a Johnson distribution with shape parameters ${\psi }_1$ and ${\psi }_2$, where $-\infty <{\psi }_1<\infty$ and ${\psi }_2>0$, if

$$Y=sinh\left(\frac{W-{\psi }_1}{{\psi }_2}\right),$$

where W is a standard normal random variable, and $sinh(x)=(exp(x)-exp(-x))/2$. The cdf of a random variable with Johnson distribution is

$$F_Y(y\mid {\psi }_1,{\psi }_2)=\mathsf{\Phi }\left({\psi }_1+{\psi }_2{sinh}^{-1}(y)\right),$$

where ${sinh}^{-1}(y)=ln(x+\sqrt{1+x^2}).$ The corresponding pdf is

$$f_Y(y\mid {\psi }_1,{\psi }_2)=\frac{{\psi }_2}{\sqrt{1+y^2}}\varphi \left({\psi }_1+{\psi }_2{sinh}^{-1}(y)\right).$$

The mean of Y is m${}_Y=-exp({\psi }_2^{-2}/2)sinh({\psi }_1/{\psi }_2),$ and its variance is

$${\mathrm{v}}_Y=\frac{1}{2}\left(exp\left({\psi }_2^{-2}\right)-1\right)\left(exp\left({\psi }_2^{-2}\right)cosh\left(\frac{2{\psi }_1}{{\psi }_2}\right)+1\right),$$

where $cosh(x)=(exp(x)+exp(-x))/2$. Finally, the $\alpha$-VaR and the $\alpha$-ES of Y are

$${\mathrm{VaR}}_Y(\alpha \mid {\psi }_1,{\psi }_2)=sinh\left(\frac{{\mathsf{\Phi }}^{-1}(\alpha )-{\psi }_1}{{\psi }_2}\right),$$

$${\mathrm{ES}}_Y(\alpha \mid {\psi }_1,{\psi }_2)=\frac{1}{2\alpha }exp(\frac{{\psi }_2^{-2}}{2})\left[exp(-\frac{{\psi }_1}{{\psi }_2})\mathsf{\Phi }\left({\mathsf{\Phi }}^{-1}(\alpha )-\frac{1}{{\psi }_2}\right)-exp(\frac{{\psi }_1}{{\psi }_2})\mathsf{\Phi }\left({\mathsf{\Phi }}^{-1}(\alpha )+\frac{1}{{\psi }_2}\right)\right].$$

3. Assessing the Performance of VaR and ES Estimates

3.1. Backtesting VaR and ES

To evaluate one-day-ahead VaR/ES forecasts, first we use the backtesting method, which is a formal statistical framework that consists on checking whether actual losses are in line with predicted losses (see [31]). We perform this analysis using a one-day rolling-window methodology. Specifically, given a sample of T daily returns, we divide the sample into two parts: the in-sample period with the first $T_0$ observations, and the out-of-sample period with the remaining $T-T_0$ observations. In our first estimation we use the data from day 1 to day $T_0$ to estimate the model by ML, and then derive the estimates of VaR${}_{T_0+1}(\alpha \mid {\mathcal{F}}_{T_0})$ and ES${}_{T_0+1}(\alpha \mid {\mathcal{F}}_{T_0})$ as described in the previous section. In our second estimation we exclude observation 1 from the estimation sample, and incorporate the observation of day $T_0+1$; thus, we proceed to estimate the model by ML using the data from day 2 to day $T_0+1,$ and then derive the estimates of VaR${}_{T_0+2}(\alpha \mid {\mathcal{F}}_{T_0+1})$ and ES${}_{T_0+2}(\alpha \mid {\mathcal{F}}_{T_0+1})$ as above. We continue in this way until getting VaR and ES estimates for the whole out-of-sample period, i.e., ${\{{\widehat{\mathrm{VaR}}}_t(\alpha \mid {\mathcal{F}}_{t-1})\}}_{t=T_0+1}^T$ and ${\{{\widehat{\mathrm{ES}}}_t(\alpha \mid {\mathcal{F}}_{t-1})\}}_{t=T_0+1}^T$. The accuracy of these sequence of estimates is then analyzed by comparing them with the sequence of actual out-of-sample returns ${\{R_t\}}_{t=T_0+1}^T$, using the procedures that are described below.

We use two procedures for backtesting VaR. First, we apply the unconditional coverage test of [21]. This test is based on the fact that, if the model is correctly specified, then the so-called hit variables $h_t\equiv \mathbb{I}(R_t<$VaR${}_t(\alpha \mid {\mathcal{F}}_{t-1}))$, where $\mathbb{I}(·)$ is the indicator function, are independent Bernoulli random variables, and hence ${\sum }_{t=T_0+1}^T{h}_t$ follows a Binomial distribution Bi$(T-T_0,\alpha )$. The test statistic is

$$L{R}_{\mathrm{UC}}=-2ln\left(\frac{{\alpha }^N{(1-\alpha )}^{T-T_0-N}}{{\widehat{\alpha }}^N{(1-\widehat{\alpha })}^{T-T_0-N}}\right),$$

where $N\equiv {\sum }_{t=T_0+1}^T{\widehat{h}}_t,$ $\widehat{\alpha }\equiv N/(T-T_0)$ and ${\widehat{h}}_t\equiv \mathbb{I}(R_t<{\widehat{\mathrm{VaR}}}_t(\alpha \mid {\mathcal{F}}_{t-1}))$. Under the null hypothesis that the model is correctly specified, the asymptotic distribution of $L{R}_{\mathrm{UC}}$ is ${\chi }_1^2;$ thus, the null hypothesis of correct specification is rejected at the $5\%$ significance level if the sample value of $L{R}_{\mathrm{UC}}$ is above ${\chi }_{1,0.05}^2=3.8415.$ Second, we apply the independence test of [22]. This test is based on the fact that, if the model is correctly specified, then hits are independent over time; hence, if we denote ${\alpha }_{ij}\equiv P(h_{t+1}=j\mid h_t=i)$ for $i,j=0,1$, then ${\alpha }_{i1}$ must be equal to $\alpha ,$ both when $i=0$ and $i=1$, and ${\alpha }_{i0}$ must be equal to $1-\alpha ,$ both when $i=0$ and $i=1$. The test statistic is

$$L{R}_{\mathrm{IND}}=-2ln\left(\frac{{\widehat{\alpha }}^{N_{01}+N_{11}}{(1-\widehat{\alpha })}^{N_{00}+N_{10}}}{{\widehat{\alpha }}_{01}^{N_{01}}{(1-{\widehat{\alpha }}_{01})}^{N_{00}}{\widehat{\alpha }}_{11}^{N_{11}}{(1-{\widehat{\alpha }}_{11})}^{N_{10}}}\right)$$

where $N_{ij}\equiv {\sum }_{t=T_0+1}^{T-1}\mathbb{I}({\widehat{h}}_{t+1}=j)\mathbb{I}({\widehat{h}}_t=i),$ for $i,j=0,1,$${\widehat{\alpha }}_{01}\equiv N_{01}/\left(N_{00}+N_{01}\right)$ and ${\widehat{\alpha }}_{11}\equiv N_{11}/\left(N_{10}+N_{11}\right)$. Under the null hypothesis that the model is correctly specified, the asymptotic distribution of $L{R}_{\mathrm{IND}}$ is also ${\chi }_1^2;$ thus, the null hypothesis of correct specification is rejected at the $5\%$ significance level if the sample value of $L{R}_{\mathrm{IND}}$ is above ${\chi }_{1,0.05}^2=3.8415.$

We also use two procedures for backtesting ES. First, we apply the robust unconditional test of [4]. The test statistic is

$$M{U}_{\mathrm{ES}}=\frac{\sqrt{T-T_0}(\overline{H}(\alpha )-\frac{\alpha }{2})}{\sqrt{\alpha (\frac{1}{3}-\frac{\alpha }{4})+\frac{T-T_0}{T_0}{\widehat{R}}_{\mathrm{ES}}^{\prime }\widehat{\Lambda }{\widehat{R}}_{\mathrm{ES}}}},$$

where $\overline{H}(\alpha )\equiv {(T-T_0)}^{-1}{\sum }_{t=T_0+1}^T{\widehat{H}}_t(\alpha ),$

$${\widehat{H}}_t(\alpha )\equiv \frac{{\widehat{h}}_t}{\alpha }\{\alpha -F_Y({\widehat{\mathrm{m}}}_Y+\frac{{\widehat{\mathrm{v}}}_Y^{1/2}}{{\widehat{\sigma }}_t}(R_t-\widehat{\mu })\mid {\widehat{\psi }}_1,{\widehat{\psi }}_2)\},$$

$\widehat{\Lambda }$ is the $7\times 7$ variance-covariance matrix of the estimates, and ${\widehat{R}}_{\mathrm{ES}}$ is a $7\times 1$ matrix whose precise definition is given in page 955 of [4]. Under the null hypothesis that the model is correctly specified, the asymptotic distribution of $M{U}_{\mathrm{ES}}$ is standard normal; thus, the null hypothesis of correct specification is rejected at the $5\%$ significance level if the absolute value of the sample value of $M{U}_{\mathrm{ES}}$ is above $z_{0.025}=1.96$. Second, we apply the robust conditional test of [4]. For a given $m\in \mathbb{N},$ the test statistic is

$$M{C}_{\mathrm{ES}}(m)=(T-T_0){\widehat{\rho }}_{(m)}^{\prime }{\widehat{\Omega }}^{-1}{\widehat{\rho }}_{(m)}$$

where ${\widehat{\rho }}_{(m)}={\left({\widehat{\rho }}_1,\dots ,{\widehat{\rho }}_m\right)}^{\prime },$${\widehat{\rho }}_j={\widehat{\gamma }}_j/{\widehat{\gamma }}_0$ for $j=0,1,\cdots ,m,$

$${\widehat{\gamma }}_j=\frac{1}{T-T_0-j}{\sum }_{t=T_0+1}^{T-j}({\widehat{H}}_{t+j}(\alpha )-\frac{\alpha }{2})({\widehat{H}}_t(\alpha )-\frac{\alpha }{2}),$$

$\widehat{\Omega }$ is an $m\times m$ matrix whose $ij$th element is ${\widehat{\Omega }}_{ij}=\mathbb{I}(i=j)+((T-T_0)/T_0){\widehat{R}}_j^{\prime }\widehat{\Lambda }{\widehat{R}}_j,$ and ${\widehat{R}}_j$ is a $7\times 1$ matrix whose precise definition is given in page 955 of [4]. Under the null hypothesis that the model is correctly specified, the asymptotic distribution of $M{C}_{\mathrm{ES}}(m)$ is ${\chi }_m^2$; thus, the null hypothesis of correct specification is rejected at the $5\%$ significance level if the sample value of $M{C}_{\mathrm{ES}}(m)$ is above ${\chi }_{m,0.05}^2$.

3.2. Assessment of Performance with Loss Functions

The main goal of the backtesting procedures described in the previous subsection is to determine if a model provides reliable VaR and ES estimates. However, it is often the case that the null hypothesis of correct specification is not rejected for several models; hence, a criterion to select one model among those that have not been rejected with backtesting techniques is required. A frequently used criterion is based on the so-called loss functions (LF). This approach was introduced in [32], and its aim is to calculate the size of noncovered losses by measuring the distance between a risk measure for period t, say RiskM${}_t$, computed with the information available up to period $t-1$, and the observed returns for that period $R_t.$ Following [23], the loss functions considered in this paper have the form

$$L(R_t,{\mathrm{RiskM}}_t)=\left\{\begin{array}{cc}f(R_t,{\mathrm{RiskM}}_t)\hfill & \mathrm{if}{R}_t<{\mathrm{RiskM}}_t,\hfill \\ 0\hfill & \mathrm{if}{R}_t\ge {\mathrm{RiskM}}_t.\hfill \end{array}\right.$$

(10)

Note that this type of loss function only pays attention to the magnitude of the hit when it actually occurs. In our empirical analysis we analyze four risk measures: VaR${}_t(0.05\mid {\mathcal{F}}_{t-1}),$ VaR${}_t(0.025\mid {\mathcal{F}}_{t-1}),$ ES${}_t(0.05\mid {\mathcal{F}}_{t-1})$ and ES${}_t(0.025\mid {\mathcal{F}}_{t-1}).$ As regards the function $f,$ we will use the following alternatives:

$$\begin{array}{c}{f}_1(R_t,{\mathrm{RiskM}}_t)=1+{(R_t-{\mathrm{RiskM}}_t)}^2{}_{}\hfill \\ f_2(R_t,{\mathrm{RiskM}}_t)={(R_t-{\mathrm{RiskM}}_t)}^2{}_{}\hfill \\ f_3(R_t,{\mathrm{RiskM}}_t)=\left|1-\left|\frac{R_t}{{\mathrm{RiskM}}_t}\right|\right|\hfill \\ f_4(R_t,{\mathrm{RiskM}}_t)=\frac{{(\left|R_t\right|-\left|{\mathrm{RiskM}}_t\right|)}^2}{\left|{\mathrm{RiskM}}_t\right|}\hfill \\ f_5(R_t,{\mathrm{RiskM}}_t)=\left|R_t-{\mathrm{RiskM}}_t\right|\hfill \end{array}$$

(11)

Function $f_1$ is used in [32], function $f_2$ is used in [33], and functions $f_3,$$f_4,$$f_5$ are used in [34]. Note that both $f_1$ and $f_2$ penalize large hits more than small ones, whereas the remaining functions stress the importance of uncovered losses but taking also into account their relative sizes.

For a given risk measure and a given loss function $f_j$, the overall performance of an estimate of the risk measure, say $\widehat{\mathrm{RiskM}}$, can be found by computing the average loss across the out-of-sample period, that is,

$${\overline{L}}_j(\widehat{\mathrm{RiskM}})=\frac{{\sum }_{t=T_0+1}^T{L}_j(R_t,{\widehat{\mathrm{RiskM}}}_t)}{T-T_0},$$

(12)

where $L_j(R_t,{\widehat{\mathrm{RiskM}}}_t)$ denotes the loss that is found according to (10), when function $f_j$ is used as $f.$ When comparing the performance of different estimates of the risk measure RiskM, the one that minimizes the average loss ${\overline{L}}_j(\widehat{\mathrm{RiskM}})$ should be preferred.

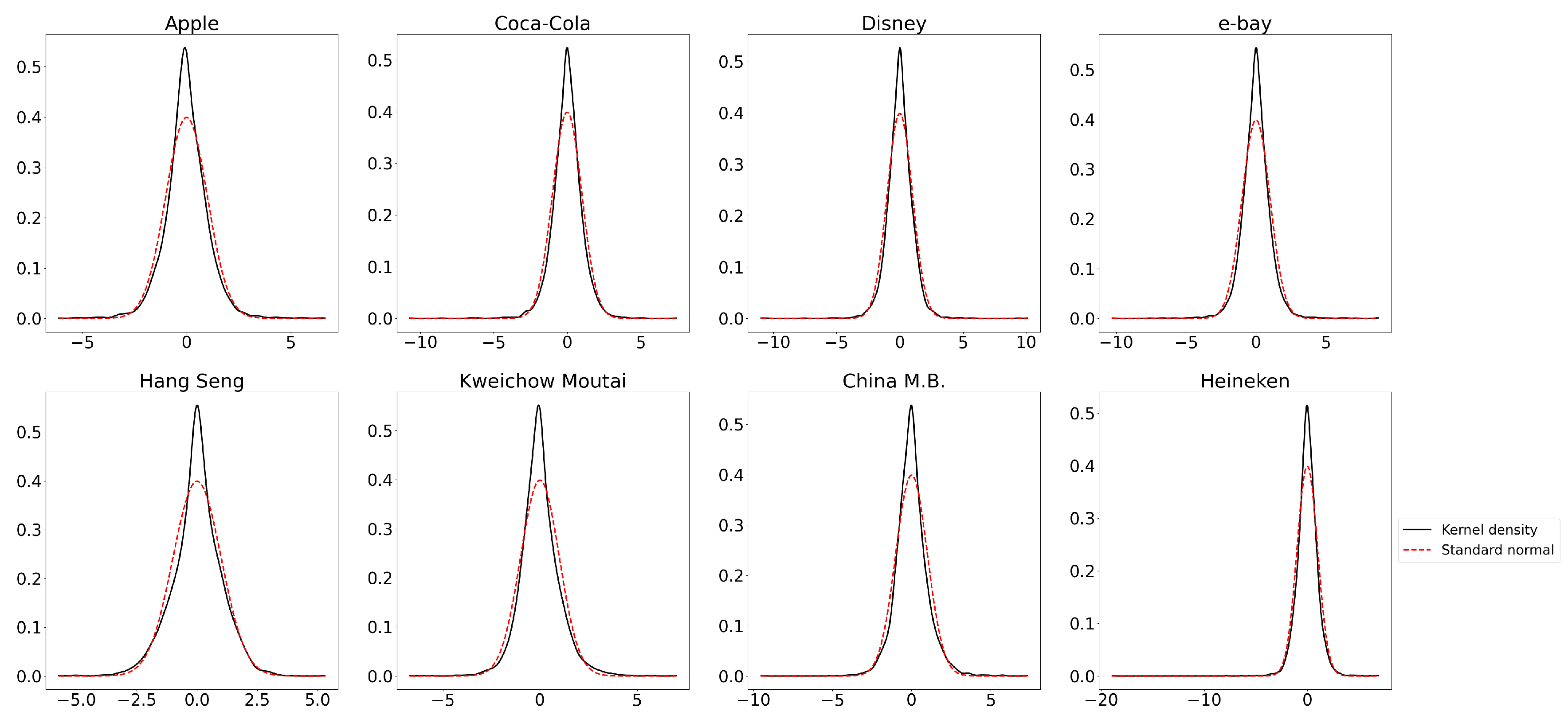
4. Empirical Results

We collect daily log-returns of several indexes, stocks and others extracted from Datastream and Yahoo Finance. Log-returns are obtained by taking the logarithmic differences of closing daily prices, i.e., $R_t=(ln(P_t)-ln(P_{t-1}))\times 100$, where $P_t$ denotes the price of the stock at time t. The selection of series is made with the aim of encompassing several markets across the world and stocks of different countries and sectors. As described in Section 3.1, the full data period of size T is divided into the in-sample period (first $T_0$ observations) and the out-of-sample period (remaining $T-T_0$ observations). The period and sample size vary across series; the number of observations in the in-sample period is $T_0=2000$ in all cases; thus, the out-of-sample period is approximately 60% of the total sample in most cases. Information about the data, including descriptive statistics, period and in-sample period, is reported in

Table 1. Descriptive Statistics for Daily Log-Returns.

Series	Mean	Std.Dev.	Max	Min	Skew.	Kurt.	Period	T
S&P500	0.02	1.16	10.96	−9.47	−0.23	9.48	11/10/2000–10/12/2019	5000
Euro Stoxx 50	−0.01	1.42	10.44	−9.01	−0.05	5.24	11/10/2000–10/12/2019	5000
BRBOVES	0.04	1.69	13.68	−12.10	−0.12	4.62	11/10/2000–10/12/2019	5000
NASCOMP	0.02	1.46	13.25	−9.59	0.08	6.83	11/10/2000–10/12/2019	5000
Hang Seng	0.01	1.39	13.40	−13.59	−0.04	9.21	11/10/2000–10/12/2019	5000
DAX	0.02	1.56	12.37	−9.60	−0.11	5.39	11/10/2000–10/12/2019	5000
FTSE100	0.00	1.33	12.22	−11.51	−0.25	9.95	11/10/2000–10/12/2019	5000
Euro to US $	0.00	0.59	3.84	−4.62	−0.10	2.78	11/10/2000–10/12/2019	5000
China Merch. Bank	0.05	2.15	9.60	−14.27	0.17	4.07	10/04/2002−10/12/2019	4353
Kweichow Moutai	0.12	2.05	9.56	−15.21	0.34	3.60	02/01/2002−10/12/2019	4421
Amazon.com	0.08	2.28	29.62	−28.46	0.54	14.83	11/10/2000–10/12/2019	5000
Apple	0.10	1.17	13.02	−19.75	−0.23	6.36	11/10/2000–10/12/2019	5000
Coca−Cola	0.01	1.79	13.00	−10.60	−0.14	11.02	11/10/2000–10/12/2019	5000
Walt Disney	0.03	1.79	14.82	−20.29	−0.21	11.00	11/10/2000–10/12/2019	5000
e−bay	0.03	2.50	26.53	−23.04	0.10	12.74	11/10/2000–10/12/2019	5000
Heineken	0.01	1.44	9.57	−21.53	−0.74	14.39	29/06/2000–10/12/2019	5000

. Note that the end of the sample period is always December 2019, in order to exclude the COVID-19 period.

In order to examine how sensitive parameter estimates are to the distribution of the errors, first we report the estimates that are obtained with each distribution using the in-sample period of one of the series, namely the Euro Stoxx 50. As a reference, we also report the estimates that are obtained when we assume that the distribution of the errors $Z_t$ is standard normal. These results can be found in

Table 2. Parameter Estimates of Euro Stoxx 50 (In-Sample Period *).

	CF	GC	Skewed-t	Johnson	Normal
$b_0$	0.0240 (0.0049)	0.0239 (0.0064)	0.0245 (0.0044)	0.0239 (0.0086)	0.0245 (0.0127)
$b_1$	0.7575 (0.0433)	0.7548 (0.0444)	0.7541 (0.0296)	0.7577 (0.0473)	0.7574 (0.1120)
$b_2$	0.0432 (0.0031)	0.0427 (0.0031)	0.0443 (0.0074)	0.0432 (0.0031)	0.0421 (0.0413)
c	2.0919 (0.2144)	2.1235 (0.2214)	2.0882 (0.2612)	2.0926 (0.2588)	2.1294 (1.1149)
$\mu$	−0.0184 (0.0248)	−0.0175 (0.0421)	−0.0244 (0.0219)	−0.0182 (0.0790)	−0.0234 (0.0350)
${\psi }_1$	−0.2613 (0.0593)	0.3873 (0.1484)	0.5695 (0.0158)	1.6762 (3.2153)
${\psi }_2$	0.3093 (0.1664)	0.1628 (0.0438)	25.7810 (14.2877)	4.2613 (4.0214)
Sample skewness of ${\widehat{Z}}_t$	−0.2933	−0.2933	−0.2941	−0.2933	−0.2923
Estimated skewness based on ${\widehat{\psi }}_1,{\widehat{\psi }}_2$	−0.2754	−0.2423	−0.2548	−0.2776
Sample kurtosis of ${\widehat{Z}}_t$	3.4112	3.4108	3.4152	3.4114	3.4070
Estimated kurtosis based on ${\widehat{\psi }}_1,{\widehat{\psi }}_2$	3.3374	3.3301	3.3275	3.3434

Note: Standard errors in parentheses. * In-sample period is from 11 October 2000 to 10 June 2008 (2000 observations).

.

The estimates of the unconditional mean parameter $\mu$ and the conditional variance parameters, $b_0$, $b_1$, $b_2$, c, are similar across distributions. The shape parameters ${\psi }_1$ and ${\psi }_2$ are not directly comparable across distributions. These parameters are related to the skewness and kurtosis of the distribution; thus, we compare the estimates of skewness and kurtosis that are found with each distribution using two procedures: first, by computing the sample skewness and sample kurtosis of the estimated errors ${\widehat{Z}}_t$; second, by computing the ML estimates of the skewness and kurtosis coefficient (the formulas that relate these coefficients with ${\psi }_1$ and ${\psi }_2$ in each distribution can be found in the references that are included in Section 2). The estimates of skewness and kurtosis across distributions are similar; in all cases left skewness and leptokurtosis are observed. In order to visually check what type of distribution could be more appropriate, in Figure 1 and Figure 2 we show kernel density estimates obtained with the estimated errors ${\widehat{Z}}_t$ of the normal model, together with the standard normal pdf. In all cases the kernel density estimates exhibit a much higher kurtosis than the standard normal pdf; additionally, a slight left skewness is also observed in most cases. These plots suggest that the normal model is not appropriate.

For each returns series described in Table 1, the estimates of VaR and ES for all distributions (including the standard normal) are backtested using the procedures described in Section 3.1. Specifically, given a coverage level $\alpha ,$ we compute the p-values that are obtained when backtesting VaR$(\alpha )$ with the test statistics $L{R}_{\mathrm{UC}}$ and $L{R}_{\mathrm{IND}}$, and we consider that the model is “successfully backtested for VaR$(\alpha )$” if both p-values are greater than 0.05; the results that are obtained when performing this exercise for coverage levels $\alpha =0.05$ and $\alpha =0.025$ are reported in

Table 3. Backtesting VaR at the 5% Significance Level.

	Coverage Level $\mathit{\alpha }=0.05$					Coverage Level $\mathit{\alpha }=0.025$
	CF	GC	Skewed-t	Johnson	Normal	CF	GC	Skewed-t	Johnson	Normal
S&P500	1	1	1	1	1	1	1	1	1	0
Euro Stoxx 50	1	1	1	1	1	1	1	1	1	0
BRBOVES	1	1	1	1	1	1	1	1	1	1
NASCOMP	1	1	1	1	1	1	1	1	1	0
Hang Seng	1	1	1	1	1	1	1	1	1	0
DAX	1	1	1	1	1	1	1	1	1	0
FTSE100	1	1	1	0	1	1	1	1	1	0
Euro to US $	1	1	1	1	1	1	1	1	1	1
China Merch. Bank	1	1	1	1	0	1	1	1	1	1
Kweichow Moutai	1	0	1	1	0	1	1	1	1	1
Amazon.com	1	0	0	0	0	1	0	0	1	0
Apple	1	1	1	1	0	1	1	1	1	1
Coca-Cola	1	1	0	0	1	0	0	1	1	1
Walt Disney	1	1	1	1	0	1	1	1	1	1
e-bay	0	1	1	1	0	1	1	1	1	1
Heineken	1	1	1	1	0	1	0	1	1	1

Note: A value of “1” means that the corresponding model is succesfully backtested; otherwise, the value is “0”.

. Similarly, we compute the p-values that are obtained when backtesting ES$(\alpha )$ with the statistics $M{U}_{\mathrm{ES}}$ and $M{C}_{\mathrm{ES}}(1),$ and we consider that the model is “successfully backtested for ES$(\alpha )$” if both p-values are greater than 0.05; the results that are obtained when performing this exercise for coverage levels $\alpha =0.05$ and $\alpha =0.025$ are reported in

Table 4. Backtesting ES at the 5% Significance Level.

	Coverage Level $\mathit{\alpha }=0.05$					Coverage Level $\mathit{\alpha }=0.025$
	CF	GC	Skewed-t	Johnson	Normal	CF	GC	Skewed-t	Johnson	Normal
S&P500	1	1	1	1	0	1	1	1	1	0
Euro Stoxx 50	1	1	1	1	0	1	1	1	1	0
BRBOVES	1	1	1	1	1	1	1	1	1	1
NASCOMP	1	1	1	1	0	1	1	1	1	0
Hang Seng	1	1	1	1	0	1	0	1	1	0
DAX	1	1	1	1	0	1	1	1	1	0
FTSE100	1	0	1	1	0	1	1	0	1	0
Euro to US $	1	1	1	1	1	1	1	1	1	1
China Merch. Bank	1	0	1	1	0	1	1	1	1	1
Kweichow Moutai	1	1	1	1	0	1	1	1	1	0
Amazon.com	1	0	0	1	0	1	1	1	1	1
Apple	1	1	1	1	1	1	1	1	1	1
Coca-Cola	1	1	1	1	1	1	1	1	1	0
Walt Disney	1	1	1	1	1	1	1	1	1	0
e-bay	1	1	1	1	1	1	1	1	1	1
Heineken	1	0	1	1	1	1	0	1	1	0

Note: A value of “1” means that the corresponding model is succesfully backtested; otherwise, the value is “0”.

.

When backtesting VaR, the normal distribution is successfully backtested only in 18 cases out of the 32 analyses that are carried out with it. The other four distributions perform much better, as they are only rejected in two cases (CF distribution), three cases (skewed-t and Johnson distributions) or five cases (GC distribution). Also note that, when comparing the results of VaR(0.05) and VaR(0.025), there are not big differences between them, except in the Johnson distribution (which fails in three cases when $\alpha =0.05$, but is always successfully backtested when $\alpha =0.025$). When backtesting ES, the normal distribution performs even worse, as it is successfully backtested only in 13 cases. The other four distributions perform much better, but some differences are observed among them: the CF and the Johnson distributions are always successfully backtested and the skewed-t distribution is only rejected in two cases; however, the GC distribution is rejected in six cases. Also note that, in terms of performance of the different distributions, the results for ES(0.05) and ES(0.025) are completely similar. It is also worth emphasizing that there are two cases (FTSE100 and Heineken with the GC model) that are successfully backtested for VaR but not for ES when coverage level is 0.05, and two other cases (Hang Seng with the GC model and FTSE100 with the skewed-t model) in which this also happens when coverage level is 0.025; note that this may happen when the model does not appropriately capture the behavior at the extreme left tail. Similar cases have also been reported, e.g., in Table 7 of [27], and in Table 2 of [35] (when analyzing FTSE100 with their statistic $T_n$.).

To sum up, the backtesting results suggest that the standard normal distribution is clearly outperformed by all four two-parameter distributions, but these results shed no clear light on whether the distributions based on polynomial expansions outperform the distributions based on parametric densities.

We proceed then to comparatively analyze the performance of the four two-parameter distributions using loss functions. When using several loss functions, it may happen that the best model according to one of the loss functions is not the same as the best model according to another loss function. A possible way to reconcile all the results is to use the sum of all loss functions and then consider that the best model is the one with lowest sum; this is, for example, the approach followed in [23]. Instead, here we will only perform comparisons between two models (first between the two polynomial expansions, second between the two parametric models, and third between the best ones in the first and second comparisons); for this reason, in each case we decide to consider that the best model is the one that yields lower loss functions for most of the five loss functions described in (11), and thus we avoid that a bad performance with one of the loss functions is decisive in the comparison. More specifically, for each of our 16 return series and for each of our 4 risk measures (that is, 64 cases), we perform the comparison of models in this way: (i) we define the “best polynomial expansion” (BPE) as follows: if neither the GC nor the CF distributions have been successfully backtested for that risk measure, we consider that there is no BPE; if one of these two distributions is successfully backtested but the other is not, then the one that is successfully backtested is considered as the BPE; and when both the CG and the CF distributions are successfully backtested, we compute the average loss functions ${\overline{L}}_j(\widehat{\mathrm{RiskM}})$ defined in (12), for $j=1,\cdots ,5,$ with each distribution, and the one that yields lower values for most of these five loss measures is considered as the BPE; (ii) we define the “best parametric density” (BPD) by comparing the skewed-t distribution and the Johnson distribution in the same way as the GC and CF distributions are compared; (iii) finally, we compare the BPE and the BPD using the median of the five relative differences (in percentage) between one and the other, that is

$$\mathrm{Median}\mathrm{of}\mathrm{Relat}.\mathrm{Diff}.=\mathrm{Median}\{100\times \frac{{\overline{L}}_j{(\widehat{\mathrm{RiskM}})}_{\mathrm{BPD}}-{\overline{L}}_j{(\widehat{\mathrm{RiskM}})}_{\mathrm{BPE}}}{{\overline{L}}_j{(\widehat{\mathrm{RiskM}})}_{\mathrm{BPD}}},\mathrm{for}j=1,\cdots ,5\},$$

Note that this value gives us with a measure of the relative gain obtained by using a polynomial expansion instead of a parametric density: a positive (negative) value tells us how much better (worse) the BPE is with respect to the BPD, in percentage. To clarify matters, in the first analysis that we perform, i.e., when analyzing the estimation of VaR$(0.05)$ for S&P500, all four distributions are successfully backtested. The average loss functions when using the GC distribution are ${\overline{L}}_1=0.1023,$ ${\overline{L}}_2=0.0543,$${\overline{L}}_3=0.02102,$${\overline{L}}_4=0.02704$ and ${\overline{L}}_5=0.03483,$ and four of these values (all but ${\overline{L}}_2$) are lower than the similar values that are obtained with the CF distribution; hence, the GC distribution is the BPE. The average loss functions when using the skewed-t distribution are ${\overline{L}}_1=0.10161,$${\overline{L}}_2=0.05027,$${\overline{L}}_3=0.02181,$${\overline{L}}_4=0.02654$ and ${\overline{L}}_5=0.0343,$ and all of them are lower than the similar values that are obtained with the Johnson distribution; hence the skewed-t is the BPD. And the median of the five relative differences between the GC distribution and the skewed-t distribution is $100\times ({\overline{L}}_{5,\text{Skewed-t}}-{\overline{L}}_{5,\mathrm{GC}})/{\overline{L}}_{5,\text{Skewed-t}}=-1.55\%,$ that is, in this case using a polynomial expansion yields slightly worse results than using a parametric density.

Table 5. Comparison of Distributions with Loss Functions: VaR.

	VaR$(0.05)$			VaR$(0.025)$
	$\begin{array}{c}\mathbf{Best}\\ \mathbf{Polynomial}\\ \mathbf{Expan}.(\mathbf{1})\end{array}$	$\begin{array}{c}\mathbf{Best}\\ \mathbf{Parametric}\\ \mathbf{Density}(\mathbf{2})\end{array}$	$\begin{array}{c}\mathbf{Median}\mathbf{of}\\ \mathbf{Relat}.\mathbf{Diff}.*\\ [(\mathbf{1})-(\mathbf{2})]/(\mathbf{2})\end{array}$	$\begin{array}{c}\mathbf{Best}\\ \mathbf{Polynomial}\\ \mathbf{Expan}.(\mathbf{1})\end{array}$	$\begin{array}{c}\mathbf{Best}\\ \mathbf{Parametric}\\ \mathbf{Density}(\mathbf{2})\end{array}$	$\begin{array}{c}\mathbf{Median}\mathbf{of}\\ \mathbf{Relat}.\mathbf{Diff}.*\\ [(\mathbf{1})-(\mathbf{2})]/(\mathbf{2})\end{array}$
S&P500	GC	Skewed-t	$-1.55\%$	GC	Skewed-t	$3.11\%$
Euro Stoxx 50	CF	Skewed-t	$-0.28\%$	CF	Johnson	$0.63\%$
BRBOVES	CF	Johnson	$0.50\%$	CF	Johnson	$0.63\%$
NASCOMP	GC	Skewed-t	$-0.61\%$	GC	Johnson	$5.51\%$
Hang Seng	GC	Johnson	$5.37\%$	CF	Johnson	$2.43\%$
DAX	CF	Johnson	$0.73\%$	CF	Johnson	$0.95\%$
FTSE100	CF	Skewed-t	$0.49\%$	CF	Johnson	$0.85\%$
Euro to US $	GC	Skewed-t	$-3.40\%$	CF	Skewed-t	$-3.31\%$
China Merch. Bank	GC	Johnson	$14.25\%$	CF	Johnson	$3.18\%$
Kweichow Moutai	CF	Johnson	$2.97\%$	CF	Johnson	$5.58\%$
Amazon.com	CF	— **	—	CF	Johnson	$3.81\%$
Apple	CF	Johnson	$1.18\%$	CF	Johnson	$1.25\%$
Coca-Cola	CF	— **	—	— **	Johnson	—
Walt Disney	CF	Johnson	$1.31\%$	CF	Johnson	$1.49\%$
e-bay	GC	Johnson	$-3.07\%$	CF	Johnson	$1.68\%$
Heineken	CF	Johnson	$1.85\%$	CF	Johnson	$2.50\%$

Note: Only distributions that are “sucessfully backtested“ are considered (excluding the normal). * A positive sign means that the best polynomial expansion performs better (has lower median loss) than the best parametric density. ** In this case no distribution of this type is sucessfully backtested.

reports the results that are found when performing this analysis for VaR$(0.05)$ and Var$(0.025),$ and

Table 6. Comparison of Distributions with Loss Functions: ES.

	ES$(0.05)$			ES$(0.025)$
	$\begin{array}{c}\mathbf{Best}\\ \mathbf{Polynomial}\\ \mathbf{Expan}.(\mathbf{1})\end{array}$	$\begin{array}{c}\mathbf{Best}\\ \mathbf{Parametric}\\ \mathbf{Density}(\mathbf{2})\end{array}$	$\begin{array}{c}\mathbf{Median}\mathbf{of}\\ \mathbf{Relat}.\mathbf{Diff}.*\\ [(\mathbf{1})-(\mathbf{2})]/(\mathbf{2})\end{array}$	$\begin{array}{c}\mathbf{Best}\\ \mathbf{Polynomial}\\ \mathbf{Expan}.(\mathbf{1})\end{array}$	$\begin{array}{c}\mathbf{Best}\\ \mathbf{Parametric}\\ \mathbf{Density}(\mathbf{2})\end{array}$	$\begin{array}{c}\mathbf{Median}\mathbf{of}\\ \mathbf{Relat}.\mathbf{Diff}.*\\ [(\mathbf{1})-(\mathbf{2})]/(\mathbf{2})\end{array}$
S&P500	GC	Skewed-t	$-3.42\%$	CF	Skewed-t	$-4.00\%$
Euro Stoxx 50	CF	Johnson	$-0.20\%$	CF	Johnson	$-1.18\%$
BRBOVES	CF	Johnson	$-0.03\%$	CF	Johnson	$-0.45\%$
NASCOMP	CF	Johnson	$-0.74\%$	CF	Johnson	$-1.77\%$
Hang Seng	CF	Johnson	$1.19\%$	CF	Johnson	$0.58\%$
DAX	CF	Johnson	$0.10\%$	CF	Johnson	$-0.34\%$
FTSE100	CF	Johnson	$0.09\%$	CF	Johnson	$-0.50\%$
Euro to US $	CF	Johnson	$1.13\%$	CF	Skewed-t	$-9.38\%$
China Merch. Bank	CF	Skewed-t	$-2.32\%$	GC	Skewed-t	$2.39\%$
Kweichow Moutai	CF	Skewed-t	$1.69\%$	CF	Skewed-t	$-0.86\%$
Amazon.com	CF	Johnson	$0.65\%$	CF	Skewed-t	$-7.03\%$
Apple	CF	Johnson	$-0.42\%$	CF	Johnson	$-1.71\%$
Coca-Cola	CF	Johnson	$-0.25\%$	CF	Skewed-t	$-2.94\%$
Walt Disney	CF	Johnson	$-0.02\%$	GC	Johnson	$2.41\%$
e-bay	CF	Johnson	$0.18\%$	CF	Johnson	$-1.21\%$
Heineken	CF	Skewed-t	$0.23\%$	CF	Skewed-t	$-3.27\%$

Note: Only distributions that are “sucessfully backtested” are considered (excluding the normal). * A positive sign means that the best polynomial expansion performs better (has lower median loss) than the best parametric density.

reports similar results when performing this analysis for ES$(0.05)$ and ES$(0.025).$

The results in Table 5 show that the polynomial expansions typically outperform the parametric densities when estimating VaR: the polynomial expansions are preferred in 25 out of the 32 analysis that are performed. More specifically, the CF distribution is clearly the dominant one: when estimating VaR$(0.025)$, it is the preferred one in 12 cases (in the other 4 cases the preferred model is twice the GC model, and once each one of the parametric densities); when estimating VaR$(0.05),$ the CF distribution still continues to be the preferred one in 9 cases (in the other 7 cases the preferred model is four times the skewed-t distribution, twice the GC distribution and once the Johnson distribution). However, the results in Table 5 also show that the gain by using a polynomial expansion instead of a parametric density is modest: the values of our measure of the relative difference between the BPE and the BPD are within the interval $[-4\%,$$6\%]$ in all but one of the 29 comparisons that are made, and most of the times (in 19 cases) the absolute value of the relative difference is below $3\%.$

The results in Table 6 show a different picture when estimating ES. Parametric densities outperform polynomial expansions in 21 out of the 32 analysis that are performed. More specifically, the Johnson distribution is now the dominant one, but the results are much less clear-cut than those of Table 5. In fact, when estimating ES$(0.05)$, in 8 cases the BPE outperforms the BPD (and in those 8 cases the CF distribution is the BPE), and in 8 cases the BPD outperforms the BPE (and in 6 of these cases the Johnson distribution is the BPD). When estimating ES(0.025) there is more evidence of a better performance of the BPD, as it outperforms the BPE in 13 cases (and in 7 of these cases the Johnson distribution is the BPD). However, it is possibly more important to emphasize that now the differences in performance are even lower than those observed in Table 5: the values of our measure of the relative difference between the BPE and the BPD are within the interval $[-4\%,$$3\%]$ in all but two of the 32 comparisons that are made, and most of the times (in 23 cases) the absolute value of the relative difference is below $2\%.$

To sum up, the distributions based on polynomial expansions (specifically, the CF distribution) outperform the parametric distributions that we consider when the risk measure of interest is VaR, but if our interest lies on the estimation of ES the parametric distributions (specifically, the Johnson distribution) provide somewhat better results than the polynomial expansions that we consider. In any case, the relative gains of using one approach instead of the other are modest, especially when estimating ES.

5. Concluding Remarks

We study the performance of alternative models for estimating the VaR and the ES of daily returns, using both backtesting tests and loss functions to rank the candidate models. All the models we consider specify a NGARCH structure for the conditional variance with constant conditional mean, but differ in the distribution assumed for the standardized errors, $Z_t$; more specifically, we examine (i) distributions based on polynomial expansions (Cornish-Fisher and Gram-Charlier), and (ii) well-known parametric distributions (skewed-t and Johnson distributions). We employ traditional tests for backtesting VaR, see [21,22], and the approach of cumulative violations proposed in [4] for backtesting ES.

The datasets we use include stock returns, indexes and exchange rates, and cover markets from around the world. The coverage levels considered here are 5% and 2.5%, which are typical values employed by regulators and risk managers in practice. The first stage of our analysis, based on the backtesting approach, provides evidence that polynomial expansions are as good as parametric densities to generate statistically correct VaR/ES estimates at both coverage levels; it also shows that the standard normal density is not appropriate in most cases. A second stage analysis, based on the use of loss function, is implemented for those successfully backtested VaR/ES models, in order to rank the models and examine whether or not polynomial expansions yield better estimates than parametric densities. The conclusion of this analysis is that polynomial expansions (specifically, the Cornish-Fisher one) usually outperform parametric densities in VaR estimation, but parametric densities (specifically, the Johnson density) slightly outperform polynomial expansions in ES estimation. However, the gains of using one approach or the other are modest, especially in the case of ES estimation.

Several interesting avenues for further research are as follow: First, examining whether an increase in the number of parameters would favor one of the two approaches over the other; this type of analysis should consider, for example, the three-parameter generalization of the Student-t density proposed in [36], or the higher-order GC expansion considered in [37]. Second, including in the analysis polynomial expansions based on alternative densities to the normal that yield closed-form expressions for ES, see, e.g., [38] for the case of the Student-t, or [39] for the case of hyperbolic secant and logistic densities. Third, extending our analysis by considering the use of joint scoring functions for VaR and ES and intraday data, in the spirit of [40].