Global Stability for a Diffusive Infection Model with Nonlinear Incidence
Abstract
1. Introduction
2. Dynamical Behaviors of System (4)
2.1. Positivity and Boundedness of Solutions
2.2. Existence of Equilibria
- (1)
- There is a unique infection-free equilibrium , when .
- (2)
- There is a unique infection equilibrium without immunity besides , when .
- (3)
- There is a unique infection equilibrium with immunity besides and , when .
2.3. Global Asymptotic Stability
3. Dynamics Behavior of System (9)
Global Stability
- (1)
- If , then implies that , , , .
- (2)
- If , then implies that , , From system (9), we obtain , .
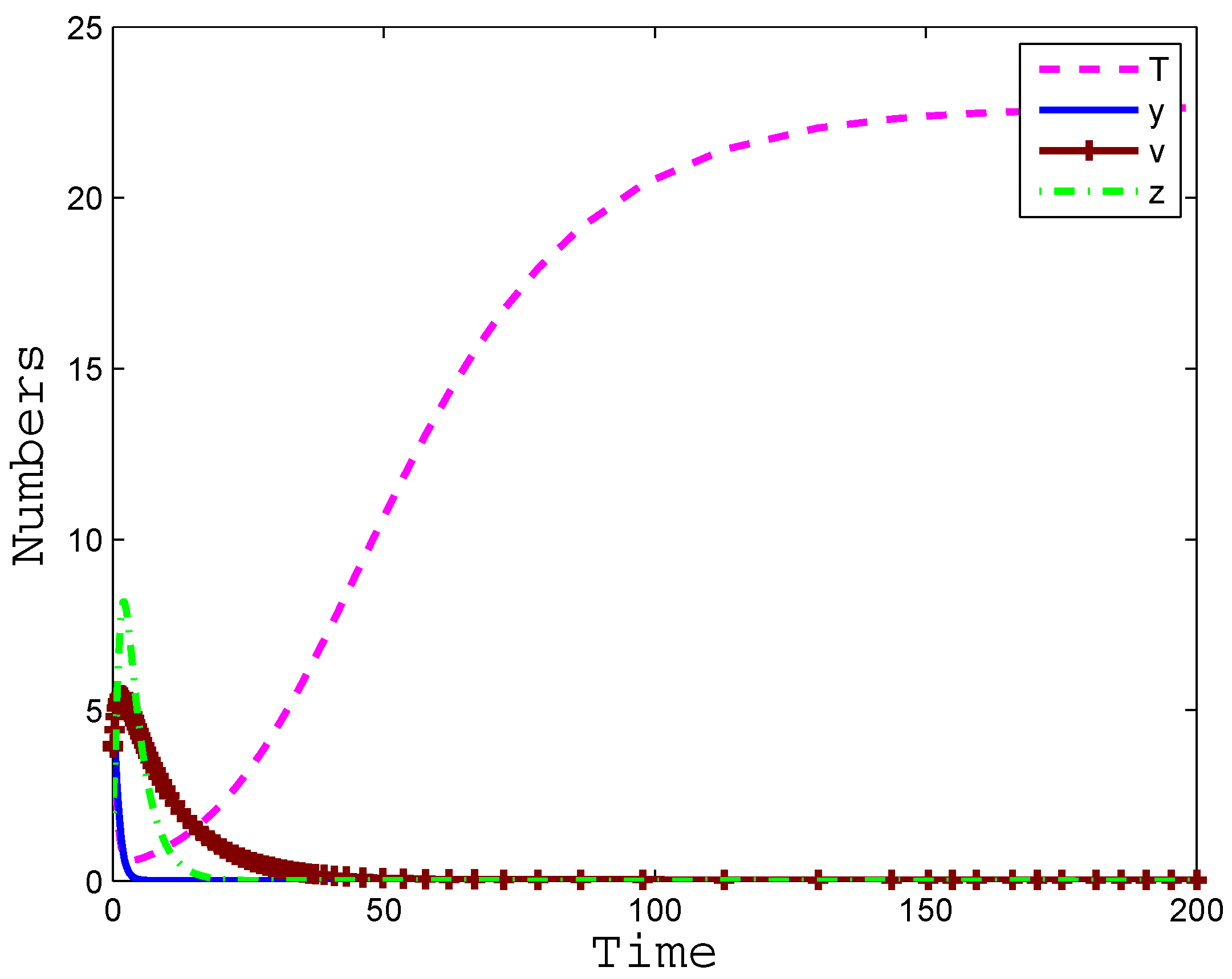
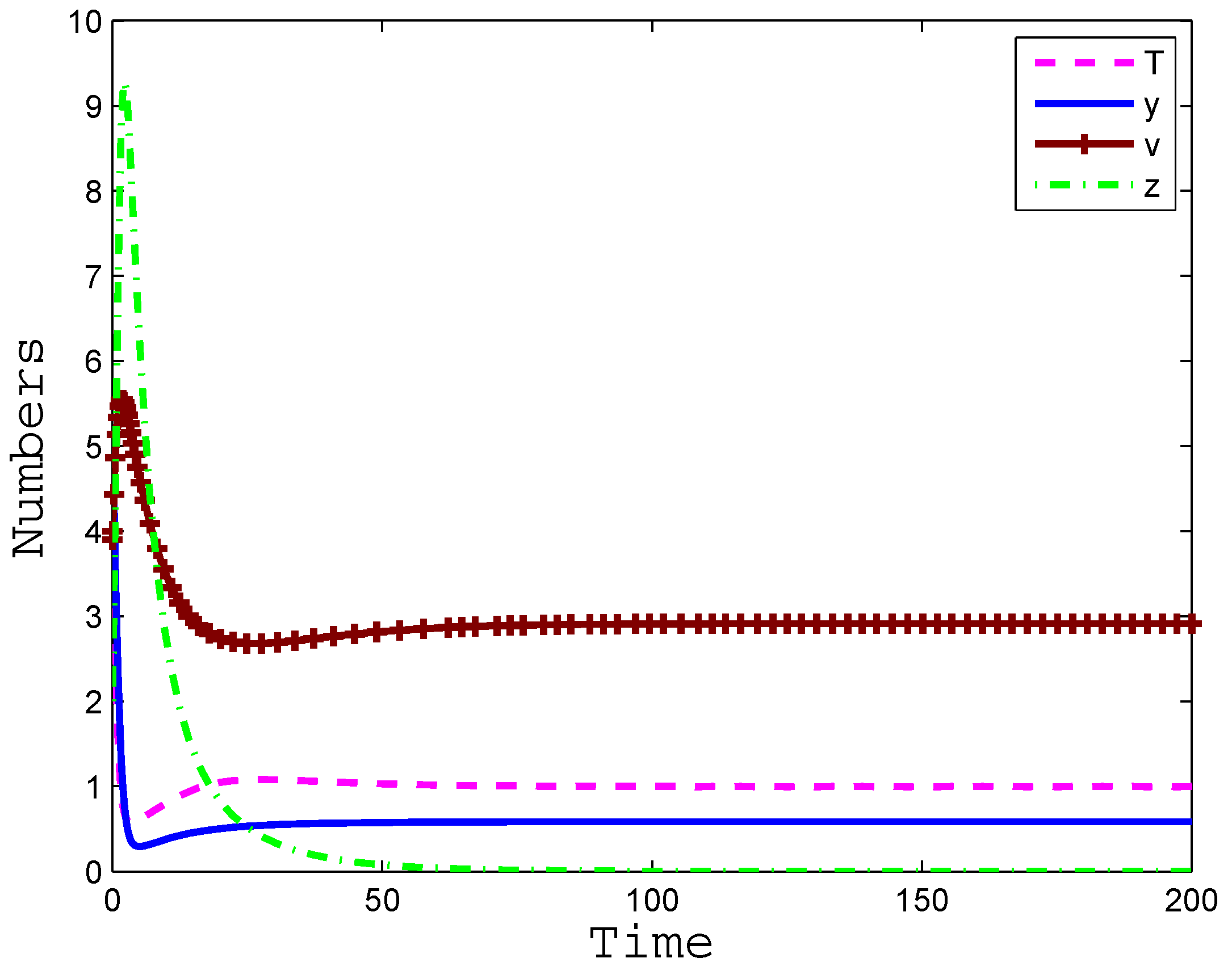
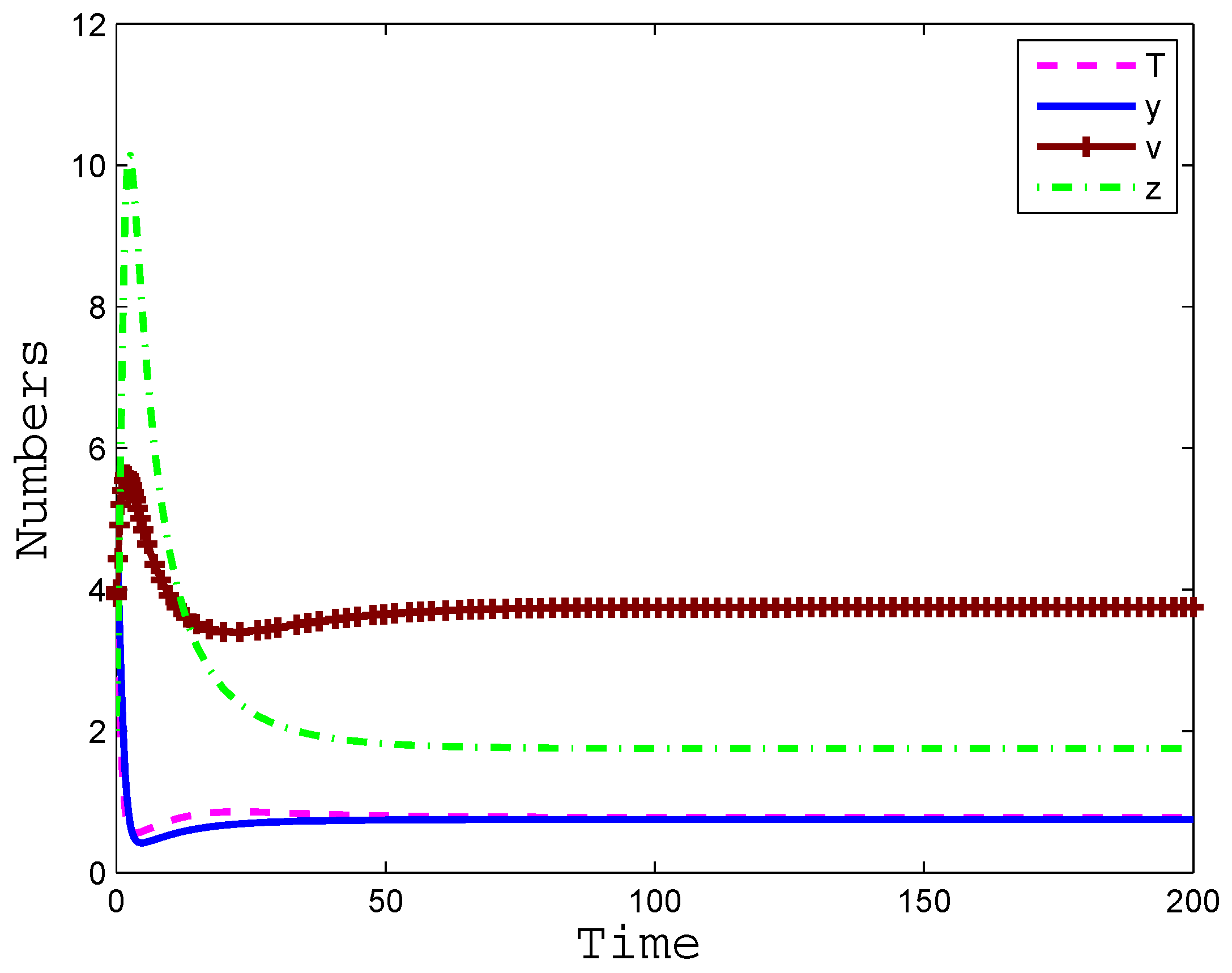
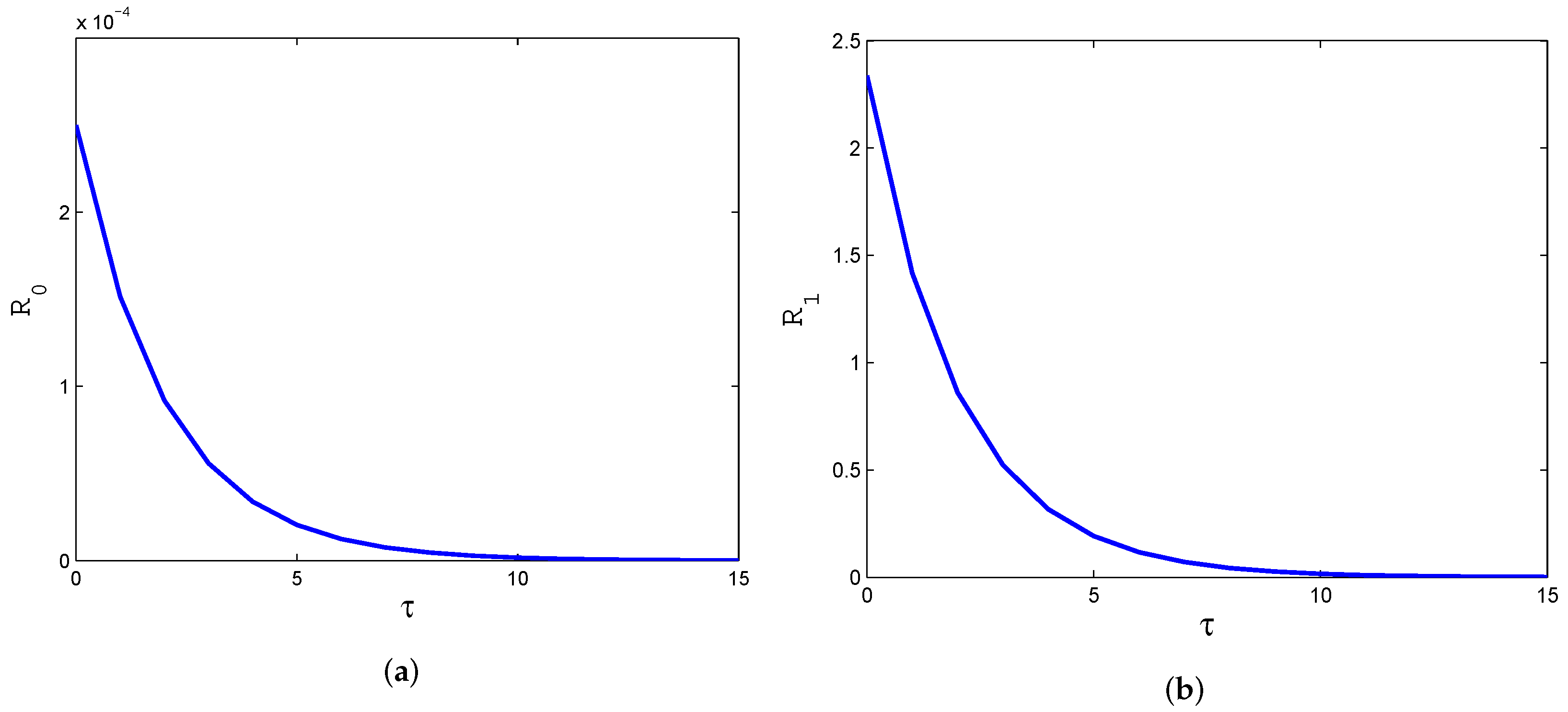
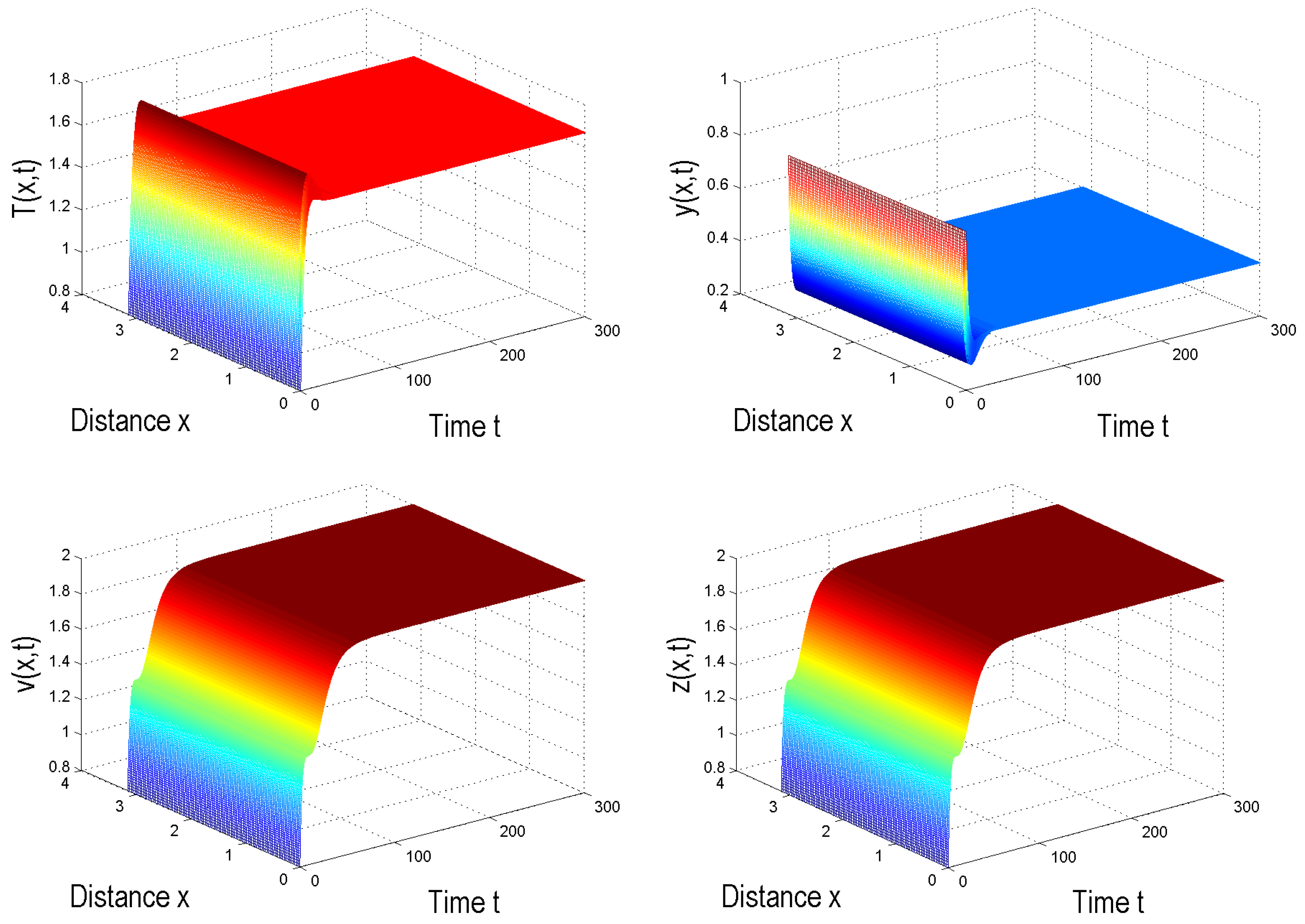
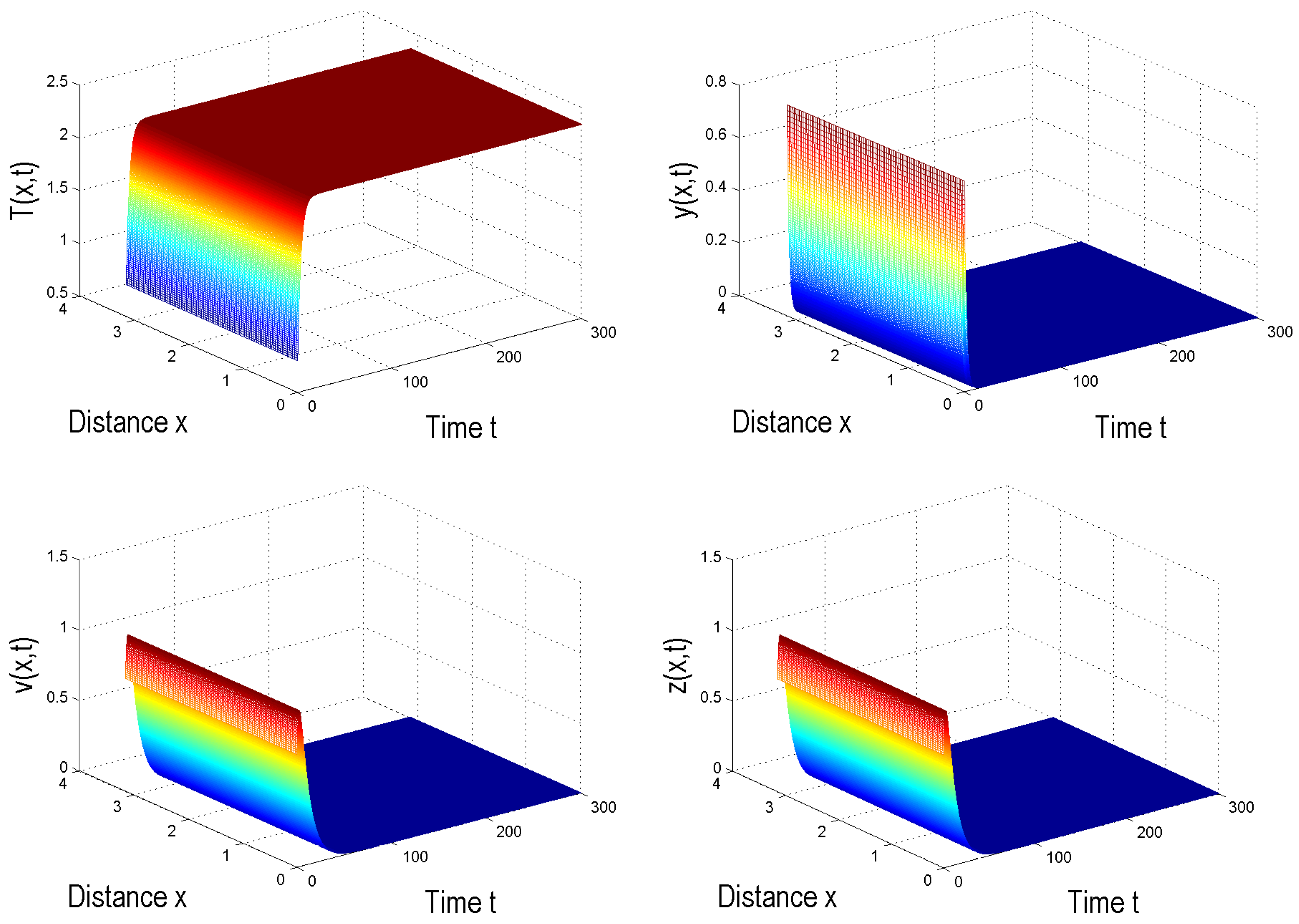
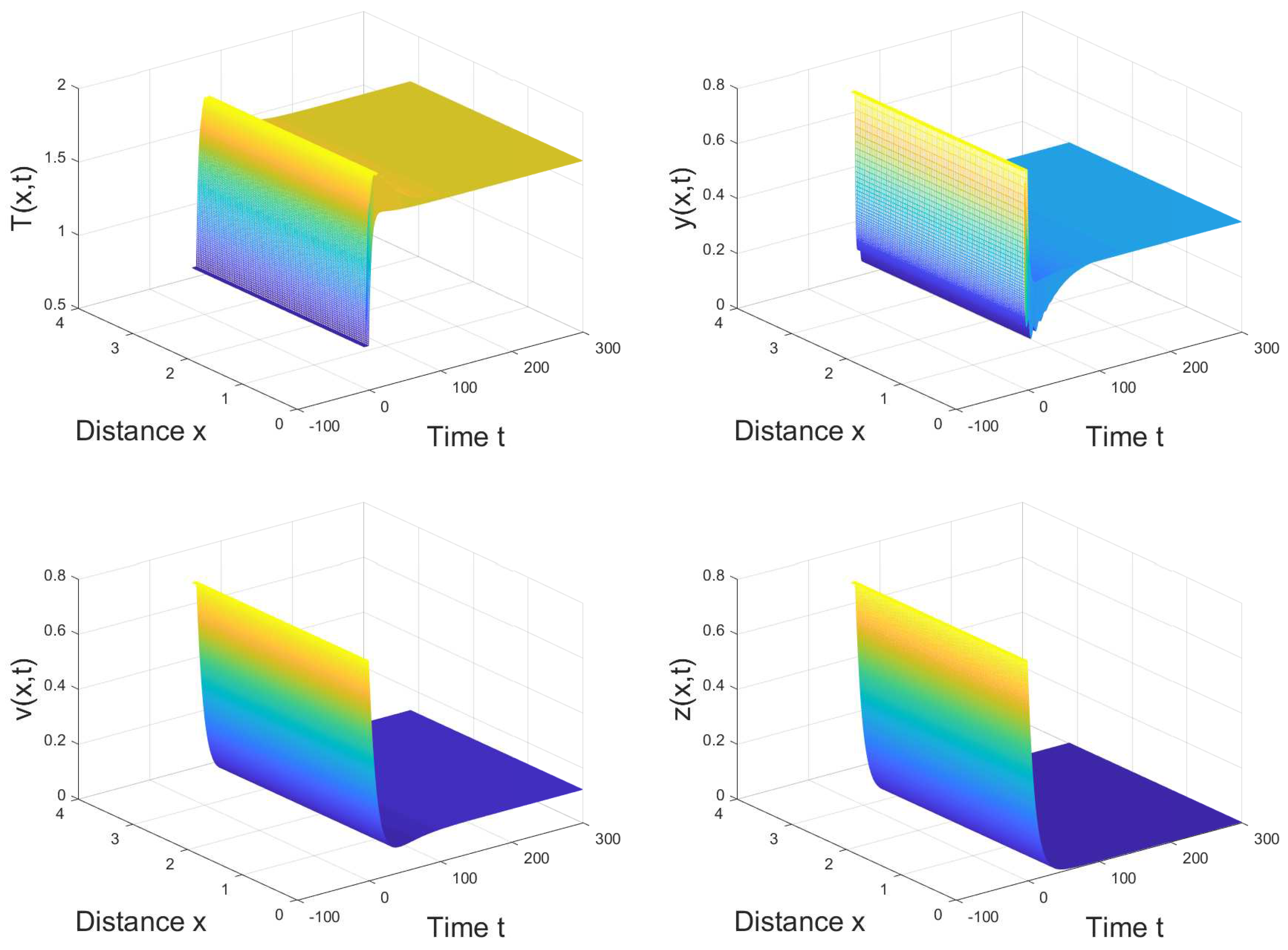
4. Numerical Simulation
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Calleri, F.; Nastasi, G.; Romano, V. Continuous-time stochastic processes for the spread of COVID-19 disease simulated via a Monte Carlo approach and comparison with deterministicmodels. J. Math. Biol. 2021, 83, 34. [Google Scholar] [CrossRef] [PubMed]
- Rihan, F.A.; Alsakaji, H.J.; Rajivganthi, C. Stochastic SIRC epidemic model with time-delay for COVID-19. Adv. Differ. Equ. 2020, 2020, 502. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. The necessity analysis of the knowledge dissemination of hypertension disease prevention in public english teaching. Indian J. Pathol. Microbiol. 2020, 82, 40. [Google Scholar]
- Zeng, Q.; Bie, B.; Guo, Q.; Yuan, Y.; Han, Q.; Han, X.; Chen, M.; Zhang, X.; Yang, Y.; Liu, M.; et al. Hyperpolarized Xe NMR signal advancement by metal-organic framework entrapment in aqueous solution. Proc. Natl. Acad. Sci. USA 2020, 117, 17558–17563. [Google Scholar] [CrossRef]
- Arnaout, R.; Nowak, M.; Wodarz, D. HIV-1 dynamics revisited: Biphasic decay by cytotoxic lymphocyte killing. Proc. Roy. Soc. Lond. B 2000, 265, 1347–1354. [Google Scholar] [CrossRef]
- Culshaw, R.; Ruan, S.; Spiteri, R. Optimal HIV treatment by maxinising immune response. J. Math. Biol. 2004, 48, 545–562. [Google Scholar] [CrossRef]
- Male, D.; Brostoff, J.; Roth, D.; Roitt, I. Immunology, 7th ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Nowak, M.; May, R. Vitus Dynamics; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Wang, K.; Wang, W.; Liu, X. Global stability in a viral infection model with lytic and nonlytic immune response. Comput. Math. Appl. 2006, 51, 1593–1610. [Google Scholar] [CrossRef][Green Version]
- Wodarz, D. Killer Cell Dynamics: Mathematical and Computational Approaches to Immunology; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Kirschner, D.E.; Webb, G.; Cloyd, M. Model of HIV-1 disease progression based on virus-induced lymph node homing and homing-induced apotosis of CD4+ lymphocytes. J. AIDS 2000, 24, 352–362. [Google Scholar]
- Weber, J.N.; Weiss, R.A. HIV infection: The cellular picture. Sci. Am. 1988, 259, 101–109. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Anderson, R.; May, R. Infections Diseases of Humans: Dynamics and Control; Oxford Univ Press: Oxford, UK, 1991. [Google Scholar]
- Boer, R.D.; Perelson, A. Target cell limited and immune control models of HIV infection, A comparison. J. Theoret. Biol. 1998, 190, 201–214. [Google Scholar] [CrossRef]
- Nowak, M.; Bangham, C. Population dynamics of immune responses to persistent viruses. Proc. Natl. Acad. Sci. USA 1996, 272, 74–79. [Google Scholar]
- Zhu, H.; Zou, X. Dynamics of a HIV-1 infection model with cell-mediated immune response and intracellular delay. Discrete Contin. Dyn. Syst. Ser. B 2009, 12, 511–524. [Google Scholar] [CrossRef]
- Wang, J.L.; Guan, L.J. Global stability for a HIV-1 infection model with cell-mediated immune response and intrecellular delay. Discrete Contin. Dyn. Syst. Ser. B 2012, 17, 297–302. [Google Scholar]
- Srivastava, H.M.; Deniz, S. A new modified semi-analytical technique for a fractional-order Ebola virus disease model. Rev. Real Acad. Cienc. Exactas Fís. Natur. Ser. A Mat. (RACSAM) 2021, 115, 137. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Jan, R.; Jan, A.; Deebani, W.; Shutaywi, M. Fractional-calculus analysis of the transmission dynamics of the dengue infection. Chaos 2021, 31, 53130. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M.; Gómez-Aguilar, J.F.; Almadiy, A.A. Some new mathematical models of the fractional-order system of human immune against IAV infection. Math. Biosci. Eng. 2020, 17, 4942–4969. [Google Scholar] [CrossRef]
- Zhu, C.C.; Zhu, J. Stability of a reaction-diffusion alcohol model with the impact of tax policy. Comput. Math. Appl. 2017, 74, 613–633. [Google Scholar] [CrossRef]
- Li, H.C.; Peng, R.; Wang, Z.A. On a Diffusive Susceptible-Infected-Susceptible Epidemic Model with Mass Action Mechanism and Birth-Death Effect: Analysis, Simulations, and Comparison with Other Mechanisms. SIAM J. Appl. Math. 2018, 78, 2129–2153. [Google Scholar] [CrossRef]
- Jin, H.Y.; Wang, Z.A. Boundedness, blowup and critical mass phenomenon incompeting chemotaxis. J. Differ. Equ. 2016, 260, 162–196. [Google Scholar] [CrossRef]
- Sigdel, R.P.; Mcluskey, C.C. Global stability for an SEI model of infection disease with immigration. Appl. Math. Comput. 2014, 243, 684–689. [Google Scholar]
- Srivastava, H.M.; Ahmad, H.; Ahmad, I.; Thounthong, P.; Khan, M.N. Numerical simulation of 3-D fractional-order convection-diffusion PDE by a local meshless method. Thermal. Sci. 2021, 25, 347–358. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Izadi, M.; Okhovati, N. Viscous splitting finite difference schemes to convection-diffusion equations with discontinuous coefficient. Appl. Anal. Optim. 2022, 6, 313–328. [Google Scholar]
- Srivastava, H.M.; Izadi, M. The Rothe–Newton approach to simulate the variable coefficient convection-diffusion equations. J. Mahani Math. Res. Cent. 2022, 11, 141–157. [Google Scholar]
- Xu, H.Y.; Li, H.; Xuan, Z.C. Some new inequalities on Laplace–Stieltjes transforms involving logarithmic growth. Fractal Fract. 2022, 6, 233. [Google Scholar] [CrossRef]
- Xu, H.Y.; Xu, L. Transcendental entire solutions for several quadratic binomial and trinomial PDEs with constant coefficients. Anal. Math. Phys. 2022, 12, 64. [Google Scholar] [CrossRef]
- Xu, H.Y.; Jiang, Y.y. Results on entire and meromorphic solutions for several systems of quadratic trinomial functional equations with two complex variables, Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Ser. A Matemáticas 2022, 116, 1–19. [Google Scholar]
- Li, H.; Xu, H.Y. Notes on solutions for some systems of complex functional equations in C2. J. Funct. Spaces 2021, 2021, 5424284. [Google Scholar]
- Xu, H.Y.; Kong, Y.Y. Entire functions represented by Laplace-Stieltjes transforms concerning the approximation and generalized order. Acta Math. Sci. 2021, 41, 646–656. [Google Scholar] [CrossRef]
- Xu, H.Y.; Liu, S.Y.; Li, Q.P. Entire solutions for several systems of nonlinear difference and partial differential-difference equations of Fermat-type. J. Math. Anal. Appl. 2020, 483, 123641. [Google Scholar] [CrossRef]
- Xu, H.Y.; Kong, Y.Y. The approximation of Laplace–Stieltjes transformations with finite order on the left half plane. Comptes Rendus Math. 2018, 356, 63–76. [Google Scholar] [CrossRef]
- Liu, X.L.; Zhu, C.C. A Non-Standard Finite Difference Scheme for a Diffusive HIV-1 Infection Model with Immune Response and Intracellular Delay. Axioms. 2022, 11, 129. [Google Scholar] [CrossRef]
- Enatsu, Y.; Nakata, Y.; Muroya, Y.; Izzo, G.; Vecchio, A. Global dynamics of difference equations for SIR epidemic models with a class of nonlinear incidence rates. J. Differ. Equ. Appl. 2012, 18, 1163–1181. [Google Scholar] [CrossRef]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Hattaf, K.; Yousfi, N. Global properties of a discrete viral infection model with general incidence rate. Math. Methods Appl. Sci. 2016, 39, 998–1004. [Google Scholar] [CrossRef]
- Shi, P.; Dong, L. Dynamical behaviors of a discrete HIV-1 virus model with bilinear infective rate. Math. Methods Appl. Sci. 2014, 37, 2271–2280. [Google Scholar]
- Wang, J.P.; Teng, Z.D.; Miao, H. Global dynamics for discrete-time analog of viral infection model with nonlinear incidence and CTL immune response. Adv. Differ. Equ. 2016, 2016, 143. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.H.; Geng, Y. Dynamic consistent NSFD Scheme for a Delayed Viral Infection Model with Immune Response and Nonlinear Incidence. Discret. Nat. Soc. 2017, 2017, 3141736. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, J. Global dynamics of a PDE in-host viral model. Appl. Anal. 2014, 93, 2312–2329. [Google Scholar]
- Fitzgibbon, W.E. Semilinear functional differential equations in Banach space. J. Differ. Equ. 1978, 29, 1–14. [Google Scholar] [CrossRef]
- Martin, R.H.; Smith, H.L. Abstract functional differential equations and reaction-diffusion systems. Trans. Am. Math. Soc. 1990, 321, 1–44. [Google Scholar]
- Martin, R.H.; Smith, H.L. Reaction-diffusion systems with time delays: Monotonicity, invariance, comparison and convergence. J. Reine Angew. Math. 1991, 413, 1–35. [Google Scholar]
- Travis, C.C.; Webb, G.F. Existence and stability for partial functional differential equations. Trans. Am. Math. Soc. 1974, 200, 395–418. [Google Scholar] [CrossRef]
- Wu, J. Theory and Applications of Parfunctional Differential Equations; Springer: New York, NY, USA, 1996. [Google Scholar]
- Protter, M.H.; Weinberger, H.F. Maximum Principles in Differential Equations; Prentice Hall: Engle-Wood Cliffs, NJ, USA, 1967. [Google Scholar]
- Henry, D. Gerometric Theory of Semilinear Parabolic Equation; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Xiang, H.; Tang, Y.L.; Huo, H.F. A viral model with intracellular delay and humoral immunity. Bull. Malays. Math. Sci. Soc. 2016. [Google Scholar] [CrossRef]
- Nelson, P.; Murray, J.; Perelson, A. A model of HIV-1 pathogenesis that includes an intracellular delay. Math. Biosci. 2000, 163, 201–215. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhu, C.-C.; Srivastava, H.M.; Xu, H. Global Stability for a Diffusive Infection Model with Nonlinear Incidence. Mathematics 2022, 10, 4296. https://doi.org/10.3390/math10224296
Liu X, Zhu C-C, Srivastava HM, Xu H. Global Stability for a Diffusive Infection Model with Nonlinear Incidence. Mathematics. 2022; 10(22):4296. https://doi.org/10.3390/math10224296
Chicago/Turabian StyleLiu, Xiaolan, Cheng-Cheng Zhu, Hari Mohan Srivastava, and Hongyan Xu. 2022. "Global Stability for a Diffusive Infection Model with Nonlinear Incidence" Mathematics 10, no. 22: 4296. https://doi.org/10.3390/math10224296
APA StyleLiu, X., Zhu, C.-C., Srivastava, H. M., & Xu, H. (2022). Global Stability for a Diffusive Infection Model with Nonlinear Incidence. Mathematics, 10(22), 4296. https://doi.org/10.3390/math10224296








