An Intensional Probability Theory: Investigating the Link between Classical and Quantum Probabilities †
Abstract
1. Introduction
2. Fundamental Conception
2.1. Intensionality of Geometrical Structuring
2.2. Foundation of Probability Theory
2.3. Geometrical Structure of Probability
3. Results
3.1. Quantum Ensembles and Measurement
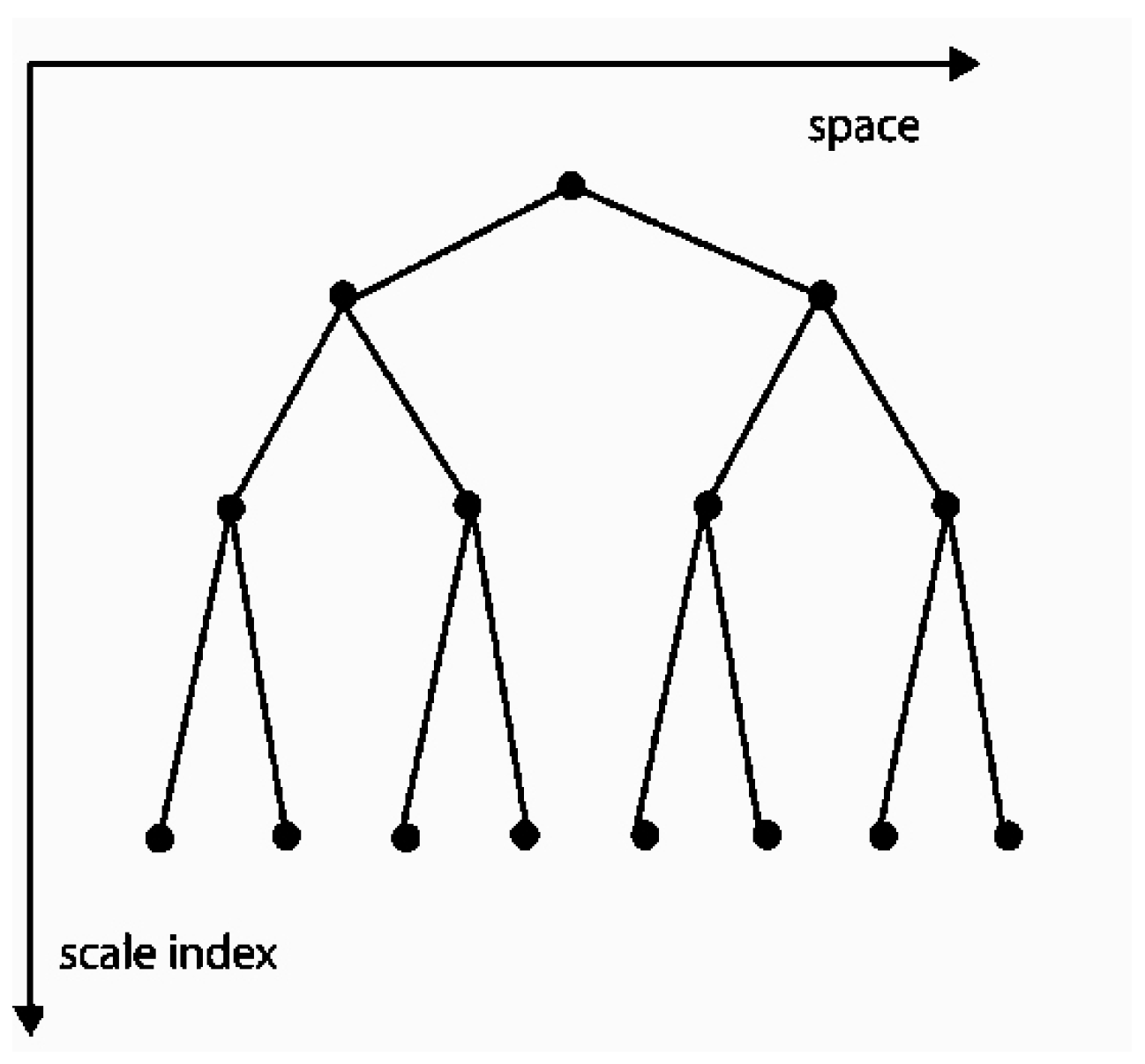
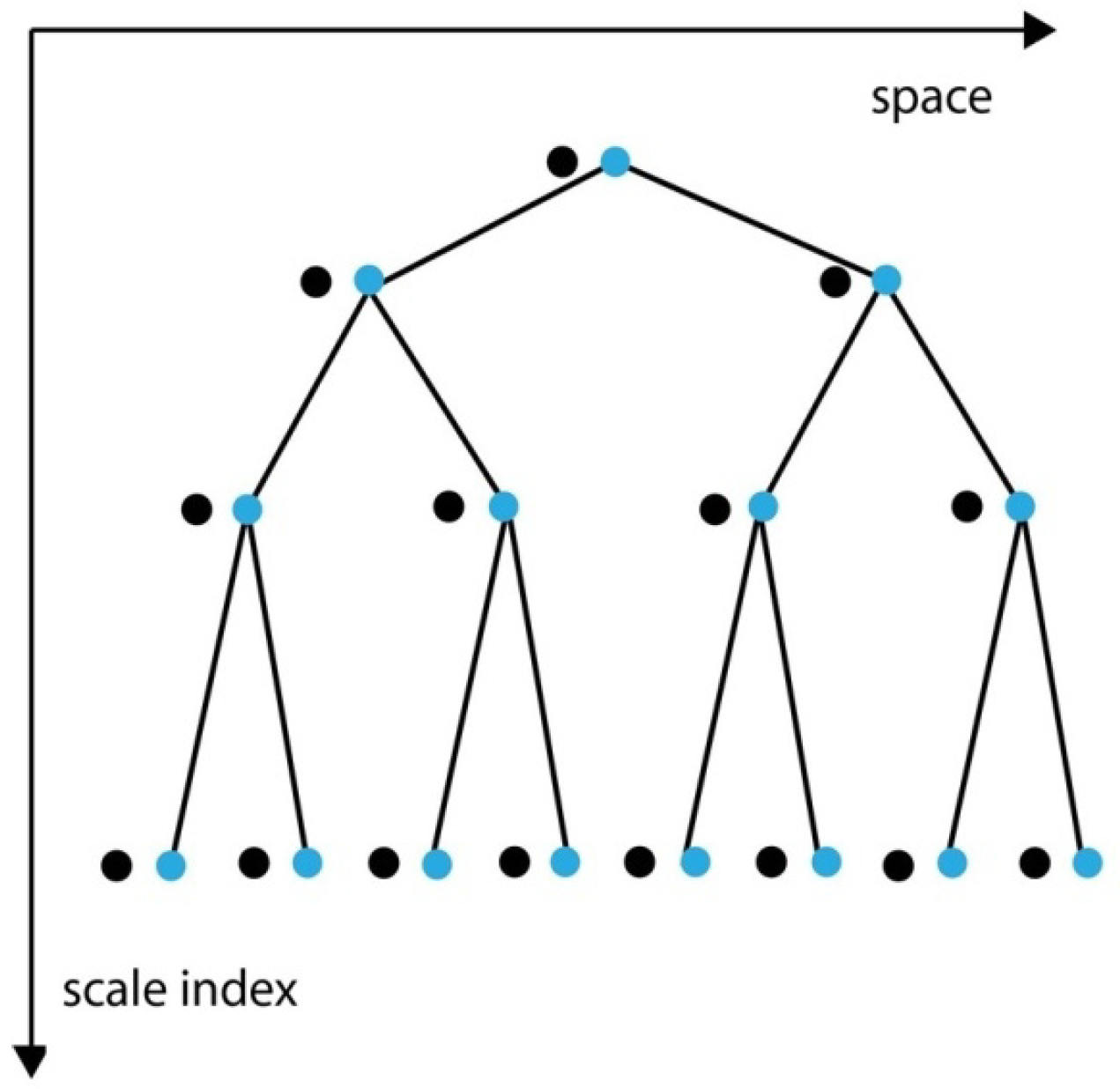
3.2. Time Continuum and Intuitionism
- (i)
- annihilation ;
- (ii)
- periodization ;
- (iii)
- translation ;
- (iv)
- evolution ;
- (v)
- basicity for every variable from and some coefficients of approximation A and details ;
- (vi)
- orthonormality and the constant variable 1 constitute an orthonormal base of .
3.3. Wavelet-Domain Hidden Markov Model
4. Discussion
4.1. The Art of Memory
4.2. Postmodern Science
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meyerson, É. Identité et Réalité; Alcan, F., Ed.; Librairies Félix Alcan et Guillaumin Réunies: Paris, France, 1908. [Google Scholar]
- Florensky, P. Smisao Idealizma; Plato: Belgrade, Serbia, 2000; pp. 103–111. [Google Scholar]
- Mijajlović, Ž.; Marković, Z.; Došen, K. Hilbertovi Problemi i Logika; Zavod za Udžbenike i Nastavna Sredstva: Belgrade, Serbia, 1986; pp. 16–17. [Google Scholar]
- Tasić, V. Mathematics and the Roots of Postmodern Thought; Oxford University Press: Oxford, UK, 2001; pp. 36–45. [Google Scholar]
- Toulmin, S. The Return to Cosmology: Postmodern Science and the Theology of Nature; University of California Press: Berkeley, CA, USA, 1982. [Google Scholar]
- Butterworth, G. Context and cognition in models of cognitive growth. In Context and Cognition; Light, P., Butterworth, G., Eds.; Lawrence Erlbaum Associates Publishers: London, UK, 1993; pp. 1–13. [Google Scholar]
- Duarte, F.J. Fundamentals of Quantum Entanglement, 2nd ed.; IOP Publishing: Bristol, UK, 2022. [Google Scholar]
- Bernasconi, J.; Gustafson, K. Contextual quick-learning and generalization by humans and machines. Netw. Comput. Neural Syst. 1998, 9, 85–106. [Google Scholar] [CrossRef]
- Cole, M.M.; Cole, S.R. The Development of Children; Freeman: San Francisco, CA, USA, 1989. [Google Scholar]
- Anderson, J.R. Cognitive Psychology and Its Implications; Freeman: New York, NY, USA, 1990. [Google Scholar]
- Yan, P.; Li, L.; Zeng, D. Quantum probability-inspired graph attention network for modeling complex text interaction. Knowl.-Based Syst. 2021, 234, 107557. [Google Scholar] [CrossRef]
- Estes, W.K. Classification and Cognition; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Pothos, E.M.; Busemeyer, J.R. Quantum Cognition. Annu. Rev. Psychol. 2022, 73, 749–778. [Google Scholar] [CrossRef]
- Cohen, M.A.; Grossberg, S. Learning, recognizing and predicting multiple groupings of patterned data using a masking field neural architecture. SPIE Dig. Opt. Comp. 1987, 752, 98–104. [Google Scholar]
- Crowther, K. Spacetime emergence: Collapsing the distinction between content and context? In From Electrons to Elephants and Elections: Exploring the Role of Content and Context; Wuppuluri, S., Stewart, I., Eds.; Springer: Dordrecht, The Netherlands, 2022; pp. 379–402. [Google Scholar]
- Stewart, I. Introduction. In From Electrons to Elephants and Elections: Exploring the Role of Content and Context; Wuppuluri, S., Stewart, I., Eds.; Springer: Dordrecht, The Netherlands, 2022; pp. ix–xxiv. [Google Scholar]
- Cohen, J. Are You Content in Your Context? Novacon Special, The Birmingham Science Fiction Group: Birmingham, UK, 1990. [Google Scholar]
- Bueno, O. Content, context, and naturalism in mathematics. In From Electrons to Elephants and Elections: Exploring the Role of Content and Context; Wuppuluri, S., Stewart, I., Eds.; Springer: Dordrecht, The Netherlands, 2022; pp. 287–306. [Google Scholar]
- Ohmdal, B. Cognitive Appraisal, Emotion, and Empathy; Lawrence Erlbaum Associates, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Jung, K.G. Foreward. In The I Ching or Book of Changes; Princeton University Press: Princeton, NJ, USA, 1977; pp. 33–69. [Google Scholar]
- Poisson, S.D. Recherches sur la Probabilite des Jugements en Matiére Criminelle et en Matière Civile, Précédées des Règles Générales du Calcul des Probabilités; Bachelier: Paris, France, 1837. [Google Scholar]
- Franklin, J. The Science of Conjecture: Evidence and Probability before Pascal; Johns Hopkins University Press: Baltimore, MD, USA, 2015. [Google Scholar]
- Garibaldi, U.; Penco, M.A. Intensional vs extensional probabilities from their origins to Laplace. Hist. Math. 1991, 18, 16–35. [Google Scholar] [CrossRef][Green Version]
- de Ronde, C.; Freytes, H.; Sergioli, G. Quantum probability: A reliable tool for an agent or a reliable source of reality. Synthese 2021, 198, 5679–5699. [Google Scholar] [CrossRef]
- Heisenberg, W. Development of concepts in the history of quantum theory. In The Physicist’s Conception of Nature; Mehra, J., Ed.; Springer: Dordrecht, The Netherlands, 1973; pp. 264–275. [Google Scholar]
- Peppe, S. Extensionalism, Naturalism, and Probability: Can Quine’s Anti-Modalism Survive Quantum Mechanics? Ph.D. Dissertation, University of New York, New York, NY, USA, 2022; pp. 73–112. [Google Scholar]
- Khrennikov, A. Contextual Approach to Quantum Formalism; Springer: Växjö, Sweden, 2009. [Google Scholar]
- Kolmogoroff, A. Grundbegriffe der Wahrscheinlichkeitsrechnung; Julius Springer: Berlin, Germany, 1933. [Google Scholar]
- López-Astorga, M.; Ragni, M.; Johnson-Laird, P.N. The probability of conditionals: A review. Psychon. B. Rev. 2022, 29, 1–20. [Google Scholar] [CrossRef]
- Khrennikov, A. Contextual probability in quantum physics, cognition, psychology, social science, and artificial intelligence. In From Electrons to Elephants and Elections: Exploring the Role of Content and Context; Wuppuluri, S., Stewart, I., Eds.; The Frontiers Collection; Springer: Dordrecht, The Netherlands, 2022; pp. 523–536. [Google Scholar]
- Müller, M. Probabilistic theories and reconstructions of quantum theory. SciPost Phys. Lect. Notes 2021, 28, 1–41. [Google Scholar] [CrossRef]
- Wendt, A. Why IR scholars should care about quantum theory, part I: Burdens of proof and uncomfortable facts, part II: Critics in the PITs. Int. Theor. 2022, 14, 119–129, 193–209. [Google Scholar] [CrossRef]
- Uspensky, B.A. Poetika Kompozicije; Semiotika Ikone; Nolit: Belgrade, Serbia, 1979. [Google Scholar]
- Milovanović, M.; Tomić, B. Fractality and self-organization in the Orthodox iconogrpahy. Complexity 2016, 21, 55–68. [Google Scholar] [CrossRef]
- Milovanović, M.; Medic-Simić, G. Aesthetical criterion in art and science. Neural. Comput. Appl. 2021, 33, 2137–2156. [Google Scholar] [CrossRef]
- Kostić, J. Samoreferencija i Teorija Pojmova. Ph.D. Dissertation, University of Belgrade, Belgrade, Serbia, 2021. [Google Scholar]
- Bloom, A. The Republic of Plato; Basic Books: New York, NY, USA, 1991; p. 527a. [Google Scholar]
- Radojčić, M. Elementarna Geometrija: Osnove i Elementi Euklidske Geometrije; Naučna Knjiga: Belgrade, Serbia, 1961. [Google Scholar]
- Janičić, P. Jedan Metod za Automatsko Dokazivanje Teorema Geometrije. Master’s Thesis, University of Belgrade, Belgrade, Serbia, 1996; pp. 4–6. [Google Scholar]
- Bell, J.L. A Primer of Infinitesimal Analysis; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Khrennikov, A. Probability and Randomness: Quantum versus Classical; Imperial College Press: London, UK, 2016. [Google Scholar]
- Accardi, L. Foundations of quantum probability. In Rendiconti del Seminario Matematico dell’Università e del Politecnico; Levrotto e Bella: Torino, Italy, 1982; pp. 249–270. [Google Scholar]
- Koopman, B.O. Quantum theory and the foundations of probability. In Applied Probability, Proceedings of Symposia in Applied Mathematics, Volume VII; MacCooll, L.A., Ed.; MC Graw Hill Book Company: New York, NY, USA; Toronto, ON, Canada; London, UK, 1957; pp. 97–102. [Google Scholar]
- Majer, U. The axiomatic method and the foundations of science: Historical roots of mathematical physics in Göttingen (1900–1930). In John von Neumann and the Foundation of Quantum Theory; Rédei, M., Stöltzner, M., Eds.; Springer-Science +Business Media: Dordrecht, The Netherlands, 2001; pp. 11–33. [Google Scholar]
- Breuer, T. Von Neumann, Gödel and quantum incompletness. In John von Neumann and the Foundation of Quantum Theory; Rédei, M., Stöltzner, M., Eds.; Springer-Science +Business Media: Dordrecht, The Netherlands, 2001; pp. 75–82. [Google Scholar]
- von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Antoniou, I.; Misra, B.; Suchanecki, Z. Time Operator: Innovation and Complexity; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Bub, J. Von Neumann’s projection postulate as a probability conditionalization rule in quantum mechanics. J. Philos. Log. 1977, 10, 381–390. [Google Scholar] [CrossRef]
- Antoniou, I.E.; Misra, B. Relativistic internal time operator. Int. J. Theor. Phys. 1992, 31, 119–136. [Google Scholar] [CrossRef]
- Heisenberg, W. The Physical Principles of the Quantum Theory; Dover Publications: New York, NY, USA, 1949; pp. 39–46. [Google Scholar]
- Prigogine, I. From Being to Becoming: Time and Complexity in the Physical Science; W. H. Freeman and Co.: New York, NY, USA, 1980; pp. 241–248. [Google Scholar]
- Milovanović, M.; Vukmirović, S.; Saulig, N. Stochastic analysis of the time continuum. Mathematics 2021, 9, 1452. [Google Scholar] [CrossRef]
- Milovanović, M. The measurement problem in statistical signal processing. Int. J. Mod. Phys. A 2022. under review. [Google Scholar]
- Antoniou, I.E.; Gustafson, K.E. The time operator of wavelets. Chaos Solit. Fractals 2000, 11, 443–452. [Google Scholar] [CrossRef]
- Antoniou, I.; Gustafson, K. Wavelets and stochastic processes. Math. Comput. Simul. 1999, 49, 81–104. [Google Scholar] [CrossRef]
- Crouse, M.C.; Nowak, R.D.; Baraniuk, R.G. Wavelet-based statistical signal processing using hidden Markov model. IEEE Trans. Sign. Proc. 1998, 46, 886–902. [Google Scholar] [CrossRef]
- Milovanović, M.; Rajković, M. Quantifying self-organization with optimal wavelets. Europhys. Lett. 2013, 102, 40004. [Google Scholar] [CrossRef]
- Heidelberger, M. The mind-body problem in the origin of logical empiricism: Herbert Feigl and psychophysical parallelism. In Logical Empiricism: Historical and Contemporary Perspectives; Parrini, P., Salmon, W.C., Salmon, M.H., Eds.; Pittsburgh University Press: Pittsburgh, PA, USA, 2003; pp. 233–262. [Google Scholar]
- Fechner, G.T. Elemente der Psychophysik; Erster Theil; Breitkopf und Härtel: Leipzig, Germany, 1860; pp. vii–xiii, 1–20. [Google Scholar]
- Misra, B.; Prigogine, I.; Courbage, M. From deterministic dynamics to probabilistic descriptions. Physica A 1979, 98A, 1–26. [Google Scholar] [CrossRef]
- Kracauer, S. Photography. Crit. Inq. 1993, 19, 421–436. [Google Scholar] [CrossRef]
- Milovanović, M. Postmodern memory. A study on aesthetics of Eastern Europe. In Beauty in Architecture. Harmony of Place; Szuba, B., Drewniak, T., Eds.; Studies in Philosophy; Culture and Contemporary Society: Berlin, Germany, 2022; pp. 363–389. [Google Scholar]
- Yates, F. The Art of Memory; Routledge: London, UK; New York, NY, USA,, 1966; p. 379. [Google Scholar]
- Courturat, L. La Logique de Leibniz d’Apres s des Documents Inedit; Alcan, F., Ed.; Ancienne Librairie Germer Bailliére: Paris, France, 1901; pp. 84–85. [Google Scholar]
- Peirce, C.S. The New Elements of Mathematics, Volume III; Eisele, C., Ed.; Mouton Publishers: The Hague and Paris; Humanities Press: Atlantic Highlands, NJ, USA, 1976; p. 124. [Google Scholar]
- Gödel, K. Russell’s mathematical logic. In Kurt Gödel Collected Works II: Publications 1938–1974; Feferman, S., Dawson, J.W., Jr., Kleene, S.C., Moore, G., Solovay, R., Heijenoort, J., Eds.; Oxford University Press: Oxford, UK, 1990; pp. 119–141. [Google Scholar]
- Trostnikov, V. Научна ли “научная картина мира”? Новый Mир 1989, 12, 257. [Google Scholar]
- Pétrovitch, M. Mécanisms Communs aux Phénomènes Disparates; Borel, É., Ed.; Librairie Felix Alcan: Paris, France, 1921. [Google Scholar]
- Petrovitch, M. Leçons sur les Spectres Mathématiques; Gauthier-Villars et, C., Ed.; Libraires du Bireau des Longitudes, de l‘Ecole Polytechnique: Paris, France, 1928. [Google Scholar]
- Milovanović, M. Značaj Petrovićevih spektara u zasnivanju matematike. In Mihailo Petrović Alas: Povodom sto Pedeset Godina od Rođenja; Milovanović, G., Pilipović, S., Mijajlović, Ž., Eds.; Serbian Academy of Sciences and Arts, Faculty of Mathematics, Mathematical Institute SANU, Mathematical Society of Serbia: Belgrade, Serbia, 2019; pp. 47–62. [Google Scholar]
- Rudeanu, S. Lattice Functions and Equations; Springer: London, UK, 2001. [Google Scholar]
- Mišić, N. Fraktali i Deterministički Haos u Strukturi Objekata i Dinamici Procesa Sistema Upravljanja. Ph.D. Dissertation, University of Belgrade, Belgrade, Serbia, 2006; p. 4. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milovanović, M.; Saulig, N. An Intensional Probability Theory: Investigating the Link between Classical and Quantum Probabilities. Mathematics 2022, 10, 4294. https://doi.org/10.3390/math10224294
Milovanović M, Saulig N. An Intensional Probability Theory: Investigating the Link between Classical and Quantum Probabilities. Mathematics. 2022; 10(22):4294. https://doi.org/10.3390/math10224294
Chicago/Turabian StyleMilovanović, Miloš, and Nicoletta Saulig. 2022. "An Intensional Probability Theory: Investigating the Link between Classical and Quantum Probabilities" Mathematics 10, no. 22: 4294. https://doi.org/10.3390/math10224294
APA StyleMilovanović, M., & Saulig, N. (2022). An Intensional Probability Theory: Investigating the Link between Classical and Quantum Probabilities. Mathematics, 10(22), 4294. https://doi.org/10.3390/math10224294





