Nonlinear Hammerstein System Identification: A Novel Application of Marine Predator Optimization Using the Key Term Separation Technique
Abstract
1. Introduction
2. System Model
3. Methodology
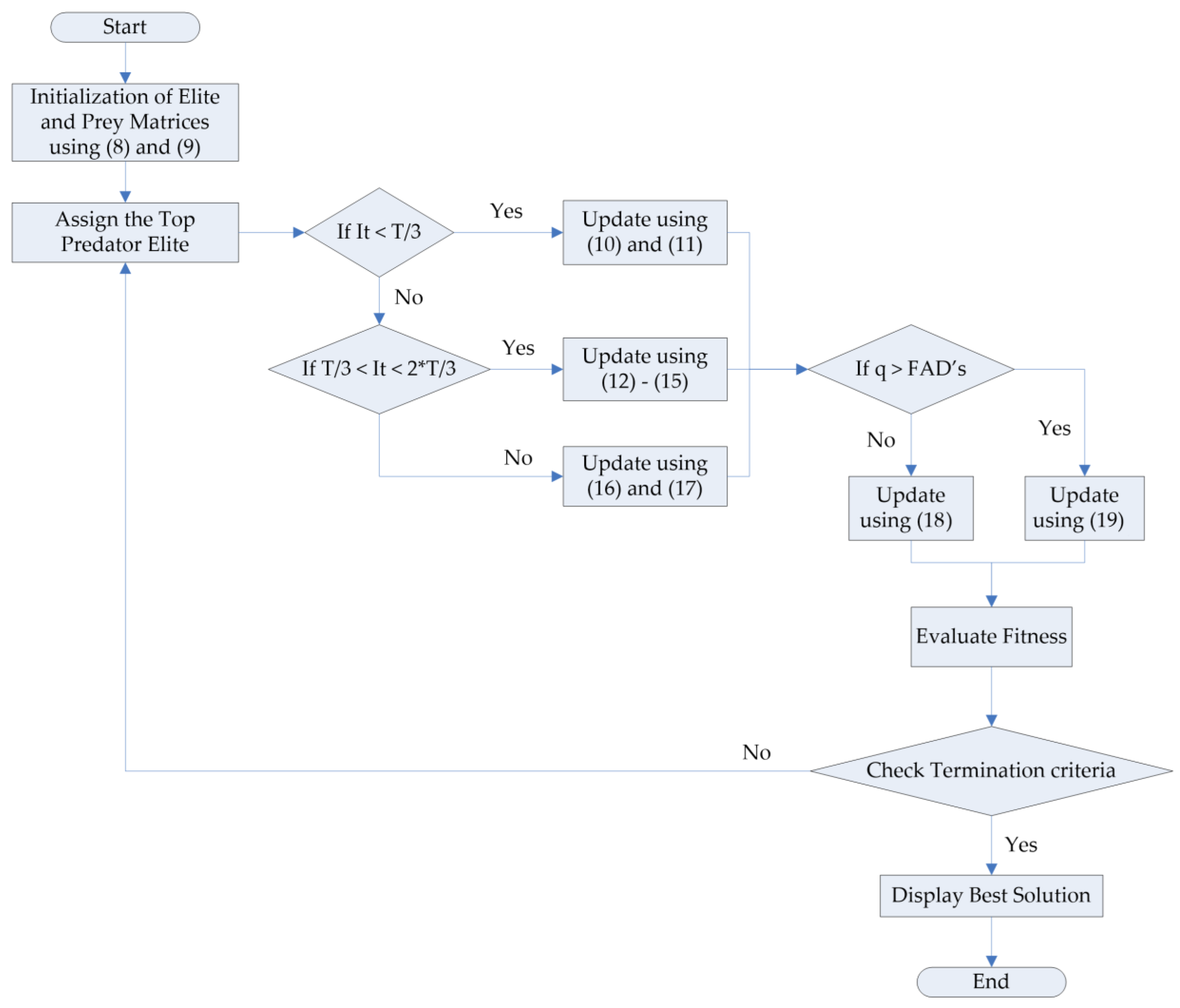
3.1. Marine Predator Algorithm
3.1.1. Formulation
3.1.2. Optimization
Phase I
Phase II
Phase III
3.1.3. Fish Aggregating Devices’ (FAD’s) Effect
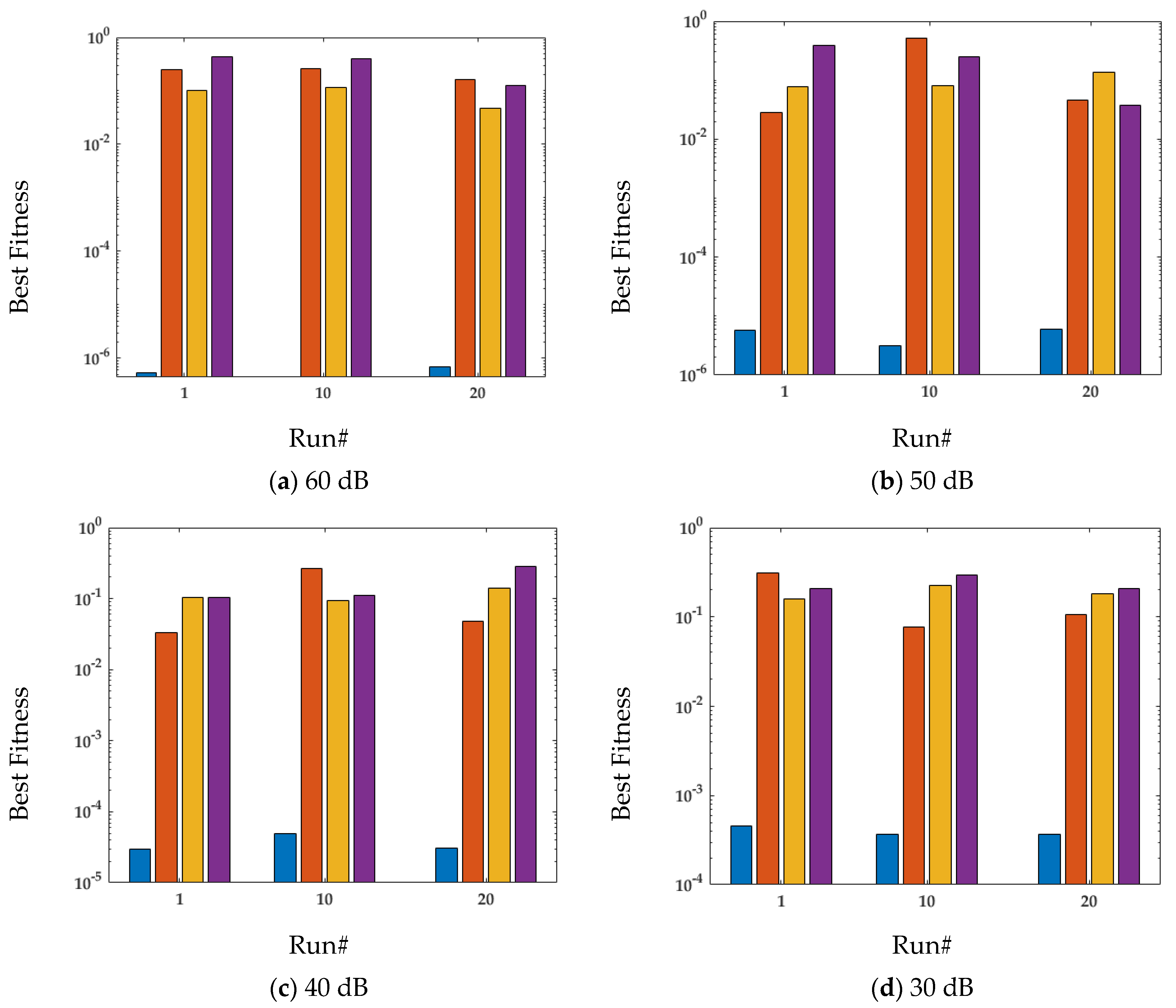
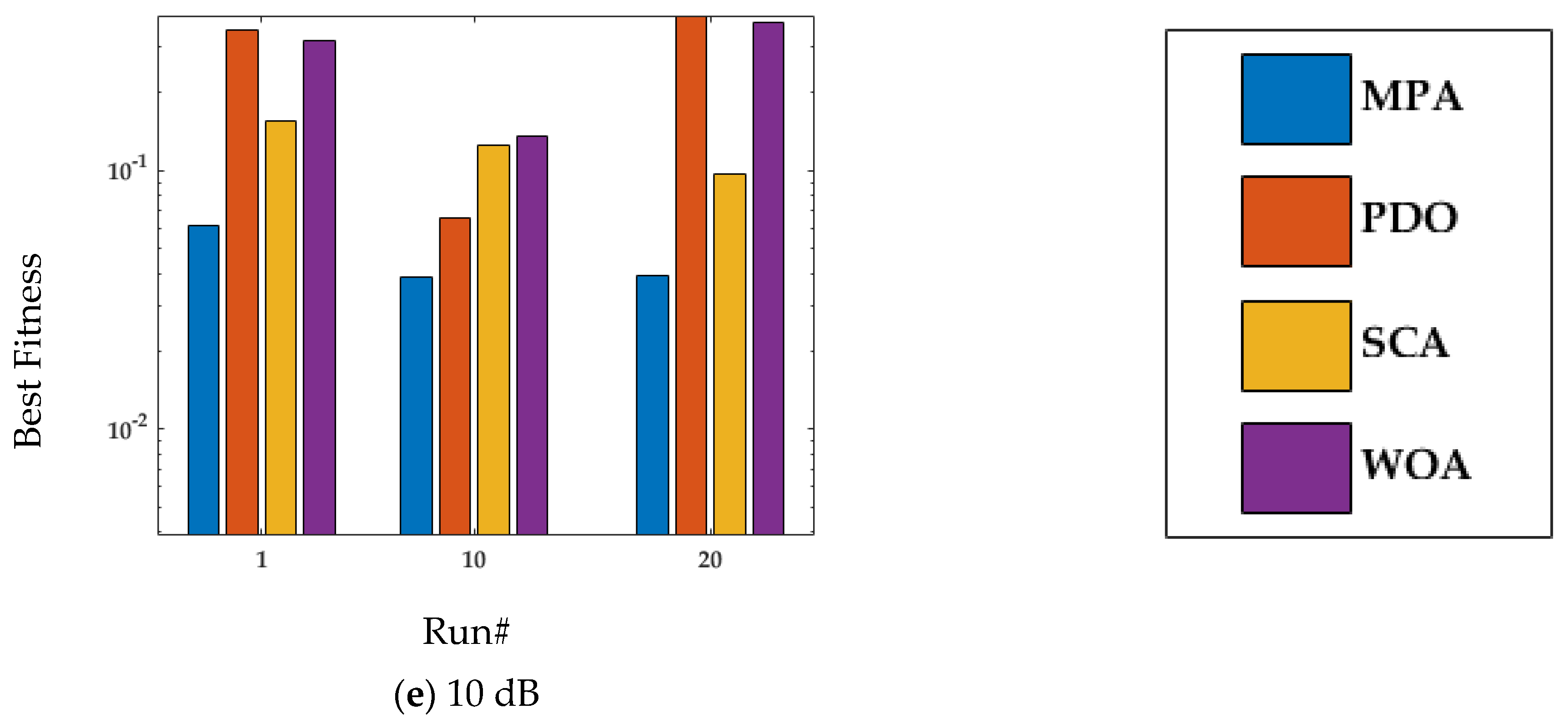
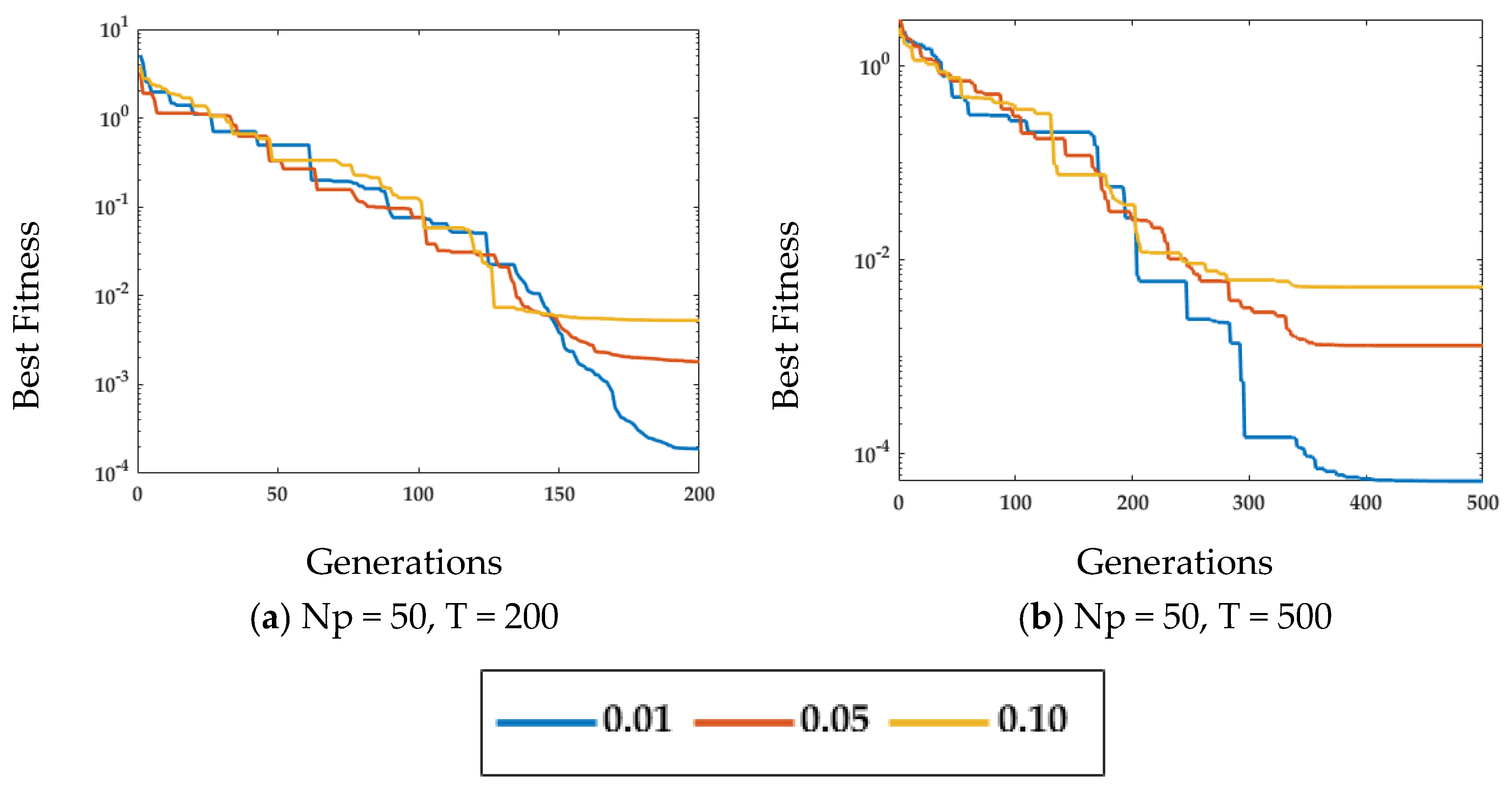
4. Performance Analysis
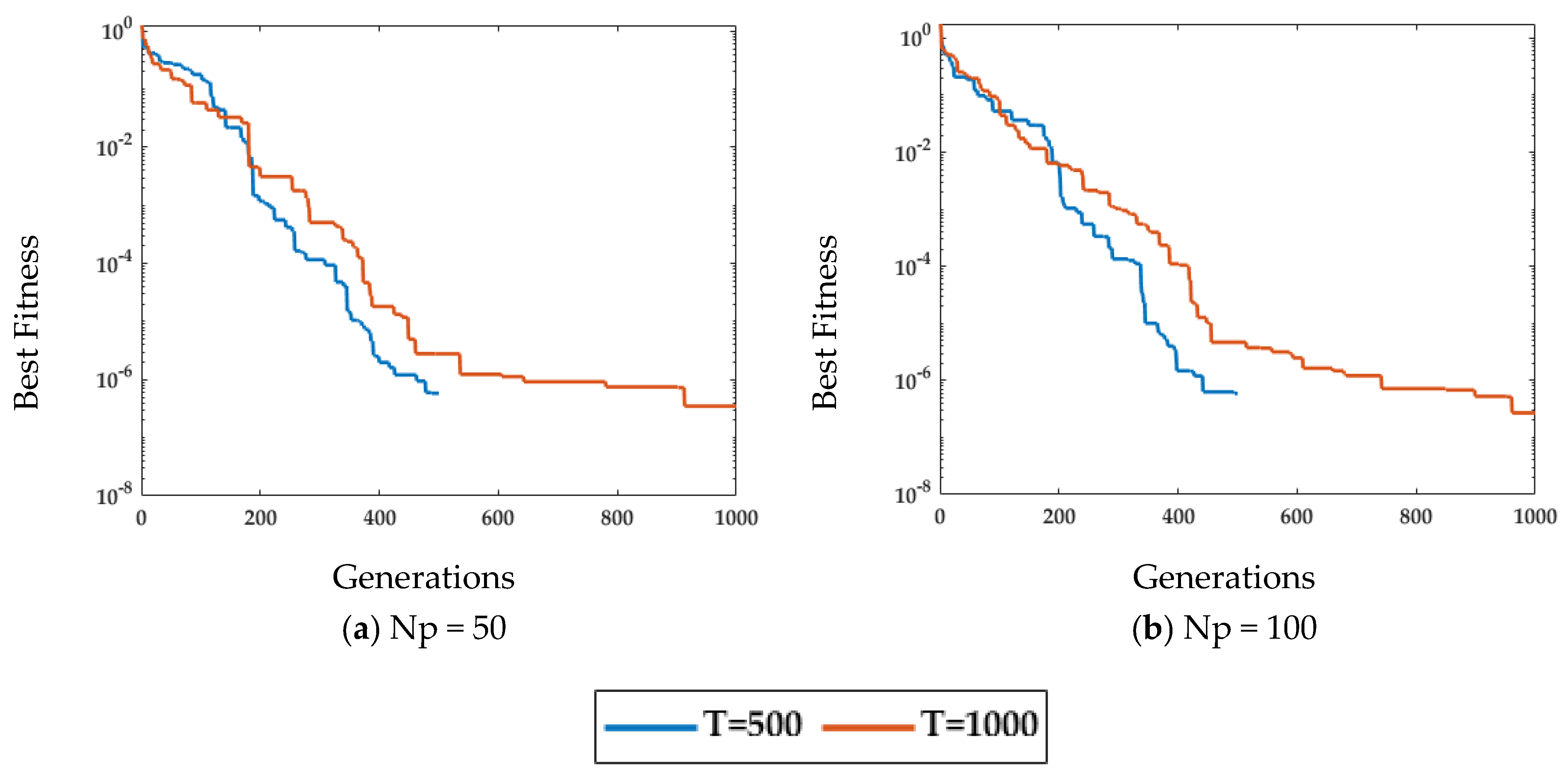
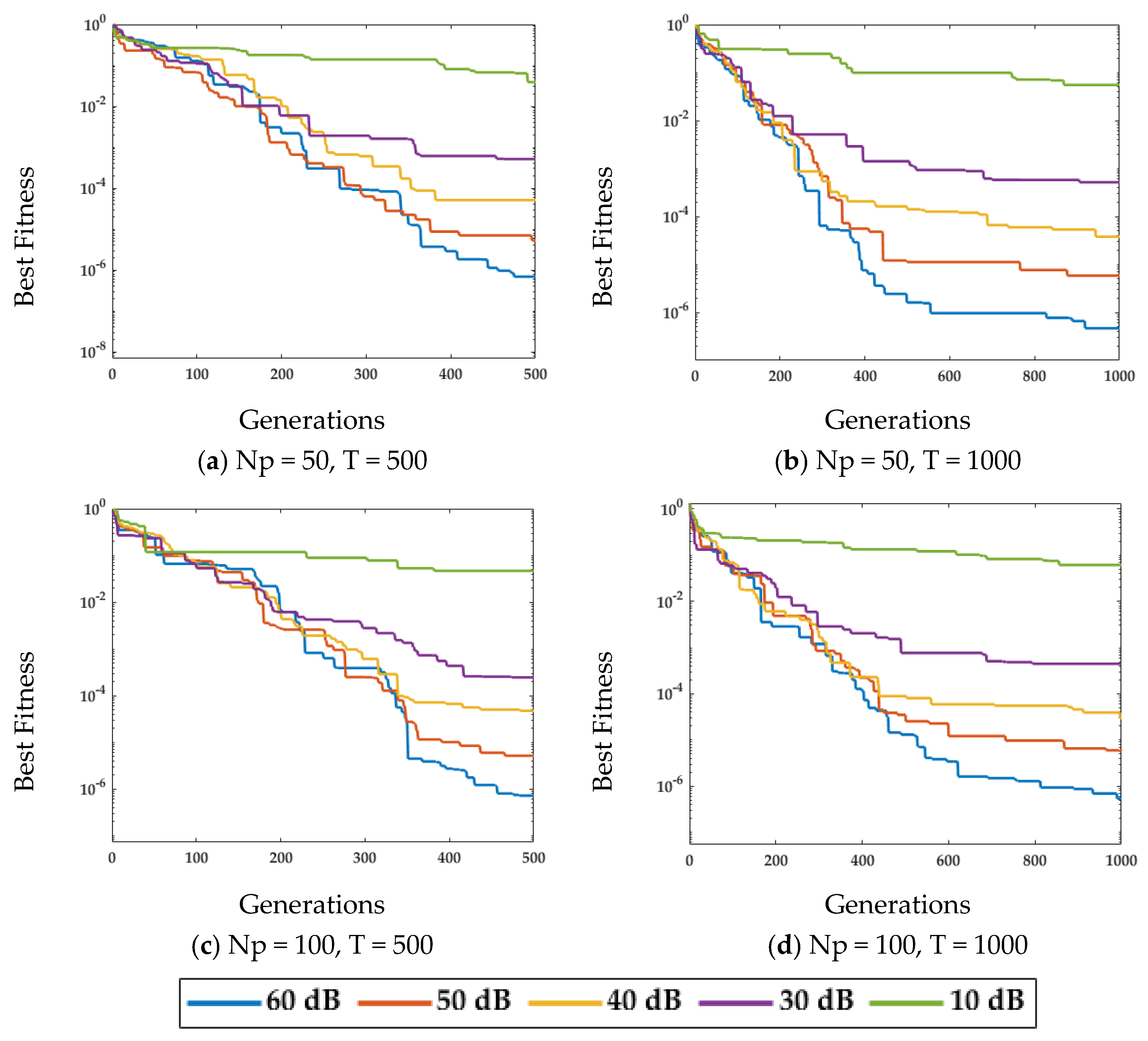
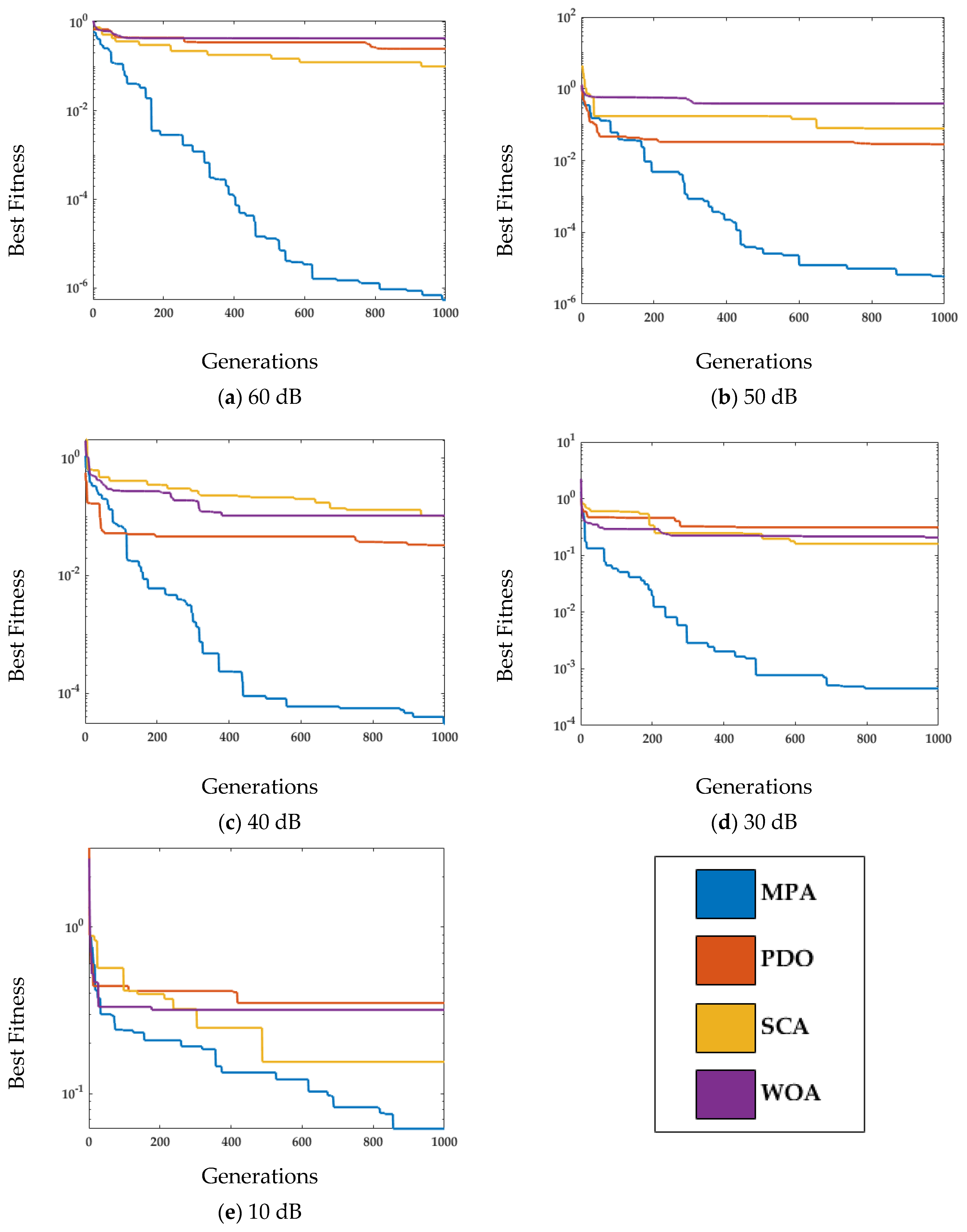
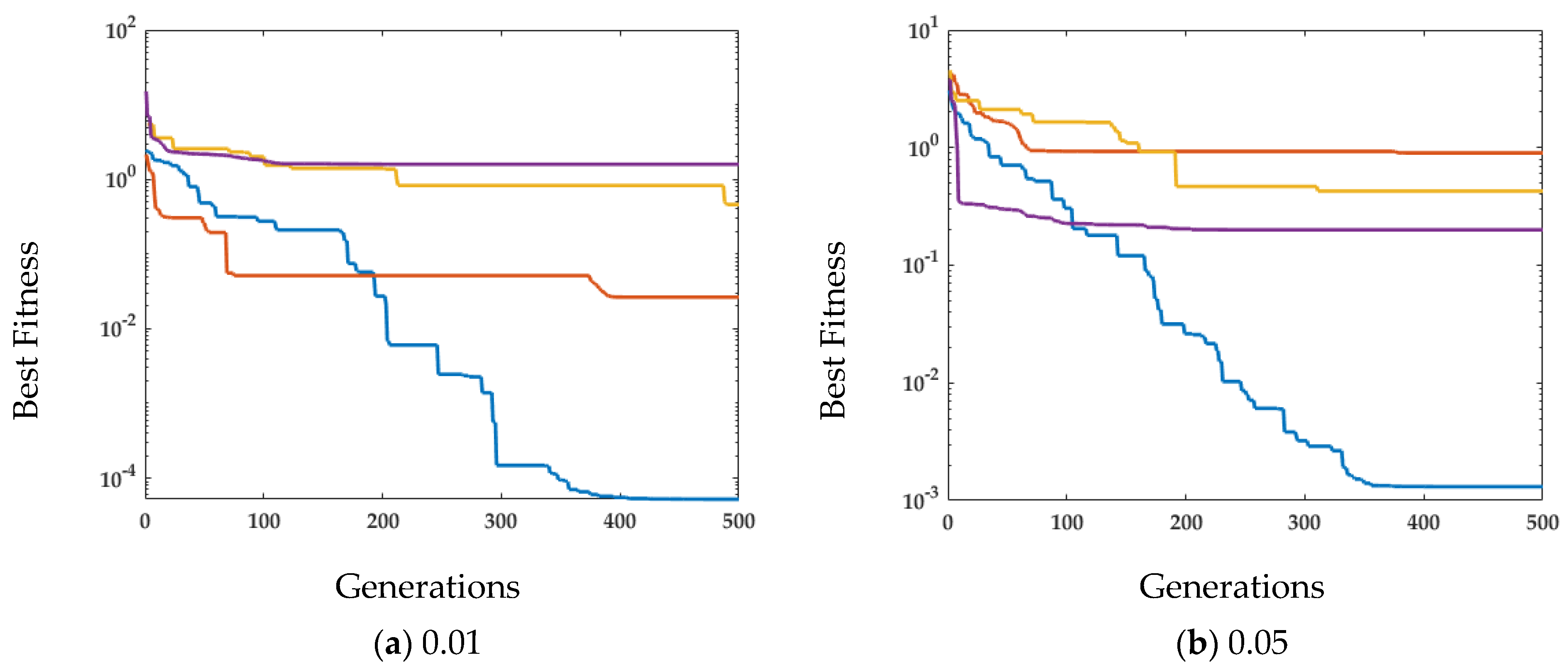
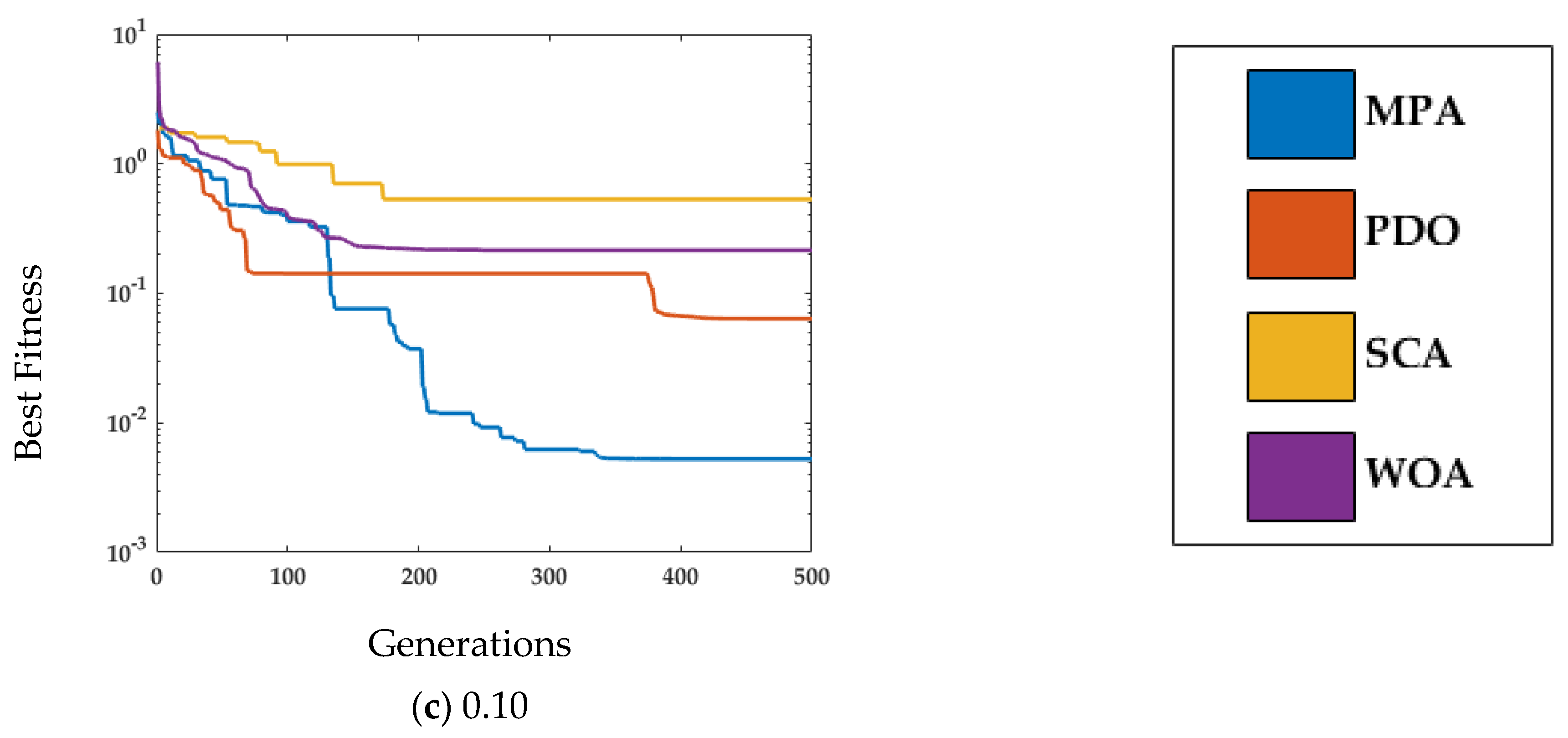
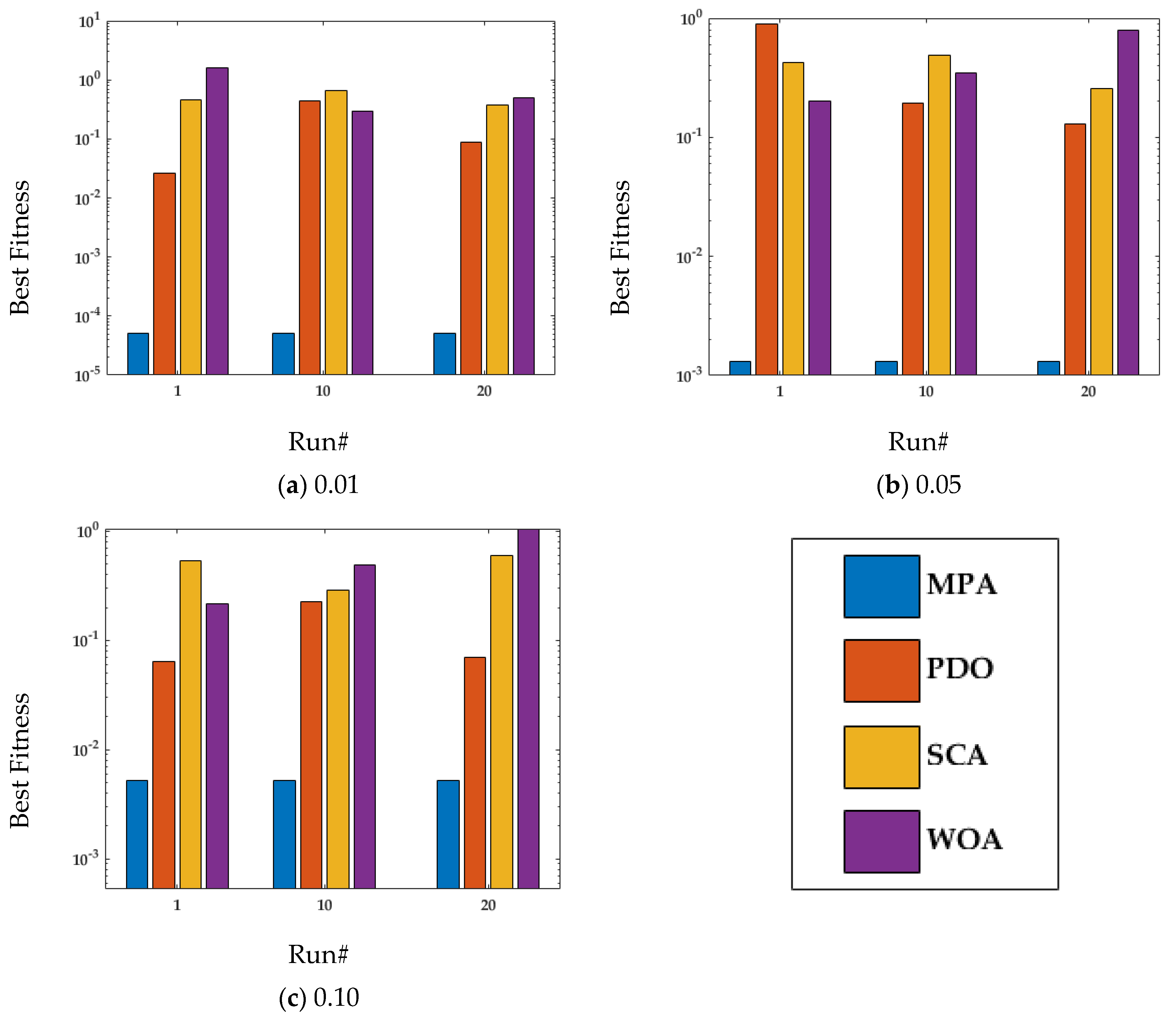
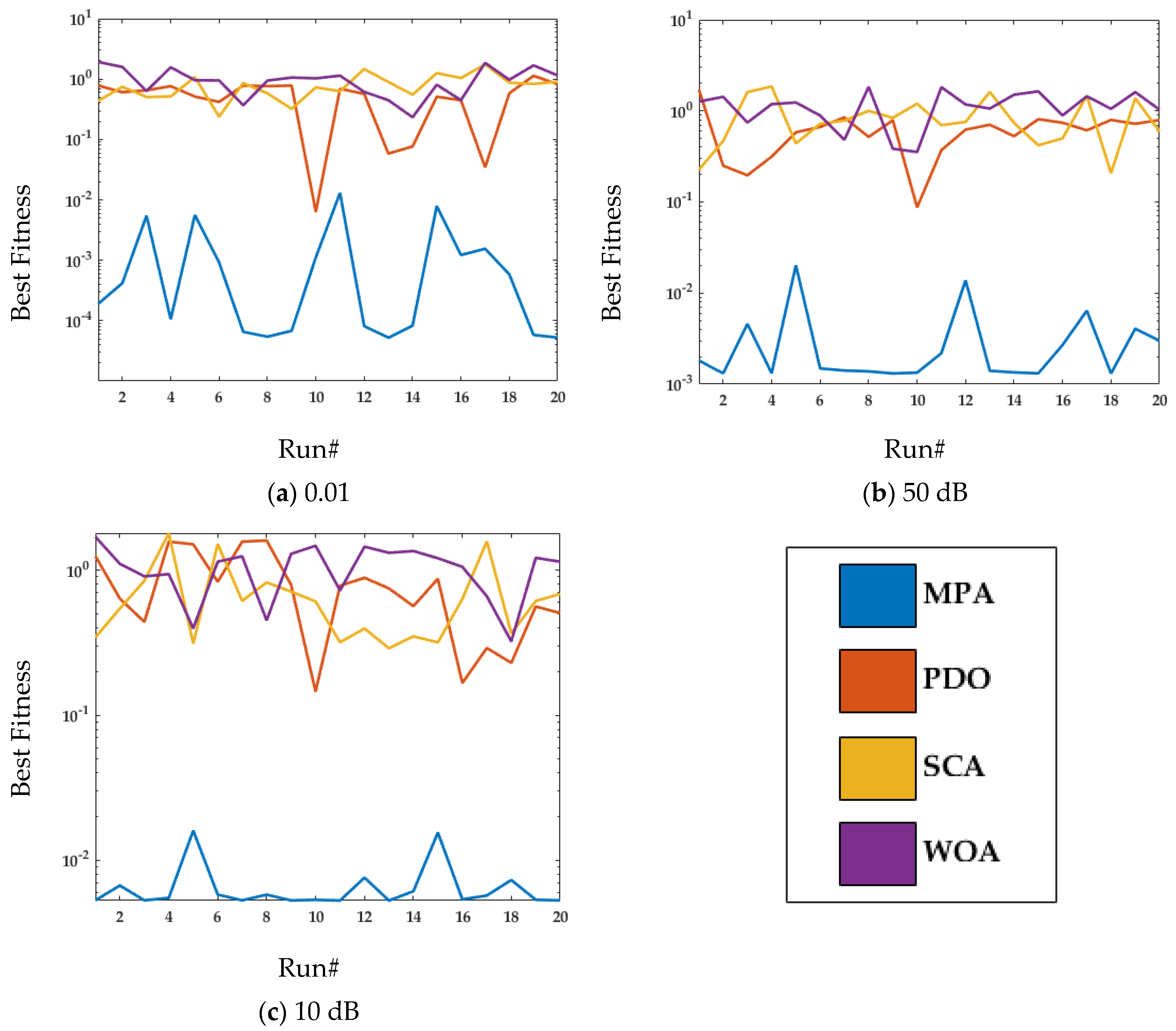
4.1. Case Study 1
4.2. Case Study 2
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schoukens, J.; Ljung, L. Nonlinear System Identification: A User-Oriented Road Map. IEEE Control Syst. 2019, 39, 28–99. [Google Scholar] [CrossRef]
- Yukai, S.; Chao, Y.; Zhigang, W.; Liuyue, B. Nonlinear System Identification of an All Movable Fin with Rotational Freeplay by Subspace-Based Method. Appl. Sci. 2020, 10, 1205. [Google Scholar] [CrossRef]
- Giri, F.; Bai, E.W. (Eds.) Block-Oriented Nonlinear System Identification; Springer: Berlin/Heidelberg, Germany, 2010; Volume 1, p. 0278-0046. [Google Scholar]
- Billings, S.A. Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Tissaoui, K. Forecasting implied volatility risk indexes: International evidence using Hammerstein-ARX approach. Int. Rev. Financial Anal. 2019, 64, 232–249. [Google Scholar] [CrossRef]
- Bai, Y.-T.; Wang, X.-Y.; Jin, X.-B.; Zhao, Z.-Y.; Zhang, B.-H. A Neuron-Based Kalman Filter with Nonlinear Autoregressive Model. Sensors 2020, 20, 299. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1987. [Google Scholar]
- Narendra, K.; Gallman, P. An iterative method for the identification of nonlinear systems using a Hammerstein model. IEEE Trans. Autom. Control 1966, 11, 546–550. [Google Scholar] [CrossRef]
- Chang, F.; Luus, R. A noniterative method for identification using Hammerstein model. IEEE Trans. Autom. Control 1971, 16, 464–468. [Google Scholar] [CrossRef]
- Vörös, J. Parameter identification of discontinuous hammerstein systems. Automatica 1997, 33, 1141–1146. [Google Scholar] [CrossRef]
- Voros, J. Recursive identification of hammerstein systems with discontinuous nonlinearities containing dead-zones. IEEE Trans. Autom. Control 2003, 48, 2203–2206. [Google Scholar] [CrossRef]
- Chen, H.; Ding, F. Hierarchical Least Squares Identification for Hammerstein Nonlinear Controlled Autoregressive Systems. Circuits Syst. Signal Process. 2014, 34, 61–75. [Google Scholar] [CrossRef]
- Ding, F.; Chen, H.; Xu, L.; Dai, J.; Li, Q.; Hayat, T. A hierarchical least squares identification algorithm for Hammerstein nonlinear systems using the key term separation. J. Frankl. Inst. 2018, 355, 3737–3752. [Google Scholar] [CrossRef]
- Chen, H.; Xiao, Y.; Ding, F. Hierarchical gradient parameter estimation algorithm for Hammerstein nonlinear systems using the key term separation principle. Appl. Math. Comput. 2014, 247, 1202–1210. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Khan, Z.A.; Zubair, S.; Raja, M.A.Z.; Dedovic, N. Normalized fractional adaptive methods for nonlinear control autoregressive systems. Appl. Math. Model. 2018, 66, 457–471. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Aslam, M.S.; Baleanu, D.; Raja, M.A.Z. Design of sign fractional optimization paradigms for parameter estimation of nonlinear Hammerstein systems. Neural Comput. Appl. 2019, 32, 8381–8399. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Raja MA, Z.; He, Y.; Khan, Z.A.; Machado, J.T. Design of multi innovation fractional LMS algorithm for parameter estimation of input nonlinear control autoregressive systems. Appl. Math. Model. 2021, 93, 412–425. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Raja, M.A.Z.; Khan, Z.A.; Cheema, K.M.; Milyani, A.H. Hierarchical Quasi-Fractional Gradient Descent Method for Parameter Estimation of Nonlinear ARX Systems Using Key Term Separation Principle. Mathematics 2021, 9, 3302. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Raja, M.A.Z.; Khan, Z.A.; Mehmood, A.; Shah, S.M. Design of fractional hierarchical gradient descent algorithm for parameter estimation of nonlinear control autoregressive systems. Chaos Solitons Fractals 2022, 157, 111913. [Google Scholar] [CrossRef]
- Gotmare, A.; Bhattacharjee, S.S.; Patidar, R.; George, N.V. Swarm and evolutionary computing algorithms for system identification and filter design: A comprehensive review. Swarm Evol. Comput. 2017, 32, 68–84. [Google Scholar] [CrossRef]
- Jui, J.J.; Ahmad, M.A. A hybrid metaheuristic algorithm for identification of continuous-time Hammerstein systems. Appl. Math. Model. 2021, 95, 339–360. [Google Scholar] [CrossRef]
- Raja MA, Z.; Shah, A.A.; Mehmood, A.; Chaudhary, N.I.; Aslam, M.S. Bio-inspired computational heuristics for parameter estimation of nonlinear Hammerstein controlled autoregressive system. Neural Comput. Appl. 2018, 29, 1455–1474. [Google Scholar] [CrossRef]
- Mehmood, A.; Aslam, M.S.; Chaudhary, N.I.; Zameer, A.; Raja, M.A.Z. Parameter estimation for Hammerstein control autoregressive systems using differential evolution. Signal Image Video Process. 2018, 12, 1603–1610. [Google Scholar] [CrossRef]
- Mehmood, A.; Raja, M.A.Z.; Shi, P.; Chaudhary, N.I. Weighted differential evolution-based heuristic computing for identification of Hammerstein systems in electrically stimulated muscle modeling. Soft Comput. 2022, 26, 8929–8945. [Google Scholar] [CrossRef]
- Mehmood, A.; Zameer, A.; Chaudhary, N.I.; Raja, M.A.Z. Backtracking search heuristics for identification of electrical muscle stimulation models using Hammerstein structure. Appl. Soft Comput. 2019, 84, 105705. [Google Scholar] [CrossRef]
- Altaf, F.; Chang, C.-L.; Chaudhary, N.I.; Raja, M.A.Z.; Cheema, K.M.; Shu, C.-M.; Milyani, A.H. Adaptive Evolutionary Computation for Nonlinear Hammerstein Control Autoregressive Systems with Key Term Separation Principle. Mathematics 2022, 10, 1001. [Google Scholar] [CrossRef]
- Nanda, S.J.; Panda, G.; Majhi, B. Improved identification of Hammerstein plants using new CPSO and IPSO algorithms. Expert Syst. Appl. 2010, 37, 6818–6831. [Google Scholar] [CrossRef]
- Gotmare, A.; Patidar, R.; George, N.V. Nonlinear system identification using a cuckoo search optimized adaptive Hammerstein model. Expert Syst. Appl. 2015, 42, 2538–2546. [Google Scholar] [CrossRef]
- Janjanam, L.; Saha, S.K.; Kar, R. Optimal Design of Hammerstein Cubic Spline Filter for Non-Linear System Modelling Based on Snake Optimiser. IEEE Trans. Ind. Electron. 2022. [Google Scholar] [CrossRef]
- Altaf, F.; Chang, C.-L.; Chaudhary, N.I.; Cheema, K.M.; Raja, M.A.Z.; Shu, C.-M.; Milyani, A.H. Novel Fractional Swarming with Key Term Separation for Input Nonlinear Control Autoregressive Systems. Fractal Fract. 2022, 6, 348. [Google Scholar] [CrossRef]
- Zheng, J.; Li, K.; Zhang, X. Wi-Fi Fingerprint-Based Indoor Localization Method via Standard Particle Swarm Optimization. Sensors 2022, 22, 5051. [Google Scholar] [CrossRef]
- Jiang, L.; Tajima, Y.; Wu, L. Application of Particle Swarm Optimization for Auto-Tuning of the Urban Flood Model. Water 2022, 14, 2819. [Google Scholar] [CrossRef]
- Mehmood, K.; Chaudhary, N.I.; Khan, Z.A.; Cheema, K.M.; Raja, M.A.Z.; Milyani, A.H.; Azhari, A.A. Dwarf Mongoose Optimization Metaheuristics for Autoregressive Exogenous Model Identification. Mathematics 2022, 10, 3821. [Google Scholar] [CrossRef]
- Alissa, K.A.; Elkamchouchi, D.H.; Tarmissi, K.; Yafoz, A.; Alsini, R.; Alghushairy, O.; Mohamed, A.; Al Duhayyim, M. Dwarf Mongoose Optimization with Machine-Learning-Driven Ransomware Detection in Internet of Things Environment. Appl. Sci. 2022, 12, 9513. [Google Scholar] [CrossRef]
- Ji, H.; Hu, H.; Peng, X. Multi-Underwater Gliders Coverage Path Planning Based on Ant Colony Optimization. Electronics 2022, 11, 3021. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, S.; Chen, M.; Liu, W. Detecting Dynamic Communities in Vehicle Movements Using Ant Colony Optimization. Appl. Sci. 2022, 12, 7608. [Google Scholar] [CrossRef]
- Al-Shammaa, A.A.; MAbdurraqeeb, A.; Noman, A.M.; Alkuhayli, A.; Farh, H.M. Hardware-In-the-Loop Validation of Direct MPPT Based Cuckoo Search Optimization for Partially Shaded Photovoltaic System. Electronics 2022, 11, 1655. [Google Scholar] [CrossRef]
- Hameed, K.; Khan, W.; Abdalla, Y.S.; Al-Harbi, F.F.; Armghan, A.; Asif, M.; Qamar, M.S.; Ali, F.; Miah, S.; Alibakhshikenari, M.; et al. Far-Field DOA Estimation of Uncorrelated RADAR Signals through Coprime Arrays in Low SNR Regime by Implementing Cuckoo Search Algorithm. Electronics 2022, 11, 558. [Google Scholar] [CrossRef]
- Mehmood, K.; Chaudhary, N.I.; Khan, Z.A.; Raja, M.A.Z.; Cheema, K.M.; Milyani, A.H. Design of Aquila Optimization Heuristic for Identification of Control Autoregressive Systems. Mathematics 2022, 10, 1749. [Google Scholar] [CrossRef]
- Lee, J.G.; Chim, S.; Park, H.H. Energy-efficient cluster-head selection for wireless sensor networks using sampling-based spider monkey optimization. Sensors 2019, 19, 5281. [Google Scholar] [CrossRef]
- He, F.; Ye, Q. A Bearing Fault Diagnosis Method Based on Wavelet Packet Transform and Convolutional Neural Network Optimized by Simulated Annealing Algorithm. Sensors 2022, 22, 1410. [Google Scholar] [CrossRef]
- Xiao, S.; Tan, X.; Wang, J. A Simulated Annealing Algorithm and Grid Map-Based UAV Coverage Path Planning Method for 3D Reconstruction. Electronics 2021, 10, 853. [Google Scholar] [CrossRef]
- Thiagarajan, K.; Anandan, M.M.; Stateczny, A.; Divakarachari, P.B.; Lingappa, H.K. Satellite Image Classification Using a Hierarchical Ensemble Learning and Correlation Coefficient-Based Gravitational Search Algorithm. Remote Sens. 2021, 13, 4351. [Google Scholar] [CrossRef]
- Owolabi, T.; Rahman, M.A. Energy Band Gap Modeling of Doped Bismuth Ferrite Multifunctional Material Using Gravitational Search Algorithm Optimized Support Vector Regression. Crystals 2021, 11, 246. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Turky, R.A.; Alghuwainem, S.; Tostado-Véliz, M.; Jurado, F. Circle Search Algorithm: A Geometry-Based Metaheuristic Optimization Algorithm. Mathematics 2022, 10, 1626. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Turky, R.A.; Alghuwainem, S.; Loo, K.-H.; Elgendy, M. Optimal PEM Fuel Cell Model Using a Novel Circle Search Algorithm. Electronics 2022, 11, 1808. [Google Scholar] [CrossRef]
- Ehteram, M.; Ahmed, A.N.; Ling, L.; Fai, C.M.; Latif, S.D.; Afan, H.A.; Banadkooki, F.B.; El-Shafie, A. Pipeline scour rates prediction-based model utilizing a multilayer perceptron-colliding body algorithm. Water 2020, 12, 902. [Google Scholar] [CrossRef]
- Yang, W.; Xia, K.; Li, T.; Xie, M.; Zhao, Y. An Improved Transient Search Optimization with Neighborhood Dimensional Learning for Global Optimization Problems. Symmetry 2021, 13, 244. [Google Scholar] [CrossRef]
- Almabrok, A.; Psarakis, M.; Dounis, A. Fast Tuning of the PID Controller in An HVAC System Using the Big Bang–Big Crunch Algorithm and FPGA Technology. Algorithms 2018, 11, 146. [Google Scholar] [CrossRef]
- Wu, T.; Li, X.; Zhou, D.; Li, N.; Shi, J. Differential Evolution Based Layer-Wise Weight Pruning for Compressing Deep Neural Networks. Sensors 2021, 21, 880. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Zhang, D.; Lu, S.; Tang, X.; Phung, T. Differential Evolution-Based Overcurrent Protection for DC Microgrids. Energies 2021, 14, 5026. [Google Scholar] [CrossRef]
- Drachal, K.; Pawłowski, M. A Review of the Applications of Genetic Algorithms to Forecasting Prices of Commodities. Economies 2021, 9, 6. [Google Scholar] [CrossRef]
- Awan, W.A.; Zaidi, A.; Hussain, M.; Hussain, N.; Syed, I. The design of a wideband antenna with notching characteristics for small devices using a genetic algorithm. Mathematics 2021, 9, 2113. [Google Scholar] [CrossRef]
- Strumberger, I.; Minovic, M.; Tuba, M.; Bacanin, N. Performance of Elephant Herding Optimization and Tree Growth Algorithm Adapted for Node Localization in Wireless Sensor Networks. Sensors 2019, 19, 2515. [Google Scholar] [CrossRef] [PubMed]
- Abualigah, L.; Diabat, A.; Sumari, P.; Gandomi, A. A Novel Evolutionary Arithmetic Optimization Algorithm for Multilevel Thresholding Segmentation of COVID-19 CT Images. Processes 2021, 9, 1155. [Google Scholar] [CrossRef]
- Sharma, A.; Khan, R.A.; Sharma, A.; Kashyap, D.; Rajput, S. A Novel Opposition-Based Arithmetic Optimization Algorithm for Parameter Extraction of PEM Fuel Cell. Electronics 2021, 10, 2834. [Google Scholar] [CrossRef]
- Faradonbeh, R.S.; Monjezi, M.; Armaghani, D.J. Genetic programing and non-linear multiple regression techniques to predict backbreak in blasting operation. Eng. Comput. 2015, 32, 123–133. [Google Scholar] [CrossRef]
- Masoumi, N.; Xiao, Y.; Rivaz, H. ARENA: Inter-modality affine registration using evolutionary strategy. Int. J. Comput. Assist. Radiol. Surg. 2018, 14, 441–450. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Shaheen, M.A.; Yousri, D.; Fathy, A.; Hasanien, H.M.; Alkuhayli, A.; Muyeen, S.M. A novel application of improved marine predators algorithm and particle swarm optimization for solving the ORPD problem. Energies 2020, 13, 5679. [Google Scholar] [CrossRef]
- Ebeed, M.; Alhejji, A.; Kamel, S.; Jurado, F. Solving the optimal reactive power dispatch using marine predators algorithm considering the uncertainties in load and wind-solar generation systems. Energies 2020, 13, 4316. [Google Scholar] [CrossRef]
- He, Q.; Lan, Z.; Zhang, D.; Yang, L.; Luo, S. Improved Marine Predator Algorithm for Wireless Sensor Network Coverage Optimization Problem. Sustainability 2022, 14, 9944. [Google Scholar] [CrossRef]
- Yang, L.; He, Q.; Yang, L.; Luo, S. A Fusion Multi-Strategy Marine Predator Algorithm for Mobile Robot Path Planning. Appl. Sci. 2022, 12, 9170. [Google Scholar] [CrossRef]
- Wadood, A.; Khan, S.; Khan, B.M.; Ali, H.; Rehman, Z. Application of Marine Predator Algorithm in Solving the Problem of Directional Overcurrent Relay in Electrical Power System. Eng. Proc. 2021, 12, 9. [Google Scholar]
- Lu, X.; Nanehkaran, Y.A.; Fard, M.K. A Method for Optimal Detection of Lung Cancer Based on Deep Learning Optimized by Marine Predators Algorithm. Comput. Intell. Neurosci. 2021, 2021, 3694723. [Google Scholar] [CrossRef] [PubMed]
- Hoang, N.-D.; Tran, X.-L. Remote Sensing–Based Urban Green Space Detection Using Marine Predators Algorithm Optimized Machine Learning Approach. Math. Probl. Eng. 2021, 2021, 5586913. [Google Scholar] [CrossRef]
- Yang, W.; Xia, K.; Li, T.; Xie, M.; Song, F. A Multi-Strategy Marine Predator Algorithm and Its Application in Joint Regularization Semi-Supervised ELM. Mathematics 2021, 9, 291. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Agushaka, J.O.; Abualigah, L.; Mirjalili, S.; Gandomi, A.H. Prairie Dog Optimization Algorithm. Neural Comput. Appl. 2022, 34, 20017–20065. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, J.; Alkhathlan, A. Informatisation of educational reform based on fractional differential equations. Appl. Math. Nonlinear Sci. 2021. [Google Scholar] [CrossRef]
- Zhang, X.; Alahmadi, D. Study on the maximum value of flight distance based on the fractional differential equation for calculating the best path of shot put. Appl. Math. Nonlinear Sci. 2021. [Google Scholar] [CrossRef]
- Che, Y.; Keir, M.Y.A. Study on the training model of football movement trajectory drop point based on fractional differential equation. Appl. Math. Nonlinear Sci. 2021, 7, 425–430. [Google Scholar] [CrossRef]
- Chandra, S.; Hayashibe, M.; Thondiyath, A. Muscle Fatigue Induced Hand Tremor Clustering in Dynamic Laparoscopic Manipulation. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 50, 5420–5431. [Google Scholar] [CrossRef]
- Xu, W.; Chu, B.; Rogers, E. Iterative learning control for robotic-assisted upper limb stroke rehabilitation in the presence of muscle fatigue. Control Eng. Pract. 2014, 31, 63–72. [Google Scholar] [CrossRef]


| Domain | Technique |
|---|---|
| Swarm Intelligence | Particle swarm optimization (PSO) [31,32] |
| Dwarf Mongoose optimization (DMO) [33,34] | |
| Ant Colony optimization (ACO) [35,36] | |
| Cuckoo search [37,38] | |
| Aquila Optimizer (AO) [39] | |
| Spider monkey optimization [40] | |
| Physics based | Simulated Annealing [41,42] |
| Gravitational search algorithm [43,44] | |
| Circle search algorithm [45,46] | |
| Colliding bodies optimizer [47] | |
| Transient search optimizer [48] | |
| Big bang big crunch [49] | |
| Evolutionary | Differential Evolution [50,51] |
| Genetic algorithm [52,53] | |
| Tree growth algorithm [54] | |
| Arithmetic optimization algorithm [55,56] | |
| Genetic programming [57] | |
| Evolutionary strategy [58] |
| Methods | T | Np | Design Parameters | Best Fitness | Avg Fitness | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MPA | 500 | 50 | −1.0999 | 0.9003 | −0.7999 | −0.6007 | −0.8994 | 0.5998 | 0.1998 | ||
| 100 | −1.1004 | 0.9004 | −0.8003 | −0.5999 | −0.8983 | 0.6010 | 0.1999 | ||||
| 1000 | 50 | −1.0997 | 0.8997 | −0.7998 | −0.5993 | −0.9028 | 0.5992 | 0.2003 | |||
| 100 | −1.0999 | 0.9000 | −0.7997 | −0.5998 | −0.9003 | 0.6002 | 0.2002 | ||||
| PDO | 500 | 50 | −1.0518 | 0.8524 | −0.6261 | −0.7220 | −0.9588 | 0.5851 | 0.2329 | 0.0097 | 0.1631 |
| 100 | −1.0600 | 0.8566 | −0.7128 | −0.6272 | −1.0817 | 0.5417 | 0.2249 | 0.0059 | 0.1618 | ||
| 1000 | 50 | −1.0701 | 0.8637 | −0.6899 | −0.8059 | −0.8724 | 0.5222 | 0.1791 | 0.0119 | 0.1677 | |
| 100 | −1.0730 | 0.8670 | −0.7100 | −0.6694 | −0.9522 | 0.5646 | 0.2155 | 0.0039 | 0.1848 | ||
| SCA | 500 | 50 | −1.1554 | 0.8944 | −1.2713 | −0.3910 | −1.3633 | 0.2760 | 0.0024 | 0.0785 | 0.1676 |
| 100 | −1.0469 | 0.8100 | −0.9144 | −0.3546 | −1.8413 | 0.2371 | 0.2565 | 0.0719 | 0.1567 | ||
| 1000 | 50 | −0.9063 | 0.6642 | −0.8466 | −0.6712 | −1.7836 | −0.0064 | 0.0990 | 0.1167 | 0.1977 | |
| 100 | −1.0292 | 0.8255 | −1.0403 | −0.3248 | −1.2033 | 0.5034 | 0.1878 | 0.0464 | 0.1285 | ||
| WOA | 500 | 50 | −1.1307 | 0.9794 | −1.0294 | −0.7458 | −0.0103 | 0.8304 | 0.2124 | 0.1346 | 0.3724 |
| 100 | −1.1050 | 0.9013 | −0.8204 | −0.7087 | −0.8466 | 0.5344 | 0.1570 | 0.0042 | 0.3019 | ||
| 1000 | 50 | −1.0270 | 0.8621 | −0.4477 | −0.6913 | −0.7818 | 0.8436 | 0.3795 | 0.0294 | 0.3219 | |
| 100 | −0.9356 | 0.7506 | −0.5725 | −0.6927 | −1.4624 | 0.4017 | 0.2705 | 0.0521 | 0.2748 | ||
| True Values | −1.1000 | 0.9000 | −0.8000 | −0.6000 | −0.9000 | 0.6000 | 0.2000 | 0 | 0 | ||
| Methods | T | Np | Design Parameters | Best Fitness | Avg Fitness | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MPA | 500 | 50 | −1.0990 | 0.8998 | −0.7971 | −0.6027 | −0.9000 | 0.6006 | 0.2000 | ||
| 100 | −1.1007 | 0.9007 | −0.8010 | −0.6005 | −0.8976 | 0.5999 | 0.1995 | ||||
| 1000 | 50 | −1.1007 | 0.9007 | −0.8016 | −0.6004 | −0.9021 | 0.5988 | 0.1989 | |||
| 100 | −1.0999 | 0.8996 | −0.7972 | −0.6010 | −0.9034 | 0.5994 | 0.2006 | ||||
| PDO | 500 | 50 | −1.0989 | 0.8856 | −0.6730 | −0.8708 | −0.8491 | 0.4867 | 0.1613 | 0.0122 | 0.2468 |
| 100 | −1.0950 | 0.8850 | −0.7609 | −0.6493 | −1.0193 | 0.5226 | 0.1898 | 0.0026 | 0.1971 | ||
| 1000 | 50 | −1.0568 | 0.8489 | −0.6975 | −0.6522 | −1.0537 | 0.5183 | 0.2255 | 0.0070 | 0.2406 | |
| 100 | −1.0821 | 0.8792 | −0.6982 | −0.7261 | −0.8873 | 0.5679 | 0.2011 | 0.0031 | 0.1237 | ||
| SCA | 500 | 50 | −1.0086 | 0.7452 | −0.4993 | −0.7635 | −1.4064 | 0.4192 | 0.2437 | 0.0902 | 0.1928 |
| 100 | −1.1220 | 1.0084 | −0.3534 | −1.1780 | −0.1565 | 0.8028 | 0.2544 | 0.0801 | 0.1949 | ||
| 1000 | 50 | −1.1596 | 0.8947 | −1.0397 | −0.4481 | −1.0611 | 0.3793 | 0.1573 | 0.0295 | 0.1382 | |
| 100 | −0.9708 | 0.7561 | −0.4713 | −0.7527 | −1.2920 | 0.4789 | 0.2752 | 0.0588 | 0.1212 | ||
| WOA | 500 | 50 | −1.0691 | 0.8544 | −0.9376 | −0.4316 | −1.1141 | 0.5184 | 0.2023 | 0.0104 | 0.3667 |
| 100 | −0.9926 | 0.8132 | −0.6119 | −0.6398 | −1.0712 | 0.6237 | 0.2896 | 0.0216 | 0.3111 | ||
| 1000 | 50 | −1.0723 | 0.9288 | −0.2641 | −0.9755 | −0.2221 | 0.9602 | 0.3590 | 0.0657 | 0.4094 | |
| 100 | −1.0765 | 0.8998 | −0.3190 | −1.1725 | −0.5884 | 0.6273 | 0.2237 | 0.0370 | 0.2990 | ||
| True Values | −1.1000 | 0.9000 | −0.8000 | −0.6000 | −0.9000 | 0.6000 | 0.2000 | 0 | 0 | ||
| Methods | T | Np | Design Parameters | Best Fitness | Avg Fitness | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MPA | 500 | 50 | −1.0976 | 0.9002 | −0.8108 | −0.5990 | −0.9099 | 0.5912 | 0.1952 | ||
| 100 | −1.0992 | 0.8985 | −0.7965 | −0.6014 | −0.9045 | 0.5973 | 0.2016 | ||||
| 1000 | 50 | −1.0978 | 0.8969 | −0.7999 | −0.6023 | −0.9044 | 0.5961 | 0.1984 | |||
| 100 | −1.0978 | 0.8965 | −0.7981 | −0.5994 | −0.9046 | 0.5976 | 0.2016 | ||||
| PDO | 500 | 50 | −1.1077 | 0.8619 | −0.7954 | −0.8527 | −0.6526 | 0.5071 | 0.1500 | 0.0260 | 0.2769 |
| 100 | −1.0527 | 0.8379 | −0.7737 | −0.6079 | −0.9045 | 0.5709 | 0.2188 | 0.0071 | 0.1967 | ||
| 1000 | 50 | −1.0243 | 0.8187 | −0.8046 | −0.5028 | −1.2278 | 0.5109 | 0.2319 | 0.0110 | 0.1863 | |
| 100 | −1.1020 | 0.8933 | −0.8539 | −0.5378 | −0.9603 | 0.5789 | 0.1965 | 0.1612 | |||
| SCA | 500 | 50 | −1.2458 | 1.0114 | −1.2823 | −0.5958 | −0.4440 | 0.6779 | 0.0084 | 0.1362 | 0.2290 |
| 100 | −1.1005 | 0.9112 | −0.7042 | −0.7149 | −0.7310 | 0.6718 | 0.2431 | 0.0195 | 0.1565 | ||
| 1000 | 50 | −1.0389 | 0.8189 | −0.8901 | −0.5615 | −1.1855 | 0.4103 | 0.2097 | 0.0556 | 0.1500 | |
| 100 | −1.1279 | 0.8664 | −1.1919 | −0.3155 | −1.4402 | 0.2008 | 0.1338 | 0.0530 | 0.1164 | ||
| WOA | 500 | 50 | −1.1736 | 0.9365 | −1.3780 | −0.3366 | −0.5491 | 0.6183 | 0.0930 | 0.0515 | 0.4267 |
| 100 | −0.4672 | 0.3825 | −0.4320 | −1.1173 | −1.9501 | −0.1694 | 0.1607 | 0.1660 | 0.4192 | ||
| 1000 | 50 | −1.0051 | 0.8141 | −0.2655 | −0.9009 | −1.0431 | 0.5755 | 0.3375 | 0.0660 | 0.4354 | |
| 100 | −0.7311 | 0.6054 | −0.3689 | −1.0833 | −1.0464 | 0.3766 | 0.2605 | 0.1053 | 0.2973 | ||
| True Values | −1.1000 | 0.9000 | −0.8000 | −0.6000 | −0.9000 | 0.6000 | 0.2000 | 0 | 0 | ||
| Methods | T | Np | Design Parameters | Best Fitness | Avg Fitness | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MPA | 500 | 50 | −1.0993 | 0.9027 | −0.8065 | −0.5937 | −0.9485 | 0.5739 | 0.2001 | ||
| 100 | −1.0884 | 0.8840 | −0.7943 | −0.6330 | −0.8651 | 0.5970 | 0.1908 | ||||
| 1000 | 50 | −1.1002 | 0.8957 | −0.7948 | −0.5956 | −0.9017 | 0.5975 | 0.2046 | |||
| 100 | −1.1034 | 0.9003 | −0.8125 | −0.5908 | −0.9229 | 0.5861 | 0.1983 | ||||
| PDO | 500 | 50 | −0.9118 | 0.6720 | −1.0179 | −0.4754 | −1.3536 | 0.2024 | 0.1578 | 0.0461 | 0.2711 |
| 100 | −1.0106 | 0.8154 | −0.6439 | −0.8667 | −0.9536 | 0.4742 | 0.1776 | 0.0095 | 0.2513 | ||
| 1000 | 50 | −0.8903 | 0.7105 | −0.6975 | −0.6399 | −1.3032 | 0.3473 | 0.2361 | 0.0230 | 0.2707 | |
| 100 | −1.0686 | 0.8515 | −0.9238 | −0.4909 | −0.9426 | 0.5455 | 0.1848 | 0.0048 | 0.1520 | ||
| SCA | 500 | 50 | −1.0744 | 0.8886 | −0.8612 | −0.4488 | −1.3053 | 0.3867 | 0.1863 | 0.0784 | 0.2060 |
| 100 | −1.1646 | 0.8605 | −1.3450 | −0.1424 | −1.3534 | 0.1530 | 0.1114 | 0.0709 | 0.1638 | ||
| 1000 | 50 | −1.0843 | 0.9227 | −0.6941 | −0.8631 | −1.0894 | 0.4127 | 0.1170 | 0.0719 | 0.1513 | |
| 100 | −1.0649 | 0.8689 | −0.8942 | −0.4560 | −0.9881 | 0.6281 | 0.2674 | 0.0489 | 0.1265 | ||
| WOA | 500 | 50 | −1.1271 | 0.9493 | 0.5670 | −1.9626 | 0.0465 | 0.8384 | 0.3408 | 0.1945 | 0.4343 |
| 100 | −0.9911 | 0.8016 | 0.0386 | −1.9189 | −0.5169 | 0.4345 | 0.1694 | 0.0826 | 0.3993 | ||
| 1000 | 50 | −1.2537 | 0.8268 | −1.9499 | 0.4810 | −1.8826 | −0.1519 | 0.0787 | 0.1643 | 0.3945 | |
| 100 | −1.1938 | 0.9840 | −0.8044 | −0.4657 | 0.0998 | 1.1197 | 0.3217 | 0.0991 | 0.3120 | ||
| True Values | −1.1000 | 0.9000 | −0.8000 | −0.6000 | −0.9000 | 0.6000 | 0.2000 | 0 | 0 | ||
| Methods | T | Np | Design Parameters | Best Fitness | Avg Fitness | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MPA | 500 | 50 | −1.0044 | 0.9248 | −0.6585 | −0.5989 | −1.2175 | 0.5851 | 0.2879 | 0.0266 | 0.0651 |
| 100 | −0.4721 | 0.3117 | 0.0368 | −1.0912 | −1.7806 | 0.1460 | 0.4641 | 0.0350 | 0.0585 | ||
| 1000 | 50 | −1.0797 | 0.8075 | −1.0865 | −0.3263 | −0.8897 | 0.5562 | 0.2113 | 0.0257 | 0.0537 | |
| 100 | −1.0986 | 0.9158 | −0.6987 | −0.6994 | −0.9153 | 0.5574 | 0.1941 | 0.0263 | 0.0417 | ||
| PDO | 500 | 50 | −0.4146 | 0.2163 | −0.3158 | −1.3845 | −1.1701 | 0.0619 | 0.1626 | 0.0591 | 0.3364 |
| 100 | −1.0651 | 0.6972 | −1.6685 | −0.2576 | −0.5222 | 0.4760 | 0.0516 | 0.0810 | 0.2740 | ||
| 1000 | 50 | −0.7514 | 0.5082 | −0.2147 | −0.6914 | −1.2349 | 0.8102 | 0.5757 | 0.0707 | 0.3043 | |
| 100 | −0.7529 | 0.5434 | −0.3480 | −1.1650 | −0.9728 | 0.3101 | 0.1813 | 0.0390 | 0.2830 | ||
| SCA | 500 | 50 | −0.6897 | 0.4400 | −0.8164 | −0.9964 | −1.5210 | −0.0562 | 0.1077 | 0.1750 | 0.2764 |
| 100 | −1.1314 | 0.8923 | −1.5527 | −0.7299 | −0.8486 | 0.2096 | 0.0101 | 0.0933 | 0.1738 | ||
| 1000 | 50 | −0.0228 | 0.0203 | −0.0002 | −2.0000 | −1.7703 | −0.2665 | 0.1090 | 0.1005 | 0.1781 | |
| 100 | −0.2253 | −0.0028 | −0.1909 | −1.6631 | −1.0498 | 0.1043 | 0.2336 | 0.0966 | 0.1620 | ||
| WOA | 500 | 50 | −0.1134 | −0.0868 | −0.3416 | −0.7243 | −0.4913 | 0.7683 | 0.4553 | 0.1016 | 0.3102 |
| 100 | −1.3169 | 0.8183 | −1.6177 | 0.1795 | −1.4909 | 0.0159 | 0.1090 | 0.0760 | 0.2376 | ||
| 1000 | 50 | −0.7933 | 0.6662 | −1.2328 | −0.5992 | −1.9345 | −0.2411 | 0.0103 | 0.0824 | 0.2924 | |
| 100 | 0.0301 | 0.1867 | −1.9827 | −1.9827 | −1.0564 | −0.1705 | 0.0200 | 0.1355 | 0.2732 | ||
| True Values | −1.1000 | 0.9000 | −0.8000 | −0.6000 | −0.9000 | 0.6000 | 0.2000 | 0 | 0 | ||
| Methods | T | Design Parameters | Best Fitness | Avg Fitness | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MPA | 200 | −1.1017 | 0.8978 | −0.8044 | −0.5999 | −0.8932 | 0.6001 | 0.1980 | ||
| 500 | −1.1018 | 0.8979 | −0.8044 | −0.5996 | −0.8920 | 0.6010 | 0.1982 | |||
| PDO | 200 | −1.0836 | 0.8766 | −0.7975 | −0.6473 | −1.0023 | 0.5269 | 0.1740 | 0.5494 | |
| 500 | −1.0899 | 0.8948 | −0.5766 | −0.6963 | −0.7177 | 0.7521 | 0.2727 | 0.0146 | 0.3834 | |
| SCA | 200 | −1.1650 | 0.9793 | −1.8630 | −1.2628 | 0.0036 | 0.6294 | 0.0072 | 0.2384 | 0.8104 |
| 500 | −1.1364 | 0.8896 | −1.6057 | −0.2327 | −0.7748 | 0.5465 | 0.0233 | 0.0867 | 0.4969 | |
| WOA | 200 | −0.9963 | 0.7957 | −0.3799 | −0.7507 | −1.3856 | 0.6501 | 0.3586 | 0.2331 | 1.0182 |
| 500 | −1.1450 | 0.9706 | −0.2738 | −0.6472 | 0.3553 | 1.4730 | 0.4975 | 0.1753 | 0.6517 | |
| True Values | −1.1000 | 0.9000 | −0.8000 | −0.6000 | −0.9000 | 0.6000 | 0.2000 | 0 | 0 | |
| Methods | T | Design Parameters | Best Fitness | Avg Fitness | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MPA | 200 | −1.1109 | 0.8910 | −0.8271 | −0.5952 | −0.8589 | 0.6044 | 0.1903 | ||
| 500 | −1.1109 | 0.8910 | −0.8262 | −0.5954 | −0.8583 | 0.6049 | 0.1906 | |||
| PDO | 200 | −1.0406 | 0.8332 | −0.4206 | −1.3664 | −0.7828 | 0.4256 | 0.1194 | 0.0872 | 0.6333 |
| 500 | −1.0866 | 0.8555 | −0.8423 | −0.6316 | −1.0984 | 0.4647 | 0.1520 | 0.0172 | 0.4124 | |
| SCA | 200 | −1.1050 | 0.8054 | −1.4742 | −0.1922 | −1.0218 | 0.5351 | 0.0089 | 0.2073 | 0.8758 |
| 500 | −1.0695 | 0.8453 | −1.1957 | −1.4701 | −0.1459 | 0.5871 | 0.0042 | 0.1845 | 0.4258 | |
| WOA | 200 | −0.9064 | 0.7102 | −0.3235 | −1.1091 | −1.2099 | 0.4528 | 0.2038 | 0.3539 | 1.1520 |
| 500 | −1.0549 | 0.8315 | −1.0059 | −0.9560 | −1.2754 | 0.1507 | −0.0263 | 0.1994 | 0.5828 | |
| True Values | −1.1000 | 0.9000 | −0.8000 | −0.6000 | −0.9000 | 0.6000 | 0.2000 | 0 | 0 | |
| Methods | T | Design Parameters | Best Fitness | Avg Fitness | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MPA | 200 | −1.1267 | 0.8856 | −0.8717 | −0.5808 | −0.8127 | 0.6069 | 0.1776 | ||
| 500 | −1.1265 | 0.8857 | −0.8653 | −0.5835 | −0.8107 | 0.6093 | 0.1794 | |||
| PDO | 200 | −1.0194 | 0.7655 | −0.6219 | −0.9296 | −1.1517 | 0.3711 | 0.1296 | 0.1452 | 0.7990 |
| 500 | −1.0938 | 0.8706 | −0.6854 | −0.7346 | −0.8723 | 0.5692 | 0.2007 | 0.0172 | 0.3089 | |
| SCA | 200 | −1.0574 | 0.9286 | −0.0290 | −1.3075 | −0.6739 | 0.5813 | 0.3124 | 0.2892 | 0.6840 |
| 500 | −1.1517 | 0.8870 | −1.4557 | −0.1035 | −1.4434 | 0.2615 | 0.0165 | 0.1655 | 0.4139 | |
| WOA | 200 | −1.1503 | 0.8178 | −1.9646 | 0.2299 | −1.9588 | −0.0416 | −0.0822 | 0.3225 | 1.0572 |
| 500 | −1.0863 | 0.8635 | −0.3088 | −0.8407 | −0.6800 | 0.8381 | 0.3392 | 0.0734 | 0.6578 | |
| True Values | −1.1000 | 0.9000 | −0.8000 | −0.6000 | −0.9000 | 0.6000 | 0.2000 | 0 | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehmood, K.; Chaudhary, N.I.; Khan, Z.A.; Cheema, K.M.; Raja, M.A.Z.; Milyani, A.H.; Azhari, A.A. Nonlinear Hammerstein System Identification: A Novel Application of Marine Predator Optimization Using the Key Term Separation Technique. Mathematics 2022, 10, 4217. https://doi.org/10.3390/math10224217
Mehmood K, Chaudhary NI, Khan ZA, Cheema KM, Raja MAZ, Milyani AH, Azhari AA. Nonlinear Hammerstein System Identification: A Novel Application of Marine Predator Optimization Using the Key Term Separation Technique. Mathematics. 2022; 10(22):4217. https://doi.org/10.3390/math10224217
Chicago/Turabian StyleMehmood, Khizer, Naveed Ishtiaq Chaudhary, Zeshan Aslam Khan, Khalid Mehmood Cheema, Muhammad Asif Zahoor Raja, Ahmad H. Milyani, and Abdullah Ahmed Azhari. 2022. "Nonlinear Hammerstein System Identification: A Novel Application of Marine Predator Optimization Using the Key Term Separation Technique" Mathematics 10, no. 22: 4217. https://doi.org/10.3390/math10224217
APA StyleMehmood, K., Chaudhary, N. I., Khan, Z. A., Cheema, K. M., Raja, M. A. Z., Milyani, A. H., & Azhari, A. A. (2022). Nonlinear Hammerstein System Identification: A Novel Application of Marine Predator Optimization Using the Key Term Separation Technique. Mathematics, 10(22), 4217. https://doi.org/10.3390/math10224217









