Novel Soliton Solutions of the Fractional Riemann Wave Equation via a Mathematical Method
Abstract
1. Introduction
2. The Conformable Derivative’s Outline
3. Analysis of the Method
4. Application of the Method
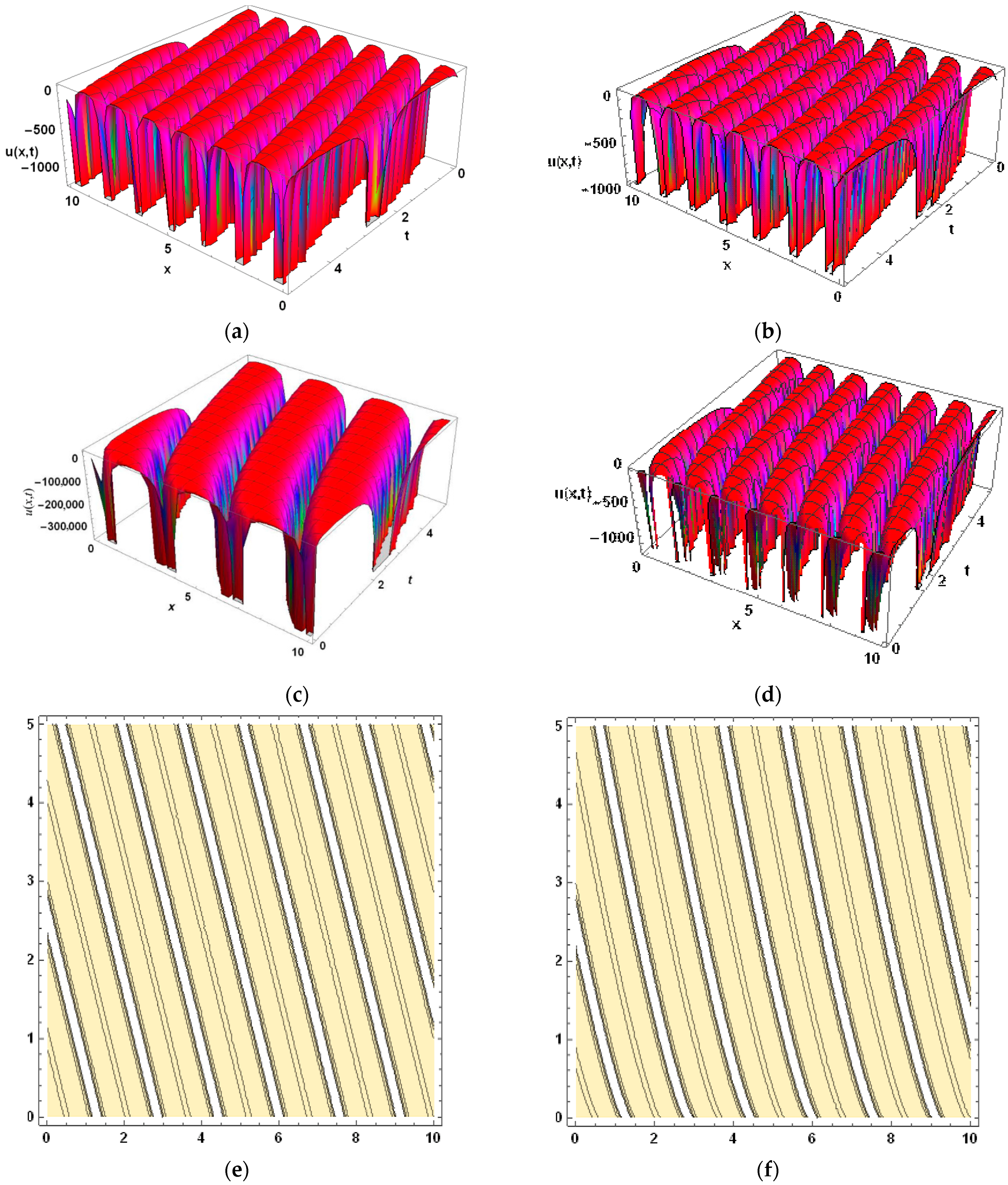
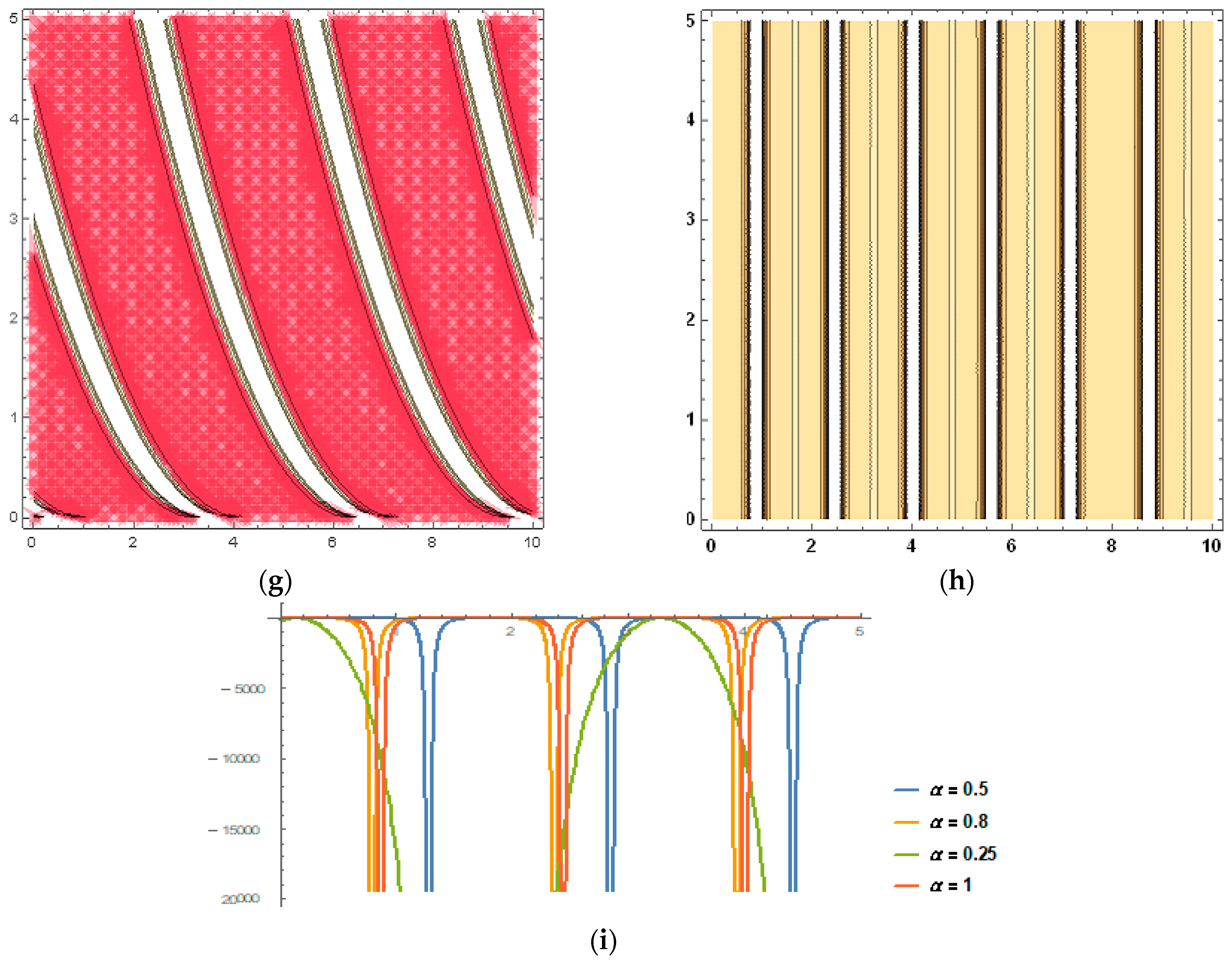
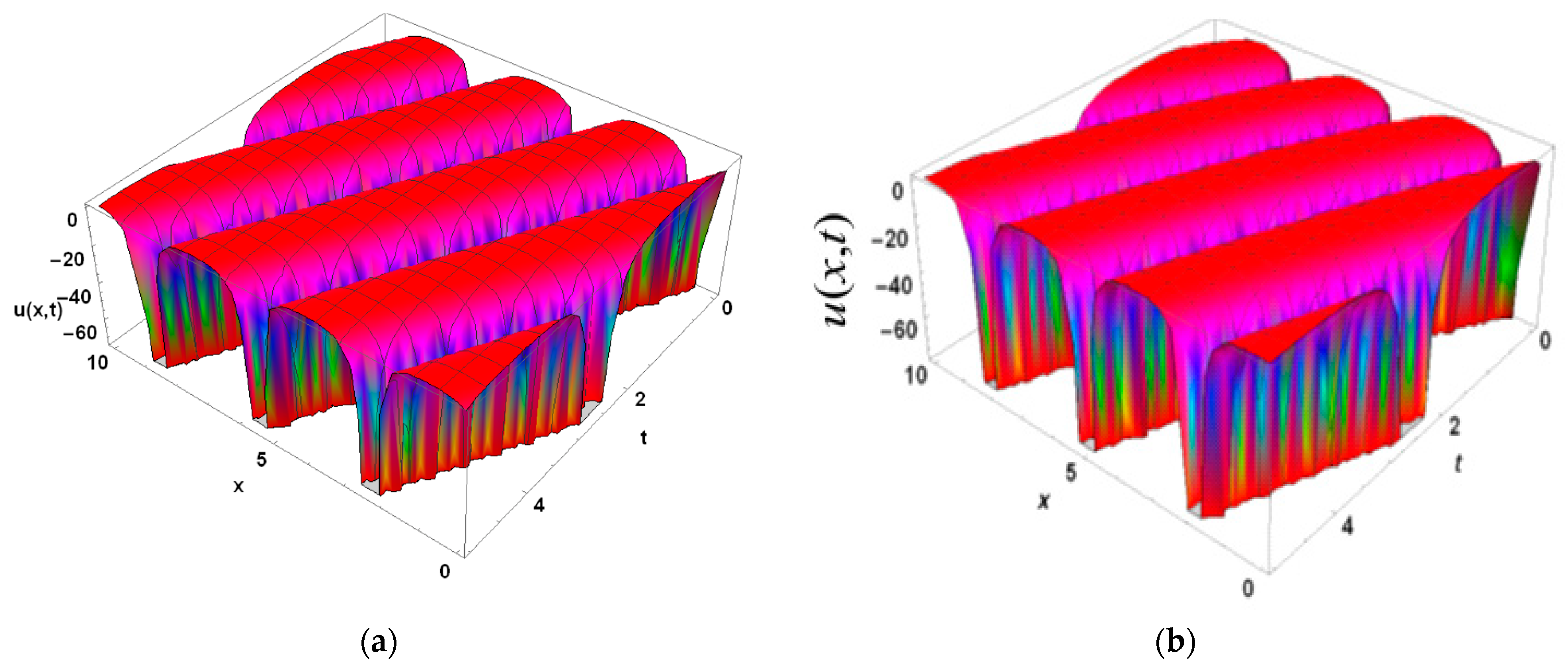
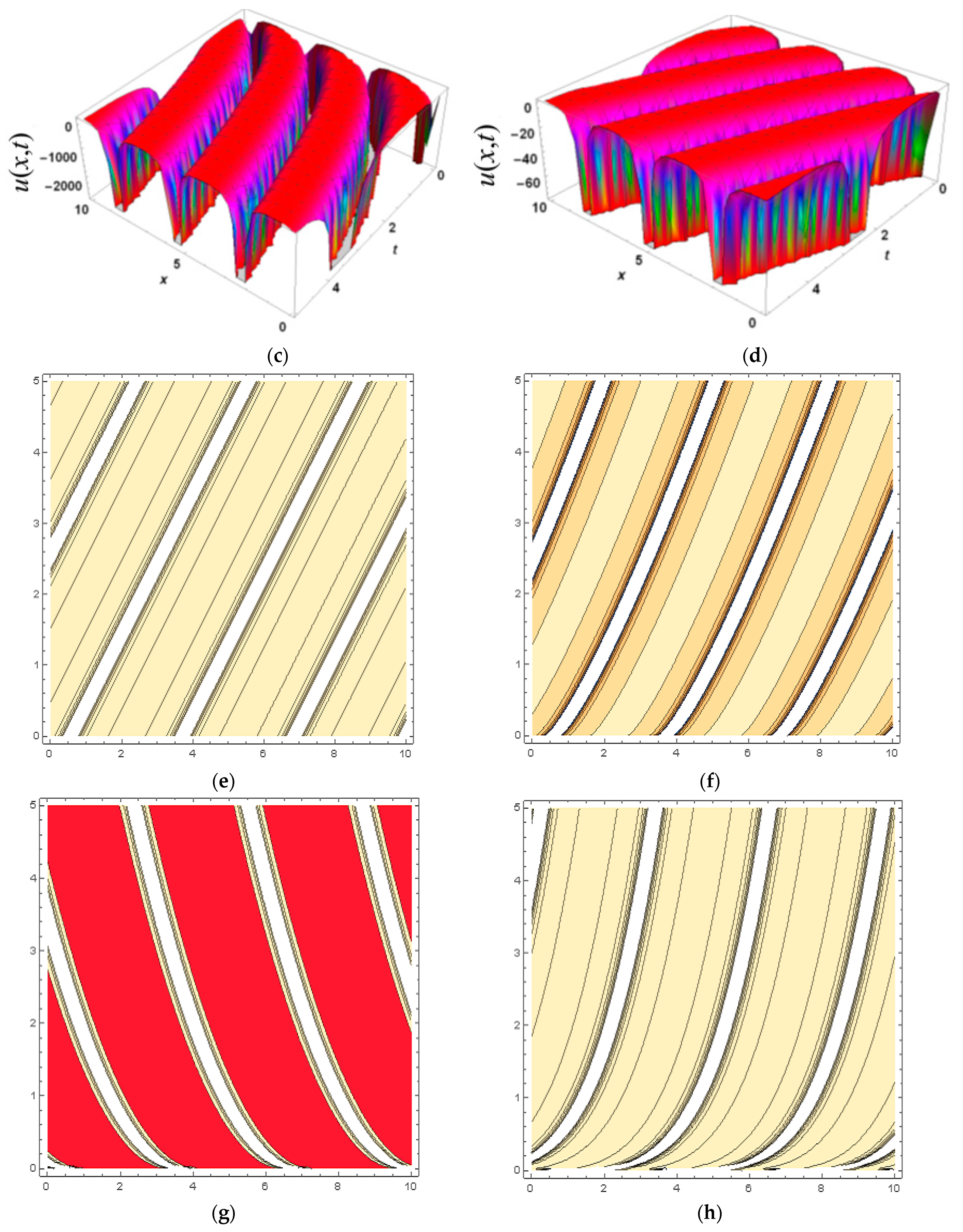
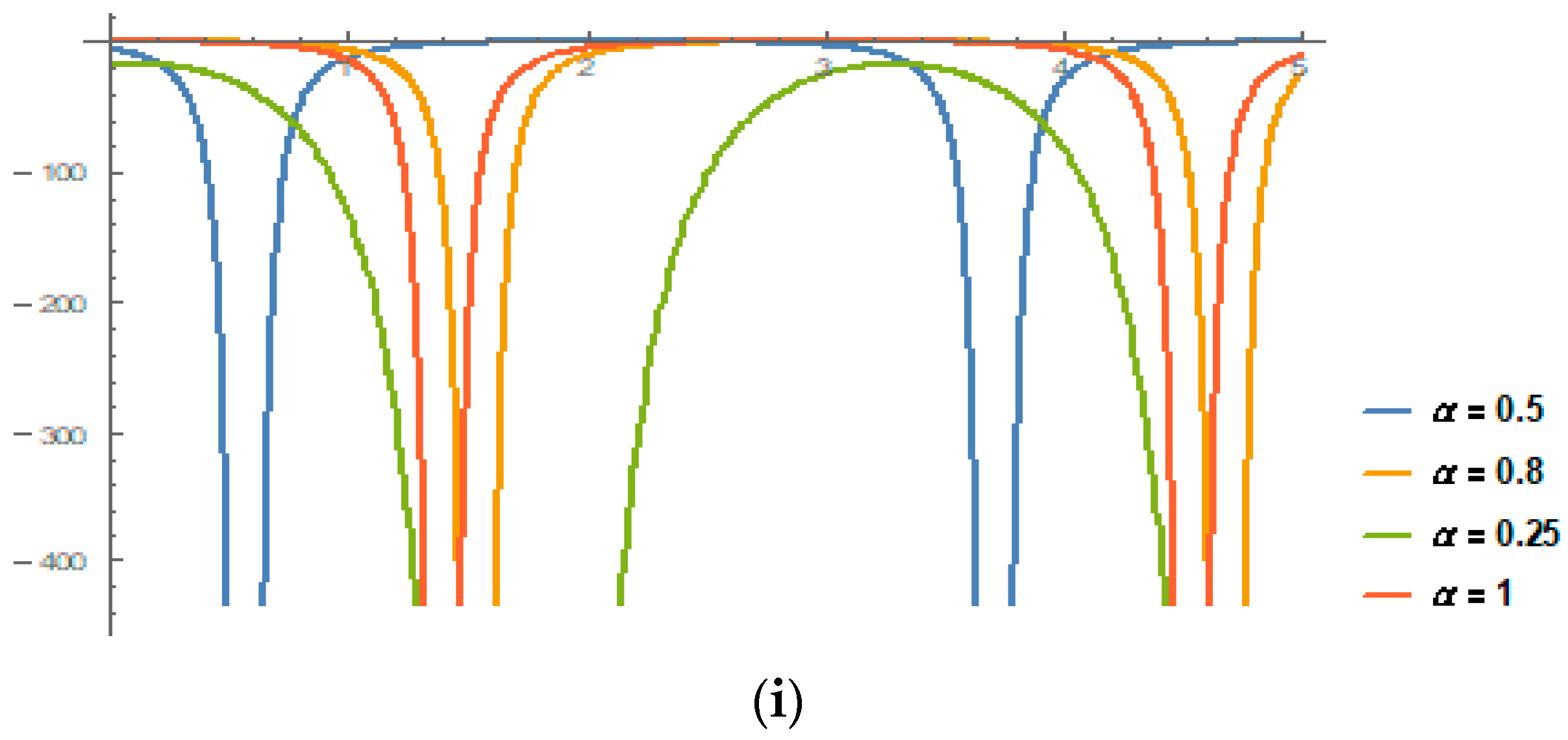
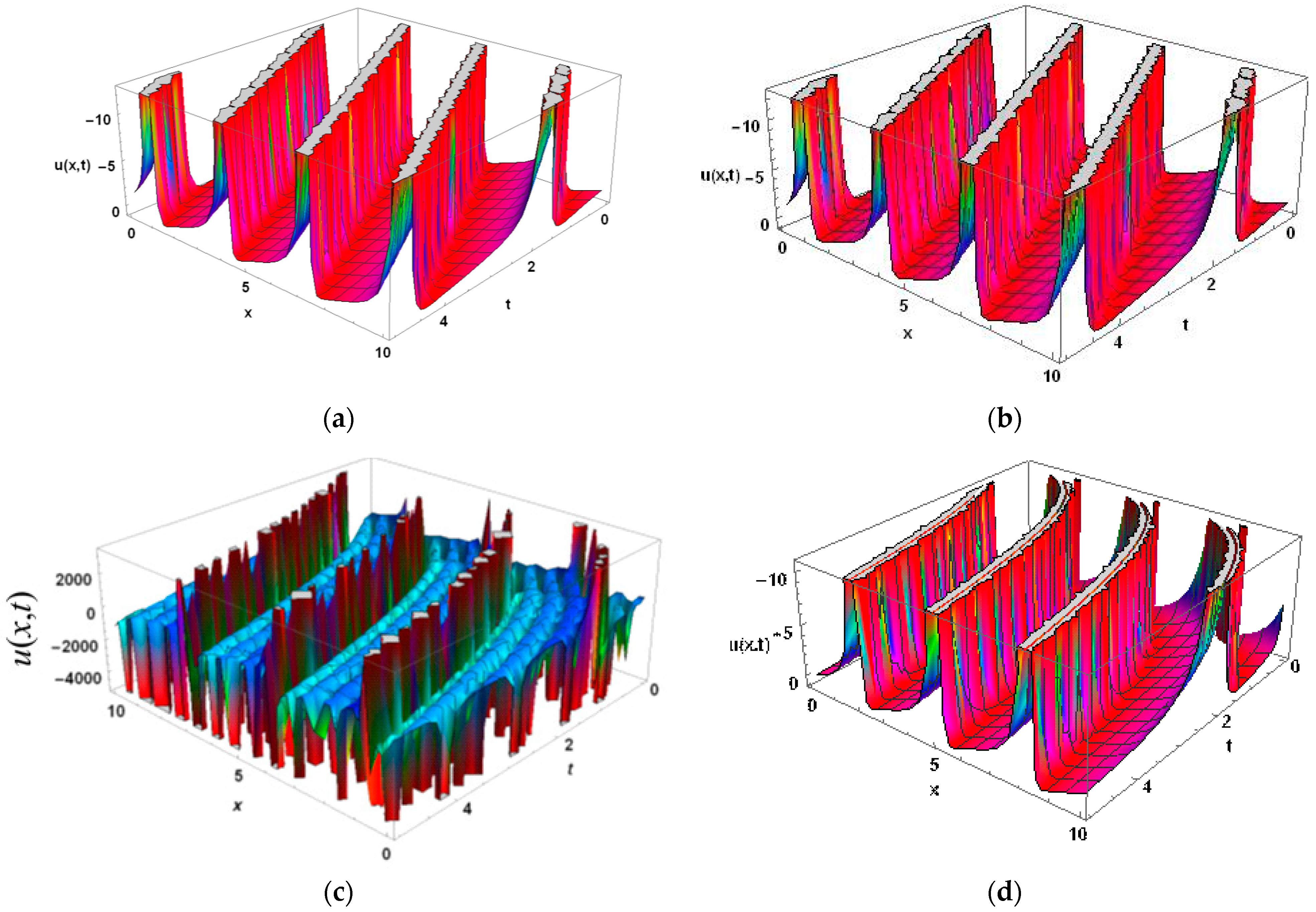
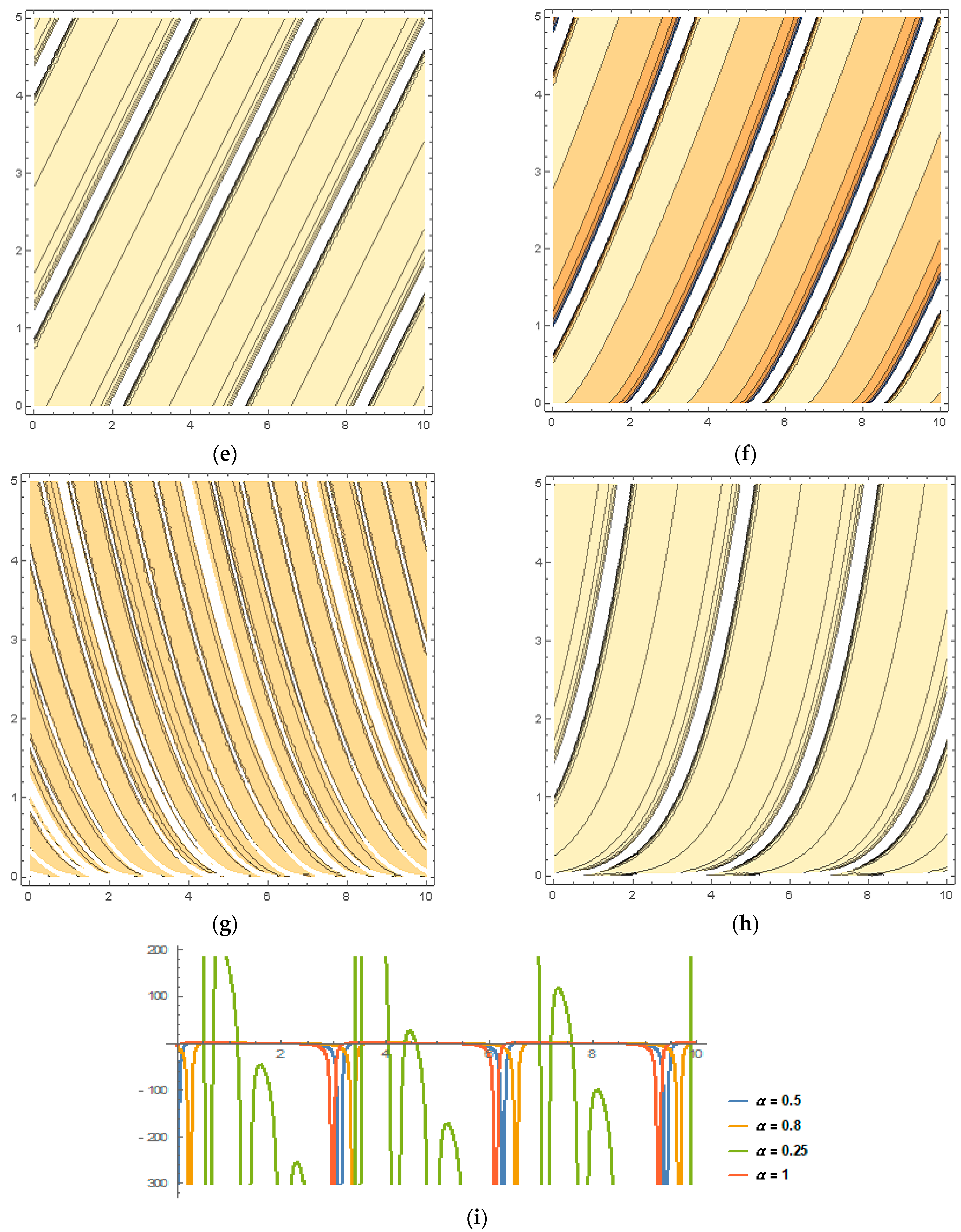
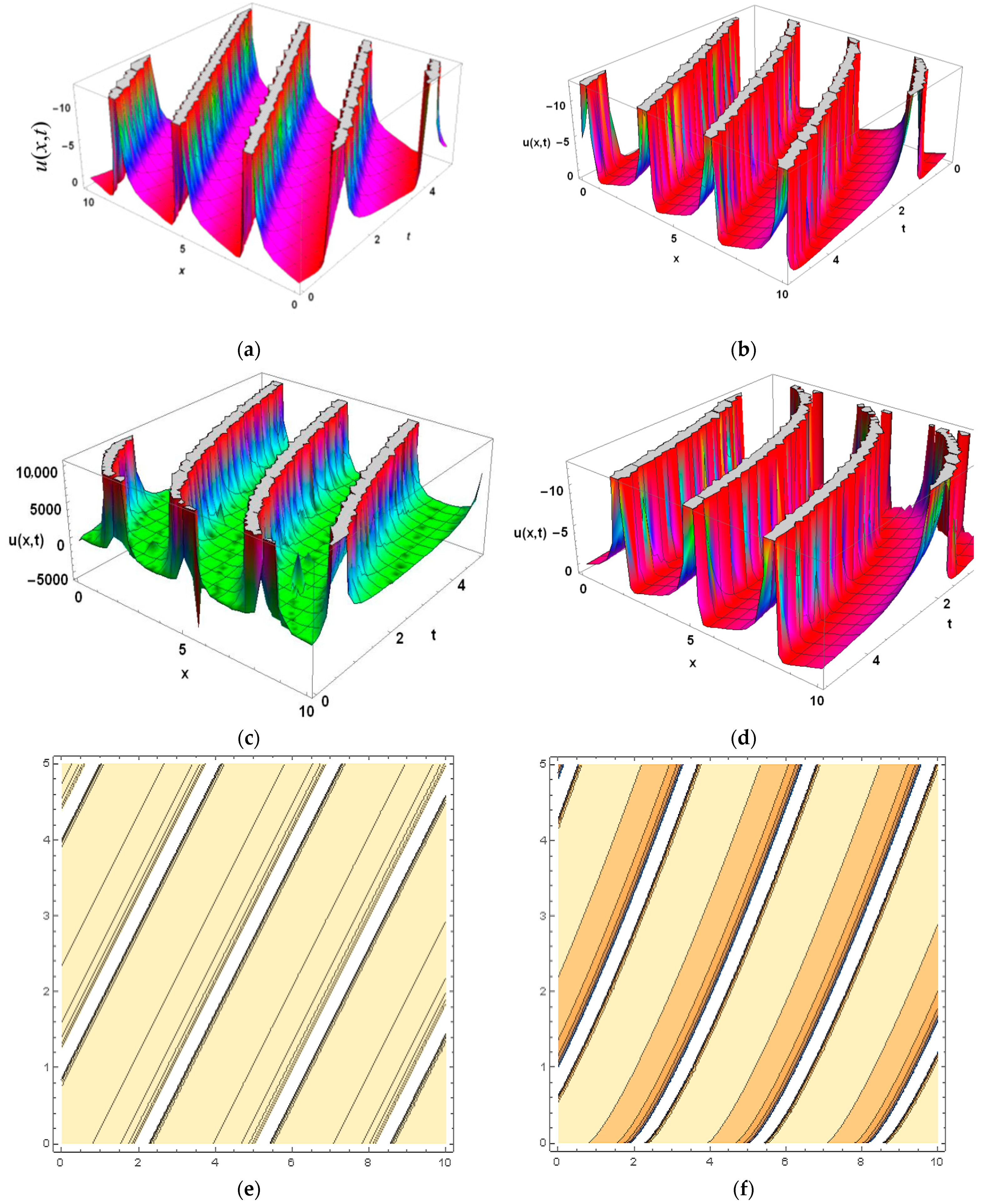
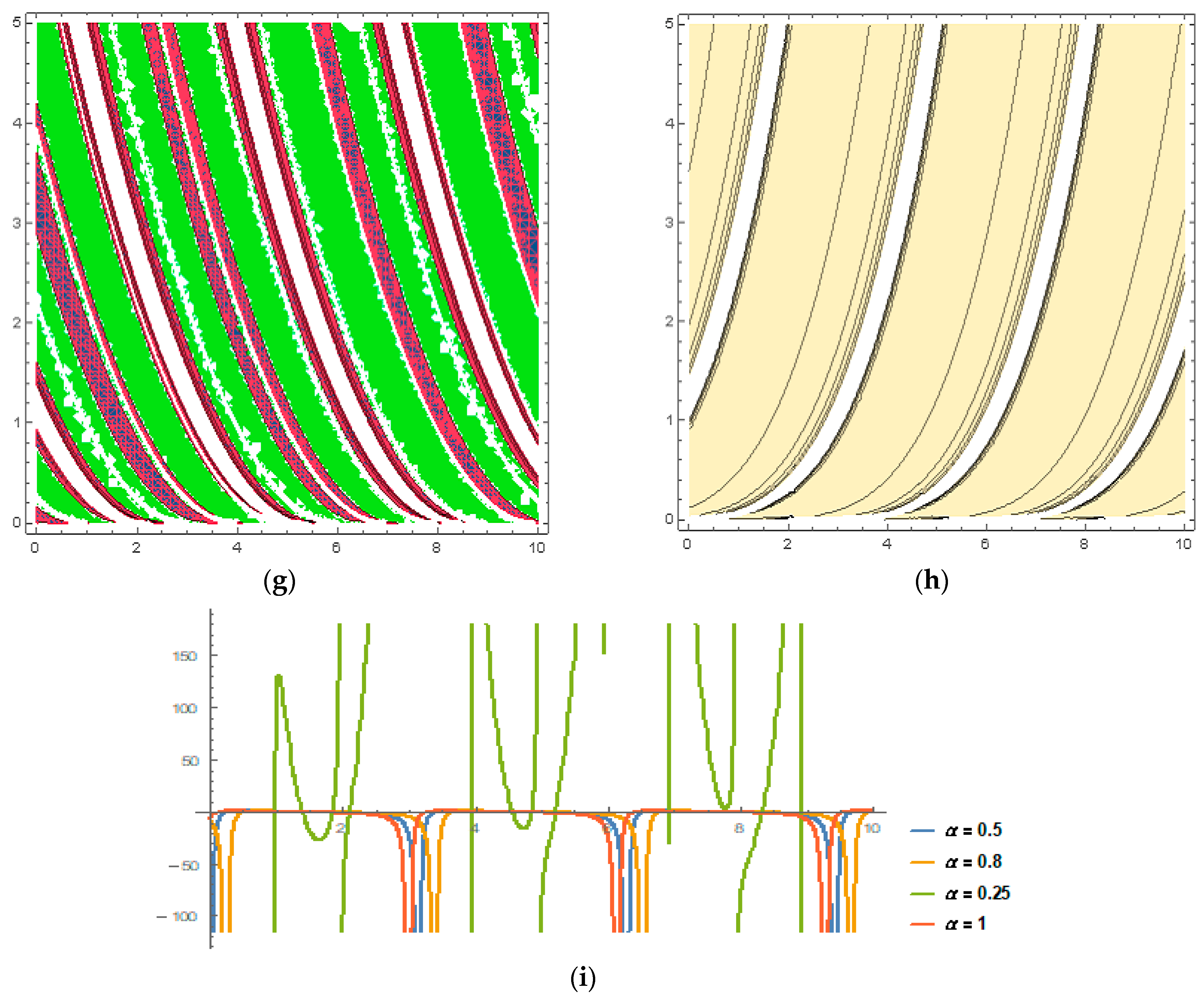
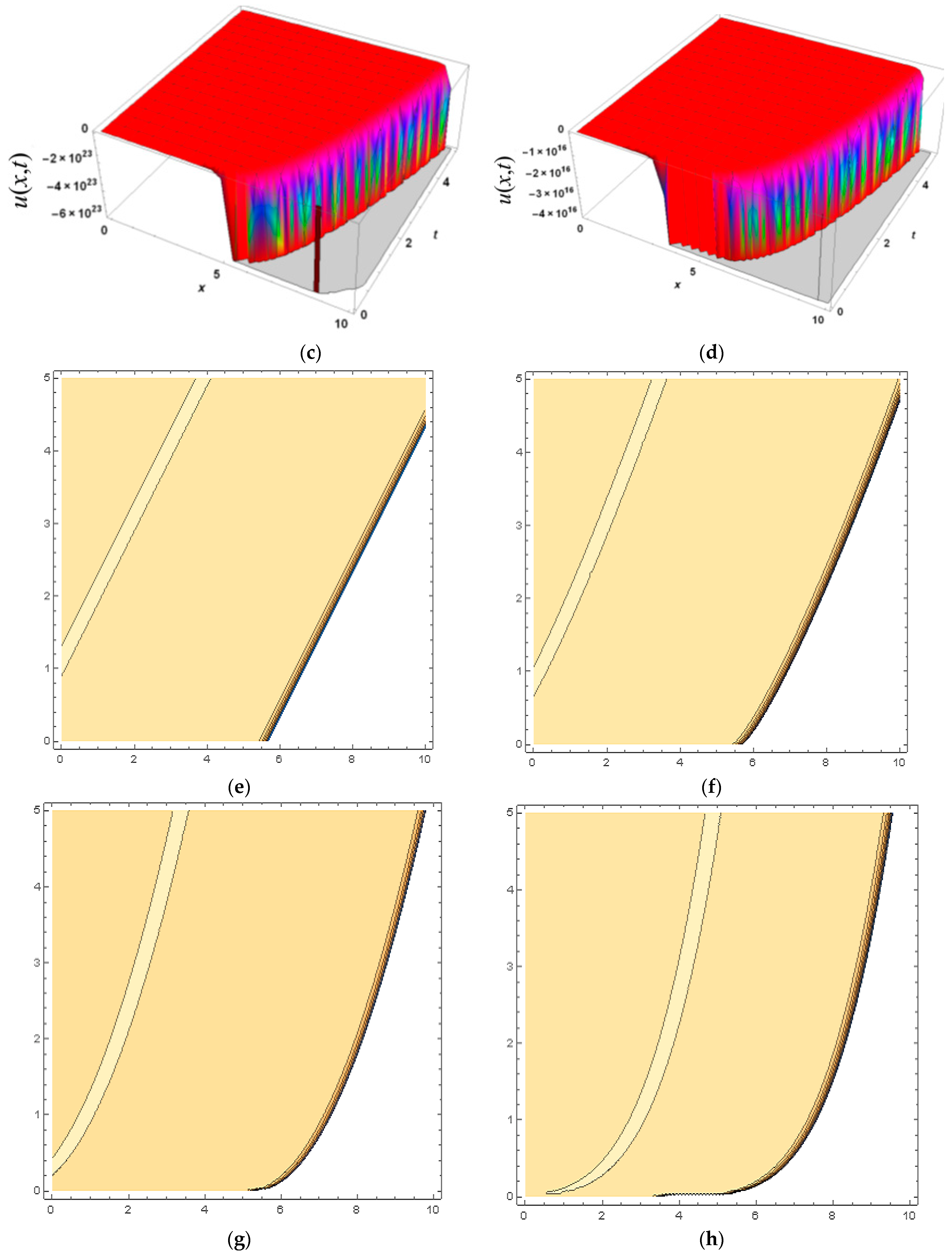
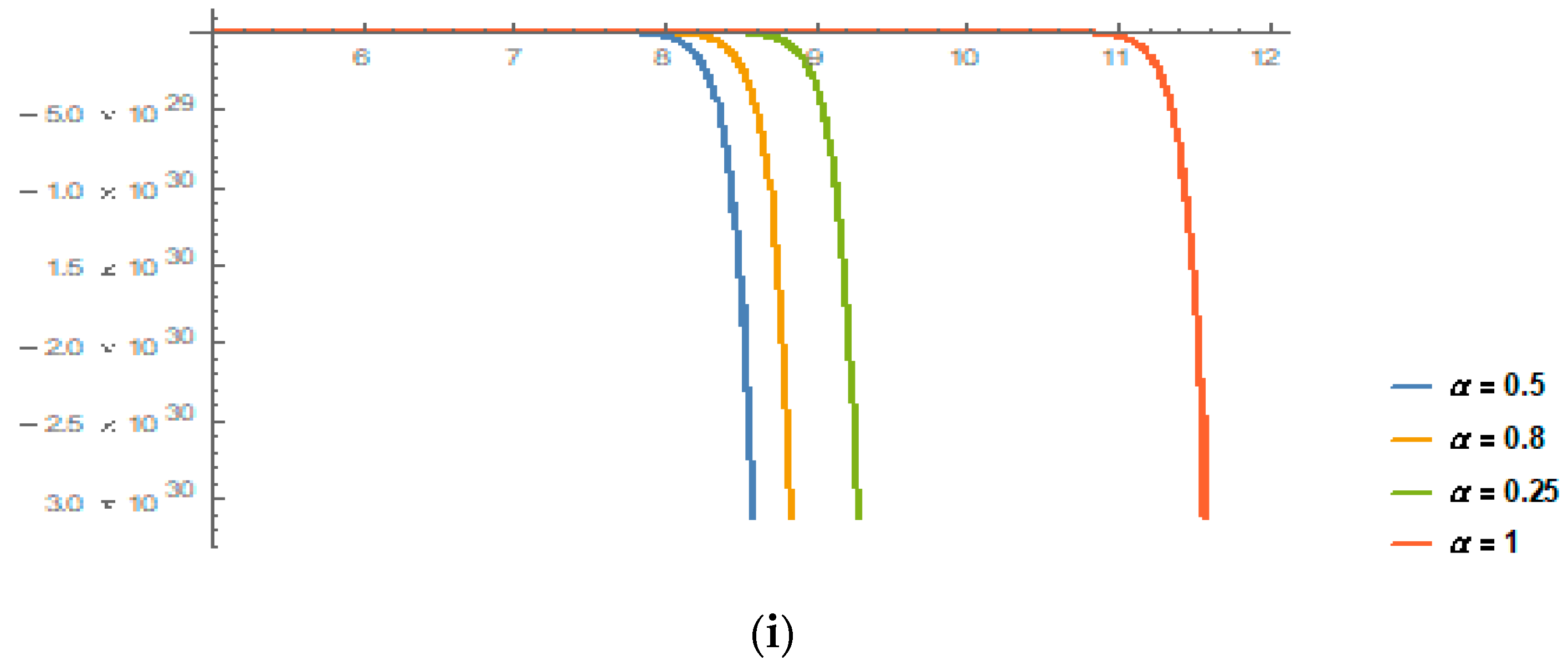
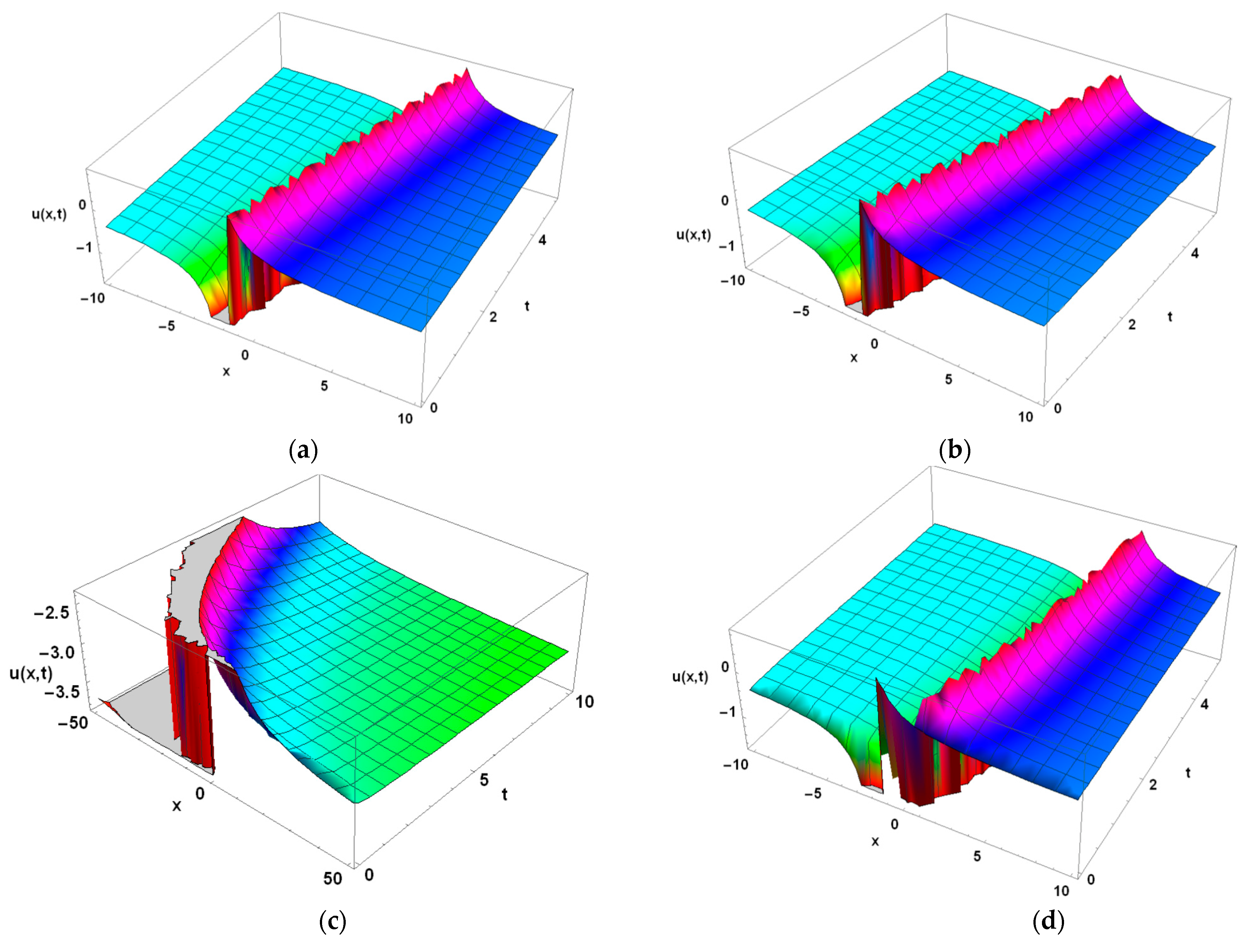
5. Physical Implications and Graphical Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdeljabbar, A.; Roshid, H.-O.; Aldurayhim, A. Bright, Dark, and Rogue Wave Soliton Solutions of the Quadratic Nonlinear Klein–Gordon Equation. Symmetry 2022, 14, 1223. [Google Scholar] [CrossRef]
- Shah, N.A.; Alyousef, H.A.; El-Tantawy, S.A.; Shah, R.; Chung, J.D. Analytical Investigation of Fractional-Order Korteweg–De-Vries-Type Equations under Atangana–Baleanu–Caputo Operator: Modeling Nonlinear Waves in a Plasma and Fluid. Symmetry 2022, 14, 739. [Google Scholar] [CrossRef]
- Shah, N.A.; Dassios, I.; Chung, J.D. A Decomposition Method for a Fractional-Order Multi-Dimensional Telegraph Equation via the Elzaki Transform. Symmetry 2021, 13, 8. [Google Scholar] [CrossRef]
- Thach, T.N.; Tuan, N.H. Stochastic pseudo-parabolic equations with fractional derivative and fractional Brownian motion. Stoch. Anal. Appl. 2022, 40, 328–351. [Google Scholar] [CrossRef]
- Thach, T.N.; Kumar, D.; Luc, N.H.; Tuan, N.H. Existence and regularity results for stochastic fractional pseudo-parabolic equations driven by white noise. Discret. Contin. Dyn. Syst.-S 2022, 15, 481. [Google Scholar] [CrossRef]
- Shah, N.A.; Agarwal, P.; Chung, J.D.; El-Zahar, E.R.; Hamed, Y.S. Analysis of Optical Solitons for Nonlinear Schrödinger Equation with Detuning Term by Iterative Transform Method. Symmetry 2020, 12, 1850. [Google Scholar] [CrossRef]
- He, W.; Chen, N.; Dassios, I.; Chung, J.D. Fractional System of Korteweg-De Vries Equations via Elzaki Transform. Mathematics 2021, 9, 673. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ilhan, O.A.; Abdulazeez, S.T.; Manafian, J.; Mohammed, S.A.; Osman, M. Novel multiple soliton solutions for some nonlinear PDEs via multiple Exp-function method. Results Phys. 2021, 21, 103769. [Google Scholar] [CrossRef]
- Ma, W.-X. N-soliton solution of a combined pKP–BKP equation. J. Geom. Phys. 2021, 165, 104191. [Google Scholar] [CrossRef]
- Zhang, S.; Zheng, X. N-soliton solutions and nonlinear dynamics for two generalized Broer–Kaup systems. Nonlinear Dyn. 2022, 107, 1179–1193. [Google Scholar] [CrossRef]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.-D.; Shah, R.; Khan, A. A Comparative Analysis of Fractional-Order Kaup–Kupershmidt Equation within Different Operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Cinar, M.; Onder, I.; Secer, A.; Yusuf, A.; Sulaiman, T.A.; Bayram, M.; Aydin, H. The analytical solutions of Zoomeron equation via extended rational sin-cos and sinh-cosh methods. Phys. Scr. 2021, 96, 094002. [Google Scholar] [CrossRef]
- Rani, A.; Zulfiqar, A.; Ahmad, J.; Hassan, Q.M.U. New soliton wave structures of fractional Gilson-Pickering equation using tanh-coth method and their applications. Results Phys. 2021, 29, 104724. [Google Scholar] [CrossRef]
- Rani, A.; Ashraf, M.; Ahmad, J.; Ul-Hassan, Q.M. Soliton solutions of the Caudrey–Dodd–Gibbon equation using three expansion methods and applications. Opt. Quantum Electron. 2022, 54, 158. [Google Scholar] [CrossRef]
- Naz, S.; Ul-Hassan, Q.M.; Zulfiqar, A. Dynamics of new optical solutions for nonlinear equations via a novel analytical technique. Opt. Quantum Electron. 2022, 54, 474. [Google Scholar] [CrossRef]
- Abdel-Salam, E.A.; Gumma, E.A. Analytical solution of nonlinear space–time fractional differential equations using the improved fractional Riccati expansion method. Ain Shams Eng. J. 2015, 6, 613–620. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alngar, M.E. Optical soliton solutions for the generalized Kudryashov equation of propagation pulse in optical fiber with power nonlinearities by three integration algorithms. Math. Methods Appl. Sci. 2021, 44, 315–324. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Shakeel, M. Soliton solutions of coupled systems by improved (G′/G)-expansion method. In Proceedings of the AIP Conference Proceedings, Tampa, FL, USA, 9–11 March 2013; pp. 156–166. [Google Scholar]
- Islam, S.R.; Bashar, M.H.; Muhammad, N. Immeasurable soliton solutions and enhanced (G′/G)-expansion method. Phys. Open 2021, 9, 100086. [Google Scholar] [CrossRef]
- Rizvi, S.; Seadawy, A.R.; Younis, M.; Ali, I.; Althobaiti, S.; Mahmoud, S.F. Soliton solutions, Painleve analysis and conservation laws for a nonlinear evolution equation. Results Phys. 2021, 23, 103999. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Zhang, J. The (G′ G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Yokus, A.; Durur, H.; Ahmad, H.; Thounthong, P.; Zhang, Y.-F. Construction of exact traveling wave solutions of the Bogoyavlenskii equation by (G′/G, 1/G)-expansion and (1/G′)-expansion techniques. Results Phys. 2020, 19, 103409. [Google Scholar] [CrossRef]
- Islam, T.; Akbar, M.A.; Azad, A.K. Traveling wave solutions to some nonlinear fractional partial differential equations through the rational (G′/G)-expansion method. J. Ocean Eng. Sci. 2018, 3, 76–81. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Alesemi, M.; Albosaily, S.; Iqbal, N.; El-Morshedy, M. The Exact Solutions of Stochastic Fractional-Space Kuramoto-Sivashinsky Equation by Using (G′ G)-Expansion Method. Mathematics 2021, 9, 2712. [Google Scholar] [CrossRef]
- Aniqa, A.; Ahmad, J. Soliton solution of fractional Sharma-Tasso-Olever equation via an efficient (G′/G)-expansion method. Ain Shams Eng. J. 2022, 13, 101528. [Google Scholar] [CrossRef]
- Younis, M.; Seadawy, A.R.; Baber, M.; Husain, S.; Iqbal, M.; Rizvi, S.; Baleanu, D. Analytical optical soliton solutions of the Schrödinger-Poisson dynamical system. Results Phys. 2021, 27, 104369. [Google Scholar] [CrossRef]
- Barman, H.K.; Aktar, M.S.; Uddin, M.H.; Akbar, M.A.; Baleanu, D.; Osman, M. Physically significant wave solutions to the Riemann wave equations and the Landau-Ginsburg-Higgs equation. Results Phys. 2004, 22, 683–691. [Google Scholar] [CrossRef]
- Geng, X.; Cao, C. Explicit solutions of the 2 + 1-dimensional breaking soliton equation. Chaos Solitons Fractals 2004, 22, 683–691. [Google Scholar] [CrossRef]
- Barman, H.K.; Seadawy, A.R.; Akbar, M.A.; Baleanu, D. Competent closed form soliton solutions to the Riemann wave equation and the Novikov-Veselov equation. Results Phys. 2020, 17, 103131. [Google Scholar] [CrossRef]
- Hong-Hai, H.; Da-Jun, Z.; Jian-Bing, Z.; Yu-Qin, Y. Rational and periodic solutions for a (2 + 1)-dimensional breaking soliton equation associated with ZS-AKNS hierarchy. Commun. Theor. Phys. 2010, 53, 430. [Google Scholar] [CrossRef]
- Roy, R.; Barman, H.K.; Islam, M.N.; Akbar, M.A. Bright-dark wave envelopes of nonlinear regularized-long-wave and Riemann wave models in plasma physics. Results Phys. 2021, 30, 104832. [Google Scholar] [CrossRef]
- Duran, S. Breaking theory of solitary waves for the Riemann wave equation in fluid dynamics. Int. J. Mod. Phys. B 2021, 35, 2150130. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Kajouni, A.; Chafiki, A.; Hilal, K.; Oukessou, M. A New Conformable Fractional Derivative and Applications. Int. J. Differ. Equ. 2021, 2021, 6245435. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. New properties of conformable derivative. Open Math. 2015, 13, 889–898. [Google Scholar] [CrossRef]
- Tuan, N.H.; Thach, T.N.; Can, N.H.; O′Regan, D. Regularization of a multidimensional diffusion equation with conformable time derivative and discrete data. Math. Methods Appl. Sci. 2021, 44, 2879–2891. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naz, S.; Rani, A.; Shakeel, M.; Shah, N.A.; Chung, J.D. Novel Soliton Solutions of the Fractional Riemann Wave Equation via a Mathematical Method. Mathematics 2022, 10, 4171. https://doi.org/10.3390/math10224171
Naz S, Rani A, Shakeel M, Shah NA, Chung JD. Novel Soliton Solutions of the Fractional Riemann Wave Equation via a Mathematical Method. Mathematics. 2022; 10(22):4171. https://doi.org/10.3390/math10224171
Chicago/Turabian StyleNaz, Shumaila, Attia Rani, Muhammad Shakeel, Nehad Ali Shah, and Jae Dong Chung. 2022. "Novel Soliton Solutions of the Fractional Riemann Wave Equation via a Mathematical Method" Mathematics 10, no. 22: 4171. https://doi.org/10.3390/math10224171
APA StyleNaz, S., Rani, A., Shakeel, M., Shah, N. A., & Chung, J. D. (2022). Novel Soliton Solutions of the Fractional Riemann Wave Equation via a Mathematical Method. Mathematics, 10(22), 4171. https://doi.org/10.3390/math10224171





