A Fitted Operator Finite Difference Approximation for Singularly Perturbed Volterra–Fredholm Integro-Differential Equations
Abstract
:1. Introduction
2. Asymptotic Properties
3. Discrete Scheme
4. The Stability and Convergence
5. Results and Discussion
| Algorithm 1: To compute the numerical solution . |
| Input: , , = , = , , , , and |
| Output: The numerical solution |
| Step 1: |
| Step 2: for |
| end |
| Step 3: for |
| if |
| end |
| if |
| end |
| if |
| end |
| if |
| end |
| end |
| Step 4: for |
| end |
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Perturbation parameter | |
| C | Generic positive constant |
| Real parameter | |
| Mesh step size | |
| Mesh node point | |
| Non-uniform mesh | |
| and | Mesh transition points |
| Maximum error | |
| Order of convergence | |
| L | Differential operator |
| T | Volterra integral operator |
| S | Fredholm integral operator |
| Exact solution of the presented problem | |
| Approximate solution of the difference problem | |
| Remainder term | |
| Error function |
References
- Amin, R.; Nazir, S.; Garcia-Magarino, I. A collocation method for numerical solution of nonlinear delay integro-differential equations for wireless sensor network and internet of things. Sensors 2020, 20, 1962. [Google Scholar] [CrossRef] [PubMed]
- Dawood, L.A.; Hamoud, A.; Mohammed, N.M. Laplace discrete decomposition method for solving nonlinear Volterra-Fredholm integro-differential equations. J. Math. Comput. Sci. 2020, 21, 158–163. [Google Scholar] [CrossRef]
- Kashkaria, B.S.H.; Syam, M.I. Evolutionary computational intelligence in solving a class of nonlinear Volterra-Fredholm integro-differential equations. J. Comput. Applied Math. 2017, 311, 314–323. [Google Scholar] [CrossRef]
- Bellomo, N.; Firmani, B.; Guerri, L. Bifurcation analysis for a nonlinear system of integro-differential equations modelling tumor-immune cells competition. Appl. Math. Lett. 1999, 12, 39–44. [Google Scholar] [CrossRef]
- Guan, L.; Prieur, C.; Zhang, L.; Prieur, C.; Georges, D.; Bellemain, P. Transport effect of Covid-19 pandemic in France. Annu. Rev. Control 2020, 50, 394–408. [Google Scholar] [CrossRef]
- Köhler-Rieper, F.; Röhl, C.H.F.; De Michecli, E. A novel deterministic forecast model for the Covid-19 epidemic based on a single ordinary integro-differential equations. Eur. Phys. J. Plus 2020, 135, 599. [Google Scholar] [CrossRef]
- Hamoud, A.A.; Bani Issa, M.; Ghadle, K.P. Existence and uniqueness results for nonlinear Volterra-Fredholm integro-differential equations. Nonlinear Funct. Anal. Appl. 2018, 23, 797–805. [Google Scholar]
- Hamoud, A.; Mohammed, N.; Ghadle, K. Existence and uniqueness results for Volterra-Fredholm integro-differential equations. Adv. Theory Nonlinear Anal. Appl. 2020, 4, 361–372. [Google Scholar] [CrossRef]
- Al-Ahmad, S.; Sulaiman, I.M.; Nawi, M.M.A.; Mamat, M.; Ahmad, M.Z. Analytical solution of systems of Volterra integro-differential equations using modified differential transform method. J. Math. Comput. Sci. 2022, 26, 1–9. [Google Scholar] [CrossRef]
- Bani Issa, M.S.H.; Hamoud, A.A. Solving systems of Volterra integro-differential equations by using semi analytical techniques. Technol. Rep. Kansai Univ. 2020, 62, 685–690. [Google Scholar]
- Tahernezad, T.; Jalilian, R. Exponential spline for the numerical solutions of linear Fredholm integro-differential equations. Adv. Differ. Equations 2020, 141, 1–15. [Google Scholar] [CrossRef]
- Segni, S.; Ghiat, M.; Guebbai, H. New approximation method for Volterra nonlinear integro-differential equations. Asian-Eur. J. Math. 2019, 12, 1950016. [Google Scholar] [CrossRef]
- Alvandi, A.; Paripour, M. The combined reproducing kernel method and Taylor series for handling nonlinear Volterra integro-differential equations with derivative type kernel. Appl. Math. Comput. 2019, 355, 151–160. [Google Scholar] [CrossRef]
- Amin, R.; Maharq, I.; Shah, K.; Elsayed, F. Numerical solution of the second order linear and nonlinear integro-differential equations using Haar wavelet method. Arab. J. Basic Appl. Sci. 2021, 28, 1–19. [Google Scholar] [CrossRef]
- Swaidan, W.; Ali, H.S. A computational method for nonlinear Fredholm integro-differential equations using Haar wavelet collocation points. J. Physics Conf. Ser. 2021, 1, 012032. [Google Scholar] [CrossRef]
- Issa, K.; Salehi, F. Approximate solution of perturbed Volterra-Fredholm integro-differential equations by Chebyshev Galerkin method. J. Math. 2017, 2017, 8213932. [Google Scholar] [CrossRef]
- Basirat, B.; Shahdadi, M.A. Numerical solution of nonlinear integro-differential equations with initial conditions by Bernstein Operational matrix of derivative. Int. J. Mod. Nonlinear Theory Appl. 2013, 2, 141–149. [Google Scholar] [CrossRef]
- Cakir, M.; Gunes, B.; Duru, H. A novel computational method for solving nonlinear Volterra integro-differential equation. Kuwait J. Sci. 2021, 48, 31–40. [Google Scholar] [CrossRef]
- Cimen, E.; Yatar, S. Numerical solution of Volterra integro-differential equtaion with delay. J. Math. Comput. Sci. 2020, 20, 255–263. [Google Scholar] [CrossRef]
- Chen, J.; He, M.; Huang, Y. A fast multiscale Galerkin method for solving second order linear Fredholm integro-differential equation with Dirichlet boundary conditions. J. Comput. Appl. Math. 2020, 364, 112352. [Google Scholar] [CrossRef]
- Hesameddini, E.; Riahi, M. Galerkin matrix method and its convergence analysis for solving system of Volterra-Fredholm integro-differential equations. Iran. J. Sci. Technol. Sci. 2019, 43, 1203–1214. [Google Scholar] [CrossRef]
- Ghomanjani, F. Numerical solution for nonlinear Volterra integro-differential equations. Palest. J. Math. 2020, 9, 164–169. [Google Scholar]
- Cao, Y.; Nikan, O.; Avazzadeh, Z. A localized meshless technique for solving 2D nonlinear integro-differential equation with multi-term kernels. Appl. Numer. Math. 2023, 183, 140–156. [Google Scholar] [CrossRef]
- Jafarzadeh, Y.; Ezzati, R. A new method for the solution of Volterra-Fredholm integro-differential equations. Tblisi Math. J. 2019, 12, 59–66. [Google Scholar] [CrossRef]
- Sharif, A.A.; Hamoud, A.A.; Ghadle, K.P. Solving nonlinear integro-differential equations by using numerical techniques. Acta Univ. Apulensis 2020, 61, 43–53. [Google Scholar]
- Shoushan, A.F.; Al-Humedi, H.O. The numerical solutions of integro-differential equations by Euler polynomials with least-squares method. Polarch J. Archaeol. Egypt/Egyptol. 2021, 18, 1740–1753. [Google Scholar]
- Iragi, B.C.; Munyakazi, J.B. New parameter-uniform discretizations of singularly perturbed Volterra integro-differential equations. Appl. Math. Int. Sci. 2018, 12, 517–529. [Google Scholar] [CrossRef]
- Iragi, B.C.; Munyakazi, J.B. A uniformly convergent numerical method for a singularly perturbed Volterra integro-differential equation. Int. J. Comput. Math. 2020, 97, 759–771. [Google Scholar] [CrossRef]
- Kudu, M.; Amirali, I.; Amiraliyev, G.M. A finite difference method for a singularly perturbed delay integro-differential equations. J. Of Computational Appl. Math. 2016, 308, 379–390. [Google Scholar] [CrossRef]
- Yapman, Ö.; Amiraliyev, G.M.; Amirali, I. Convergence analysis of fitted numerical method for a singularly perturbed nonlinear Volterra integro-differential equation with delay. J. Comput. And Applied Math. 2019, 355, 301–309. [Google Scholar] [CrossRef]
- Amiraliyev, G.M.; Yapman, Ö.; Kudu, M. A fitted approximate method for a Volterra delay-integro-differential equation with initial layer. Hacet. J. Math. Stat. 2019, 48, 1417–1429. [Google Scholar] [CrossRef]
- Mbroh, N.A.; Noutchie, S.C.O.; Massoukou, R.Y.M. A second order finite difference scheme for singularly perturbed Volterra integro-differential equation. Alex. Eng. J. 2020, 59, 2441–2447. [Google Scholar] [CrossRef]
- Yapman, Ö.; Amiraliyev, G.M. A novel second order fitted computational method for a singularly perturbed Volterra integro-differential equation. Int. J. Comput. Math. 2019, 97, 1293–1302. [Google Scholar] [CrossRef]
- Tao, X.; Zhang, Y. The coupled method for singularly perturbed Volterra integro-differential equations. Adv. Differ. Equations 2019, 217, 2139. [Google Scholar] [CrossRef]
- Panda, A.; Mohapatra, J.; Amirali, I. A second-order post-processing technique for singularly perturbed Volterra integro-differential equations. Mediterr. J. Math. 2021, 18, 1–25. [Google Scholar] [CrossRef]
- Amiraliyev, G.M.; Durmaz, M.E.; Kudu, M. Uniform convergence results for singularly perturbed Fredholm integro-differential equation. J. Of Mathematical Anal. 2018, 9, 55–64. [Google Scholar]
- Amiraliyev, G.M.; Durmaz, M.E.; Kudu, M. Fitted second order numerical method for a singularly perturbed Fredholm integro-differential equations. Bull. Belg. Math. Soc. Simon Stevin 2020, 27, 71–88. [Google Scholar] [CrossRef]
- Cimen, E.; Cakir, M. A uniform numerical method for solving singularly perturbed Fredholm integro-differential problem. Comput. Appl. Math. 2021, 40, 1–14. [Google Scholar] [CrossRef]
- Durmaz, M.E.; Amiraliyev, G.M. A robust numerical method for a singularly perturbed Fredholm integro-differential equation. Mediterr. J. Math. 2021, 18, 1–17. [Google Scholar] [CrossRef]
- Cakir, M.; Gunes, B. Exponentially fitted difference scheme for singularly perturbed mixed integro-differential equations. Georgian Math. J. 2022, 29, 193–203. [Google Scholar] [CrossRef]
- Cakir, M.; Gunes, B. A new difference method for the singularly perturbed Volterra-Fredholm integro-differential equations on a Shishkin mesh. Hacet. J. Math. Stat. 2022, 51, 787–799. [Google Scholar]
- Amiraliyev, G.M.; Durmaz, M.E.; Kudu, M. A numerical method for a second order singularly perturbed Fredholm integro-differential equation. Miskolc Math. Notes 2021, 22, 37–48. [Google Scholar]
- Boglaev, I.P. Approximate solution of a nonlinear boundary value problem with a small parameter for the highest-order differential. USSR Comput. Math. Math. Phys. 1984, 24, 30–35. [Google Scholar] [CrossRef]
- Amiraliyev, G.M.; Mamedov, Y.D. Difference schemes on the uniform mesh for singularly perturbed pseudo-parabolic equations. Tr. J. Math. 1995, 19, 207–222. [Google Scholar]
- Samarski, A.A. The Theory of Difference Schemes; M.V. Lomonosov State University: Moscow, Russia, 2021. [Google Scholar]


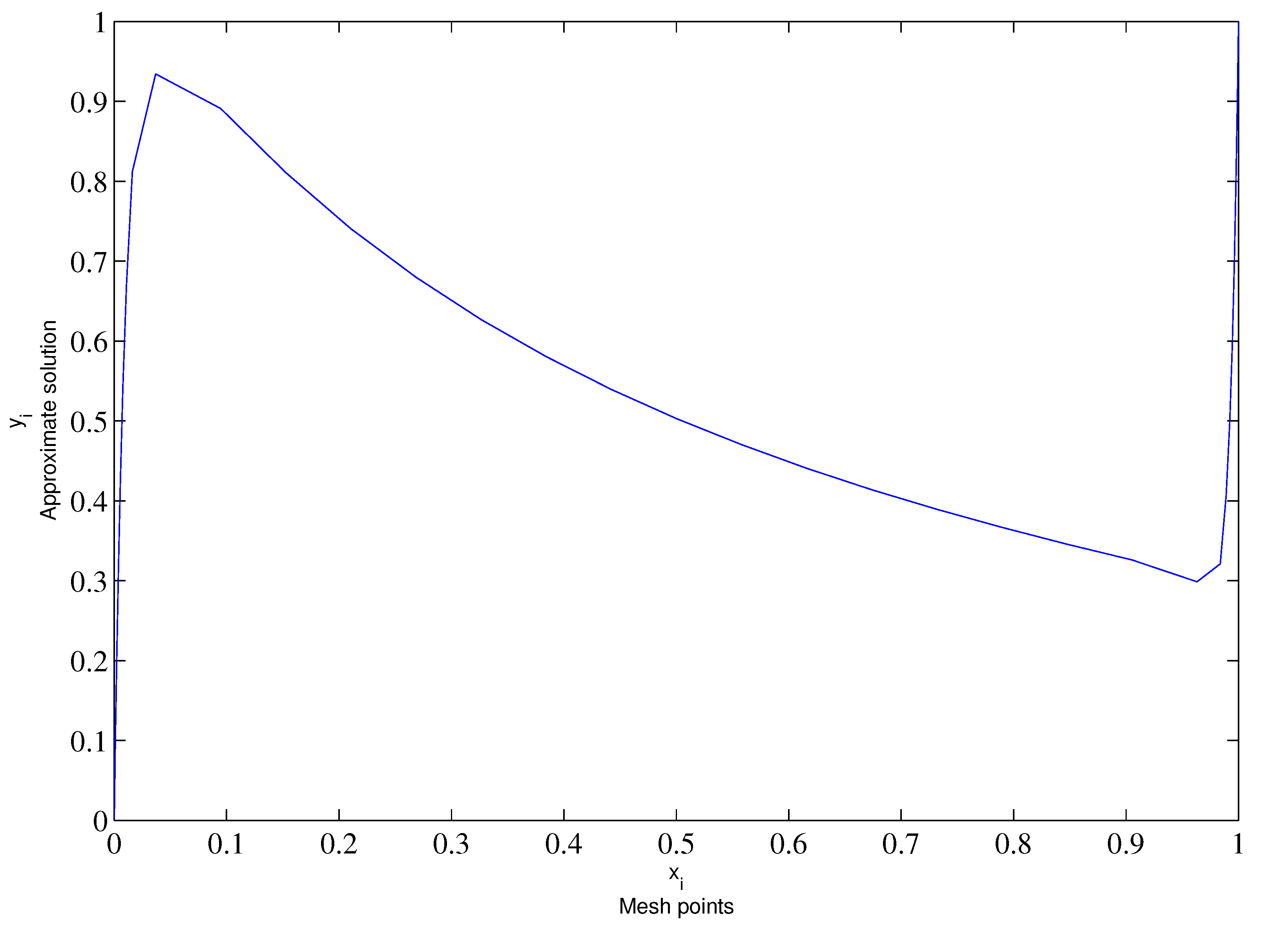
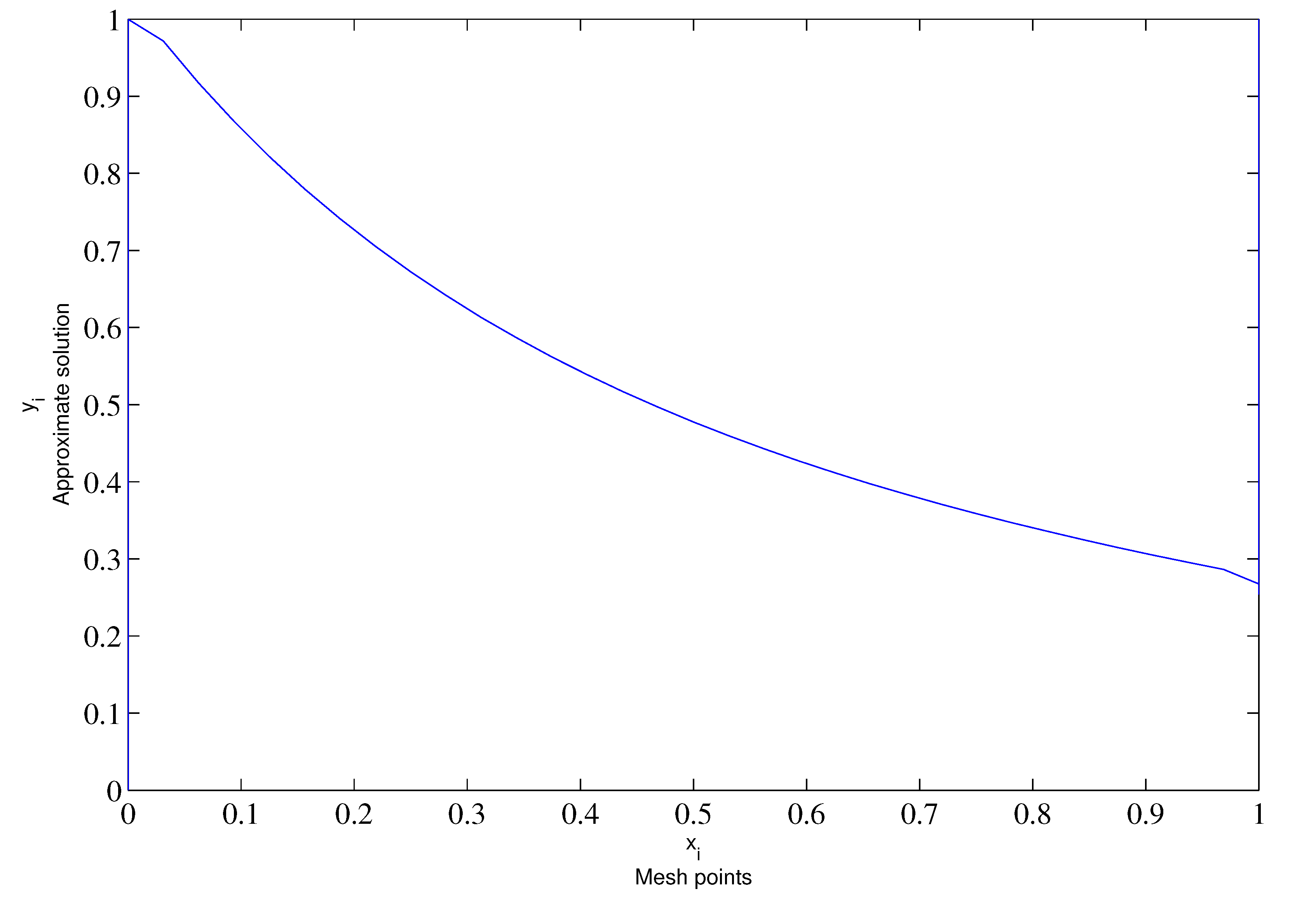
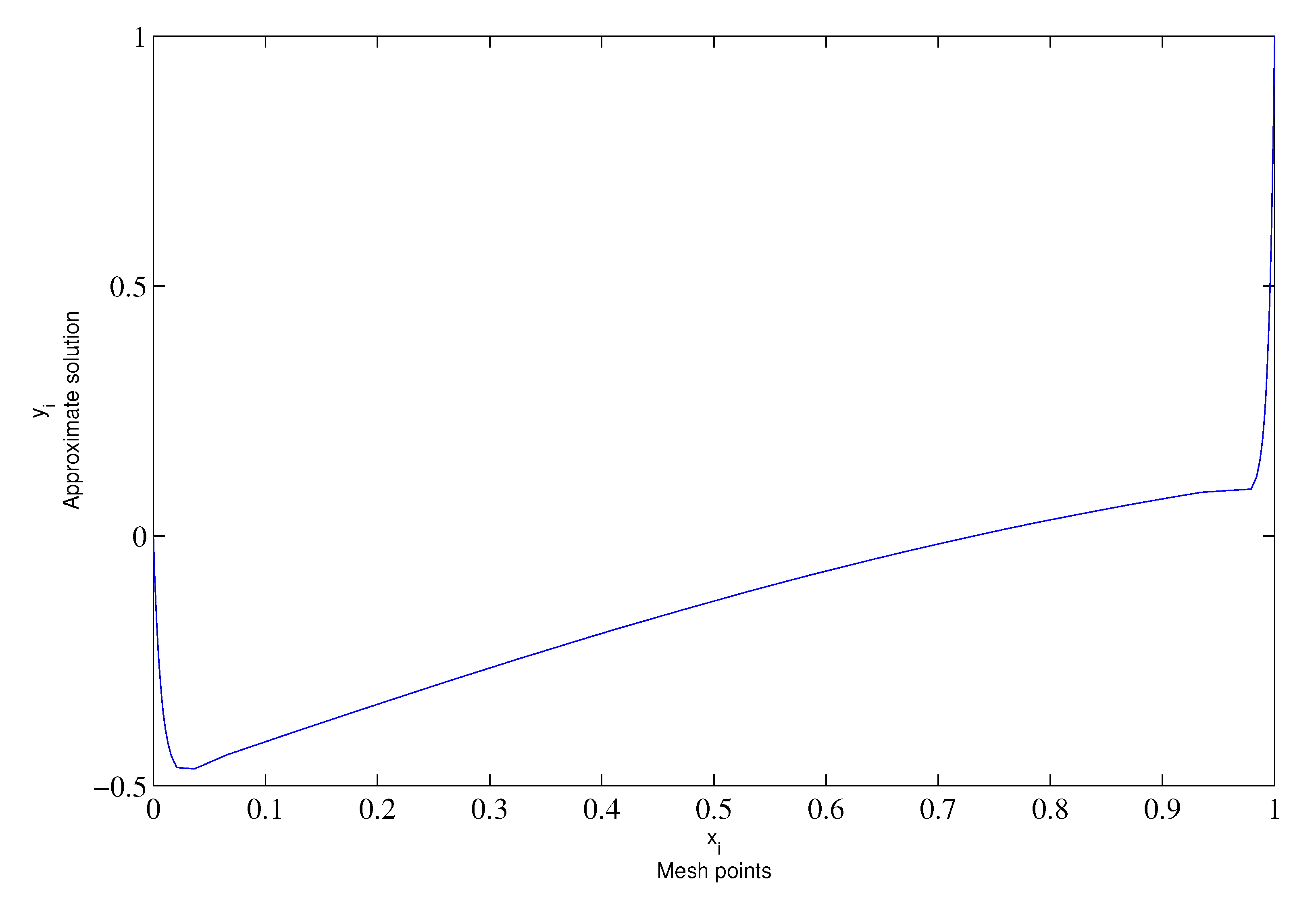
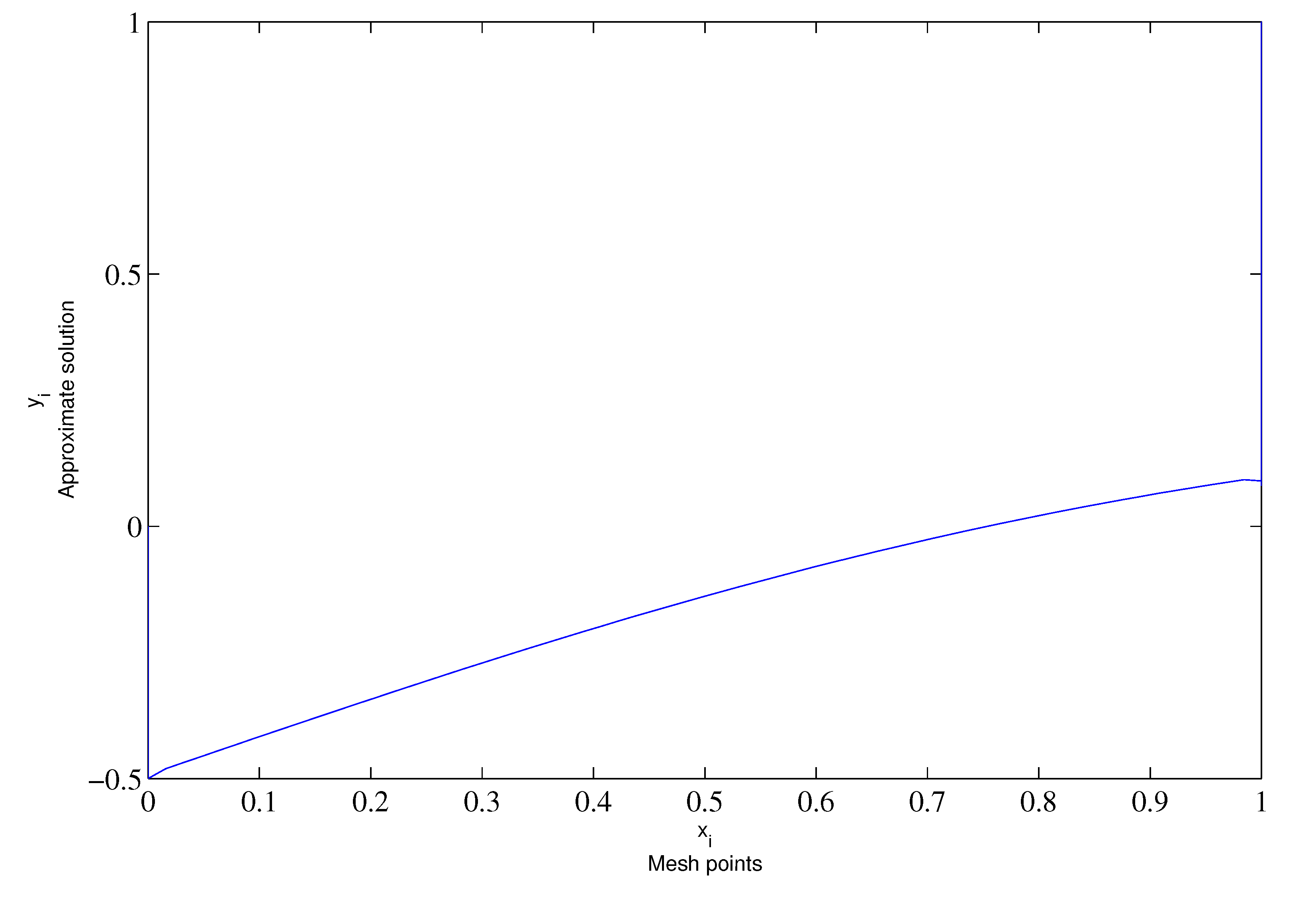
| 1.81764 | |||||
| 2.772958 | |||||
| 1.233841 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cakir, M.; Gunes, B. A Fitted Operator Finite Difference Approximation for Singularly Perturbed Volterra–Fredholm Integro-Differential Equations. Mathematics 2022, 10, 3560. https://doi.org/10.3390/math10193560
Cakir M, Gunes B. A Fitted Operator Finite Difference Approximation for Singularly Perturbed Volterra–Fredholm Integro-Differential Equations. Mathematics. 2022; 10(19):3560. https://doi.org/10.3390/math10193560
Chicago/Turabian StyleCakir, Musa, and Baransel Gunes. 2022. "A Fitted Operator Finite Difference Approximation for Singularly Perturbed Volterra–Fredholm Integro-Differential Equations" Mathematics 10, no. 19: 3560. https://doi.org/10.3390/math10193560
APA StyleCakir, M., & Gunes, B. (2022). A Fitted Operator Finite Difference Approximation for Singularly Perturbed Volterra–Fredholm Integro-Differential Equations. Mathematics, 10(19), 3560. https://doi.org/10.3390/math10193560






