Abstract
Freeway networks, despite being built to handle the transportation needs of large traffic volumes, have suffered in recent years from an increase in demand that is rarely resolvable through infrastructure improvements. Therefore, the implementation of particular control methods constitutes, in many instances, the only viable solution for enhancing the performance of freeway traffic systems. The topic is fraught with ambiguity, and there is no tool for understanding the entire system mathematically; hence, a fuzzy suggested algorithm seems not just appropriate but essential. In this study, a fuzzy cognitive map-based model and a fuzzy rule-based system are proposed as tools to analyze freeway traffic data with the objective of traffic flow modeling at a macroscopic level in order to address congestion-related issues as the primary goal of the traffic control strategies. In addition to presenting a framework of fuzzy system-based controllers in freeway traffic, the results of this study demonstrated that a fuzzy inference system and fuzzy cognitive maps are capable of congestion level prediction, traffic flow simulation, and scenario analysis, thereby enhancing the performance of the traffic control strategies involving the implementation of ramp management policies, controlling vehicle movement within the freeway by mainstream control, and routing control.
Keywords:
fuzzy system; inference system; fuzzy cognitive map; congestion prediction; control strategy; freeway networks MSC:
03B52
1. Introduction
Over the course of the last few decades, there has been a steady increase in the amount of vehicular traffic, which has led to a number of adverse consequences for both society and the environment [1]. As a direct result of the ramifications of these factors, there has been an increased requirement for the development of surveillance and control strategies for freeway traffic networks [2]. These networks, despite being constructed to fulfill the mobility requirements of heavy traffic flows, have been negatively affected in recent years by the rising demand, which is rarely solvable through the implementation of appropriate infrastructure improvements [3]. As a consequence, the implementation of particular traffic management measures constitutes, in many scenarios, the only feasible solution to the problem of how to enhance the operation of freeway vehicular networks, largely linked to physical and economic constraints [4,5].
Taking all of this into account, the continued development of planning and management tools for traffic systems is of the utmost importance, since it is the only method to enhance the effectiveness of the existing freeway network without making significant improvements to the underlying infrastructure [6]. As a result of a significant component of the freeway network being incapable of meeting the present mobility needs, which is having an effect on drivers in the form of increased congestion, exacerbated air pollution, and diminishing safety, many studies have been carried out in order to develop the methodologies of planning and control for freeway traffic networks. Former scholars were primarily focused on finding ways to alleviate congestion-associated problems, but the present global frameworks for eco-innovation in transportation systems need the implementation of far improved strategies [7]. Because of this, common methods to control traffic need to be rethought in order to provide a more justifiable perspective. This is necessary because, once this is done, control purposes will include not only the optimum utilization of freeway network capacity but also the minimization of emission, fuel consumption, and accidents [6].
In addition, the complexity of the traffic control problem derives from the natural dynamic character, nonlinearity, and volatility of the traffic network system. Generally, when the demand flow surpasses the capacity of a particular segment of freeway, congestion occurs. It is commonly accepted that such a complex problem cannot be described precisely using a mathematical method, such as statistical regression, which is incapable of addressing the complexities of freeway traffic dynamics and the interconnections among components. Moreover, engaged variables are primarily associated with uncertain features since they are directly influenced by human behavior and decisions; hence, these variables and the amount of uncertainty in their quantities must be accounted for within the framework of the system’s computation [8]. This is mostly related to the problem’s extreme complexity and the vast number of characteristics that can influence the control actions. For this reason, various distinct strategies have been employed lately, ranging among the following: using macroscopic traffic simulation and variable speed limit control to manage traffic flow in the main stream of the freeway by a generic fuzzy system-based approach [9,10], back propagation neural network and single neuron-based freeway traffic density control [11,12,13,14], including even certain combinations of fuzzy neural network control methods [15]. Although substantial progress has been made in this area of research with regard to congestion-related unique challenges, these techniques still require specialized knowledge to extract parameters with causal relationships and rules, as well as a vast amount of training data.
Accordingly, as a continuation of the research presented at the IPMU 2022 conference [16], this work is extended to a novel framework in which the flow of traffic at a macroscopic scale is measured to approximate computation of freeway traffic data. This computation is performed by using a combination method of Fuzzy Cognitive Maps (FCM) to simulate traffic flow and various scenarios analysis (e.g., lane-drop scenario) as well as the Fuzzy Inference System (FIS) to address congestion-related issues as the core of the traffic control improvement strategy. This study aims to contribute to the establishment of a responsive traffic control and management system in addition to offering a generic framework for fuzzy system-based controllers in freeway traffic. Modeling and processing imprecise traffic data at the macroscopic level and minimizing the negative economic, social, and environmental effects of congestion in freeway networks are the primary contributions of the suggested system. MATLAB Fuzzy Logic Toolbox R2022a and the FCMpy library [17] simulate and validate the resulting FIS and FCM models, respectively.
This study is presented in five sections. The second section discusses traffic control methods. In Section 3, following presenting the case study, a FIS developed for congestion scale calculation and an FCM designed for flow computation are presented. In Section 4, the products of both fuzzy system-based methodologies are examined, and finally in Section 5, possible future directions are stated.
2. Traffic Control Strategies
Effective mobility involves a wide range of challenges, including environmental conservation and social and economic development. Since freeways are still the main popular way to move people and goods, they are essential to the expansion of the economy and the maintenance of social harmony. In response, various methods for efficient traffic control in freeway systems have been developed. A common and accepted choice is road-based traffic control. It is accomplished by macrolevel controls on traffic flow, through which the use of a number of regulating mechanisms (Figure 1) can be used to manage the flow of traffic. These mechanisms include ramp management, i.e., ramp metering in conjunction with traffic lights at onramps; mainstream control, e.g., variable speed limits, keep-lane directives, lane control, and congestion warnings; and route guiding, i.e., typically specific signs are posted at crossroads [18].
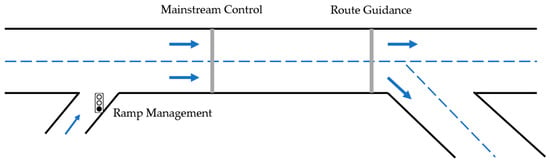
Figure 1.
Main traffic control strategies.
In light of the complexity of the problem, scholars have been looking at transportation-related challenges for a number of years [19]. In response to these challenges, the traditional freeway traffic control systems’ primary focus has shifted to the reduction of traffic congestion as its primary goal. As was mentioned, with the dramatic expansion of goods transportation in bulk as well as passengers, mobility systems have facilitated the growth of society and the economy. Meanwhile, this expansion caused congestion to rise, through which the quality of the current mobility service has declined. Such a phenomenon can take many different forms, from just creating bottlenecks and lengthening travel times to seriously degrading the system and halting vehicle traffic. Furthermore, as demonstrated by the experiments carried out in [20], frequent exposure to congestion raises user irritability since users perceive the extra time needed to get to their destination as wasted time that may be spent on other activities. Finding the right traffic control measures is one way to hasten the process of mitigating congestion and creating a functional mobility system [21]. An effective modeling strategy for defining traffic flow behaviors must be created in order to establish these control measures. In order to mathematically reflect the dynamic behavior of real-world traffic systems, traffic flow models are adopted. Traffic flow models are being used to determine planning actions, analyze the impact of infrastructure upgrades or alterations to existing freeway configurations, and build, visualize, and assess certain operational procedures in addition to evaluating and predicting the system. A wide range of traffic flow models with various qualities and functionality have been constructed, starting with work by [22] in the 1950s. Traffic models have been categorized using a range of methodologies [23]. According to their degree of attributes, macroscopic, microscopic, and mesoscopic models are the most prominent standardized approaches for traffic flow modeling. The key categorization characteristics for these approaches are depicted in Figure 2.
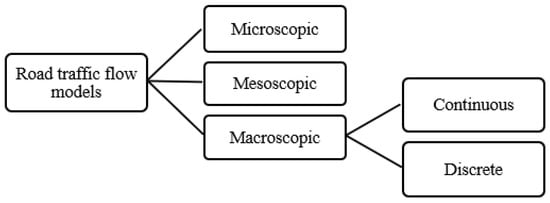
Figure 2.
Modeling freeway traffic approaches [6].
The macroscopic approach is the most prevalent and established level of traffic regulation. The continuous or discrete nature of the characteristics expressing time and space is used to effectively categorize macroscopic forms. Given their low processing complexity and adaptability for real-time control systems in extended networks, macroscopic discrete approaches are the preferred method for freeway traffic control. In this work, the method concentrates on discrete macroscopic properties to compute hourly vehicle dynamic patterns. Additionally, discrete parameters are employed rather than continuous values (temporally and spatially), in which freeways are represented as a set of sections with fixed lengths and time is equally divided into separate spans, accordingly [24]. As a result, modeling these features mainly depends on conventional mathematical approaches, which are frequently unable to capture the complexity of road traffic patterns and complicated relationships between pertinent components. Furthermore, due to the constant vibrant responses of drivers imposing these components, they are strongly influenced by ambiguous and uncertain attributes. Accordingly, conventional mathematical approaches are unable to model all features of the components and their varied degrees of vagueness within the system. Therefore, fuzzy system-based techniques are not just sufficient but also essential to be taken into account in the associated way of reasoning.
3. Fuzzy System-Based Controllers in Transportation
As an integral aspect of computational intelligence, fuzzy systems approximate exact computation through the application of methodologies and procedures that mimic human observation, reasoning, and decision-making. Fuzzy systems provide the framework for integrating objective and subjective variables to optimally process quantitative and linguistic information. These methods have found widespread application in transportation engineering. Speed advisory boards in [25] utilize data from measurements and the insight of experts to set speed limits on freeways. Further studies discuss existing and upcoming challenges in traffic network control and management by assessing some popular computational intelligence models and evaluating their implementation for traffic signal control [26]. An optimized monetary system for seaport services is presented in [27] using a fuzzy system-based approach. To make lane-changing operations in construction zones more realistic, researchers in [28] created a fuzzy system-based framework that takes drivers’ characteristics into consideration and imitates them.
While fuzzy systems approaches have been utilized for a number of traffic-related issues, their potential for controlling traffic to maximize efficiency on highway networks has been underestimated. Effective mobility, on the other hand, is a relatively new topic of study that is receiving a growing degree of interest from the scientific community of traffic control specialists. Next, a Fuzzy Inference System (FIS) and a Fuzzy Cognitive Map (FCM), both of which were conceptualized and built in [29,30], are used in combination (see Figure 3) for traffic control with the goal of enhancing mobility in large-scale freeway networks. With the suggested fuzzy system-based controllers, a general framework for supervised vehicular traffic is provided in Figure 3. As the application of the proposed framework, vehicle level data can be clustered and computed by FIS in linguistic terms to predict the Level of Congestion (LOC) as the output variable of the system, and then the level of intervention based on the LOC may be assigned. Subsequently, an assumption that can be made here is that fuzzy rule-based inference and FCM may be considered to manage local (e.g., ramp metering, main stream control) and global (coordinated ramp control, route guidance) control actions, respectively.
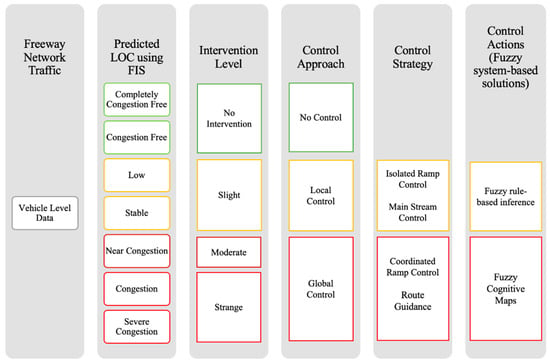
Figure 3.
A framework of fuzzy system-based controllers in freeway traffic.
3.1. The Case Study
The suggested FIS and FCM models were created using datasets from Hungarian motorway networks, whose users experience diverse and complex congestion behaviors; primarily as a result of two main sources: Hungary’s prominent position in the transit system and the 25 percent growth in the number of certified automobiles between 2010 and 2018 [31,32]. These problems produce intricate behavior in the flow of traffic on the roads, involving variations in both spatial and temporal scales. The E-toll system is the source of the used data in this study, which consists of freeway segment tollway data with the following variables: the highway’s name, the segment’s name (identifier), the number of e-tolls collected in each segment (links) and its length as well as the number of lanes. These linkages are comprised of a total of 2446 unique segments, wherein each measured between 100 and 18,000 m in length. In building the FIS algorithm and clustering ranges for input and output parameters, the full dataset and freeway segments are assessed. However, in order to maintain the efficacy and reliability of the constructed FCM, 58 segments were selected to represent the whole set of highway segments between Budapest and the Austrian border.
Most traffic models on roads attempt to paint a comprehensive picture of how traffic variables change across time and space, and this recognition of the importance of geographic context for the dataset under study is reflected in the models’ construction. Therefore, as a great advantage, the location-specific patterns of road traffic can be reflected in this dataset as well. Figure 4 depicts an example of a link between three different segments labeled A, B, and C. Since the presented dataset is a time series, it can be used to foretell how traffic would behave on downstream road segments given the current conditions in the upstream ones.
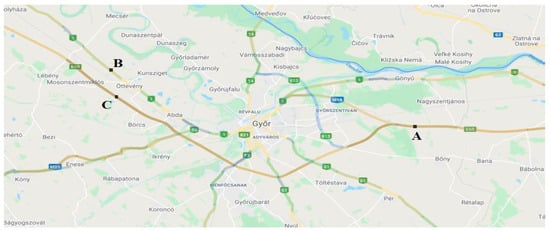
Figure 4.
An illustration of segment linkages between A as upstream segment and B, C as downstream segments.
Figure 5 shows the causal linkages and correlations between the segments on a logarithmic scale, where the overall performance of road traffic may be observed over time, indicating how flow in an upstream segment may influence traffic flow in a downstream one. The computed correlation of road traffic flow between segments exposes that A and B correlate (0.03), A and C correlate (0.90), and B and C correlate (0.10). Various inferences and correlation analysis may be done using these values to determine the behavior patterns and intensity of freeway traffic flow.
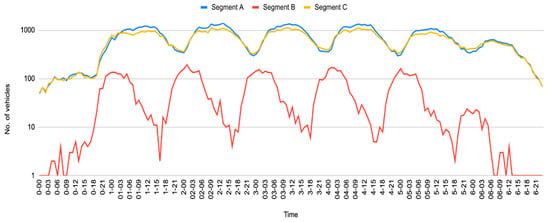
Figure 5.
A logarithmic scale view of the traffic’s causal connections on the subsequent segments.
3.2. The Fuzzy Inference System
The original fuzzy set theory [33] developed by Zadeh has been utilized to handle a variety of industrial and scientific issues in numerous technology and science fields. The qualities of fuzzy sets and the possibility of their expression in linguistic terms give a computational approach for characterizing and addressing problems involving imprecision and ambiguity. This study accordingly offers a fuzzy inference approach to identify traffic congestion founded on the Mamdani method [34] deployed in MATLAB’s Fuzzy Logic Toolbox R2022a. The created model is focused on evaluating and predicting the degree of highway network congestion. In Figure 6, the configuration of the model fuzzy inference system in MATLAB with relevant variables is depicted.
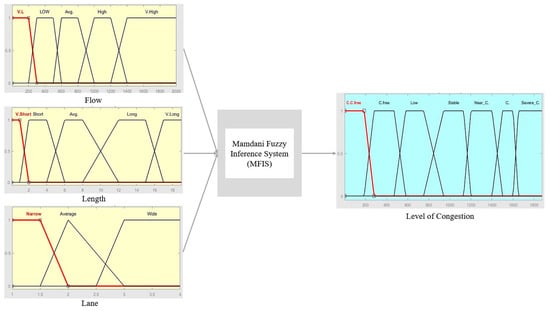
Figure 6.
Detailed illustration of the presented FIS.
The first phase in creating a fuzzy inference system is determining the attributes that will be used to determine the input and output values of the system. The system uses the length of the segment, number of lanes, and flow as input elements to compute the level of congestion as the system’s output. The projected Mamdani fuzzy inference technique is broken down into four main stages of development:
- Identifying the acceptable numerical interval for involved linguistic parameters (Table 1 and Table 2). The input parameters are as follows:
 Table 1. Input variables clustering ranges.
Table 1. Input variables clustering ranges. Table 2. Output variable clustering ranges.
Table 2. Output variable clustering ranges.- Flow, rate expressed in terms of vehicles per minute,where q is the quantity of vehicles on average (n) passing a certain point in time (T).
- Length of each segment of freeway in kilometers.
- Lane, the number of lanes of the given segment.
- 2.
- Given that they capture and express the characteristics of the fuzzy set employed in the case study, triangular and trapezoidal membership functions are utilized to assess how directly the input and output parameters match. Equations (2) and (3) explain triangular and trapezoidal membership functions, respectively:
- 3.
- Input–output links are constrained by if-then fuzzy rules. A total of 75 rules were implemented, mainly founded on the percentile distribution of the data, and expert evaluation. These rules were applied via the MATLAB Fuzzy Rule Editor in order to create the inference and nonlinear surface model.
- 4.
- Centroid of Area (COA) was utilized as the defuzzification operator to determine the corresponding action (i.e., in this study congestion level) to be conducted. The following denotes COA:where z is the fuzzy system output and aggregated output membership function is given as .
3.3. The Fuzzy Cognitive Map
As an extension of conventional cognitive maps [35], Kosko [36] introduced the concept of the Fuzzy Cognitive Map (FCM) to solve restrictions related to the binary structure of the initial cognitive map model. FCM merges the idea of cognitive maps and the concept of fuzzy sets, first proposed by Zadeh [33], with the added concept of signed fuzzy impacts to construct a unique type of artificial neural network or fuzzy bipolar graph. These characteristics help to create fuzzy nodes (components or concepts) that utilize the non-binary features of the modeled system’s components and gradual intensifications of their causal linkages. Figure 7 depicts a schematic illustration of a simple FCM; using weighted arcs, interconnections and connections among nodes are modeled.
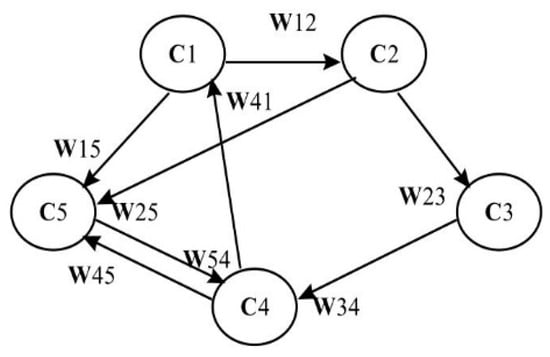
Figure 7.
A fundamental illustration of FCM [25].
In the development of an FCM-based road traffic flow model, determining activation values for nodes (segments) related to weight assignments is crucial. An inference rule developed from Equations (5) and (6) is used by the presented model to assign activation values. The suggested integration thus emphasizes two crucial aspects: nodes can both reflect their past values (i.e., previous traffic density in the given node or segment) and activation values may be derived utilizing the values of the connected nodes and their associated causal weights at each time step. Involved methods and the proposed inference rule are as follows:
- Calculating the density of segment i in link m at different time frames [37]:
- Calculating the value of concept Ci at time t, wherein the value of Ci may represent the calculated density in the given segment [38]:
- Calculating the value of concept Ci at time t, wherein the value of Ci may represent the calculated density in the given segment [30]:
Consequently, every freeway segment is signified by a node, the value of which is taken as the density of segment of link and the weighted arcs are set to a constant parameter based on variables as a rough estimate of the capacity; where signifies the lengths of the segments of link m, and signifies the quantity of the available lanes in link m. Accordingly, these parameters are used to set up the nodes and weights. Then, the system has the right to interact; following every iteration, new values are made and put into the new state vector. This approach will be continued until the simulation exhibits a stabilized state at a specified numerical boundary and reaches equilibrium (see further details in [30]).
4. Results and Discussion
FIS and FCM are designed in relation to traffic control approaches, i.e., mainstream control, ramp management, and route guiding, in freeway networks based on a macro-level data analysis. In this part, the features of each fuzzy system-based technique are examined in greater detail.
4.1. FIS in Congestion Level Prediction
Mainstream control is utilized to regulate the flow of vehicles driving on the main lanes, typically by delivering appropriate signals to drivers via variable message signs (VMS) or other means such as traffic lights. On a macroscopic scale, these management procedures aim to standardize traffic conditions, avoid the recurrence of congestion, and limit the chance of vehicle collisions. A further objective is to address the appearance of one-time congestion issues by increasing system reliability in low-capacity conditions. [39]. The projected FIS attempts to enhance freeway mobility and safety by providing or mandating suitable speed restrictions displayed via VMSs. As explained in the third section, using three forms of available data, the level of congestion for every segment is calculated, including the number of vehicles in a given timestep, the length and the lane of each segment. These inputs provide approximations of the segment’s rough capacity to fulfill newly created demand that may cause an alteration in the Level of Congestion (LOC).
Figure 8 shows how operative the proposed FIS might be in generalizing complex nonlinear connections between congestion levels and the involved features of the traffic; in which the interdependence of the input variables and LOC can be demonstrated using a fuzzy control surface in a graphical insight view. It indicates that a correlation exists between LOC and the input parameters. When the length is between 4 and 6 km and the number of lanes is 2 or 3, the LOC undergoes the greatest change (Figure 8A). Whenever the length variable is between 1 and 6 km, each segment with a rising flow rate of more than 200 vehicles experiences an intense reaction (approximately a 50 percent increase) in the LOC (Figure 8B). Increasing or reducing the number of lanes has the greatest impact on the LOC. Segments with 3 or 4 lanes will not experience severe congestion; however, an increase of 200 vehicles per hour in segments with fewer than two lanes can increase the LOC by more than 50 percent (Figure 8C).

Figure 8.
Rule surface of LOC for length and lane (A), and length and flow (B), and flow and lane (C).
When input data are inserted into the designed FIS, congestion severity can be predicted. If real-time input parameter properties are entered as shown in Figure 9, as an example of the proposed model application: The LOC would be anticipated as 243, which is classified based on the assigned membership function, for the level of congestion-free, given the flow rate of 239, two-lane segment, and its length of 9.5 km.
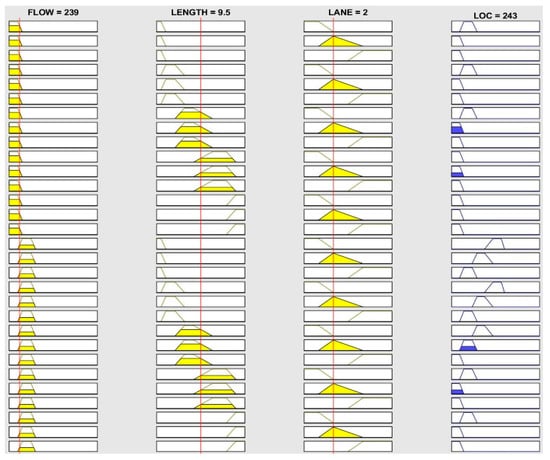
Figure 9.
An example of the assigned fuzzy rules in the lookup diagram.
Measuring congestion is essential for optimizing traffic management and control. The creation of an effective transportation system is largely determined by the current road mobility patterns. Therefore, the method applied to evaluate the severity of congestion ought to be sufficiently realistic to enable decision-makers to take the needed steps to alleviate congestion and to rapidly construct an effective transportation system. Consequently, transportation engineers have recognized the exact features that are normally prescribed in a congestion degree [40,41]. An effective evaluation of congestion should primarily include the following: non-technical companies should be capable of easily comprehending and evaluating the results of the analysis; it should provide a consistent range of possible values; be relevant to all road types; and be capable of predictive and statistical analysis. In addition to these traits, in contrast to conventional approaches to traffic detection, the presented approach has an intelligent discipline recognized as approximate reasoning [8,42] that sacrifices exact traffic-connected qualities (e.g., geometric features such as junctions, bifurcations, offramps, and onramps) that may be selected in both microscopic and mesoscopic types of traffic modeling in order to achieve substantially lower computational contributions and time.
4.2. FCM in Traffic Flow Simulation
A range of interdependent and connected components describe the complex road traffic flow rules. Thus, FCM is provided as a computational intelligence method of resolving the imprecision and volatility within highway networks. From the perspective of macroscopic modeling, these uncertainties are mostly associated with road traffic flow, density, and estimated capacity-related variables that might increase the likelihood of a breakdown and change the condition of traffic from free flow to congested flow [24]. In the projected FCM, segments of each link (freeway) are allocated as nodes (concepts), whose values are determined by their computed densities. Figure 10 shows a geographical description of the selected freeways.
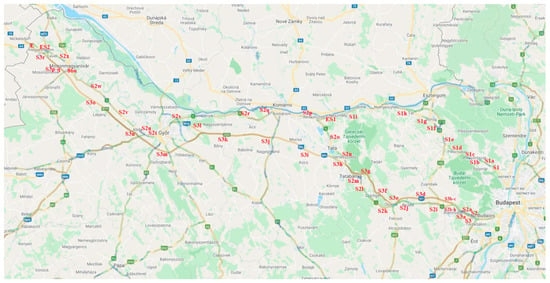
Figure 10.
Geographical locations of the selected segments.
Figure 11 illustrates the FCM with initialized weights and notes. FCM commences performance analysis of the process. In each iteration of the FCM, the state of notes is determined using Equation (7). Higher activation values in the nodes (segments) are reflected by larger nodes in the simulated FCM; these larger nodes signify higher density and display activation values with a stronger influence on the network. Three alternate highways between Budapest and the Austrian border are depicted by S1, S2, and S3 and their 58 segments as nodes in the network. S1 contains nine nodes that end at node ES1 and merges with one of the S2 nodes; S3, as the preferred route, also interacts closely with the nodes in S2, which both end at node E as the last Hungarian segment before entering Austrian territory.
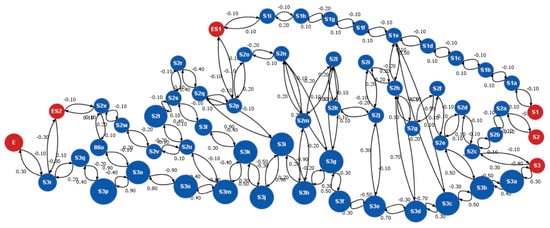
Figure 11.
FCM illustration of the causal relationships among selected freeway segments in Figure 10.
Table 3 and its corresponding Figure 12 depict the FCM traffic flow simulation of the initial states, in which the road segments are denoted by nodes, e.g., S3a, S3b, …, and the computed values show the segments’ density to illustrate how changes in inconstant attributes (e.g., a variation in the flow rate or a change in the quantity of lanes) alter system behavior. This model provides diverse solutions for implementing the most commonly used traffic control strategies, such as ramp management and route guidance. Consequently, as one of the most frequent causes of severe LOC, i.e., based on Figure 8C, a lane-drop scenario is simulated in a two-lane segment (S3h). Though a lane was dropped, the density reduced slightly, which clearly indicates that the remaining lane’s traffic density increased significantly and reached severe LOC. Compared to their initial states, the density values of connected segments vary, i.e., S3g and S3i can be observed in Table 4 and its corresponding Figure 13, in which the density of S3i falls by 11%, and thereafter there is a minor decline in S3j, though in the upstream nodes, S3g and S3f rise by 16% and 8%, respectively.

Table 3.
Initial simulation result of the traffic flow density in the chosen network, adapted from [16].
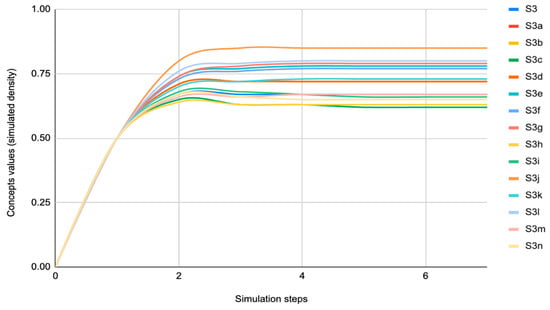
Figure 12.
Corresponding graph of Table 3.

Table 4.
Traffic flow density in one lane reduction scenario, adapted from [16].
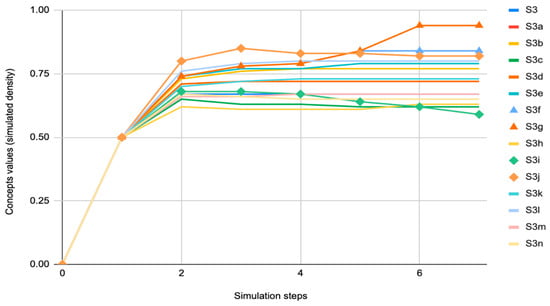
Figure 13.
Corresponding graph of Table 4.
Simulations confirmed the FCM’s viability as a computational intelligence tool, not only at the macroscopic modeling level to examine the overall behavior of road traffic flow, but also in terms of studying and tracking relevant changes inside freeway networks. These features provide useful information and can contribute to positive outcomes connected to traffic control techniques, namely, the prediction and monitoring of the road traffic flow state in complex networks for lowering traffic emissions and enhancing road safety; for planning reasons, such as evaluating the impact of new road projects or comparing the effects of alternative development scenarios; anticipating the impact of changes in road capacity, e.g., in repairing needs; recognizing dynamic congestion patterns and error-prone places in order to optimize ramp management and route guidance for eco-routing [43].
Furthermore, modern approaches, despite their distinct characteristics, are able to operate online based on real-time qualities originating from the road network, as opposed to the primitive traffic control with fixed plans generated from past data. These traffic control approaches, such as mainstream control, ramp management, and route guiding, can be fed by the analysis and forecasts made possible by the given FIS and FCM. Additionally, in classifying traffic controllers, local approaches are founded on localized data produced by sensors situated near the actuators, whereas in the global control approach, the gathered segment data are not regarded individually, but rather as an input to evaluate the state of the whole freeway network [20]. Consequently, in the presented framework (see Figure 3), FIS might be offered as a local traffic controller that can be used for mainstream control methods, and FCM can be provided as a global traffic controller that can evaluate the system dynamics supporting ramp metering and route guidance.
5. Conclusions and Future Direction
The explosive growth of road traffic flow modeling needs a particular focus on assessing the capabilities of various computational intelligence approaches in this domain. Consequently, this study presented FIS and FCM as two computational intelligence approaches for assessing freeway traffic data pertaining to traffic flow modeling at the macroscopic level for resolving congestion-related concerns at the heart of mobility effectiveness improvement strategies. Due to the world’s growing population, there is no surety that congestion can be eradicated entirely. However, these approaches are offered to ease congestion to a fair extent.
This study develops innovative solutions of FIS and FCM in the analysis of complex freeway networks, with a focus on critical vehicular traffic congestion control strategies, such as ramp management, mainstream control, and route guidance, with the primary objective of enhancing freeway safety and reducing emissions. In addition, mobility effectiveness can be enhanced by employing these techniques as the primary reason for designing and managing transportation networks. According to the complexity of the problem, it is probable that the FIS and FCM models cannot capture all of the contributions of a macroscopic traffic flow control technique; hence, the generated results may differ from the actual condition of freeway traffic. Yet, any estimating method will inevitably include a trade-off between model performance and operating time; therefore, methods based on fuzzy systems offer substantial advantages for traffic control techniques from this standpoint. Moreover, the dataset for this study does not include all segments that have the ability to impact road traffic behavior, but only those that are part of the e-toll network. Notably, by including new mapping and data, the precision of the representation of freeway networks can be greatly increased, resulting in more accurate but also more complex FCM models with finer simulation outcomes. The next step in this area of investigation should focus on developing a real-time route guidance generation method by combining FCM with other algorithms like Dijkstra and Q-learning to confront the stochastic nature of the traffic conditions and all involved segments in the freeway networks, with a special emphasis on bottleneck locations.
Author Contributions
Methodology, Writing—review & editing, M.A. and M.F.H.; Project administration, L.T.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Hungarian Office for Research Innovation and Development (NKFIH), grant number K-124055.
Acknowledgments
The authors gratefully acknowledge Gergely Mikulai and the Hungarian national toll payment services for their work on providing the original dataset.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, K.; Batterman, S. Air pollution and health risks due to vehicle traffic. Sci. Total Environ. 2013, 450, 307–316. [Google Scholar] [CrossRef] [PubMed]
- Ramazani, A.; Vahdat-Nejad, H. A new context-aware approach to traffic congestion estimation. In Proceedings of the 2014 4th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 29–30 October 2014; pp. 504–508. [Google Scholar]
- Cambridge Systematics. Traffic Congestion and Reliability: Trends and Advanced Strategies for Congestion Mitigation; Cambridge Systematics Inc.: Cambridge, MA, USA, 2005. [Google Scholar]
- Faris, H.; Yazid, S. Development of Communication Technology on VANET with a Combination of Ad-hoc, Cellular and GPS Signals as a Solution Traffic Problems. In Proceedings of the 2019 7th International Conference on Information and Communication Technology (ICoICT), Kuala Lumpur, Malaysia, 24–26 July 2019; pp. 1–9. [Google Scholar]
- Ferrara, A.; Sacone, S.; Siri, S. Freeway Traffic Modelling and Control; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Pasquale, C.; Sacone, S.; Siri, S.; Ferrara, A. Traffic control for freeway networks with sustainability-related objectives: Review and future challenges. Annu. Rev. Control 2019, 48, 312–324. [Google Scholar] [CrossRef]
- Mavi, R.K.; Fathi, A.; Saen, R.F.; Mavi, N.K. Eco-innovation in transportation industry: A double frontier common weights analysis with ideal point method for Malmquist productivity index. Resour. Conserv. Recycl. 2019, 147, 39–48. [Google Scholar] [CrossRef]
- Amini, M.; Hatwagner, M.F.; Mikulai, G.C.; Koczy, L.T. A vehicular traffic congestion predictor system using Mamdani fuzzy inference. Syst. Theor. Control Comput. J. 2021, 1, 49–57. [Google Scholar] [CrossRef]
- Yu, X.; Xu, W.; Alam, F.; Potgieter, J.; Fang, C. Genetic fuzzy logic approach to local ramp metering control using microscopic traffic simulation. In Proceedings of the 2012 19th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Auckland, New Zealand, 28–30 November 2012; pp. 290–297. [Google Scholar]
- Ghods, A.; Kian, A.; Tabibi, M. Adaptive freeway ramp metering and variable speed limit control: A genetic-fuzzy approach. IEEE Intell. Transp. Syst. Mag. 2009, 1, 27–36. [Google Scholar] [CrossRef]
- Liang, X.; Fan, Y. Freeway ramp pid controller regulated by bp neural network. In Proceedings of the 2009 Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 713–717. [Google Scholar]
- Liang, X.; Li, J.; Luo, N. Single neuron-based freeway traffic density control via ramp metering. In Proceedings of the 2010 2nd International Conference on Information Engineering and Computer Science (ICIECS), Wuhan, China, 25–26 December 2010; pp. 1–4. [Google Scholar]
- Li, J.; Liang, X. Freeway ramp control based on single neuron. In Proceedings of the 2009 IEEE International Conference on Intelligent Computing and Intelligent Systems (ICIS), Shanghai, China, 19–23 July; Volume 2, pp. 122–125.
- Qi, C.; Hou, Z.; Li, X. Freeway feedback ramp metering based on neuron adaptive control algorithm. In Proceedings of the 2008 International Conference on Intelligent Computation Technology and Automation (ICICTA), Changsha, China, 20–22 October 2008; Volume 1, pp. 349–353. [Google Scholar]
- Feng, C.; Yuanhua, J.; Jian, L.; Huixin, Y.; Zhonghai, N. Design of fuzzy neural network control method for ramp metering. In Proceedings of the 2011 Third International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Shanghai, China, 6–7 January 2011; Volume 1, pp. 966–969. [Google Scholar]
- Amini, M.; Hatwagner, M.F.; Koczy, L.T. Fuzzy System-Based Solutions for Traffic Control in Freeway Networks Toward Sustainable Improvement. In Information Processing and Management of Uncertainty in Knowledge-Based Systems; IPMU 2022. Communications in Computer and Information Science; Springer: Cham, Switzerland, 2022; Volume 1602. [Google Scholar] [CrossRef]
- Mkhitaryan, S.; Giabbanelli, P.J.; Wozniak, M.K.; Napoles, G.; de Vries, N.K.; Crutzen, R. FCMpy: A Python Module for Constructing and Analyzing Fuzzy Cognitive Maps. arXiv 2021, arXiv:2111.12749. [Google Scholar] [CrossRef]
- Siri, S.; Pasquale, C.; Sacone, S.; Ferrara, A. Freeway traffic control: A survey. Automatica 2021, 130, 109655. [Google Scholar] [CrossRef]
- Castillo, H.; Pitfield, D.E. ELASTIC-A methodological framework for identifying and selecting sustainable transport indicators. Transp. Res. Part D 2010, 15, 179–188. [Google Scholar] [CrossRef]
- Lajunen, T.; Parker, D.; Summala, H. Does traffic congestion increase driver aggression? Transp. Res. Part F 1999, 2, 225–236. [Google Scholar] [CrossRef]
- Ferrara, A.; Sacone, S.; Siri, S. An overview of traffic control schemes for freeway systems. Free. Traffic Model. Control. 2018, 193–234. [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, G.B. On kinematic waves II: A theory of traffic flow on long crowded roads. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1955, 229, 317–345. [Google Scholar]
- Hoogendoorn, S.P.; Bovy PH, L. State-of-the-art of vehicular traffic flow modelling. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2001, 215, 283–303. [Google Scholar] [CrossRef]
- Ferrara, A.; Sacone, S.; Siri, S. First-Order Macroscopic Traffic Models. In Freeway Traffic Modelling and Control; Advances in Industrial Control Series; Springer: Cham, Switzerland, 2018; Volume 3, pp. 47–84. [Google Scholar]
- Ngo, C.Y.; Victor, O.K.L. Freeway traffic control using fuzzy logic controllers. Inform. Sci. 1994, 1, 59–76. [Google Scholar] [CrossRef]
- Zhao, D.; Dai, Y.; Zhang, Z. Computational intelligence in urban traffic signal control: A survey. IEEE Trans. Syst. Man Cybern. 2012, 42, 485–494. [Google Scholar] [CrossRef]
- John, A.; Yang, Z.; Riahi, R. Application of a collaborative modeling and strategic fuzzy decision support system for selecting appropriate resilience strategies for seaport operations. J. Traff. Transp. Eng. Engl. Ed. 2014, 1, 159–179. [Google Scholar]
- Li, Q.; Qiao, F.; Yu, L. Socio-demographic impacts on lane-changing response time and distance in work zone with drivers’ smart advisory system. J. Traff. Transp. Eng. Engl. Ed. 2015, 2, 313–326. [Google Scholar] [CrossRef]
- Amini, M.; Hatwagner, M.F.; Mikulai, G.C.; Koczy, L.T. An intelligent traffic congestion detection approach based on fuzzy inference system. In Proceedings of the 2021 IEEE 15th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 19–21 May 2021; pp. 97–104. [Google Scholar] [CrossRef]
- Amini, M.; Hatwagner, M.F.; Mikulai, G.C.; Koczy, L.T. Developing a macroscopic model based on fuzzy cognitive map for road traffic flow simulation. Infocommun. J. 2021, 13, 14–23. [Google Scholar] [CrossRef]
- László, F.T.; Péter, T. Hungary’s ITS National Report. ITS National Report. 2018. Available online: https://ec.europa.eu/transport/sites/transport/files/2018_hu_its_progress_report_2017.pdf (accessed on 8 October 2022).
- European Commission. EU Transport in Figures—Statistical Pocketbook 2020, Number of Registered Passenger Cars in Hungary from 1990 to 2018; European Commission: Brussels, Belgium, 2020. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man. Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Axelrod, R. Structure of Decision: The Cognitive Maps of Political Elites; Princeton University Press: Princeton, NJ, USA, 1976; Available online: https://www.jstor.org/stable/j.ctt13x0vw3 (accessed on 8 October 2022).
- Kosko, B. Fuzzy cognitive maps. Int. J. Man. Mach. Stud. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Messmer, A.; Papageorgiou, M. METANET: A macroscopic simulation program for motorway networks. Traffic Eng. Control 1990, 31, 466–470. Available online: https://www.researchgate.net/publication/282285780_METANET_a_macroscopic_simulation_program_for_motorway_networks (accessed on 8 October 2022).
- Stylios, C.D.; Groumpos, P.P. Modeling Complex Systems Using Fuzzy Cognitive Maps. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2004, 34, 155–162. [Google Scholar] [CrossRef]
- Iordanidou, G.-R.; Roncoli, C.; Papamichail, I.; Papageorgiou, M. Feedback-based mainstream traffic flow control for multiple bottlenecks on motorways. IEEE Trans. Intell. Transp. Syst. 2015, 16, 610–621. [Google Scholar]
- Afrin, T.; Yodo, N. A survey of road traffic congestion measures towards a sustainable and resilient transportation system. Sustainability 2020, 12, 4660. [Google Scholar] [CrossRef]
- Aftabuzzaman, M. Measuring traffic congestion—A critical review. In Proceedings of the 30th Australasian Transport Research Forum (ATRF), Melbourne, VIC, Australia, 25–27 September 2007. [Google Scholar]
- Turner, S.M.; Lomax, T.J.; Levinson, H.S. Measuring and Estimating Congestion Using Travel Time–Based Procedures. Transp. Res. Rec. 1996, 1564, 11–19. [Google Scholar] [CrossRef]
- Jabbarpour, M.R.; Zarrabi, H.; Khokhar, R.H.; Shamshirband, S.; Choo, K.K.R. Applications of computational intelligence in vehicle traffic congestion problem: A survey. Soft Comput. 2018, 22, 2299–2320. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).