A Novel Formulation of the Fractional Derivative with the Order
Abstract
1. Introduction
2. New Definition of Fractional Derivative
- Using the definition of the new fractional derivative and the properties of the integral, this relationship can be easily proven.
- Using Equation (2) and since ,the following relationship can be obtained:using part integral, the above relationship can be written as follows:
- Using the definition of the new derivative and since , then thus, Equation (11) is true. □
- By definition of new fractional derivative and integral of the exponential function, it is possible to prove the following relationship:
- Relationship No. 2 can easily be proven using the new derivative definition and the integral of the sine function:
- Similarly, relationship No. 3 can be proved. □
- From Equations (2) and (20), we obtain:by using the integral by part of the last relationship becomes as follows:
- Using Equations (2) and (20), we obtain:by the Leibniz integral rule and properties of differential operator the above relationship can be written as follows:□
3. Integral Transforms of the New Derivative
4. Initial Value Problems with New Derivative
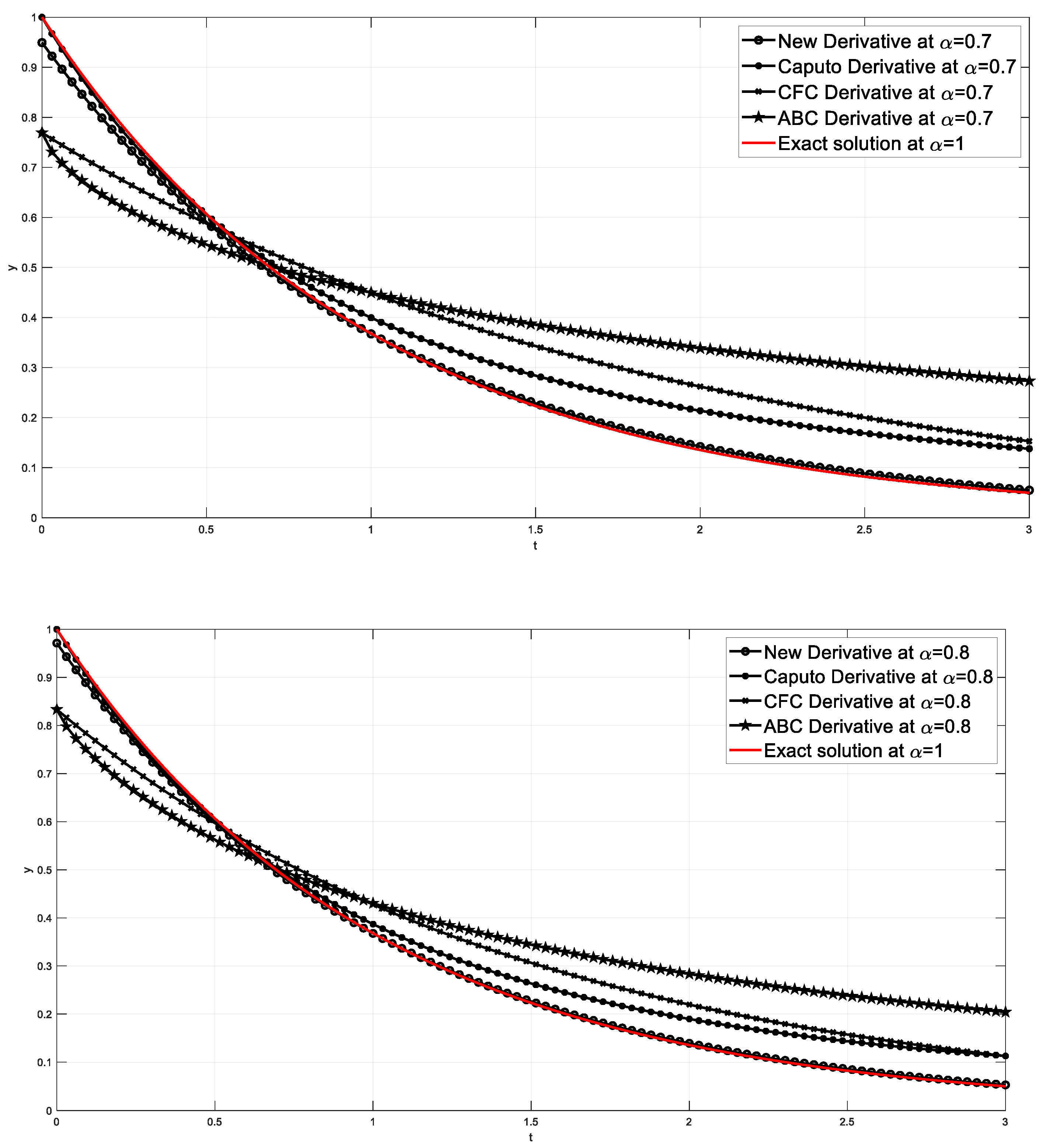
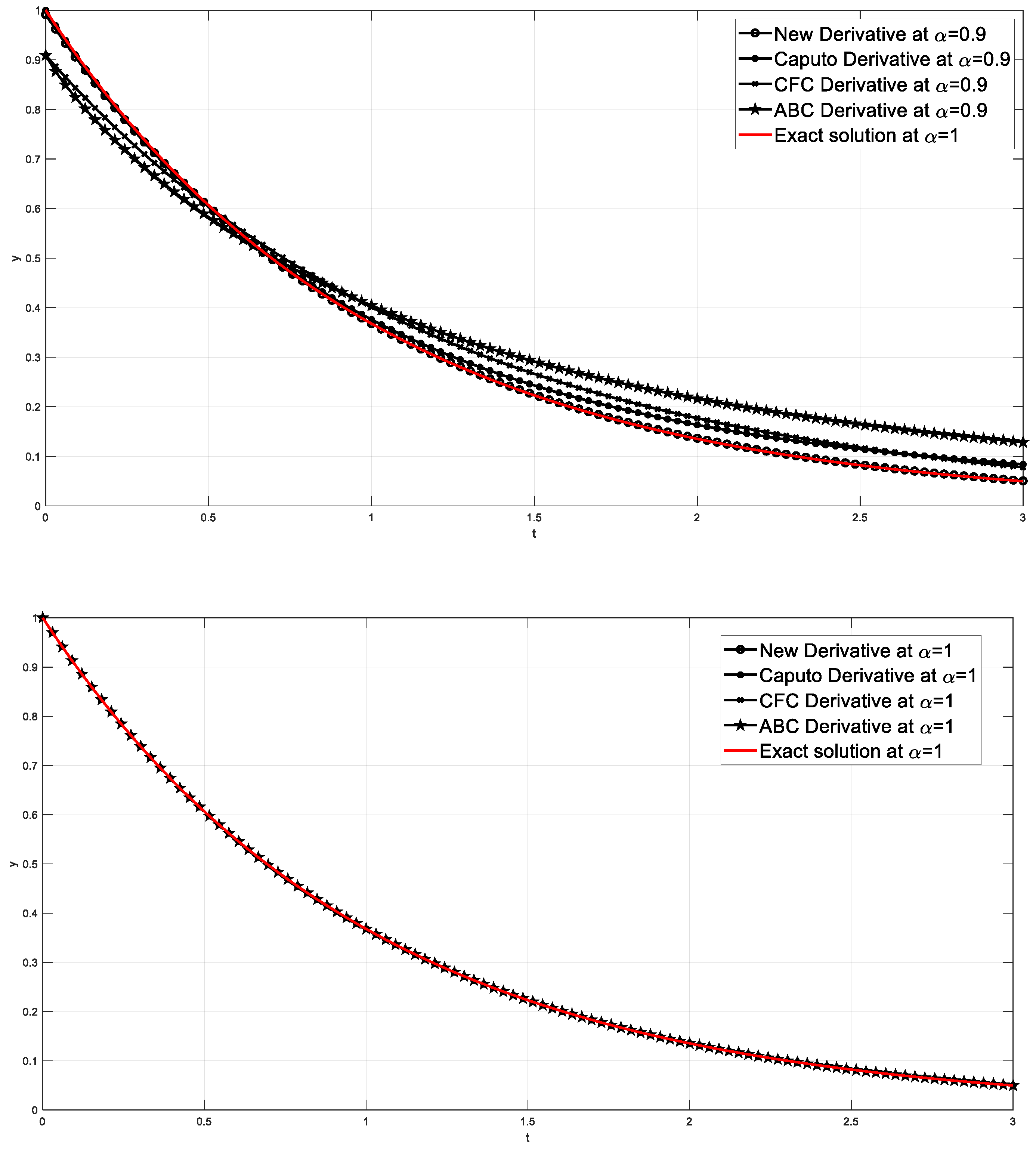
5. Illustrative Examples
| 0.2143 | 0.8016 | 0.8024 | 0.7629 | 0.7367 | 0.8071 | 0.0055 | 0.0047 | 0.0442 | 0.0704 |
| 0.4286 | 0.6482 | 0.6473 | 0.6402 | 0.6165 | 0.6514 | 0.0032 | 0.0041 | 0.0112 | 0.0349 |
| 0.6429 | 0.5241 | 0.5253 | 0.5373 | 0.5226 | 0.5258 | 0.0016 | 0.0005 | 0.0115 | 0.0032 |
| 0.8571 | 0.4238 | 0.4289 | 0.4509 | 0.4469 | 0.4244 | 0.0005 | 0.0046 | 0.0265 | 0.0226 |
| 1.0714 | 0.3427 | 0.3525 | 0.3784 | 0.3851 | 0.3425 | 0.0002 | 0.0100 | 0.0358 | 0.0426 |
| 1.2857 | 0.2771 | 0.2917 | 0.3175 | 0.3339 | 0.2765 | 0.0007 | 0.0152 | 0.0411 | 0.0575 |
| 1.5000 | 0.2241 | 0.2431 | 0.2664 | 0.2913 | 0.2231 | 0.0010 | 0.0200 | 0.0433 | 0.0681 |
| 1.7143 | 0.1812 | 0.2041 | 0.2236 | 0.2554 | 0.1801 | 0.0011 | 0.0240 | 0.0435 | 0.0754 |
| 1.9286 | 0.1465 | 0.1726 | 0.1876 | 0.2252 | 0.1454 | 0.0012 | 0.0273 | 0.0423 | 0.0798 |
| 2.1429 | 0.1185 | 0.1471 | 0.1575 | 0.1994 | 0.1173 | 0.0012 | 0.0298 | 0.0401 | 0.0821 |
| 2.3571 | 0.0958 | 0.1264 | 0.1321 | 0.1775 | 0.0947 | 0.0011 | 0.0317 | 0.0375 | 0.0828 |
| 2.5714 | 0.0775 | 0.1094 | 0.1109 | 0.1586 | 0.0764 | 0.0010 | 0.0330 | 0.0345 | 0.0822 |
| 2.7857 | 0.0626 | 0.0954 | 0.0931 | 0.1424 | 0.0617 | 0.0010 | 0.0338 | 0.0314 | 0.0808 |
| 3.0000 | 0.0507 | 0.0839 | 0.0781 | 0.1284 | 0.0498 | 0.0009 | 0.0341 | 0.0283 | 0.0786 |
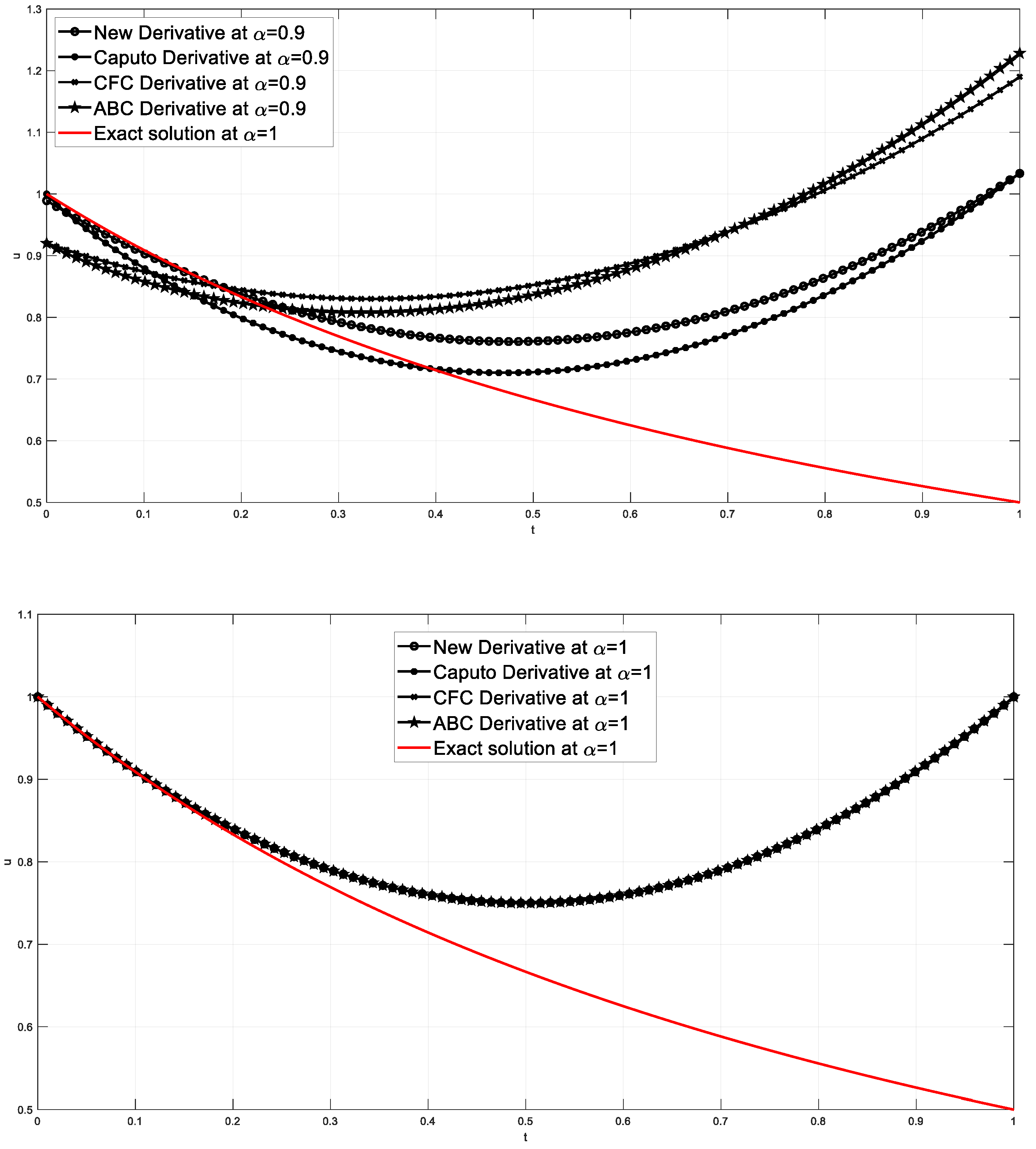
| 0.0714 | 0.0714 | 0.0667 | 0.0667 | 0.0667 | 0.0667 | 0.0667 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.1429 | 0.1429 | 0.1254 | 0.1254 | 0.1254 | 0.1254 | 0.1250 | 0.0004 | 0.0004 | 0.0004 | 0.0004 |
| 0.2143 | 0.2143 | 0.1782 | 0.1782 | 0.1782 | 0.1782 | 0.1765 | 0.0017 | 0.0017 | 0.0017 | 0.0017 |
| 0.2857 | 0.2857 | 0.2274 | 0.2274 | 0.2274 | 0.2274 | 0.2222 | 0.0052 | 0.0052 | 0.0052 | 0.0052 |
| 0.3571 | 0.3571 | 0.2751 | 0.2751 | 0.2751 | 0.2751 | 0.2632 | 0.0120 | 0.0120 | 0.0120 | 0.0120 |
| 0.4286 | 0.4286 | 0.3236 | 0.3236 | 0.3236 | 0.3236 | 0.3000 | 0.0236 | 0.0236 | 0.0236 | 0.0236 |
| 0.5000 | 0.5000 | 0.3750 | 0.3750 | 0.3750 | 0.3750 | 0.3333 | 0.0417 | 0.0417 | 0.0417 | 0.0417 |
| 0.5714 | 0.5714 | 0.4315 | 0.4315 | 0.4315 | 0.4315 | 0.3636 | 0.0679 | 0.0679 | 0.0679 | 0.0679 |
| 0.6429 | 0.6429 | 0.4953 | 0.4953 | 0.4953 | 0.4953 | 0.3913 | 0.1040 | 0.1040 | 0.1040 | 0.1040 |
| 0.7143 | 0.7143 | 0.5685 | 0.5685 | 0.5685 | 0.5685 | 0.4167 | 0.1518 | 0.1518 | 0.1518 | 0.1518 |
| 0.7857 | 0.7857 | 0.6534 | 0.6534 | 0.6534 | 0.6534 | 0.4400 | 0.2134 | 0.2134 | 0.2134 | 0.2134 |
| 0.8571 | 0.8571 | 0.7522 | 0.7522 | 0.7522 | 0.7522 | 0.4615 | 0.2906 | 0.2906 | 0.2906 | 0.2906 |
| 0.9286 | 0.9286 | 0.8670 | 0.8670 | 0.8670 | 0.8670 | 0.4815 | 0.3855 | 0.3855 | 0.3855 | 0.3855 |
| 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.5000 | 0.5000 | 0.5000 | 0.5000 | 0.5000 |
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Das, S. Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1. [Google Scholar]
- Veeresha, P.; Prakasha, D.G.; Baleanu, D. Analysis of fractional Swift Hohenberg equation using a novel computational technique. Math. Methods Appl. Sci. 2019, 43, 1970–1987. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baleanu, D. An efficient technique for fractional coupled system arisen in magnetothermoelasticity with rotation using Mittag–Leffler kernel. J. Comput. Nonlinear Dyn. 2021, 16, 011002. [Google Scholar] [CrossRef]
- Veeresha, P.; Malagi, N.S.; Prakasha, D.G.; Baskonus, H.M. An efficient technique to analyze the fractional model of vector-borne diseases. Phys. Scr. 2022, 97, 054004. [Google Scholar] [CrossRef]
- Sunitha, M.; Gamaoun, F.; Abdulrahman, A.; Malagi, N.S.; Singh, S.; Gowda, R.J. An efficient analytical approach with novel integral transform to study the two-dimensional solute transport problem. Ain Shams Eng. J. 2022, 101878. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Hussein, M.A.; Jassim, H.K. New approximate analytical technique for the solution of two dimensional fractional differential equations. NeuroQuantology 2022, 20, 3690–3705. [Google Scholar]
- Yang, X.-J.; Srivastava, H.; Machado, J.A.T. A new fractional derivative without singular kernel: Application to the modelling of the steady heat flow. Therm. Sci. 2016, 20, 753–756. [Google Scholar] [CrossRef]
- Atangana, A.; Dumitru, B. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Alzaki, L.K.; Jassim, H.K. Time-Fractional Differential Equations with an Approximate Solution. J. Niger. Soc. Phys. Sci. 2022, 4, 818. [Google Scholar] [CrossRef]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Peter, O.J.; Shaikh, A.S.; Ibrahim, M.O.; Nisar, K.S.; Baleanu, D.; Khan, I.; Abioye, A.I. Analysis and dynamics of fractional order mathematical model of COVID-19 in Nigeria using atangana-baleanu operator. Comput. Mater. Contin. 2021, 66, 1823–1848. [Google Scholar] [CrossRef]
- Laskin, N. Fractional schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef]
- Baleanu, D.; Jassim, H.K. Exact Solution of Two-dimensional Fractional Partial Differential Equations. Fractal Fract. 2020, 4, 21. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K.; Baleanu, D.; Chu, Y.-M. On the approximate solutions for a system of coupled Korteweg-de Vries equations with local fractional derivative. Fractals 2021, 29, 1–7. [Google Scholar] [CrossRef]
- Cesarone, F.; Caputo, M.; Cametti, C. Memory formalism in the passive diffusion across a biological membrane. J. Membr. Sci. 2004, 250, 79–84. [Google Scholar] [CrossRef]
- Caputo, M.; Cametti, C. Memory diffusion in two cases of biological interest. J. Theor. Biol. 2008, 254, 697–703. [Google Scholar] [CrossRef]
- Caputo, M. Modeling Social and Economic Cycles. In Alternative Public Economics; Forte, F., Navarra, P., Mudambi, R., Eds.; Elgar: Cheltenham, UK, 2014. [Google Scholar]
- Jumarie, G. New stochastic fractional models of the Malthusian growth, the Poissonian birth process and optimal management of populations. Math. Comput. Model. 2006, 44, 231–254. [Google Scholar] [CrossRef]
- Iaffaldano, G.; Caputo, M.; Martino, S. Experimental and theoretical memory diffusion of water in sand. Hydrol. Earth Syst. Sci. 2006, 10, 93–100. [Google Scholar] [CrossRef]
- El Shaed, M. A Fractional Calculus Model of Semilunar Heart Valve Vibrations. In Proceedings of the ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 2–6 September 2006. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Inc. Publishers: Danbury, CT, USA, 2006. [Google Scholar]
- Bokhari, A. Application of Shehu transform to Atangana-Baleanu derivatives. J. Math. Comput. Sci. 2019, 20, 101–107. [Google Scholar] [CrossRef]
- Patel, T.; Ramakanta, M. Adomian decomposition Sumudu transform method for solving fully nonlinear fractional order power-law fin-type problems. Int. J. Math. Comput. 2015, 27, 7–16. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Jafari, H. A new general integral transform for solving integral equations. J. Adv. Res. 2020, 32, 133–138. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jassim, H.K.; Hussein, M.A.
A Novel Formulation of the Fractional Derivative with the Order
Jassim HK, Hussein MA.
A Novel Formulation of the Fractional Derivative with the Order
Jassim, Hassan Kamil, and Mohammed A. Hussein.
2022. "A Novel Formulation of the Fractional Derivative with the Order
Jassim, H. K., & Hussein, M. A.
(2022). A Novel Formulation of the Fractional Derivative with the Order






